Как искать экстремумы функции: Как найти экстремум (точки минимума и максимума) функции

Точки экстремума функции, необходимые и достаточные условия экстремума

Содержание:

• Необходимое условие экстремума
• Первое достаточное условие экстремума
• Второе достаточное условие экстремума

Определение

Точка $x_{0}$ называется точкой локального максимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности выполняется неравенство: $f(x) \leq f\left(x_{0}\right)$.

Точка $x_{0}$ называется точкой локального минимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности $f(x) \geq f\left(x_{0}\right)$.

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума — локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка $x_{0}$ называется точкой строгого локального максимума

функции $y=f(x)$, если для всех $x$ из окрестности этой точки будет справедливо строгое неравенство $f(x) \lt f\left(x_{0}\right)$. {2}+1}=-1$.

Ответ. $y_{\min }=y(0)=-1$

Остались вопросы?

Здесь вы найдете ответы.

Что подразумевается под понятием «экстремум»?

Экстремум представляет собой значение функции на определенном интервале в момент достижения им минимального или максимального показания. Под понятием «экстремумы» или по-другому минимумы/максимумы подразумевается значение функции (у).

Точка экстремума – что это такое?

Если в определенной точке достигается экстремум или, иными словами, максимальное/минимальное значение функции на заданном интервале, то эта точка носит название точки экстремума. Из этого следует, что при достижении минимума, точка экстремума будет названа точкой минимума, и, наоборот, при достижении максимума эта точка будет называться точкой максимума. В случае, когда указываются точки экстремумов (или минимумов/максимумов) подразумеваются иксы, в которых достигаются минимальные или максимальные значения.

Что имеется в виду под понятием «точка минимума функции»?

Любая точка x₀ будет определена в качестве точки минимума функции y = f(x) при соблюдении условия о том, что имеется такая V, представляющая собой окрестность (x₀ — V; x₀+V) упомянутой ранее точки, из которой для каждого значения x x₀ действительно следующее неравенство:

f(x)>f(x₀).

Как описать точку минимума функции?

Под понятием «минимум функции» имеется в виду та точка на ней, в которой функция имеет значение, являющееся наименьшим среди всех значений, приобретаемых ею в любой из других соседних точек. Другими словами, это означает, что в случае, когда функция, достигнув определенной точки, прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и представляет собой точку ее минимума.

Каким образом можно вычислить значение функции y=x⁴-4x³+6x²-4x, которого она достигает в точке своего минимума?

Для ответа на поставленный вопрос нужно отыскать точку минимума указанной функции, в которой ее значение перестает падать. Это можно сделать следующим образом:

y’ = 4x³ — 12x² + 12x – 4

Предположив, что минимальное значение данной функции равно 0, можно переписать равенство в следующем виде:

4x³ — 12x² + 12x — 4 = 0

Сократим данное уравнение на 4:

x³ — 3x² + 3x — 1 = 0

Получившееся равенство также может быть записано в следующем виде после перемены местами слагаемых:

(x³ — 1) + (-3x² + 3x) = 0

Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:

(x — 1)(x² + x + 1) -3x(x — 1) = 0

Это же уравнение может выглядеть так:

(x -1)(x² + x + 1- 3x) = 0

Произведем сложение слагаемых х и -3х:

(x — 1) (x² -2x + 1) = 0

Теперь для упрощения можно переписать уравнение в таком виде:

(x — 1)(x-1)² = 0

Получившееся равенство:

(x — 1)³ = 0

В этом случае х = 1

-∞ 1 +∞

Знаками «+» и «-» обозначены значения производной.

После проведенных вычислений было установлено, что х = 1, что является точкой минимума функции:

у = 1⁴- 4*1³ + 6*1² — 4*1 = 1 — 4 +6 — 4 = -1

Какие расчеты нужно произвести, для того чтобы вычислить точку максимума для функции y = -x/x²+484?

Точкой максимума называется то значение х, достигнув которого, производная начинает менять свой знак с плюса на минус.

Зная это, можно перейти к поиску точки максимума для функции, указанной в задании.

Для этого нужно начать с поиска производной, используя следующую формулу:

(U/V)’ = (U’V — UV’)/V²

Подставляем приведенные в задании значения и получаем:

y’ = (-(x² + 484) — 2x)/(x² + 484)² = (-x²-484 -2x)/(x² +484)²

Теперь следует приравнять производную к 0 и начать решать получившееся уравнение:

(-x²-484 -2x)/(x² +484)² = 0

Упростим уравнение и получим:

(-x²-484 -2x) = 0

(x² +484)² ≠ 0

-x²-484 -2x = 0

Избавимся от минусов в уравнении:

x² + 2x +484 = 0

D

В результате вычислений стало ясно, что корней нет. Это значит, что невозможно поставить их на числовой прямой, для того чтобы проверить знаки производной по соседству с этими точками. На основании этого можно сделать вывод о том, что указанная в задании функция не имеет точек экстремума.

Что представляет собой точка максимума функции?

Под точкой максимума функции понимается та точка, в которой она достигает значения, являющегося наибольшим среди тех значений, что достигаются ею в соседних точках. Это означает, что в точке, при пересечении которой функция прекращает расти, и наблюдается ее падение, и достигается ее максимум.

Имеется график производной функции. Каким образом можно вычислить точки ее максимума и минимума?

В случае, если имеется график производной функции, и при этом требуется определить ее экстремумы, то необходимо вычислить точки пересечения этого графика производной с осью Ох. По-другому они называются «нулями» производной. В случае, когда, пересекая конкретную точку, график производной восходит из области со знаком «-» в область со знаком «+», и в это время производная меняет свой знак на противоположный, функция также изменяется с убывания на рост. В этом случае данная точка, которая пересекается графиком производной, представляет собой точку минимума. Если же при пересечении графиком производной какой-либо точки он идет из положительной в отрицательную область, а функция из возрастания меняется на убывание, то речь идет о точке ее максимума.

Как можно вычислить экстремумы и точки экстремума функции y=4x⁴+2x²+1?

Для того чтобы найти ответ на поставленный вопрос, сначала нужно приравнять функцию к 0:

у = 0

Это же означает, что:

4X⁴ + 2X² + 1 = 0

Введем обозначения:

Х2 = А, при этом А больше 0.

С учетом введенных обозначений равенство будет иметь следующий вид:

4A² + 2A + 1 = 0

D = 4 — 4 = 0 ; √ D = 0

A = (- 2) : 4 = (- 0,5) (

Очевидно, что корней нет.

Ответ: х = 0, у = 1.

Дана функция y = x² -3x+2. Как можно вычислить экстремум этой функции?

Имеется функция y = x² -3x+2, которую также можно переписать в следующем виде:

у = -0,25+ (x-1,5)²

Отсюда следует, что:

miny = — 0,25 при условии, что х-1,5 = 0

Можно сделать вывод о том, что х = 1,5.

Запишем производную данной функции:

y ‘= (x² -3x+2)’ =2x -3

А затем приравняем ее к 0:

y ‘ = 0, значит:

2x -3 = 0.

Это позволяет сделать вывод о том, что:

x = 3/2.

Получается, что, если x

Если же x >3/2, то производная y’ > 0, и в этом случае функция возрастает.

x =3/2=1,5 – это единственная точка экстремума, которая является точкой минимума.

miny =(1,5)² -3*1,5+2 = -0,25.

Как раскрыть понятие «критическая точка функции»?

Критическая точка функции представляет собой ту точку, при пересечении с которой производная данной функции становится равной 0, либо она вовсе не существует.

Возможно ли привести доказательства того, что функция f(x) =2x — 3/x не может иметь критической точки?

Для начала нужно определить, что под критической точкой функции подразумевается та точка, при пересечении с которой производная приобретает нулевое значение, либо же эта производная просто не существует в этой точке, что означает, что функцию в данной точке невозможно дифференцировать.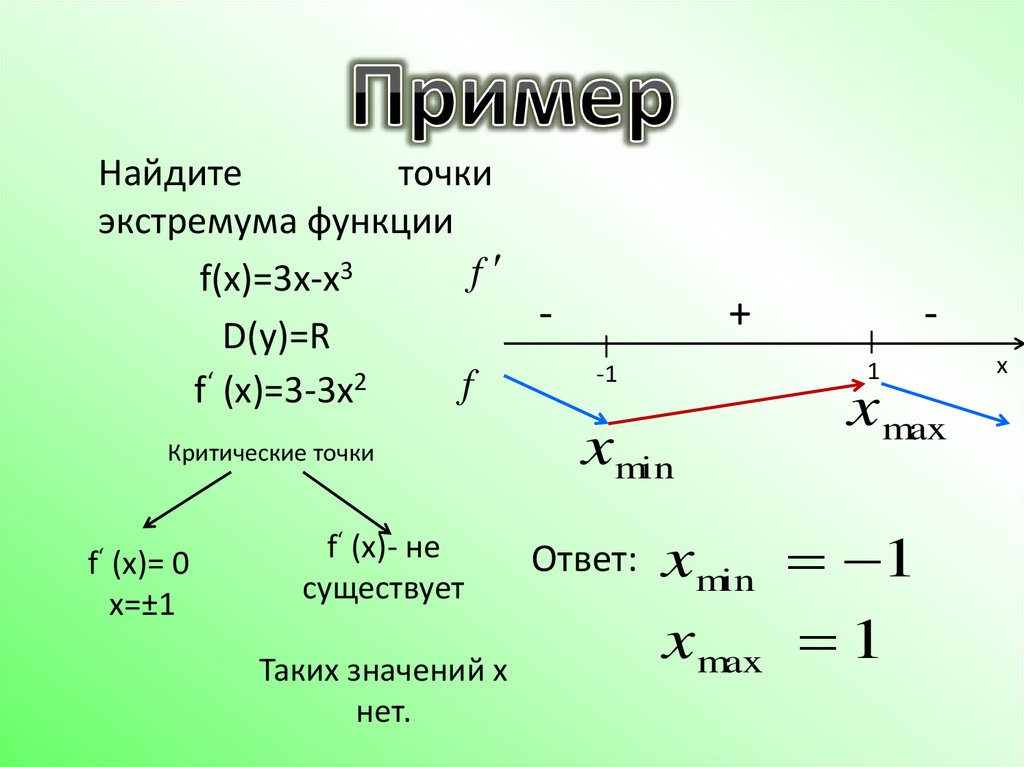

Проверим, применимо ли это утверждение к упомянутой в задании функции:

f ‘(x) =(sin2x — 3x)’ = 2sin2x-3

Приравняем производную функции к 0:

f ‘(x) = 0, это значит, что 2sin2x-3 = 0.

Следовательно:

sin2x= 3 2 не имеет решения

Ответ: заданная функция не имеет критических точек и существует при любых х.

Каким способом можно определить критические точки функции y=|x|/1+x²?

Под критическими точками функции понимаются те точки, в которых ее производная равна 0 или вовсе не существует.

В задании дана функция:

y=|x|/(1+x²)

Предположим, что x

y=-x/(1+x²)

Запишем производную функции и приравняем ее к 0:

y`=(-1-x²+2x²)/(1+x²)²=(x²-1)/(1+x²)²=(x-1)(x+1)/(1+x²)²=0

х = 1 не соответствует условию, значит х = -1.

Теперь предположим, что x≥0.

Снова записываем производную имеющейся функции и приравниваем ее к 0:

y`=(1+x²-2x²)/(1+x²)²=(1-x²)/(1+x²)²=(1-x)(x+1)/(1+x²)²=0

х = — 1 не отвечает условию, значит х = 1.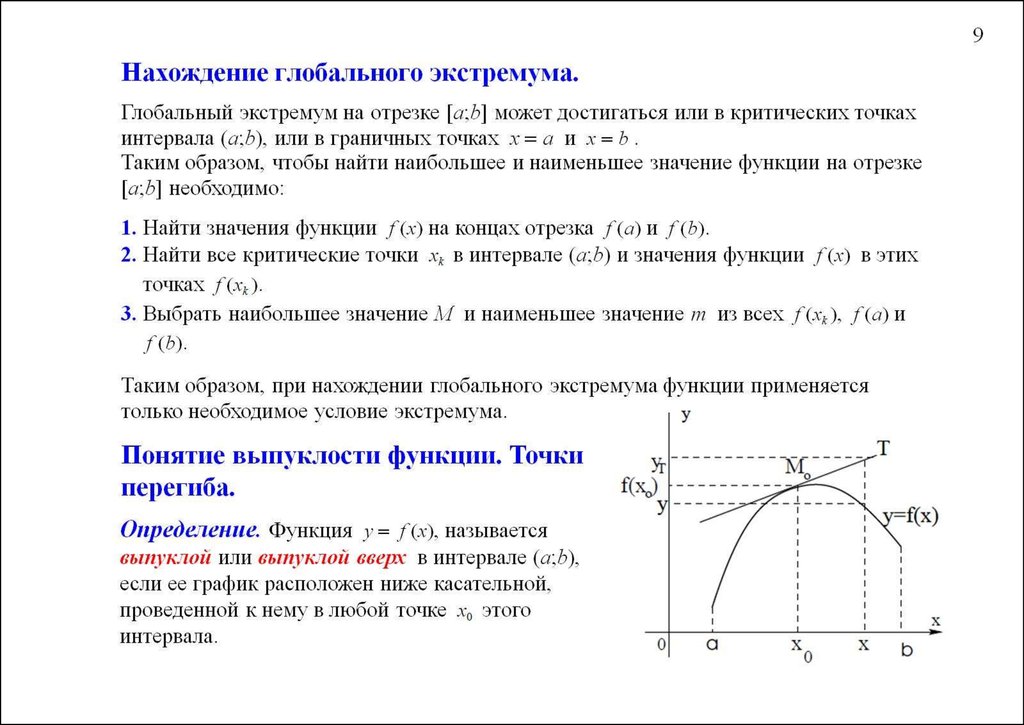

Ответ: х = 1, х = -1.

Читать дальше: наибольшее и наименьшее значение функции.

Экстремумы функции онлайн

С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.

• Решение онлайн
• Видеоинструкция
• Оформление Word
• Также решают

Найти наибольшее и наименьшее значение функции

y =

на отрезке [;]

Включать теорию

Правила ввода функций:

Вместе с этим калькулятором также используют следующие:
Асимптоты функции

Уравнение касательной к графику функции

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление пределов

Необходимое условие экстремума функции одной переменной

Уравнение f’₀(x^*) = 0 — это необходимое условие экстремума функции одной переменной, т. е. в точке x^* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x^с, в которых функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x^* выполняется условие:

f’₀(x^*) = 0
f»₀(x^*) > 0

то точка x^* является точкой локального (глобального) минимума функции.

Если в точке x^* выполняется условие:

f’₀(x^*) = 0
f»₀(x^*) < 0

то точка x^* — локальный (глобальный) максимум.

Пример №1. Найти наибольшее и наименьшее значения функции: на отрезке [1; 3].
Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)=⁵/₂, f(3)=3 ⁸/₈₁
Ответ: f_min=⁵/₂ при x=2; f_max=9 при x=1

Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).
Решение.
Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±^π/₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x=^π/₃+2πk, k∈Z – точки минимума функции; , значит x=-^π/₃+2πk, k∈Z – точки максимума функции.

Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x²

Наибольший объем цилиндра

Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.
Решение:

Объем цилиндра равен: V = πr²H
где H = 2h,
Подставим эти значения в целевую функцию.

V → max
Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса Производная онлайн и приравняем ее к нулю.
dV/dh = 2πR² — 6πh²
dV/dh = 0
2πR² — 6πh² = 0 или R² = 3h²
Откуда


При высоте и радиусе основания размеры цилиндра будут наибольшими.

Исчисление I. Нахождение абсолютных экстремумов

Онлайн-заметки Пола
Главная / Исчисление I / Применение производных / Нахождение абсолютных экстремумов

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4.4. Нахождение абсолютных экстремумов

Пришло время рассмотреть наше первое крупное применение производных в этой главе. Учитывая непрерывную функцию \(f\left( x \right)\), на интервале \(\left[ {a,b} \right]\) мы хотим определить абсолютные экстремумы функции. Для этого нам понадобятся многие из идей, которые мы рассмотрели в предыдущем разделе.

Во-первых, поскольку у нас есть замкнутый интервал (, т.е. и интервал, включающий конечные точки), и мы предполагаем, что функция непрерывна, теорема об экстремальном значении говорит нам, что мы действительно можем это сделать. Это, конечно, хорошо. Мы не хотим пытаться найти то, чего может и не быть.

Далее, в предыдущем разделе мы видели, что абсолютные экстремумы могут возникать в конечных точках или в относительных экстремумах. Кроме того, из предыдущего раздела мы знаем, что список критических точек также является списком всех возможных относительных экстремумов. Таким образом, конечные точки вместе со списком всех критических точек фактически будут списком всех возможных абсолютных экстремумов.

Теперь нам просто нужно вспомнить, что абсолютные экстремумы — это не что иное, как наибольшее и наименьшее значения, которые может принимать функция, поэтому все, что нам действительно нужно сделать, это получить список возможных абсолютных экстремумов, подставить эти точки в нашу функцию и затем определите наибольшее и наименьшее значения.

Вот процедура нахождения абсолютных экстремумов.

Нахождение абсолютных экстремумов \(f\left( x \right)\) на \(\left[ {a,b} \right]\)

0. Проверка непрерывности функции на интервале \(\left [ {яркий]\).
1. Найдите все критические точки \(f\left( x \right)\), которые находятся в интервале \(\left[ {a,b} \right]\). Это имеет смысл, если подумать. Поскольку нас интересует только то, что функция делает в этом интервале, нас не интересуют критические точки, выходящие за пределы интервала.
2. Оцените функцию в критических точках, найденных на шаге 1, и в конечных точках.
3. Определите абсолютные экстремумы.

В этой процедуре нет ничего особенного. Мы назвали первый шаг в процессе шагом 0, главным образом потому, что все функции, которые мы собираемся здесь рассмотреть, будут непрерывными, но с этим нужно быть осторожным. Этот процесс будет работать только в том случае, если у нас есть функция, непрерывная на заданном интервале. Наиболее трудоемким этапом этого процесса является второй этап (шаг 1), на котором мы находим критические точки. Также важно отметить, что все, что нам нужно, это критические точки, находящиеся в интервале. 2} + 6t — 12 = 6\left( {t + 2} \right)\left( {t — 1} \right)\]

Похоже, у нас будет две критические точки, \(t = — 2\) и \(t = 1\). Обратите внимание, что на самом деле нам нужно нечто большее, чем просто критические точки. Нам нужны только критические точки функции, лежащие в рассматриваемом интервале. Оба они попадают в интервал, поэтому мы будем использовать их оба. Это может показаться глупым упоминать сейчас, но об этом часто забывают, обычно когда это становится важным, и поэтому мы будем упоминать об этом при каждой возможности, чтобы убедиться, что об этом не забыли.

Теперь мы оцениваем функцию в критических точках и конечных точках интервала.

\[\begin{align*}g\left( { — 2} \right) & = 24\hspace{1.0in} & g\left( 1 \right) & = — 3\\ g\left( { — 4 } \right) &= — 28\hspace{1.0in} & g\left( 2 \right) & = 8\end{align*}\]

Абсолютные экстремумы — это наибольшая и наименьшая функция, которые когда-либо будут, и эти четыре точки представляют единственные места в интервале, где могут возникать абсолютные экстремумы. Итак, из этого списка мы видим, что абсолютный максимум \(g\left( t \right)\) равен 24, и он приходится на \(t = — 2\) (критическая точка) и абсолютный минимум \( g\left( t \right)\) равно -28, что происходит в \(t = — 4\) (конечная точка). 92} — 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ {0,2} \right]\]

Показать решение

Обратите внимание, что эта проблема практически идентична первой. Разница лишь в интервале, на котором мы работаем. Однако это небольшое изменение полностью изменит наш ответ. С этим изменением мы исключили оба ответа из первого примера.

Первый шаг — снова найти критические точки. Из первого примера мы знаем, что это \(t = — 2\) и \(t = 1\).. Здесь важно напомнить, что нам нужны только критические точки, которые действительно попадают в рассматриваемый интервал. Это означает, что нам нужно только \(t = 1\), так как \(t = — 2\) выходит за пределы интервала.

Теперь оцените функцию в одной критической точке интервала и в двух конечных точках.

\[g\left( 1 \right) = — 3\hspace{0.5in}g\left( 0 \right) = 4\hspace{0.5in}g\left( 2 \right) = 8\]

Из этого списка значений мы видим, что абсолютный максимум равен 8 и произойдет при \(t = 2\), а абсолютный минимум равен -3, что произойдет при \(t = 1\).

Как мы видели в этом примере, простое изменение интервала может полностью изменить ответ. Это также показало нам, что нам нужно быть осторожными, чтобы исключить критические точки, которые не находятся в интервале. Если бы мы забыли об этом и включили \(t = — 2\), мы бы получили неправильный абсолютный максимум!

Это еще одна большая ошибка, которую ученики допускают в этих задачах. Слишком часто они забывают исключить критические точки, которые не входят в интервал. Если ваш инструктор похож на меня, это будет означать, что вы получите неправильный ответ. Несложно убедиться, что критическая точка вне интервала больше или меньше любой из точек в интервале.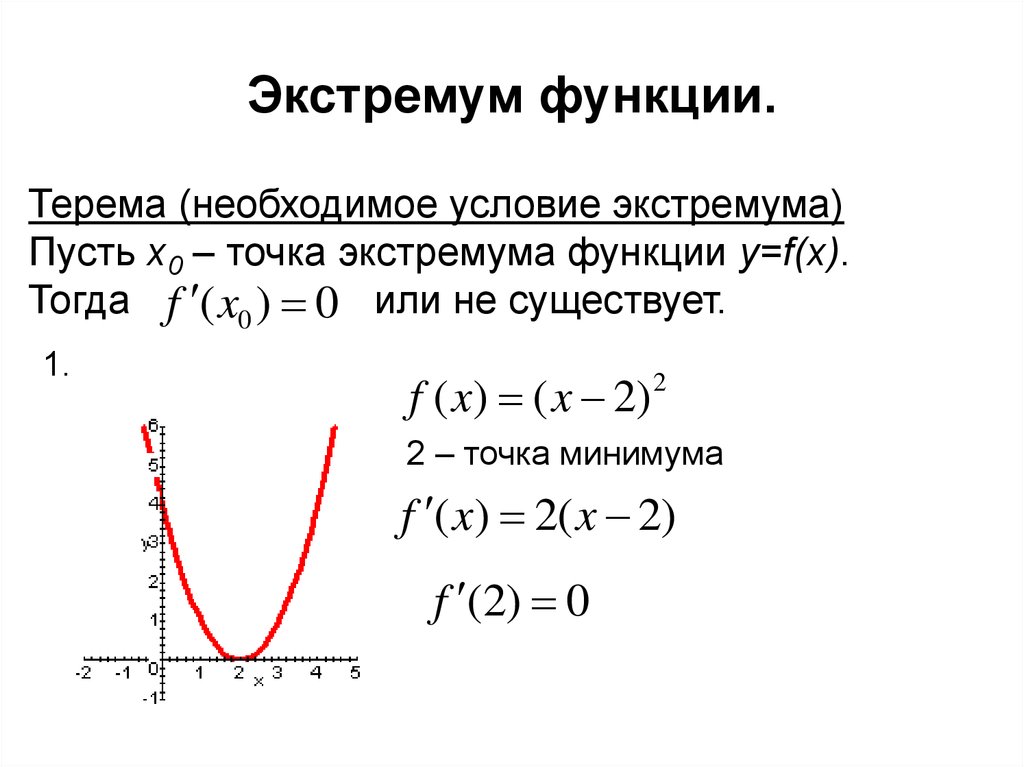

Пример 3 Предположим, что популяция (в тысячах) определенного вида насекомых через \(t\) месяцев определяется следующей формулой. \[P\left( t \right) = 3\,t + \sin \left( {4t} \right) + 100\]

Определить минимальную и максимальную популяцию за первые 4 месяца.

Показать решение

Вопрос, который мы действительно задаем, состоит в том, чтобы найти абсолютные экстремумы \(P\left( t \right)\) на интервале \(\left[ {0,4} \right]\). Поскольку эта функция непрерывна везде, мы знаем, что можем это сделать.

Начнем с производной.

\[P’\влево( t \вправо) = 3 + 4\cos \влево({4t} \вправо)\]

Нам нужны критические точки функции. Производная существует везде, поэтому критических точек от нее нет. Итак, все, что нам нужно сделать, это определить, где производная равна нулю.

\[\begin{align*}3 + 4\cos \left( {4t} \right) & = 0\\ \cos \left( {4t} \right) & = — \frac{3}{4}\ конец {выравнивание *} \]

Решения для этого,

\[\begin{массив}{*{20}{c}}{4t = 2,4189+ 2\pi n,\,\,\,\,n = 0, \pm 1, \pm 2, \ldots }\\{4t = 3,8643 + 2\pi n,\,\,\,\,n = 0, \pm 1, \pm 2, \ldots }\end{array}\hspace{0,25in} \Rightarrow \hspace{0,25in}\begin{array}{*{20}{c}}{t = 0,6047 + \displaystyle \frac{{\pi n}}{2},\,\,\,\,n = 0, \pm 1, \pm 2, \ldots}\\{t = 0,9661 + \displaystyle \ frac{{\pi n}}{2},\,\,\,\,n = 0, \pm 1, \pm 2, \ldots}\end{массив}\]

Итак, это все критические точки. Нам нужно определить те, которые попадают в интервал \(\left[ {0,4} \right]\). Нам нечего делать, кроме как подставлять некоторые \(n\) в формулы, пока мы не получим их все.

\(n = 0\) :

\[t = 0,6047\hspace{1,0 дюйма} t = 0,9661\]

Нам понадобятся обе эти критические точки.

\(n = 1\)

\[t = 0,6047 + \ frac {\ pi} {2} = 2,1755 \ hspace {1,0 дюйм} t = 0,9661 + \ frac {\ pi} {2} = 2,5369 \]

Нам это понадобится.

\(n = 2\)

\[t = 0,6047 + \pi = 3,7463\hspace{1,0 дюйма} t = 0,9661 + \пи = 4,1077\]

В данном случае нам нужен только первый, так как второй находится вне интервала.

В интервале есть пять критических точек. Они есть,

\[0,6047,\,\,\,0,9661,\,\,\,2,1755,\,\,\,2,5369,\,\,\,3,7463\]

Наконец, чтобы определить абсолютный минимум и максимум населения, нам нужно только подставить эти значения в функцию, а также две конечные точки. Вот оценки функций.

\[\begin{align*}P\left( 0 \right) & = 100. 0\hspace{1.0in} & P\left( 4 \right) & = 111.7121\\ P\left( {0,6047} \right) & = 102,4756\hspace{1,0in} & P\left( {0,9661} \right) & = 102,2368\\ P\left( {2,1755} \right) & = 107,1880\hspace{1.0in} & P\left( {2,5369} \right) & = 106,9492\\ P\влево({3,7463}\вправо) & = 111,9004 & & \end{выравнивание*}\]

Из этих оценок видно, что минимальная численность населения составляет 100 000 (помните, что \(P\) выражается в тысячах…), что происходит при \(t = 0\), а максимальная численность населения составляет 111 900, что происходит при \(t = 3,7463). \).

Убедитесь, что вы можете правильно решать триггерные уравнения. Если бы мы забыли \(2\pi n\), мы бы пропустили три последние критические точки в интервале и, следовательно, получили бы неправильный ответ, поскольку максимальная популяция была в последней критической точке. 92}}}{8}}}\]

Определить минимальную и максимальную сумму денег на счете в течение первых 10 лет его открытия.

Показать решение

Здесь мы действительно запрашиваем абсолютные экстремумы \(A\left( t \right)\) на интервале \(\left[ {0,10} \right]\). Как и в предыдущих примерах, эта функция везде непрерывна, и мы знаем, что это можно сделать.

Сначала нам понадобится производная, чтобы мы могли найти критические точки. 92} = 4\hspace{0,5 дюйма} \Стрелка вправо \hspace{0,25 дюйма}\,\,\,\,t = \pm 2\]

У нас есть две критические точки, однако только \(t = 2\) на самом деле находится в интервале, поэтому мы будем использовать только эту критическую точку.

Теперь оценим функцию в единственной критической точке и в конечных точках интервала. Вот эти оценки функций.

\[A\влево( 0 \вправо) = 2000\hspace{0,5 дюйма}A\влево( 2 \вправо) = 1990,66\hspace{0,5 дюйма}A\влево({10}\вправо) = 1999,94\]

Таким образом, максимальная сумма на счете будет равна 2000 долларов США, что произойдет в \(t = 0\), а минимальная сумма на счете будет равна 199,66 долларов США, что произойдет на отметке 2 года.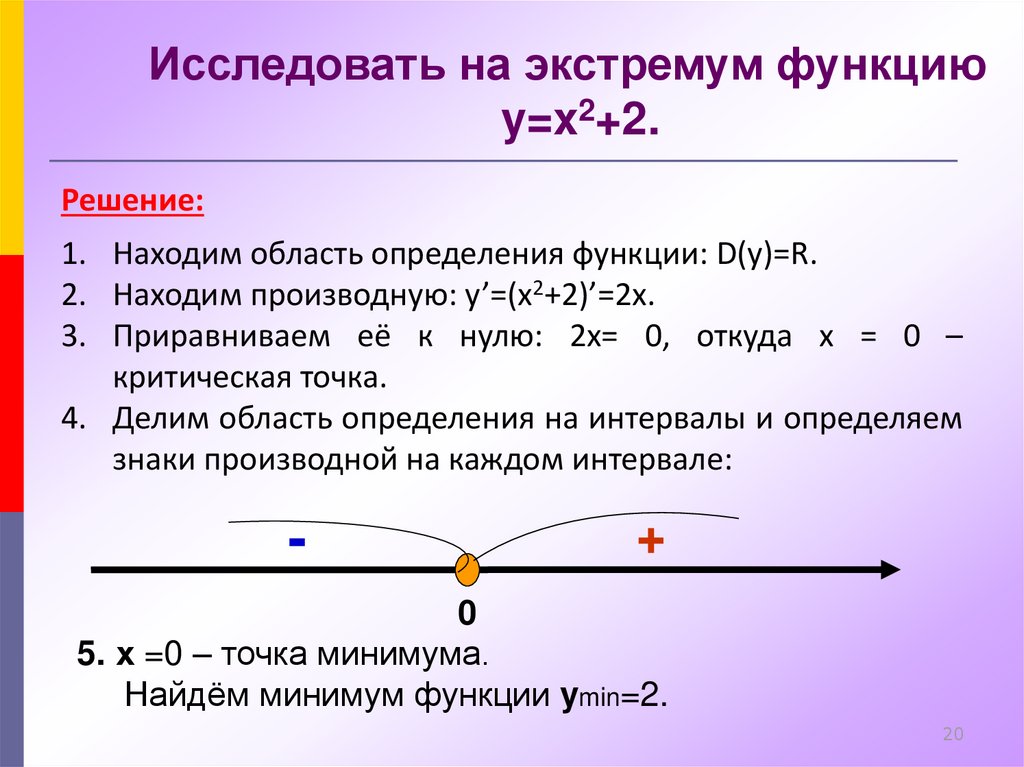 {\frac{2}{3}}}\hspace{0,5in}{\mbox{on}}\ hspace{0.5in}\left[ { — 5,\, — 1} \right]\] 9{\ гидроразрыва {1} {3}}}}} \ конец {выравнивание *} \]

Итак, похоже, у нас есть две критические точки.

\[\begin{align*}y & = — 4\hspace{0.5in} & & {\mbox{Поскольку производная здесь не существует.}}\\ y & = — \frac{{12}}{ 5} \hspace{0.5in} & & {\mbox{Потому что здесь производная равна нулю.}}\end{align*}\]

Оба они находятся в интервале, поэтому давайте оценим функцию в этих точках и в конечных точках интервала.

\[\begin{align*}Q\left( { — 4} \right) & = 0 & \hspace{0.5in} & & Q\left( { — \frac{{12}}{5}} \right ) & = — 9.849\\ Q\left( { — 5} \right) & = — 15 & \hspace{0.5in} & & Q\left( { — 1} \right) & = — 6.241\end{align *}\]

Функция имеет абсолютный нулевой максимум в точке \(y = — 4\), а абсолютный минимум функции будет равен -15 в точке \(y = — 5\).

Итак, если бы мы проигнорировали или забыли о критической точке, в которой производная не существует (\(y = — 4\)) мы бы не получили правильного ответа.

В этом разделе мы увидели, как можно использовать производную для определения абсолютных экстремумов функции. Это важное применение деривативов, которое время от времени будет возникать, поэтому не забывайте об этом.

Как найти локальные экстремумы с помощью теста первой производной Исчисление для чайников

Исследовать книгу Купить на Amazon

Все локальные максимумы и минимумы на графике функции, называемые локальными экстремумами, возникают в критических точках функции (где производная равна нулю или не определена). Не забывайте, однако, что не все критические точки обязательно являются локальными экстремумами.

Первым шагом в поиске локальных экстремумов функции является нахождение ее критических чисел ( x -значений критических точек). Затем вы используете тест первой производной. Этот тест основан на идеях уровня Нобелевской премии, согласно которым, когда вы преодолеваете вершину холма, вы сначала поднимаетесь, а затем спускаетесь, и что когда вы въезжаете в долину и выезжаете из нее, вы спускаетесь, а затем вверх. Этот математический материал довольно удивителен, а?

На рисунке показан график

Чтобы найти критические числа этой функции, выполните следующие действия:

1. Найдите первую производную от f , используя степенное правило.

2. Установите производную равной нулю и найдите x.

   x = 0, –2 или 2.

   Эти три значения x- являются критическими числами f. Дополнительные критические числа могли бы существовать, если бы первая производная была неопределенной при некоторых x -значения, а потому что производная

   определено для всех входных значений, приведенный выше набор решений, 0, –2 и 2, представляет собой полный список критических чисел. Поскольку производная (и наклон) 90 208 f 90 209 равна нулю при этих трех критических числах, кривая имеет горизонтальные касательные при этих числах.

Теперь, когда у вас есть список критических чисел, вам нужно определить, возникают ли пики или впадины, или ни то, ни другое при этих значениях x . Вы можете сделать это с помощью теста первой производной. Вот как:

1. Возьмите числовую прямую и запишите найденные критические числа: 0, –2 и 2.

   Вы делите эту числовую прямую на четыре области: слева от –2, от –2 до 0, от 0 до 2 и справа от 2.

2. Выберите значение из каждой области, подставьте его в первую производную и отметьте, будет ли ваш результат положительным или отрицательным.

   В этом примере вы можете использовать числа –3, –1, 1 и 3 для проверки областей.

   Эти четыре результата являются соответственно положительными, отрицательными, отрицательными и положительными.

3. Возьмите свою числовую прямую, отметьте каждую область соответствующим положительным или отрицательным знаком и укажите, где функция увеличивается и уменьшается.

   Увеличивается, когда производная положительна, и уменьшается, когда производная отрицательна. В результате получается так называемый знаковый график функции.

   Этот рисунок просто говорит вам то, что вы уже знаете, если смотрели на график f — что функция идет вверх до –2, вниз от –2 до 0, далее вниз от 0 до 2 и снова вверх от 2 на.

   А вот и ракетостроение. Функция переключается с возрастания на убывание при –2; другими словами, вы поднимаетесь до -2, а затем падаете. Итак, при –2 у вас есть холм или локальный максимум. И наоборот, поскольку функция переключается с убывания на возрастание в 2, у вас есть впадина или локальный минимум. А поскольку знак первой производной не меняется при нуле, в этом значении x нет ни минимума, ни максимума.

4. Получите значения функций (другими словами, высоты) этих двух локальных экстремумов, вставив x- значений в исходную функцию.

   Таким образом, локальный максимум находится в точке (–2, 64), а локальный минимум – в точке (2, –64).

   No related posts.