04. Матрицы и операции над ними
Матрицы и определители матриц широко используются при решении систем линейных уравнений, линейном программировании, исследовании систем дифференциальных уравнений. Аппарат теории матриц применяется в вычислительной математике, физике, моделировании практических задач в технике, экономике и бизнесе.
Матрицей называется прямоугольная таблица, составленная из элементов некоторого множества. Матрицы обычно обозначают заглавными буквами латинского алфавита в виде , если важно знать ее размеры, или буквами . Записывается матрица в следующем виде .
Элементы матрицы нумеруются двумя индексами. Первый индекс обозначает номер строки, а второй – номер столбца, на пересечении которых находится этот элемент в матрице. Матрица называется числовой, если ее элементы вещественные или комплексные числа; функциональной, если ее элементы – функции; блочной, если ее элементы – другие матрицы. Если число строк матрицы равно числу ее столбцов, то матрицу называют квадратной.
Некоторые матрицы имеют специальные обозначения и названия.
Произвольная матрица называется нулевой, если все ее элементы равны нулю. Например, матрица – нулевая размером два на три.
Квадратная матрица называется единичной, если все ее элементы на главной диагонали равны единице, а все остальные элементы равны нулю.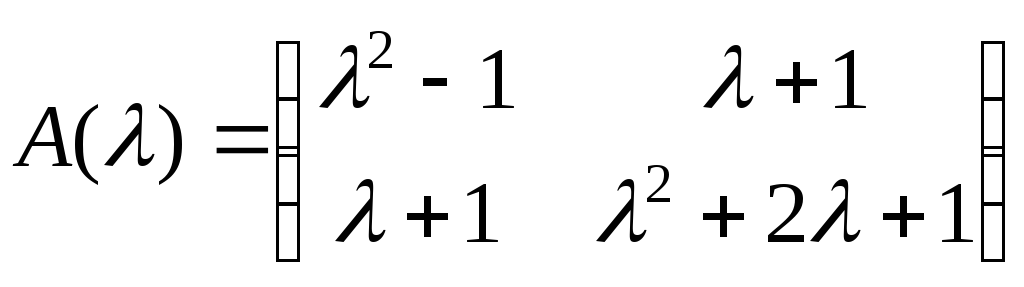
Квадратная матрица называется диагональной, если ее элементы, стоящие выше и ниже главной диагонали равны нулю. Например, матрица — диагональная.
Если в матрице размером заменить строки на столбцы с тем же номером, то получится новая матрица размером , которую называют транспонированной к исходной матрице . Таким образом, по определению для всех элементов транспонированной матрицы выполняются соотношения: . Например, транспонированной по отношению к матрице размером две строки на три столбца будет матрица размером три строки на два столбца. Если дважды транспонировать матрицу, то в результате получится исходная матрица.
Матрицы и Называют равными, если они имеют одинаковые размеры и все их соответствующие элементы равны, т. е. , если .
Например, числовая матрица равна квадратной, функциональной матрице , но они записаны в различных формах.
Квадратная матрица Называется симметричной, если она совпадает с транспонированной матрицей, т. е. . Например, матрица — симметричная, и видно, что она симметрична относительно главной диагонали. Отметим также, что диагональная и единичная матрицы являются симметричными, так как они совпадают со своими транспонированными матрицами, что проверяется непосредственно.
е. . Например, матрица — симметричная, и видно, что она симметрична относительно главной диагонали. Отметим также, что диагональная и единичная матрицы являются симметричными, так как они совпадают со своими транспонированными матрицами, что проверяется непосредственно.
Для матриц введены две основные операции: сложение матриц и умножение матрицы на число (вещественное или комплексное).
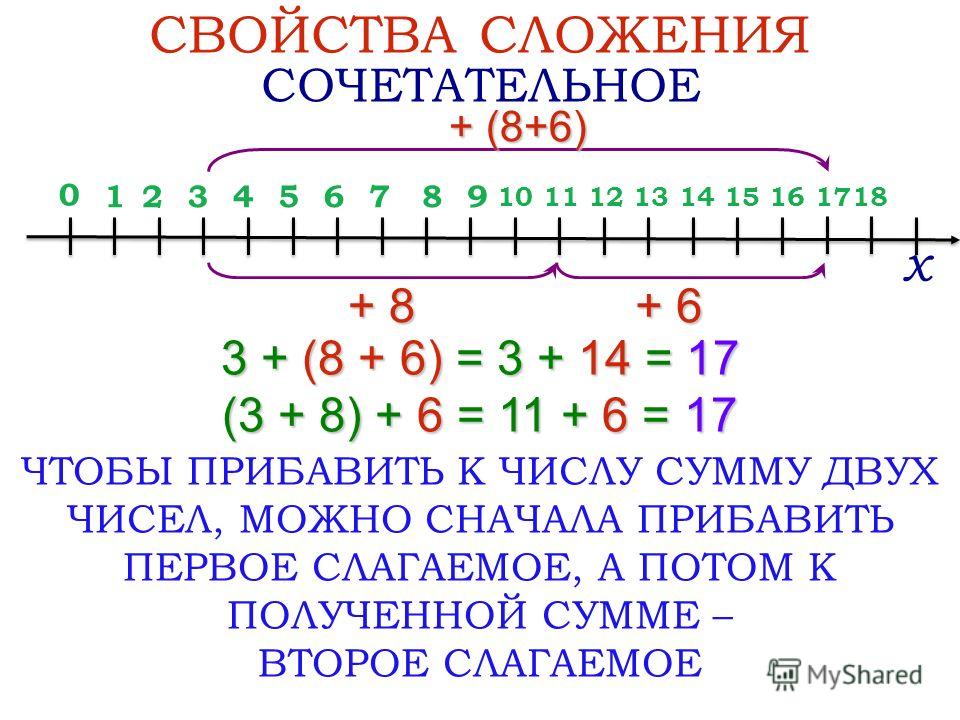
Суммой двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть .
Так, если и , то .
Для операции сложения матриц выполняются свойства коммутативности И ассоциативности , которые следуют из соответствующих свойств чисел. Если к любой матрице прибавить слева или справа нулевую матрицу, то исходная матрица не изменится; таким образом, выполняются равенства . Для любой матрицы существует единственная противоположная матрица , такая что , что также следует из аксиоматических свойств чисел.
и , то .
Произведением матрицы на число (вещественное или комплексное) называется матрица , полученная из исходной матрицы умножением всех ее элементов на число , то есть .
Например, пусть . Тогда .
Для основных матричных операций выполняются, дополнительно к вышеуказанным четырем свойствам, следующие четыре свойства:
— ассоциативность умножения на числа ,
— две дистрибутивности и . Все свойства матриц следуют из соответствующих свойств чисел.
Таким образом, для матриц относительно основных операций сложения и умножения на число выполняются все восемь аксиом линейного пространства. Это позволяет считать матрицы элементами некоторого конкретного линейного пространства и обращаться с ними как с векторами. Отметим, что арифметические векторы по их определению совпадают с матрицами – строками или матрицами – столбцами. Следовательно, арифметические векторы также удовлетворяют всем восьми свойствам абстрактного линейного пространства и могут, как и матрицы, называться векторами.
Следовательно, арифметические векторы также удовлетворяют всем восьми свойствам абстрактного линейного пространства и могут, как и матрицы, называться векторами.
Операция умножения первой матрицы на вторую матрицу Не является основной. Эта операция определяется только в том случае, когда число столбцов первой равно числу строк второй (длина строк первой матрицы равна высоте столбцов второй матрицы).
Произведением матрицы размера на матрицу размера называется матрица размера , все элементы которой находятся по формулам
.
Таким образом, для нахождения элементов последовательно выбираются строки и столбцы, причем при каждом выборе элементы строки умножаются на соответствующие элементы столбца и все такие парные произведения складываются. Пусть, например, первая матрица имеет размер две строки на два столбца, вторая матрица- такой же размер. Тогда матрица , равная их произведению , находится по определяющим формулам в виде и также имеет размер две строки на два столбца. Так как матрицы И Квадратные, то их можно перемножить в обратном порядке, то есть найти
Так как матрицы И Квадратные, то их можно перемножить в обратном порядке, то есть найти
.
Мы получили в нашем случае, что . Этот контрпример доказывает, что в общем случае умножение матриц не подчиняется закону коммутативности. Существуют матрицы, для которых свойство коммутативности выполняется. Такие матрицы называют коммутирующими, и они обязательно должны быть квадратными.
Покажем, например, что матрицы и коммутирующие. Действительно
,
,
Что и доказывает наше утверждение.
Если матрица Не является квадратной, то есть , то ее нельзя умножить саму на себя, так как число столбцов первой матрицы не будет равно числу строк второй матрицы. Однако если ее транспонировать, то определено как произведение размера , так и произведение размера . Рассмотрим для примера матрицу – строку вида . Транспонированная к ней матрица будет матрицей – столбцом вида . Произведение будет иметь размер три на три, а произведение будет иметь размер одна строка на один столбец. Сформируем далее матрицу
Сформируем далее матрицу
.
В этой формуле символом обозначен определитель матрицы , состоящей из одного элемента. Как показывается ниже, определитель такой матрицы равен значению этого единственного элемента. Полученная матрица симметричная и при умножении на себя дает единичную матрицу.
Основные свойства, связанные с умножением матриц, доказываются в общем виде на основе соответствующих свойств чисел путем непосредственного сопоставления матриц слева и справа от знака равенства:
1) ,
2) ,
3) ,
4) ,
5) ,
6) .
| < Предыдущая | Следующая > |
|---|
Лекция по теме «Матрица, действия над матрицами»
I. Определение матрицы.
Матрицей называют совокупность чисел, расположенных в прямоугольной таблице
,
состоящей из m строк и n столбцов.
Числа называют элементами матрицы. Первый индекс в обозначении элемента ( i ) указывает на номер строки, а второй индекс ( j )- на номер столбца, в которых расположен этот элемент.
В нашем случае () матрица называется прямоугольной размера . Если число строк в матрице равно числу столбцов (m=n), то матрицу называют квадратной порядка m.
Матрица, состоящая из одного столбца (n=1), называется матрицей-столбцом, а число строк в ней ( m ) — высотой столбца:
или .
Матрица, имеющая только одну строку (m=1), называется матрицей-строкой, а число столбцов в ней ( n ) — длиной строки:
или .
Два столбца равны, если они имеют одну одинаковую
высоту и равные элементы с одинаковыми номерами. Две строки равны, если они
имеют одинаковую длину и равны их соответствующие элементы.
II. Определение детерминанта.
Для квадратной матрицы может быть введено понятие детерминанта (определителя). Детерминант матрицы [A] обозначают
или .
Детерминантом матрицы порядка n>1 называют число
, (1)
где — детерминант матрицы порядка n-1, полученной из матрицы [A] вычеркиванием первой строки и k -ого столбца.
Матрица порядка 1 состоит из одного числа, и ее детерминант по определению считают равным этому числу:
. (2)
Детерминант матрицы второго порядка в соответствии с (1) и (2) можно вычислить по следующей формуле:
.
Для матрицы третьего порядка
В соответствии с определением детерминант матрицы
четвертого порядка может быть выражен через определитель третьего порядка, тот
в свою очередь через определители второго порядка и т. д.
д.
Число называют дополнительным минором элемента . Для произвольного элемента матрицы также можно ввести понятия дополнительного минора: — это определитель матрицы, получаемой из исходной вычеркиванием i -ой строки и j-ого столбца. Например, для матрицы [A] третьего порядка дополнительным минором элемента будет определитель
.
Определитель матрицы может быть вычислен по формулам разложения детерминанта по произвольной строке или столбцу:
по строке: , (3)
по столбцу: . (4)
Числа называют алгебраическими дополнениями элементов матрицы A. Они равны соответствующим минорам, взятым со своим знаком.
С помощью алгебраических дополнений формулы (3) и (4) могут быть записаны в виде:
, (3¢)
. (4¢)
(4¢)
Пример: записать определитель матрицы третьего порядка, используя формулы разложения по второй строке и третьему столбцу:
III. Свойства детерминантов.
Перечислим следующие основные свойства детерминантов:
1) определитель не изменится, если все строки матрицы заменить столбцами с соответствующими номерами:
.
Cправедливость этого свойства следует из возможности вычисления детерминанта по формулам разложения по строке или столбцу.
2) при перестановке местами двух строк или двух столбцов определителя, он должен быть умножен на -1:
.
3) если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
4) умножение всех элементов одного столбца или одной строки на любое число k равносильно умножению определителя на это число:
.
5) если все элементы некоторого столбца или строки матрицы равны нулю, то и ее определитель равен нулю.
6) если соответствующие элементы двух столбцов или двух строк матрицы пропорциональны, то ее определитель равен нулю:
7) если каждый элемент i-ого столбца или строки матрицы представляет собой сумму двух слагаемых, то ее определитель может быть вычислен как сумма двух определителей:
8) если к элементам некоторой строки (или некоторого столбца) матрицы прибавить соответствующие элементы другой строки (или другого столбца), умноженные на одно и тоже число, то величина определителя при этом не изменится:
.
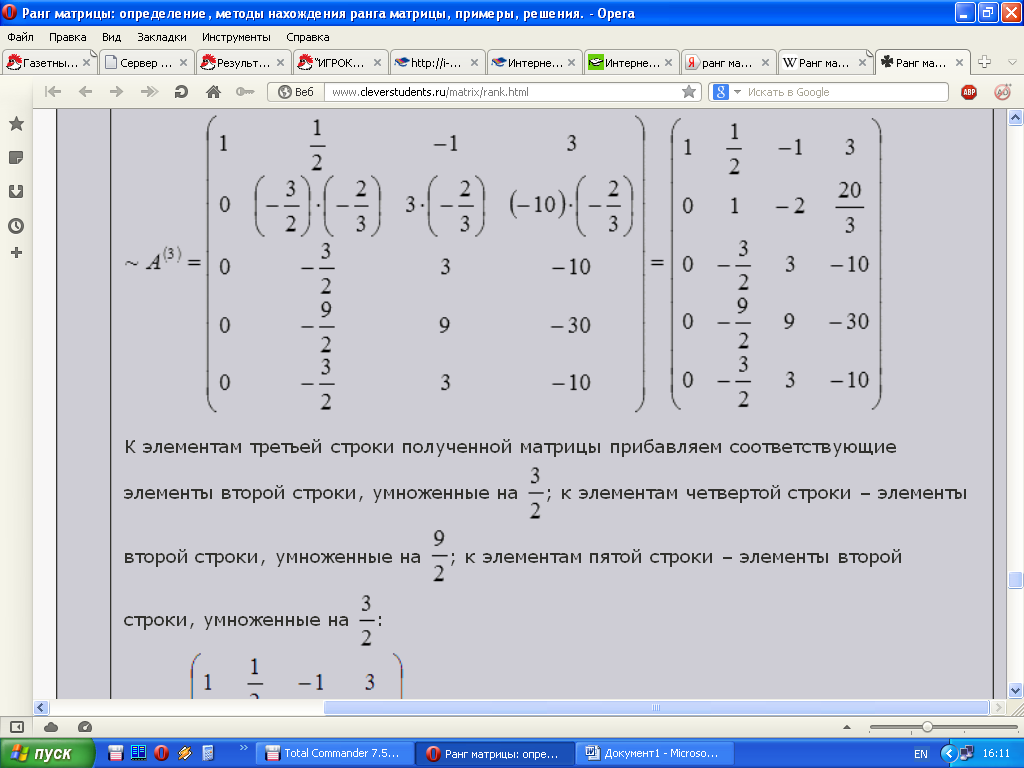
IV. Ранг матрицы.
Рассмотрим некоторую не обязательно квадратную матрицу [A] размером . Выберем какие-нибудь r номеров ее строк и r номеров столбцов
. Минором порядка r
матрицы [A] называется определитель матрицы порядка r,
образованной элементами, расположенными на пересечении выбранных строк и
столбцов.
Если считать, что , то
. (5)
Пусть задана матрица [A] размером :
.
Составим все ее миноры третьего порядка. Они должны включать строки матрицы [A] с номерами 1, 2, 3 и три столбца матрицы [A]. Это могут быть столбцы с номерами 1, 2, 3; или 1, 3, 4; или 2, 3, 4 или 1, 2, 4. Тогда можно составить для этой матрицы четыре минора третьего порядка:
Для данной матрицы миноры четвертого порядка не существуют, т.к. у нее только три строки. Примерами миноров второго порядка являются:
Определение: в матрице [A] размером минор
порядка r называется базисным, если он отличен от
нуля, а все миноры порядка r+1 равны нулю или не существуют. (В последнем случае r равно меньшему из чисел т или п).
В матрице может быть несколько базисных миноров.
Пример. Найдем базисные миноры матрицы:
Миноров третьего порядка для этой матрицы не существует.
, т.к. есть нулевой столбец
Миноры второго порядка, содержащие первый столбец, также равны нулю.
Ненулевыми для данной матрицы оказываются только миноры первого порядка:. Они и являются базисными.
Если матрица нулевая, т.е. все ее элементы равны нулю, то у нее вообще нет базисного минора.
Определение : рангом матрицы называется порядок ее базисного минора. Если матрица нулевая, то ее ранг считают равным нулю.
В соответствии с определением можно указать ранги матриц, рассмотренных в следующем примере: RgA=2, RgB=1.
V. Действия над матрицами.
Будем рассматривать матрицы [A]
и [B] одного и того же размера .
Для двух таких матриц вводятся линейные операции сложения и умножения на число. Суммой матриц [A] и [B] является матрица [C]
=[A]+[B] того же размера, каждый элемент которой
вычисляется по формуле
Суммой матриц [A] и [B] является матрица [C]
=[A]+[B] того же размера, каждый элемент которой
вычисляется по формуле
При умножении матрицы [A] на вещественное число каждый ее элемент умножается на это число:
т.е. в результате умножения матрицы на число получаем матрицу тех же размеров.
Еще одна операция над матрицей — транспонирование. Транспонирование заключается в замене строк матрицы ее столбцами с соответствующими номерами. Если транспонированию подвергается матрица [A] размером , то результатом будет матрица [A]T размером , называемая транспонированной по отношению к матрице [A]. Элементы транспонированной матрицы .
Для двух матриц [A] и [B]
размерами и соответственно вводится операция умножения.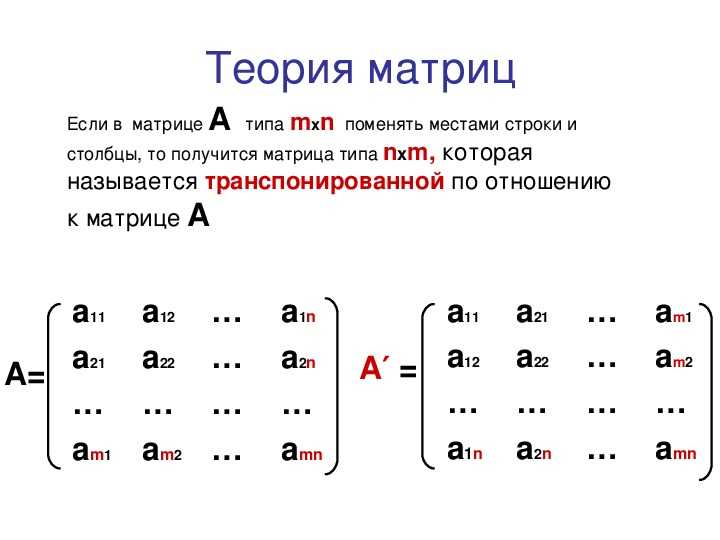 Произведением матриц [A] и
[B] указанных размеров является третья матрица [C]
размером :
Произведением матриц [A] и
[B] указанных размеров является третья матрица [C]
размером :
,
причем , т.е. элемент, стоящий в i -ой строке и j-ом столбце можно найти как сумму произведений элементов матрицы [A], стоящих в i -ой строке, и элементов матрицы [B], стоящих в j -ом столбце.
Перемножать можно только матрицы, для которых число столбцов в первой равно числу строк во второй матрице. Две квадратные матрицы можно перемножать только в том случае, когда они имеют одинаковый порядок. Для операции умножения двух матриц не справедлив переместительный закон, т.е. в общем случае
.
Примеры:
При выполнении операций над матрицами полезно иметь в виду следующие соотношения между определителями:
.
Пример: для матриц и
VI. Некоторые специальные виды матриц.
Некоторые специальные виды матриц.
Среди квадратных матриц выделяют некоторые матрицы специальных видов:
1) диагональные матрицы — имеют ненулевые элементы, стоящие только на главной диагонали, т.е. ;
2) единичные матрицы — на главной диагонали стоят единицы, а все остальные элементы — нули:
3) нулевая матрица — все элементы равны нулям;
4) симметричные матрицы — для них выполняется условие
, т.е. ;
5) кососимметричные матрицы: , т.е. .
6) вырожденные матрицы имеют нулевой определитель, т.е..
7) унимодулярные матрицы имеют определитель, равный 1.
Перечислим некоторые свойства таких матриц:
Если матрицу [A] сложить с нулевой матрицей [0] , то получим матрицу [A]:
[A]+[0]=[A].
При умножении матрицы [A] на единичную матрицу слева или справа, матрица не изменяется:
.
Матрица [B] называется обратной по отношению к матрице [A], если их произведение равно единичной матрице:
.
Матрицу, обратную к данной, обозначают . Вырожденные матрицы не имеют обратных.
Одним из методов нахождения матрицы, обратной к данной, является метод присоединенной матрицы. В соответствии с этим методом
,
где [AV] — матрица, присоединенная к матрице [A] .
Каждый элемент матрицы [AV] определяется как алгебраическое дополнение соответствующего элемента матрицы [A]; т.е.
.
Пример: найти матрицу, обратную к матрице
Найдем определитель матрицы [А]: .
Найдем алгебраические дополнения элементов матрицы [А]:
и составим присоединенную матрицу
.
Вычислим в соответствии с формулой элементы обратной матрицы:
.
Проверим результат умножением
.
Матрицы сложения и вычитания
Матрицы складывать и вычитать легко. Если вы знаете, как складывать и вычитать целые числа, этот урок будет проще простого. Во-первых, внимательно изучите рисунок ниже, чтобы увидеть, как это делается для матрицы 2 × 2.
На основе примера на рисунке выше, чтобы сложить или вычесть матрицы, мы добавляем или вычитаем их соответствующие элементы. Например, мы добавляем 8 и 9, чтобы получить 17.
Даны две матрицы размера m × n A = [a ij ] и B = [b ij ], где a и b расположены в строке i и столбце j.
Сумма A + B = [a ij ] + [b ij ]
Разность A — B = [a ij ] — [ b ij ]
два2 Использование 2 матрицы,- элементы в первой строке и первом столбце равны a 11 и b 11
- элементы в первой строке и втором столбце равны a 12 8 и b 10034
- Элементы во втором ряду и первом столбце — 21 и B 21
- Элементы во втором ряду и второй столбец — 22 и B 22
Уведомление о том, как.
 получим сумму соответствующих элементов в следующем сложении матриц:
получим сумму соответствующих элементов в следующем сложении матриц:$$ А + В = \begin{bmatrix} а_{11} и а_{12}\\ а_{21} и а_{22}\\ \end{bmatrix} + \begin{bmatrix} б_{11} и б_{12}\\ б_{21} и б_{22}\\ \end{bmatrix} «=» \begin{bmatrix} а_{11} + b_{11} и а_{12} + b_{12}\\ a_{21} + b_{21} и a_{22} + b_{22}\\ \end{bmatrix} $$
Обратите также внимание на то, как мы получаем разность соответствующих элементов при следующем вычитании матриц:
$$ А — В = \begin{bmatrix} а_{11} и а_{12}\\ а_{21} и а_{22}\\ \end{bmatrix} — \begin{bmatrix} б_{11} и б_{12}\\ б_{21} и б_{22}\\ \end{bmatrix} «=» \begin{bmatrix} а_{11} — б_{11} и а_{12} — б_{12}\\ а_{21} — б_{21} и а_{22} — б_{22}\\ \end{bmatrix} $$
Важно знать следующее правило: при сложении и вычитании матриц сначала убедитесь, что матрицы имеют одинаковые размеры. Предположим, вы добавляете две матрицы.
Тогда это означает, что количество строк в первой матрице должно быть равно количеству строк во второй матрице.
 Точно так же количество столбцов в первой матрице должно быть равно количеству столбцов во второй матрице.
Точно так же количество столбцов в первой матрице должно быть равно количеству столбцов во второй матрице.По порядку слов вы можете добавить или вычесть 2×3 с 2×3 или 3×3 с 3×3. Однако вы не можете добавить 3×2 к 2×3 или 2×2 к 3×3.
Другие примеры, показывающие, как складывать и вычитать матрицы
Сложение матриц
Добавьте две матрицы, показанные ниже:
1 -4 0 8 -1 6 0 3 2 + 9 3 7 -8 0 5 -3 2 9 Добавление матрицы
Добавьте две матрицы, показанные ниже:
1 -4 0 8 -1 6 0 3 2 + 9 3 7 -8 0 5 -3 2 9
Правило для сложения и вычитания матрицВы можете добавлять элементы в одну и ту же позицию или элементы в одну строку и один столбец.
 Мы показываем эти элементы одним цветом, чтобы сделать их кристально четкими.
Мы показываем эти элементы одним цветом, чтобы сделать их кристально четкими.1 -4 0 8 -1 6 0 3 2 + 9 3 7 -8 0 5 -3 2 9 1 + 9 -4 + 3 0 + 7 8 + -8 -1 + 0 6 + 5 0 + -3 3 + 2 2 + 9 10 -1 7 0 -1 11 -3 5 11 1 -4 0 8 -1 6 0 3 2 + 9 3 7 -8 0 5 -3 2 9 1 + 9 -4 + 3 0 + 7 8 + -8 -1 + 0 6 + 5 0 + -3 3 + 2 2 + 9 10 -1 7 0 -1 11 -3 5 11 Вычитание матриц
Вычитание матриц аналогично сложению матриц, за исключением того, что вы вычитаете элементы из одной строки и одного столбца.

Вычтите две следующие матрицы:
9 7 1 -2 0 4 8 -5 3 — 6 1 8 -3 0 9 -1 2 1 9 — 6 7 — 1 1 — 8 -2 — -3 0 — 0 4 — 9 8 — -1 -5 — 2 3 — 1 3 6 -7 1 0 -5 9 -7 2 Вычитание матриц аналогично сложению матриц, за исключением того, что вы вычитаете элементы из одной и той же строки и одного столбца.

Вычтите две следующие матрицы:
9 7 1 -2 0 4 8 -5 3 — 6 1 8 -3 0 9 -1 2 1 9 — 6 7 — 1 1 — 8 -2 — -3 0 — 0 4 — 9 8 — -1 -5 — 2 3 — 1 3 6 -7 1 0 -5 9 -7 2 Связь с реальным миром
У вас есть бизнес по продаже рубашек и брюк.
 Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — это неделя №1 , а матрица справа — это неделя №2.
Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — это неделя №1 , а матрица справа — это неделя №2. В строке №1 указано количество брюк, проданных вами, а в строке №2 — количество рубашек, проданных с понедельника по пятницу.
Например, вы продали 40 штанов в среду (неделя 1).
Вы продали 28 рубашек в пятницу (2-я неделя)
Сколько штанов и рубашек вы продали за две недели?
Просто выполните сложение матриц!
50 25 40 80 10 30 90 60 12 45 + 20 30 70 65 80 55 35 75 14 28 50 + 20 25 + 30 40 + 70 80 + 65 10 + 80 30 + 55 90 + 35 60 + 75 12 + 14 45 + 28 70 55 110 145 90 85 125 135 26 73 Связь с реальным миром
У вас есть бизнес по продаже рубашек и брюк.
 Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1, матрица справа — неделя №2.
Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1, матрица справа — неделя №2.В строке №1 указано количество брюк, проданных вами, а в строке №2 — количество рубашек, проданных с понедельника по пятницу.
Например, вы продали 40 штанов в среду (неделя 1).
Вы продали 28 рубашек в пятницу (2-я неделя)
Сколько штанов и рубашек вы продали за две недели?
Просто выполните сложение матриц!
50 25 40 80 10 30 90 60 12 45 + 20 30 70 65 80 55 35 75 14 28 50 + 20 25 + 30 40 + 70 80 + 65 10 + 80 30 + 55 90 + 35 60 + 75 12 + 14 45 + 28 70 55 110 145 90 85 125 135 26 73 Тест на сложение и вычитание матриц.
 Проверьте, насколько хорошо вы поняли этот урок.
Проверьте, насколько хорошо вы поняли этот урок.Квадратичная формула: простые шаги
26, 23 января 11:44
Узнайте о квадратной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.
Подробнее
Формула площади — список важных формул
25, 23 января 05:54
Какова формула площади двумерной фигуры? Вот список тех, которые вы должны знать!
Подробнее
Матрицы — документация по SymPy 1.11
>>> из импорта sympy * >>> init_printing(use_unicode=Истина)
Чтобы создать матрицу в SymPy, используйте объект
Matrix. Матрица построена путем предоставления списка векторов-строк, составляющих матрицу. Например, построить матрицу\[\begin{split}\left[\begin{array}{cc}1 & -1\\3 & 4\\0 & 2\end{массив}\right]\end{split}\]
использовать
>>> Матрица([[1, -1], [3, 4], [0, 2]]) ⎡1 -1⎤ ⎢ ⎥ ⎢3 4 ⎥ ⎢ ⎥ ⎣0 2 ⎦
Чтобы упростить создание векторов-столбцов, список элементов считается вектор-столбец.

>>> Матрица([1, 2, 3]) ⎡1⎤ ⎢ ⎥ ⎢2⎥ ⎢ ⎥ ⎣3⎦
Матрицы управляются так же, как и любые другие объекты в SymPy или Python.
>>> М = Матрица([[1, 2, 3], [3, 2, 1]]) >>> N = Матрица ([0, 1, 1]) >>> М*Н ⎡5⎤ ⎢ ⎥ ⎣3⎦
Важно отметить, что в матрицах SymPy, в отличие от любых других объект в SymPy, они изменяемы. Это означает, что они могут быть изменены в место, как мы увидим ниже. Недостатком этого является то, что
Matrixне может использоваться в местах, требующих неизменности, например, внутри других SymPy выражения или как ключи к словарям. Если вам нужна неизменяемая версияMatrix, используйтеImmutableMatrix.Основные операции
Вот некоторые основные операции с
Matrix.Форма
Чтобы получить форму матрицы, используйте
функцию shape().>>> из формы импорта sympy >>> М = Матрица([[1, 2, 3], [-2, 0, 4]]) >>> М ⎡1 2 3⎤ ⎢ ⎥ ⎣-2 0 4⎦ >>> Форма (М) (2, 3)
Доступ к строкам и столбцам
Чтобы получить отдельную строку или столбец матрицы, используйте
rowилиcol. Для
например,
Для
например, M.row(0)получит первую строку.M.col(-1)получит последний столбец.>>> М.ряд(0) [1 2 3] >>> М.кол(-1) ⎡3⎤ ⎢ ⎥ ⎣4⎦
Удаление и вставка строк и столбцов
Чтобы удалить строку или столбец, используйте
row_delилиcol_del. Эти операции будем дорабатывать матрицу вместо .>>> M.col_del(0) >>> М ⎡2 3⎤ ⎢ ⎥ ⎣0 4⎦ >>> M.row_del(1) >>> М [2 3]
Чтобы вставить строки или столбцы, используйте
row_insertилиcol_insert. Эти операции не работают на месте .>>> М [2 3] >>> M = M.row_insert(1, Matrix([[0, 4]])) >>> М ⎡2 3⎤ ⎢ ⎥ ⎣0 4⎦ >>> M = M.col_insert(0, Matrix([1, -2])) >>> М ⎡1 2 3⎤ ⎢ ⎥ ⎣-2 0 4⎦
Если не указано иное, методы, упомянутые ниже, не работают в место. Как правило, метод, который не работает на месте, возвращает новый
Matrixи метод, который работает на месте, вернутNone.
Основные методы
Как отмечалось выше, выполняются простые операции, такие как сложение и умножение. просто используя
+,*и**. Чтобы найти обратную матрицу, достаточно поднять его до-1власть.>>> М = Матрица ([[1, 3], [-2, 3]]) >>> N = Матрица ([[0, 3], [0, 7]]) >>> М + Н ⎡1 6 ⎤ ⎢ ⎥ ⎣-2 10⎦ >>> М*Н ⎡0 24⎤ ⎢ ⎥ ⎣0 15⎦ >>> 3*м ⎡3 9⎤ ⎢ ⎥ ⎣-6 9⎦ >>> М**2 ⎡-5 12⎤ ⎢ ⎥ ⎣-8 3 ⎦ >>> М**-1 ⎡1/3 -1/3⎤ ⎢ ⎥ ⎣2/9 1/9 ⎦ >>> Н**-1 Traceback (последний последний вызов): ... NonInvertibleMatrixError: Matrix det == 0; не обратимый.
Чтобы транспонировать матрицу, используйте
T.>>> M = Матрица ([[1, 2, 3], [4, 5, 6]]) >>> М ⎡1 2 3⎤ ⎢ ⎥ ⎣4 5 6⎦ >>> М.Т. ⎡1 4⎤ ⎢ ⎥ ⎢2 5⎥ ⎢ ⎥ ⎣3 6⎦
Матричные конструкторы
Существует несколько конструкторов для создания общих матриц. Чтобы создать идентификационная матрица, используйте
глаз.
eye(n)создаст единичную матрицу \(n\times n\).>>> глаз(3) ⎡1 0 0⎤ ⎢ ⎥ ⎢0 1 0⎥ ⎢ ⎥ ⎣0 0 1⎦ >>> глаз(4) ⎡1 0 0 0⎤ ⎢ ⎥ ⎢0 1 0 0⎥ ⎢ ⎥ ⎢0 0 1 0⎥ ⎢ ⎥ ⎣0 0 0 1⎦
Чтобы создать матрицу всех нулей, используйте
нулей.нулей(n, m)создает \(n\times m\) матрица \(0\)s.>>> нули (2, 3) ⎡0 0 0⎤ ⎢ ⎥ ⎣0 0 0⎦
Аналогично,
единицсоздает матрицу единиц.>>> единицы (3, 2) ⎡1 1⎤ ⎢ ⎥ ⎢1 1⎥ ⎢ ⎥ ⎣1 1⎦
Для создания диагональных матриц используйте
diag. Аргументы дляdiagмогут быть либо числа, либо матрицы. Число интерпретируется как \(1\times 1\) матрица. Матрицы уложены по диагонали. Остальные элементы заполнено \(0\)s.>>> диаг.(1, 2, 3) ⎡1 0 0⎤ ⎢ ⎥ ⎢0 2 0⎥ ⎢ ⎥ ⎣0 0 3⎦ >>> диаг(-1, единицы(2, 2), матрица([5, 7, 5])) ⎡-1 0 0 0⎤ ⎢ ⎥ ⎢0 1 1 0⎥ ⎢ ⎥ ⎢0 1 1 0⎥ ⎢ ⎥ ⎢0 0 0 5⎥ ⎢ ⎥ ⎢0 0 0 7⎥ ⎢ ⎥ ⎣0 0 0 5⎦
Расширенные методы
Определитель
Чтобы вычислить определитель матрицы, используйте
det.
>>> М = Матрица([[1, 0, 1], [2, -1, 3], [4, 3, 2]]) >>> М ⎡1 0 1⎤ ⎢ ⎥ ⎢2 -1 3⎥ ⎢ ⎥ ⎣4 3 2⎦ >>> М.дет() -1
РЕФ
Чтобы преобразовать матрицу в сокращенную форму эшелона строк, используйте
rref.rrefвозвращает кортеж из двух элементов. Первая представляет собой уменьшенную эшелонированную форму строки, а второй — это кортеж индексов опорных столбцов.>>> M = Matrix([[1, 0, 1, 3], [2, 3, 4, 7], [-1, -3, -3, -4]]) >>> М ⎡1 0 1 3 ⎤ ⎢ ⎥ ⎢2 3 4 7 ⎥ ⎢ ⎥ ⎣-1-3-3-4⎦ >>> М.rref() ⎛⎡1 0 1 3 ⎤ ⎞ ⎜⎢ ⎥ ⎟ ⎜⎢0 1 2/3 1/3⎥, (0, 1)⎟ ⎜⎢ ⎥ ⎟ ⎝⎣0 0 0 0 ⎦ ⎠
Примечание
Первый элемент кортежа, возвращенный
rrefотносится к типуМатрица. Второй типtuple.Пустое пространство
Чтобы найти нулевое пространство матрицы, используйте
нулевое пространство.nullspaceвозвращаетсписоквекторов-столбцов, которые охватывают нулевое пространство матрицы.
>>> М = Матрица([[1, 2, 3, 0, 0], [4, 10, 0, 0, 1]]) >>> М ⎡1 2 3 0 0⎤ ⎢ ⎥ ⎣4 10 0 0 1⎦ >>> М.nullspace() ⎡⎡-15⎤ ⎡0⎤ ⎡ 1 ⎤⎤ ⎢⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎥ ⎢⎢ 6 ⎥ ⎢0⎥ ⎢-1/2⎥⎥ ⎢⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎥ ⎢⎢ 1 ⎥, ⎢0⎥, ⎢ 0 ⎥⎥ ⎢⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎥ ⎢⎢ 0 ⎥ ⎢1⎥ ⎢ 0 ⎥⎥ ⎢⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎥ ⎣⎣ 0 ⎦ ⎣0⎦ ⎣ 1 ⎦⎦
Пространство столбцов
Чтобы найти пространство столбцов матрицы, используйте
пространство столбцов.columnspaceвозвращаетсписоквекторов-столбцов, которые охватывают пространство столбцов матрицы.>>> М = Матрица ([[1, 1, 2], [2, 1, 3], [3, 1, 4]]) >>> М ⎡1 1 2⎤ ⎢ ⎥ ⎢2 1 3⎥ ⎢ ⎥ ⎣3 1 4⎦ >>> M.columnspace() ⎡⎡1⎤ ⎡1⎤⎤ ⎢⎢ ⎥ ⎢ ⎥⎥ ⎢⎢2⎥, ⎢1⎥⎥ ⎢⎢ ⎥ ⎢ ⎥⎥ ⎣⎣3⎦ ⎣1⎦⎦
Собственные значения, собственные векторы и диагонализация
Чтобы найти собственные значения матрицы, используйте
собственных значений.собственных значенийвозвращает словарь изсобственных значений: алгебраическая_множественностьпар (аналогично выход корней).
>>> М = Матрица([[3, -2, 4, -2], [5, 3, -3, -2], [5, -2, 2, -2], [5, -2 , -3, 3]]) >>> М ⎡3 -2 4 -2⎤ ⎢ ⎥ ⎢5 3 -3 -2⎥ ⎢ ⎥ ⎢5 -2 2 -2⎥ ⎢ ⎥ ⎣5 -2 -3 3 ⎦ >>> M.eigenvals() {-2:1, 3:1, 5:2}Это означает, что
Mимеет собственные значения -2, 3 и 5, и что собственные значения -2 и 3 имеют алгебраическую кратность 1 и что собственное значение 5 имеет алгебраическую кратность 2.Чтобы найти собственные векторы матрицы, используйте
собственных векторов.собственных вектороввозвращает список кортежей вида(собственное значение, алгебраическая_кратность, [собственные векторы]).>>> М.собственные векторы() ⎡⎛ ⎡⎡0⎤⎤⎞ ⎛ ⎡⎡1⎤⎤⎞ ⎛ ⎡⎡1⎤ ⎡0 ⎤⎤⎞⎤ ⎢⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥ ⎢ ⎥⎥⎟⎥ ⎢⎜ ⎢⎢1⎥⎥⎟ ⎜ ⎢⎢1⎥⎥⎟ ⎜ ⎢⎢1⎥ ⎢-1⎥⎥⎟⎥ ⎢⎜-2, 1, ⎢⎢ ⎥⎥⎟, ⎜3, 1, ⎢⎢ ⎥⎥⎟, ⎜5, 2, ⎢⎢ ⎥, ⎢ ⎥⎥⎟⎥ ⎢⎜ ⎢⎢1⎥⎥⎟ ⎜ ⎢⎢1⎥⎥⎟ ⎜ ⎢⎢1⎥ ⎢0 ⎥⎥⎟⎥ ⎢⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥⎥⎟ ⎜ ⎢⎢ ⎥ ⎢ ⎥⎥⎟⎥ ⎣⎝ ⎣⎣1⎦⎦⎠ ⎝ ⎣⎣1⎦⎦⎠ ⎝ ⎣⎣0⎦ ⎣1 ⎦⎦⎠⎦ 9{-1}\).
>>> P, D = M.diagonalize() >>> П ⎡0 1 1 0 ⎤ ⎢ ⎥ ⎢1 1 1 -1⎥ ⎢ ⎥ ⎢1 1 1 0 ⎥ ⎢ ⎥ ⎣1 1 0 1 ⎦ >>> Д ⎡-2 0 0 0⎤ ⎢ ⎥ ⎢0 3 0 0⎥ ⎢ ⎥ ⎢0 0 5 0⎥ ⎢ ⎥ ⎣0 0 0 5⎦ >>> П*Д*П**-1 ⎡3 -2 4 -2⎤ ⎢ ⎥ ⎢5 3 -3 -2⎥ ⎢ ⎥ ⎢5 -2 2 -2⎥ ⎢ ⎥ ⎣5 -2 -3 3 ⎦ >>> П*Д*П**-1 == М Истинный
Обратите внимание, что, поскольку
собственных векторовтакже включают собственные значения, вы должны использовать это вместособственных значений, если вам также нужны собственные векторы. Однако, как вычисление собственных векторов часто может быть дорогостоящим,собственных значенийдолжны быть предпочтительнее, если вы хотите найти только собственные значения.Если вам нужен только характеристический полином, используйте
charpoly. Это эффективнее, чемсобственных значений, потому что иногда могут быть дорого просчитывать.>>> лямда = символы('лямда') >>> p = M.charpoly(лямда) >>> фактор(p. as_expr())
2
(λ - 5) ⋅ (λ - 3) ⋅ (λ + 2)
as_expr())
2
(λ - 5) ⋅ (λ - 3) ⋅ (λ + 2)
Возможные проблемы
Нулевое тестирование
Если ваши операции с матрицами не выполняются или возвращают неверные ответы, общие причины, вероятно, связаны с нулевым тестированием. Если есть выражение, не прошедшее правильную проверку нулями, это может вызвать проблемы с поиском опорных точек для исключения Гаусса, или решить, является ли матрица обратимой, или любые функции высокого уровня, которые зависят от предшествующих процедур.
В настоящее время метод нулевого тестирования SymPy по умолчанию
_iszeroтолько гарантированно быть точным в некоторой ограниченной области чисел и символов, и любые сложные выражения за пределами его разрешимости рассматриваются какNone, который ведет себя аналогично логическомуFalse.Список методов, использующих процедуры нулевого тестирования, следующий:
эшелон_форма,ис_эшелон,ранг,rref,пустое пространство,собственные векторы,inverse_ADJ,inverse_GE,inverse_LU,LUdecomposition,LUdecomposition_Simple,LUsolveУ них есть свойство
iszerofunc, открытое для пользователя, чтобы указать нулевое тестирование метод, который может принимать любую функцию с одним вводом и логическим выводом, по умолчанию с_iszero.
Вот пример решения проблемы, вызванной занижением нуля. В то время выход для этой конкретной матрицы с тех пор был улучшен, метод ниже все еще интересно. [1] [2] [3]
>>> из импорта sympy * >>> q = Символ ("q", положительный = Истина) >>> m = Матрица([ ... [-2*кош(д/3), ехр(-д), 1], ... [ ехр(д), -2*кош(д/3), 1], ... [1, 1, -2*кош(д/3)]]) >>> m.nullspace() []Вы можете отследить, какое выражение недооценивается, внедрив пользовательский нулевой тест с включенными предупреждениями.
>>> предупреждения об импорте >>> >>> определение my_iszero(x): ... пытаться: ... результат = x.is_zero ... кроме AttributeError: ... результат = нет ... ... # Предупреждения, если оцениваются как None ... если результат None: ... warnings.warn("Нулевая проверка {} оценена как None".format(x)) ... вернуть результат ... >>> m.nullspace(iszerofunc=my_iszero) __основной__:9: UserWarning: Нулевое тестирование 4*cosh(q/3)**2 — 1 оценивается как None __main__:9: UserWarning: Нулевое тестирование (-exp(q) - 2*cosh(q/3))*(-2*cosh(q/3) - exp(-q)) - (4*cosh(q) /3)**2 - 1)**2 оценивается как None __main__:9: UserWarning: Нулевое тестирование 2*exp(q)*cosh(q/3) - 16*cosh(q/3)**4 + 12*cosh(q/3)**2 + 2*exp (-q)*cosh(q/3) оценивается как None __main__:9: UserWarning: Нулевое тестирование -(4*cosh(q/3)**2 - 1)*exp(-q) - 2*cosh(q/3) - exp(-q) оценено как None []В этом случае
(-exp(q) - 2*cosh(q/3))*(-2*cosh(q/3) - exp(-q)) - (4*cosh(q/3)**2 - 1 )**2должен дать ноль, но нулевая проверка не уловила. возможно, это означает, что следует ввести более сильный нулевой тест.
Для этого конкретного примера переписывание в экспоненты и применение упрощения будет
усилить нулевой тест для гипербол,
будучи безвредным для других многочленов или трансцендентных функций.
возможно, это означает, что следует ввести более сильный нулевой тест.
Для этого конкретного примера переписывание в экспоненты и применение упрощения будет
усилить нулевой тест для гипербол,
будучи безвредным для других многочленов или трансцендентных функций.>>> определение my_iszero(x): ... пытаться: ... результат = x.rewrite(exp).simplify().is_zero ... кроме AttributeError: ... результат = нет ... ... # Предупреждения, если оцениваются как None ... если результат None: ... warnings.warn("Нулевая проверка {} оценена как None".format(x)) ... вернуть результат ... >>> m.nullspace(iszerofunc=my_iszero) __основной__:9: UserWarning: Нулевая проверка -2*cosh(q/3) - exp(-q) оценена как None ⎡⎡ ⎛ д ⎛q⎞⎞ -д 2⎛q⎞ ⎤⎤ ⎢⎢- ⎜- ℯ - 2⋅кош⎜─⎟⎟⋅ℯ + 4⋅кош ⎜─⎟ - 1⎥⎥ ⎢⎢ ⎝ ⎝3⎠⎠ ⎝3⎠ ⎥⎥ ⎢⎢───────────────────────────────────────── ⎢⎢ ⎛ 2⎛q⎞ ⎞ ⎛q⎞ ⎥⎥ ⎢⎢ 2⋅⎜4⋅кош ⎜─⎟ - 1⎟⋅кош⎜─⎟ ⎥⎥ ⎢⎢ ⎝ ⎝3⎠ ⎠ ⎝3⎠ ⎥⎥ ⎢⎢ ⎥⎥ ⎢⎢ ⎛ q ⎛q⎞⎞ ⎥⎥ ⎢⎢ -⎜- ℯ - 2⋅кош⎜─⎟⎟ ⎥⎥ ⎢⎢ ⎝ ⎝3⎠⎠ ⎥⎥ ⎢⎢ ──────────────────── ⎥⎥ ⎢⎢ 2⎛q⎞ ⎥⎥ ⎢⎢ 4⋅кош ⎜─⎟ - 1 ⎥⎥ ⎢⎢ ⎝3⎠ ⎥⎥ ⎢⎢ ⎥⎥ ⎣⎣ 1 ⎦⎦Вы можете ясно видеть, что
nullspaceвозвращает правильный результат после введения альтернативный нулевой тест.
Обратите внимание, что этот подход действителен только для некоторых ограниченных случаев матриц содержит только числовые, гиперболические и экспоненциальные числа. Для других матриц следует использовать другой метод, выбранный для их доменов.
Возможные предложения: либо воспользоваться переписыванием, либо упрощение, с компромиссом скорости [4] , или с использованием случайного числового тестирования с компромиссом точности [5] .
Если вам интересно, почему не существует универсального алгоритма нулевого тестирования, который мог бы работать с любыми символическими объектами, это из-за постоянной проблемы, утверждающей, что нулевое тестирование неразрешимо [6] , и не только SymPy, но и другие системы компьютерной алгебры [7] [8] столкнется с той же фундаментальной проблемой.
Однако обнаружение любых сбоев при нулевом тесте может дать несколько хороших примеров для улучшить SymPy, поэтому, если вы столкнулись с ним, вы можете сообщить о проблеме Трекер проблем SymPy [9], чтобы получить подробную помощь от сообщества.


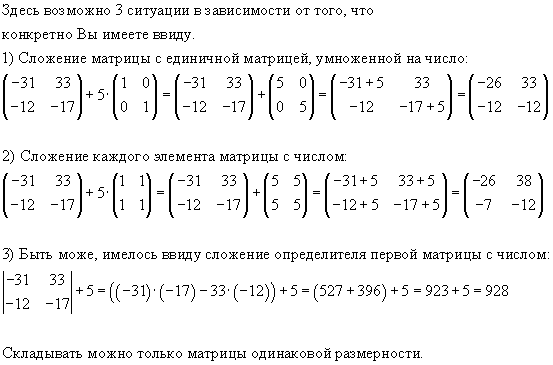 получим сумму соответствующих элементов в следующем сложении матриц:
получим сумму соответствующих элементов в следующем сложении матриц: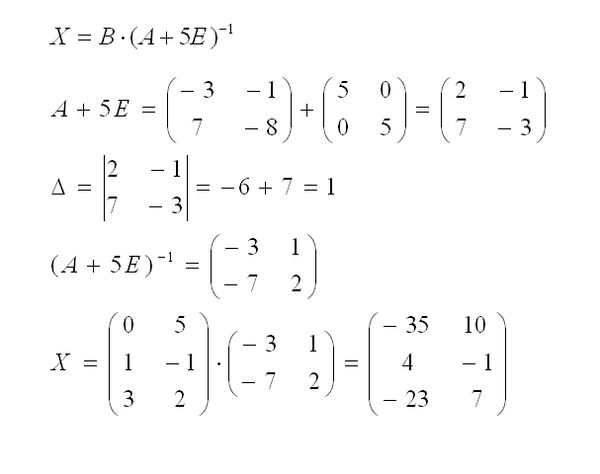 Точно так же количество столбцов в первой матрице должно быть равно количеству столбцов во второй матрице.
Точно так же количество столбцов в первой матрице должно быть равно количеству столбцов во второй матрице. Мы показываем эти элементы одним цветом, чтобы сделать их кристально четкими.
Мы показываем эти элементы одним цветом, чтобы сделать их кристально четкими.

 Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — это неделя №1 , а матрица справа — это неделя №2.
Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — это неделя №1 , а матрица справа — это неделя №2.  Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1, матрица справа — неделя №2.
Приведенные ниже матрицы представляют собой количество рубашек и брюк, которые вы продали за две недели. Матрица слева — неделя №1, матрица справа — неделя №2. Проверьте, насколько хорошо вы поняли этот урок.
Проверьте, насколько хорошо вы поняли этот урок.
 Для
например,
Для
например, 




 as_expr())
2
(λ - 5) ⋅ (λ - 3) ⋅ (λ + 2)
as_expr())
2
(λ - 5) ⋅ (λ - 3) ⋅ (λ + 2)

 возможно, это означает, что следует ввести более сильный нулевой тест.
Для этого конкретного примера переписывание в экспоненты и применение упрощения будет
усилить нулевой тест для гипербол,
будучи безвредным для других многочленов или трансцендентных функций.
возможно, это означает, что следует ввести более сильный нулевой тест.
Для этого конкретного примера переписывание в экспоненты и применение упрощения будет
усилить нулевой тест для гипербол,
будучи безвредным для других многочленов или трансцендентных функций.
