Как косинус перевести в тангенс: Найти тангенс фи, если известен косинус фи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )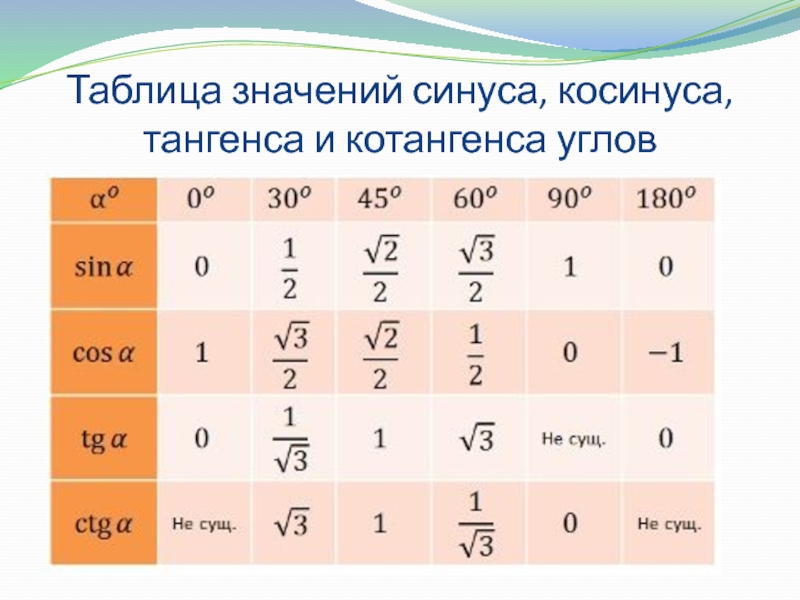
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значение sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значение
arcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Тригонометрические функции комплексного числа

  • Полином Чебышева с свободным членом
  • Создать вектор(диофант) по матрице
  • Египетские дроби. Часть вторая
  • Египетские (аликвотные) дроби
  • По сегменту определить радиус окружности
  • Круг и площадь, отсекаемая перпендикулярами
  • Деление треугольника на равные площади параллельными
  • Определение основных параметров целого числа
  • Свойства обратных тригонометрических функций
  • Разделить шар на равные объемы параллельными плоскостями
  • Взаимосвязь между организмами с различными типами обмена веществ
  • Аутотрофные и миксотрофные организмы
  • Рассечение круга прямыми на равные площади
  • Период нечетной дроби онлайн. Первые полторы тысяч разложений.
  • Представить дробь, как сумму её множителей
  • Решение системы из двух однородных диофантовых уравнений
  • Расчет основных параметров четырехполюсника
  • Цепочка остатков от деления в кольце целого числа
  • Система счисления на базе ряда Фибоначчи онлайн
  • Уравнение пятой степени. Частное решение.
  • Рассчитать площадь треугольника по трем сторонам онлайн
  • Общее решение линейного диофантового неоднородного уравнения
  • Частное решение диофантового уравнения с несколькими неизвестными
  • Онлайн разложение дробно рациональной функции
  • Корни характеристического уравнения
Расчетное комплексное число(радианы или градусы)
Точность вычисления от 1 до 14
Синус числа
Косинус числа
Тангенс числа
Котангенс числа
Если исходное число было в градусах, то
Синус числа (если заданное число было в градусах)
Косинус числа (если заданное число было в градусах)
Тангенс числа (если заданное число было в градусах)
Котангенс числа (если заданное число было в градусах)

В статье рассматривается  способы расчета и выдача значений  основных тригонометрических функций 

Синус комплексного числа

Если представить  комплексное число  как \(z=x+iy\)

То синус числа, выраженный через гиперболические функции

\(sin(z)=sin(x)ch(y)+icos(x)sh(y)\)

Косинус комплексного числа

Если представить \(z=x+iy\)

То косинус числа, выраженный через гиперболические функции

\(cos(z)=cos(x)ch(y)-isin(x)sh(y)\)

Введите в поле  число, комплексное или вещественное и  программа выдаст результат

Тангенс комплексного числа

Если представить  \(z=x+iy\)

То тангенс числа, выраженный через синус и косинус

\(\operatorname{tg}z{}=\cfrac{sin(z)}{cos(x)}\)

или  

\(\operatorname{tg}\,z{}=\cfrac{sin(2x)}{cos(2x)+ch(2y)}+i\cfrac{sh(2y)}{cos(2x)+ch(2y)}\)

Котангенс комплексного числа

Котангенс комплексного числа также  легко решается

\(\operatorname{ctg}\,z{}=\cfrac{cos(z)}{sin(x)}\)

 

 

  • Тригонометрическое уравнение как многочлен >>
Поиск по сайту
  • Русский и английский алфавит в одну строку
  • Часовая и минутная стрелка онлайн. Угол между ними.
  • Массовая доля химического вещества онлайн
  • Декoдировать текст \u0xxx онлайн
  • Универсальный калькулятор комплексных чисел онлайн
  • Перемешать буквы в тексте онлайн
  • Частотный анализ текста онлайн
  • Поворот точек на произвольный угол онлайн
  • Обратный и дополнительный код числа онлайн
  • Площадь многоугольника по координатам онлайн
  • Остаток числа в степени по модулю
  • Расчет пропорций и соотношений
  • Как перевести градусы в минуты и секунды
  • Расчет процентов онлайн
  • Растворимость металлов в различных жидкостях
  • Поиск объекта по географическим координатам
  • DameWare Mini Control. Настройка.
  • Время восхода и захода Солнца и Луны для местности
  • Калькулятор географических координат
  • Расчет значения функции Эйлера
  • Теория графов. Матрица смежности онлайн
  • Перевод числа в код Грея и обратно
  • Произвольный треугольник по заданным параметрам
  • НОД двух многочленов. Greatest Common Factor (GCF)
  • Географические координаты любых городов мира
  • Площадь пересечения окружностей на плоскости
  • Непрерывные, цепные дроби онлайн
  • Сообщество животных. Кто как называется?
  • Онлайн определение эквивалентного сопротивления
  • Проекция точки на плоскость онлайн
  • Из показательной в алгебраическую. Подробно
  • Калькулятор онлайн расчета количества рабочих дней
  • Система комплексных линейных уравнений
  • Расчет заряда и разряда конденсатора через сопротивление
  • Расчет понижающего конденсатора
  • Месторождения золота и его спутники
  • Определение формулы касательной к окружности
  • Построить ненаправленный граф по матрице
  • Дата выхода на работу из отпуска, декрета онлайн
  • Каноническое уравнение гиперболы по двум точкам
Онлайн расчеты
Подписаться письмом
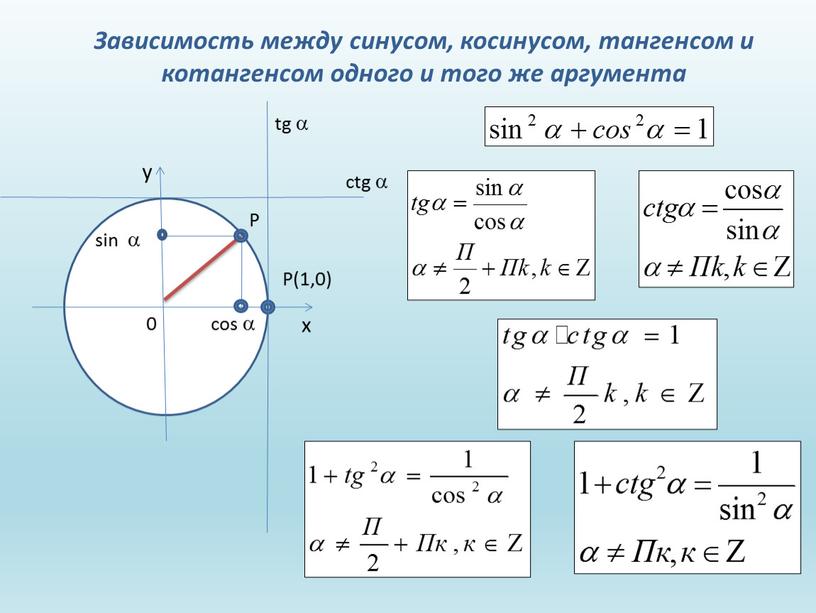
2} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}$ по теореме Пифагора. Таким образом, известное правило SOH-CAH-TOA дает:

$$\sin(\frac{\pi}{6}) = \cos(\frac{\pi}{3}) = \frac{1/2 {1} = \frac{1}{2}$$ $ $ \ sin (\ frac {\ pi} {3}) = \ cos (\ frac {\ pi} {6}) = \ frac {\ sqrt {3}/2} {1} = \ frac {\ sqrt {3}}{2}$$ $$\tan(\frac{\pi}{6}) = \cot(\frac{\pi}{3}) = \frac{\sqrt{3}/2}{1/2} = \sqrt{ 3}$$ $$\tan(\frac{\pi}{3}) = \cot(\frac{\pi}{6}) = \frac{1/2}{\sqrt{3}/2} = \frac{ 1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$$

Если известны точные значения $\sin$ и $\cos$ для двух углов $\alpha$ и $\ beta$, вы можете вычислить их как сумму и разность этих углов, используя тождества: 92(\frac{\theta}{2}) = 1$, получаем систему квадратных уравнений с решениями:

$$\sin(\frac{\theta}{2}) = \pm \sqrt{ \frac{1 — \cos(\theta)}{2}}$$ $$\cos(\frac{\theta}{2}) = \pm \sqrt{\frac{1 + \cos(\theta)}{2}}$$

Где выбор знаков зависит от того, какой квадрант угол равен дюймам.

Из этих тождеств мы можем разделить пополам любой угол с известным косинусом. Например, начиная с $\cos(\frac{\pi}{2}) = 0$, мы имеем

$$\sin(\frac{\pi}{4}) = \sqrt{\frac{1 — 0}{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$$ $ $ \ cos (\ frac {\ pi} {4}) = \ sqrt {\ frac {1 + 0} {2}} = \ frac {1} {\ sqrt {2}} = \ frac {\ sqrt { 2}}{2}$$

Вероятно, вы уже знаете $\frac{\pi}{4}$ как «особый» угол равнобедренного прямоугольного треугольника. Но мы можем сделать еще одну итерацию, чтобы получить $\frac{\pi}{8}$.

$$\sin(\frac{\pi}{8}) = \sqrt{\frac{1 — \frac{\sqrt{2}}{2}}{2}} = \frac{\sqrt{ 2 — \sqrt{2}}}{2}$$ $ $ \ cos (\ frac {\ pi} {8}) = \ sqrt {\ frac {1 + \ frac {\ sqrt {2}} {2}} {2}} = \ frac {\ sqrt {2 + \sqrt{2}}}{2}$$

Для другого примера, учитывая $\cos(\frac{\pi}{6}) = \frac{\sqrt{3}}{2}$ из вашего вопрос, мы можем найти:

92{\theta} — 1}} \right)$$

Или, используя тождество Пифагора,

$$\sin({\frac{\theta}{3}}) = \frac{1}{2 } \left( \sqrt[3]{-\sin(\theta) + i\cos(\theta)} + \sqrt[3]{-\sin(\theta) — i\cos(\theta)} \ правильно)$$ $$\cos(\frac{\theta}{3}) = \frac{1}{2} \left(\sqrt[3]{\cos(\theta) + i \sin(\theta)} + \ sqrt[3]{\cos(\theta) — i \sin(\theta)} \right)$$

Да, там есть $i$, но поскольку мы добавляем два сопряженных термина, они отменить и дать реальный номер.

Обратите внимание, что поскольку в этих формулах используются кубические корни, а не только квадратные, $\sin(\frac{\theta}{3})$ и $\cos(\frac{\theta}{3})$ не являются, в общие, конструктивные числа. Таким образом, в классической геометрии, с ее упором на циркуль и линейку, невозможно разделить произвольный угол на три части.

Четвертование угла

Просто дважды разделите его пополам.

Но для дробей со старшим знаменателем

В общем случае, чтобы найти $\sin(\frac{\theta}{n})$ и $\cos(\frac{\theta}{n})$, где $n $ — простое число, вам нужно решить полиномиальное уравнение $n$-й степени. К сожалению, общей формулы для решения многочленов степени 5 и выше не существует. И из-за этого невозможно иметь выражение в замкнутой форме для тригонометрических функций любого произвольного рационального кратного $\pi$.

Существуют, однако, некоторые особые углы, которые имеют выражения в замкнутой форме для своих триггерных функций, несмотря на то, что формулы половинного угла и третьего угла неприменимы. Например, $\frac{\pi}{5} = 36°$ обладает этим свойством

$$\sin(\frac{\pi}{5}) = \sqrt{\frac{5 — \sqrt{5 }}{8}} = \frac{\sqrt{2(5 — \sqrt{5})}}{4}$$ $$\cos(\frac{\pi}{5}) = \frac{1 + \sqrt{5}}{4}$$

И из этого факта, плюс существование решений в замкнутой форме для деления угла пополам и пополам, следует, что любое целое число градусов ($1° = \frac{\pi}{180}$) должно иметь точные выражения для его триггерные функции, хотя это может включать несколько неудобных слоев радикалов.

Учебник Excel по тригонометрии

Физика
Лаборатория		 Excel
Учебник
#6

5. Отображение символов
E
Тригонометрия 7. График
F

При решении тригонометрических выражений, таких как синус, косинус и тангенс, очень важно понимать, что Excel использует радианы, а не градусов для выполнения этих вычислений! Если угол в градусах вы должны сначала преобразовать его в радианы.

Есть два простых способа сделать это.

  1. Напомним, что p = 180°. Поэтому, если угол в градусах, умножьте его на p/180°, чтобы преобразовать его в радианы. В Excel это преобразование можно записать как PI()/180 . Для Например, чтобы преобразовать 45° в радианы, выражение Excel будет таким: 45*PI()/180, что равно 0,7854 радиана.
  2. Excel имеет встроенную функцию, известную как RADIANS(угол) где угол угол в градусах, который вы хотите преобразовать к радианам. Например, выражение Excel, используемое для преобразования 270° в радианах будет RADIANS(270), что равняется 4,712389 радианам

    Вы можете использовать функцию ГРАДУСОВ(угол) перевести радианы в градусы. Например, ГРАДУСЫ(ПИ( )) равняется 180.

Excel использует несколько встроенных триггерных функций. Те, которые вы будете использовать чаще всего отображаются в таблице ниже. Обратите внимание, что аргументы для функций SIN(), COS() и TAN() по умолчанию радиан . Кроме того, функции ASIN(), ACOS() и ATAN() возвращаемые значения в терминах радиан . (При работе со степенями вам потребуется должным образом используйте функции ГРАДУСЫ() и РАДИАНЫ() для преобразования в правильные единицы измерения.)

Математика
Выражение 		Эксель
Выражение 		Примеры Excel
синус: sin(q) SIN(номер) SIN(30) равно -0,98803, синус 30 радиан

SIN(RADIANS(30)) равно 0,5, синус 30°

косинус: cos(q) COS(номер) COS(1. 5) равно 0,07074, косинусу 1,5 радиана

COS(RADIANS(1.5)) равно 0,99966, синус 1,5°

тангенс: tan(q) ТАН(номер) TAN(2) равно -2,18504, тангенсу 2 радиана

TAN(РАДИАНЫ(2)) равно 0,03492, тангенс 2°

арксинус: sin -1 (x) ASIN(номер) ASIN(0,5) равно 0,523599 радианам

DEGREES(ASIN(0.5)) равно 30°, арксинус 0,5

arccos: cos -1 (x) ACOS(номер) ACOS(-0,5) равно 2,09440 радиан

DEGREES(ACOS(-0.5)) равен 120°, арккосинус -0.5

арктангенс: тангенс -1 (x) АТАН(номер) ATAN(1) равно 0,785398 радиан

DEGREES(ATAN(1)) равно 45°, арктангенс 1

Ниже приведены несколько примеров задач, связанных с тригонометрией, и способы их решения. мы использовали Excel, чтобы решить их.

Скажем, например, мы хотим знать высоту дерева в показанный выше рисунок. Мы знаем, что если мы стоим на расстоянии 76 м от основания дерева ( х = 76 м) линия вид на верхушку дерева составляет 32° по отношению к горизонту (q = 32°). Мы знаем это

Решение для высоты дерева, ч , находим . Снимок экрана ниже показано, как мы использовали Excel, чтобы определить, что высота дерево 47 м.

Обратите внимание на использование функции RADIANS() в пример выше.


В следующем примере мы хотим знать угол запуска, a, рампы для водных лыж, изображенной выше. Мы учитывая, что A = 3,5 м, B = 10,2 м и b = 45,0°. Чтобы найти a, мы можем использовать Закон синусов который в данном случае можно записать

Мы можем переписать это уравнение как . Использование арксинуса (обратный синус) можно найти угол a используя уравнение

Снимок экрана ниже показано, как мы использовали Excel, чтобы определить, что угол запуска угол наклона 14,04°.

Обратите внимание на использование ГРАДУСОВ() и РАДИАНОВ(). функцию в приведенном выше примере.



В нашем последнем примере тригонометрии мы будем использовать Excel для изучения триггерная личность

Обратите внимание на приведенный ниже снимок экрана, что эта идентичность верна. когда q дано в радианах и градусов .

Обратите внимание на единицы измерения угла q размещены в разных ячейках, чем числа. Если мы поместим числа и единицы в одну ячейку, Excel не сможет расшифровать число и поэтому мы не будем иметь возможность ссылаться на ячейки для использования в любом уравнении!


См.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта