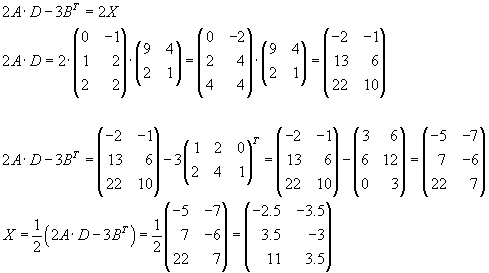Как матрицу возвести в квадрат: Возведение матрицы в степень | Мозган калькулятор онлайн

alexxlab / / Разное

Java Archives • Страница 9 из 17 • Vertex Academy

Java Java Start 

Vertex Academy задача на числа фибоначчи java,числа фибоначчи java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Выведите на экран

Больше

Java Java Start 

Vertex Academy найти минимальное число из 2 чисел java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Необходимо написать метод,

Больше

Java Java Start 

Vertex Academy возвести в степень java,как написать метод возведения в степень java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Необходимо написать метод,

Больше

Java Java Start 

Vertex Academy как проверить четное число или нет java,четное или нечетное число java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Напишите метод, который

Больше

Java Java Start 

Vertex Academy метод на true или false java,написать метод на true false java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Напишите метод, который

Больше

Java Java Start 

Vertex Academy возвести число в куб java,задача возвести число в куб java,как написать метод возведения числа в куб java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Напишите метод, с

Больше

Java Java Start 

Vertex Academy возведение в степень java,возвести в степень java,вывести квадрат числа java,задача возведение числа в степень java

Задача на написание метода возведения числа в квадрат java. Детальные пояснения. Уровень — для начинающих. Задачи по java на методы.

Больше

Java Java Start 

26 января, 2018 Vertex Academy задача на транспонирование матрицы java,как транспонировать матрицу в java,переставить столбцы в матрице java,переставить строчки в матрице java,поменять строчки и столбцы в матрице java,транспонирование матрицы java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Напишите программу Transpose.java, которая будет

Больше

Java Java Start 

Vertex Academy как определить количество строк в строке java,определить количество слов в строке java

Данная статья написана командой Vertex Academy.

Это одна из статей из нашего «Самоучителя по Java.» Напишите программу HowMany.java, которая определит,

Больше

Java Java Start 

Vertex Academy раздача карт в покере java

Данная статья написана командой Vertex Academy. Это одна из статей из нашего «Самоучителя по Java.» Условие задачи: Напишите программу Deal.java,

Больше

««<…7891011…>»»

Вычислить матрицу неточностей—Справка | ArcGIS Desktop

Доступно с лицензией Spatial Analyst.

  • Краткая информация
  • Использование
  • Синтаксис
  • Пример кода
  • Параметры среды
  • Информация о лицензиях

Краткая информация

Вычисляет матрицу неточностей на основе ошибок пропуска и невыполнения, и получает значение Каппа. Оно является показателем согласованности между классифицированной картой и базовыми данными.

Этот инструмент использует выходные данные инструмента Создать точки оценки точности или Обновить точки оценки точности.

Использование

  • Этот инструмент вычисляет матрицу несоответствий, используя произвольные точки оценки точности. Точки оценки точности создаются инструментом Создать точки оценки точности и обновляются при помощи инструмента Обновить точки оценки точности. Эти инструменты гарантируют, что каждая точка имеет корректные значения класса в полях CLASSIFIED и GROUND_TRUTH. Инструмент вычисляет точность пользователя и точность построителя для каждого класса, а также общий индекс Kappa. Диапазон точности варьируется от 0 до 1, при этом 1 означает 100% точность. Ниже приведен пример матрицы несоответствий.

    c_1

    c_2

    c_3

    Всего

    U_Accuracy

    Kappa

    c_1

    49

    4

    4

    57

    0. 8594

    0

    c_2

    2

    40

    2

    44

    0.9091

    0

    c_3

    3

    3

    59

    65

    0.9077

    0

    Всего

    54

    47

    65

    166

    0

    0

    P_Accuracy

    0. 9074

    0.8511

    0.9077

    0

    0.8916

    0

    Kappa

    0

    0

    0

    0

    0

    0.8357

    Пример матрицы несоответствий

  • Точность пользователя дает ложноположительные результаты, если пикселы ошибочно классифицируются как некий известный класс, когда их следовало классифицировать как нечто другое. Примером может служить классифицированное изображение, где пиксел указан как непроницаемый, а базовые данные указывают, что это лес. Непроницаемый класс имеет дополнительные пикселы, которые он не должен иметь в соответствии с базовыми данными.

    Точность пользователя называют также ошибками достоверности или ошибкой типа 1. Данные для расчета коэффициента ошибок считываются со строк таблицы.

    Строка Всего показывает число точек, которые согласно базовым данным должны были определиться как заданный класс.

  • Точность построителя является ложноотрицательной, когда пикселы известного класса классифицируются как нечто иное, чем этот самый класс. Примером может служить классифицированное изображение, где пиксел указан как лес, а на самом деле он должен быть непроницаемым. В этом случае, непроницаемый класс – это отсутствующие пикселы в соответствии с базовыми данными.

    Точность построителя также называют ошибками пропуска и невыполнения или ошибкой типа 2. Данные для расчета этого коэффициента ошибок считываются со столбцов таблицы.

    Столбец Всего показывает число точек, которые согласно классифицированной карте определились как заданный класс.

  • Индекс Kappa дает общую оценку точности классификации.

Синтаксис

ComputeConfusionMatrix (in_accuracy_assessment_points, out_confusion_matrix)
ПараметрОбъяснениеТип данных

in_accuracy_assessment_points

Класс объектов точек оценок точности создается инструментом Создать точки оценки точности, он содержит поля CLASSIFIED и GROUND_TRUTH.

Feature Layer

out_confusion_matrix

Имя выходного файла матрицы несоответствий в табличном формате.

Формат таблицы определяется выходным местоположением и путем к ней. По умолчанию выходными данными будет таблица базы геоданных. Если путь не в базе геоданных, укажите расширение .dbf, чтобы он был в формате dBASE.

Table

Пример кода

ComputeConfusionMatrix, пример 1 (автономный скрипт)

Пример вычисления матрицы несоответствий на основе точек оценки точности.

import arcpy
from arcpy.sa import *
arcpy.gp.ComputeConfusionMatrix("aapnt2.shp", "confm.dbf")

Параметры среды

  • Автоподтверждение
  • Текущая рабочая область
  • Выходное ключевое слово CONFIG
  • Временная рабочая область

Информация о лицензиях

  • ArcGIS Desktop Basic: Требует Spatial Analyst
  • ArcGIS Desktop Standard: Требует Spatial Analyst
  • ArcGIS Desktop Advanced: Требует Spatial Analyst

Связанные разделы

Глава 13 Свойства квадратных матриц

В этой главе вы узнаете о некоторых свойствах квадратных матриц, встречающихся в статистических и психометрических приложениях. Эти свойства также полезны для вычислений.

13.1 След матрицы

След квадратной матрицы представляет собой сумму элементов вдоль главной диагонали. 8 Например, рассмотрим матрицу Y :

\[ \underset{3\times 3}{\mathbf{Y}} = \begin{bmatrix} \цвет{красный}0 и 1 и 0 \\ 1 и \цвет{красный}3 и -8\\ 10 и 4 & \цвет{красный}{-2} \end{bmatrix} \]

След Y равен \(0 + 3 + -2 = 1\). Чтобы вычислить трассировку с помощью R, мы используем функции sum() и

diag() .

 # Создать матрицу
Y = матрица (
  данные = с (0, 1, 0, 1, 3, -8, 10, 4, -2),
  по ряду = ИСТИНА,
  nкол = 3
  )
# Вычислить трассировку Y
sum(diag(Y)) 
 [1] 1

Вы также можете использовать функцию tr() из библиотеки psych для вычисления трассировки.

 библиотека (психология)
тр(Y) 
 [1] 1

13.2 Определитель

Каждая квадратная матрица имеет связанное с ней уникальное скалярное значение, называемое определителем . Определитель, обозначаемый \(\left| \mathbf{A} \right|\) или \(\mathrm{det}(\mathbf{A})\), имеет множество применений в статистических и психометрических приложениях. Например, определитель матрицы дисперсии-ковариации предоставляет информацию о обобщенной дисперсии нескольких переменных. Это также полезно для вычисления нескольких многомерных статистических данных.

Мы проиллюстрируем процесс вычисления определителя для матрицы \(1 \times 1\), \(2 \times 2\) и \(3 \times 3\). За пределами матрицы \(3 \times 3\) определитель вычислить сложнее, и эти методы здесь обсуждаться не будут. На практике для нахождения определителя используется вычисление.

13.2.1 Определитель для матрицы \(1 \times 1\).

Определитель скалярной матрицы \(1 \times 1\) равен скаляру, а именно \(\mathrm{det}\big([a_1]\big) = a_1\). Например, рассмотрим скалярную матрицу, имеющую элемент \(-1\):

\[ \begin{vmatrix}-1\конец{vmatrix} = -1 \]

Определитель этой матрицы равен \(-1\).

13.2.2 Определитель для матрицы \(2 \times 2\).

Определитель матрицы \(2\times 2\) A , заданный как

\[ \underset{2\times 2}{\mathbf{A}} = \begin{bmatrix} а_{11} и а_{12} \\ а_{21} и а_{22} \end{bmatrix} \]

— это скаляр \(a_{11}(a_{22}) — a_{12}(a_{21})\). То есть мы берем произведение элементов по главной диагонали (показано розовым цветом ниже) и вычитаем произведение элементов по диагонали (показано синим цветом ниже).

9\mathrm{Термин~2} } \конец{разделить} \]

В качестве примера рассмотрим матрицу Y :

\[ \mathbf{Y} = \begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} \]

Определитель числа Y :

\[ \начать{разделить} \mathrm{det}(\mathbf{Y}) &= \begin{vmatrix} 1 и 2 \\ 3 и 4 \end{vmatrix} \\[2ex] &= 1(4) — 2(3) \\[2ex] &= -2 \конец{разделить} \]

13.2.3 Определитель для матрицы \(3 \times 3\).

Определитель матрицы \(3\x 3\) А , где

\[ \underset{3\times 3}{\mathbf{A}} = \begin{bmatrix} а_{11} и а_{12} и а_{13} \\ а_{21} и а_{22} и а_{23} \\ а_{31} и а_{32} и а_{33} \end{bmatrix} \]

определяется как:

\[ \начать{разделить} \mathrm{det}(\mathbf{A}) = &a_{11}(a_{22})(a_{33}) + a_{12}(a_{23})(a_{31}) + a_{13 }(а_{21})(а_{32}) -\\ &a_{13}(a_{22})(a_{31}) — a_{11}(a_{23})(a_{32}) — a_{12}(a_{21})(a_{33}) \конец{разделить} \]

Хотя это выглядит сложно, процедура его нахождения легко описана. Запишите матрицу A и дополнительно добавить первые два столбца справа от матрицы. Эти дополнительные столбцы показаны ниже красным цветом.

\[ \mathbf{A} = \begin{bmatrix} а_{11} и а_{12} и а_{13} \\ а_{21} и а_{22} и а_{23} \\ а_{31} и а_{32} и а_{33} \end{bmatrix} \color{red}{\begin{matrix}a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{ матрица}} \]

Первые три члена произведения в определителе вычисляются путем: умножения элементов, найденных на главной диагонали (первый член произведения), и элементов в оставшихся двух параллельных диагоналях (показаны розовым ниже). Точно так же второй набор из трех произведений находится путем умножения элементов на противоположной диагонали и элементов на двух параллельных диагоналях (показаны синим цветом ниже).

Рисунок 13.2: Процедура нахождения членов произведения в определителе для матрицы 3×3. Первые три члена вычисляются путем умножения элементов вдоль каждой из розовых стрелок, а второй набор из трех членов вычисляется путем умножения элементов вдоль каждой из синих стрелок.

Мы складываем первые три термина продукта и вычитаем три последних термина продукта. Это дает нам определитель.

\[ \начать{разделить} \mathrm{det}(\mathbf{A}) = ~&\color{#CC79\mathrm{Термин~3}} \color{#56B4E9}{-}\\ &\color{#56B4E9}{\underbrace{a_{13}(a_{22})(a_{31})}_\mathrm{Term~4} — \underbrace{a_{11}(a_{23}) (a_{32})}_\mathrm{Term~5} — \underbrace{a_{12}(a_{21})(a_{33})}_\mathrm{Term~6}} \конец{разделить} \]

В качестве примера рассмотрим следующую матрицу \(3 \times 3\):

\[ \underset{3\times 3}{\mathbf{X}} = \begin{bmatrix} 3 и 5 и 0 \\ 1 и 2 и 1 \\ 3 и 6 и 4 \end{bmatrix} \]

Определитель числа X :

\[ \начать{разделить} \mathrm{det}(\mathbf{X}) &= \begin{vmatrix} 3 и 5 и 0 \\ 1 и 2 и 1 \\ 3 и 6 и 4 \end{vmatrix} \\[2ex] &= 3(2)(4) + 5(1)(3) + 0(1)(6) — 0(2)(3) — 3(1)(6) — 5(1)(4) \ \[2ex] &= 24 + 15 + 0 — 0 — 18 — 20 \\[2ex] &= 1 \конец{разделить} \]

13.2.4 Использование R для нахождения определителя

Мы можем использовать функцию det() для вычисления определителя, используя R. Ниже мы используем эту функцию для вычисления определителя для каждой из матриц, приведенных в примеры выше.

 # Создать матрицу
Y = матрица (
  данные = с (1, 2, 3, 4),
  по ряду = ИСТИНА,
  nкол = 2
)
# Найти определитель
det(Y) 
 [1] -2 
 # Создать матрицу
Х = матрица (
  данные = с (3, 5, 0, 1, 2, 1, 3, 6, 4),
  по ряду = ИСТИНА,
  nкол = 3
)
# Найти определитель
det(X) 
 [1] 1

13.2.5 Свойства определителя

У определителя есть несколько полезных свойств. Для каждого из этих свойств A и B являются матрицами, а \(\lambda\) является скаляром. 9{-1}\mathbf{A} = \mathbf{I} \]

То есть, когда мы умножаем (или предварительно умножаем) квадратную матрицу на обратную, мы получаем единичную матрицу \(n \times n\). Не все квадратные матрицы имеют обратную. Если квадратная матрица имеет обратную, мы говорим, что она обратимая или неособая .

Обычно мы используем компьютер, чтобы найти обратную матрицу. {-1}\), мы:

  • Вычислить определитель числа A .
  • Создайте новую матрицу, назовите ее B , где мы поменяем местами элементы на главной диагонали A и поменяем знаки на элементах вне диагоналей.
  • Умножьте B на обратную величину определителя.

В качестве примера рассмотрим следующую матрицу \(2 \times 2\):

\[ \mathbf{A} = \begin{bmatrix} 2 и 1 \\ 1 и 3 \end{bmatrix} \]

Определитель 9{-1}\mathbf{A} &= \begin{bmatrix} \frac{3}{5} & -\frac{1}{5} \\ -\frac{1}{5} и \frac{2}{5} \end{bmatrix}\begin{bmatrix} 2 и 1 \\ 1 и 3 \end{bmatrix} \\[2ex] &= \begin{bmatrix} 1 и 0 \\ 0 и 1 \end{bmatrix} \конец{разделить} \]

13.3.1 Нахождение обратного с помощью R

Чтобы найти обратное с помощью R, мы можем использовать функцию solve() . Если вам нужны дробные элементы (а не десятичные элементы), вы можете использовать функцию Fractions() из {MASS} пакет для преобразования десятичного вывода в дроби.

 # Создать матрицу
А = матрица (
  данные = с (2, 1, 1, 3),
  по ряду = ИСТИНА,
  nкол = 2
)
# Найти инверсию
решить(А) 
 [1] [2]
[1,] 0,6 -0,2
[2,] -0.2 0.4 
 # Найти обратное (вывести в виде дробей)
MASS::fractions(solve(A)) 
 [1] [2]
[1,] 3/5 -1/5
[2,] -1/5 2/5

Если вы получаете сообщение о том, что система «точно сингулярна» или «вычислительно сингулярна», матрица не имеет обратной (или не может быть вычислена). В этом случае мы бы сказали, что 9{-1}\) обратны диагональным элементам D .

  • Обратная неособая симметричная матрица также является симметричной матрицей.

    • 13.4 Упражнения

    Для каждой из следующих матриц вычислите (вручную) след, определитель и обратную. Затем используйте R, чтобы проверить свою работу.

    1. \(\mathbf{A} = \begin{bmatrix}2 и 4 \\3 и 6 \end{bmatrix}\)
    1. \(\mathbf{B} = \begin{bmatrix}2 & -1 \\3 & 3 \end{bmatrix}\)

    Для каждой из следующих матриц вычислите (вручную) трассу и определитель. Затем используйте R, чтобы проверить свою работу. Также используйте R, чтобы найти обратное.

    1. \(\mathbf{C} = \begin{bmatrix}2 & -1 & 3 \\3 & 3 & 4\\1 & 2 & 2 \end{bmatrix}\)
    1. \(\mathbf{D} = \begin{bmatrix}2 & -1 & 3 \\3 & 3 & 4\\5 & 2 & 7 \end{bmatrix}\)

    1. Поскольку прямоугольные матрицы также имеют главную диагональ, мы также можем вычислить след прямоугольной матрицы. Однако в статистических и психометрических приложениях (например, при анализе основных компонентов) трассировка в основном вычисляется на квадратных матрицах.↩︎

    линейная алгебра — Какой самый быстрый способ взять степени квадратной матрицы?

    спросил

    Изменено 1 месяц назад

    Просмотрено 13 тысяч раз

    $\begingroup$

    Итак, я знаю, что вы можете использовать алгоритм Штрассена для умножения двух матриц за семь операций, но как насчет умножения двух абсолютно одинаковых матриц. Есть ли более быстрый способ сделать это (например, уменьшив количество умножений на итерацию до чего-то меньшего, чем 7)? 92 = \begin{pmatrix} 0 & 0 & AB \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}.$$ Таким образом, возведение матрицы в квадрат асимптотически не лучше, чем обычное произведение. Конечно, на практике разница постоянных коэффициентов очень значительна.

    Получение степени лучше всего достигается повторным возведением в квадрат. Другой метод — диагонализация, но я думаю, что обычно собственные значения находятся с помощью степенного метода, а не наоборот.

    $\endgroup$

    5 9k P,$$

    , а поскольку $B$ является диагональной матрицей, для умножения матриц требуется всего $2$ умножения. Нечто подобное можно сделать с матрицами нормальной формы Джордана. Общий метод состоит в использовании двоичного возведения в степень для уменьшения количества умножений матриц, которые необходимо выполнить, с N до $\log(N)$.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *