Все формулы объемов геометрических тел
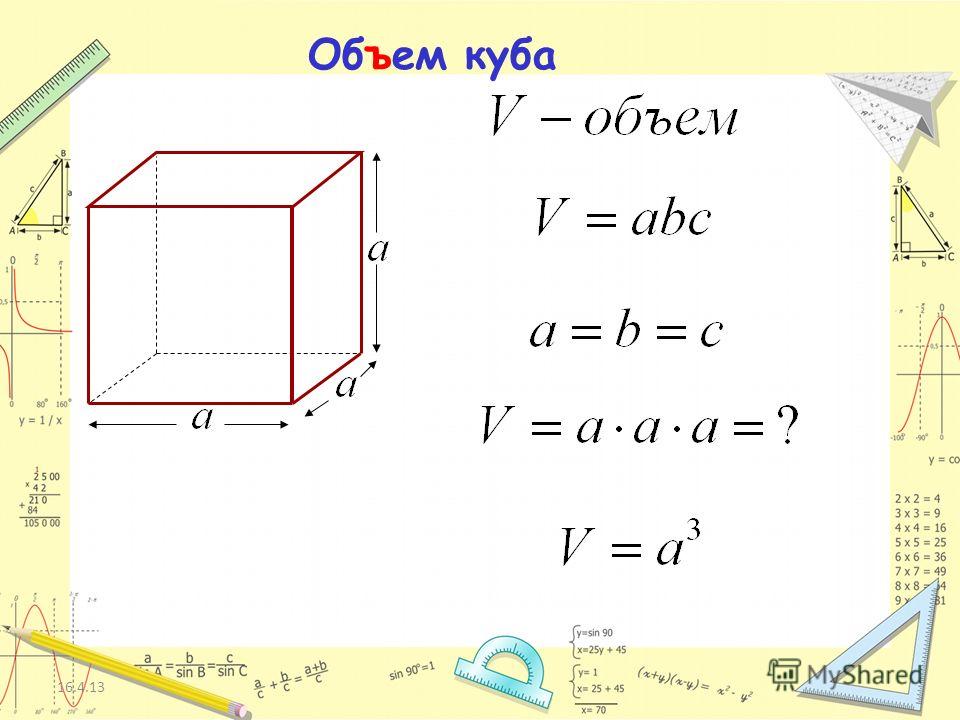
1. Расчет объема куба
a — сторона куба
Формула объема куба, (V):
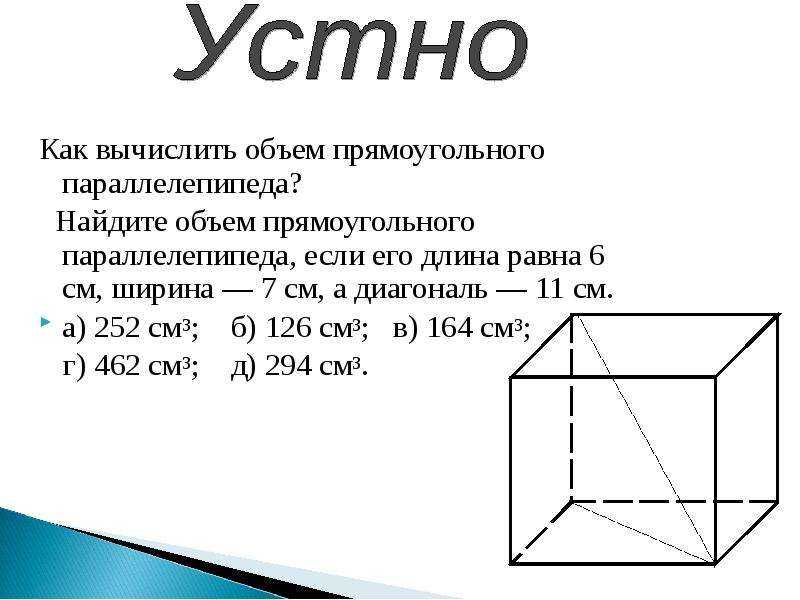
2. Найти по формуле, объем прямоугольного параллелепипеда
a, b, c — стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R — радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):
4.

h — высота цилиндра
r — радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):
5. Как найти объем конуса ?
R — радиус основания
H — высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r — радиус верхнего основания
R — радиус нижнего основания
h — высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса ( V ):
8.
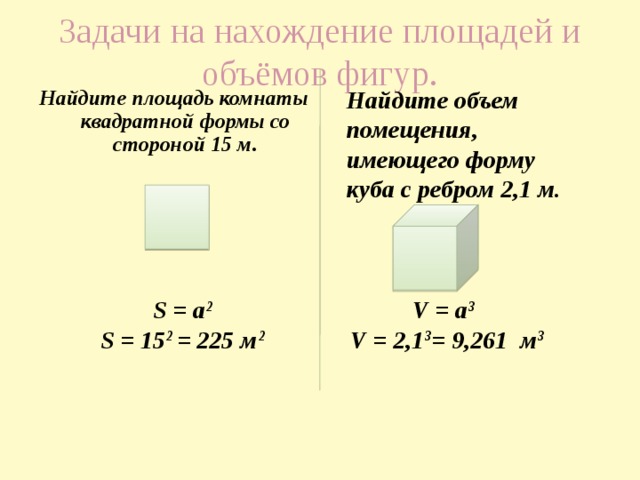 Объем правильного тетраэдра
Объем правильного тетраэдраПравильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.
а — ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a — сторона основания
h — высота пирамиды
Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h — высота пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон ( V):
12. Расчет объема пирамиды
h — высота пирамиды
S — площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны — высота и площадь основания (V):
13.
 Расчёт объёма усечённой пирамиды
Расчёт объёма усечённой пирамидыh — высота пирамиды
Sниж — площадь нижнего основания, ABCDE
Sверх — площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):
14. Объем шарового сегмента, формула
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
R — радиус шара
h — высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
15. Объем шарового сектора
R — радиус шара
h — высота сегмента
π ≈ 3.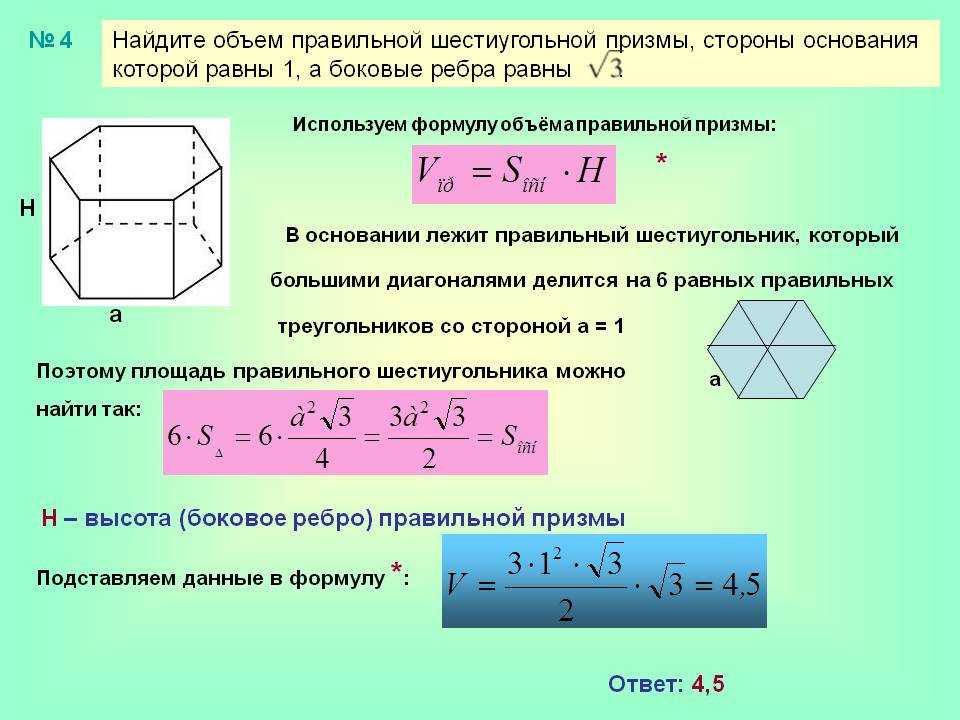 14
14
Формула объема шарового сектора, (V):
16. Объем шарового слоя
h — высота шарового слоя
R
— радиус нижнего основанияr — радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
Как найти объем чисел. Объем
Для того чтобы определить плотность вещества, надо массу тела разделить на его объем:
Массу тела можно определить с помощью весов. А как найти объем тела?
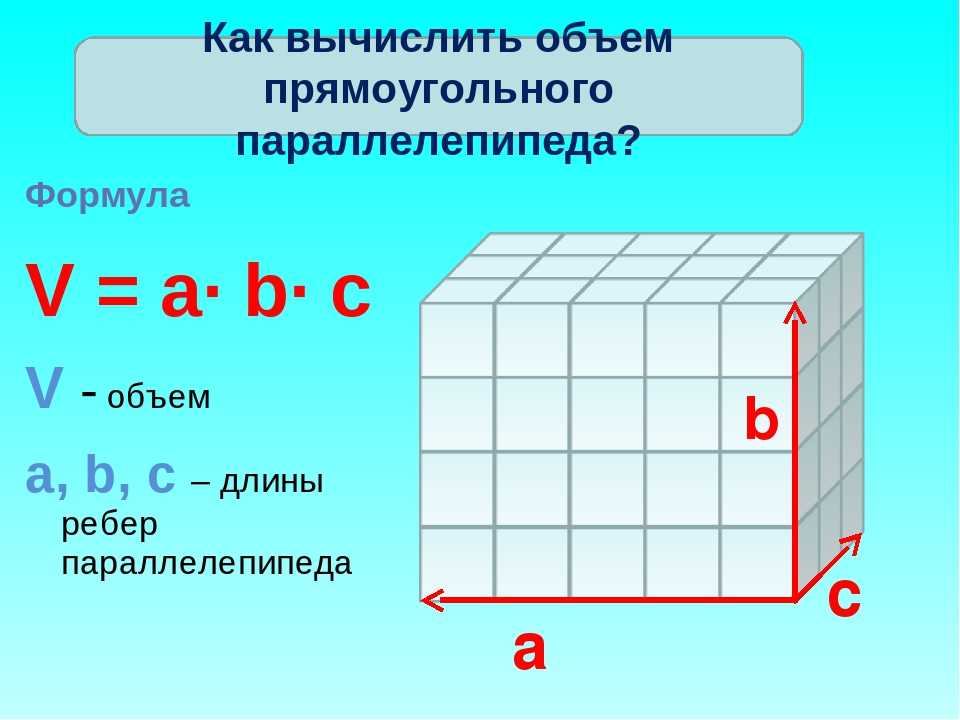
Если тело имеет форму прямоугольного параллелепипеда (рис. 24), то его объем находится по формуле
V = аbс .
Если же у него какая-то другая форма, то его объем можно найти методом, который был открыт древнегреческим ученым Архимедом в III в. до н. э.
Архимед родился в Сиракузах на острове Сицилия. Его отец, астроном Фидий, был родственником Гиерона, ставшего в 270 г. до н. э. царем города, в котором они жили.
до н. э. царем города, в котором они жили.
До нас дошли не все сочинения Архимеда. О многих его открытиях стало известно благодаря более поздним авторам, в сохранившихся трудах которых описываются его изобретения. Так, например, римский архитектор Витрувий (I в. до н. э.) в одном из своих сочинений рассказал следующую историю:
После этого был сделан донос, что из короны была взята часть золота и вместо него примешано такое же количество серебра.
Затем, пишет Витрувий, Архимед взял сосуд, доверху наполненный водой, и опустил в него золотой слиток, равный по весу короне. Измерив объем вытесненной воды, он снова наполнил сосуд водой и опустил в него корону. Объем воды, вытесненной короной, оказался больше объема воды, вытесненной золотым слитком. Больший объем короны означал, что в ней присутствует менее плотное, чем золото, вещество. Поэтому опыт, проделанный Архимедом, показал, что часть золота была похищена.
Итак, для определения объема тела, имеющего неправильную форму, достаточно измерить объем воды, вытесняемой данным телом. Располагая измерительным цилиндром (мензуркой), это сделать несложно.
В тех случаях, когда известны масса и плотность тела, его объем можно найти по формуле, вытекающей из формулы (10.1):
Отсюда видно, что для определения объема тела надо массу этого тела разделить на его плотность .
Если, наоборот, объем тела известен, то, зная, из какого вещества оно состоит, можно найти его массу:
m = ρV . (10.3)
Чтобы определить массу тела, надо плотность тела умножить на его объем.
1. Какие способы определения объема вы знаете? 2. Что вам известно об Архимеде? 3. Как можно найти массу тела по его плотности и объему?
Содержимое:
Объем – это количество занимаемого телом пространства, а плотность равна массе тела, поделенной на его объем. Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см 3) или кубических метрах (м 3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см 3) или граммы на миллилитр (г/мл).
Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см 3) или кубических метрах (м 3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см 3) или граммы на миллилитр (г/мл).
Шаги
Часть 1 Вычисление объема тела правильной формы
- 1 Определите форму тела. Знание формы позволит вам выбрать правильную формулу и провести измерения, необходимые для расчета объема.
- Сфера представляет собой идеально круглый трехмерный объект, все точки поверхности которого отстоят на равном расстоянии от центра. Иными словами, сферическое тело похоже на круглый мяч.
- Конус – это трехмерная фигура, в основании которой лежит круг, а вершину составляет единственная точка, называемая вершиной конуса. Конус можно представить также в виде пирамиды с круглым основанием.

- Куб представляет собой трехмерную фигуру, составленную из шести одинаковых квадратных граней.
- Прямоугольный параллелепипед , называемый также прямоугольной призмой, похож на куб: он также имеет шесть граней, однако в этом случае они представляют собой прямоугольники, а не квадраты.
- Цилиндр – это трехмерная фигура, состоящая из одинаковых круглых концов, края которых соединены округлой поверхностью.
- Пирамида является трехмерной фигурой, в основании которой лежит многоугольник, который соединен с вершиной боковыми гранями. Правильной пирамидой называется такая пирамида, в основании которой лежит правильный многоугольник, все стороны и углы которого равны между собой.
- Если тело имеет неправильную форму, его объем можно найти, полностью погрузив его в воду.
- 2 Выберите для вычисления объема правильное уравнение. Для тела каждого типа существует своя формула, позволяющая рассчитать занимаемый им объем.
 Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье.
Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье.- Сфера : V = (4/3) π r 3 , где r – радиус сферы, а π – константа, равная примерно 3,14.
- Конус : V = (1/3) π r 2 h , где r – радиус круглого основания, h – высота конуса, π – константа, равная приблизительно 3,14.
- Куб : V = s 3 , где s – длина ребра куба (стороны любой из его квадратных граней).
- Прямоугольный параллелепипед : V = l x w x h , где l – длина прямоугольной грани, w – ее ширина, h – высота параллелепипеда (призмы).
- Цилиндр : V= π r 2 h , где r – радиус круглого основания, h – высота цилиндра, π – константа, составляющая примерно 3,14.
- Пирамида : V= (1/3) b x h , где b – площадь основания пирамиды (l x w), h – высота пирамиды.
- 3 Произведите необходимые измерения. Они будут зависеть от того, с телом какого вида вы имеете дело.
 Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.
Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.- Радиус круга равен половине его диаметра. Измерьте диаметр, приложив к середине круга линейку, после чего поделите полученный результат на 2.
- Радиус сферы измерить немного сложнее, однако и это не составит труда, если вы воспользуетесь методами, подробно изложенными в статье.
- Длину, ширину и высоту тела можно определить, приложив к нему линейку в соответствующих местах и записав результаты измерений.
- 4 Вычислите объем. Выяснив форму тела, выберите подходящую формулу и измерьте входящие в нее величины. Подставьте в формулу измеренные значения и выполните необходимые математические действия. В результате вы получите объем тела.
- Помните о том, что ответ должен выражаться в кубических единицах независимо от того, какой системой единиц вы пользуетесь (метрической либо другой).
 После полученной величины обязательно напишите единицы, в которых она измеряется.
После полученной величины обязательно напишите единицы, в которых она измеряется.
- Помните о том, что ответ должен выражаться в кубических единицах независимо от того, какой системой единиц вы пользуетесь (метрической либо другой).
Часть 2 Вычисление объема тела неправильной формы
- 1 Определите объем тела по количеству вытесняемой им воды. Тело может иметь неправильную форму, что затрудняет измерение его размеров и ведет к неточному определению объема. В этом случае прекрасно работает метод, заключающийся в определении объема воды, вытесняемой телом при полном погружении.
- Данный метод можно применить и для нахождения объема тел правильной формы, чтобы избежать вычислений.
- 2 Наполните водой мерный цилиндр (мензурку). Это лабораторная емкость с метками на боковой поверхности, позволяющая измерять объем жидкостей. Выберите достаточно большой цилиндр, чтобы в него полностью поместился измеряемый объект. Необходимо наполнить цилиндр водой так, чтобы в нее можно было полностью погрузить объект, но при этом она не выливалась. Запишите начальный объем воды без измеряемого тела.

- Наблюдая первоначальный объем воды, наклонитесь так, чтобы ваши глаза находились на одном уровне с поверхностью жидкости, после чего запишите высоту, на которой расположено дно мениска. Мениск – это внешняя поверхность воды, которая искривляется при контакте с другими поверхностями (в нашем случае это стенки сосуда).
- 3 Аккуратно поместите в емкость измеряемое тело. Делайте это плавно, чтобы не уронить объект, поскольку в этом случае часть воды может выплеснуться из мерного цилиндра. Убедитесь в том, что тело полностью погрузилось в воду. Запишите новые показания уровня воды в емкости, вновь расположившись так, чтобы ваши глаза находились на одном уровне с мениском.
- Если при погружении тела часть воды выплеснулась, попробуйте повторить с самого начала, налив меньше воды или взяв больший мерный цилиндр.
- 4 Вычтите из окончательного уровня воды его первоначальное значение. Количество вытесненной предметом воды будет равняться его объему в кубических сантиметрах.
 Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.
Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.- Например, если сначала уровень воды был 35 мл, а после опускания в нее предмета поднялся до 65 мл, объем этого предмета составляет 65 – 35 = 30 мл, или 30 см 3 .
Часть 3 Вычисление плотности
- 1 Определите массу предмета. Масса объекта соответствует количеству материи, из которой он состоит. Массу находят путем прямого взвешивания на весах, она измеряется в граммах или килограммах.
- Возьмите точные измерительные весы и поместите на них предмет. Запишите показания весов в свой блокнот.
- Массу тела можно определить и при помощи чашечных весов. Положив объект на одну чашу, на вторую поместите гирьки с известными массами так, чтобы обе чаши уравновесили друг друга, расположившись на одинаковой высоте. В этом случае искомая масса предмета будет равна сумме масс использованных гирек.
- Перед взвешиванием проследите, чтобы предмет не был влажным, иначе погрешность измерений возрастет.

- 2 Определите объем тела. Если предмет имеет правильную форму, для определения его объема используйте одну из формул, приведенных выше. Если форма тела неправильна, измерьте объем, погрузив его в воду, как описано выше.
- 3 Вычислите плотность. Согласно определению, плотность равна массе, деленной на объем. Таким образом, поделите измеренную массу на вычисленный объем. В результате вы получите плотность тела, измеренную в г/см 3 .
- Например, вычислим плотность предмета объемом 8 см 3 и массой 24 г.
- плотность = масса / объем
- d = 24 г / 8 см 3
- d = 3 г/см 3
- Нередко предметы состоят из нескольких частей, имеющих правильные геометрические формы. В этом случае разделите составляющие элементы на группы, относящиеся к той или иной правильной форме, найдите объем каждого элемента, а затем сложите их вместе, определив тем самым общий объем всего предмета.
- Можно определить объем какого-либо предмета как путем вычислений, так и погружением в воду, после чего сравнить полученные результаты.

Предупреждения
- Будьте внимательны: прежде чем приступать к вычислениям, обязательно переведите все измеренные величины в метрическую систему (систему единиц СИ).
Количество коробок
Результат:
Объем одной коробки(м 3):
Общий объем(м 3):
Используйте полученный
результат для
оформления заявки
| d= | м см | |
| h= | м см |
Количество труб
Результат:
Объем одной трубы(м 3):
Общий объем(м 3):
Используйте полученный
результат для
оформления заявки
У вас возник вопрос о доставке , а так же возникла необходимость знать, как вычислить объем груза, нужна наша помощь? Как вычислить объем груза мы знаем, на этой странице вы видите калькулятор, который точно выполнит расчеты.
А вообще, для какой цели рассчитывается объем?
Объем рассчитать необходимо для того, чтобы избежать недоразумений при погрузке груженых коробок в транспортное средство. Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.
Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.
Во-первых , все знают — в процессе доставки важна каждая деталь, и немаловажно без ошибок посчитать объем груза в целом. Посчитать объем груза как уже говорилось поможет наш калькулятор объемов, он сделает это быстро и надежно!
Второе — калькулятор объемов, о его начини на нашем сайте, уже сказано выше, как видите, мы заботимся о наших клиентах. Калькулятор объемов, вот что может максимально облегчить работу с расчетами, и напрочь убить ваши сомнения.
Что мы вам даём?
Что же еще необходимо?
Например…
Вы предприниматель, который занимается перевозками из Китая, и Вам постоянно необходим калькулятор расчета объема. Калькулятор расчета объемов вы быстро найдёте на страницах нашего сайта, и выполните свои расчеты сейчас же.
В наше время предпринимательство держится на Китайском производстве товаров, а от куда возникла потребность рассчитать объем? Рассчитать объем необходимо для того что бы узнать общий объём груза, и далее выбрать вид транспорта.
Чем же является расчет объемов в доставке? И какую роль он играет?
Расчёт объема — это насколько, вы уже поняли очень важный этап в доставке, и доверять его надо в надёжные руки профессионалов. Расчёт объема груза надо делать тщательно, учитывая все размеры, и переведя их в метры кубические.
Но к сожалению, не все справляются с этими расчетами.
Еще в школьные времена мы изучали то как посчитать объем груза в м3, но к сожалению, всего этого не запомнишь. Как посчитать объем груза в м3 — бывают случаи когда этот вопрос встаёт на первое место, например во время доставки.
Для этого данная страница и существует!
Ведь эта страница для того и предназначена, чтобы помогать Вам в расчёте доставки.
Что бы выполнить расчет объема коробки, не надо стараться это делать самостоятельно, просто надо заполнить пустые поля. Расчет объема коробки автоматически выполнится нашим калькулятором, если вы сомневаетесь, проверьте сами.
Для этого мы и напомнили Вам формулу объемов.
Расчет объема груза в кубометрах необходим Вам для того, чтобы подать правильную заявку для его перевозки. Расчет объема груза в кубометрах, т. е. знание самого объема поможет определиться с тем какой вид доставки Вам подойдет.
А теперь перейдем к основному , поговорим о том, как совершать расчеты и для чего они необходимы.
Для начала разберемся…
Рассчитать объем груза не всегда просто, как кажется, всё это из-за того что, коробки могут быть разнообразной формы. Рассчитать объем груза прямоугольной коробки, пустяк, а вот остальных тяжеловато, необходимо знать формулы.
Для начала определим форму, для этого сначала узнаем, какие они существуют.
Какую форму может иметь коробка:
- Прямоугольника;
- Цилиндра;
- Усеченной пирамиды (очень редко).
Затем следуют измерения
Перед тем, как вычислить объем коробки измерим её, но запомните, чем точнее сделаны измерения, тем легче Вам. «Как вычислить объем коробки?» — что делать дальше: определить, какой она формы (куба или прямоугольника), размеры.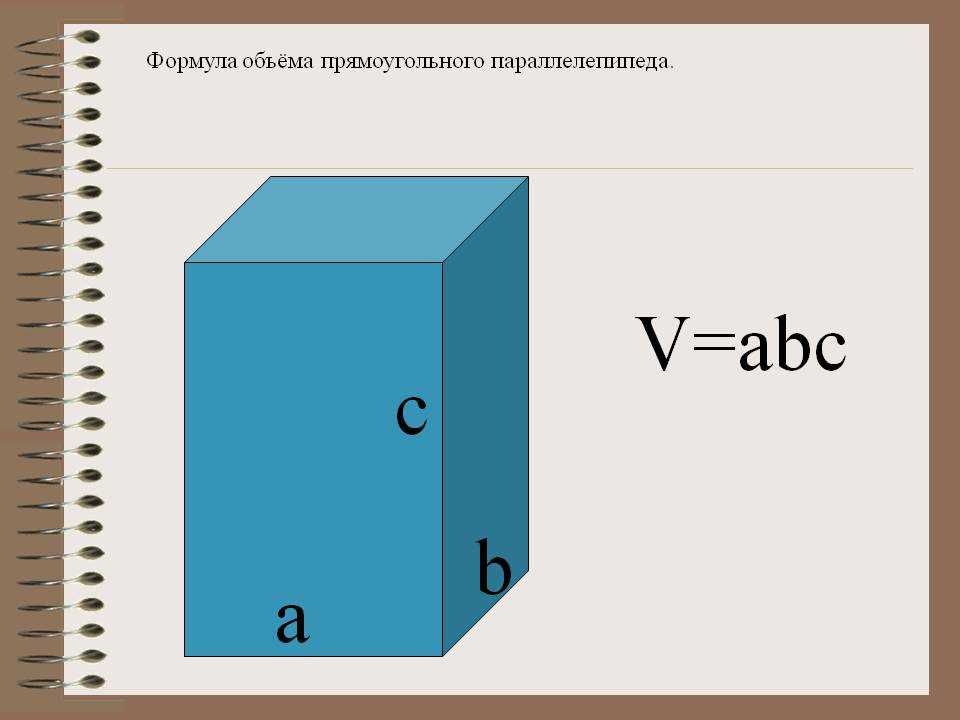
Что нам дает знание объёма?
Знание объёма коробки не позволит допустить недоразумений при погрузке товаров в любой вид транспорта, который может быть. От объёма коробки практически не чего не зависит, скорее наоборот все зависит от размеров самого товара.
А почему? Тут всё очевидно, прежде чем приобрести коробку, надо узнать размер груза, который Вы собираетесь перевозить через границу.
Ну вот Вы знаете размеры груза, теперь остаётся посчитать его объем (что бы приобрести коробу).
Итак , для того чтобы узнать, как рассчитать объем груза в м3 формула потребуется в первую же очередь. Как рассчитать объём груза в м3 формула поможет без сомнений в этом вопросе, вот так она выглядит V=a*b*h, всё очень просто.
Тем более она уже вам известна.
Хотим напомнить о том что…
Что бы Вам стало легче определить, какой вид транспорта выбрать для доставки, надо рассчитать объем груза в м3. Рассчитать объем груза в м3 очень просто, тут необходимо знать точные размеры, которые затем необходимо перемножить.
Единицы необходимо пе6реводить именно в м3, иначе не получится посчитать доставку.
А что делать, если форма коробки не прямоугольная, а округлая? Ведь это большая редкость, но все же бывает.
Можно объем посчитать коробки или ёмкости в основании которых лежит круг, и для этого так же существует формула. Объем посчитать коробки формой круга позволяет выражение V *r2*h, размеры прежде всего надо безошибочно измерить.
Калькулятор объемов
Предоставляем к вашему вниманию калькулятор: объем грузов в м3, с помощью него вы можете самостоятельно делать расчёты. Калькулятор объем грузов расположен на наем сайте специально для вашего удобства, и для быстроты расчетов.
Для чего нужен калькулятор расчета объема груза?
Мы с вами деловые люди и потерянное время порой несёт в себе большие минусы. Хотите получать грузы быстро и надёжно? И при этом в максимально короткие сроки узнавать цены на их перевозку и доставку?
Вот именно здесь, поможет калькулятор объёма груза!
Наш калькулятор объёмов позволяет вам рассчитать объём груза в м3, поэтому вопрос о объёме коробки больше не возникнет. Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза.
Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза.
Итак, с помощью калькулятора объёма Вы решаете несколько вопросов:
Как вычислить объем груза (или коробки)? Не забывайте о количественной единице, которую вы берёте в расчёт.
Столкнулись с одним из них или возник подобный? Наша компания рада предложить для Вашего удобства объем в метрах кубических коробки посчитать, с помощью удобного калькулятора.
А напоследок, давайте вспомним математику!
Какая проблема самая распространённая?
Многие путают то как вычислять объём плоских фигур и объемных, т. к., ошибаются в понятиях, точнее затрудняются с ответом. Как вычислять объём не надо знать, хватит того, что вы укажете размеры, главное не забывайте, что их 3.
Закончив все расчеты, остается еще одна задача.
А какой Вам нужен транспорт?
Напомним, в доставке кроме того, как рассчитать кубатуру есть еще не менее важные вещи, например размещение товаров.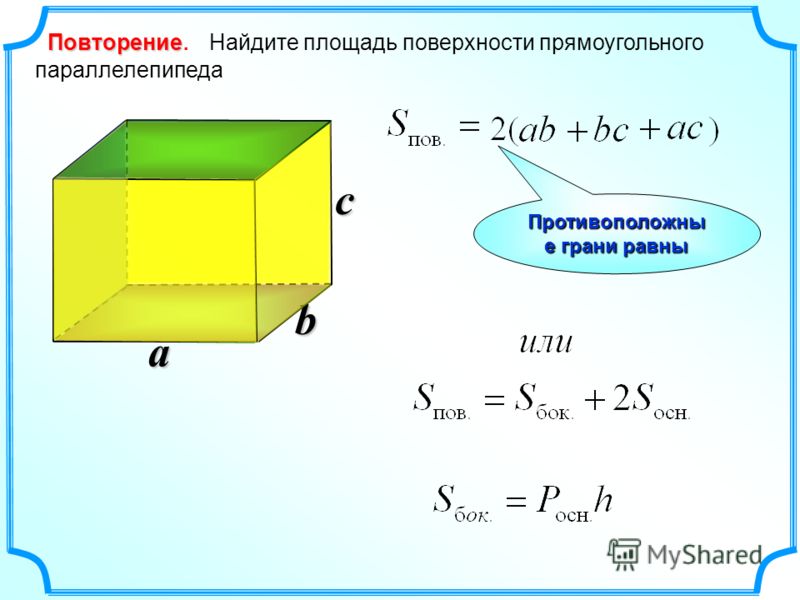 Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас.
Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас.
Химия и физика всегда подразумевают вычисление различных величин, в том числе и объём вещества. Объем вещества можно рассчитать при помощи некоторых формул. Главное знать, в каком состоянии находится данное вещество. Агрегатных состояний, в которых могут пребывать частицы, существует четыре:
- газообразное;
- жидкое;
- твёрдое;
- плазменное.
Для вычисления объёма каждого из них есть своя конкретная формула. Для того чтобы найти объем, нужно иметь определённые данные. К ним относятся масса, молярная масса, а также для газов (идеальных) — газовая постоянная.
Процесс нахождения объема вещества
Давайте рассмотрим, как найти объём вещества, если оно находится, к примеру, в газообразном состоянии. Для подсчёта нужно выяснить условия задачи: что известно, какие параметры даются. Формула, по которой можно определить, каков объём данного газа, такова:
Необходимо молярное количество имеющегося вещества (именуемого n) умножить на молярный его объём (Vm). Так можно узнать объём (V). Когда газ находится в нормальных условиях — н. у., то его Vm — объём в молях составляет 22,4 л./моль. Если в условии сказано, сколько вещества в молях имеется (n), то нужно подставить данные в формулу и выяснить конечный результат.
Так можно узнать объём (V). Когда газ находится в нормальных условиях — н. у., то его Vm — объём в молях составляет 22,4 л./моль. Если в условии сказано, сколько вещества в молях имеется (n), то нужно подставить данные в формулу и выяснить конечный результат.
Если условия не предусматривают указания данных о молярном количестве (n), его нужно выяснить. Есть формула, которая поможет сделать вычисление:
Нужно массу вещества (в граммах) разделить на его молярную массу. Теперь можно сделать вычисление и определить молярное количество. М — это константа, которую можно посмотреть в таблице Менделеева. Под каждым элементом есть число, которое обозначает его массу в молях.
Определение объема вещества в миллилитрах
Как определить объём вещества в миллилитрах? Что может быть указано в условиях задачи: масса (в граммах), консистенция в молях, количество данного вам вещества, а также его плотность. Существует такая формула, по которой можно подсчитать объём:
Масса в граммах должна быть разделена на плотность указанного вещества.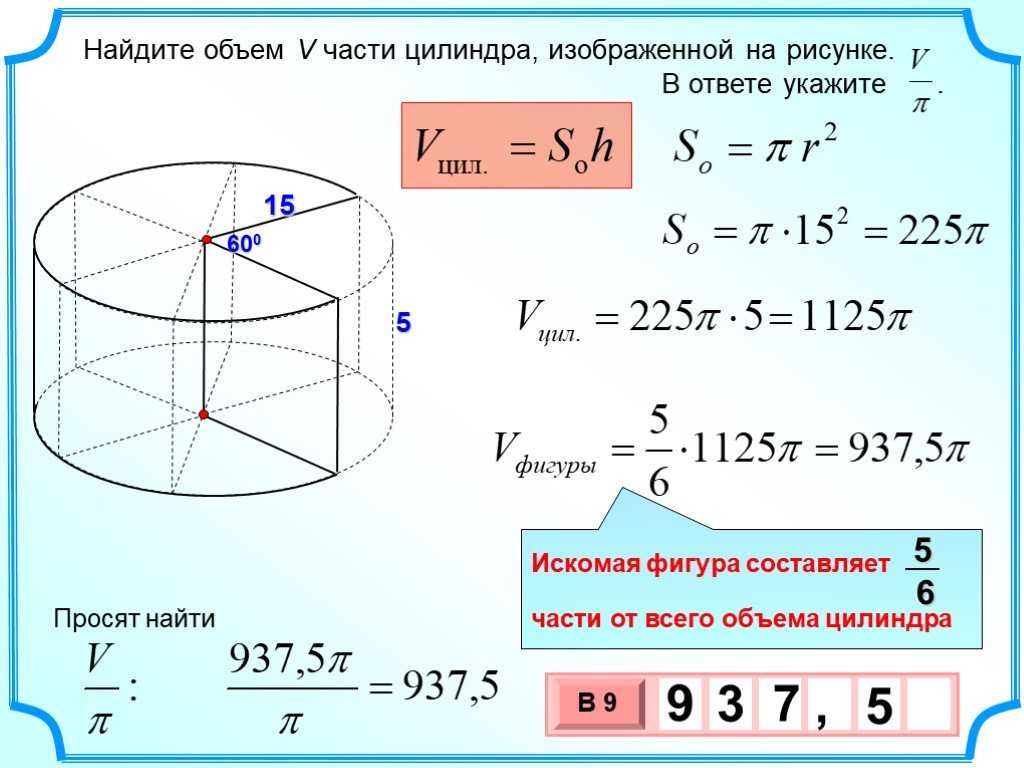
Если вам не известна масса, то её можно рассчитать так:
Молярное количество вещества нужно умножить на его молярную массу. Для того чтобы правильно подсчитать молярную массу (М), нужно знать формулу того вещества, которое даётся в условии задачи. Нужно сложить атомную массу каждого из элементов вещества. Также если нужно узнать плотность вещества, можно пользоваться такой обратной формулой:
Если вам известно молярное количество (n) и концентрация (с) вещества, можно также подсчитать объём. Формула будет выглядеть следующим образом:
Вам необходимо молярное количество данного в задаче вещества разделить на его молярную концентрацию. Отсюда можно вывести формулу для нахождения концентрации.
Чтобы правильно решать задачи по физике и химии, вам нужно знать некоторые формулы и иметь под рукой таблицу Менделеева, тогда успех вам гарантирован.
Любое геометрическое тело можно охарактеризовать площадью (S) поверхности и объемом (V). Площадь и объем совсем не одно и то же. Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Параллелепипед: определение, виды и свойства
Параллелепипед – это четырехугольная призма, в основании которой находится параллелограмм. Для чего же может потребоваться формула нахождения объема фигуры? Подобную форму имеют книги, упаковочные коробки и еще множество вещей из повседневной жизни. Комнаты в жилых и офисных домах, как правило, являются прямоугольными параллелепипедами. Для установки вентиляции, кондиционеров и определение количества обогревательных элементов в комнате необходимо рассчитать объем помещения.
У фигуры 6 граней – параллелограммов и 12 ребер, две произвольно выбранные грани называют основаниями. Параллелепипед может быть нескольких видов. Различия обусловлены углами между смежными ребрами. Формулы для нахождения V-ов различных многоугольников немного отличаются.
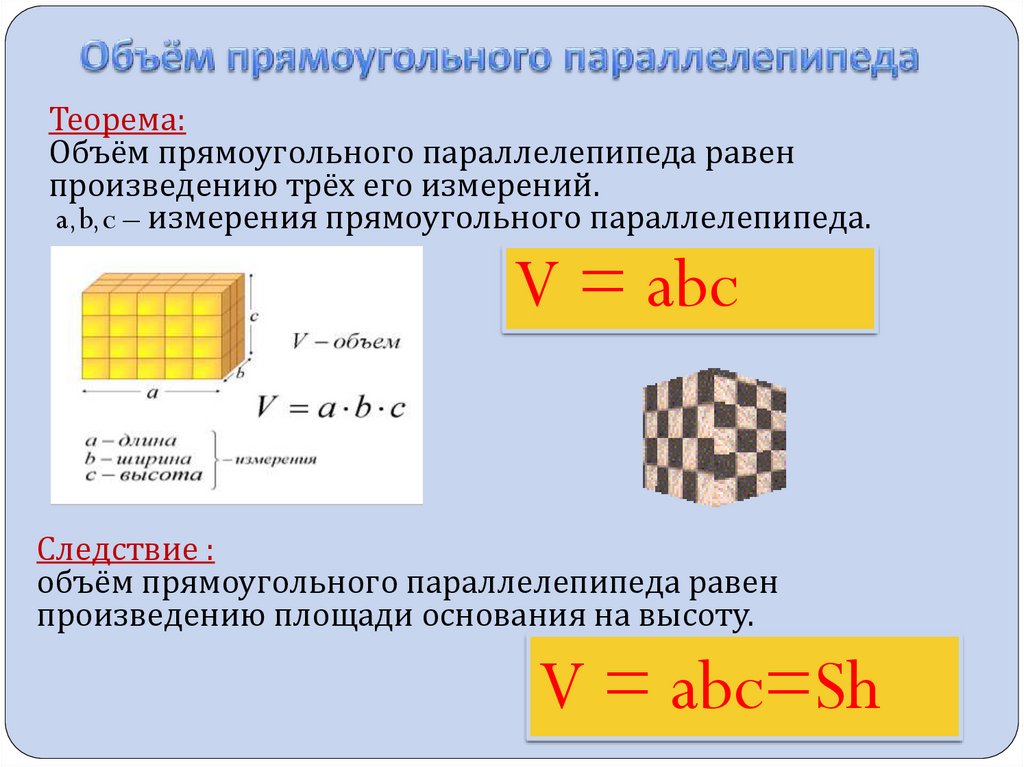
Если 6 граней геометрической фигуры представляют собой прямоугольники, то ее тоже называют прямоугольной.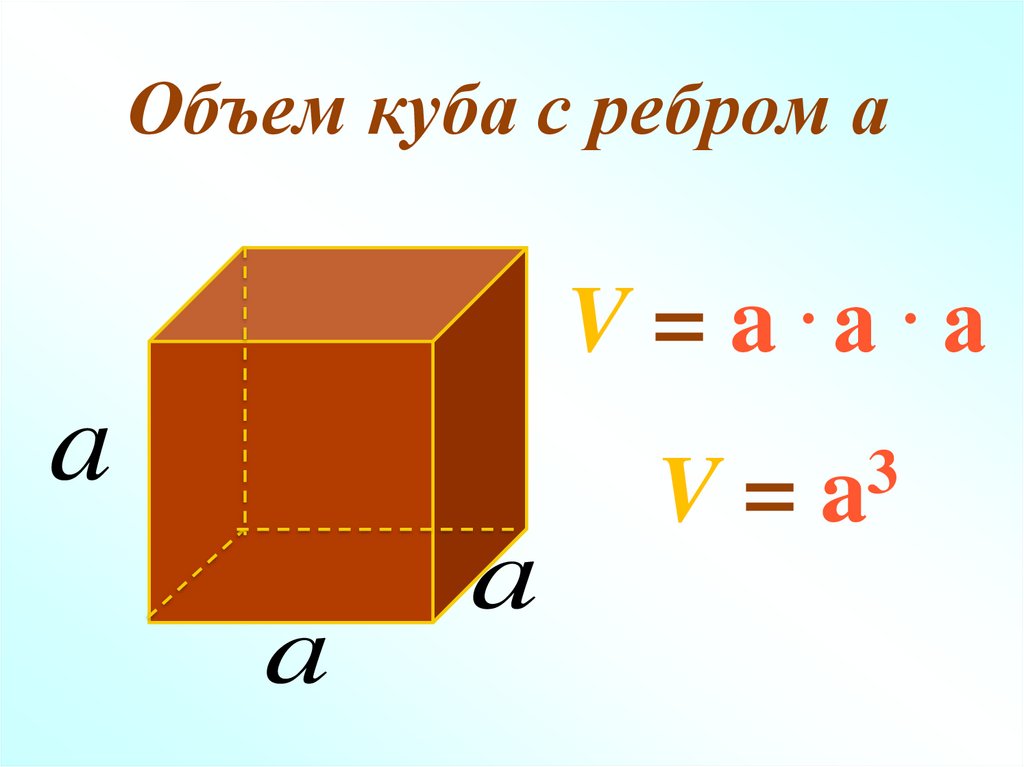 Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Для решения задач понадобятся знания не только готовых формул, но свойств фигуры. Перечень основных свойств прямоугольной призмы невелик и очень прост для понимания:
- Противолежащие грани фигуры равны и параллельны. Это значит, что ребра расположенные напротив одинаковы по длине и углу наклона.
- Все боковые грани прямого параллелепипеда – прямоугольники.
- Четыре главные диагонали геометрической фигуры пересекаются в одной точкой, и делятся ею пополам.
- Квадрат диагонали параллелепипеда равен суме квадратов измерений фигуры (следует из теоремы Пифагора).
Теорема Пифагора гласит, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади треугольника, построенного на гипотенузе того же треугольника.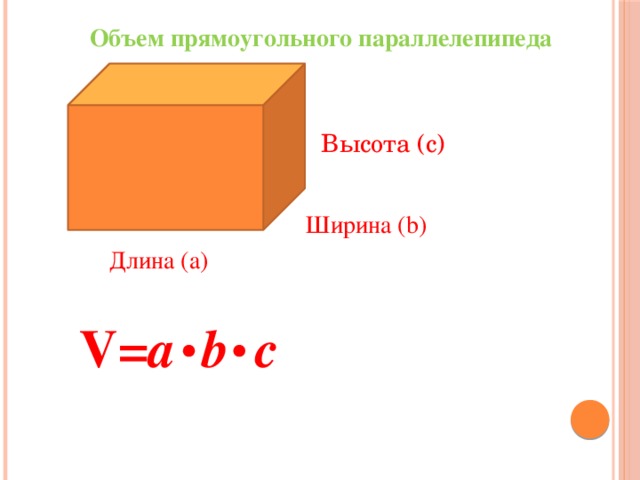
Доказательство последнего свойства можно разобрать на изображении представленном ниже. Ход решения поставленной задачи прост и не требует подробных объяснений.
Формула объема прямоугольного параллелепипеда
Формула нахождения для всех видов геометрической фигуры одна: V=S*h, где V- искомый объем, S – площадь основания параллелепипеда, h – высота, опущенная из противоположной вершины и перпендикулярная основанию. В прямоугольнике h совпадает с одной из сторон фигуры, поэтому чтобы найти объем прямоугольной призмы необходимо перемножить три измерения.
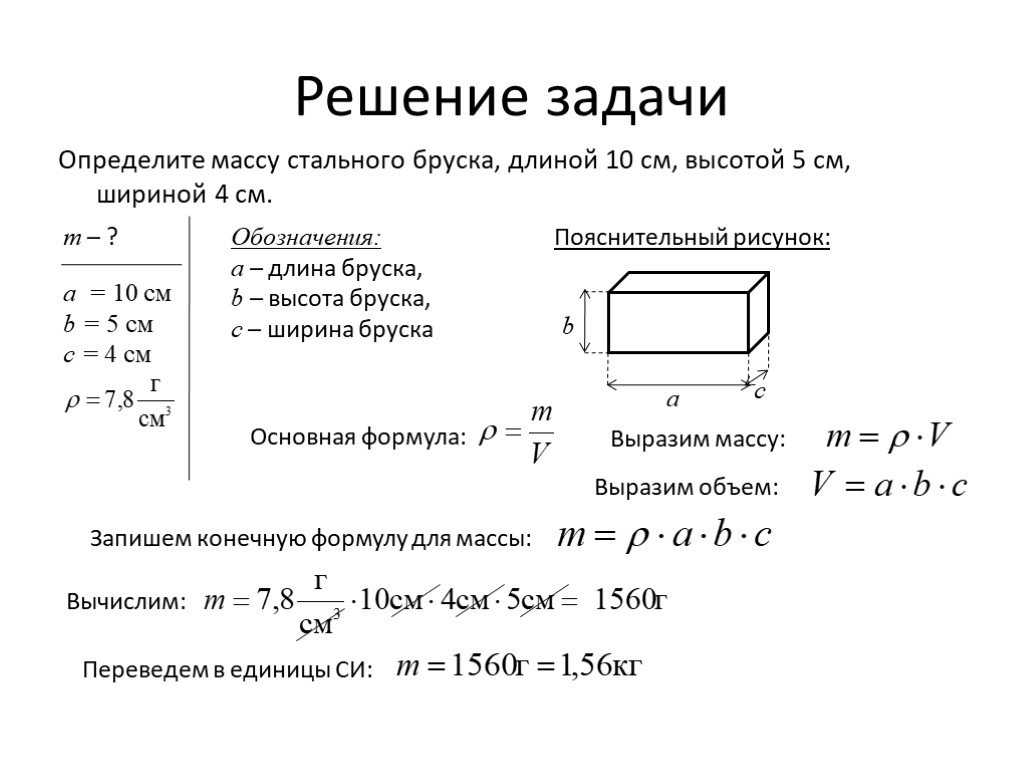
Объем принято выражать в см3. Зная все три значения a, b и c найти объем фигуры совсем не сложно. Наиболее часто встречающийся тип задач в ЕГЭ – это поиск объема или диагонали параллелепипеда. Решить многие типовые задания ЕГЭ без формулы объема прямоугольника – невозможно. Пример задания и оформления его решения приведен на рисунке ниже.
Примечание 1 . Площадь поверхности прямоугольной призмы можно найти, если умножить на 2 сумму площадей трех граней фигуры: основания (ab) и двух смежных боковых граней (bc + ac).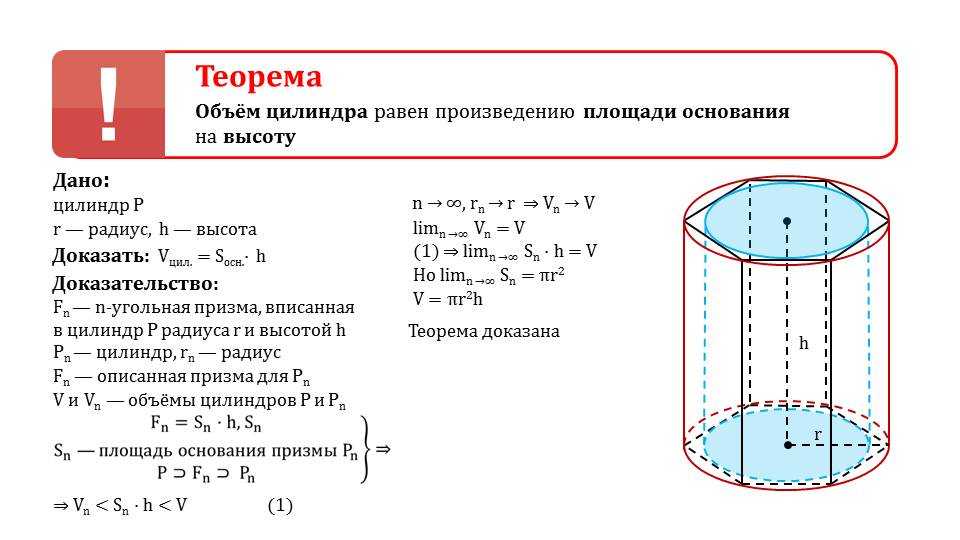
Примечание 2 . Площадь поверхности боковых граней легко узнать умножив периметр основания на высоту параллелепипеда.
Исходя из первого свойства параллелепипедов AB = A1B1, а грань B1D1 = BD. Согласно следствиям из теоремы Пифагора сумма всех углов в прямоугольном треугольнике равна 180°, а катет, лежащий против угла в 30°, равен гипотенузы. Применив данные знания для треугольника, легко находим длину сторон AB и AD. Затем перемножаем полученные значения и вычисляем объем параллелепипеда.
Формула для нахождения объема наклонного параллелепипеда
Чтобы найти объем наклонного параллелепипеда необходимо площадь основания фигуры умножить на высоту, опущенную на данное основание из противоположного угла.
Таким образом, искомый V можно представить в виде h — количества листов с площадью S основания, так объем колоды складывается из V-ов всех карт.
Примеры решения задач
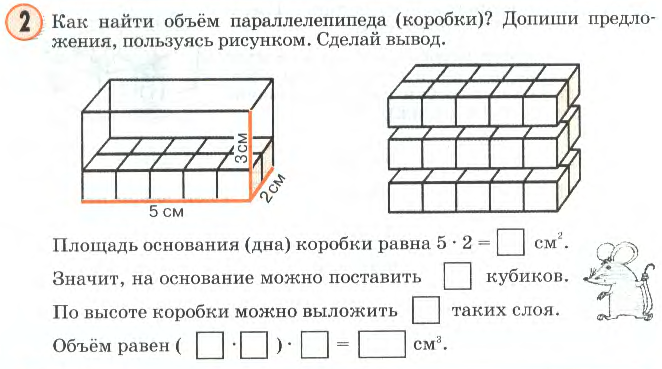
Задания единого экзамена должны быть выполнены за определенное время.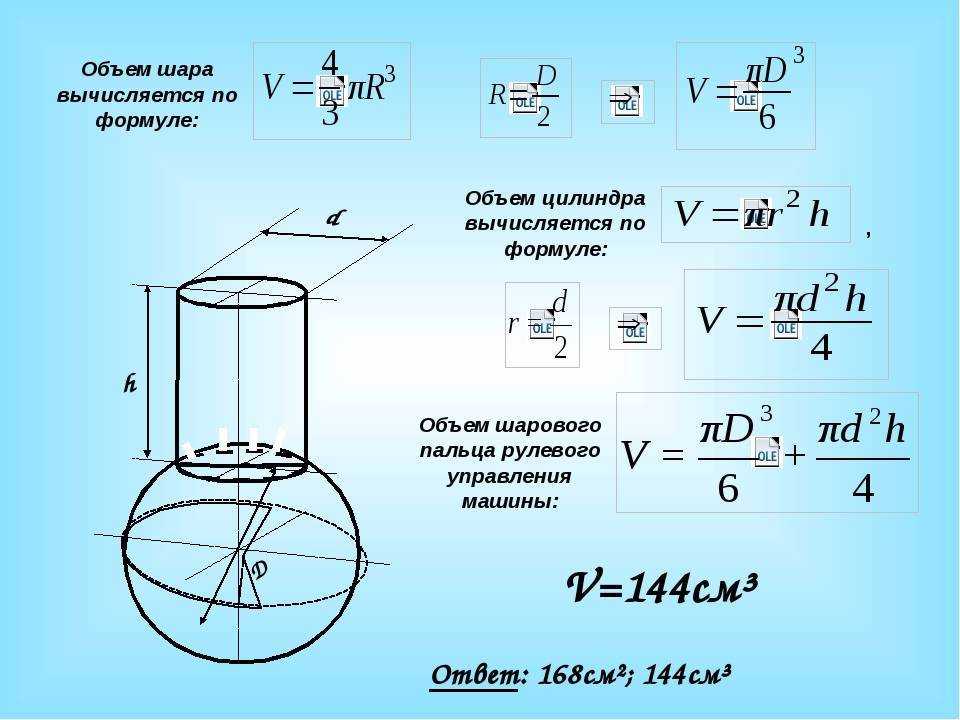 Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Как видно из примера на изображении выше, ничего сложного в решении подобных задач нет. Задания из более сложных разделов предполагают знания теоремы Пифагора и ее следствий, а так же формулу длины диагонали фигуры. Для успешного решения заданий тестов достаточно заранее ознакомится с образцами типовых задач.
Как правильно с помощью формул найти объем прямоугольного параллелепипеда?
Прямоугольный параллелепипед, с точки зрения математики, является объемной фигурой с шестью гранями. Увидеть его можно, если посмотреть на прямоугольный бассейн, кирпич или спичечный коробок.
Эта фигура очень часто встречается в повседневной жизни, однако, нередко возникает необходимость узнать ее объем, что для многих представляет некоторые трудности. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.
Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.
Во многих других ситуациях возникает проблема, как найти объем параллелепипеда правильно.
Между тем вычислить это значение очень просто. Достаточно лишь знать ширину, длину и высоту предмета или объекта. И также необходимо знать формулу, с помощью которой и находят объем данной геометрической фигуры.
Содержание:
- Основные особенности и формула для расчета
- Формула расчета в двух вариантах
- О чем еще следует знать для правильности расчета?
- Видео
Основные особенности и формула для расчета
Для того чтобы найти объем параллелепипеда необходимо:
- определить длину, высоту и ширину объекта;
- и после этого перемножить данные значения друг на друга;
- получившиеся данные и будут объемом.
Это все предельно просто и не таит никаких подводных камней.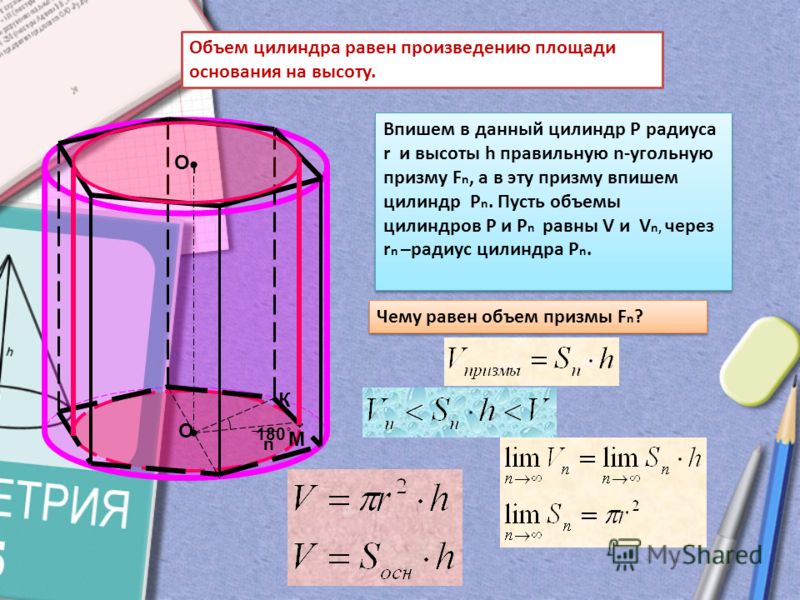 Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.
Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.
При этом важно знать, что определить параметр можно в сантиметрах, кубометрах, дециметрах и некоторых других размерностях в зависимости от требований. Если говорить о Международной системе единиц (СИ), параметр рассчитывают в сантиметрах. Это оптимальный вариант. Но при желании всегда можно перевести значение в требуемые размерности.
Формула расчета в двух вариантах
Итак, для расчета по формуле нужно знать длину, ширину и высоту измеряемого предмета. Эти данные следует обозначить соответственно как А, B и C, а объем обычно представляют буквой V. Формула для определения объема прямоугольного параллелепипеда при этом будет выглядеть следующим образом: V = A x B x C.
Если определятся объем бассейна, то необходимо его длину, ширину и глубину перемножить. Для более простого восприятия давайте разберем правила расчета объема параллелепипеда на примере. Допустим, что его длина составляет 10 метров, ширина достигает 3 метров, а глубина — 1,5.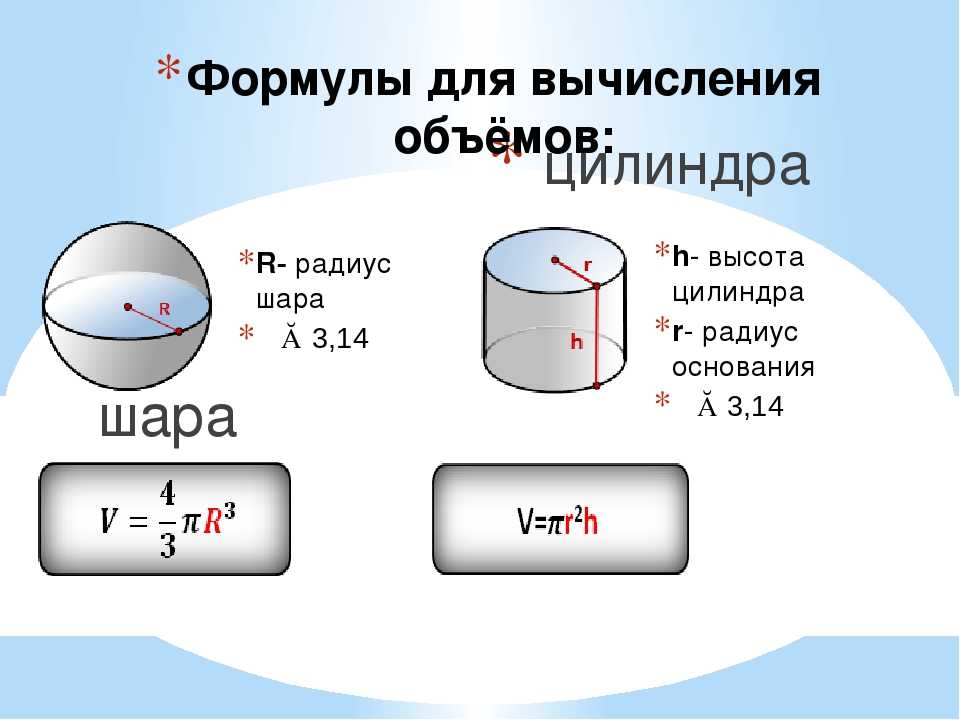 В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.
В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.
Можно выделить и другую формулу, которая имеет некоторое отличие. Она представляет собой произведение площади основания на высоту. Формула выглядит следующим образом: V = S x h. Здесь h — высота параллелепипеда. S — площадь основания, которая представлена произведением двух сторон основания. Обычно их обозначают, как a и b: S = a x b.
При расчете можно пользоваться любой из двух приведенных формул. Обе являются верными и позволяют получить точные данные. Последний вариант удобен, когда уже известна площадь основания. Если же она неизвестна, проще перемножать сразу три линейных размера, исключая необходимость в лишней процедуре.
О чем еще следует знать для правильности расчета?
Для вычисления объема параллелепипеда необходимо понять, что это за фигура. Она представляет собой призму, основание которой — параллелограмм. Параллелепипед имеет 6 граней, каждый из которых является параллелограммом.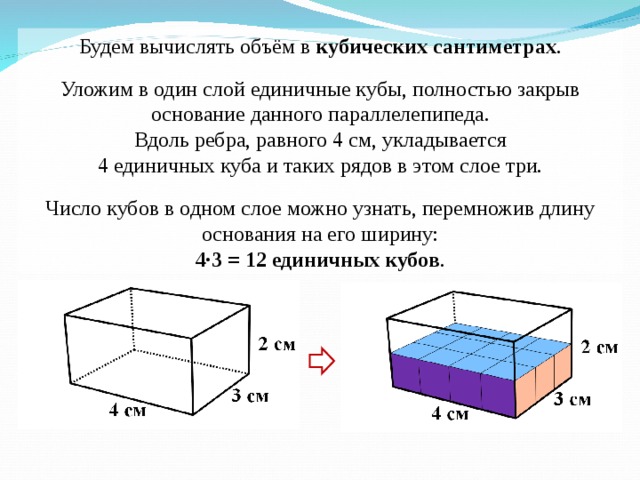 При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
- Прямоугольный параллелепипед. Эта фигура представляет собой параллелепипед, который имеет все грани в виде прямоугольников.
- Прямым параллелепипедом является фигура, у которой 4 боковые грани — прямоугольники.
- Куб — это еще один вид параллелепипеда. Он представляет собой прямоугольный параллелепипед, все стороны которого равны между собой. Другими словами, все шесть граней такой фигуры, как куб — это равные квадраты.
И также важно помнить о том, что в процессе выполнения расчета у каждой составляющей формулы должна быть одна и та же размерность. Если опустить это простое правило, получить верный результат не удастся. Если вы выполняете расчеты просто на уроках математики, проблемой могут стать только неудовлетворительные оценки. А при проектировании и наличии ошибок в расчетах проблемы могут быть более серьезными.
Не стоит думать, что основные математические формулы по определению объемов геометрических фигур встречаются исключительно на уроках математики. В большинстве случаев они пригодятся и в последующей жизни. В частности, во время ремонтных или строительных работ, при проектировании и декорированию интерьера, а также в ряде других случаев. Именно тогда без правильной формулы обойтись не удастся.
Можно подвести итог: объем параллелепипеда равен произведению трех линейных размеров — длины, ширины, высоты. Параметр напрямую зависит от трех единиц измерения при любом вращении и повороте. Результат будет неизменным.
Видео
Видео поможет вам научиться находить объем прямоугольного параллелепипеда.
Как найти объём сосуда
Понятие объёма
Можно провести аналогию понятия объема сосуда с понятием площади. Напомним, что понятие площади применимо к плоскости.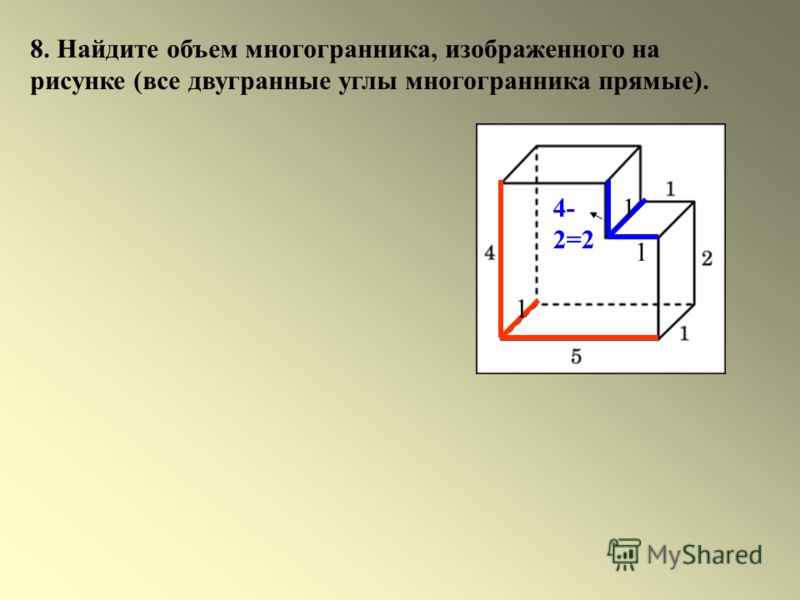 3$ — эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
3$ — эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
Основные свойства объёмов:
- У равных сосудов равные объёмы.
- В случае, когда сосуд состоит из нескольких сосудов, то его объём равен сумме всех этих сосудов.
Эти свойства аналогичны свойствам длин отрезков и площадей многоугольников.
Часто требуется найти объём параллелепипеда, пирамиды, цилиндра, конуса и шара. Параллельно с формулами объёма дадим ключевые определения. Чтобы рассмотреть такую фигуру как параллелепипед, необходимо дать два важных определения:
- Многогранник — это тело, ограниченное несколькими многоугольниками (гранями). Стороны граней называют рёбрами, а концы рёбер — вершинами.
- Призма — это многогранник, который составлен из двух параллельных многоугольников (оснований призмы), вершины которых соединены параллельными и равными друг другу отрезками (боковыми ребрами призмы), образующими параллелограммы (боковые грани призмы).

Нахождение объёма параллелепипеда
Параллелепипед — это многогранник, составленный из 6-ти прямоугольников. Или это четырёхугольная призма, в которой основания — параллелограммы. Форму параллелепипеда имеют коробки, комнаты и многие другие предметы из нашей повседневной жизни.
В случае, когда у параллелепипеда боковые ребра перпендикулярны к плоскостям оснований, а боковые грани и основания — прямоугольники, то этот параллелепипед называют прямоугольным (прямым).
Для нахождения объёма прямоугольного параллелепипеда необходимы его измерения. Измерения параллелепипеда — это длины трёх рёбер с общей вершиной. В речи мы называем измерениями «длину», «ширину» и «высоту» (например, при измерении комнаты).
Определение 1
Объём прямоугольного параллелепипеда равен произведению трёх его измерений: $V=abc$.
Если площадь основания $S=ac$, а высота $h=b$, то формула объёма может быть следующей: $V=Sh$.
Нахождение объёма пирамиды
Пирамида — это многогранник, образованный из $n$-угольника (в качестве основания) и треугольников (в качестве боковых граней), построенных путем соединения одной точки (вершины пирамиды) отрезками (боковыми рёбрами) с вершинами многоугольника.
Рисунок 1. Пирамида. Автор24 — интернет-биржа студенческих работ
Определение 2
Объём пирамиды равен одной трети произведения площади основания на высоту. В данном случае высота представляет собой перпендикулярный к плоскости основания отрезок, который соединяет вершину пирамиды с плоскостью её основания.
$V=\frac{Sh}{3}$.
Нахождение объёма цилиндра
Цилиндр — некоторое тело (или сосуд), полученное в результате вращения некоторого прямоугольника вокруг своей оси (одной из сторон прямоугольника).
Рисунок 2. Цилиндр. Автор24 — интернет-биржа студенческих работ
Определение 3
Объём цилиндра равен произведению площади основания на высоту: $V=Sh$.
Нахождение объёма конуса
Конус — это некоторое тело (сосуд), полученное в результате вращения прямоугольного треугольника вокруг его катета.
Рисунок 3. Конус. Автор24 — интернет-биржа студенческих работ
Определение 4
Объём конуса равен одной трети произведения площади основания на высоту: $V=\frac{Sh}{3}$. 3$, где $R$ — радиус шара.
3$, где $R$ — радиус шара.
Таким образом, мы перечислили все основные формулы объёма основных фигур в стереометрии.
Как найти объем и площадь прямоугольного параллелепипеда?
Как найти объем и площадь прямоугольного параллелепипеда?
Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см. V = 9 * 6 * 3 = 162 см3. Ответ: объем прямоугольного параллелепипеда равен 162 см3. Объем параллелепипеда равен произведению площади основания на высоту.
Как найти сторону у параллелепипеда?
Боковое ребро параллелепипеда
- a = V / bc. Если известна площадь боковой поверхности и два ребра (b, c), находим неизвестное ребро (а) путем деления площади боковой поверхности (S) на удвоенную сумму двух известных ребер 2 (b+c).
- a = Sб.п. / 2 (a+c) …
- a = (Sп.п. — 2bc) / 2 (b+c) …
- a = √D2 + d2 = √D2 + b2 + c2
Как найти объем формула?
Формула объема.
| Фигура | Формула | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Куб.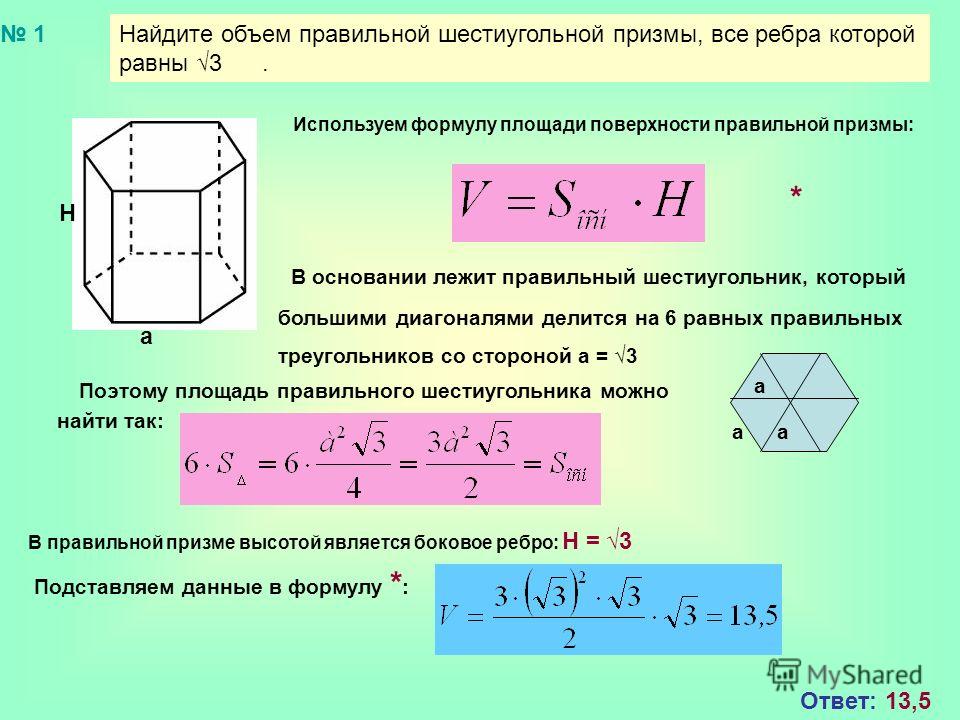 3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту 3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высотуЧто нужно сделать чтобы узнать объем?Для вычисления объема прямоугольных фигур (прямоугольный параллелепипед, куб) используйте формулу: объем = L × W × H (длину умножить на ширину умножить на высоту). Эту формулу можно рассматривать как произведение площади поверхности одной из граней фигуры на ребро, перпендикулярное этой грани. Как находить объем фигур?4. Объем фигур
Как найти объем через площадь и высоту?Умножаешь площадь на высоту и получится объем! В Вашем случае это 50 метров кубических. Как найти объем куба формула 5 класс?Формула вычисления объема куба
Как посчитать объем коробки по размерам?Объем вычисляем по известной формуле: v = l х w х h, где v – объем коробки. Наглядно это выглядит так: допустим, длина коробки составила 70 см, ширина – 40 см, высота 50 см. Полученный объем будет составлять 140000 кубических сантиметров. Как рассчитать литраж в аквариуме?Пошаговая инструкция по вычислению литража Вашего аквариума: То есть получается: — 100 см* 50 см* 60 см = 300000 кубических сантиметров; Теперь, чтобы получить количество литров, умножаем это значение на 0,001: — 300000 куб. Как узнать сколько надо грунта в аквариум?Например, аквариум объемом 100 литров будет содержать 100 дм3 воды, или 1000000 см3 воды. Массу грунта вычисляем по формуле: m = р·V, где: Масса, кг. Плотность, кг/см3….Следовательно, масса 1 см грунта на всей площади дна аквариума: m = р·V = р·А·В·1 см, где:
Как рассчитать вес аквариума с водой?Метрическая система мер: умножьте длину аквариума на его ширину и высоту, выраженные в сантиметрах, чтобы получить его объем в кубических сантиметрах (см3). Разделите эту величину на 1000, чтобы перевести ее в литры. 1 литр воды весит 1 килограмм. Сколько можно рыбок в аквариум на 50 литров?Для аквариумистов сколько можно рыбок сажать в емкость, есть формула: на 2 см длины тела животного необходимо обеспечить 2 литра воды. Так на 50 литровый аквариум можно приобретать: Гуппи не больше 20 рыбок. Кого можно поселить в аквариум на 50 литров?Кого заселить
Сколько Неонов на 50 литров?Сколько можно Неонов красных в 50 литровый аквариум — 20 шт. Сколько можно Неонов обыкновенных в 50 литровый аквариум — 20 шт. Кого можно поселить в аквариум 60 литров?в общем можно. неоны расбора кардиналы пецилия моллинезия гуппи меченосцы, гурами из цихлид можно прикупить пару размирези , чернополосики , хромисы. Сколько неонов можно в 60 литров?Сколько можно Неонов обыкновенных в 60 литровый аквариум — 24 шт. Сколько рыб можно держать в аквариуме 60 литров?Количество рыб в аквариуме 60 литров зависит от вида, и может быть следующим: Гуппи – 24 шт. Что нужно для аквариума на 60 литров?Рыбки для аквариума 60 литров:
Что нужно для аквариума на 50 литров?Оборудование и материалы:
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000. Подсчет объема коробки в литрахПри транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м3 зная равенство: 1 м3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л. Объем цилиндрической полостиОбъем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных. На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны. Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. Теория Цилиндр может быть правильным или наклонным Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов. Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов. Рассмотрим правильный цилиндр. Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Радиус основания цилиндра, является радиусом цилиндра. Ось цилиндра – это прямая, соединяющая центра оснований цилиндра. Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому. Объем прямого цилиндраЦилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros». Объем цилиндра через площадь основания и высоту цилиндраОбъем цилиндра равен произведению площади основания цилиндра на его высоту. [ LARGE V = S cdot H ] где: Поверхности цилиндраНаружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая. Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой. Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке). Сечения цилиндраПри сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями. Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса Как рассчитать объем цилиндра с помощью калькулятораКалькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
Выберите соответствующий шаг и введите исходные данные в соответствующие поля. Также важно указать единицы измерения по условиям задачи. Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема. Формула расчета объема цилиндраОбъем цилиндра вычисляется как произведение площади основания на высоту цилиндра. Так как основанием цилиндра является круг, площадь основания можно рассчитать через радиус или диаметр. Найти объем цилиндраВыберите известные величины: Введите данные:
Вводить можно числа или дроби (-2.4, 5/7, …).
Источники
Расчет объема | SkillsYouNeedНа этой странице объясняется, как рассчитать объем твердых предметов, т.е. сколько вы могли бы вместить в предмет, если, например, вы наполнили его жидкостью. Площадь — это мера того, сколько места находится внутри двухмерного объекта (дополнительную информацию см. на нашей странице: Расчет площади). Объем — это мера пространства внутри трехмерного объекта. Наша страница о трехмерных фигурах объясняет основы таких фигур. В реальном мире вычисление объема, вероятно, не будет использоваться так часто, как вычисление площади. Тем не менее, это может быть важно. Возможность рассчитать объем позволит вам, например, определить, сколько места у вас есть для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете поместить в банку. Это также может быть полезно для понимания того, что имеют в виду СМИ, когда говорят о мощности плотины или расходе реки. Примечание по единицам измерения Площадь выражается в квадратных единицах ( 2 ), поскольку она измеряется в двух измерениях (например, длина × ширина). Объем выражается в кубических единицах ( 3 ), поскольку он измеряется в трех измерениях (например, длина × ширина × глубина). Кубические единицы включают см3, м3 и кубические футы. Кубические единицы включают 3 см, 3 м и кубические футы. ВНИМАНИЕ! Объем также может быть выражен как емкость по жидкости. Метрическая система В метрической системе вместимость жидкости измеряется в литрах, что напрямую сравнимо с кубическим измерением, поскольку 1 мл = 1 см 3 . Имперская/английская система В имперской/английской системе эквивалентными единицами измерения являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше всего придерживаться либо жидких, либо твердых единиц объема. Для получения дополнительной информации см. нашу страницу о системах измерения. Основные формулы для вычисления объемаОбъем тел, основанных на прямоугольниках В то время как основная формула площади прямоугольной формы равна длине × ширине, основная формула для объема равна длине × ширине То, как вы ссылаетесь на различные измерения, не влияет на расчет: вы можете, например, использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются вместе. Вы можете умножать в любом порядке, поскольку это не изменит ответ (см. Коробка с размерами 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем: | ||||||||||||||||||||||||||||||||||||||||

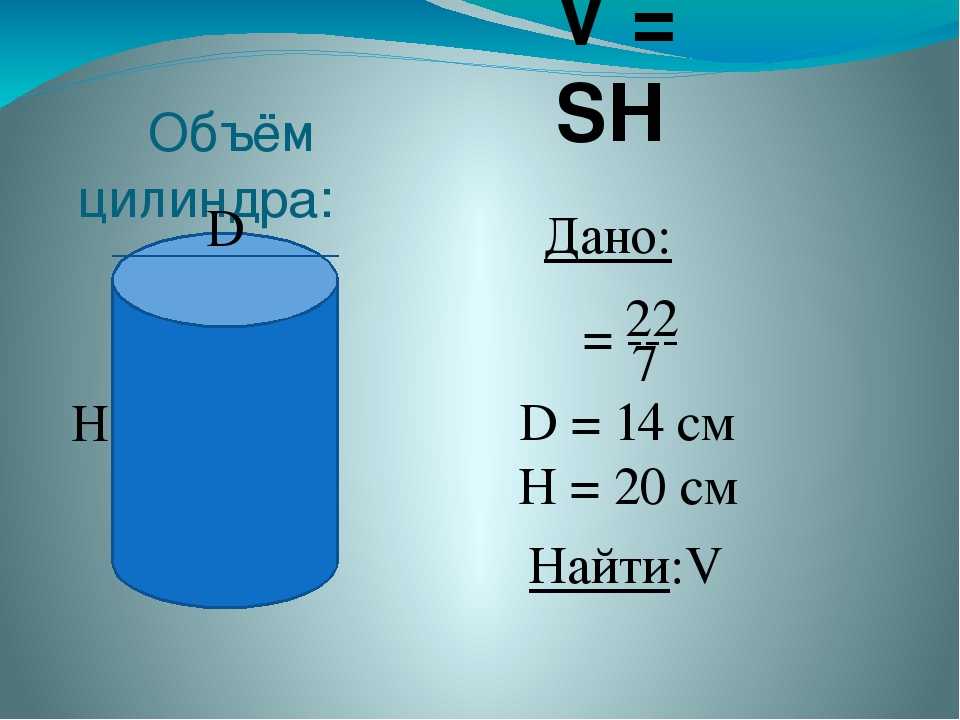
 Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье.
Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье. Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.
Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.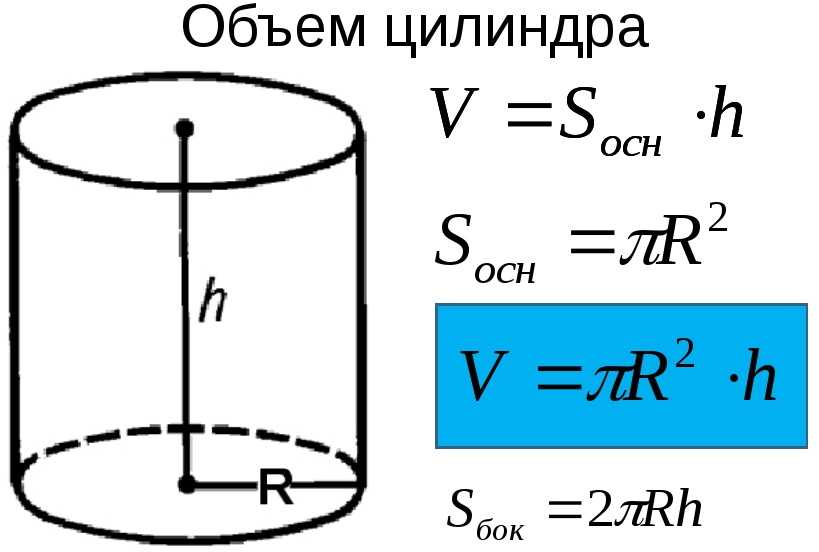 После полученной величины обязательно напишите единицы, в которых она измеряется.
После полученной величины обязательно напишите единицы, в которых она измеряется.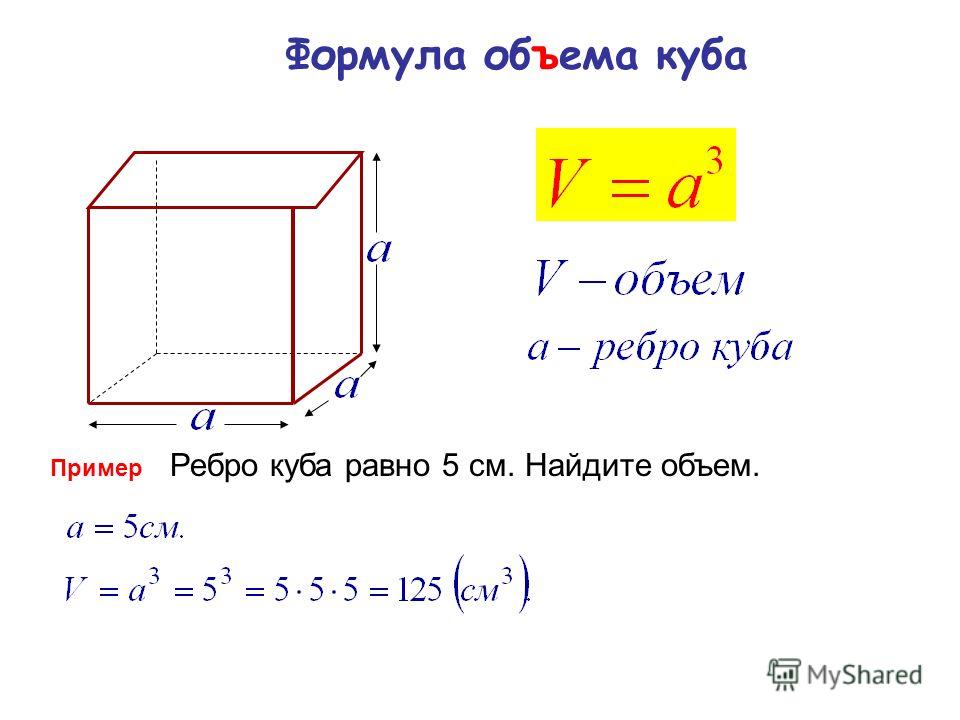
 Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.
Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.
 Площадь умножить на высоту. 2,5 х 20 =50 куб.
Площадь умножить на высоту. 2,5 х 20 =50 куб.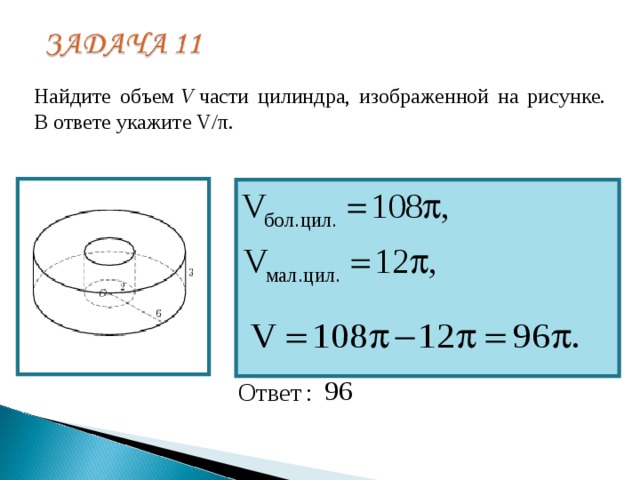
 Меченосцев можно подсаживать до 10 животных.
Меченосцев можно подсаживать до 10 животных. Меченосцы – 6 шт. Моллинезии – 6 шт.
Меченосцы – 6 шт. Моллинезии – 6 шт. 2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту: 14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3 Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.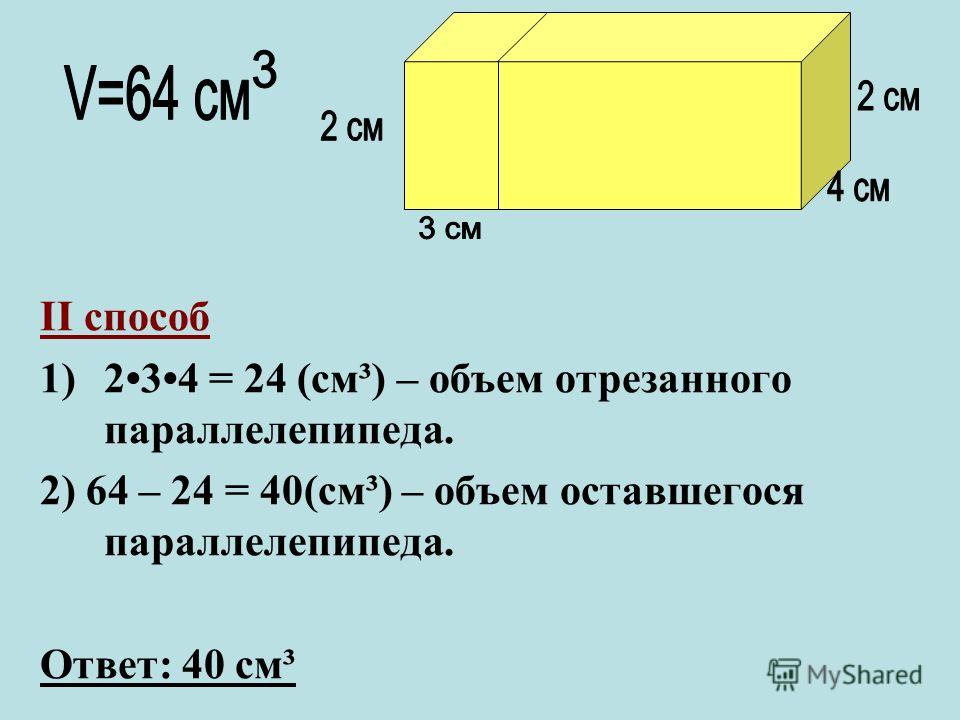
 Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом: То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.