Как посчитать квадрат числа без калькулятора?
Вычислить квадрат числа относительно просто: достаточно умножить имя сам. и квадрат 5,7 равно 32,49, так как 5,7 × 5,7 = 32,49.
Итак, что такое квадратный корень из 25? В математике а квадратный корень числа х является число r такое, что r2 = х. Например: 1. квадратный корень из 25 5 потому что 52 = 25.
Как сделать расчеты без калькулятора? Пальцами обеих рук можно вычисление весь стол из 9. Положите руки перед собой, пальцы вытянуты. Теперь посчитайте число, которое вы хотите умножить на 9 слева направо на пальцах, начиная с большого пальца левой руки. Просто согните соответствующий палец.
Как сделать кубический корень на калькуляторе TI? Нажмите клавишу «Математика» на TI-83 . Нажмите » 4″, чтобы выбрать функцию квадратный корень . La calculatrice автоматически вставляет «(«, чтобы открыть выражение.
Что такое квадратный корень из 3?
La квадратный корень из трех, обозначенный √3 ou 31/2, является действительное число в математике, примерно равное 1,732.
Как извлечь кубический корень на калькуляторе TI 30? Второй соответствует квадратный корень. Он находится «за» 0, поэтому вы должны использовать «2-й» ключ: в результате вы получите 4 (нет необходимости набирать «=»).
Как быстро вычислить число в квадрате?
Как найти квадрат числа? в квадрат определяется для всех имя n в результате умножения этого имя сам по себе и обозначается цифрой 2 в качестве надстрочного индекса: n2 = п × п.
Как посчитать квадрат суммы?
Le квадрат суммы получается путем добавления квадрат каждого из терминов и всех «двойных произведений».
Чему равен квадратный корень из 20?
Так, например, квадратный корень из 20 примерно равно 4,47213595499957939…, этоявляетсято есть число, близкое к 4 с половиной.
Чему равен квадратный корень из 16? от 4 до квадрат равно 16. Корень квадрат 16 есть донк 4.
Чему равен квадратный корень из 8? а, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15… Но один квадратный корень не всегда может быть записано в виде десятичной дроби… rac(8)²=8 по определению квадрат de квадратный корень из, это имеет. … Примеры: 38 = 3,8 х10; 0,0562 = 5,62 х 10-2; – 97631 = – 9763 1 х 104 …
Как посчитать дробь без калькулятора?
4) Добавить Фракции
И тебе даже не нужен calculatrice. Начните со сложения знаменателей, чтобы получить знаменатель окончательного результата. Затем умножьте левый знаменатель на правый числитель и правый знаменатель на левый числитель.
Как научиться быстро считать? Например, 36 х 4 = 36 х 2 х 2 = 72 х 2 = 144.
3 .
Как сделать квадратный корень на TI 83? Выполнение простых расчетов с помощью TI
Переместите числитель и знаменатель с помощью джойстика. Подтверждаем клавишей ввода и находим 58. Нажмите «2de x2», чтобы получить квадратный корень.
Какое число в квадрате дано 3?
Таблица чисел в квадрате
| Имя | число в квадрате |
|---|---|
| 3 | 3²=9 |
| 4 | 4²=16 |
| 5 | 5²=25 |
| 6 | 6²=36 |
• 5 февраля 2020 г.
Чему равен квадратный корень из 5? квадратный корень из пяти, обозначенный √5 ou 51/2, является действительное число, замечательное в математике и приблизительно равное 2,236.
Чему равен квадратный корень из 8?
Таблица квадратного корня
| X | √ х |
|---|---|
| 8 | 2. 82843 |
| 9 | 3 |
| Дикс | 3.16228 |
| 11 | 3,31662 |
Не забудьте поделиться статьей ✨
[Случай] Используйте tkinter, чтобы сделать калькулятор, верно? (Версия третья)
Content
- Введение в дело
- Готов к работе
- Интерфейсный модуль
- Сводка кода
- Сделать скриншот
- постскриптум
Введение в дело
Это будет последняя версия нашего небольшого проекта (возможно), на этот раз мы добавим математические функции расчета.
pi、e、sin()、cos()、tan()、
n !, log (), gcd (), power operation, квадратный корень
Мы узнаем: 1. Как реализовать факториальную операцию. 2. Как найти наибольший общий делитель двух чисел.
Готов к работе
- Python 3.x
- Наибольший общий делитель:Самый большойФактор, также называемыйНаибольший общий делитель、Самый большойФактор, относится к двум или более общим целым числам.
Реализация функции. Используйте встроенный в Python метод pow ().
Реализация функции. Используйте встроенный в Python метод pow ().>>> pow(2, 3) 8
- Реализация функции gcd. Используйте модуль gcd в математическом модуле python.
>>> from math import gcd >>> gcd(3, 6) 3
- Реализация функции квадратного корня. Используйте модуль sqrt в математическом модуле python.
>>> from math import sqrt >>> sqrt(4) 2.0
Сводка кода
# coding: utf-8
# !/usr/bin/python
"""
@ Файл: Calculator.py
@Author : jiaming
@Modify Time: 2020/4/26 21:27
@Contact : https://jiaming.blog.csdn.net/
@Version : 3.0
@Desciption: 1. Никаких математических расчетов, знак процента выполнен!
2. Курсор находится в конце готово!
3. Клавиша возврата может вернуться только к последнему выполненному символу!
"""
# log(10,2)
from math import sin, cos, pi, e, tan, gcd, log, sqrt, factorial
import tkinter as tk
# Содержимое текстового поля
TEXT_str = ''
def get_value():
"""
оценивать
:return:
"""
try:
print(«Требуется выражение:», TEXT_str)
value = str(eval(TEXT_str))
return value
except BaseException:
print('Ошибка! ')
return ''
def menu(Entry_word=None):
"""
Меню
:return:
"""
menu = tk. ":
Entry_word.insert(tk.INSERT, "pow(,)")
TEXT_str = Entry_word.get()
elif s == "%":
Entry_word.insert(tk.INSERT, "*0.01")
TEXT_str = Entry_word.get()
elif s == "cancel":
pass
else:
Entry_word.insert(tk.INSERT, s)
TEXT_str = Entry_word.get()
menu.destroy()
# Кнопка "Поместить"
key = 0
for i in range(0, 3):
for j in range(0, 4):
if menu_list[key] == "cancel":
btn = tk.Button(
menu,
text=menu_list[key],
width=10,
height=2,
relief=tk.GROOVE,
command=lambda idx=key: btn_command_menu(idx),
bg="orange"
)
else:
btn = tk.Button(
menu,
text=menu_list[key],
width=10,
height=2,
relief=tk. GROOVE,
command=lambda idx=key: btn_command_menu(idx))
btn.grid(row=i, column=j)
key += 1
menu.mainloop()
def main():
"""
Интерфейс калькулятора рисования
"""
# Настройка основных параметров интерфейсных объектов
root = tk.Tk()
root.title(«Калькулятор (Версия 3)»)
root.geometry('335x265+250+250')
# Установите, можно ли растягивать интерфейс по желанию
root.resizable(False, False)
text_list = [
'AC', 'BS', '( )', 'menu',
'7', '8', '9', '+',
'4', '5', '6', '-',
'1', '2', '3', '*',
'.', '0', '=', '/',
]
# Разместить текстовое поле
Entry_word = tk.Entry(root, width=30, font=('Arial', 15))
Entry_word.grid(row=0, column=0, columnspan=4)
def btn_command(idx=None):
"""
Событие кнопки
:param idx:
:return:
"""
global TEXT_str
# Распечатать текстовое значение кнопки
s = text_list[idx]
print("войти:", s)
if s == '=':
# Нажмите знак равенства, чтобы вызвать функцию оценки
value_str = get_value()
TEXT_str = '' # Желаемое выражение
Entry_word.
delete(0, tk.END) # Очистить все содержимое поля ввода
Entry_word.insert(tk.END, value_str) # Вставляем вычисленное значение в поле ввода value_str
elif s == 'menu':
# меню
menu(Entry_word=Entry_word) # Вызвать интерфейс меню
elif s == 'AC':
TEXT_str = '' # Желаемое выражение
Entry_word.delete(0, tk.END) # Очистить все содержимое поля ввода
elif s == 'BS':
# print(Entry_word.index(tk.INSERT))
Entry_word.delete(Entry_word.index(tk.INSERT) - 1,
Entry_word.index(tk.INSERT))
TEXT_str = Entry_word.get()
elif s == '( )':
Entry_word.insert(tk.INSERT, '()')
TEXT_str = Entry_word.get()
else:
# Другой
Entry_word.insert(tk.INSERT, s)
TEXT_str = Entry_word.get()
# Кнопка "Поместить"
key = 0
for i in range(1, 6):
for j in range(0, 4):
if text_list[key] == "=":
btn = tk. Button(
root,
text=text_list[key],
width=10,
height=2,
relief=tk.GROOVE,
command=lambda idx=key: btn_command(idx),
bg="orange"
)
elif text_list[key] == "menu":
btn = tk.Button(
root,
text=text_list[key],
width=10,
height=2,
relief=tk.GROOVE,
command=lambda idx=key: btn_command(idx),
bg="gray"
)
else:
btn = tk.Button(
root,
text=text_list[key],
width=10,
height=2,
relief=tk.GROOVE,
command=lambda idx=key: btn_command(idx))
btn.grid(row=i, column=j)
key += 1
root.mainloop()
if __name__ == "__main__":
main()
GROOVE,
command=lambda idx=key: btn_command_menu(idx))
btn.grid(row=i, column=j)
key += 1
menu.mainloop()
def main():
"""
Интерфейс калькулятора рисования
"""
# Настройка основных параметров интерфейсных объектов
root = tk.Tk()
root.title(«Калькулятор (Версия 3)»)
root.geometry('335x265+250+250')
# Установите, можно ли растягивать интерфейс по желанию
root.resizable(False, False)
text_list = [
'AC', 'BS', '( )', 'menu',
'7', '8', '9', '+',
'4', '5', '6', '-',
'1', '2', '3', '*',
'.', '0', '=', '/',
]
# Разместить текстовое поле
Entry_word = tk.Entry(root, width=30, font=('Arial', 15))
Entry_word.grid(row=0, column=0, columnspan=4)
def btn_command(idx=None):
"""
Событие кнопки
:param idx:
:return:
"""
global TEXT_str
# Распечатать текстовое значение кнопки
s = text_list[idx]
print("войти:", s)
if s == '=':
# Нажмите знак равенства, чтобы вызвать функцию оценки
value_str = get_value()
TEXT_str = '' # Желаемое выражение
Entry_word.
Сделать скриншот
постскриптум
Вышесказанное касается того, как использовать tkinter для создания простого калькулятора (версия 3).
Добро пожаловать, подписывайтесь на меняМои знания о колонке, Есть больше замечательных знаний о python ~
| Квадраты и квадратные корни
К
Харис Алик
Харис увлеченно изучает информационные технологии и любит облегчать проблемы других во всех сферах жизни. В свободное время предпочитает читать и писать тексты. Он также любит стратегические игры и музыку. Коммуникабельный, амбициозный, креативный, ответственный, целеустремленный и мотивированный к работе человек. Социально активный, с большим опытом работы с молодежью, связями с общественностью и планированием проектов.
Последнее обновление: 4 апреля 2022 г.
5 / 5 ( 15 голоса )
Этот калькулятор квадратного корня поможет вам найти главный квадратный корень, а также корни других действительных чисел.
Тем временем посмотрите другие калькуляторы, связанные с математикой, такие как Калькулятор логарифмов, Площадь трапеции, Конденсированные логарифмы, или, может быть, вы хотите узнать больше о тригонометрии, так что отправляйтесь к этому Калькулятору кофункций. Кроме того, мы рекомендуем вам узнать больше о постулате сложения сегментов.
Что такое квадратный корень?
Квадратным корнем называется выражение, в котором одно число умножается само на себя. Укоренение — это вычислительная операция, в которой у нас есть корни. В основном мы выражаем это знаком √. Натуральное число под корнем называется радиантом, а выражение выше корня — показателем степени. Мы часто используем его почти в каждом случае, написанном без экспоненты.
Символ квадратного корня
Символ « √ » для квадратного корня впервые был использован в печати в 1525 году в книге Кристофа Рудольфа «Косс».
История
Эта таблица была составлена между 1800 г. до н.э. и 1600 г. до н.э. Йельским вавилонянином, на ней показаны: \sqrt{2}\text{и}\frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}
разделены как 1; 24,51,10 и 0; 42,25,35 основано на 60 числах на квадрате, пересеченном двумя диагоналями. Они нашли процедуру определения стоимости этого. Они использовали вычисление приблизительного значения алгоритмов извлечения квадратного корня.
Для его расчета он использовал итерационный метод. В Йельском университете хранятся глиняные таблички с клинописными табличками 17 века до н.э., на которых находится процедура определения диагонали квадрата на странице 30.
Немецкий ученый Михаэль Штифель в 15 веке в своей книге Arthitmetica Integra использовал корневые символы. Обозначение корня, скорее всего, происходит от первой буквы латинского слова radix.
Как вычислить квадратный корень?
Продукт сначала вычисляется, а затем рутируется.
Этот продукт также может быть укоренен, так что каждый фактор укоренен отдельно. Квадратный корень из частного равен частному из квадратных корней. Если мы укореняем сумму или разность, мы должны сначала вычислить их значение и только потом укоренять. В вычислениях выделение и корень имеют приоритет над другими вычислительными операциями.
Как найти квадратный корень без калькулятора?
Чтобы найти квадратный корень из целого числа, вы также можете разделить целое число на числа, пока не получите ответ, который будет представлять собой число, которое вы разделили на . Например, , 16 разделить на 4 равно 4. 4 разделить на 2 равно 2 и так далее. Или просто используйте этот калькулятор квадратного корня.
Квадратный корень из отрицательного числа
Квадрат любого положительного и отрицательного числа дает положительный результат, а квадрат 0 равен 0. Таким образом, никакое отрицательное число не может иметь действительный квадратный корень.
Однако можно работать и с комплексными числами, которые имеют решения для квадратного корня из отрицательного числа. Это делается путем введения нового числа, обозначаемого i. И это называется воображаемой единицей.
Как упростить вычисление квадратных корней?
Упрощение квадратных корней кажется сложным, но на самом деле это не так. Чтобы упростить квадратный корень, вам просто нужно разложить число на множители и извлечь корни любых полных квадратов, которые вы найдете, из знака радикала. Как только вы запомните несколько типичных правильных квадратов и научитесь разлагать числа на множители, вы будете на пути к упрощению извлечения квадратного корня.
Совершенные квадраты
Совершенные квадраты — это квадраты следующих целых чисел:
| Square | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| Result | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Часто задаваемые вопросы
Квадратный корень из 2
Квадратный корень из 2 приблизительно равен 1,4142 — положительное действительное число.
При умножении на себя получаем число 2.
Квадратный корень из 3
Квадратный корень из 3 — это положительное действительное число, которое при умножении само на себя дает число 3. Корень из 3 приблизительно равен 1,7320508075.
Является ли квадратный корень из 2 рациональным числом?
Да , 2 — рациональное число. Мы знаем, что рациональное число имеет форму p/q, где q не равно нулю.
Обязательно ознакомьтесь с нашим Калькулятором квадратных уравнений!
Как вычислить квадратный корень
Квадратные корни полезны в повседневной жизни. Какими бы сложными они ни были для понимания в школе, вам нужно их понять, потому что они применимы в реальной жизни. В этой статье вы узнаете все, что вам нужно знать, чтобы уметь находить квадратные корни. К тому времени, когда вы закончите читать, вы станете своим собственным калькулятором квадратного корня, получая точные результаты в конце каждого уравнения.
Что такое квадратный корень?
квадратный корень из — это число, которое при умножении само на себя дает определенное количество. Любая пара цифр, умноженная друг на друга, может быть квадратным корнем. Символ квадратного корня — √.
Ниже приведены примеров квадратных корней:
- Квадратный корень из 16 равен 4, потому что 4 x 4 = 16
- Квадратный корень из 25 равен 5, потому что 5 х 5 = 25
- Квадратный корень из 36 равен 6, потому что 6 x 6 = 36
Для чего используются квадратные корни?
Как только вы научитесь находить квадратный корень из чисел, вы поймете, что у него много применений в реальной жизни. Ниже приведены примеры использования квадратного корня в повседневной жизни.
Финансы
Функция квадратного корня обычно используется в финансах. Это важный инструмент для расчета доходности инвестиций, которые созрели или обесценились за двухлетний период.
Формула квадратного корня для расчета коэффициента доходности выглядит следующим образом:
R = √(V2 / V0) – 1
R= коэффициент доходности
V2= конечное значение
V0= начальное значение
Подставим теперь в это уравнение несколько действительных чисел:
Майк инвестировал 100 долларов в Disney в 2020 году
Два года спустя он продал свои акции за 196 долларов
Теперь у нас есть реальный сценарий ввода чисел в формулу. Поэтому:
V2 = 196
V0 = 100
Следовательно:
R = √ (196/100) — 1
R = √ (1,96) — 1
R = 1,4 — 1
R (1,96) — 1
R = 1,4 — 1
R (1,96) — 1
= 0,4
В этом примере мы видим, что квадратное число не обязательно должно быть целым числом. Десятичные цифры также могут быть квадратными числами.
Теорема Пифагора
Помимо использования в финансах, квадратные корни также используются в математических формулах, а именно в теореме Пифагора.
Теорема Пифагора — это уравнение, используемое для вычисления длины стороны треугольника. Он часто используется в строительстве и строительных работах, чтобы обеспечить использование правильных измерений.
Теорема используется для вывода площади гипотенузы прямоугольного треугольника:
√(a2 + b2) = c
c = гипотенуза
a = первая сторона
b = вторая сторона
Если у вас есть треугольник, две стороны которого равны 6 футам и 8 футам соответственно, и вам нужно найти длину самой длинной стороны, вам нужно использовать приведенную выше формулу как следующим образом:
√(62 + 82) = c
√(36 + 64) = c
√(100) = c
10 = c
Длина самой длинной стороны равна 10 футам. Всегда не забывайте включать правильную единицу измерения. В противном случае ваш ответ будет неправильным.
Что такое БОДМАС в математике?
Как упростить квадратный корень
Если у вас есть большие многозначные числа, вы можете упростить их, чтобы с ними было легче работать.
Чтобы упростить квадратный корень, вам нужно определить, существуют ли идеальные квадраты, найдя множители для имеющегося у вас числа.
Возьмем, к примеру, √75
75 = 5 x 5 x 3
Это эквивалентно
5² x 3 = 75
Следовательно,
√59 x 3 √75 = √750003
То же, что и
√75 = √5² x √3
Это можно упростить до
√75 = 5√3
Квадратный корень из
, если вас попросят вычислить квадратный корень из числа, это будет положительное число. Квадратный корень из числа может быть как положительным, так и отрицательным, поскольку при умножении отрицательного числа на другое отрицательное число получается положительное число. Если вас спросят, чему равен квадратный корень из 25, ответ может быть либо 5, либо -5, поскольку оба этих числа, умноженные сами на себя, дадут ответ 25. Найдите репетитора по математике
Как найти квадратный корень из числа
Метод вычитания
Если у вас есть идеальный квадрат, это самый простой способ найти квадратный корень из числа. Все, что вам нужно сделать, это вычитать нечетные числа из исходного числа, из которого вы пытаетесь найти квадратный корень, пока не получите ноль.
Например, если вы пытаетесь найти квадратный корень из 25:
25 – 1 = 24
24 – 3 = 21
21 – 5 = 16
16 – 7 = 9
9 – 9 = 0
Поскольку вам потребовалось 5 попыток, чтобы получить число 0, вы можете сделать вывод, что 5 – это квадратный корень из 25.
Метод оценки
Оценка ответа на математический вопрос эквивалентна обоснованному предположению на основе имеющейся у вас информации. В этом случае вы используете известные вам квадратные числа, окружаете искомое число и работаете с ним. Это хорошо работает для любого числа, квадрат которого не идеален.
Попробуем найти √15 методом оценки. Ближайшая к 15 пара цифр в идеальном квадрате — это √16, что равно 4. Но 16 слишком велико, поэтому возведем в квадрат 3. Получится 9, которое, как мы знаем, слишком мало. Мы можем сделать вывод, что квадрат 15 лежит где-то между 3 и 4. Теперь нам нужно выяснить, ближе ли квадрат 15 к 3 или 4. Для этого нам нужно возвести в квадрат 3,5 и 4, что дает нам ответы 12.25 и 16 соответственно. В результате мы знаем, что √15 должно лежать между 3,5 и 4 и ближе к 4.
Затем вам нужно методом проб и ошибок найти точное квадратное число 15. Например, вы можете взять 3,8 в квадрате и увидеть, что оно равно 14,44. Однако вы знаете, что он должен быть больше, чем это. Следовательно, вы должны проверить 3,9 в квадрате, что соответствует 15,21.
Это слишком большое значение. Поэтому вам нужно попробовать числа, лежащие между 3,8 и 3,9. В конце концов вы обнаружите, что √15 = 3,872. Этот процесс не рекомендуется из-за того, что он занимает много времени, а также из-за того, что вы имеете дело со сложными числа с десятичной точкой . Легче просто сделать это на калькуляторе.
Метод деления в длину
Алгоритм деления в длину — это более точный способ найти ответы для чисел, не имеющих идеального квадрата. Возьмем для примера 2025. Первое, что вам нужно сделать, это разбить число на более управляемые числа. В этом случае вы бы разделили 20 и 25.
Далее вам нужно найти наибольший целочисленный квадрат самого левого числа. В данном случае это число равно 20. Наибольшее квадратное целое число 20 равно 4, поскольку 4 x 4 = 16. Затем вы отнимаете квадратное число 16 от 20, что дает нам 4.
Вы должны записать число 4 и поставить рядом с ним оставшиеся 25 от исходного числа, в результате чего у вас получится 425. При этом также напишите число 4 в крайнем правом углу текущего уравнения. Теперь вы должны умножить эти 4 на 2, что оставит вам 8. Запишите 8 в этом уравнении.
Теперь вам нужно заполнить уравнение 8 _ x _ =
Чтобы найти нужные вам числа, вам нужно вычислить максимально возможное квадратное целое число для второго из ваших исходных чисел, которое равно 25. Это полный квадрат, и ответ равен 5. У вас остается следующее уравнение:
85 x 5 = 425
Два квадрата, которые у вас получились, это 4 и 5, поэтому ваше окончательное число квадратов и ответ на √2025 равны 45.
Все, что вам нужно сделать, это вычитать нечетные числа из исходного числа, из которого вы пытаетесь найти квадратный корень, пока не получите ноль.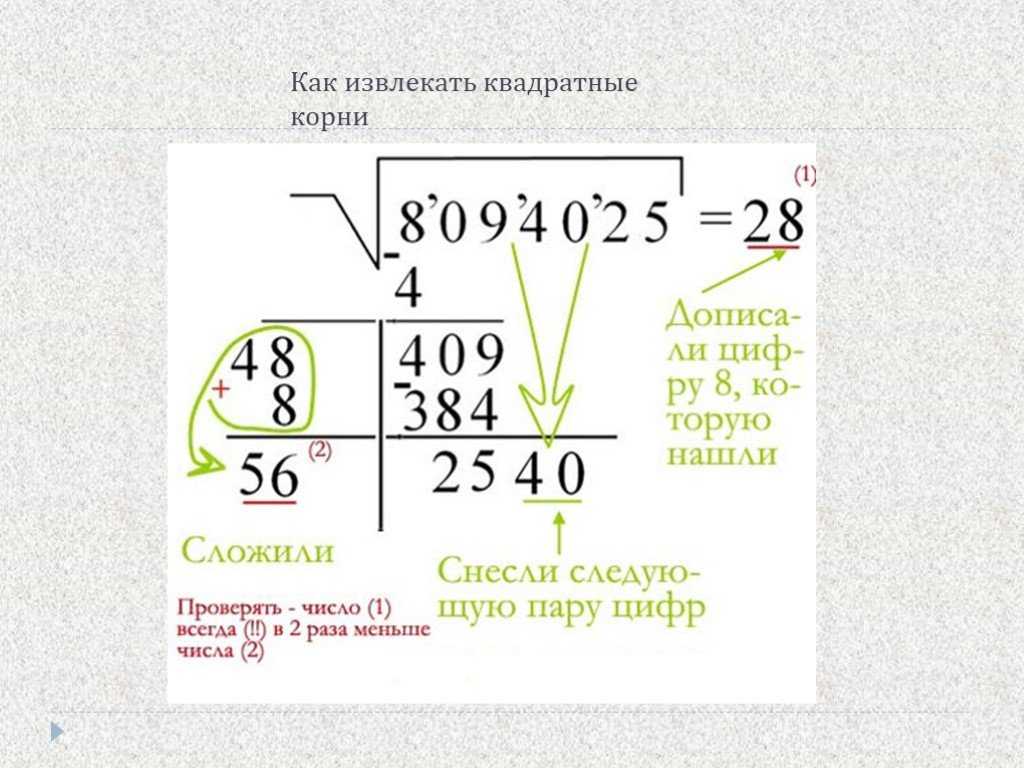
Теперь нам нужно выяснить, ближе ли квадрат 15 к 3 или 4. Для этого нам нужно возвести в квадрат 3,5 и 4, что дает нам ответы 12.25 и 16 соответственно. В результате мы знаем, что √15 должно лежать между 3,5 и 4 и ближе к 4. 
Возьмем для примера 2025. Первое, что вам нужно сделать, это разбить число на более управляемые числа. В этом случае вы бы разделили 20 и 25. 