Когда определитель матрицы равен нулю: Свойства определителя матрицы | Мозган калькулятор онлайн

Если определитель матрицы равен нулю, то обратная к ней не существует — Студопедия

Поделись  

Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.

Определение 14.9 Квадратную матрицу назовем вырожденной или особенной матрицей, если , и невырожденной или неособенной матрицей, если .

Предложение 14.21 Если обратная матрица существует, то она единственна.

Доказательство. Пусть две матрицы и являются обратными для матрицы . Тогда

и

Следовательно, .

Предложение 14.22 Если квадратная матрица является невырожденной, то обратная для нее существует и

(14.14)

 

где — алгебраические дополнения к элементам .

Доказательство. Так как для невырожденной матрицы правая часть равенства (14. 14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, что и что . Докажем первое из этих равенств, второе доказывается аналогично.

Пусть . Найдем элементы матрицы , учитывая, что :

Если , то по предложению 14.17 сумма справа равна нулю, то есть при .

Если , то

Сумма справа представляет собой разложение определителя матрицы по -ой строке (предложение 14.16). Таким образом,

Итак, в матрице диагональные элементы равны 1, а остальные равны нулю, то есть .

Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему.

Теорема 14.1 Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица  — невырожденная, обратная матрица единственна, и справедлива формула (14.14).

Замечание 14.12 Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер

столбца, а второй — номер строки, в которые нужно записать вычисленное алгебраическое дополнение.

Пример 14.7 Найдите обратную матрицу для матрицы .

Решение. Находим определитель

Так как , то матрица  — невырожденная, и обратная для нее существует.

Находим алгебраические дополнения:

Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй — строке:

(14.15)

 

Полученная матрица и служит ответом к задаче.

Замечание 14.13 В предыдущем примере было бы точнее ответ записать так:

(14.16)

 

Однако запись (14.15) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (14.15) предпочтительнее, если элементы матриц — целые числа. И наоборот, если элементы матрицы  — десятичные дроби, то обратную матрицу лучше записать без множителя впереди.

Замечание 14.14 При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.

Пример 14.8 Найдите обратную матрицу для матрицы .



Свойства определителей

1. Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

Определи́тель — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Минором порядка k матрицы А называется определитель, составленный из элементов, стоящих на пересечении любых k строк и k столбцов данной матрицы.

Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.

— Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

— Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

— Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

— Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

— Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

— Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

— Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

— Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей формула Бине-Коши).

Правило разложения определителя по строке (столбцу).

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы детерминант определяется как

Для матрицы определитель задаётся рекурсивно:

, где — дополнительный минор к элементу a1j. Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы такова:

= a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке)

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

Здесь x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].

— Система называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.

— Система называется квадратной, если число m уравнений равно числу n неизвестных.

— Решение системы — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему обращает все её уравнения в тождества.

— Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

— Совместная система вида может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств: c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

— Совместная система вида называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Обычно ранг матрицы A обозначается () или .

Пример: Делим первую строку на 3.

Теперь вычитаем из второго и третьего столбца первый с коэффициентами 2/3 и 1/3 соответственно.

Вычитаем из второй и третьей строки первую с коэффициентами 2 и 1 соответственно.

и т.д. В итоге получим матрицу: Следовательно ранг матрицы равен 3.

[решено] Какой из следующих определителей имеет нулевое значение? 1. \(\

Какой из следующих определителей имеет нулевое значение?

1. \(\left| {\begin{array}{*{20}{c}} {41}&1&5\\ {79}&7&9 \\ {29}&5&3 \end{массив}} \right|\)

2. \(\left| {\begin{array}{*{20}{c}} 1&a&{b + c}\\ 1&b& {c + a}\\ 1&c&{a + b} \end{массив}} \right|\)

3.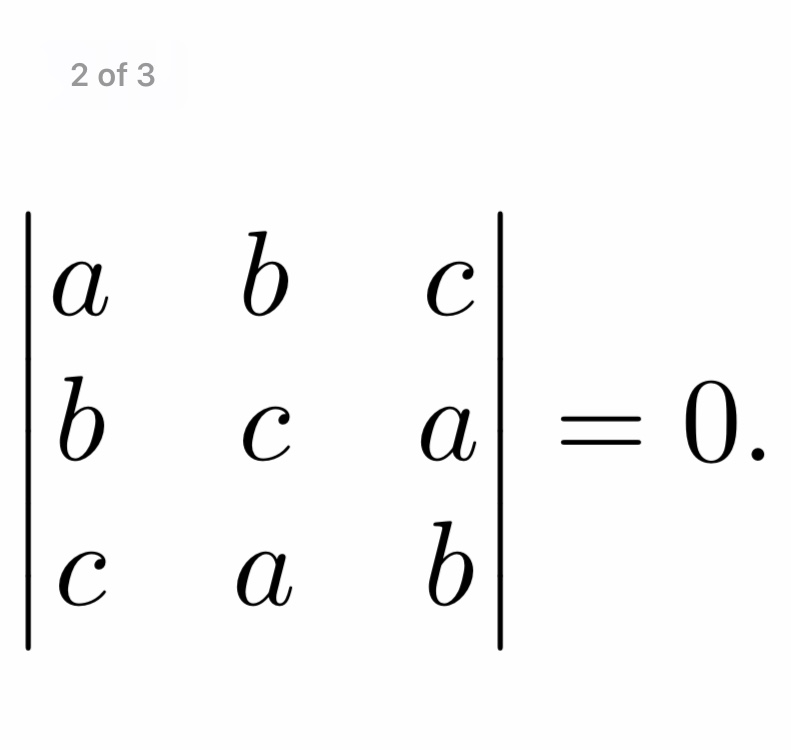 \(\left| {\begin{array}{*{20}{c}} 0&c&b\ \ { — c}&0&a\\ { — b}&{ — a}&0 \end{массив}} \right|\)

Выберите правильный ответ, используя приведенный ниже код.

1. 1 и 2 только
2. 2 и 3 только
3. 1 и 3 только
4. 1, 2 и 3

Вариант 4: 1, 2 и 3

БЕСПЛАТНЫЙ

Электрические заряды и закон Кулона (Основой))

82,6 тыс. пользователей

10 вопросов

10 баллов

10 минут

Понятие :

• Элементарные преобразования не изменяют значение определителя матрицы.
• Если любые две строки (столбца) матрицы совпадают, то значение определителя равно нулю
• Если все элементы одной строки (столбца) умножить на одну и ту же величину, скажем, k, то значение нового определителя в k раз больше значения исходного определителя.
• Если \(A = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{{ a_{33}}} \end{array}} \right]\) – квадратных матриц порядка 3 9.0039 , то определитель A определяется как:

          |А| = A ₁₁ × {(A ₂₂ × A ₃₃ ) — ( ₂₃ × A ₃₂ )} — ₁₂ × {A ₂₁ × A ₃₃ ) — A ₂₁ × A ₃₃ ) — A ₂₁ × A ₃₃ ) — A ₂₁ × A ₃₃ ) — A ₂₁ × a ₃₃ ) — A ₂₁ × a _{3 3}) — A ₂₁ × A ₃ × {A ₂₁ × a ₃ × (A ₂₃ × A ₃₁ )} + A ₁₃ × {(A ₂₁ × A ₃₂ ) — A ₂₂ × A ₃₁ )}

9002 888899.999999999999999999999999888888888888888888888888888888888888тели ₃₁ ). :

Код 1 : \(\left| {\begin{array}{*{20}{c}} {41}&1&5\\ {79}&7&9\\ {29}&5&3 \end{array}} \right|\)

Применить C ₁ ↔ C ₁  — 8 ⋅ C ₃  на указанном выше определителе получаем

\(\ Стрелка вправо \ влево | {\ begin {array} {* {20} {c}} {41} & 1 & 5 \\ {79} & 7 & 9 \\ {29} & 5 & 3 \ end {array}} \ right | = \ left | {\ begin{array}{*{20}{c}} {1}&1&5\\ {7}&7&9\\ {5}&5&3 \end{array}} \right|\)

Как мы знаем, если любые два строки (столбцы) матрицы одинаковы, то значение определителя равно нулю.

\(\Стрелка вправо \влево| {\begin{array}{*{20}{c}} {41}&1&5\\ {79}&7&9\\ {29}&5&3 \end{массив}} \right| = 0\)

Итак, матрица, представленная кодом 1 , имеет значение определителя 0 .

Код 2 : \(\left| {\begin{array}{*{20}{c}} 1&a&{b + c}\\ 1&b&{c + a}\\ 1&c&{a + b} \ end{array}} \right|\)

Apply C ₃ ↔ C ₂  + C ₃  на указанный выше определитель получаем

\(\Стрелка вправо \влево| {\begin{array}{*{20}{c}} 1&a&{b + c}\\ 1&b&{c + a}\\ 1&c&{a + b} \end{array} } \right| = \left| {\begin{array}{*{20}{c}} 1&a&{a + b + c}\\ 1&b&{b + c + a}\\ 1&c&{a + b + c } \end{array}} \right|\)

Поскольку мы знаем, что если все элементы одной строки (столбца) умножить на одну и ту же величину, скажем, k, то значение нового определителя в k раз больше значения исходного определитель.

\(\Стрелка вправо \влево| {\begin{array}{*{20}{c}} 1&a&{b + c}\\ 1&b&{c + a}\\ 1&c&{a + b} \end{array }} \right| = (a + b + c) \left| {\begin{array}{*{20}{c}} 1&a&{1}\\ 1&b&{1}\\ 1&c&{1} \end{ массив}} \справа|\)

Как известно, если любые две строки (столбца) матрицы совпадают, то значение определителя равно нулю.

\(\Стрелка вправо \влево| {\begin{array}{*{20}{c}} 1&a&{b + c}\\ 1&b&{c + a}\\ 1&c&{a + b} \end{array }} \right| = 0\)

Итак, матрица, представленная кодом 2, имеет значение определителя равное нулю.

Код 3: \(\left| {\begin{array}{*{20}{c}} 0&c&b\\ { — c}&0&a\\ { — b}&{ — a}&0 \end{array} } \справа|\)

 

\(\Стрелка вправо \влево| {\begin{array}{*{20}{c}} 0&c&b\\ { — c}&0&a\\ { — b}&{ — a}&0 \end{array}} \right| = 0 \cdot (0 \ + a) — c \cdot (0 \ + ab) + b \cdot (ac \ — 0) = 0\)

Итак, матрица, представленная кодом 3, имеет определяющее значение нуль.

Значит, вариант D правильный

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления NDA

Последнее обновление: 21 декабря 2022 г.

UPSC NDA (I) Срок подачи заявок продлен до 12 января 2023 г. до 18:00. Союзная комиссия по государственной службе (UPSC) выпустила Уведомление NDA I 2023 о 395 вакансиях. Процесс отбора на экзамен включает в себя письменный экзамен и собеседование SSB. Кандидаты, прошедшие успешный отбор в соответствии с UPSC NDA, получат заработную плату в диапазоне от рупий до от 15 600 до рупий. 39 100. Ожидается, что будет выпущено новое уведомление для UPSC NDA.

Свойства определителей | Superprof

Что такое детерминанты?

В линейной алгебре мы можем вычислить определители квадратных матриц. Квадратная матрица — это матрица, имеющая одинаковое количество строк и столбцов. Например, квадратная матрица порядка 2×2 имеет две строки и два столбца. Точно так же квадратная матрица порядка 3×3 имеет три строки и три столбца. Точно так же у нас есть матрицы более высокого порядка, такие как 4×4, 5×5 и так далее. Детерминанты можно использовать для анализа или поиска решений линейных уравнений. Помимо линейной алгебры, детерминанты имеют множество приложений в таких областях, как инженерия, экономика, естественные науки и социальные науки.

Определитель матрицы A обозначается как |A| или det A. Определитель матрицы 2×2 легко вычислить. Например, рассмотрим следующую квадратную матрицу.

Определитель вышеуказанной матрицы будет обозначаться как |B|. Он вычисляется путем умножения диагоналей и помещения между ними знака минус.

|Б| = mp — no

Определители матриц 3×3 и 4×4 вычисляются с использованием других и несколько сложных процедур, чем эта. Вы также можете использовать матричный калькулятор для вычисления определителей производных высших порядков.

В этой статье мы обсудим некоторые свойства определителей.

 

Лучшие репетиторы по математике

Поехали

1. Свойство отражения

Если строки матрицы преобразовать в столбцы, а столбцы в строки, то определитель не изменится. Это свойство известно как свойство отражения определителей. Можно также сказать, что определитель матрицы и ее транспонированный равны. Чтобы найти транспонированную матрицу, мы превращаем строки в столбцы, а столбцы в строки.

 

2. All-zero Свойство

Если каждый элемент в строке или столбце равен нулю, то определитель матрицы равен нулю.

 

3. Свойство пропорциональности или повторения

Если все элементы строки или столбца в матрице идентичны или пропорциональны элементам какой-либо другой строки или столбца, то определитель матрицы равен нулю.

Например, рассмотрим следующую матрицу, в которой вторая строка пропорциональна первой строке.

Так как элементы второй строки получаются умножением элементов первой строки на число 3, то определитель матрицы равен нулю.

 

4. Свойство переключения

Если поменять местами любые две строки или столбца, то определитель матрицы меняет знак. Это значит, что если до перестановки она была положительной, то после смены позиции станет отрицательной, и наоборот.

Например, рассмотрим следующую матрицу:

Определитель этой матрицы равен |A| = 18 — 15 = 3

Теперь посмотрим, что происходит при перестановке строк или столбцов.

Мы поменяли местами ряды. Определитель матрицы будет |A| = 15 — 18 = -3.

 

5. Свойство треугольника

Если каждый элемент в матрице выше или ниже главной диагонали равен нулю, определитель равен произведению элементов на диагонали.

Например, рассмотрим следующую матрицу:

Определитель матрицы будет:

 

некоторая ненулевая константа, то определитель такой матрицы будет умножен на эту же константу.

Например, рассмотрим следующую матрицу:

Ее определитель равен |A| = 8 — 2 = 6

Умножим все элементы приведенной выше матрицы на 2.

|A| = 16 -4 = 12

В примере выше видно, что после умножения одной строки на число 2 определитель новой матрицы также умножается на то же число 2.

 

7. Свойство суммы

 

Решить матрицы, используя свойства определителей

 

Пример 10003

 

 

Решение

В этом примере нам даны две матрицы. Нам нужно найти определители этих матриц. Начнем с матрицы A.

Вы можете видеть, что в приведенной выше матрице строки и столбцы пропорциональны друг другу. Другими словами, мы можем сказать, что когда мы добавляем 3 к каждому элементу в строке 1, мы получаем строку 2. Точно так же, когда мы добавляем 3 к каждому элементу в строке 2, мы получаем строку 3.

Свойство пропорциональности или повторяемости говорит о том, что определитель такой матрицы равен нулю. Отсюда можно сказать, что:

Теперь перейдем к матрице B. В матрице B все элементы выше и ниже главной диагонали равны нулям. По свойству треугольности определитель такой матрицы равен произведению элементов диагонали. Следовательно, определитель матрицы B равен:

 

Пример 2

Вычислите определитель следующей матрицы, используя свойства определителей:

Решение

Вы можете видеть, что в этой матрице все элементы в первой строке кратны 5.

No related posts.