Как находить асимптоты: Как найти асимптоты графика функции, примеры решений

2

Задание 20. Нахождение асимптот графика функции – 1 ч — Студопедия

Поделись  

Цель: формирование умения находить асимптоты графика функции.

Задание для самостоятельной внеаудиторной работы:

&20.1.Запомните основные виды асимптот графика функции.Проанализируйте, в каких случаях график функции имеет вертикальную асимптоту, в каких — горизонтальную или наклонную.

&20.2.Детально изучите и постарайтесь освоить алгоритм, позволяющий находить асимптоты графика функции.

?20.3. Найдите асимптоты графика функции:

а) ; б) ; в) ; г) .

¶ 20.4. Найдите асимптоты графика функции:

а) ; б) .

Методические указания по выполнению работы:

Для успешного решения задач необходимо знание следующего теоретического материала:

Поиск асимптот является одним из важных этапов построения графиков функций.

Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная.

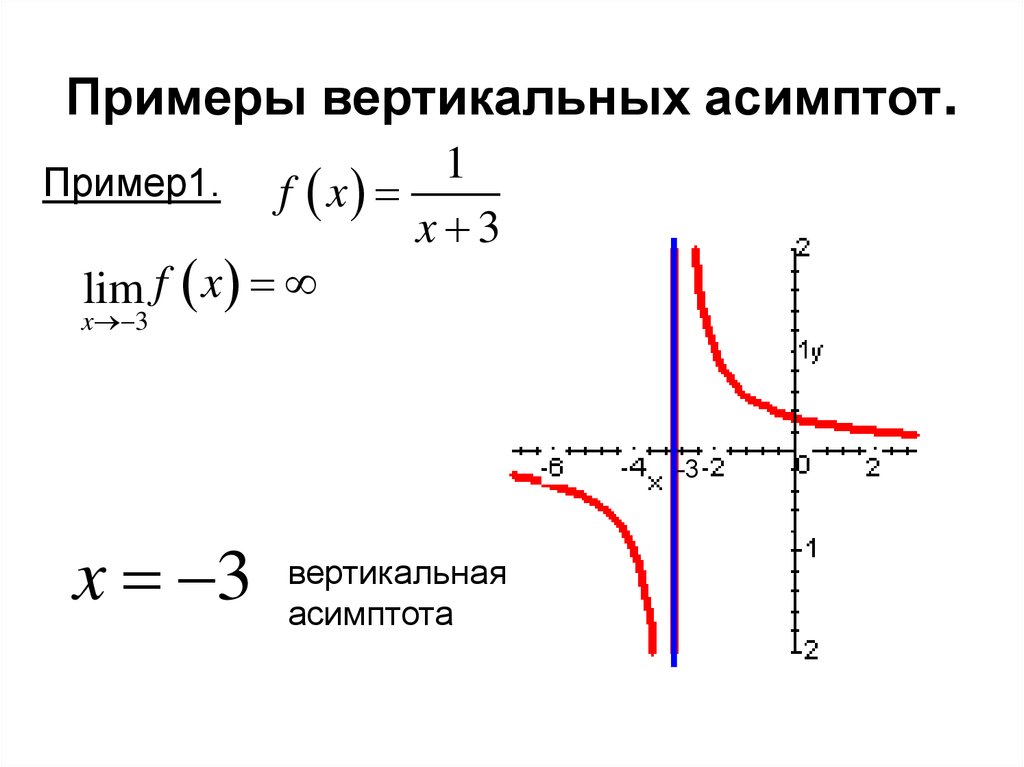
1. Прямая х=а называется вертикальной асимптотой функции , если .

2. Прямая у=с называется горизонтальной асимптотой функции , если .

3. Прямая у=kx+b называется наклонной асимптотой функции , если .

На чертеже асимптоты принято обозначать пунктирными линиями.

Рассмотрим следующий искусственно составленный график функции (рис.1), на примере которого хорошо видны все виды асимптот:

у=f(x)

у=kx+b

Рис. 1

х=а – вертикальная асимптота

у=c – горизонтальная асимптота

у=kx+b – наклонная асимптота

Горизонтальные и наклонные асимптоты рассматриваются только при условии →∞.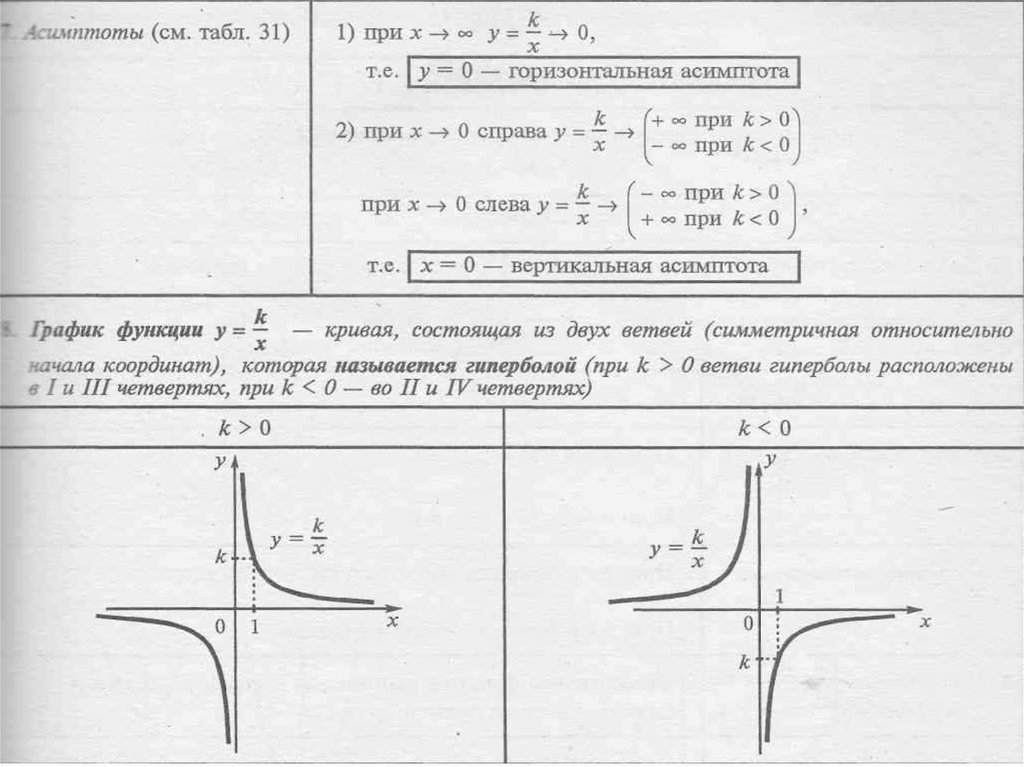

Иногда их различают на горизонтальные и наклонные асимптоты при →+∞ и →-∞.

Для поиска асимптот удобно использовать следующий алгоритм:

1. Для поиска вертикальных асимптот находим точки, не принадлежащие области определения (х=а) и проверяем следующее условие: если , то х=а – вертикальная асимптота.

Вертикальных асимптот может быть одна, несколько или не быть совсем.

1. Для поиска горизонтальных асимптот находим .

• Если с – число, то у=с – горизонтальная асимптота;
• Если с – бесконечность, то горизонтальных асимптот нет.

1. Для поиска наклонных асимптот находим .

• Если k – число, отличное от 0, то находим . Тогда у=kx+b – наклонная асимптота;
• Если k – бесконечность, то наклонных асимптот нет.

Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.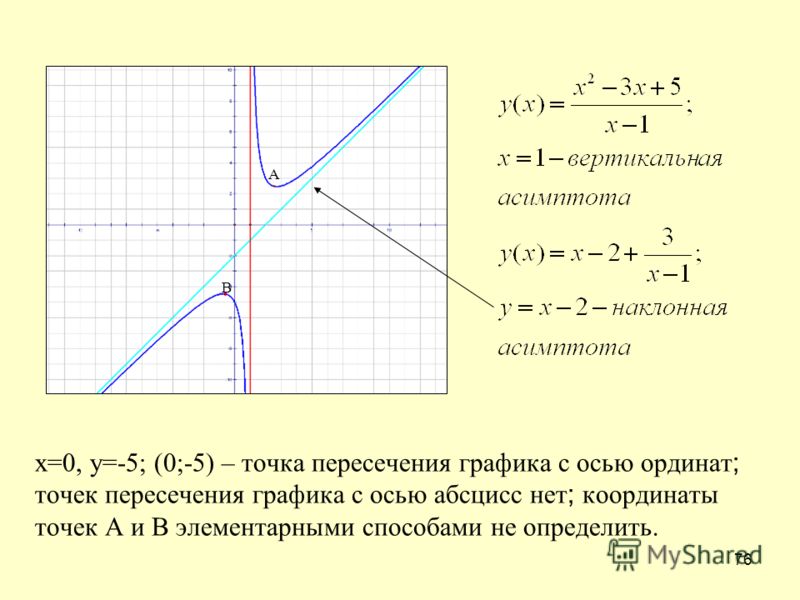

Рассмотрим примеры нахождения асимптот функции:

Пример 1. Найдите асимптоты графика функции .

Решение. 1. Найдем область определения функции: х-1≠0; х≠1.

Проверим, является ли прямая х=1 вертикальной асимптотой. Для этого вычислим предел функции в точке х=1: .

Получили, что , следовательно, х=1 — вертикальная асимптота.

2. Для поиска горизонтальных асимптот находим : с= .

Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с=2 (число), то у=2 – горизонтальная асимптота.

Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.

Таким образом, данная функция имеет вертикальную асимптоту х=1 и горизонтальную асимптоту у=2.

Ответ: графикфункции имеет вертикальную асимптоту х=1 и горизонтальную асимптоту у=2.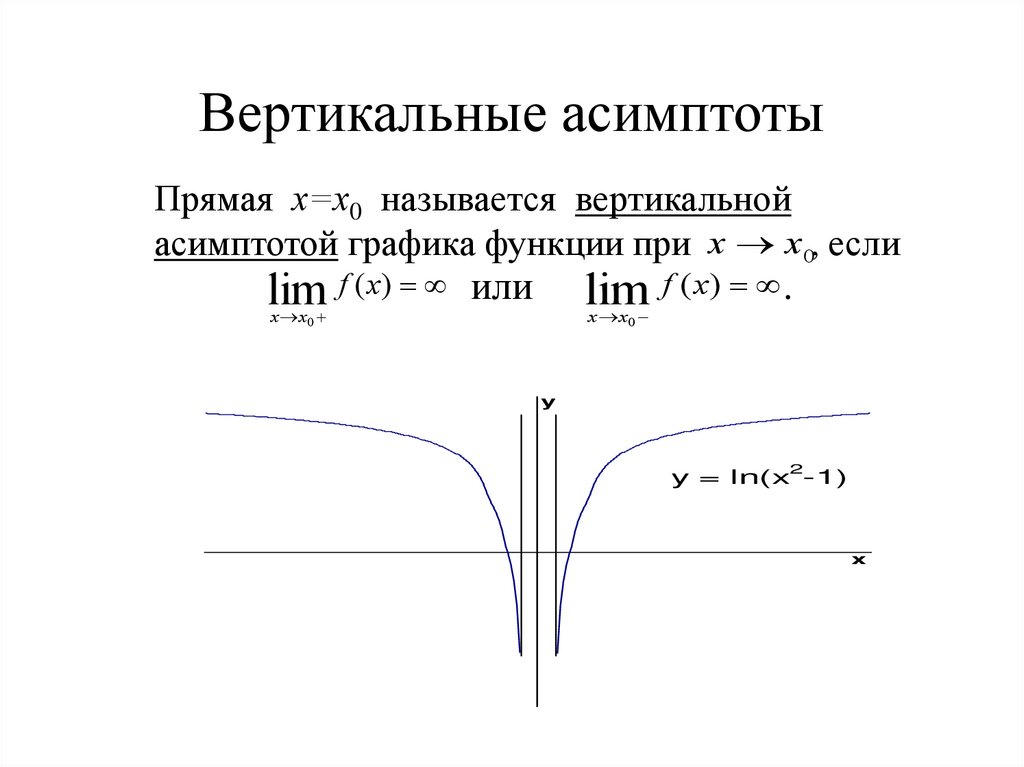

Пример 2. Найдите асимптоты графика функции .

Решение. 1. Найдем область определения функции: х-2≠0; х≠2.

Проверим, является ли прямая х=2 вертикальной асимптотой. Для этого вычислим предел функции в точке х=2: .

Получили, что , следовательно, х=2 — вертикальная асимптота.

2. Для поиска горизонтальных асимптот находим : с= .

Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя:

с= = . Т.к. с – бесконечность, то горизонтальных асимптот нет.

3. Для поиска наклонных асимптот находим :

= = = .

Получили неопределенность вида , воспользуемся правилом Лопиталя: = =1.Итак, 1. Найдем b по формуле: .

b= = =

= = .

Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.

Таким образом, данная функция имеет вертикальную асимптоту х=2 и наклонную асимптоту у=x+2.

Ответ: график функции имеет вертикальную асимптоту х=2 и наклонную асимптоту у=x+2.

Список литературы:

1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский — М.: Издательский центр «Академия», 2012. – 320с. – Глава 6, §6.9, стр. 144 – 146.

2. Валуцэ И.И. Математика для техникумов на базе средней школы: Учебное пособие. / И.И. Валуцэ, Г.Д. Дилигул.– 2-е изд., перераб. и доп. – М.: Наука, 1989. – 576 с. – Глава 7, § 41, стр. 231-232.



404 Cтраница не найдена

Размер:

AAA

Изображения Вкл. Выкл.

Обычная версия сайта

К сожалению запрашиваемая страница не найдена.

Но вы можете воспользоваться поиском или картой сайта ниже

Университет Майкопский государственный технологический университет – один из ведущих вузов юга России. История университета Анонсы Объявления Медиа Представителям СМИ Газета «Технолог» О нас пишут Ректорат Структура Филиал Политехнический колледж Медицинский институт Лечебный факультет Педиатрический факультет Фармацевтический факультет Стоматологический факультет Факультет послевузовского профессионального образования Факультеты Кафедры Ученый совет Дополнительное профессиональное образование Бережливый вуз – МГТУ Новости Объявления Лист проблем Лист предложений (Кайдзен) Реализуемые проекты Архив проектов Фабрика процессов Рабочая группа «Бережливый вуз-МГТУ» Вакансии Профсоюз Противодействие терроризму и экстремизму Противодействие коррупции WorldSkills в МГТУ Научная библиотека МГТУ Реквизиты и контакты Работа МГТУ в условиях предотвращения COVID-19 Документы, регламентирующие образовательную деятельность Абитуриентам Подача документов онлайн Абитуриенту 2022 Экран приёма 2022 Иностранным абитуриентам Международная деятельность Общие сведения Кафедры Новости Центр Международного образования Академическая мобильность и международное сотрудничество Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Как стать участником программ академической мобильности Дни открытых дверей в МГТУ Подготовительные курсы Подготовительное отделение Курсы для выпускников СПО Курсы подготовки к сдаче ОГЭ и ЕГЭ Онлайн-курсы для подготовки к экзаменам Подготовка школьников к участию в олимпиадах Малая технологическая академия Профильный класс Индивидуальный проект Кружковое движение юных технологов Олимпиады, конкурсы, фестивали Архив Веб-консультации для абитуриентов Олимпиады для школьников Отборочный этап Заключительный этап Итоги олимпиад Профориентационная работа Стоимость обучения Студентам Студенческая жизнь Стипендии Организация НИРС в МГТУ Студенческое научное общество Студенческие научные мероприятия Конкурсы Команда Enactus МГТУ Академическая мобильность и международное сотрудничество Образовательные программы Подготовка кадров высшей квалификации Аспирантура Ординатура Расписание занятий Расписание звонков Онлайн-сервисы Социальная поддержка студентов Общежития Трудоустройство обучающихся и выпускников Информация о Центре Цели и задачи центра Контактная информация Положение о центре Договоры о сотрудничестве с организациями, предприятиями Партнеры Работодателям Размещение вакансий Ярмарки Вакансий Студентам и выпускникам Вакансии Стажировки Карьерные мероприятия Карьерные сайты Сегодня Современный Государственный Университет — это один из самых крупных многопрофильных вузов Поволжья, обеспечивающий формирование интеллектуального потенциала и способствующий социально-экономическому развитию региона. HeadHunter Работа в России Факультетус Карьерные возможности для лиц с инвалидностью и ОВЗ Трудоустройство иностранных студентов Обеспеченность ПО Инклюзивное образование Условия обучения лиц с ограниченными возможностями Доступная среда Ассоциация выпускников МГТУ Перевод из другого вуза Вакантные места для перевода

Наука и инновации Научная инфраструктура Проректор по научной работе и инновационному развитию Научно-технический совет Управление научной деятельностью Управление аспирантуры и докторантуры Точка кипения МГТУ О Точке кипения МГТУ Руководитель и сотрудники Документы Контакты Центр коллективного пользования Центр народной дипломатии и межкультурных коммуникаций Студенческое научное общество Новости Научные издания Научный журнал «Новые технологии» Научный журнал «Вестник МГТУ» Научный журнал «Актуальные вопросы науки и образования» Публикационная активность Конкурсы, гранты Научные направления и результаты научно-исследовательской деятельности Основные научные направления университета Отчет о научно-исследовательской деятельности в университете Результативность научных исследований и разработок МГТУ Финансируемые научно-исследовательские работы Объекты интеллектуальной собственности МГТУ Результативность научной деятельности организаций, подведомственных Минобрнауки России (Анкеты по референтным группам) Студенческое научное общество Инновационная инфраструктура Федеральная инновационная площадка Проблемные научно-исследовательские лаборатории Научно-исследовательская лаборатория «Совершенствование системы управления региональной экономикой» Научно-исследовательская лаборатория проблем развития региональной экономики Научно-исследовательская лаборатория организации и технологии защиты информации Научно-исследовательская лаборатория функциональной диагностики (НИЛФД) лечебного факультета медицинского института ФГБОУ ВПО «МГТУ» Научно-исследовательская лаборатория «Инновационных проектов и нанотехнологий» Научно-техническая и опытно-экспериментальная база Центр коллективного пользования Конференции Международная научно-практическая конференция «Актуальные вопросы науки и образования» VI Международная научно-практическая онлайн-конференция Международная деятельность Иностранным студентам Международные партнеры Академические обмены, иностранные преподаватели Академическая мобильность и фонды Индивидуальная мобильность студентов и аспирантов Как стать участником программ академической мобильности Объявления Факультет международного образования Сведения об образовательной организации

Горизонтальные асимптоты и пересечения | Колледж Алгебра

Результаты обучения

• Используйте степень числителя и знаменателя рациональной функции, чтобы определить, какой вид горизонтальной асимптоты она будет иметь.
• Рассчитать наклонные асимптоты.
• Определите точки пересечения рациональной функции в факторизованной форме.

В то время как вертикальные асимптоты описывают поведение графика, когда выход становится очень большим или очень маленьким, горизонтальные асимптоты помогают описать поведение графика как .0013 ввод становится очень большим или очень маленьким. Напомним, что поведение конца многочлена будет отражать поведение старшего члена. Точно так же конечное поведение рациональной функции будет отражать отношение старших членов функций числителя и знаменателя.

Есть три разных результата при проверке горизонтальных асимптот:

Случай 1: Если степень знаменателя > степени числителя, существует горизонтальная асимптота при [latex]y=0[/latex] . 9{2}}=\frac{4}{x}[/latex]. Это говорит нам о том, что при неограниченном увеличении или уменьшении входных данных эта функция будет вести себя аналогично функции [latex]g\left(x\right)=\frac{4}{x}[/latex], а выходные данные будет приближаться к нулю, что приводит к горизонтальной асимптоте при [latex]y=0[/latex].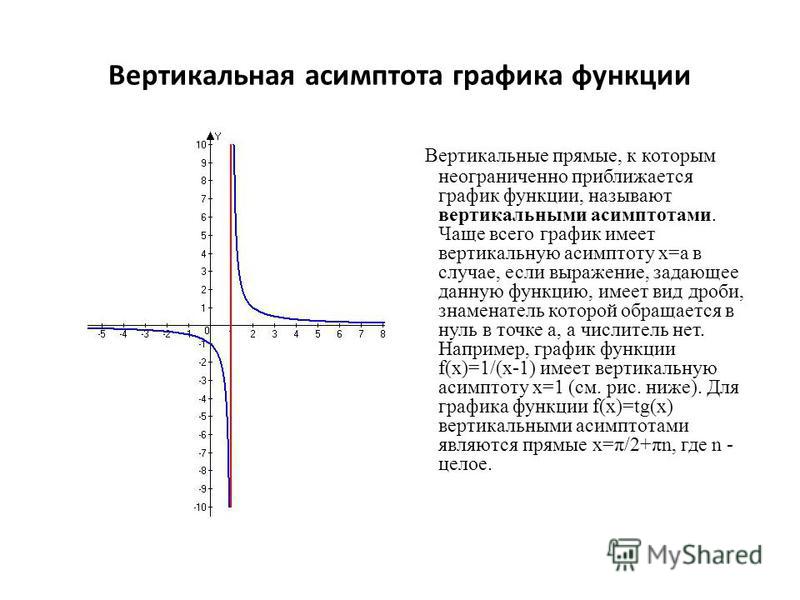 Обратите внимание, что этот график пересекает горизонтальную асимптоту.

Горизонтальная асимптота [латекс]y=0[/латекс], когда [латекс]f\left(x\right)=\dfrac{p\left(x\right)}{q\left(x\right)}, q\left(x\right)\ne{0}\text{, где степень }p<\text{степень q}[/latex]. 9{2}}{x}=3x[/латекс]. Это говорит нам о том, что при неограниченном увеличении или уменьшении входных данных эта функция будет вести себя аналогично функции [латекс]г\влево(х\вправо)=3х[/латекс]. По мере того, как входы становятся большими, выходы будут расти, а не выравниваться, поэтому этот график не имеет горизонтальной асимптоты. Однако график [latex]g\left(x\right)=3x[/latex] выглядит как диагональная линия, и поскольку [latex]f[/latex] будет вести себя аналогично [latex]g[/latex] , он будет приближаться к линии, близкой к [latex]y=3x[/latex]. Эта линия представляет собой наклонную асимптоту (ПРИМЕЧАНИЕ: график самой функции является всего лишь «наброском» в пределах параметров асимптоты). 9{2}-2x+1}{x - 1}[/латекс]. Частное равно [латекс]3x+1[/латекс], а остаток равен 2. Наклонная асимптота представляет собой график прямой [латекс]г\влево(х\вправо)=3х+1[/латекс].

Случай 3: Если степень знаменателя = степени числителя, существует горизонтальная асимптота при [latex]y=\frac{{a}_{n}}{{b}_{n}} [/latex], где [latex]{a}_{n}[/latex] и [latex]{b}_{n}[/latex] — старшие коэффициенты [latex]p\left(x\right )[/латекс] и [латекс]q\left(x\right)[/latex] для [латекс]f\left(x\right)=\frac{p\left(x\right)}{q\left (x\right)},q\left(x\right)\ne 0[/latex]. 9{2}}=3[/латекс]. Это говорит нам о том, что по мере увеличения входных данных эта функция будет вести себя как функция [латекс]г\влево(х\вправо)=3[/латекс], которая представляет собой горизонтальную линию. Поскольку [латекс]x\to \pm \infty ,f\left(x\right)\to 3[/latex], получается горизонтальная асимптота при [latex]y=3[/latex]. Обратите внимание, что этот график пересекает горизонтальную асимптоту.

Горизонтальная асимптота, когда [латекс]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0\text{, где степень }p=\text{степень }q[/латекс].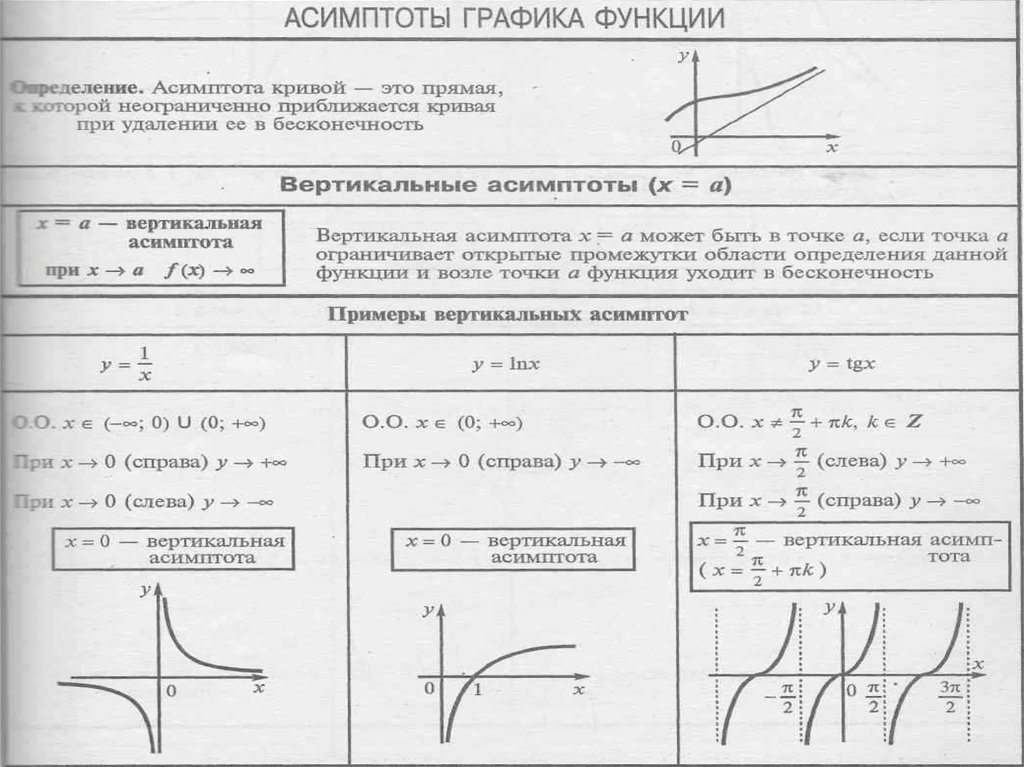

Обратите внимание, что хотя график рациональной функции никогда не пересекает вертикальную асимптоту , график может пересекать или не пересекать горизонтальную или наклонную асимптоту. Кроме того, хотя график рациональной функции может иметь много вертикальных асимптот, график будет иметь не более одной горизонтальной (или наклонной) асимптоты.

Следует отметить, что если степень числителя больше степени знаменателя более чем на единицу, конечное поведение графика будет имитировать поведение сокращенной конечной дроби. Например, если бы у нас была функция 9{4}[/latex],

поведение графика в конце будет похоже на поведение четного многочлена с положительным старшим коэффициентом.

As [latex]x\to \pm \infty , f\left(x\right)\to \infty [/latex]

 

Общее примечание: горизонтальные асимптоты рациональных функций

Горизонтальная асимптота рациональной функции можно определить, глядя на степени числителя и знаменателя.

• Степень числителя меньше степени знаменателя: горизонтальная асимптота в
• [латекс]y=0[/латекс]
• Степень числителя больше степени знаменателя на единицу : нет горизонтальной асимптоты; наклонная асимптота.
• Степень числителя равна степени знаменателя: горизонтальная асимптота при отношении старших коэффициентов.

Пример: определение горизонтальной и наклонной асимптот

Для функций ниже определите горизонтальную или наклонную асимптоту. 9{3}-8}[/латекс]

Показать раствор

Попробуйте

Посмотрите это видео, чтобы увидеть больше рабочих примеров определения того, какой тип горизонтальной асимптоты будет иметь рациональная функция.

Пример: определение горизонтальных асимптот

Ранее в задаче о концентрации сахара мы создали уравнение [латекс]C\left(t\right)=\dfrac{5+t}{100+10t}[/latex] .

Найдите горизонтальную асимптоту и интерпретируйте ее в контексте задачи.

Показать раствор

Пример: определение горизонтальной и вертикальной асимптот

Найдите горизонтальную и вертикальную асимптоты функции

[латекс]f\left(x\right)=\dfrac{\left(x — 2\right)\left(x +3\вправо)}{\влево(x — 1\вправо)\влево(x+2\вправо)\влево(x — 5\вправо)}[/latex]

Показать решение

Попробуйте

Найдите вертикальную и горизонтальную асимптоты функции:

[латекс]f\left(x\right)=\dfrac{\left(2x — 1\right)\left(2x+1\right) )}{\влево(х — 2\вправо)\влево(х+3\вправо)}[/латекс]

Показать раствор

A Общее примечание: пересечения рациональных функций

рациональная функция будет иметь y -пересечение, когда вход равен нулю, если функция определена в нуле. У рациональной функции не будет [latex]y[/latex]-перехвата, если функция не определена в нуле.

Аналогично, рациональная функция будет иметь [latex]x[/latex]-перехваты на входах, которые приводят к нулю на выходе. Поскольку дробь равна нулю только тогда, когда числитель равен нулю, пересечения [latex]x[/latex] могут происходить только тогда, когда числитель рациональной функции равен нулю.

Пример: нахождение точек пересечения рациональной функции

Найдите точки пересечения [латекс]f\left(x\right)=\dfrac{\left(x — 2\right)\left(x+3\right) }{\влево(x — 1\вправо)\влево(x+2\вправо)\влево(x — 5\вправо)}[/латекс].

Показать решение

Попробуйте

Для заданной функции обратного квадрата, которая сдвигается вправо на 3 единицы и вниз на 4 единицы, запишите это как рациональную функцию. Затем найдите точки пересечения [latex]x[/latex]– и [latex]y[/latex] и горизонтальную и вертикальную асимптоты.

Показать раствор

Посмотрите следующее видео, чтобы увидеть больше рабочих примеров нахождения асимптот, точек пересечения и дыр рациональных функций.

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Как найти горизонтальные асимптоты

Горизонтальная асимптота — это горизонтальная линия на графике, до которой выход функции приближается, но никогда не достигает. В более математических терминах функция будет приближаться к горизонтальной асимптоте тогда и только тогда, когда вход функции растет до бесконечности или отрицательной бесконечности, а выход функции приближается к постоянному значению с. Символически это можно представить двумя предельными выражениями:

По сути, график функции будет иметь горизонтальную асимптоту, если выход функции приближается к некоторой константе, когда x растет произвольно большим в положительном или отрицательном направлении. Если одно из приведенных выше выражений верно, то график функции будет иметь горизонтальную асимптоту на линии y=c. Примером может служить функция ƒ(x)=(8x²-6)/(2x²+3) . Построение графика этой функции дает нам:

Эта рациональная функция имеет горизонтальную асимптоту при y=4. Обратите внимание, что по мере неограниченного роста значения x в любом направлении синий график приближается к пунктирной красной линии при y=4, но никогда не касается ее. Другие виды асимптот включают вертикальные асимптоты и наклонные асимптоты. Любая рациональная функция имеет не более одной горизонтальной или наклонной асимптоты, но может иметь много вертикальных асимптот.

Горизонтальная асимптота также может быть определена через производные. В двух словах, функция имеет горизонтальную асимптоту, если для ее производной x стремится к бесконечности, предел уравнения производной равен 0. Это соответствует касательным линиям графика, приближающимся к горизонтальной асимптоте, все ближе и ближе к наклону 0

Есть несколько простых правил для определения того, имеет ли рациональная функция горизонтальную асимптоту. Но чтобы понять их, нам сначала нужно взглянуть на идею степень многочлена.

Степень многочлена

Многочлен — это выражение, состоящее из ряда переменных и коэффициентов, связанных только с операторами сложения, вычитания и умножения. Общая форма полинома —

AX ^N + по ^M

, где A и B — константы, A и B — это константы, A и B — A и B — A и B — A и B . неопределенно ), а n и m — некоторые неотрицательные целые числа. Так, например, 3x ² +4x-6 является полиномиальным выражением, поскольку оно состоит из комбинации коэффициентов и переменных, связанных оператором сложения. Аналогично, 9x ⁴ -3xz ³ +7y ² также является полиномом с тремя отдельными переменными.

степень многочлена можно определить, сложив вместе степени его отдельных членов монома. Степень терма равна сумме верхних индексов показателей степени переменной (переменных) в одном мономиальном терме. Степень всего многочлена равна наибольшей степени его отдельных членов монома.

. +2x ¹ y ¹ -7x ⁰ y ⁰ , имеет 4 термина. Первый член 4z ⁴ x ³ имеет степень 7 (3+4), второй член 6x ³ y ² имеет степень 5 (3+2), третий член 2x ¹ y ¹ степень 2 (1+1) и четвертый член 7x ⁰ y ⁰  степень 0 (0+0). Поскольку 7 является мономом с наивысшей степенью, степень всего полинома равна 7. Правила нахождения горизонтальных асимптот. Имеет ли рациональная функция в виде R(x)=P(x)/Q(x) горизонтальную асимптоту, зависит от степени многочленов числителя и знаменателя P(x) и Q(x).

Общие правила следующие:

• Если степень вершины < степень основания , то функция имеет горизонтальную асимптоту при y=0. В функции ƒ(x) = (x+4)/(x ² -3x) степень члена в знаменателе больше, чем у члена в числителе, поэтому функция имеет горизонтальную асимптоту при y=0.
• Если степень вершины = степень основания , разделите коэффициенты членов высшей степени. Например, в функции ƒ(x)=(8x²-6)/(2x²+3) степень верхнего и нижнего многочленов равна 2. Деление коэффициентов членов высшей степени дает 8/2= 9.0021 4.  Таким образом, функция имеет горизонтальную асимптоту при y=4.
• Если степень вершины > степени основания , то функция не имеет горизонтальной асимптоты. ƒ(x) = (2x ² )/(x-5) не имеет горизонтальной асимптоты, поскольку степень полинома числителя больше степени полинома знаменателя.

В особых случаях, когда степень числителя больше знаменателя ровно на 1, график будет иметь наклонную асимптоту.

Как и все, что связано с функциями, графическое изображение уравнения может помочь вам определить любые горизонтальные асимптоты. Хотя построение графика не является способом доказать, что функция имеет горизонтальную асимптоту, оно может быть полезным и указать правильное направление для ее поиска.

Задачи с решениями

Давайте рассмотрим некоторые задачи, чтобы привыкнуть к этим правилам нахождения горизонтальных асимптот.

Найдите горизонтальные асимптоты (если есть) следующих функций:

1. ƒ(x)=(3x²-5)/(x²-2x+1)
2. ƒ(x)=(x ² -9)/(x+1)
3. ƒ(x)= (x-12)/(2x ³ +5x-3)
4. ƒ(x)=(3x ³ +3x)/(2x ³ -2x)

1

2

2

2

2

2

2

2 (1)

Для ƒ(x)=(3x²-5)/(x²-2x+1) нам сначала нужно определить степень полиномов числителя и знаменателя. И верхняя, и нижняя функции имеют степень 2 (3x ² и x ² ), поэтому деление коэффициентов перед старшими членами дает нам 3/1=3. Таким образом, функция ƒ(x)=(3x²-5)/(x²-2x+1) имеет горизонтальную асимптоту в  г=3 .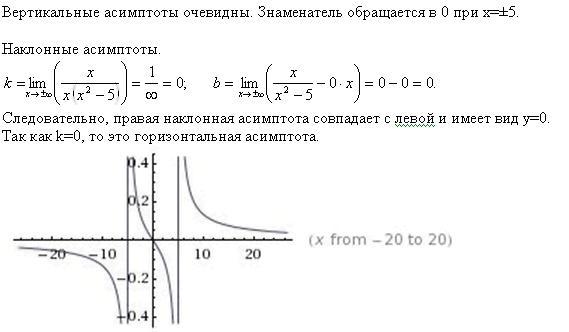 График этой функции дает нам:

В самом деле, по мере того, как x растет сколь угодно большим в положительном и отрицательном направлениях, выход функции ƒ(x)=(3x²-5)/(x²-2x+1) приближается к прямой в точке y =3. Обратите внимание, что этот график пересекает свою горизонтальную асимптоту в одной точке, прежде чем бесконечно приближаться к ней.

(2)

Для ƒ(x)=(x ² -9)/(x+1) нам снова нужно определить степень верхнего и нижнего членов. Степень вершины равна 2 (х ² ) и степень дна 1 (х). Поскольку степень числителя больше степени знаменателя, эта функция не имеет горизонтальных асимптот . Действительно, построение графика функции ƒ(x)=(x ² -9)/(x+1) дает нам:

Как мы видим, нет горизонтальной линии, к которой приближается этот график. Этот график, однако, имеет наклонную асимптоту, так как разница в градусах вершины и низа равна ровно 1 (он также имеет вертикальную асимптоту при x=-1)

(3)

Для ƒ(x)=(x-12)/(2x ³ +5x-3) степень верха равна 1 (x), а степень низа равна 3 (х ³ ). Поскольку градус наверху меньше, чем градус внизу, график имеет горизонтальную асимптоту при y=0. Опять же, построение графика этой функции дает нам:

Поскольку значение x становится очень большим в обоих направлениях, мы можем видеть, что график становится все ближе и ближе к линии при y=0.

(4)

Для ƒ(x)=(3x ³ +3x)/(2x ³ -2x) мы ясно видим, что и верхний, и нижний члены имеют степень 3 (3x ³ и 2x ³ ). Поскольку степени и вершины, и основания равны, мы делим коэффициенты перед старшими членами, чтобы получить 3/2. Таким образом, график имеет горизонтальную асимптоту на линии y=2/3. График этой функции дает нам:

Мы видим, что график приближается к линии при y=2/3. По мере того, как значения x становятся очень, очень большими, выход становится все ближе и ближе к 2/3. Эта функция также имеет 2 вертикальные асимптоты при -1 и 1,9. 0017

Примеры горизонтальных асимптот в реальном мире

Асимптоты в целом могут показаться просто математическим курьезом. В конце концов, пределы и бесконечности, связанные с асимптотами, могут показаться бессмысленными в контексте физического мира. Однако асимптотические рассуждения распространены в науках, и функции, содержащие асимптоты, используются для моделирования различных процессов или отношений между величинами. Очень часто процессы, стремящиеся к некоторому равновесному значению, можно моделировать с помощью горизонтальных асимптот.

Например, предположим, что мы растворяем какое-то растворенное вещество в растворителе. Для любого данного растворителя относительно некоторого растворенного вещества существует максимальное количество растворенного вещества, которое растворитель может растворить до того, как растворитель станет полностью насыщенным. Как только растворитель полностью насыщается растворенным веществом, растворитель больше не растворяет растворенное вещество.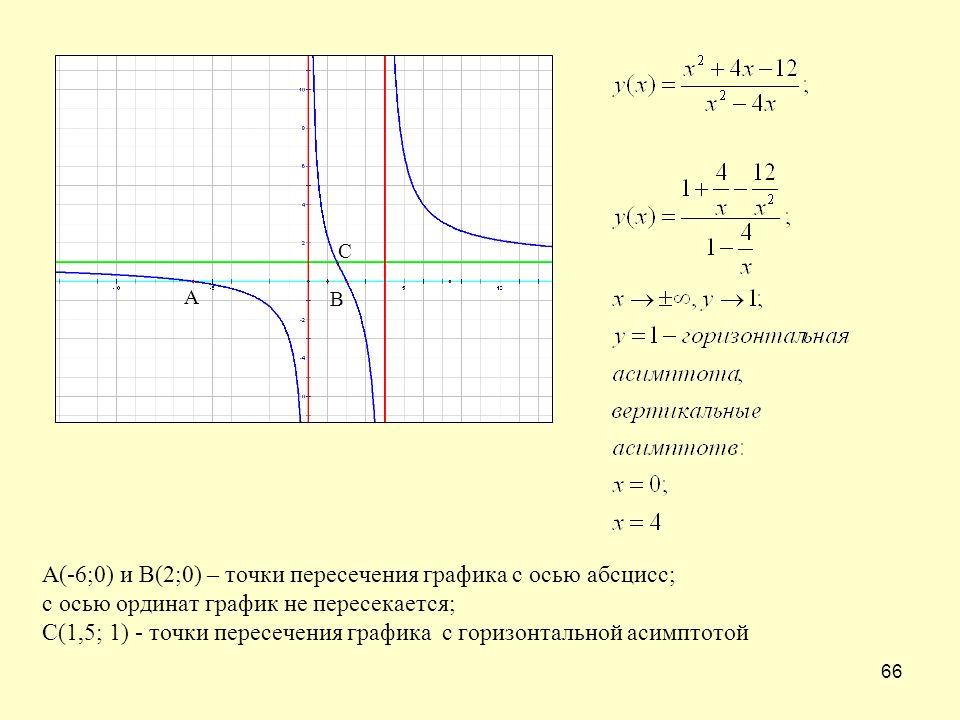

График зависимости количества добавленного растворенного вещества по оси x от концентрации растворенного вещества по оси y покажет, что по мере увеличения количества растворенного вещества (значение x) общая концентрация растворенного вещества (значение y ) увеличивается, пока не достигнет некоторой критической концентрации, после чего концентрация (значение y) больше не будет увеличиваться. Этот график будет иметь горизонтальную асимптоту на этой линии, которая равна концентрации, которая является точкой насыщения растворителя. Точные числовые характеристики будут зависеть от химического характера растворителя и растворенного вещества, но для любого растворителя и растворенного вещества существует точка, в которой растворенное вещество максимально сконцентрировано и больше не растворяется.

Точно так же моделирование скоростей диффузии жидкостей часто включает асимптотические рассуждения. По мере увеличения времени газ будет диффундировать, чтобы в равной степени заполнить контейнер. Вначале газ имеет очень высокую концентрацию, которая начинает падать по мере распространения газа в камере. В конце концов, молекулы газа достигнут точки, в которой они будут максимально равномерно распределены по контейнеру, после чего концентрация уже не может падать. График времени по оси x и концентрации по оси y даст вам красивую кривую, которая начинается при высокой концентрации, медленно спадает, а затем в конце концов приближается к некоторой горизонтальной асимптоте при некотором критическом значении концентрации — точке, в которой газ полностью равномерно распределены в контейнере.

Solving Higher-Degree Polynomials and Asymptotes of Rational Functions

Key Terms

Synthetic division

Asymptote

Vertical asymptote

Horizontal asymptote

Slant asymptote

 

Цели

Использовать синтетическое деление для факторизации многочленов более высокой степени

Найти асимптоты рациональных функций

 

Полиномы более высоких степеней

 

 

Уравнения, содержащие линейные или даже квадратичные полиномы, достаточно просты, но если речь идет о полиномах более высоких степеней, это может быть трудно или невозможно выполнить вручную. В этих случаях может понадобиться графический калькулятор или компьютер. Тем не менее, мы можем приблизительно найти корни многочленов более высоких степеней, построив графики функций (даже вручную), а в некоторых случаях мы можем использовать метод, называемый синтетическим делением, чтобы найти их и разложить многочлен на множители.

 

 

Многочлен с корнем x = a имеет бином ( x — a ) в качестве множителя. Thus, if f ( x ) is a polynomial of degree n where f ( a ) = 0, then

 

 

 

 

where g ( x ) является полиномом степени n – 1. Рассмотрим простой пример: f ( x ) = x ² – 1. Корень этого квадратного многочлена равен x = 1, поэтому он имеет множитель – 1):

 

 

 

 

Here, our remaining polynomial g ( x ) is simply x + 1, which corresponds to the root at x = – 1. Для общего полинома F ( x ) Определено следующим образом,

, где CA _N = 10012, где CA _N = 1, 10013.

 

 

Здесь константы a _i являются корнями f. Другими словами, многочлен степени n имеет n корней, но не все эти корни могут быть уникальными, как в случае с x ³ , что может быть учтено в выражении ( x – 0) ( x – 0) ( x – 0 ). (Кроме того, эти корни могут быть комплексными, как в случае с квадратичной функцией x ² + 1 — однако мы не будем рассматривать эту ситуацию.) Хотя это выражение делится на три двучлена, все соответствующие корни равны равен нулю.

 

 

Как только вы найдете корень полиномиальной функции, вы можете вынести соответствующий бином из полинома, оставив полином более низкой степени в качестве другого множителя. Иногда это упрощает нахождение оставшихся корней, хотя иногда задача остается такой же сложной. Чтобы найти этот полином более низкой степени, мы можем использовать метод, называемый синтетическое деление, более или менее длинное деление многочленов. Давайте рассмотрим пример:

Скажем, мы на графике функции или иным образом определили, что один из корней на x = 2. Мы знаем, что фактор F F F F F F F F F F F F F F F F F F F F F F F F F F f F x = 2. Мы знаем, что фактор F . бином x – 2:

Хотите узнать больше? Почему бы не пройти онлайн-курс Precalculus?

 

 

Вот процедура нахождения г ( x ).

 

 

1. Настройка подразделения. Нарисуйте перевернутую разделительную скобку, как показано ниже. За скобками напишите координату корня; внутри напишите коэффициенты полинома, который вы переводите из членов более высокого порядка в члены низшего порядка (включая нулевые коэффициенты).

 

 

2. Перенести первый коэффициент. Перенесите коэффициент старшего порядка ниже скобки.

3. Умножьте значение корня на последнее значение, которое вы написали под скобкой, затем запишите произведение под следующим коэффициентом внутри скобки. Теперь добавьте значения в этот столбец и запишите значение под скобкой в ​​том же столбце.

 

 

 

 

4. Повторяйте шаг 3, пока не дойдете до конца кронштейна. Последнее число, которое вы пишете под скобкой, должно быть равно нулю; если нет, то либо вы допустили ошибку, либо значение корня за скобками не является корнем многочлена.

21. Используйте нулевое значение вне скобок для записи биномиального множителя; используйте числа под скобками в качестве коэффициентов для нового многочлена.

Практическая задача:

. Найдите остальные корни многочлена.

 

 

Решение: Во-первых, мы можем выделить x ² из многочлена, чтобы несколько упростить его.

Поскольку корень многочлена равен x = –2, мы знаем, что он имеет множитель a04 + 904 x a03 ( x = –2). Давайте воспользуемся синтетическим делением, чтобы разделить этот двучлен. Во-первых, поставьте задачу.

Теперь выполните деление. Только результат показан ниже.

 

 

 

 

Thus, the polynomial can be expressed as follows:

 

 

 

 

Factor the quadratic:

 

 

 

Таким образом, корнями многочлена являются 0 (что встречается «дважды»), 1, –2 и 3.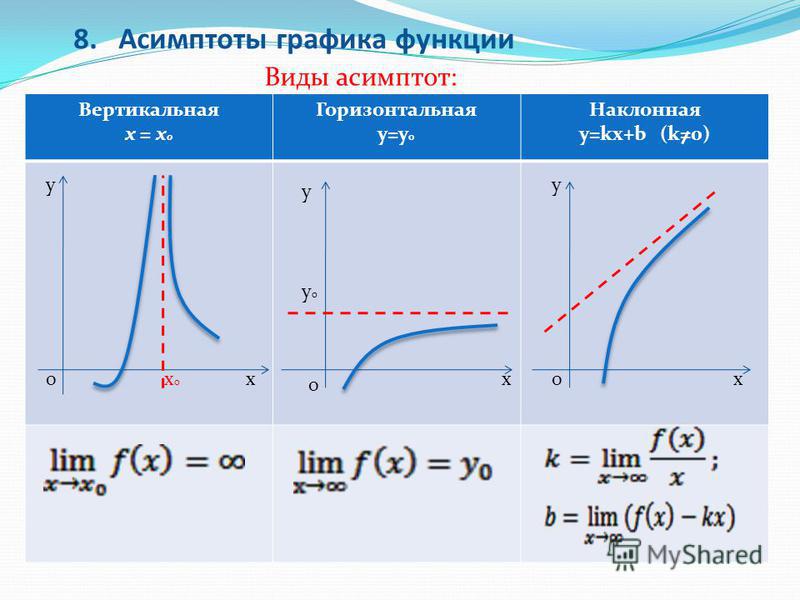 0014

 

 

Одной из особенностей рациональных функций, на которую стоит обратить внимание, является наличие (или отсутствие) асимптот: прямых, к которым функция приближается произвольно, но никогда не касается и не пересекает их. Рассмотрим простую рациональную функцию ; график этой функции показан ниже.

Обратите внимание, что определено для всех x , кроме нуля, — и это проявляется как функция, 9произвольно близкая к получению x 0013 y — ось, но никогда не касаясь ее. Другими словами, выберите значение x; независимо от того, насколько он мал, f ( x ) определен до тех пор, пока x не равно нулю. Таким образом, ось y- ( x = 0) является вертикальной асимптотой функции . Кроме того, обратите внимание, что никакое значение x , каким бы большим оно ни было, не может сделать функцию равной нулю.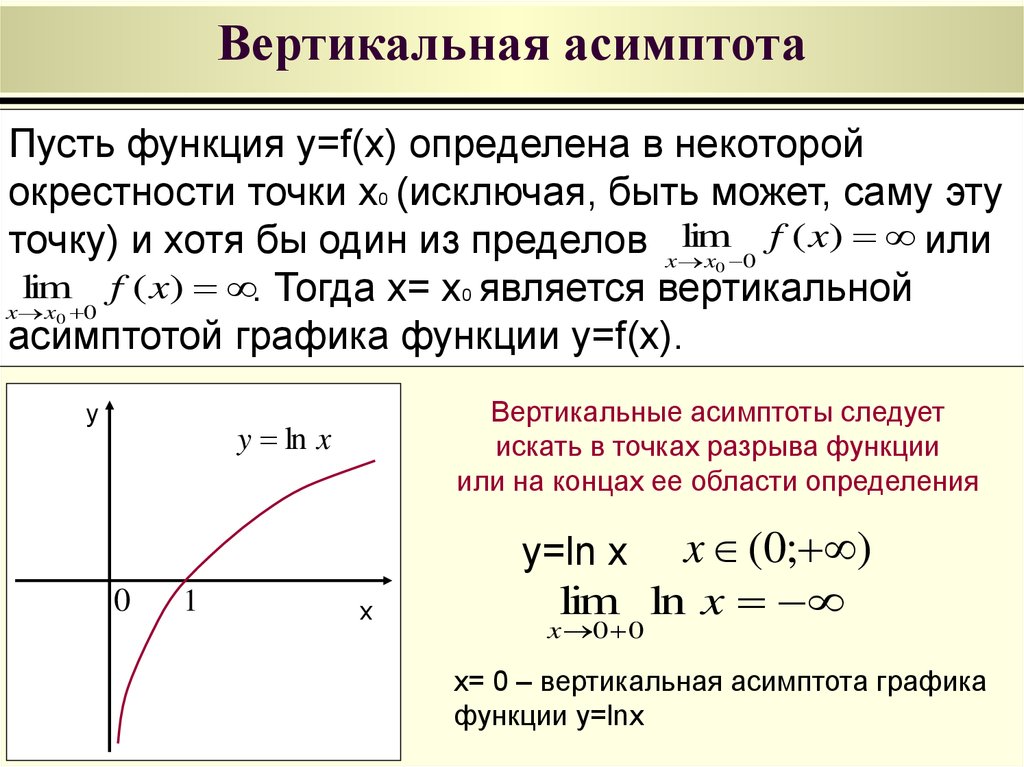 Тем не менее, чем больше x , тем ближе f ( x ) попадает на ось x . Таким образом, ось x ( y = 0) является горизонтальной асимптотой от . Эти асимптоты добавлены к графику ниже.

Асимптотами могут быть любые линии на координатной плоскости, и найти выражения для этих линий иногда бывает сложно. Встречаются и простые случаи, подобные приведенным выше. Обратите внимание, что всякий раз, когда домен (или диапазон) имеет вид ( a , b ) и ( b , c ), существует асимптота для значения независимой (или зависимой) переменной b. Обратите внимание, что для , например, областью является (-∞, 0) и (0, ∞). Таким образом, асимптота существует при x = 0. (Обратите внимание, что не все асимптоты соответствуют функциям! Любая асимптота x = a является прямой, но не функцией. ) Дополнительный момент, который следует отметить об асимптотах, заключается в том, что функция может фактически пересекать асимптоту в некоторой точке, но это пересечение не связано с той частью функции, которая демонстрирует асимптотическое поведение. То есть функция может приближаться к асимптоте, когда независимая переменная становится очень большой, но она также может пересекать асимптоту при малом значении 9.0013 x, подобно x = 0. Это пересечение не означает, что асимптота не существует.

 

 

 

Практическая задача: Постройте график функции и найдите ее асимптоты. Вам не нужно определять функции для этих асимптот.

 

 

Решение: Сначала нарисуйте график функции.

Ясно, что функция имеет асимптоту в точке x = 1: это соответствует корню многочлена в знаменателе функции. Чуть менее очевидно, однако, наличие другой, «диагональной» асимптоты.