4.2. Симплекс-метод решения задач линейного программирования
302
4.2. Симплекс-метод решения задач
линейного программирования
___________________________________________________________________________________________________________
Основная идея симплекс-метода
Основываясь на определениях данных в предыдущей лекции, мы можем найти оптимальное решение задачи линейного программирования, записанной в стандартной форме, путем простого перебора всех базисных (допустимых) решений. Но, конечно, такая процедура не эффективна. Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограниченное количество допустимых базисных решений [19].
Алгоритм
симплекс-метода всегда начинается с
некоторого допустимого базисного
решения и затем пытается найти другое
допустимое базисное решение, «улучшающее»
значение целевой функции. Это возможно
только в том случае, если возрастание какой-либо нулевой (небазисной) переменной
ведет к улучшению значения целевой
функции.
Пример 1.
Рассмотрим детали выполнения симплекс-метода при решении следующей задачи.
Компания Тиккурила производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2. Основные данные задачи сведены в таблицу.
Расход сырья (в тоннах) на тонну краски | Максимально возможный ежедневный расход сырья | ||
Для наружных работ | Для внутренних работ | ||
Сырье М1 | 6 | 4 | 24 |
Сырье М2 | 1 | 2 | 6 |
Доход (в $1000) на тонну краски | 5 | 4 | |
Отдел
маркетинга компании ограничил ежедневное
производство краски для внутренних
работ до 2 тонн (из-за отсутствия
надлежащего спроса), а также поставил
условие, чтобы ежедневное производство
краски для внутренних работ не превышало
более чем на тонну аналогичный показатель
производства краски для внешних работ.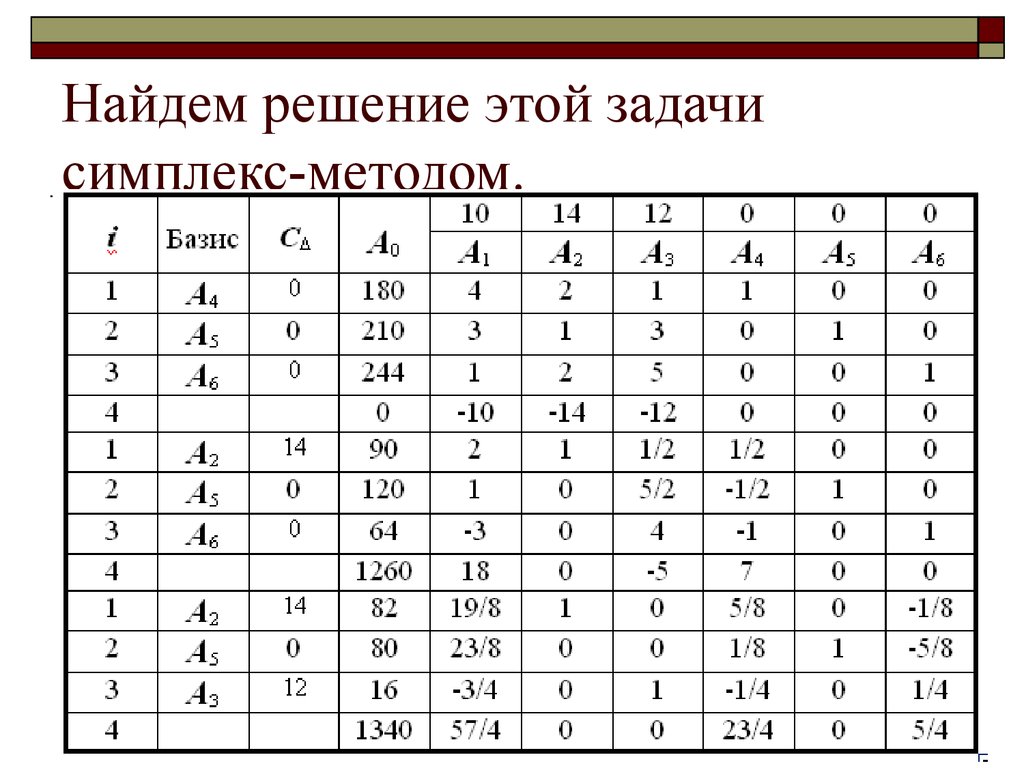 Компания хочет определить оптимальное
(наилучшее) соотношение между видами
выпускаемой продукции для максимизации
общего ежедневного дохода.
Компания хочет определить оптимальное
(наилучшее) соотношение между видами
выпускаемой продукции для максимизации
общего ежедневного дохода.
Переменные задачи: 1= объем ежедневного производства краски для наружных работ (тонны), 2 = объем ежедневного производства краски для внутренних работ (тонны).
Краска обоих видов производится из сырья М1 и М2. Первые два ограничения задачи порождены ограниченными ежедневными запасами сырья. Другие два отображают ограниченный рыночный спрос на краску. Прибыль от одной тонны краски для наружных работ составляет $5000, а краски для внутренних работ – $4000. Целевая функция задачи должна максимизировать общую прибыль. Для удобства вычислений доходность производства красок масштабирована в тысячах долларов.
Эта задача в стандартной форме записывается так:
максимизировать
при ограничениях
Здесь s1, s2, s3, s4 –
дополнительные (остаточные) переменные,
добавленные в неравенства для
преобразования их в равенства.
Задачу ЛП в стандартной форме можно представить в виде следующей компактной таблицы.
Нижние четыре строки этой таблицы представляют равенства ограничений; значения правых частей этих равенств даны в столбце «Решение». Строка z = W() получена из равенства
W() – 5 1– 4 2 = z – 5 1– 4 2= 0.
Дополнительные
переменные s1, s2, s3 и s4 составляют очевидное начальное допустимое
базисное решение. При этом, поскольку небазисные
переменные 1 и 2 равны нулю, значения s1, s2, s3 и s4 автоматически отображаются в столбце
«Решение»: s1 = 24, s2= 6, s 3 = 1 и s4 = 2. Значение целевой функции при этом
решении равно нулю.
Значение целевой функции при этом
решении равно нулю.
Будет
ли это начальное решение оптимальным?
Конечно, нет, поскольку переменные 1 и 2 здесь равны нулю, а возрастание этих
переменных даже на единицу приводит к
увеличению значения целевой функции W() = 5 1+
4 2 на 5 (при увеличении на единицу 1)
или на 4 единицы (при увеличении на
единицу 2). Поскольку в формуле целевой функции
коэффициент при переменной 1 больше, чем коэффициент при 2,
переменную 1 следует ввести в число базисных переменных
(в этом случае она станет 
Включаемая (вводимая) переменная 1 должна принять положительное значение. На рис. 4.2.1 видно, что, исходя из начальной точки A ( 1 = 0, 2 = 0), наибольшее значение, которое можно присвоить переменной 1 (не выходя из пространства допустимых решений), равно 4, что соответствует точке B ( 1 = 4, 2 = 0). Это означает, что решение переместилось от крайней точки A в крайнюю точку В.
Рис. 4.2.1
Поскольку
симплекс-метод не должен основываться
на графическом представлении задачи
ЛП, необходимо определить, как выбрать
точку B алгебраически. Из рисунка 4.2.1 видно,
что B является одной из точек пересечения
прямых, соответствующих ограничениям,
с осью 1. Алгебраически точку пересечения можно
найти как отношение правой части равенства (значение в
столбце «Решение») к коэффициенту
при переменной 1 в этом равенстве, как показано в следующей
таблице.
Алгебраически точку пересечения можно
найти как отношение правой части равенства (значение в
столбце «Решение») к коэффициенту
при переменной 1 в этом равенстве, как показано в следующей
таблице.
Нас интересуют только неотрицательные отношения (или точки пересечения на положительной полуоси
Минимальное
неотрицательное отношение равно значению
вводимой переменной 1в
новом решении,
а именно 1=
4 (сравните с точкой B на рис. 1). Значение целевой функции
при этом значении 1 возрастет
до 20 (= 54).
1). Значение целевой функции
при этом значении 1 возрастет
до 20 (= 54).
Теперь
среди текущих базисных переменных s1, s2, s3 и s4 следует
определить исключаемую
переменную, которая примет
нулевое значение после введения в базис
переменной 1.
(Напомним, что в этом примере должно
быть в точности 4 базисные переменные.)
Поскольку наименьшее
(неотрицательное) отношение соответствует
переменной s1,
в точке B именно
эта переменная обращается в нуль.
Таким образом, переменная s1 будет исключаемой, в этом случае переменная 1 автоматически получает значение 4.
Замена исключаемой переменной s1 на
вводимую переменную 1 приводит
к новому базисному решению ( 1, s2, s3, s4).
Процесс вычисления нового базисного решения состоит из двух этапов [19]:
Симплекс метод. Решение задач линейного программирования симплекс методом
Решение задач линейного программирования симплекс методом
курсовая работа
Симплекс метод — метод линейного программирования, который реализует рациональный перебор базисных допустимых решений, в виде конечного итеративного процесса, необходимо улучшающего значение целевой функции на каждом шаге.
Применение симплекс-метода для задачи линейного программирования предполагает предварительное приведение ее формальной постановки к канонической форме с n неотрицательными переменными: (X1, …, Xn), где требуется минимизация линейной целевой функции при m линейных ограничениях типа равенств. Среди переменных задачи выбирается начальный базис из m переменных, для определенности (X1, …, Xm), которые должны иметь неотрицательные значения, когда остальные (n-m) свободные переменные равны 0. Целевая функция и ограничения равенства преобразуются к диагональной форме относительно базисных переменных, переменных, где каждая базисная переменная входит только в одно уравнение с коэффициентом 1.
Данная формальная модель задачи линейного программирования обычно задается в форме, так называемой симплекс-таблицы, удобной для выполнения операций симплекс-метода:
Симплекс-таблица
1 | X1 | X2 | . | Xm | Xm+1 | … | Xn | ||
X0 | A0,0 | 0 | 0 | … | 0 | A0,m+1 | … | A0,n | |
X1 | A1,0 | 1 | 0 | … | 0 | A1,m+1 | … | A1,n | |
X2 | A2,0 | 0 | 1 | … | 0 | A2,m+1 | … | A2,n | |
… | … | … | … | . | … | … | … | … | |
Xm | Am,0 | 0 | 0 | … | 1 | Am,m+1 | … | Am,n |
Верхняя строка симплекс-таблицы представляет целевую функцию задачи. Каждая строка симплекс-таблицы, кроме первой, соответствует определенному ограничению-равенству задачи. Свободные члены ограничений составляют крайний левый столбец таблицы. Слева от таблицы записаны текущие базисные переменные (X1, …, Xm). Сверху от таблицы приведен набор всех переменных задачи, где Xm+1, …, Xn — свободные переменные задачи.
На начальном шаге алгоритма симплекс-метода должно быть выбрано базисное допустимое решение (X1, …, Xm) >= 0 при Xj = 0 (j = m+1, . .., n), следовательно, все свободные члены ограничений Ai,0 >= 0 (i = 1, …, m). Когда это условие выполнено, симплекс-таблица называется прямо-допустимой, так как в этом случае базисные переменные, равные Ai,0, определяют допустимое решение прямой задачи линейного программирования. Если все коэффициенты целевой функции A0,j >= 0 (j = 1, …, m), то симплекс-таблица называется двойственно-допустимой, поскольку соответствующее решение является допустимым для двойственной задачи линейного программирования.
.., n), следовательно, все свободные члены ограничений Ai,0 >= 0 (i = 1, …, m). Когда это условие выполнено, симплекс-таблица называется прямо-допустимой, так как в этом случае базисные переменные, равные Ai,0, определяют допустимое решение прямой задачи линейного программирования. Если все коэффициенты целевой функции A0,j >= 0 (j = 1, …, m), то симплекс-таблица называется двойственно-допустимой, поскольку соответствующее решение является допустимым для двойственной задачи линейного программирования.
Если симплекс-таблица является одновременно прямо и двойственно допустимой, т.е. одновременно все Ai,0 >= 0 и A0,j >= 0, то решение оптимально.
Действительно, поскольку допустимыми являются лишь неотрицательные значения управляемых параметров, то изменение целевой функции за счет вариации свободных переменных, через которые она выражена, возможно только в сторону увеличения, т.e. будет ухудшаться. Если среди ее коэффициентов имеются A0,j < 0, то значение целевой функции еще можно уменьшить (т. e. улучшить), увеличивая значение любой свободной переменной Xj с отрицательным коэффициентом A0,j при побочном уменьшении базисных переменных, чтобы оставались справедливы ограничения задачи. Теоретически можно использовать любую свободную переменную Xj с A0,j < 0, но на практике обычно действуют в соответствии со стратегией наискорейшего спуска, выбирая минимальный элемент A0,p < 0 из всех отрицательных A0,j < 0:
e. улучшить), увеличивая значение любой свободной переменной Xj с отрицательным коэффициентом A0,j при побочном уменьшении базисных переменных, чтобы оставались справедливы ограничения задачи. Теоретически можно использовать любую свободную переменную Xj с A0,j < 0, но на практике обычно действуют в соответствии со стратегией наискорейшего спуска, выбирая минимальный элемент A0,p < 0 из всех отрицательных A0,j < 0:
A0,p = min A0,j < 0.
j
Столбец p симплекс-таблицы, соответствующий выбранному коэффициенту A0,p < 0, называется ведущим столбцом. Свободная переменная ведущего столбца должна быть введена в базис вместо одной из текущих базисных переменных. Очевидно, из базиса следует исключить такую переменную Xq, которая раньше других обращается в нуль при увеличении переменной Xp ведущего столбца.
Её индекс легко определить, если среди положительных элементов ведущего столбца p найти элемент, минимизирующий отношение (Ai,0 / Ai,p):
Aq,0 Ai,0
—— = min —— , i = 1,. ..,m.
..,m.
Aq,p i Ai,p
Элемент Aq,p называется ведущим элементом, cтрока q симплекс-таблицы, содержащая ведущий элемент, называется, соответственно, ведущей строкой. Переменная ведущей строки Xq заменяется в базисе переменной ведущего столбца Xp и становится свободной переменной с значением 0, в то время как новая базисная переменная Xp достигнет максимально возможного значения, равного: max Xp = ( Aq,0 / Aq,p).
После указанного взаимообразного обмена переменными Xp и Xq между наборами свободных и базисных переменных нужно модифицировать исходную каноническую модель задачи путем приведения ее к диагональной форме относительно нового множества базисных переменных. Для указанного преобразования можно формально использовать процедуру исключения Гаусса, которая, как известно, состоит из двух элементарных операций, применяемых к системе алгебраических уравнений ( в данном случае ограничений — равенств):
· умножение уравнения E1(X) = 0 на константу K1 и замена уравнения E1(X) = 0 уравнением K1*E1(X) = 0;
· сложение уравнений E1(X) = 0 и E2(X) = 0 c последующей заменой уравнения E2(X) = 0 уравнением E1(X) + E2(X) = 0.
Исключения Гаусса позволяют привести систему уравнений к диагональной форме относительно желаемого множества переменных. В данном случае исключение Гаусса применяется так, чтобы все элементы симплекс-таблицы в ведущем столбце, кроме ведущего элемента Aq,p, стали нулевыми, а ведущий элемент стал равным единице:
Ai,p = 0, если i не равно q
и
Ai,p = 1, если i = q.
Указанные шаги симплекс-метода повторяются, пока не будет получена симплекс-таблица, которая одновременно является прямо и двойственно допустимой. Если положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные — нулю, то будет получено оптимальное решение.
Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой перебор базисных допустимых решений. Однако, трудные для симплекс метода задачи на практике встречаются крайне редко, что объясняет широкое распространение и большую популярность данного метода линейного программирования по сравнению с другими подходами.
Однако, трудные для симплекс метода задачи на практике встречаются крайне редко, что объясняет широкое распространение и большую популярность данного метода линейного программирования по сравнению с другими подходами.
Двойственный симплекс-метод решения задач линейного программирования
Метод, при котором вначале симплекс-методом решается одна из взаимно двойственных задач, а затем оптимум и оптимальное решение другой задачи находятся с помощью теорем двойственности, называется двойственным симплекс-методом.
Теорема 1 (Первая теорема двойственности). Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и
другая, причем оптимальные значения их целевых функций равны:
. (7.1)
Если целевая функция исходной задачи не ограничена, то система ограничений двойственной задачи несовместна.
Примечание: утверждение, обратное по отношению ко второй части первой теоремы двойственности, в общем случае неверно.
Установим соответствие между переменными взаимно двойственных задач.
Теорема 2. Компоненты оптимального плана двойственной задачи (обладающие условием неотрицательности) равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
Компоненты оптимального плана двойственной задачи (не ограниченные по знаку) равны значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
Теорема 3. Положительным (ненулевым) компонентам оптимального решения одной из задач симметричной двойственной пары соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых и :
Теорема 4 (Третья теорема двойственности). Компоненты оптимального плана двойственной задачи равны значениям частных производных линейной функции по соответствующим аргументам, т.е.
Компоненты оптимального плана двойственной задачи равны значениям частных производных линейной функции по соответствующим аргументам, т.е.
. (7.2)
Экономическая интерпретация третьей теоремы двойственности: компоненты оптимального плана двойственной задачи показывают, на сколько денежных единиц изменится максимальная прибыль (выручка) от реализации продукции при изменении запаса соответствующего ресурса на одну единицу.
Пример 9.1. На основе решения примера 5.2 (файл «Алгоритм и примеры симплекс-метода») определим двойственным симплекс- методом оптимальное решение двойственной задачи.
Исходная задача | Двойственная задача |
Данная двойственная пара является симметричной. Задачи записаны в стандартной форме, приведем их к каноническому виду:
Задачи записаны в стандартной форме, приведем их к каноническому виду:
Исходная задача | Двойственная задача |
Установим соответствие между переменными взаимно двойственных задач.
На основе решения примера 5.2. симплекс-таблица последней итерации (таблица 5.10) имеет вид:
Таблица 9.3
Симплекс-таблица оптимального решения исходной задачи
В соответствии с теоремой 2, оптимальные значения переменных и будут равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
По таблице 9.3 выпишем целевую функцию исходной задачи, выраженную через свободные переменные ее оптимального решения:
.
Следовательно, , .
Переменные , , и не присутствуют в целевой функции (т.е. коэффициенты при них равны нулю), следовательно, оптимальные значения соответствующих им переменных , , и равны нулю.
В соответствии с теоремой 1, .
Таким образом, оптимальное значение целевой функции , которое достигается при .
Ответ: , .
Пример 9.2. На основе решения исходной задачи найти оптимальное решение двойственной задачи используя двойственный симплекс-метод.
Исходная задача | Двойственная задача |
Данная двойственная пара является несимметричной. Приведем к каноническому виду двойственную задачу.
Приведем к каноническому виду двойственную задачу.
Исходная задача | Двойственная задача |
Для установления соответствия переменных двойственной пары введем в исходную задачу две недостающие фиктивные переменные.
Исходная задача | Двойственная задача |
Установим соответствие между переменными взаимно двойственных задач.
Таблица 9. 4
4
Соответствие переменных двойственной пары
Решим исходную задачу симплекс-методом.
Используя метод Жордана-Гаусса, выделим в системе ограничений исходной задачи в качестве базисных переменные и (примечание: не использовать в качестве базисных фиктивные переменные).
В результате преобразований получим следующую матрицу коэффициентов:
.
Система ограничений исходной задачи примет следующий вид:
Выразим базисные переменные через свободные, в результате исходная задача примет следующий вид:
Подставив полученные значения базисных переменных в целевую функцию, она примет следующий вид:
В результате решения симплекс-методом преобразованной исходной задачи на последней итерации получим следующую симплекс-таблицу:
Таблица 9.5
Симплекс-таблица оптимального решения исходной задачи
СП БП | |||||
3 | -1/3 | 5/3 | -1/3 | 2/3 | |
3 | 1/3 | 4/3 | -2/3 | 1/3 | |
12 | 5/3 | 23/3 | -7/3 | 5/3 |
Примечание: при проверке признаков несовместности системы ограничений, неограниченности целевой функции, оптимальности найденного допустимого базисного решения, а также определении разрешающего элемента, колонки фиктивных переменных не учитываются.
В соответствии с теоремой 3, оптимальные значения переменных и будут равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
Так как переменные , не ограничены по знаку, то их оптимальные значения будут равны значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
.
Согласно таблице соответствия переменных (таблица 9.4):
, , , .
Переменные и не присутствуют в целевой функции (т.е. коэффициенты при них равны нулю), следовательно, оптимальные значения соответствующих им переменных и равны нулю.
В соответствии с теоремой 1, .
Таким образом, оптимальное значение целевой функции , которое достигается при .
Ответ: , .
Симплекс-метод решения линейного программирования
Симплекс-метод
Симплекс-метод — это метод определения оптимального значения линейной программы вручную. Метод дает оптимальное решение, удовлетворяющее заданным ограничениям, и дает максимальное значение дзета. Чтобы использовать симплекс-метод, данная модель линейного программирования должна иметь стандартную форму, в которую затем могут быть введены резервные переменные. Используя табличные и сводные переменные, можно найти оптимальное решение.
Переменная Slack
Переменные Slack — это дополнительные переменные, которые вводятся в линейные ограничения линейной программы для их преобразования из ограничений неравенства в ограничения равенства.
Избыточная переменная
Избыточные переменные — это переменные, вычитаемые из линейных ограничений линейной программы для преобразования их из ограничений неравенства в ограничения равенства.
Если неравенство ≤ (меньше или равно), то мы добавляем резервную переменную + S, чтобы заменить ≤ на =.
Например: 2×1 + x2 ≤ 3 — это неравенство.
Тогда 2×1 + x2 + s = 3; s — резервная переменная
Если неравенство ≥(больше или равно), то мы вычитаем избыточную переменную — S, чтобы изменить ≥ на =.
Например: 2×1 + 3×2 ≥ 5 является неравенством.
Тогда 2×1 + 3×2 — s = 5; s — избыточная переменная
Стандартная форма задачи максимизации с двумя переменными
Стандартная форма — базовый формат для всех линейных программ перед поиском оптимального решения и имеет три требования: (1) должна быть задачей максимизации, (2 ) все линейные ограничения должны находиться в неравенстве меньше или равно, (3) все переменные неотрицательны.
Пример:
z = 7×1 + 5×2
, подлежащий
x1 + 2×2 ≤ 6
4×1 + 3×2 ≤ 12
x1, x2 ≥ 0
Основное решение
. n переменных (m < n). Любое решение, полученное путем решения для m переменных с нулевыми оставшимися (n – m) переменными, называется базовым решением.
Базовое допустимое решение
Базовое решение, которое также удовлетворяет неотрицательным ограничениям, называется базовым допустимым решением.
Ограниченные, неограниченные, пустые решения
Если значение целевой функции Z имеет как максимальное значение, так и минимальное значение, такое решение является ограниченным решением.
Если значение целевой функции Z можно неограниченно увеличивать или уменьшать, такие решения называются неограниченными решениями. Неограниченное решение имеет минимальные значения, но не имеет максимального значения.
Пустое решение не имеет ни максимального, ни минимального значения.
Основная теорема LP
Фундаментальная теорема линейного программирования гласит, что если есть решение, то оно находится на границе допустимой области, а не внутри области.
Базовые переменные
Базовые переменные — это переменные, которые неотрицательны с точки зрения оптимального решения.
Небазовые переменные
Небазовые переменные — это переменные, которые равны нулю с точки зрения оптимального решения.
Симплексная таблица
Симплексная таблица используется для выполнения операций со строками в модели линейного программирования, а также для проверки оптимальности.
Проверка оптимальности
Оптимальные решения максимизирующей модели линейного программирования — это значения, присвоенные переменным в целевой функции, чтобы получить наибольшее значение дзета. Оптимальное решение существовало бы в угловых точках графика всей модели.
Упражнение 1 (Пошаговое объяснение)
Используйте симплекс-метод, чтобы найти оптимальные решения следующей задачи ЛП.
Макс. Z = 7×1 + 5×2
с учетом
x1 + 2×2 ≤ 6
4×1 + 3×2 ≤ 12
x1, x2 ≥ 0
Решение:
Шаг 1: Стандартная форма
Стандартная форма необходима, поскольку она создает идеальную отправную точку для максимально эффективного решения симплекс-метода.
Макс. P = 7×1 + 5×2
при условии
x1 + 2×2 ≤ 6
4×1 + 3×2 ≤ 12
x1, x2 ≥ 0
просто умножьте левую и правую части целевой функции на -1.
-1 × [-Z = -8×1 — 10×2 — 7×3]
Z = 8×1 + 10×2 + 7×3
Максимизация: Z = 8×1 + 10×2 + 7×3 -к неравенству к неравенству меньше или равно можно сделать так же, как это было сделано к целевой функции. Умножая на -1 с обеих сторон, неравенство можно изменить на меньше или равно.
-1 × [x1 — 5×2 — x3 ≥ -8 ]
x1 + 5×2 + x3 ≤ 8
Шаг 2. Определение переменных резерва
Пусть x3 и x4 неотрицательные переменные резерва,
x1 + 2×2 + x3 = 6
4×1 + 3×2 + x4 = 12
7×1 + 5×2 = P
Теперь заданная задача ЛП в стандартной форме
1.x1 + 2.x2 + 1.x3 + 0.x4 + 0.P = 6
4.x1 + 3.x2 + 0.x3 + 1.x4 + 0.P = 12
-7.x1 + -5.x2 + 0.x3 + 0.x4 + 1.P = 0
Шаг 3: Настройка таблицы
Таблица состоит из коэффициента, соответствующего линейным переменным ограничения, и коэффициентов целевая функция.
Уравнения исходной симплексной таблицы следующие:
Шаг 4: Проверка оптимальности
Для проверки оптимальности с помощью таблицы все значения в последней строке должны содержать значения, большие или равные нулю. Если значение меньше нуля, это означает, что переменная не достигла своего оптимального значения. Как видно из предыдущей таблицы, в нижней строке присутствуют два отрицательных значения, указывающие на то, что это решение не является оптимальным. Если таблица не оптимальна, следующим шагом будет определение опорного элемента, на котором будет основываться новая таблица.
Если значение меньше нуля, это означает, что переменная не достигла своего оптимального значения. Как видно из предыдущей таблицы, в нижней строке присутствуют два отрицательных значения, указывающие на то, что это решение не является оптимальным. Если таблица не оптимальна, следующим шагом будет определение опорного элемента, на котором будет основываться новая таблица.
Шаг 5. Идентификация опорного элемента
Опорный элемент можно определить, взглянув на нижнюю строку таблицы и индикатор. Выберите наименьшее отрицательное значение в нижней строке. Этот столбец, содержащий наименьшее отрицательное значение, будет сводным столбцом. Одно из значений, лежащих в опорном столбце, будет опорным элементом. Чтобы найти индикатор, разделите бета-значения линейных ограничений на соответствующие им значения из сводного столбца.
∵ -7 — это самое большое значение (наименьшее значение), поэтому первый столбец является сводным столбцом.
∵ = 6 и = 3(мин) [3<6]
∴ 4 — опорный элемент.
Шаг 6: Создайте новую таблицу
1) Чтобы оптимизировать сводную переменную, ее необходимо преобразовать в единичное значение (значение 1). Чтобы преобразовать значение, умножьте строку, содержащую опорную переменную, на обратную величину опорного значения. В приведенном ниже примере исходная переменная равна 4, поэтому умножьте всю строку на 1/4.
R2 → R2/4
2) После того, как значение единицы будет определено, другие значения в столбце, содержащем значение единицы, станут равными нулю. Это связано с тем, что x2 во втором ограничении оптимизируется, что требует, чтобы x2 в других уравнениях был равен нулю.
R1 → R1 — R2
R3 → 7R2 + R3
После завершения новой таблицы модель можно проверить на наличие оптимального решения.
∴ Все записи в последней строке неотрицательны.
Итак, оптимальное решение получено.
Таким образом, максимум P=21, когда x1=3 и x2=0
Наконец, Max P = 7×1 + 5×2 = 7,3 + 0 = 21 определен как неоптимальный, необходимо будет определить новый опорный элемент. Шаги повторяются, начиная с шага 5, и проверяется оптимальность до тех пор, пока не будут получены оптимальные значения.
Шаги повторяются, начиная с шага 5, и проверяется оптимальность до тех пор, пока не будут получены оптимальные значения.
Упражнение 2
Используйте симплекс-метод, чтобы найти оптимальные решения следующей задачи ЛП.
Макс. Z = 3×1 + 5×2
, подлежащий
3×1 + 2×2 ≤ 18
x1 ≤ 4
x2 ≤ 6
x1, x2 ≥ 0
Решение:
x3, x4 и x5 не являются невингическими. переменные резерва,
3×1 + 2×2 + x3 = 18
x1+ x4 = 4
x2 + x5 = 6
3×1 + 5×2 = Z
.x1 + 2.x2 + 1.x3 + 0.x4 + 0.x5 + 0.Z = 18
1.x1 + 0.x2 + 0.x3 + 1.x4 + 0.x5 + 0.Z = 4
0.x1 + 1.x2 + 0.x3 + 0.x4 + 1.x5 + 0.Z = 6
3.x1 + 5.x2 + 1.x3 + 0.x4 + 0.x5 + 0 .Z = 0
Уравнения в исходной симплексной таблице выглядят следующим образом:
∵ -5 — это самое большое значение (наименьшее значение), поэтому второй столбец является опорным столбцом.
∵ = 9 и = 5(мин) [5<18]
∴ 1 — опорный элемент.
R1 → R1 — 2R3
R4 → R4 + 5R3
∵ -3 — это самое большое значение (наименьшее значение), поэтому первый столбец является опорным.
∵ = 2(min) и = 4 [2<4]
∴ 3 — опорный элемент.
R1 → R1/3
R2 → R2 — R1
R4 → R4 + 3R1
∴ Все записи в последней строке неотрицательны.
Итак, оптимальное решение получено.
Таким образом, максимум Z=36, когда x1=2 и x2=6
Наконец, Max Z= 3×1+ 5×2 = 3,2 + 5,6 = 36
Двойная задача ЛП
можно решить симплексным методом.
Но если данная задача ЛП относится к типу минимизации, то ее можно решить, превратившись в задачу максимизации, которая называется двойственной задачей данной задачи ЛП.
Двойная задача минимизации LP
Мин. C = AX + By
с
A1X + B1Y ≤ C1
A2X + B2Y ≤ C2
C1, C2 ≥ 0
x, y ≥ 0
здесь,
A = Агмерная матрикса с образованной матриксом. ограничения и целевая функция
ограничения и целевая функция
Соответствующая двойственная задача данной задачи минимизации выглядит следующим образом:
Макс. P = c1x + c2y
с учетом AT
По теореме двойственности минимизация C = максимизация P
Упражнение 3
Минимизация P = 7×1 + x2
при условии
3×1 — 2×2 ≤ -6 ≥
x 1903×20003x1, x2 ≥ 0
Решение:
Стандартная форма:
минимизация p = 7×1 + x2
с при условии
3×1 -2×2 ≤ -6 или, -3×1 + 2×2 ≥ 6
x1 + 3×2 ≤ -3×1 + 2×2 ≥ 6 0003
x1 + 3×2 ≤ -6 rt. 15
x1, x2 ≥ 0
Пусть A — расширенная матрица, образованная коэффициентами ограничений с целевой функцией внизу.
Теперь соответствующий двойной LP:0003
2y1 + 3y2 ≤ 1
y1, y2 ≥ 0
Пусть x1 и x2 не связные слабые переменные,
-3y1 + y2 + x1 = 7
2y1 + 3y2 + x2 = 1
-6y1 + — 15y2 + P* = 0
Теперь заданная задача ЛП в стандартной форме имеет вид 3. y2 + 0.x1 + 1.x2 + 0.P* = 1
y2 + 0.x1 + 1.x2 + 0.P* = 1
-6y1 + -15y2+ 0.x1 + 0.x2 + 1.P* = 0
Уравнения исходной симплексной таблицы выглядят следующим образом. :
∵ -15 — это самое большое значение (наименьшее значение), поэтому второй столбец является опорным столбцом.
∵ = 7 и = 0,33 (мин) [0,33<7]
∴ 3 — опорный элемент.
R2 → R2/3
R1 → R1 — R2
R3 → R3 + 15R2
Итак, оптимальное решение получено.
Таким образом, максимум P*=5, когда x1= 0 и x2= 5
Наконец, Max P*= 7×1 + x2 = 0 + 5 = 5.
двенадцать математика Программирование 2
3.3а. Решение стандартных задач максимизации с использованием симплекс-метода | Конечная математика |
В предыдущем разделе мы обнаружили, что графический метод решения задач линейного программирования, хотя и занимает много времени, позволяет нам видеть области решения и определять угловые точки. Однако это невозможно при наличии нескольких переменных. Мы можем визуализировать до трех измерений, но даже это может быть сложно при наличии многочисленных ограничений.
Однако это невозможно при наличии нескольких переменных. Мы можем визуализировать до трех измерений, но даже это может быть сложно при наличии многочисленных ограничений.
Для решения задач линейного программирования, содержащих более двух переменных, математики разработали то, что сейчас известно как
симплекс-метод . Это эффективный алгоритм (набор механических шагов), который «переключается» через угловые точки, пока не найдет ту, которая максимизирует целевую функцию. Хотя заманчиво, есть несколько вещей, на которые нам нужно обратить внимание, прежде чем использовать его.
Прежде чем приступить к математическим деталям, давайте рассмотрим пример задачи линейного программирования, которая
будет соответствовать симплексному методу:
Пример 1
Симплексным методом можно решить следующую систему:
Целевая функция: P = 2 x + 3 y + z
С учетом ограничений: 3 x + 2 y ≤ 5 2 x + y – z ≤ 13 z ≤ 4 x,y,z≥0 С математической точки зрения, чтобы использовать симплекс-метод для решения задачи линейного программирования, нам нужна стандартная задача максимизации: Наличие ограничений с верхним пределом должно иметь смысл, поскольку при максимизации количества у нас, вероятно, есть ограничения на то, что мы можем сделать. Если бы у нас не было крышек, то мы могли бы продолжать увеличивать, скажем, прибыль, бесконечно! Это противоречит тому, что мы знаем о реальном мире. Чтобы использовать симплекс-метод, технически или вручную, мы должны настроить начальную симплекс-таблицу , которая представляет собой матрицу, содержащую информацию о задаче линейного программирования, которую мы хотим решить. Во-первых, матрицы плохо справляются с неравенствами. Consider the following linear programming problem Maximize: P = 7 x + 12 y Subject to: 2 x + 3 y ≤ 6 3 x + 7 y ≤12 Поскольку мы знаем, что левые части обоих неравенств будут меньшими, чем соответствующие значения справа, мы можем быть уверены, что добавление «чего-то» слева сторона сделает их точно равными. То есть: 2 x + 3 y + S 1 = 6 3 x + 7 Y + S Стандартная задача максимизации
 .. a n x n ле V
.. a n x n ле V 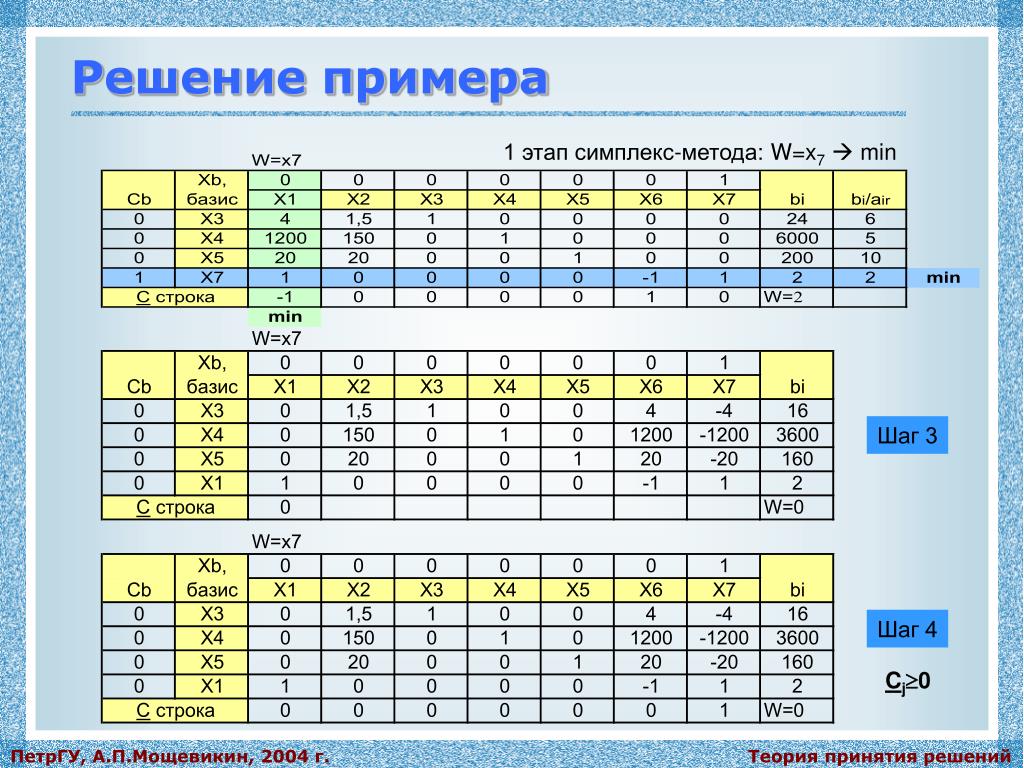 Во-первых, у матрицы нет простого способа отслеживать направление неравенства. Уже одно это препятствует использованию неравенств в матрицах. Как же нам избежать этого?
Во-первых, у матрицы нет простого способа отслеживать направление неравенства. Уже одно это препятствует использованию неравенств в матрицах. Как же нам избежать этого?
2+3+S 1 = 6 или S 1 = 1
3+7+S 2 = 12. или S
или S
Важно отметить, что эти две переменные, с 1 и s 2 , не обязательно совпадают. Они просто воздействуют на неравенство, убирая «слабину», из-за которой левая сторона не выглядит как правая. Следовательно, мы называем их слабыми переменными . Это позаботится о неравенствах для нас. Поскольку расширенные матрицы содержат все переменные слева и константы справа, мы перепишем целевую функцию в соответствии с этим форматом:
–7 x – 12 y + P =0
Теперь мы можем написать исходную систему уравнений Для этого нам потребуется матрица, которая может обрабатывать x , y , s 1 , s 2 и P . Мы установили начальную симплексную таблицу . Обратите внимание, что горизонтальные и вертикальные линии используются просто для отделения коэффициентов ограничений от констант и коэффициентов целевой функции. Также обратите внимание, что столбцы переменных резерва вместе с выходными данными целевой функции образуют единичную матрицу. Приведем алгоритм решения, однако заметим, что он не совсем интуитивен. Мы сосредоточимся на этом методе в качестве одного примера, а затем продолжим использовать технологию для выполнения процесса за нас. Сначала мы выбираем опорный столбец, который будет столбцом, содержащим наибольший отрицательный коэффициент в строке, содержащей целевую функцию. Обратите внимание, что наибольшее отрицательное число принадлежит члену, который вносит наибольший вклад в целевую функцию. Таким образом, нашей опорной точкой является столбец y . Сделайте это, вычислив отношение каждой константы ограничения к соответствующему коэффициенту в опорном столбце — это называется тестовым коэффициентом . Выберите строку с наименьшим тестовым коэффициентом. Сначала вычисляем тестовые коэффициенты: [6÷3=212÷7≈1,7]\displaystyle{\begin{bmatrix}{6÷3=2}\\{12÷7≈1,7}\end {bmatrix}}[6÷3=212÷7≈1,7] Поскольку тестовый коэффициент меньше для строки 2, мы выбираем ее в качестве опорной строки. Значение в рамке теперь называется нашим шарнир . Чтобы объяснить, почему мы это делаем, заметим, что 2 и 1,7 — это просто вертикальные точки пересечения двух неравенств. Мы выбираем меньшую, чтобы убедиться, что у нас есть угловая точка, которая находится в нашей допустимой области: Умножьте R2 на (1/7), чтобы преобразовать 7 в 1. Затем используйте 1, чтобы исключить 3 из R1: -3R 2 +R 1 →R 1 И используйте 1, чтобы исключить -12 в R3: 12R 2 +R 3 →R 3 Получаем следующую матрицу (может быть, вам удобнее в виде дробей) Что мы сделали? Во-первых, мы максимально увеличили вклад коэффициента 2-2 y в целевую функцию. Мы оптимизировали функцию? Не совсем, так как мы по-прежнему видим, что в первом столбце есть отрицательное значение. Это говорит нам о том, что еще может внести свой вклад в целевую функцию. Чтобы устранить это, мы сначала находим опорную строку, получая тестовые отношения: [5/701−3/70∣6/73/7101/70∣12/7−13/70012/71∣144/7] \ displaystyle {\ begin {bmatrix} {5/7} & {0} &{1}&{-3/7}&{0}&{|}{6/7}\\{3/7}&{1}&{0}&{1/7}&{0}& {|}{12/7}\\{-13/7}&{0}&{0}&{12/7}&{1}&{|}{144/7}\end{bmatrix}}⎣ ⎡5/73/7−13/7010100−3/71/712/7001∣6/7∣12/7∣144/7⎦ ⎤ [ (6/7)÷(5/7)≈1,212÷3≈4]\displaystyle{\begin{bmatrix}{(6/7)÷(5/7)≈1,2}\\{12÷3≈4} \end{bmatrix}}[(6/7)÷(5/7)≈1,212÷3≈4] С 1,2 Интересно, что этот тестовый коэффициент соответствует входному значению пересечения двух линий! Точно так же мы приступаем к исключению всех неосновных значений. Умножьте R1 на (1/0,71), чтобы преобразовать 0,71 в 1. Затем используйте 1, чтобы исключить 3 из R3: -3R 1 +R 2 →R 2 И используйте 1, чтобы исключить -12 в R3: 1.86R 1 +R 3 →R 3 Получаем следующую матрицу [107/5−3/50∣6/501−3/52/50∣6/50013/53/51∣114/5]\displaystyle{\begin{bmatrix}{1}& {0}&{7/5}&{-3/5}&{0}&{|}{6/5}\\{0}&{1}&{-3/5}&{2/5 }&{0}&{|}{6/5}\\{0}&{0}&{13/5}&{3/5}&{1}&{|}{114/5}\end {bmatrix}}⎣ ⎡1000107/5−3/513/5−3/52/53/5001∣6/5∣6/5∣114/5⎦ ⎤ Есть не остается никаких дополнительных отрицательных записей в строке целевой функции. Таким образом, мы имеем следующую матрицу: [107/5−3/50∣6/501−3/52/50∣6/50013/53/51∣114/5]\displaystyle{\begin{bmatrix}{1 }&{0}&{7/5}&{-3/5}&{0}&{|}{6/5}\\{0}&{1}&{-3/5}&{2 /5}&{0}&{|}{6/5}\\{0}&{0}&{13/5}&{3/5}&{1}&{|}{114/5} \end{bmatrix}}⎣ ⎡1000107/5−3/513/5−3/52/53/5001∣6/5∣6/5∣114/5⎦ ⎤ Итак, мы готовы читать решения. Чтобы идентифицировать набор решений, мы фокусируемся только на столбцах с ровно одним ненулевым элементом — они называются базовыми переменными (таким образом, столбцы с более чем одним ненулевым элементом называются неосновными переменными ). Заметим, что оба столбца x any являются базовыми переменными. На самом деле нас не интересуют резервные переменные, так же как мы игнорируем неравенства при поиске пересечений. Теперь мы видим, что [107/5−3/50∣6/501−3/52/50∣6/50013/53/51∣114/5]\displaystyle{\begin{bmatrix}{1}&{0}&{ 7/5}&{-3/5}&{0}&{|}{6/5}\\{0}&{1}&{-3/5}&{2/5}&{0} &{|}{6/5}\\{0}&{0}&{13/5}&{3/5}&{1}&{|}{114/5}\end{bmatrix}}⎣ ⎡1000107/5−3/513/5−3/52/53/5001∣6/5∣6/5∣114/5⎦ ⎤ Настройка переменные резерва равны 0, дает: x ≈ 1,2 y ≈ 1,2 P = 22,8 Таким образом, x=1. Хотя этот процесс несколько интуитивно понятен, он имеет за собой больше, чем мы показываем. И вместо того, чтобы проходить эти изнурительные шаги до тошноты, мы позволим нашей технологии следовать этим шагам. Для этого нам понадобится специальная программа, которая будет распределена по классу, Для выполнения симплекс-метода с графическим калькулятором необходимы следующие программы: Pivot и Pivot1 не используются напрямую. Вместо этого программа Simplex обращается к этим двум приложениям, чтобы помочь ей с довольно длинным и утомительным кодом. Как работает код? Используя инструкции, он находит сводные столбцы, сводные строки, выполняет исключение Гаусса, проверяет наличие отрицательных значений в строке целевой функции и повторяет этот процесс до тех пор, пока не будут удалены все отрицательные значения. Теперь, когда мы показали, что симплекс-метод работает даже для двух входных переменных, давайте продемонстрируем ситуацию, когда этот метод особенно полезен. Новая авиакомпания решила выйти на рынок. Он рассматривает возможность предложения рейсов из Феникса, штат Аризона, и первоначально хотел бы отправиться в три разных места: Сан-Диего, Сан-Франциско и Лас-Вегас. Расстояния каждого рейса туда и обратно, вылетающего из Феникса, составляют (приблизительно): 720 миль, 1500 миль и 1140 миль соответственно. Компания хотела бы использовать лозунг: «Средняя цена за рейс никогда не превышает 200 долларов». Что касается расходов, ожидается, что рейсы в Сан-Диего будут стоить около 10% стоимости авиабилетов. Точно так же в Сан-Франциско будет 12%, а в Лас-Вегасе 14% стоимости авиабилетов. Компания хочет, чтобы общая средняя стоимость составляла не более 10% от заработанной стоимости авиабилетов. Недавнее исследование рынка позволяет компании сделать вывод, что она, вероятно, могла бы продать около 1900 билетов в Сан-Диего, 700 билетов в Сан-Франциско и 1000 билетов в Лас-Вегас. Мы хотим знать стоимость авиабилетов по каждому направлению. Let, x = цена билета туда и обратно до Сан-Диего y = цена билета туда и обратно до Сан-Франциско z = цена билета туда и обратно до Лас-Вегаса Компания хочет максимизировать общий доход. Это основано на сумме количества проданных билетов, умноженной на цену билета, которая составляет: R = 1900 x + 700 y + 1000 z С учетом ограничений: 3 Математически, Поскольку оба ограничения имеют правильную форму, мы можем перейти к настройке исходной симплексной таблицы. The rewritten objective function is: –1900 x – 700 y – 1000 z + R = 0 And simplified constraints are: x + y + z ≤ 600 (Умножить обе стороны на 3) 14 y + 40 z ≤ 0 x,y≥0 Каждая из двух переменных ограничения, поэтому мы должны переписать их. следующим образом: x + Y + Z + S 1 = 600 14 Y + 404442 Z + S + 404442 Z + S + 404442 Z + y + 404442 Z + y + 404442 Z + y + 404442. следующие переменные столбцы: x , y , z , s 1 , s 2 , R , и столбец констант, всего 7 столбцов. [111100∣60001440010∣0−1900−700−1000001∣0]\displaystyle{\begin{bmatrix}{1}&{1}&{1}&{1}&{ 0}&{0}&{|}{600}\\{0}&{14}&{40}&{0}&{1}&{0}&{|}{0}\\{-1900 }&{-700}&{-1000}&{0}&{0}&{1}&{|}{0}\end{bmatrix}}⎣ ⎡10−1900114−700140−1000100010001∣600∣0∣0⎦ ⎤ Теперь таблица готова для решения с помощью Simplex. Поворот на 1-й столбец и 1-й ряд. (Вы не можете делить на 0, чтобы получить сводную строку) [111100∣60001440010∣0012009001∣1140000]\displaystyle{\begin{bmatrix}{1}&{1}&{1}&{1}& {0}&{0}&{|}{600}\\{0}&{14}&{40}&{0}&{1}&{0}&{|}{0}\\{0 }&{1200}&{900}&{1900}&{0}&{1}&{|}{1140000}\end{bmatrix}}⎣ ⎡ 100 1141200 140900 101900 010 001 ∣600∣1140000 ⎦ ⎤ , поскольку только x будет базовым, мы можем увидеть, что x = 600 является решением. Интересно, что одни только поездки в Сан-Диего приносят наибольший доход, исходя из заданных ограничений. Почему это? Если мы посмотрим на ограничения, то увидим, что компания вполне уверена, что сможет продать 1900 рейсов в Сан-Диего. Компания также несколько озадачена тем, что билеты будут продаваться по 600 долларов за штуку. На этом этапе он может решить добавить в модель некоторые дополнительные ограничения. Предположим, авиалайнер из примера 2 решает, что он может взимать не более 150 долларов США за билет до Сан-Диего, чтобы конкурировать с другими авиалайнерами, которые летают в тот же пункт назначения. Мы используем ту же исходную таблицу, но должны иметь дело со следующим новым ограничением: x ≤ 150 Добавляя третью резервную переменную, мы имеем x + с 4 3 950 Это добавит в нашу таблицу один столбец и одну строку: {1}&{0}&{0}&{0}&{|}{600}\\{0}&{14}&{40}&{0}&{1}&{0}&{0 }&{|}{0}\\{1}&{0}&{0}&{0}&{0}&{1}&{0}&{|}{150}\\{-1900}&{-700}&{-1000}&{0}&{0}&{0}&{1}&{|}{0}\end{bmatrix}}⎣ ⎡101−1900 1140−700 1400−1000 1000 0100 0010 0001 ∣600∣0∣150∣0 ⎦ ⎤ Решение с помощью Simplex дает [00−13/71−1/14 10∣4500120/701/1400∣01000010∣15000100005019001∣285000]\displaystyle{\begin{bmatrix}{0}&{0}&{-13/7}&{1}&{-1/14}&{- 1}&{0}&{|}{450}\\{0}&{1}&{20/7}&{0}&{1/14}&{0}&{0}&{|} {0}\\{1}&{0}&{0}&{0}&{0}&{1}&{0}&{|}{150}\\{0}&{0}&{ 1000}&{0}&{50}&{1900}&{1}&{|}{285000}\end{bmatrix}}⎣ ⎡00100100−13/720/7010001000−1/141/14050−10119000001∣ 450∣0∣150∣285000⎦ ⎤ Решение: x=150, y=0, z=450 и R=285000 Компания по производству обедов встреча. Мы хотим максимизировать количество сэндвичей, поэтому пусть: x = количество сэндвичей с ветчиной y = количество легких сэндвичей с ветчиной z = количество вегетарианских сэндвичей Общее количество сэндвичей определяется как S = x + y + z Ограничения будут даны с учетом общего количества доступных ингредиентов. Всего у компании имеется 10(40) = 400 ломтиков ветчины, 18(14) = 252 ломтика хлеба, 200 порций овощей и 15(60) = 900 ломтиков сыра. В лучшем случае компания может использовать вышеуказанные суммы. Есть два сэндвича с ветчиной: для первого требуется 4 ломтика ветчины, а для второго — только 2 на сэндвич. То есть 4 x + 2 y ≤ 400 То есть общее количество ломтиков ветчины не может превышать 400. Для каждого бутерброда требуется 2 ломтика хлеба, поэтому 2 x + 2 y + 2 z ≤ 252 В сэндвичах с ветчиной 1 и 2 порции овощей соответственно, а в вегетарианском сэндвиче 3 порции овощей. Итак, 1 x + 2 y + 3 z ≤ 200 Для обоих сэндвичей с ветчиной требуется один ломтик сыра, а для вегетарианского сэндвича требуется два ломтика сыра, поэтому 1 x + 1 3 y 3 x + 7 у + с 2 = 12 –7 x – 12 y + P =0  Разместим в таком порядке. Наконец, симплекс-метод требует, чтобы целевая функция была указана в нижней строке матрицы, так что мы имеем:
Разместим в таком порядке. Наконец, симплекс-метод требует, чтобы целевая функция была указана в нижней строке матрицы, так что мы имеем: 1. Выберите сводную колонку
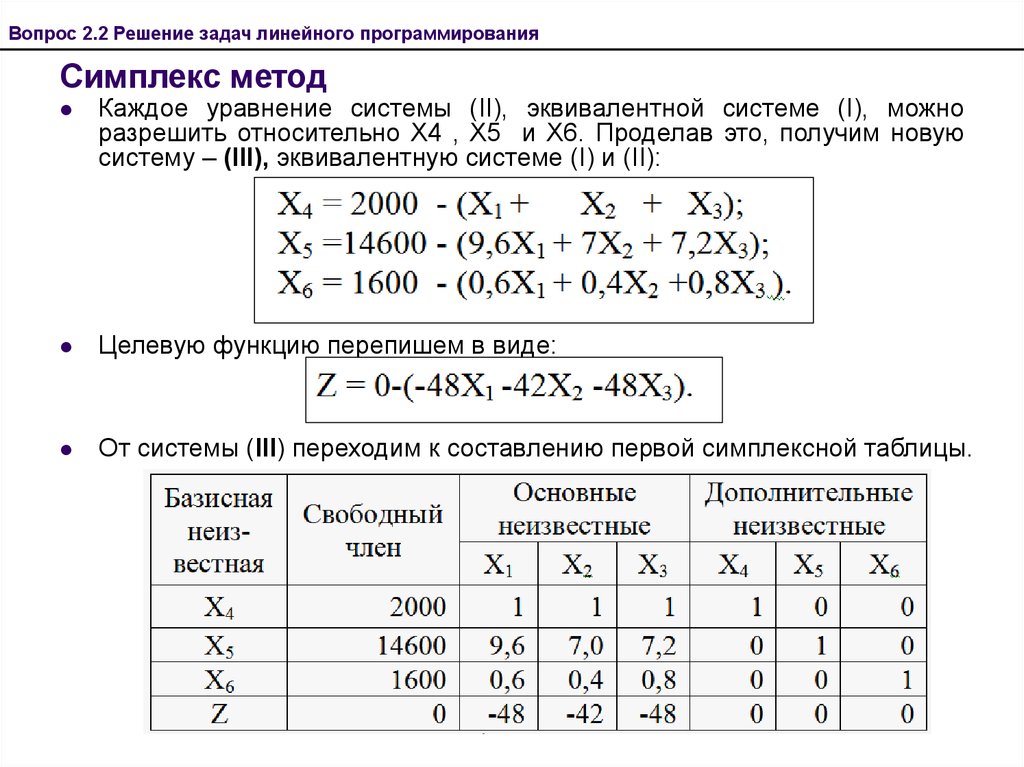 Это сделано намеренно, поскольку мы хотим сосредоточиться на значениях, которые максимально увеличивают вывод.
Это сделано намеренно, поскольку мы хотим сосредоточиться на значениях, которые максимально увеличивают вывод. 2. Выберите сводную строку
3.
 Используя исключение Гаусса, исключим строки 1 и 3
Используя исключение Гаусса, исключим строки 1 и 3

4. Определите набор решений
 2, y=1.2, P=22.8 является решением задачи линейного программирования. То есть входные данные x=1,2 и y=1,2 дадут максимальное значение целевой функции 22,8
2, y=1.2, P=22.8 является решением задачи линейного программирования. То есть входные данные x=1,2 и y=1,2 дадут максимальное значение целевой функции 22,8
Пример 2
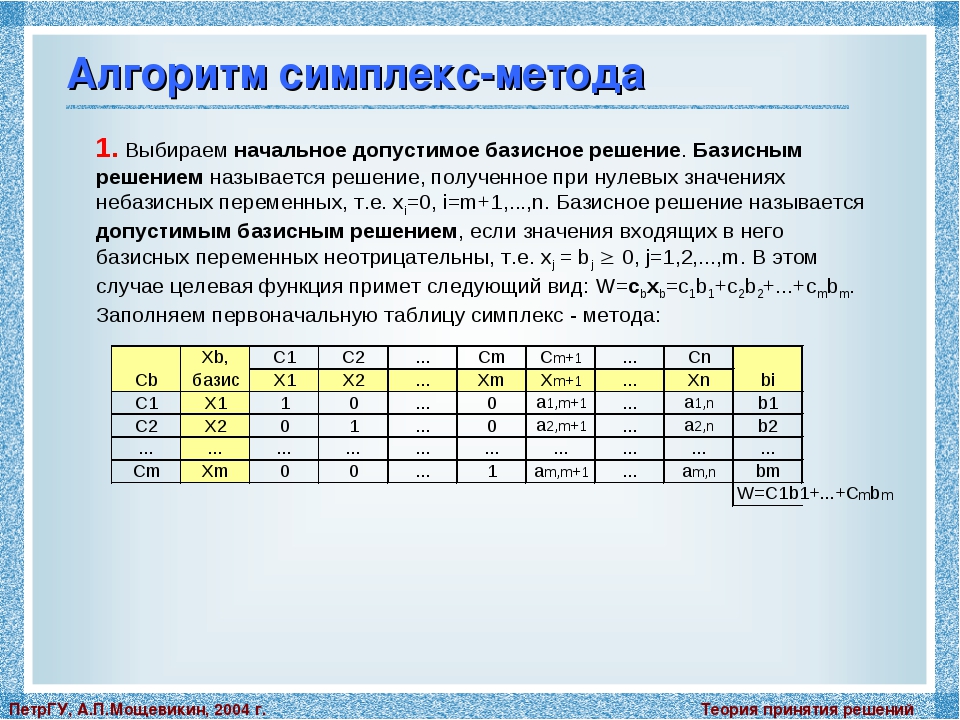 В этих условиях и при условии, что все проданные билеты являются рейсами туда и обратно, сколько компания должна взимать за каждый билет, чтобы максимизировать свой общий доход?
В этих условиях и при условии, что все проданные билеты являются рейсами туда и обратно, сколько компания должна взимать за каждый билет, чтобы максимизировать свой общий доход? Решение
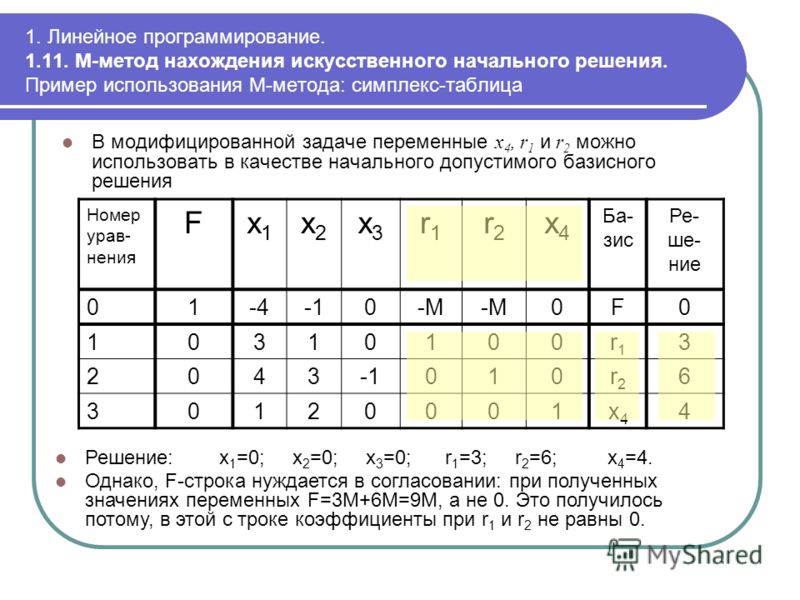 В качестве примечания: будьте очень осторожны при использовании симплексного метода, так как невыполнение требований делает недействительными полученные результаты.
В качестве примечания: будьте очень осторожны при использовании симплексного метода, так как невыполнение требований делает недействительными полученные результаты. У нас есть два ограничения и одна целевая функция, всего три строки. Теперь запишем исходную симплексную таблицу:
У нас есть два ограничения и одна целевая функция, всего три строки. Теперь запишем исходную симплексную таблицу: Тот факт, что y и z являются неосновными переменными, мы устанавливаем y = z = 0. То есть они не способствуют максимизации дохода. Кроме того, R является активной переменной, поэтому мы видим, что R = 1 140 000 долларов — это максимальный доход, который компания может получить с учетом ограничений. Они должны продавать билеты в Сан-Диего за 600 долларов и не продавать рейсы в другие города. Как вы могли догадаться, компания, вероятно, немного ошеломлена. Мы рассмотрим это в следующем примере.
Тот факт, что y и z являются неосновными переменными, мы устанавливаем y = z = 0. То есть они не способствуют максимизации дохода. Кроме того, R является активной переменной, поэтому мы видим, что R = 1 140 000 долларов — это максимальный доход, который компания может получить с учетом ограничений. Они должны продавать билеты в Сан-Диего за 600 долларов и не продавать рейсы в другие города. Как вы могли догадаться, компания, вероятно, немного ошеломлена. Мы рассмотрим это в следующем примере. Пример 3
 Предполагая, что все остальные ограничения будут по-прежнему использоваться, как это повлияет на цены билетов и максимальный доход?
Предполагая, что все остальные ограничения будут по-прежнему использоваться, как это повлияет на цены билетов и максимальный доход? Решение
Пример 4
 Здесь вам предложат сэндвичи с ветчиной, легкие сэндвичи с ветчиной и вегетарианские сэндвичи. Сэндвич с ветчиной состоит из 1 порции овощей, 4 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. Легкий бутерброд с ветчиной состоит из 2 порций овощей, 2 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. В вегетарианском бутерброде 3 порции овощей, 2 ломтика сыра и 2 ломтика хлеба. Всего доступно 10 мешков ветчины, по 40 ломтиков в каждом; Доступно 18 буханок хлеба, по 14 ломтиков в каждой; Доступны 200 порций овощей и 15 пакетов сыра, по 60 ломтиков в каждом. Учитывая ресурсы, сколько каждого бутерброда можно произвести, если цель состоит в том, чтобы максимизировать количество бутербродов?
Здесь вам предложат сэндвичи с ветчиной, легкие сэндвичи с ветчиной и вегетарианские сэндвичи. Сэндвич с ветчиной состоит из 1 порции овощей, 4 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. Легкий бутерброд с ветчиной состоит из 2 порций овощей, 2 ломтиков ветчины, 1 ломтика сыра и 2 ломтиков хлеба. В вегетарианском бутерброде 3 порции овощей, 2 ломтика сыра и 2 ломтика хлеба. Всего доступно 10 мешков ветчины, по 40 ломтиков в каждом; Доступно 18 буханок хлеба, по 14 ломтиков в каждой; Доступны 200 порций овощей и 15 пакетов сыра, по 60 ломтиков в каждом. Учитывая ресурсы, сколько каждого бутерброда можно произвести, если цель состоит в том, чтобы максимизировать количество бутербродов? Решение
 То есть у компании есть ограниченное количество ветчины, овощей, сыра и хлеба.
То есть у компании есть ограниченное количество ветчины, овощей, сыра и хлеба.
| Увеличить: S = x + y + z |
| Тема: 4 x + 2 y ≤ 400 |
| 2 x + 2 y + 2 z ≤ 252 |
| x + 2 y + 3 z ≤ 200 |
| 1 x + 1 y + 2 z ≤ 900 |
| x, y, z≥0 |
Эти ограничения удовлетворяют требованиям симплекс-метода, поэтому продолжаем.
Incorporating slack variables, we get:
4 x + 2 y + 0 z + s 1 = 400
2 x + 2 y + 2 z + с 2 = 252
x + 2 y + 3 z + s 3 = 200
x + y + 2 z + s 4 = 900
– x – y — z + S = 0
Первоначальная простой таблица состоит из:
[42010000∣40022201000∣25212300100∣20011200010∣900-1 —1001000∣25212300100∣111200010∣900-1 —1001000] \ SIVERSTYL &{2}&{0}&{1}&{0}&{0}&{0}&{0}{|}&{400}\\{2}&{2}&{2}&{ 0}&{1}&{0}&{0}&{0}{|}&{252}\\{1}&{2}&{3}&{0}&{0}&{1} &{0}&{0}{|}&{200}\\{1}&{1}&{2}&{0}&{0}&{0}&{1}&{0}{| }&{900}\\{-1}&{-1}&{-1}&{0}&{0}&{0}&{0}&{1}{|}&{0}\end{bmatrix} }⎣
⎡4211−12221−10232−1100000100000100000100∣0∣0∣0∣1∣4002522009000⎦
⎤
номер в нижней строке одинаков для трех столбцов, мы можем использовать любой столбец.
 Можно также использовать первый столбец. Наименьшее частное получается при делении 4 на 400, поэтому строка 1 является сводным столбцом. Поворот на «4» в R1C1 дает результат.
Можно также использовать первый столбец. Наименьшее частное получается при делении 4 на 400, поэтому строка 1 является сводным столбцом. Поворот на «4» в R1C1 дает результат.[11/201/40000∣100012−1/21000∣5203/23−1/40100∣10001/22−1/40010∣8000−1/2−11/40001∣100]\displaystyle{\begin{bmatrix {1}&{1/2}&{0}&{1/4}&{0}&{0}&{0}&{0}{|}&{100}\\{0}&{ 1}&{2}&{-1/2}&{1}&{0}&{0}&{0}{|}&{52}\\{0}&{3/2}&{3 }&{-1/4}&{0}&{1}&{0}&{0}{|}&{100}\\{0}&{1/2}&{2}&{-1 /4}&{0}&{0}&{1}&{0}{|}&{800}\\{0}&{-1/2}&{-1}&{1/4}& {0}&{0}&{0}&{1}{|}&{100}\end{bmatrix}}⎣
⎡100001/213/21/2−1/20232−11/4−1/2−1/4−1/41/40100000100000100∣0∣ 0∣0∣1∣10052100800100⎦
⎤
Примечание: мы увеличили S с 0 до 200, но в нижней строке у нас все еще есть минус. Поскольку «-1» более отрицательное, чем «-1/2», мы вернемся к столбцу 3. После деления положительных чисел над «-1» на константы мы получим наименьшее частное в строке 2. Поворот на «2 » в выходах R2C3.
Поворот на «2 » в выходах R2C3.
[xyzs1s2s3s4S11/201/40000∣10001/21−1/41/2000∣260001/2−3/2100∣220−1/201/4−1010∣7480001/200trix01∣126]\displaystyle{\begin{bma {x}&{y}&{z}&{s1}&{s2}&{s3}&{s4}&{S}\\{1}&{1/2}&{0}&{1 /4}&{0}&{0}&{0}&{0}{|}&{100}\\{0}&{1/2}&{1}&{-1/4}&{ 1/2}&{0}&{0}&{0}{|}&{26}\\{0}&{0}&{0}&{1/2}&{-3/2}& {1}&{0}&{0}{|}&{22}\\{0}&{-1/2}&{0}&{1/4}&{-1}&{0}& {1}&{0}{|}&{748}\\{0}&{0}&{0}&{1/2}&{0}&{0}&{0}&{1}{ |}&{126}\end{bmatrix}}⎣
⎡x10000y1/21/20−1/20z01000s11/4−1/41/21/41/2s201/2−3/2−10s300100s400010S0∣0∣ 0∣0∣1∣1002622748126⎦
⎤
Теперь у нас есть оптимальное решение
- x=100 (основная переменная в строке 1)
- y=0 (неосновная переменная)
- z=26 (базовая переменная, строка 2)
- s1=0 (неосновная переменная)
- s2=0 (неосновная переменная)
- s3=22 (базовая переменная, строка 3)
- s4=748 (базовая переменная, строка 4)
- S=126 (базовая переменная, строка 5)
Конечно, нас действительно интересуют только: x=100, y=0, z=26, S=126 Мы обнаружили, что 100 сэндвичей с ветчиной, 26 вегетарианских сэндвичей и 0 сэндвичей с легкой ветчиной должны быть приготовлены, чтобы максимизировать общее количество приготовленных сэндвичей.
Переменные запаса не важны в решении. Именно в достижении решения.
Дополнительные примеры см. в следующем разделе. Во многих задачах используются индексированные переменные, такие как x 1 , x 2 , x 3 и т. д. Это особенно удобно, если у вас несколько переменных. Вы увидите это в последующих примерах.
Дополнительные ресурсы перечислены ниже:
Милош Подманик, By the Numbers, «Решение стандартных задач максимизации с использованием симплекс-метода», под лицензией CC BY-NC-SA 3.0.
MathIsGreatFun, «MAT217 HW 2.2 #1», под лицензией Standard YouTube.
MathIsGreatFun, «MAT217 2.2 #2», под лицензией Standard YouTube.
MathIsGreatFun, «MAT217 2.2 #3», под лицензией Standard YouTube.
MathIsGreatFun, «MATh317 2.2 #4», под лицензией Standard YouTube.
Симплексный метод для стандартных задач
Симплексный метод для стандартных задач
|
| ИНДЕКС УСЛОВИЯ |
|
Симплекс-метод заменяет ограничения (неравенства) уравнениями в
задачи линейного программирования, а затем решает задачу по матрице
манипуляция. Набор решений для измененной задачи имеет более высокий
размерности, чем множество решений исходной задачи, но
легче изучать с матрицами. Набор решений для измененной задачи имеет более высокий
размерности, чем множество решений исходной задачи, но
легче изучать с матрицами. |
Ссылка : Что такое СТАНДАРТНАЯ ЗАДАЧА МАКСИМИЗАЦИИ?
Ссылка : Доступен пример SIMPLEX METHOD для стандартной задачи.
|
|
| Запишите исправленную задачу в виде таблицы с
ряд целей (= нижний ряд)
состоящая из отрицаний коэффициентов
целевая функция z ; z будут развернуты.
Нижний правый угол — это значение z , когда x, y,… равны нулю ; таким образом, z обычно начинается с нуля. См. пример? См. пример? | |
| ||
|
|
| Симплексный метод будет перемещать ISM по одному столбцу за раз ; после каждого такой ход, мы приходим (или «прыгаем») к новой угловой точке (базовое решение) с большую объективную ценность. Поскольку множество решений имеет конечное число углы, этот процесс в конечном итоге дает наибольшую ценность целевая функция. |
ИНДИКАТОР (для стандартных задач максимизации) — это
число в нижней (целевой) строке таблицы, исключая
крайний правый номер. Таким образом, здесь СТРОКА ИНДИКАТОРОВ является нижней строкой, но
для нестандартных задач индикатор
строка будет другой строкой. Таким образом, здесь СТРОКА ИНДИКАТОРОВ является нижней строкой, но
для нестандартных задач индикатор
строка будет другой строкой. |
FIRST FIND THE PIVOT : (Rolf 8 th ed., стр. 294)
| Сводная колонка — это колонка, содержащая наибольшее количество отрицательных значений. индикатор. Если ни один индикатор не является отрицательным, таблица представляет собой ОКОНЧАТЕЛЬНАЯ ТАБЛИЦА : см. шаг 8. |
| Сформируйте КОЭФФИЦИЕНТЫ (частные) для каждой строки : , разделите самое правое число на число в опорном столбце этой строки. |
|
|
«ПРЫЖОК» : перемещение подматрицы идентичности (ISM), следовательно, переход к новой угловой точке.
| Примените операцию поворота (Rolf 8 th ed., стр. 98) к таблица, включая нижнюю (целевую) строку. Сводная колонка станет столбцом нового ISM в новой таблице. Обратите внимание, какой столбец заменяется и где находится новый ISM ; его столбцы могут быть не в обычном порядке : , не беспокойтесь. Проверить ПОВОРОТНЫЙ ДВИГАТЕЛЬ, чтобы ускорить практику. |
|
|

 ..
.. ..
.. Для каждой таблицы координаты ее основного решения
заключаются в следующем (Rolf 8 -е -е изд., с. 287 или
См. пример?) :
Для каждой таблицы координаты ее основного решения
заключаются в следующем (Rolf 8 -е -е изд., с. 287 или
См. пример?) : 
