Как находить d f: определения, формулы и примеры решений

Дифференциал функции — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Понятие дифференциала функции
Рассмотрим некоторую функцию у = f (x), определенную в окрестности точки х0.
В окрестности точки х0 выберем точку х, и найдем значение функции в этой точке.
f (x)
y
х х х0 — приращение аргумента
f
f ( x0 )
f f ( x) f ( x0 ) f ( x0 x) f ( x0 ) — приращение функции
х
0
x0
x
x
Определение

Предел отношения приращения функции в точке х0 к приращению аргумента при стремлении
приращения аргумента к 0 (если этот предел существует и конечен) называется производной
функции у = f (x) в точке х0 и обозначается f ( x0 ).
f
f ( x0 ) lim
x 0 х
Обозначения производной:
f ( x), f х , y ( x), y x ,
dy df
,
dx dx
Пусть функция у = f (x) имеет в точке х0 отличную от нуля производную:
f
0
x 0 х
f ( x0 ) lim
По основной теореме о пределах, в окрестности точки х0 имеет место равенство:
f
f ( x0 ) ( х),
х
(х) – функция, бесконечно малая при х 0
Следовательно, f f ( x0 ) х ( х) х ( lim
x 0
f ( x0 ) х
f ( x0 ) 0,
х
lim
x 0
( х) х
х
( х) 0)
f ( x0 ) х – главная часть приращения функции
Определение
Дифференциалом функции у = f (x) в точке х0 называется главная часть приращения этой
функции в точке х0 и обозначается d f(x0 )
df f ( x0 ) х
Дифференциал независимой переменной х равен приращению ∆х:
y f ( x) x y x 1 df dx 1 x dx x
Итак,
Следовательно,
df f ( x) dx
df
f (x)
dx
Пример 1
Дана функция
f ( x) x 4 sin 3x
Найти df в точке х0=0
Решение:
df f ( x) dx ( x 4 sin 3x) dx (4 x 3 3 cos 3x)dx
df ( x0 ) (4 03 3 cos 0)dx 3dx
Пример 2
Дана функция
f ( x) earctg x 7 х 3
Найти df
Решение:
1
df f ( x) dx (earctg x 7 х 3) dx earctg x
7 dx
2
1 x
2. 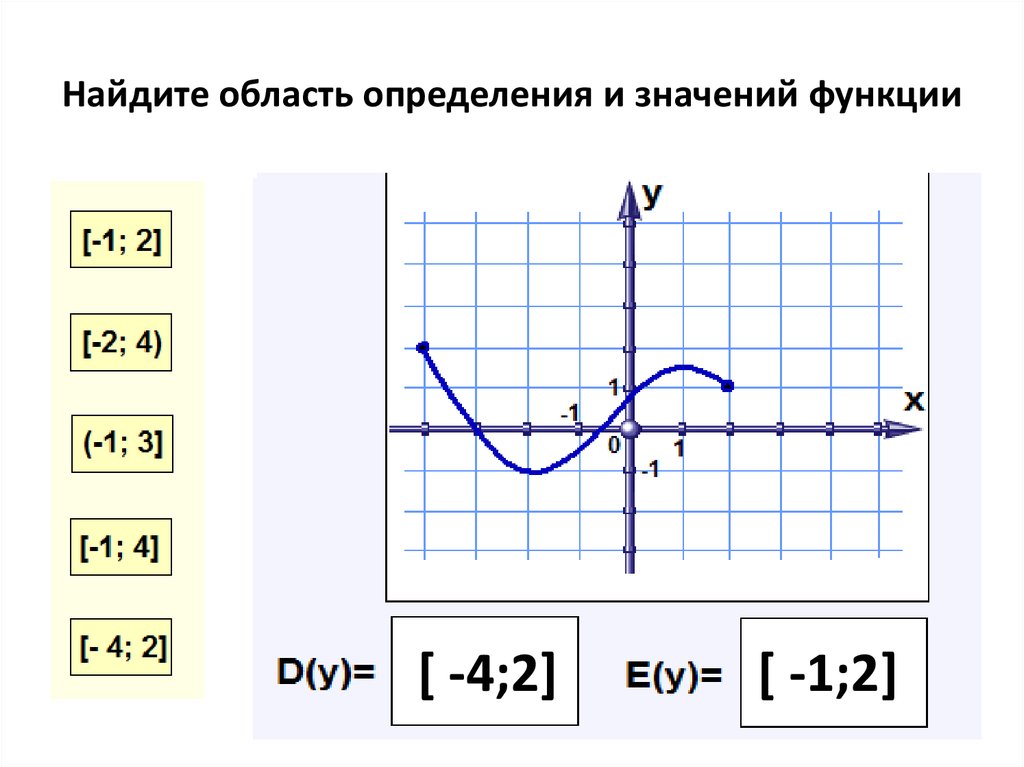Геометрический смысл дифференциала функции
К графику функции у = f (x) проведем касательную в точке х0
y
f (x)
B
df
A
f
M
f ( x0 )
х
0
f ( x0 ) tg tg АМВ
x0
x
x
AB AB AB f ( x ) x AB df
0
MA x
Дифференциал функции y = f (x) в точке х0 равен приращению ординаты касательной к
графику функции в этой точке, когда аргумент получает приращение х
3. Свойства дифференциала
1. d С 0
2. d (u v) du dv
3. d (u v) v du udv
u v du udv
4. d
(v 0)
2
v
v
5. Пусть y f (u( x)) – сложная функция, тогда
dy f x dx f u u x dx f u du
Итак,
f x dx f u du
инвариантность формы 1-го дифференциала
4. Применение дифференциала к приближенным
вычислениям
Приращение функции
f f ( x0 ) х ( х) х df ( х) х f df
Абсолютная погрешность при замене f на df равна f df ( х) х
бесконечно малая более высокого порядка, чем х при х 0
Пример
Вычислить 2,015
Решение:
Рассмотрим функцию f ( x) x 5
Пусть x0 2, x 0,01, тогда x0 x 2, 01
Задача сводится к нахождению
f ( x0 x) f ( x0 ) f
f ( x0 x) (2 0,01) 5
f ( x0 ) f (2) 25 32
f d f ( х5 ) x 5x 4 x
f ( x0 x) 32 0,8 32,8
Итак, 2,015 32,8
d f ( x0 ) 5 24 0,01 0,8
5. Дифференциалы высших порядков
Пусть у = f (x), x – независимая переменная,
d f = f΄(x)∙dx – дифференциал (первый дифференциал).
Определение
Вторым дифференциалом d 2f функции у = f (x) называют дифференциал от первого
дифференциала d f, рассматриваемого как функция от х (dx считаем константой).
Таким образом,
d 2f= d (d f) = d (f ΄(x)∙dx) = dx∙d (f ΄(x)) = dx∙f ΄΄(x)∙dx = f ΄΄(x)∙(dx)2.
Итак, d 2f=f ΄΄(x)∙dx2.
Аналогично определяются третий и выше дифференциалы:
d 3f=f (3)(x)∙dx3, d 4f=f (4)(x)∙dx4
Итак, d nf=f (n)(x)∙dxn
Пример
Дана функция
f ( x) x 4 sin 3x
Найти d 2f
Решение:
d 2 f f ( x) dx 2 ( x 4 sin 3x) dx 2 (4 x 3 3 cos 3x) dx 2 (12 х 2 9 sin 3x)dx 2
СПАСИБО ЗА ВНИМАНИЕ!

English     Русский Правила

python — Как найти значение, возле которого было максимальное кол-во соседей со значением примерно равным исходному значению?

Вопрос задан

1 год 5 месяцев назад

Изменён 1 год 5 месяцев назад

Просмотрен 107 раз

Есть DataFrame по ссылке.

Есть в DataFrame колонка close и необходимо найти значение/я по данной колонке возле которой было наиболее максимальное кол-во соседей (значений примерно равных исходному значению).

Пример: цена 1.17632 возле которой были обнаружены соседи (значения в пределах +/- 0.0005) в кол-ве 13 штук

---

PS саму идею сделал, но думаю не совсем корреткно её выполнил:

def find_protorgovok(name_df, delta: float):
    """"поиск сильных проторговок, name_df - имя dataframe, в ко-м будем 
    искать проторговки, delta - параметр погрешность
    в пунктах для поиска соседей рядом"""
    df = name_df[["time", 'open', 'high', 'low', 'close']]
    df_open = df[['open']].round(5)
    df_close = df[['close']].round(5)
    df_low = df[['low']].round(5)
    df_high = df[['high']].round(5)
    # delta = 0.0005  # погрешность в пунктах
    a_massiv = np.array([])  # создаем пустой массив
    # near_values = []
    counts_values = []  # список где будут хранится все значения ока-ся рядом(соседи)
    # цикл по столбцу "df_close" from df_list сверху/вниз
    for i in trange(len(df_close)):  
        # value = df.
  iloc[i][df.columns[j]]            # get value_df; i - номер строки, j - номер столбца
        value = df_close.iloc[i][df_close.columns[0]]  # get value from df_close
        #  print(i, value)
        a_massiv = np.append(a_massiv, value)  # добавляем каждое новое value from df_column в массив array
        minElement = np.amin(a_massiv)  # находим min- элемент массива [a_massiv] с добавленными элементами
        #  print(f"a_massiv: {a_massiv}")
        #  print(f"minElement: {minElement}")
        # ---- start my_function --
        distance_high = minElement + delta  # значение рядом (сверху) со минимльным значением
        distance_low = minElement - delta  # значение рядом (снизу) со минимльным значением
        # df_list = [df_close, df_low, df_high]        # список столбцов нашего df для iterate for columns from df_list
        #  near_values = []                            # create empty list
        if distance_low < value < distance_high:  # если значение value находится рядом с нашим minimum of a_massiv
            #  print(f"номер строки i: {i}, from: {df_close.

  

  
 columns[0]}")  # df_item.columns[0] - str(имя колонки)
            b = value
            #  print(f"найден сосед рядом b: {b}, min= {minElement}")
            #    near_values.append(b)
            counts_values.append(minElement)  # добавляем нужные значения в список counts_values
        time.sleep(0.1)
    # print(f"near_values: {len(near_values)}")
    # print(f"counts_values: {counts_values}, len counts_values: {len(counts_values)}")
    b_list = []  # создаем пустой массив для цены
    d_list = []  # создаем пустой массив для кол-ва появлений
    # поиск максимально встречющегося элемента в списке counts_values - содержащем все значения которые были рядом
    for i in range(len(df_close)):  # проверка счетчика появлений значения до 45 - раз
        new_list = [e for e in set(counts_values) if counts_values.count(e) == i]
        if new_list:
            if i > 3 and len(new_list) == 1:  # выводим только если появления более > 3 раз
                b_list.append(i)
                d_list.
  append(new_list[0])
                print(f"price : {new_list[0]}, кол-во появлений: {i}")  # [1, 3]
    dict_df = dict(zip(d_list, b_list))
    # print(f"dict : {dict_df}")
    df = pd.DataFrame(dict_df.items(), columns=['Цена', 'кол-во_появлений'])
    print(f"df : \n{df}")
    return df

• python
• pandas
• dataframe
• numpy
• оптимизация

6

Если я правильно понял условие задачи:

def count_close_points(x, ser, delta=0.005):
    return ((x - delta <= ser) & (ser <= x + delta)).sum()
delta = 0.0005
d = {x: count_close_points(x, df["close"], delta) for x in df["close"].unique()}
val = max(d, key=d.get)
cnt = d[val]
print(f'Value [{val}] has [{cnt}] "neighbours"')

вывод:

Value [1.17761] has [42] "neighbours"

2

Зарегистрируйтесь или войдите

Регистрация через Google

Регистрация через Facebook

Регистрация через почту

Отправить без регистрации

Почта

Необходима, но никому не показывается

Отправить без регистрации

Почта

Необходима, но никому не показывается

Нажимая на кнопку «Отправить ответ», вы соглашаетесь с нашими пользовательским соглашением, политикой конфиденциальности и политикой о куки

Объяснение

степеней свободы в статистике: формула и пример

Что такое степени свободы?

Степени свободы относятся к максимальному количеству логически независимых значений, то есть значений, которые могут свободно изменяться в выборке данных. После выбора количества степеней свободы необходимо выбрать конкретные элементы выборки данных, если есть невыполненные требования к выборке данных.

Ключевые выводы

• Степени свободы относятся к максимальному количеству логически независимых значений, т.е. значений, которые могут изменяться в выборке данных.
• Степени свободы вычисляются путем вычитания единицы из числа элементов в выборке данных.
• Степени свободы обычно обсуждаются в связи с различными формами проверки гипотез в статистике, такими как хи-квадрат.
• Вычисление степеней свободы является ключевым моментом при попытке понять важность статистики хи-квадрат и обоснованность нулевой гипотезы.
• Степени свободы также могут описывать деловые ситуации, когда руководство должно принять решение, определяющее результат другой переменной.

Понимание степеней свободы

Степени свободы — это количество независимых переменных, которые можно оценить при статистическом анализе. Эти значения этих переменных не имеют ограничений, хотя значения налагают ограничения на другие переменные, если набор данных должен соответствовать параметрам оценки.

В наборе данных некоторые начальные числа могут быть выбраны случайным образом. Однако, если набор данных должен составлять определенную сумму или среднее значение, например, число в наборе данных ограничено для оценки значений всех других значений в наборе данных, тогда выполняется требование набора.

Примеры степеней свободы

Самый простой способ концептуально понять степени свободы — это рассмотреть несколько примеров.

Пример 1: Рассмотрим выборку данных, состоящую из пяти положительных целых чисел. Значения пяти целых чисел должны иметь среднее значение шесть. Если четыре элемента в наборе данных равны {3, 8, 5 и 4}, пятое число должно быть равно 10. Поскольку первые четыре числа могут быть выбраны случайным образом, степени свободы равны четырем.

Пример 2 : Рассмотрим выборку данных, состоящую из пяти положительных целых чисел. Значения могут быть любым числом без известной взаимосвязи между ними. Поскольку все пять чисел могут быть выбраны случайным образом без каких-либо ограничений, степеней свободы четыре.

Пример 3: Рассмотрим выборку данных, состоящую из одного целого числа. Это целое число должно быть нечетным. Поскольку существуют ограничения на один элемент в наборе данных, степени свободы равны нулю.

Степени свободы Формула

Формула для определения степеней свободы:

Д ф «=» Н − 1 где: Д ф «=» степени свободы Н «=» размер образца \begin{align} &\text{D}_\text{f} = N — 1 \\ &\textbf{где:} \\ &\text{D}_\text{f} = \text{степени свобода} \\ &N = \text{размер образца} \\ \end{выровнено} ​Df​=N−1, где:Df​=степени свободыN=размер выборки​

Например, представьте себе задачу выбора 10 бейсболистов, чей средний показатель отбивания мяча должен быть равен 0,250. Общее количество игроков, которые составят наш набор данных, является размером выборки, поэтому N = 10. В этом примере 9(10 — 1) бейсболисты теоретически могут быть выбраны случайным образом, при этом 10-й бейсболист должен иметь определенное среднее количество ударов, чтобы соответствовать ограничению среднего показателя 0,250.

В некоторых расчетах степеней свободы с несколькими параметрами или отношениями используется формула Df = N — P, где P — количество различных параметров или отношений. Например, в t-тесте с двумя выборками используется N — 2, поскольку необходимо оценить два параметра.

История степеней свободы

Самая ранняя и самая основная концепция степеней свободы была отмечена в начале 1800-х годов и переплелась в работах математика и астронома Карла Фридриха Гаусса. Современное использование и понимание этого термина были изложены впервые Уильямом Сили Госсетом, английским статистиком, в его статье «Вероятная ошибка среднего», опубликованной в Biometrika в 1908 году под псевдонимом, чтобы сохранить его анонимность.

В своих трудах Госсет специально не использовал термин «степени свободы». Тем не менее, он давал объяснение этой концепции в ходе разработки того, что в конечном итоге стало известно как Т-распределение Стьюдента. Фактический термин не был популярен до 1922. Английский биолог и статистик Рональд Фишер начал использовать термин «степени свободы», когда начал публиковать отчеты и данные о своей работе по построению хи-квадратов.

Тесты хи-квадрат

Степени свободы обычно обсуждаются в связи с различными формами проверки гипотез в статистике, такими как хи-квадрат. При попытке понять важность статистики хи-квадрат и достоверность нулевой гипотезы важно рассчитать степени свободы.

Существует два разных вида тестов хи-квадрат: тест независимости, который задает вопрос о взаимосвязи, например: «Есть ли связь между полом и результатами SAT?»; и тест на соответствие, который спрашивает что-то вроде «Если монету подбросить 100 раз, выпадет ли она орлом 50 раз и решкой 50 раз?»

Для этих тестов используются степени свободы, чтобы определить, можно ли отвергнуть определенную нулевую гипотезу на основе общего количества переменных и выборок в эксперименте. Например, при рассмотрении студентов и выбора курса размер выборки в 30 или 40 студентов, вероятно, недостаточно велик для получения значимых данных. Получение таких же или подобных результатов исследования с использованием выборки в 400 или 500 студентов является более достоверным.

Т-тест

Чтобы выполнить t-критерий, вы должны вычислить значение t для выборки и сравнить его с критическим значением. Критическое значение будет варьироваться, и вы можете определить правильное критическое значение, используя распределение t набора данных с правильными степенями свободы.

Наборы с более низкими степенями свободы имеют более высокую вероятность экстремальных значений, в то время как более высокие степени свободы (т. е. размер выборки не менее 30) будут намного ближе к кривой нормального распределения. Это связано с тем, что меньшие размеры выборки будут соответствовать меньшим степеням свободы, что приведет к более толстым хвостам t-распределения.

В приведенных выше примерах многие ситуации можно использовать в качестве t-критерия с одной выборкой. Например, «Пример 1», в котором выбрано пять значений, но в сумме они должны составлять определенное среднее значение, может быть определен как t-критерий с одной выборкой. Это связано с тем, что на переменную накладывается только одно ограничение.

Применение степеней свободы

В статистике степени свободы определяют форму t-распределения, используемого в t-тестах при расчете p-значения. В зависимости от размера выборки разные степени свободы будут отображать разные t-распределения. Вычисление степеней свободы также имеет решающее значение при попытке понять важность статистики хи-квадрат и достоверность нулевой гипотезы.

Степени свободы также имеют концептуальные применения за пределами статистики. Поскольку бизнес сталкивается с необходимостью принятия решений, один выбор может фиксировать результат другой переменной. Рассмотрим компанию, решающую, сколько сырья закупить в рамках своего производственного процесса. У компании есть два элемента в этом наборе данных: количество сырья, которое необходимо приобрести, и общая стоимость сырья.

Компания свободно выбирает один из двух пунктов, но их выбор будет определять исход другого. Устанавливая количество приобретаемого сырья, компания не имеет права голоса в отношении общей потраченной суммы. Установив общую сумму расходов, компания может быть ограничена в количестве сырья, которое она может приобрести. Поскольку он может свободно выбирать только одно из двух, в этой ситуации у него есть одна степень свободы.

Как определить степени свободы?

При определении среднего значения набора данных степени свободы рассчитываются как количество элементов в наборе минус один. Это связано с тем, что все элементы в этом наборе могут быть выбраны случайным образом, пока не останется один элемент; что один элемент должен соответствовать заданному среднему значению.

О чем говорят вам степени свободы?

Степени свободы говорят вам, сколько юнитов в наборе можно выбрать без ограничений, чтобы по-прежнему соблюдать заданное правило, контролирующее набор. Например, рассмотрим набор из пяти элементов, среднее значение которых в сумме составляет 20. Степени свободы говорят вам, сколько элементов (4) можно выбрать случайным образом, прежде чем должны быть введены ограничения. В этом примере, как только первые четыре элемента выбраны, вы больше не можете произвольно выбирать точку данных, потому что вы должны «принудительно сбалансировать» заданное среднее значение.

Всегда ли степень свободы равна 1?

Степени свободы — это всегда количество единиц в заданном наборе минус 1. Оно всегда минус один, потому что, если в наборе данных есть параметры, последний элемент данных должен быть очень конкретным, чтобы убедиться, что все остальные точки соответствуют к этому исходу.

Практический результат

В некоторых процессах статистического анализа может потребоваться указание количества независимых значений, которые могут изменяться в ходе анализа, чтобы по-прежнему удовлетворять требованиям ограничений. Этот показатель представляет собой степени свободы, количество единиц в размере выборки, которые могут быть выбраны случайным образом, прежде чем нужно будет выбрать конкретное значение.

Как найти степени свободы

Опубликован в 7 июля 2022 г. к Шон Терни. Отредактировано 10 ноября 2022 г.

Степени свободы , часто представленные как v или df , — это количество независимых фрагментов информации, используемых для расчета статистики. Он рассчитывается как размер выборки минус количество ограничений.

Степени свободы обычно указываются в скобках рядом со статистикой теста вместе с результатами статистического теста.

Пример: Степени свободы Предположим, вы случайным образом выбираете 10 взрослых американцев и измеряете их ежедневное потребление кальция. Вы используете однообразный тест t , чтобы определить, соответствует ли среднесуточная доза взрослых американцев рекомендуемому количеству 1000 мг.

Тестовая статистика, t , имеет 9 степеней свободы:

ДФ = n − 1

df = 10 − 1

дф = 9

Вы вычисляете значение t , равное 1,41, для выборки, которая соответствует значению p , равному 0,19. Вы сообщаете о своих результатах:

«Среднее ежедневное потребление кальция участниками не отличалось от рекомендуемого количества 1000 мг, t (9) = 1,41, p = 0,19».

Содержание

1. Что такое степени свободы?
2. Степени свободы и проверка гипотез
3. Как рассчитать степени свободы
4. Тест по степеням свободы
5. Часто задаваемые вопросы о степенях свободы

Что такое степени свободы?

В логической статистике вы оцениваете параметр генеральной совокупности, вычисляя статистику выборки. Количество независимых частей информации, используемых для расчета статистики, называется степенями свободы . Степени свободы статистики зависят от размера выборки:

• Когда размер выборки мал , имеется только несколько независимых фрагментов информации и, следовательно, лишь несколько степеней свободы.
• Когда размер выборки большой , имеется много независимых фрагментов информации и, следовательно, много степеней свободы.

Примечание. Хотя степени свободы тесно связаны с размером выборки, это не одно и то же. Степеней свободы всегда меньше, чем размер выборки.

При оценке параметра необходимо ввести ограничения в том, как значения связаны друг с другом. В результате фрагменты информации не все являются независимыми. Иными словами, не все значения в выборке могут варьироваться .

Следующая аналогия и пример показывают, что означает свобода изменения значения и как на него влияют ограничения.

Свободно варьироваться: аналог десерта

Пример. Аналогия с десертом. Представьте, что ваша соседка по комнате сладкоежка, поэтому она рада узнать, что столовая вашего колледжа предлагает семь вариантов десертов. Однажды она решает, что хочет иметь разный десерт каждый день.

Решив каждый день есть разные десерты, ваша соседка по комнате накладывает ограничения на ее выбор десертов.

В понедельник она может выбрать любой из семи десертов. Во вторник она может выбрать любой из шести оставшихся вариантов десерта. В среду она может выбрать любой из пяти оставшихся вариантов и так далее.

К воскресенью у нее были все варианты десертов, кроме одного. У нее нет выбора в воскресенье, так как остается только один вариант.

Из-за ограничений ваша соседка по комнате могла выбирать себе десерт только шесть дней из семи. Ее выбор десерта мог свободно варьироваться в течение этих шести дней. Напротив, ее выбор десерта в последний день не мог свободно варьироваться; это зависело от ее выбора десерта за предыдущие шесть дней.

Произвольное изменение: пример суммы

Пример: SumSuppose Я прошу вас выбрать пять целых чисел, сумма которых равна 100.

Требование суммирования до 100 является ограничением на ваш выбор числа.

В качестве первого числа вы можете выбрать любое целое число. Что бы вы ни выбрали, сумма пяти чисел все равно может равняться 100. Это также относится ко второму, третьему и четвертому числам.

У вас нет выбора для окончательного числа; оно имеет только одно возможное значение и не может свободно изменяться. Например, представьте, что вы выбрали 15, 27, 42 и 3 в качестве первых четырех чисел. Чтобы сумма чисел равнялась 100, окончательное число должно быть 13.

Из-за ограничения можно было выбрать только четыре из пяти чисел. Первые четыре числа можно было свободно варьировать. Напротив, пятое число не могло свободно варьироваться; это зависело от остальных четырех чисел.

Степени свободы и проверка гипотез

Степени свободы статистики теста определяют критическое значение теста гипотезы. Критическое значение вычисляется из нулевого распределения и является пороговым значением, чтобы решить, следует ли отклонить нулевую гипотезу.

Степени свободы влияют на критическое значение, изменяя форму нулевого распределения. Нулевые распределения статистики Стьюдента t , критерия хи-квадрат и других статистик изменяются в зависимости от степеней свободы, но каждое из них меняется по-разному.

Студенческая

т раздача

Чтобы выполнить тест t , вы вычисляете t для образца и сравниваете его с критическим значением. Чтобы найти правильное критическое значение, вам нужно использовать распределение Стьюдента t с соответствующими степенями свободы.

Нулевое распределение Стьюдента t изменяется со степенями свободы:

• Когда df = 1, распределение является сильно лептокуртичным, что означает, что вероятность экстремальных значений выше, чем при нормальном распределении.
• По мере увеличения df распределение становится более узким и менее лептокуртичным. Оно становится возрастающим, похожим на стандартное нормальное распределение
.
• Когда df ≥ 30, Распределение Стьюдента t почти такое же, как стандартное нормальное распределение. Если у вас размер выборки больше 30, вы можете использовать стандартное нормальное распределение (также известное как z ) вместо распределения Стьюдента t .

Это изменение формы распределения интуитивно понятно. Распределение t имеет меньший разброс по мере увеличения числа степеней свободы из-за увеличения достоверности оценки. Представьте себе повторную выборку населения и вычисление Стьюдента t ; чем больше размер выборки, тем меньше будет варьироваться статистика теста между выборками.

Пример: Степени свободы и проверка гипотез Предположим, вы хотите использовать одну выборку t тест для проверки нулевой гипотезы о том, что среднее ежедневное потребление кальция взрослыми американцами равно рекомендуемому количеству 1000 мг.

Вы берете случайную выборку из 10 взрослых и измеряете их ежедневное потребление кальция.

Одновыборочный тест t определяет, когда среднее значение генеральной совокупности отличается от определенного значения. Однако вы не знаете среднее значение генеральной совокупности, поэтому сначала вам нужно оценить его, используя среднее значение выборки. Вы подсчитали, что среднее значение образца составляет 820 мг.

Предполагая, что среднее значение генеральной совокупности имеет определенное значение, вы накладываете ограничение на выборку: значения в выборке должны иметь среднее значение 820 мг. Следовательно, окончательное значение не может свободно изменяться; он имеет только одно возможное значение.

Например, представьте, что девять из десяти человек в выборке ежедневно потребляют 410, 1230, 870, 1110, 570, 390, 1030, 1080 и 630 мг кальция. Десятый человек должен ежедневно потреблять 880 мг кальция, чтобы образец имел среднее значение 820 мг.

Из-за ограничения только девять значений в выборке могут свободно изменяться. Тестовая статистика t имеет девять степеней свободы.

Чтобы найти критическое значение, нужно использовать распределение t для девяти степеней свободы. Если t выборки больше критического значения, то вы отвергаете нулевую гипотезу.

Распределение хи-квадрат

Чтобы выполнить тест хи-квадрат, вы сравниваете хи-квадрат образца с критическим значением. Чтобы найти правильное критическое значение, вам нужно использовать распределение хи-квадрат с соответствующими степенями свободы.

Нуль-распределение хи-квадрата изменяется со степенями свободы, но иначе, чем распределение Стьюдента t :

• Когда df < 3, , распределение вероятностей имеет форму перевернутой буквы «J».
• При df ≥ 3, распределение вероятностей имеет форму горба с пиком горба, расположенным на Χ ² = df − 2. Горб наклонен вправо, что означает, что распределение длиннее справа от его пика.
• Когда df > 90, распределение хи-квадрат аппроксимируется нормальным распределением.

Что может сделать корректура для вашей статьи?

Редакторы Scribbr не только исправляют грамматические и орфографические ошибки, но и улучшают качество письма, следя за тем, чтобы в статье не было неясных выражений, избыточных слов и неудобных формулировок.

См. пример редактирования

Как вычислить степени свободы

Степени свободы статистики равны размеру выборки минус количество ограничений. В большинстве случаев ограничения представляют собой параметры, которые оцениваются как промежуточные шаги при расчете статистики.

п − р

Где:

• n размер выборки

• r количество ограничений, обычно такое же, как и количество оцениваемых параметров

Степени свободы не могут быть отрицательными. В результате количество параметров, которые вы оцениваете, не может превышать размер вашей выборки.

Формулы для конкретных тестов

Может быть сложно определить количество ограничений. Часто бывает проще использовать формулы для конкретных тестов, чтобы определить степени свободы тестовой статистики.

В таблице ниже приведены формулы для расчета степеней свободы для нескольких часто используемых тестов.

Тест	Формула	Примечания
Один образец t испытание	дф = п — 1
Независимые образцы т тест	df = n 1  + n 2 − 2	Где n 1 — размер выборки группы 1, а n 2 — размер выборки группы 2
Зависимые образцы т тест	дф = п — 1	Где n количество пар
Простая линейная регрессия	дф = п — 2
Хи-квадрат критерия согласия	дф = к — 1	Где k — количество групп
Критерий независимости хи-квадрат	df = ( r − 1) * ( c − 1)	Где r — количество строк (групп одной переменной), а c — количество столбцов (групп другой переменной) в таблице непредвиденных обстоятельств
Однофакторный дисперсионный анализ	Межгрупповой df = k −  1 Внутригрупповой df = N − k Всего df − N 1 90	Где k — количество групп, а N — сумма объемов выборки всех групп

 

Викторина «Степени свободы»

Часто задаваемые вопросы о степенях свободы

org/FAQPage»>

Как проверить гипотезу, используя критическое значение t?

Чтобы проверить гипотезу, используя критическое значение t , выполните следующие четыре шага:

1. Рассчитайте значение t для вашей выборки.
2. Найдите критическое значение t в таблице t .
3. Определите, превышает ли (абсолютное) значение t критическое значение t .
4. Отклонить нулевую гипотезу, если значение выборки t больше критического значения t . В противном случае не отвергайте нулевую гипотезу.

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Терни, С. (2022, 10 ноября). Как найти степени свободы | Определение и формула. Скриббр. Проверено 21 февраля 2023 г., с https://www.scribbr.com/statistics/степени-оф-фридом/

Процитировать эту статью

Полезна ли эта статья?

Вы уже проголосовали. Спасибо 🙂 Ваш голос сохранен 🙂 Обработка вашего голоса…

Во время учебы в магистратуре и докторантуре Шон научился применять научные и статистические методы в своих исследованиях в области экологии. Теперь он любит учить студентов, как собирать и анализировать данные для собственных диссертаций и исследовательских проектов.