Урок на тему «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»
Тема урока: «Определение геометрической прогрессии. Формула п-го члена геометрической прогрессии»
Цель урока: познакомить учащихся с понятием геометрической прогрессии, формулой
n-ого члена геометрической прогрессии.
Задачи урока:
— образовательная: обеспечить восприятие, осмысление и первичное запоминание учащимися понятий «геометрическая прогрессия», «знаменатель геометрической прогрессии», «формулы n-го члена»; организовать деятельность учащихся по воспроизведению изученного материала и упражнениям в его применении по образцу; сформировать у учащихся умение находить знаменатель и n-ый член геометрической прогрессии.
— развивающая: способствовать развитию наблюдательности, умения анализировать, применять приемы сравнения, переноса знаний в новую ситуацию;
— воспитательная: побуждать учащихся к преодолению трудностей, к самоконтролю, взаимоконтролю в
процессе умственной деятельности.
Тип урока: урок изучения нового материала.
Ход урока:
- Организационный момент.
Здравствуйте, ребята! Сегодня у нас на уроке присутствуют гости, давайте их поприветствуем. Присаживайтесь.
-Сегодняшний урок я начну словами А.С. Пушкина:
СЛАЙД 1
«О сколько нам открытий чудных …
Готовит просвещенья дух,
И опыт – сын ошибок трудных,
И гений – парадоксов друг»
Сегодня на уроке мы продолжим изучать числовые последовательности, и вы сможете самостоятельно сделать по-настоящему чудные открытия в данной области. Итак, начнем.
Откройте тетради, запишите число, классная работа.
2.Актуализация опорных знаний учащихся.
-Как я уже сказала, мы продолжаем изучать числовые последовательности, а вначале вспомним то, что мы знаем об уже изученной арифметической прогрессии:
— Какая последовательность называется арифметической прогрессией?
— Запишите формулу n-го члена арифметической прогрессии?
— Что в этой формуле d и как ее найти?
— Что достаточно указать, чтобы задать арифметическую прогрессию?
—
Запишите формулу суммы первых n членов арифметической прогрессии.
— Какую еще формулу для нахождения суммы первых n членов вы знаете?
— Приведите примеры арифметических прогрессий.
— Посмотрите на последовательности. СЛАЙД 2.
-3; -6; -9; -12; -15;…
7; 14; 21; 28; 35; …
15; 10; 5; 0; -5; …
1; 3; 9; 27; 81;…
— Какие из этих последовательностей можно объединить по общему свойству? (1-3 арифметические прогрессии)
— Чем отличается 4-ая последовательность от других? (Умножая предыдущий член на одно и тоже число)
3. Изучение нового материала.
— Ребята, такие последовательности называются геометрической прогрессией
-Как вы думаете, какой будет тема урока? (Геометрическая прогрессия)
— Тема нашего урока «Определение геометрической прогрессии формула N-го члена геометрической прогрессии». Запишите ее в тетрадь.
-Сегодня на уроке мы дадим определение
геометрической прогрессии, введем обозначение геометрической прогрессии, ее
элементов, выведим формулу для n-го члена геометрической
прогрессии.
Геометрическую прогрессию чаще всего обозначают (bn), чтобы не путать ее с арифметической, хотя это условности.
-Так какая последовательность называется геометрической прогрессией?
-Постоянное число, на которое умножают, обозначим буквой q, это знаменатель геометрической прогрессии. q≠0
Чтобы задать геометрическую прогрессию, достаточно знать первый член геометрической прогрессии и знаменатель. Запишем рекуррентную формулу, вытекающую из определения геометрической прогрессии b n+1=bnq, bn≠0. Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т.е. при любом натуральном n верно равенство bn+1/bn=q.
-Члены геометрической прогрессии не могут равняться 0, так как мы отметили, что bn≠0 и q≠0 .
— Итак, мы «открыли» определение
геометрической прогрессии, записали ее рекуррентную формулу, формулу для
нахождения знаменателя геометрической прогрессии. Но это не все открытия на
сегодня.
Но это не все открытия на
сегодня.
— Выберите из данных последовательностей геометрическую прогрессию, назовите ее первый член и знаменатель. СЛАЙД 3
1; 3; 9; 27; 81;…
32; 16; 8; 4; 2;…
-10; -12; -14; -16;…
-1/5; 1; -5; 25; -125;…
— Запишите их в тетрадь.
— Какая последовательность не подошла? Почему?
— Задачи, связанные с геометрической прогрессией, имеют практический характер и встречаются в различных областях. В таких как физика, экономика, биология, геометрия. Такие задачи мы рассмотрим на последующих уроках. А сейчас Юля расскажет нам легенду о шахматах (выступает Юля). СЛАЙД 4
В книге Перельмана Я. И. «Живая математика», есть легенда о шахматах: «…Шахматная игра была придумана в Индии, и, когда индусский царь Шерам познакомился с нею, он был восхищен её остроумием и разнообразием возможных в ней положений.
Узнав, что она изобретена одним из его
подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.
Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
— Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, — сказал царь…
— Повелитель, — сказал Сета, — прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.
— Простое пшеничное зерно? – изумился царь.
— Да, повелитель. За вторую клетку прикажи выдать 2 зерна, за третью 4, за четвертую – 8, за пятую – 16, за шестую – 32…
— Довольно, — с раздражением прервал его
царь. – Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию:
за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна
моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь
моею милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения
доброты своего государя. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей.
Сета улыбнулся. Покинул залу и стал дожидаться у ворот дворца.
За обедом царь вспомнил об изобретателе шахмат и послал узнать, унёс ли уже безрассудный Сета свою жалкую награду.
— Повелитель, — был ответ, — приказание твоё исполняется. Придворные математики исчисляют число следуемых зерен…
Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение.
Царь приказал ввести его.
— Прежде чем скажешь о твоем деле, — объявил Шерам, — я желаю услышать, выдана ли, наконец, Сете та ничтожная награда, которую он себе назначил.
— Ради этого я и осмелился явиться перед тобой в столь ранний час, — ответил старик. – Мы добросовестно исчислили всё количество зерен, которое желает получить Сета. Число это так велико…
— Как бы велико оно ни было, — надменно перебил царь, житницы мои не оскудеют. Награда обещана и должна быть выдана… СЛАЙД 5
— Не в твоей власти, повелитель, исполнять подобные желания… »
— Как мы узнали из этой легенды, о
геометрической прогрессии знали еще в древние времена. А почему царь не смог
наградить изобретателя игры? Как вы думаете? (это было большое число)
А почему царь не смог
наградить изобретателя игры? Как вы думаете? (это было большое число)
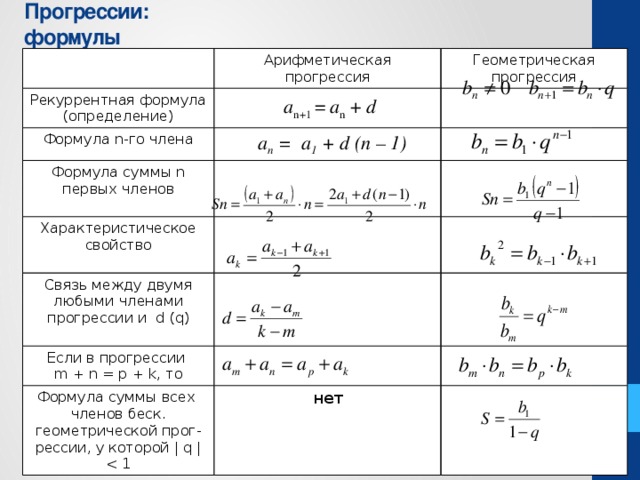
— Для того чтобы узнать, сколько зерна приходилось за 64 клетку шахматной доски, выведем формулу n-го члена геометрической прогрессии:
bn+1=bnq
b2=b1q,
b3=b2q=(b1q)q= b1q2,
b4=b3q=( b1q2)q= b1q3
b5=b4q= (b1q3)q= b1q4
bn= b1qn-1 – формула n-го члена геометрической прогрессии.
Теперь подставим значения в формулу и узнаем, сколько зерна необходимо отдать Шераму за 64 клетку шахматной доски:
b64=b1q64-1
b1=1, b2=2, q=2
b64=1*263
-Если это посчитать, то на 64 поле получится
9 223 372 036 854 775 808 (9 квинтильонов 223 квадрильона
372 триллиона 36 биллионов 854 миллиона 775 тысяч 808 ) Если бы принцу удалось
засеять пшеницей площадь всей поверхности Земли, считая и моря и океаны, и
горы, и пустыни, и Арктику, и Антарктиду, и получить богатый урожай, то,
пожалуй, лет за пять он смог бы рассчитаться с просителем. Так стоило ли принцу
смеяться?
Так стоило ли принцу
смеяться?
4. Закрепление
1) №623 стр. 156
— Откройте ваши учебники на странице 156, найдите №623, прочитайте задание. Желающие?
2) № 625 стр. 157 (у доски)
3) № 627 стр. 157 (у доски)
4) Задание 6 страница 16 из сборника ОГЭ— Задания на геометрическую прогрессию встречаются и в вашем экзамене по математике. Откройте свои сборники для подготовки к ОГЭ по математике на странице 16 и прочитайте задание 6. (Читают)
— О какой последовательности здесь идет речь?
— Как можно найти знаменатель геометрической прогрессии? Посчитаем устно чему он будет равен? (4)
5. Самостоятельная работа с самопроверкой по вариантам.
Ф.И. учащегося вариант 1 |
1.
2. Чему может быть равен знаменатель геометрической прогрессии, если b1 = 10, а b2 = 40? А) 2 B) 4 C) 5;
|
Ф.И. учащегося вариант 2 |
1. Первый член геометрической
прогрессии равен 4, знаменатель – равен 3. Найти 5-ый член прогрессии. 2. Чему может быть равен знаменатель геометрической прогрессии, если b1=6, а b2=12. А) 5; B) 2; C) 4;
|
Ф. |
1. Первый член геометрической
прогрессии равен 2, знаменатель – равен 10. Найти 4-ый член прогрессии.
2. Чему может быть равен знаменатель геометрической прогрессии, если b1=8, а b2=24? А) 4; B) 3; C) 5;
|
Ф.И. учащегося вариант 4 |
1. Первый член геометрической
прогрессии равен 6, знаменатель – равен 2. Найти 4-ый член прогрессии.
2. А) 3; B) 7; C) 8;
|
— Проверьте правильность своего решения СЛАЙД 7
6. Итог урока.
— Подведем итог сегодняшнего урока. Вспомним эпиграф нашего урока: СЛАЙД 8
«О сколько нам открытий чудных …
Готовит просвещенья дух,
И опыт – сын ошибок трудных,
И гений – парадоксов друг»
А. С. Пушкин
— Что же нового
мы «открыли» на уроке?
— Какую последовательность называют геометрической прогрессией?
— Как найти знаменатель геометрической прогрессии?
— Что достаточно знать, чтобы задать геометрическую прогрессию?
— Назовите формулу n-го члена геометрической прогрессии.
— На следующих уроках нам предстоит сделать
еще немало открытий о геометрической прогрессии.
7. Задание на дом: Пункт 27 (страницы 153-155), № 626, № 628 СЛАЙД 9
8. Выставление отметок.
-Большое спасибо за урок и помните, что «Человек, вооруженный знаниями способен решить любые задачи».
Презентация по алгебре 9 класс «Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии»
Самостоятельная работа:
В а р и а н т 1.
- Найдите двадцать третий член арифметической прогрессии ( а п ), если а 1 = 15 и d = 3 .
- Найдите сумму первых шестидесяти членов последовательности ( b n ) , заданной формулой
В а р и а н т 2.
- Найдите восемнадцатый член арифметической прогрессии ( а п ),если а 1 = 70 и d = -3 .

- Найдите сумму первых сорока членов последовательности ( b n ), заданной формулой
b n = 3n – 1 .
b n = 4n – 2 .
Рассмотрите последовательности и выявите закономерности:
а) — 3; — 5; — 7; — 9; …
б) — 2; — 4; — 8; — 16; …
в) 2; 4; 8; 16; 32; 64; …
г) 2; 6; 18; 54; 162…
Определение геометрической прогрессии. Формула n -го члена геометрической прогрессии.
Цели урока:
- Сформулировать определение геометрической прогрессии.
- Вывести формулу n -го члена геометрической прогрессии
- Находить любой член геометрической прогрессии, его порядковый номер, используя формулу n -го члена и свойство геометрической прогрессии .

Пример:
(b n ): 2, 6, 18, 54, 162,…
Здесь каждый член после первого в 3 раза больше предыдущего. То есть каждый последующий член является результатом умножения предыдущего члена на 3:
2 · 3 = 6;
6 · 3 = 18
18 · 3 = 54
54 · 3 = 162.
Геометрическая прогрессия – это такая последовательность отличных от нуля чисел, которая получается в результате умножения каждого последующего члена на одно и то же число, не равное нулю.
Последовательность (b n ) – геометрическая прогрессия, если для любого натурального n выполняется условие:
b n ≠ 0 и b n+1 = b n . q, где q – некоторое число.
Выразим из формулы q
q – знаменатель геометрической прогрессии
Знаменатель геометрической прогрессии – это число, равное отношению любого её члена, начиная со второго, к предыдущему члену прогрессии. Его обычно обозначают буквой q.
Пример :
(b n ) – геометрическая прогрессия.
b 1 = 1, q = 0,1. Найдите несколько первых членов этой прогрессии.
b 2 = b 1 . q = 1 . 0,1 = 0,1
b 4 = b 3 . q = 0,01 . 0,1 = 0,001
b 3 = b 2 . q = 0,1 . 0,1 = 0,01
b 5 = b 4 . q = 0,001 . 0,1 = 0,0001
Вывод формулы n – первых членов
геометрической прогрессии
( b n ) – геометрическая прогрессия. Зная b 1 и q, найдите последовательно первые пять членов этой прогрессии.
Зная b 1 и q, найдите последовательно первые пять членов этой прогрессии.
b 2 = b 1 . q
b 3 = b 2 . q = b 1 . q . q = b 1 . q 2
b 4 = b 3 . q = b 1 . q 2 . q = b 1 . q 3
b 5 = b 4 . q = b 1 . q 3 = b 1 . q 3 . q = b 1 . q 4
b n = b 1 . q n-1 — формула n-го члена геометрическойпрогрессии
Пример 1 : В геометрической прогрессии,
b 1 = 2, а знаменатель q = 1,5.
Найти 4-й член этой прогрессии.
Дано: b 1 = 2 q = 1,5 n = 4 Найти: b 4 — ?
Решение. Применяем формулу: b n = b 1 · q n – 1 , подставляя в нее соответствующие значения:
b 4 = 2 · 1,5 4 – 1 = 2 · 1,5 3 = 2 · 3,375 = 6,75.
Ответ: 6,75.
Пример 2 : Найти пятый член геометрической прогрессии, если первый и третий члены равны соответственно 12 и 192.
Дано: b 1 = 12, b 3 = 192 Найти: b 5 — ?
Решение.
- Найдем знаменатель геометрической прогрессии.
В качестве первого шага с помощью формулы п-го члена запишем формулу для b 3 :
b 3 = b 1 · q 3 – 1 = b 1 · q 2
Найдем знаменатель геометрической прогрессии:
или
2) Найдем значение b 5 . Если q = 4, то
Если q = 4, то
b 5 = b 1 q 5-1 = 12 · 4 4 = 12 · 256 = 3072 .
При q = –4 результат будет тот же. Таким образом,
задача имеет одно решение.
Ответ: 3072.
Свойства геометрической прогрессии
1) Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних членов, стоящих перед ним и после него: b n 2 = b n-1 · b n+1
Доказательство.
(b n ) – геометрическая прогрессия.
b n = b n-1 . q, b n+1 = b n . q все члены геометрической прогрессии отличны от нуля, то
b n 2 = b n-1 · b n+1
2) Верно и обратное утверждение: если в последовательности чисел квадрат любого ее члена, начиная со второго, равен произведению двух соседних членов, стоящих перед ним и после него, то эта последовательность является геометрической прогрессией
Пример :
Вернемся к геометрической прогрессии 2, 6, 18, 54, 162,. ..
..
Возьмем четвертый член и возведем его в квадрат: 54 2 = 2916.
Теперь перемножим члены, стоящие слева и справа от числа 54: 18 · 162 = 2916.
Как видим, квадрат третьего члена равен произведению соседних второго и четвертого членов.
Вывод
- d0
арифметическая прогрессия возрастающая
- d
арифметическая прогрессия убывающая
- q 1
геометрическая прогрессия возрастающая
- 0
геометрическая прогрессия убывающая
Формула n -го члена прогрессии
Пусть заданы а 1 и d
а 2 =а 1 + d
a 3 =a 2 +d=a 1 +d+d= а 1 + 2d
a 4 =a 3 +d= а 1 + 3d
…………………………… . .
.
a n =a 1 +(n-1)d
Пусть заданы b 1 и q
b 2 = b 1 ∙ q
b 3 = b 2 ∙ q= b 1 ∙ q ∙ q=b 1 ∙ q 2
b 4 =b 1 ∙ q 3
…………………………………………… .. b n = b 1 ∙ q n-1
Чтобы задать
арифметическую геометрическую
прогрессию, достаточно указать её
первый член и первый член и
разность знаменатель
Работа в тетрадях Задание 1.
Дано: ( b n ) — геометрическая прогрессия
b 1 = 5 q = 3
Найти: b 3 ; b 5 .
Решение: используя формулу b n = b 1 q n-1
b 3 =b 1 q 2 = 5 . 3 2 =5 . 9=45
b 5 =b 1 q 4 = 5 . 3 4 =5 . 81 =4 0 5
3 4 =5 . 81 =4 0 5
Ответ: 45; 4 0 5.
Решение
Работа в тетрадях Задание 2.
Дано: ( b n ) — геометрическая прогрессия
b 4 = 40 q = 2
Найти: b 1 .
Решение: используя формулу b n = b 1 q n-1
b 4 =b 1 q 3 ; b 1 = b 4 : q 3 =40:2 3 =40 : 8=5
Ответ: 5.
Решение
Работа в тетрадях Задание 3.
Дано: ( b n ) — геометрическая прогрессия
b 1 = -2, b 4 =-54.
Найти: q .
Решение: используя формулу b n = b 1 q n-1
b 4 =b 1 q 3 ; -54=(-2) q 3 ; q 3 = -54:(-2)=27;
q =3
Ответ: 3.
Решение
Подготовка к ГИА
Заданы три первых члена числовых последовательностей. Известно, что
одна из этих последовательностей
не является ни геометрической, ни арифметической прогрессией.
Укажите её.
А. 1; 2; 3;…
Б. 1; 2; 4;…
В. 1; 4; 16;…
Г. 1; 4; 9;…
Подготовка к ГИА
Заданы три первых члена числовых последовательностей. Известно, что
одна из этих последовательностей
не является геометрической
прогрессией. Укажите её.
-3; 1; ;…
-3; -9; -27;…
-3; 5; -7;…
-3; ;-1 ; …
Подготовка к ГИА
- Последовательности ( a n ) , ( b n ), ( c n )
заданы формулами n -го члена.
Поставьте в соответствие каждой
последовательности верное утверждение.
УТВЕРЖДЕНИЕ
- Последовательность –
арифметическая прогрессия
2) Последовательность –
геометрическая прогрессия
3) Последовательность не
является ни арифметической,
ни геометрической прогрессией
ФОРМУЛА
А)
Б)
В)
А
2
Б
1
В
3
Домашнее задание
n-й член геометрической последовательности
Горячая математика Учитывая
геометрическая последовательность
с первым сроком
а
1
и
обыкновенное отношение
р
, н
й
(или общий) термин дан кем-то
а
н
«=»
а
1
⋅
р
н
−
1
.
Пример 1:
Найди 6 й член геометрической прогрессии 3 , 12 , 48 , … .
а 1 «=» 3 , р «=» 12 3 «=» 4 а 6 «=» 3 ⋅ 4 6 − 1 «=» 3 ⋅ 4 5 «=» 3072
Пример 2:
Найди
7
й
термин для геометрической последовательности, в которой
а
2
«=»
24
и
а
5
«=»
3
.
Заменять 24 для а 2 и 3 для а 5 в формуле
а н «=» а 1 ⋅ р н − 1 .
а 2 «=» а 1 ⋅ р 2 − 1 → 24 «=» а 1 р а 5 «=» а 1 ⋅ р 5 − 1 → 3 «=» а 1 р 4
Решите первое уравнение для а 1 : а 1 «=» 24 р
Подставьте это выражение вместо
а
1
во втором уравнении и решить для
р
.
3 «=» 24 р ⋅ р 4 3 «=» 24 р 3 1 8 «=» р 3 так р «=» 1 2
Заменитель р в первом уравнении и решить а 1 .
24 «=» а 1 ( 1 2 ) 48 «=» а 1
Теперь используйте формулу, чтобы найти
а
7
.
а 7 «=» 48 ( 1 2 ) 7 − 1 «=» 48 ⋅ 1 64 «=» 3 4
Смотрите также: сигма-обозначение ряда и н й член арифметической прогрессии
Загрузите наши бесплатные приложения для обучения и книги для подготовки к экзаменам
Все об общем члене или N-м члене геометрической прогрессии
Геометрическая прогрессия или последовательность, известная также как геометрический ряд, представляет собой последовательность чисел, в которой частное любых двух последовательных членов последовательности является константой, называемой общим числом последовательности. соотношение. Формула x sub n равняется a, умноженному на r в степени n – 1, где an — первый член последовательности, а r — знаменатель, дает общий член или n-й член любой геометрической последовательности. Мы используем эту формулу, потому что записывать последовательность до тех пор, пока мы не достигнем нужного числа, не всегда возможно.
соотношение. Формула x sub n равняется a, умноженному на r в степени n – 1, где an — первый член последовательности, а r — знаменатель, дает общий член или n-й член любой геометрической последовательности. Мы используем эту формулу, потому что записывать последовательность до тех пор, пока мы не достигнем нужного числа, не всегда возможно.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность чисел, образованная путем деления или умножения предыдущего члена на то же число. Обычное отношение — это то же или подобное число.
N-й член геометрической прогрессии
«n-й» член — это формула, которую можно использовать для нахождения любого члена ряда, где «n» — номер члена. Или Любой термин в последовательности можно найти, используя правило n-го члена. Найдите разницу между каждой фразой и напишите это число перед n, чтобы получить n-й термин. Поскольку этот ряд увеличивается на два, мы начнем с записи последовательности 2n.
Ниже приведена формула для вычисления общего члена, члена n или последнего члена геометрической прогрессии:
an= член n
a1=первый член
r=знаменатель
n=позиция члена
Чтобы получить общее значение введенных членов геометрического ряда, примените формулу суммы геометрической прогрессии или ряда. Конечные геометрические ряды и бесконечные геометрические ряды — это два типа геометрических рядов. В результате существует несколько формул расчета суммы членов ряда, которые приведены ниже:
Сумма n членов геометрической прогрессии
Геометрический ряд — это набор чисел с геометрической последовательностью. Он получается путем объединения членов геометрической прогрессии.
1. Конечный геометрический ряд
Количество членов n, первый член а1, знаменатель r.
Например: Вычислите S10, 10-ю частичную сумму бесконечной геометрической последовательности 24+12+6+…
Решение: Сначала найдите r
2.
 Бесконечный геометрический ряд
Бесконечный геометрический рядИспользуйте формулу для получения суммы бесконечного геометрического ряда с отношениями, абсолютные значения которых меньше единицы.
S=a1/1-r
Первый член равен a1, а знаменатель равен r.
Например: Вычислите сумму бесконечного геометрического ряда 27+18+12+8+…
Решение: Сначала найдите r:
Заключение
В этой статье мы приходим к выводу, что следующее число в геометрической прогрессии получается путем умножения каждого целого числа на один и тот же коэффициент. Любой член ряда можно найти по формуле n-го члена. Буква «н» означает число. Подставляя различные значения для номера термина, мы можем создать ряд, используя n-й термин (n). в геометрической прогрессии найдите n-й член. Для начала разделите второй член на первый, чтобы получить знаменатель r. Затем по формуле an=arn-1 вычислить n-й член, используя первый член a и обыкновенное отношение r.

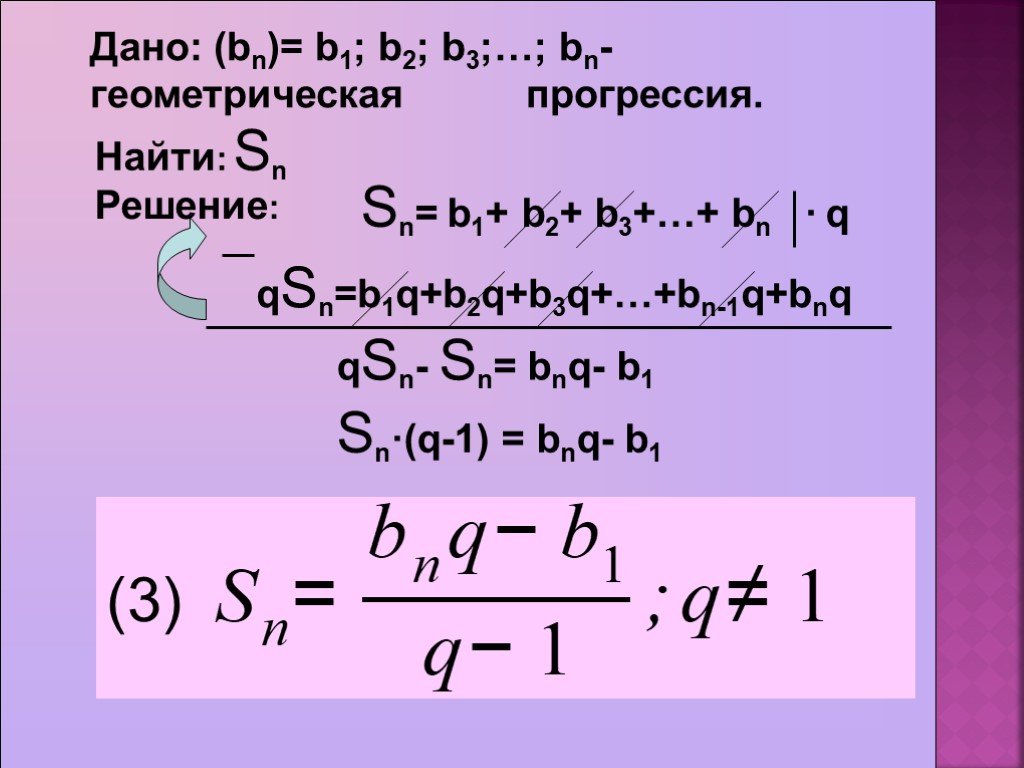 Первый член геометрической
прогрессии равен 5, знаменатель – равен 3. Найти 4-ый член прогрессии.
Первый член геометрической
прогрессии равен 5, знаменатель – равен 3. Найти 4-ый член прогрессии. И.
учащегося
вариант 3
И.
учащегося
вариант 3 Чему может быть равен знаменатель геометрической
прогрессии, если b1=2, а b2=14?
Чему может быть равен знаменатель геометрической
прогрессии, если b1=2, а b2=14?
