Как находить кратное чисел: Как найти НОД и НОК

Как найти кратное число. Делители и кратные числа

Как найти наименьшее общее кратное?

Нужно найти каждый множитель каждого из двух чисел, у которых находим наименьшее общее кратное, а потом перемножить друг на друга множители, которые совпали у первого и второго числа. Результатом произведения будет искомое кратное.

Например у нас есть числа 3 и 5 и нам надо найти НОК(наименьшее общее кратное). Нам надо умножать и тройку и пятрку на все числа начиная с 1 2 3 … и т д пока мы не увидим одинаковое число и там и там.

Множим тройку и получаем: 3, 6, 9, 12, 15

Множим пятрку и получаем: 5, 10, 15

Метод разложения на простые множители — самый классический для нахождения наименьшего общего кратного (НОК) для нескольких чисел. Наглядно и просто продемонстрирован этот метод в следующем видеоролике:

Складывать, умножать, делить, приводить к общему знаменателю и другие арифметические действия очень увлекательное занятие, особенно восхищают примеры, занимающие целый лист.

Итак найти общее кратное для двух чисел, которое будет являться самым маленьким числом на которое делятся два числа. Хочу заметить, что не обязательно в дальнейшем прибегать к формулам, чтобы найти искомое, если можешь считать в уме (а это можно натренировать), то цифры сами всплывают в голове и потом дроби щелкаются как орешки.

Для начала усвоим, что можно умножить два числа друг на друга, а потом эту цифру уменьшать и делить поочередно на данные два числа, так мы найдем наименьшее кратное.

Например, два числа 15 и 6. Умножаем и получаем 90. Это явно больше число. Причем 15 делится на 3 и 6 делится на 3, значит 90 тоже делим на 3. Получаем 30. Пробуем 30 разделить 15 равно 2. И 30 делим 6 равно 5. Так как 2 это предел, то получается, что наименьшее кратное для чисел 15 и 6 будет 30.

С цифрами побольше будет немного трудней. но если знать, какие цифры дают нулевой остаток при делении или умножении, то трудностей, в принципе, больших нет.

• Как найти НОК

  Вот видео, в котором вам будет предложено два способа нахождения наименьшего общего кратного (НОК). 1 = 4457 = 560.

  НОК(16, 20, 28) = 560.

  Таким образом, в итоге расчета получилось число 560. Оно является наименьшим общим кратным, то есть делится на каждое из трх чисел без остатка.

  Наименьшее общее кратное число — это такая цифра, которая разделится на несколько предложенных чисел без остатка. Для того, чтобы такую цифру высчитать, надо взять каждое число и разложить его на простые множители. Те цифры, которые совпадают, убираем. Оставляет всех по одной, перемножаем их между собой по очереди и получаем искомое — наименьшее общее кратное.

  НОК, или наименьшее общее кратное , — это наименьшее натуральное число двух и более чисел, которое делится на каждое из данных чисел без остатка.

  Вот пример того, как найти наименьшее общее кратное 30 и 42.

  • Первым делом нужно разложить данные числа на простые множители.

  Для 30 — это 2 х 3 х 5.

  Для 42 — это 2 х 3 х 7. Так как 2 и 3 имеются в разложении числа 30, то вычеркиваем их.

  • Выписываем множители, которые входят в разложение числа 30. Это 2 х 3 х 5 .
  • Теперь нужно домножить их на недостающий множитель, который имеем при разложении 42,а это 7. Получаем 2 х 3 х 5 х 7.
  • Находим, чему равно 2 х 3 х 5 х 7 и получаем 210.

  В итоге получаем, что НОК чисел 30 и 42 равен 210.

  Чтобы найти наименьшее общее кратное , нужно выполнить последовательно несколько простых действий. Рассмотрим это на примере двух чисел: 8 и 12

1. Разлагаем оба числа на простые множители: 8=2*2*2 и 12=3*2*2
2. Сокращаем одинаковые множители у одного из чисел. В нашем случае совпадают 2*2, сократим их для числа 12, тогда у 12 останется один множитель: 3.
3. Находим произведение всех оставшихся множителей: 2*2*2*3=24

Проверяя, убеждаемся, что 24 делится и на 8 и на 12, причем это наименьшее натуральное число, которое делится на каждое из этих чисел. Вот мы и нашли наименьшее общее кратное .

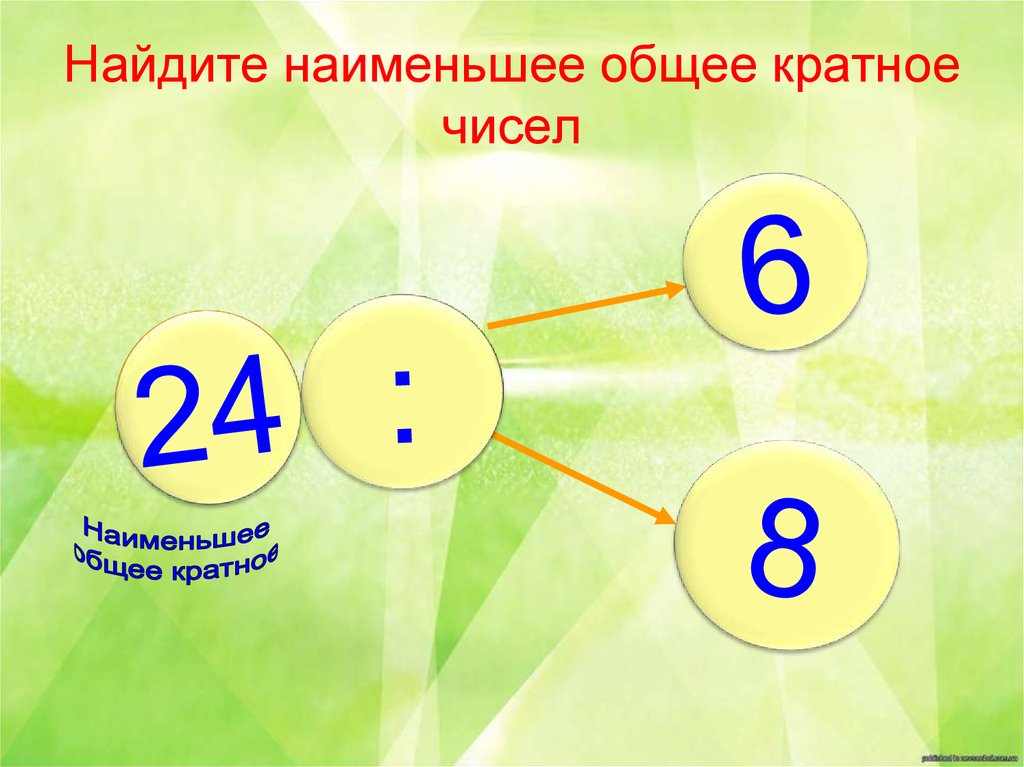
Попробую объяснить на примере цифр 6 и 8. Наименьшее общее кратное — это число, которое можно разделить на эти числа(в нашем случае 6 и 8) и остатка не будет.

Итак, начинаем умножать сначала 6 на 1, 2, 3 и т. д и 8 на 1, 2, 3 и т. д.

Рассмотрим решение следующей задачи. Шаг мальчика составляет 75 см, а шаг девочки 60 см. Необходимо найти наименьшее расстояние, на котором они оба сделают по целому числу шагов.

Решение. Весь путь который пройдут ребята, должен делиться без остатка на 60 и на 70, так как они должны сделать каждый целое число шагов. Другими словами, в ответе должно быть число, кратное как 75 так и 60.

Сначала будем выписывать все кратные числа, для числа 75. Получаем:

• 75, 150, 225, 300, 375, 450, 525, 600, 675, … .

Теперь выпишем числа, которые будут кратны 60. Получаем:

• 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660, … .

Теперь находим числа которые есть в обоих рядах.

• Общими кратными чисел будут числа, 300, 600, и т. д.

Самое наименьшее из них, это число 300. Оно в данном случае будет называться наименьшим общим кратным чисел 75 и 60.

Возвращаясь к условию задачи, наименьшее расстояние, на котором ребята сделают целое число шагов будет 300 см. Мальчик пройдет этот путь за 4 шага, а девочке потребуется сделать 5 шагов.

Определение наименьшего общего кратного

• Наименьшим общим кратным двух натуральных чисел a и b называется наименьшее натуральное число, которое кратно как a, так и b.

Для того, чтобы найти наименьшее общее кратное двух чисел, не обязательно выписывть подряд все кратные для этих чисел.

Можно воспользоваться следующим методом.

Как найти наименьшее общее кратное

Сначала необходимо разложить данные числа на простые множители.

• 60 = 2*2*3*5,
• 75=3*5*5.

Теперь выпишем все множители которые есть в разложении первого числа (2,2,3,5) и добавим к нему все недостающие множители из разложения второго числа (5).

Получим в итоге ряд простых чисел: 2,2,3,5,5. Произведение этих чисел и будет наименьшим общим сомножителем для данных чисел. 2*2*3*5*5 = 300.

Общая схема нахождения наименьшего общего кратного

• 1. Разложить числа на простые множители.
• 2. Выписать простые множители которые входят в состав одного из них.
• 3. Добавить к этим множителям все те, которые есть в разложении остальных, но нет в выбранном.
• 4. Найти произведение всех выписанных сомножителей.

Данный способ универсален. С его помощью можно найти наименьшее общее кратное любого количества натуральных чисел.

Тема «Кратные числа» изучается в 5 классе общеобразовательной школы. Ее целью является совершенствование письменных и устных навыков математических вычислений. На этом уроке вводятся новые понятия — «кратные числа» и «делители», отрабатывается техника нахождения делителей и кратных натурального числа, умение находить НОК различными способами.

Эта тема является очень важной. Знания по ней можно применить при решении примеров с дробями. Для этого нужно найти общий знаменатель путем расчета наименьшего общего кратного (НОК).

Кратным А считается целое число, которое делится на А без остатка.

Каждое натуральное число имеет бесконечное количество кратных ему чисел. Наименьшим считается оно само. Кратное не может быть меньше самого числа.

Нужно доказать, что число 125 кратно числу 5. Для этого нужно первое число разделить на второе. Если 125 делится на 5 без остатка, то ответ положительный.

Данный способ применим для небольших чисел.

При расчёте НОК встречаются особые случаи.

1. Если необходимо найти общее кратное для 2-х чисел (например, 80 и 20), где одно из них (80) делится без остатка на другое (20), то это число (80) и есть наименьшее кратное этих двух чисел.

НОК (80, 20) = 80.

2. Если два не имеют общего делителя, то можно сказать, что их НОК — это произведение этих двух чисел.

НОК (6, 7) = 42.

Рассмотрим последний пример. 6 и 7 по отношению к 42 являются делителями. Они делят кратное число без остатка.

В этом примере 6 и 7 являются парными делителями. Их произведение равно самому кратному числу (42).

Число называется простым, если делится только само на себя или на 1 (3:1=3; 3:3=1). Остальные называются составными.

В другом примере нужно определить, является ли 9 делителем по отношению к 42.

42:9=4 (остаток 6)

Ответ: 9 не является делителем числа 42, потому что в ответе есть остаток.

Делитель отличается от кратного тем, что делитель — это то число, на которое делят натуральные числа, а кратное само делится на это число.

Наибольший общий делитель чисел a и b , умноженный на их наименьшее кратное, даст произведение самих чисел a и b .

А именно: НОД (а, b) х НОК (а, b) = а х b.

Общие кратные числа для более сложных чисел находят следующим способом.

Например, найти НОК для 168, 180, 3024.

Эти числа раскладываем на простые множители, записываем в виде произведения степеней:

168=2³х3¹х7¹

2⁴х3³х5¹х7¹=15120

НОК (168, 180, 3024) = 15120.

Общие кратные

Проще говоря, любое целое число, которое делится на каждое из данных чисел, является общим кратным данных целых чисел.

Можно находить общее кратное двух и большего количества целых чисел.

Пример 1

Вычислить общее кратное двух чисел: $2$ и $5$.

Решение .

По определению общим кратным чисел $2$ и $5$ является число $10$, т.к. оно кратно числу $2$ и числу $5$:

Общими кратными чисел $2$ и $5$ также будут числа $–10, 20, –20, 30, –30$ и т.д., т.к. все они делятся на числа $2$ и $5$.

Замечание 1

Нуль является общим кратным любого количества ненулевых целых чисел.

Согласно свойствам делимости, если некоторое число является общим кратным нескольких чисел, то и противоположное по знаку число также будет общим кратным заданных чисел. Это видно из рассмотренного примера.

Для заданных целых чисел всегда можно найти их общее кратное.

Пример 2

Вычислить общее кратное чисел $111$ и $55$.

Решение .

Перемножим заданные числа: $111\div 55=6105$. Несложно убедится, что число $6105$ делится на число $111$ и на число $55$:

$6105\div 111=55$;

$6105\div 55=111$.

Таким образом, число $6105$ – общее кратное чисел $111$ и $55$.

Ответ : общее кратное чисел $111$ и $55$ равно $6105$.

Но, как мы уже видели из предыдущего примера, это общее кратное не одно. Другими общими кратными будут числа $–6105, 12210, –12210, 61050, –61050$ и т.д. Таким образом, мы пришли к следующему выводу:

Замечание 2

Любой набор целых чисел имеет бесконечное множество общих кратных.

На практике ограничиваются нахождением общих кратных только целых положительных (натуральных) чисел, т.к. множества кратных данного числа и ему противоположного совпадают.

Определение наименьшего общего кратного

Наиболее часто из всех кратных заданных чисел используют наименьшее общее кратное (НОК).

Определение 2

Наименьшее положительное общее кратное заданных целых чисел является наименьшим общим кратным этих чисел.

Пример 3

Вычислить НОК чисел $4$ и $7$.

Решение .

Т.к. у данных чисел нет общих делителей, то $НОК(4,7)=28$.

Ответ : $НОК (4,7)=28$.

Нахождение НОК через НОД

Т.к. существует связь между НОК и НОД, с ее помощью можно вычислить НОК двух целых положительных чисел :

Замечание 3

Пример 4

Вычислить НОК чисел $232$ и $84$.

Решение .

Воспользуемся формулой для нахождения НОК через НОД:

$НОК (a,b)=\frac{a\cdot b}{НОД (a,b)}$

Найдем НОД чисел $232$ и $84$ с помощью алгоритма Эвклида:

$232=84\cdot 2+64$,

$84=64\cdot 1+20$,

$64=20\cdot 3+4$,

Т.е. $НОД (232, 84)=4$.

Найдем $НОК (232, 84)$:

$НОК (232,84)=\frac{232\cdot 84}{4}=58\cdot 84=4872$

Ответ : $НОК (232,84)=4872$.

Пример 5

Вычислить $НОК (23, 46)$.

Решение .

Т.к. $46$ делится нацело на $23$, то $НОД (23, 46)=23$. Найдем НОК:

$НОК (23,46)=\frac{23\cdot 46}{23}=46$

Ответ : $НОК (23,46)=46$.

Таким образом, можно сформулировать правило :

Замечание 4

Наименьшее общее кратное двух чисел непосредственно связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.

Теорема.

Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b , деленному на наибольший общий делитель чисел a и b , то есть, НОК(a, b)=a·b:НОД(a, b) .

Доказательство.

Пусть М – какое-нибудь кратное чисел a и b . То есть, М делится на a , и по определению делимости существует некоторое целое число k такое, что справедливо равенство M=a·k . Но М делится и на b , тогда a·k делится на b .

Обозначим НОД(a, b) как d . Тогда можно записать равенства a=a 1 ·d и b=b 1 ·d , причем a 1 =a:d и b 1 =b:d будут взаимно простыми числами . Следовательно, полученное в предыдущем абзаце условие, что a·k делится на b , можно переформулировать так: a 1 ·d·k делится на b 1 ·d , а это в силу свойств делимости эквивалентно условию, что a 1 ·k делится на b 1 .

Также нужно записать два важных следствия из рассмотренной теоремы.

Общие кратные двух чисел совпадают с кратными их наименьшего общего кратного.

Это действительно так, так как любое общее кратное M чисел a и b определяется равенством M=НОК(a, b)·t при некотором целом значении t .

Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.

Обоснование этого факта достаточно очевидно. Так как a и b взаимно простые, то НОД(a, b)=1 , следовательно, НОК(a, b)=a·b:НОД(a, b)=a·b:1=a·b .

Наименьшее общее кратное трех и большего количества чисел

Нахождение наименьшего общего кратного трех и большего количества чисел можно свести к последовательному нахождению НОК двух чисел. Как это делается, указано в следующей теореме.a 1 , a 2 , …, a k совпадают с общими кратными чисел m k-1 и a k , следовательно, совпадают с кратными числа m k . А так как наименьшим положительным кратным числа m k является само число m k , то наименьшим общим кратным чисел a 1 , a 2 , …, a k является m k .

Список литературы.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Виноградов И.М. Основы теории чисел.
• Михелович Ш.Х. Теория чисел.
• Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.

Как найти наименьшее общее кратное чисел: двух, нескольких

Наименьшее общее кратное используется, например, для приведения обыкновенных дробей к общему знаменателю, что позволит сложить, вычесть или сравнить их.

В данной статье мы разберемся, каким образом выполняется эта операция, а также разберем практические примеры для закрепления изложенного материала.

• Определение наименьшего общего кратного
• Нахождение НОК
  • Для двух/небольших чисел
  • Для нескольких/больших чисел
  • Иные случаи

Определение наименьшего общего кратного

Число b является кратным числа a, если b нацело (без остатка) делится на a. Произносится как “b кратно a“. Обозначается буквой К.

Примеры кратных:

• кратные числа 3 или К(3): 6, 9, 12,15, 18 и т.д.
• кратные числа 7 или К(7): 14, 21, 28, 35, 42 и т.д.

Кратных чисел может быть бесконечное множество.

Общее кратное двух натуральных чисел – такое число, которое нацело делится на оба этих числа.

Наименьшее общее кратное двух натуральных чисел – наименьшее число из общих кратных этих чисел. Обозначается как НОК.

Например, НОК (5, 9) – это наименьшее общее кратное чисел 5 и 9.

Нахождение НОК

Чтобы найти наименьшее общее кратное, можно воспользоваться одним из двух способов ниже:

Для двух/небольших чисел

Когда мы имеем дело с двумя числами (или небольшими), процесс нахождения НОК состоит из следующих действий:

1. Записываем в ряд кратные для каждого числа по возрастанию.
2. Находим первое совпадение в полученных рядах чисел. Это и есть НОК.

Пример
Найдем наименьшее общее кратное чисел 6 и 14.

Решение
Кратные числа 6: 12, 18, 24, 30, 36, 42, 48 и т.д.
Кратные числа 14: 28, 42, 56 и т.д.

Таким образом, НОК (6, 14) = 42.

Для нескольких/больших чисел

Данный способ подойдет, если мы имеем дело с большим числами, или когда требуется найти НОК для трех и более чисел.

1. Сперва раскладываем числа на простые множители – простые числа, которые делят число нацело (их количество для разных чисел, также, может быть разным). Для удобства начинаем с самого маленького значения и заканчиваем самым большим.
2. Среди множителей мЕньшего числа находим тот, который не вошел в состав бОльшего. То же самое проделываем со следующим по возрастанию числом/числами.
3. Умножаем бОльшее число на найденные дополнительные множители и получаем НОК.

Пример
Давайте найдем НОК (12, 28, 32).

Решение
Разложим данные числа на простые множители.

Среди множителей меньшего числа (12) в состав бОльшего (32) не входит цифра 3, среди множителей среднего числа (28) – цифра 7.

Следовательно, НОК (12, 28, 32) = 32 ⋅ 3 ⋅ 7 = 672.

Иные случаи

1. Если одно из чисел, для которых требуется найти наименьшее общее кратное, нацело делится на другие числа, то это число и есть НОК.

Например: НОК (20, 40, 80) = 80.

2. НОК взаимно простых чисел является произведение данных чисел, т.к. они не имеют общих простых множителей.

Например: НОК (3, 5) = 3 ⋅ 5 = 15.

Как найти кратные — Математика с мамой

Что такое кратные?

Множители — это числа, образованные путем умножения числа на любое другое число. Проще говоря, кратными данному числу являются любые числа, находящиеся в таблице умножения этого числа. Например, числа, кратные 2, равны 2, 4, 6, 8, 10, 12 и так далее.

Многие кратные являются кратными более чем одному числу.

Здесь мы видим, что 6 одновременно кратно 2 и кратно 3.

Это потому, что 2 × 3 = 6 и 3 × 2 = 6.

6 — третье кратное 2, а 6 — второе кратное 3.

В любом предложении умножения числа, которые умножаются вместе, являются множителями ответа. Это означает, что они делятся точно на ответ.

В любом предложении с умножением ответ кратен числам, которые умножаются вместе.

Как найти кратные числа

Чтобы найти числа, кратные числу, умножьте это число на любое целое число. Например, 5 × 3 = 15, поэтому 15 — это третье кратное 5.

Например, первые 5 кратных 4 равны 4, 8, 12, 16 и 20.

1 × 4 = 4, поэтому первое кратное 4 равно 4.

2 × 4 = 8, поэтому второе кратное 4 равно 8.

3 × 4 = 12, поэтому третье кратное 4 равно 12.

4 × 4 = 16, поэтому 4-е кратное 4 равно 16.

5 × 4 = 20, поэтому 5-е кратное 4 равно 20.

Мы видим, что числа, кратные 4, каждый раз увеличиваются на 4.

Чтобы перечислить числа, кратные числу, начните с нуля и продолжайте добавлять это число. Разность между кратными любого заданного числа всегда равна данному числу. Если вы знаете кратное число, вы можете найти следующее кратное, прибавив к нему число.

Здесь мы перечислим первые пять кратных 6.

Мы можем начать с 0 и считать до шести.

Первые пять кратных 6 — это 6, 12, 18, 24 и 30.

Мы видим, что 6 + 6 = 12, 12 + 6 = 18, 18 + 6 = 24 и 24 + 6 = 30.

Мы также можем найти числа, кратные 6, умножив 6 на любое число.

1 × 6 = 6, поэтому первое кратное 6 равно 6.

2 × 6 = 12, поэтому второе кратное 6 равно 12.

3 × 6 = 18, поэтому третье кратное 6 равно 18.

4 × 6 = 24, поэтому 4-е кратное 6 равно 24.

5 × 6 = 30, поэтому 5-е кратное 6 равно 30.

В следующем примере мы перечислим первые пять чисел, кратных 8.

Мы можем начать с нуля и считать восьмерками.

Первые пять кратных 8 — это 8, 16, 24, 32 и 40.

8 + 8 = 16, 16 + 8 = 24, 24 + 8 = 32 и 32 + 8 = 40.

Мы также можем найти числа, кратные 8, умножив 8 на любое число.

1 × 8 = 8, поэтому первое кратное 8 равно 8.

2 × 8 = 16, поэтому второе кратное 8 равно 16.

3 × 8 = 24, поэтому третье кратное 8 равно 24.

4 × 8 = 32, поэтому 4-е кратное 8 равно 32.

5 × 8 = 40, поэтому пятое кратное 8 равно 40.

Списки составных частей

Вот список первых 12 кратных первых 12 чисел:

Кратность 1 равна 1, 2, 3, 4, 5, 6, 7, 8, 9., 10, 11 и 12.

Число, кратное 2, равно 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 и 24.

Число, кратное 3, равно 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 и 36.

Число, кратное 4, равно 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44 и 48.

Число, кратное 5, равно 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55 и 60.

Число, кратное 6, равно 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66 и 72.

Кратность 7 равна 7, 14, 21, 28, 35, 42, 49., 56, 63, 70, 77 и 84.

Число, кратное 8, равно 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88 и 96.

Число, кратное 9, равно 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 и 108.

10 кратны 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110 и 120.

Число, кратное 11, равно 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121 и 132.

Число, кратное 12, равно 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132 и 144.

Как найти кратные числа в математике

Введение

Умножение и деление — две важные операции в математике. Мы можем умножить число на любое число. Точно так же число можно разделить на любое число. Два важных термина, связанных с умножением и делением чисел, — это множители и кратные. Понимание одного из них будет неполным без изучения другого. Поэтому, прежде чем мы двинемся дальше и узнаем о множителях, давайте узнаем, что мы подразумеваем под множителями числа.

Что такое факторы?

Множитель числа — это точный делитель этого числа. Другими словами, делителем числа называется такое число, на которое оно полностью делится без остатка. Например, каждое из чисел 1, 2, 3, 4, 6 и 12 является делителем 12. Однако ни одно из чисел 5, 7, 8, 9, 10 и 11 не является делителем 12. 

Что такое кратность?

Кратным целому числу является произведение этого числа на любое счетное число. Если мы умножим 3 на 1, 2, 3, 4, 5, 6….. получим

3 x 1 = 3

3 x 2 = 6

3 x 3 = 9

3 x 4 = 12

3 x 5 = 15

3 x 6 = 04, 07 30 90 и т. д. , 9 , 12 , 15 , 18 и т. д. кратны 3.

Давайте теперь посмотрим на свойства, которым удовлетворяют кратные числа.

Свойства кратных

1. Каждое кратное числа больше или равно этому числу. Например, числа, кратные 5, равны 5, 10, 15, 20, 25, ……. . На самом деле кратные числа получаются путем умножения числа на 1, 2, 3, 4, 5, 6…. и так далее. Следовательно, наименьшим кратным числа является само число. Следовательно, каждое кратное числа больше или равно самому числу.
2. Наименьшим кратным числа является само число. Поскольку каждое число можно умножить на 1, чтобы получить то же самое число, следовательно, каждое число кратно самому себе.
3. Количество кратных заданному числу бесконечно. Например, числа, кратные 7, равны 7, 14, 21, 28, 35 и так далее. Мы видим, что это бесконечный список. Следовательно, количество кратных данному числу бесконечно.
4. Все числа, кратные 2, являются четными числами. Мы знаем, что 2, 4, 6, 8, 10, 12 и так далее кратны 2. Кроме того, все эти числа 2, 4, 6, 8, 10, 12….. являются четными числами. Следовательно, все числа, кратные 2, являются четными числами.

Давайте разберемся с кратными на примере.

Пример

Запишите первые пять чисел, кратных 17.

Решение

Чтобы получить первые пять чисел из 17, умножим их на 1, 2, 3 и 5. Получим –

17 х 1 = 17

17 х 2 = 34

17 х 3 = 51

17 х 4 = 68 , 51, 68 и 85.

Общие кратные числа

Теперь мы поняли, что мы подразумеваем под числовыми кратными. Теперь, если мы посмотрим на два или более чисел одновременно, мы можем получить некоторые общие кратные этих чисел. Например, если у нас есть два числа 4 и 6, мы можем легко сказать, что 12 является общим кратным как 4, так и 6, поскольку 4 x 3 = 12 и 6 x2 = 12. Это означает, что два или более числа могут иметь общие кратные. . Те кратные, которые являются общими среди кратных двух или более чисел, известны как общие кратные этих чисел.

Давайте разберемся в этом на примере – 

Пример

Список 3 общих кратных 3, 4 и 9

Решение

Нам даны три числа 3, 4 и 9, и нам нужно найти их общие кратные три числа.

Сначала запишем кратные данных чисел отдельно. У нас будет,

Кратные 3 равны 3, 6, 9, 12, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105, 108, 111 ……….

Число, кратное 4, равно 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104, 108, 112 ……..

Число, кратное 9, равно 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117 …….

Из приведенных выше кратных 3, 4 и 9 мы видим, что общие кратные 3, 4 и 6 равны 36, 72 и 108.

Следовательно, общие кратные 3, 4 и 6 равны 36, 72 и 108.

Из приведенного выше видно, что, хотя список кратных не имеет конца, всегда есть первое кратное числа или группы чисел. Следовательно, мы не можем определить наибольшее кратное числа или группы чисел, но мы всегда можем перечислить первое кратное числа. В случае группы чисел это первое кратное также является наименьшим общим кратным этих чисел.

Давайте выясним, что мы подразумеваем под наименьшим общим кратным чисел.

Наименьшее общее кратное ( LCM )

Если число кратно двум или более числам, оно называется общим кратным чисел. Например, мы знаем, что

2 x 3 = 6

Следовательно, 6 кратно и 2, и 3. Следовательно, 6 называется общим кратным 2 и 3.

Наименьшее общее кратное ( L C M ) из двух или более чисел определяется как наименьшее число (отличное от нуля), кратное этим числам. Другими словами, наименьшее общее кратное двух или более чисел — это наименьшее число, которое делится на все данные числа. Это означает, что не может быть числа, которое делится на данные числа и меньше наименьшего общего кратного.

Давайте разберемся с этим на примере.

Предположим, у нас есть два числа, 8 и 12.

Проверим кратность этих двух чисел. У нас есть,

Кратные числа 8 = 8, 16, 24, 32, 40, 48, 56, 64, 72 и так далее…..

Кратные числа 12 = 12, 24, 48, 60, 72 и т. д. …………

Из приведенного выше видно, что общие кратные 8 и 12 равны 24, 48, 72 и так далее. Среди этих 24 есть наименьшее общее кратное этих двух чисел. Следовательно, 12 — это наименьшее общее кратное или LCM чисел 8 и 12.

Мы только что видели, что, записывая кратные каждого числа, мы можем сравнить их кратные и найти среди них наименьшее общее кратное. Но является ли это единственным способом найти наименьшее общее кратное или у нас есть определенные шаги, с помощью которых мы можем найти L C M двух или более чисел? Давайте узнаем.

Как найти наименьшее общее кратное (LCM)?

Есть два основных метода, с помощью которых мы можем найти L C M двух или более чисел. Эти методы – 

1. Метод простой факторизации
2. Метод общего деления

Давайте обсудим эти методы один за другим.

Метод простой факторизации

Как следует из названия, метод простой факторизации включает в себя нахождение простых множителей заданных чисел, а затем вычисление наименьшего общего кратного ( L C M ). В этом методе для нахождения L C M используются следующие шаги – 

1. Получите заданные числа.
2. Найдите простые множители каждого числа.
3. Разложите каждое число как произведение его простых множителей
4. Найдите произведение всех различных простых множителей с наибольшей степенью при разложении каждого числа на простые множители.
5. Число, полученное на предыдущем шаге, является требуемым L C M заданных чисел.

 Давайте разберем приведенные выше шаги на примере.

Пример

Найдите LCM чисел 40, 36 и 126, используя метод простой факторизации.

Решение

Нам даны числа 40, 36 и 126, и мы должны найти L C M этих чисел. Выполняя описанные выше шаги, давайте сначала найдем простые множители каждого из заданных чисел. У нас есть,

Простые множители 40 равны –

40 = 2 x 2 x 2 x 5

Простые множители 36 равны –

36 = 2 x 2 x 3 x 3

126 есть – 

126 = 2 x 3 x 3 x 7

Мы можем видеть в приведенных выше простых разложениях приведенных выше чисел, что число 2 встречается максимум три раза, как и в случае с числом 40. Точно так же число 3 появляется как множитель для максимального числа 2, что имеет место в 36 и 126. Простые множители 5 и 7 встречаются только в 40 и 126 соответственно. Следовательно, искомая LCM чисел 40, 36 и 126 будет равна 9.0007

L C M из 40, 36 и 126 = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Следовательно, L C M из 40, 36 и 126 = 2520

Общий метод деления2

3 Следующие шаги выполняются, чтобы найти L C M двух или более чисел, используя метод общего деления – 

1. Получите заданные числа.
2. Расположите данные числа в ряд через запятую.
3. Получите число, которое делится ровно на два из заданных чисел.
4. Разделите числа, которые делятся на число, выбранное в предыдущем шаге, и запишите частное под ними. Перенесите числа, которые не делятся.
5. Повторяйте вышеуказанные шаги до тех пор, пока никакие два заданных числа не будут делиться на одно и то же число.
6. Найдите произведение делителей и целых чисел, чтобы получить требуемое L C M заданных чисел.

Давайте разберем приведенные выше шаги на примере.

Пример

Найдите L C M чисел 624 и 936, используя метод общего деления.

Решение

Нам даны числа 624 и 936, и нам нужно найти L C M, используя 624 и 936. 624 и 936 = 2 x 2 x 2 x 3 x 13 x 2 x 3 = 1872

Следовательно, L C M чисел 624 и 936 = 1872

Применение наименьшего общего кратного ( L C M)

Теперь мы рассмотрим некоторые приложения LCM при решении некоторых практических задач. Рассмотрим несколько примеров.

Пример 1 Определите два ближайших к 10000 числа, которые делятся на 2, 3, 4, 5, 6 и 7.

Решение , 3, 4, 5, 6 и 7 являются их LCM. но мы должны найти два числа, ближайших к 10000, которые точно делятся на заданные числа, т.е. 2, 3, 4, 5, 6 и 7. Мы можем видеть что такие числа кратны L C M данных чисел. Чтобы найти LCM 2, 3, 4, 5, 6 и 7, мы имеем

Следовательно, LCM чисел 2, 3, 4, 5, 6 и 7 равно 420.

Число, ближайшее к 10000 и точно делящееся на каждое из 2, 3, 4, 5, 6 и 7, также должно точно делиться на их L C M, т. е. 420. Разделим теперь 10000 на 420. Получим, что остаток равен 340. 

Число чуть меньше 10000 и точно делится на 420 и точно делится на 420

= 10000 + ( 420 – 340 ) = 10080

Отсюда два ближайших к 10000 числа, которые делятся на 2, 3, 4, 5, 6, а также на 79660 и 10080.

Пример 2 камера, позволяющая делать 36 кадров. Оба они хотят иметь возможность сделать одинаковое количество фотографий и заполнить рулоны пленки. Сколько рулонов должен купить каждый?

Решение Нам сообщили, что у Сэма есть камера, позволяющая делать 24 кадра, а у Питера камера, позволяющая делать 36 кадров. Оба они хотят иметь возможность сделать одинаковое количество фотографий и заполнить рулоны пленки.

Так как пленка в камере Сэма может сделать 24 кадра, а пленка в камере Питера может сделать 36 кадров, и обе они хотят сделать одинаковое количество фотографий, заполняя рулоны пленки, поэтому общее количество экспозиций, сделанных каждым, будет LCM для 36 и 24. Следовательно, давайте найдем LCM для 36 и 24.

У нас есть,

Из вышеизложенного мы можем видеть, что LCM для 36 и 24  = 2 x 2 x 3 x 3 x 2 = 72

  Следовательно, количество рулонов, которое должен купить Сэм, будет $\frac{72}{24}$  = 3

Точно так же число булочек, которое должен купить Питер, будет $\frac{72}{36}$  = 2

Ключевые факты и сводка

1. Множитель числа — это точный делитель этого числа.
2. Кратным целому числу является произведение этого числа на любое счетное число.
3. Если число кратно двум или более числам, оно называется общим кратным чисел.
4. Каждое число, кратное этому числу, больше или равно ему.
5. Наименьшим кратным числа является само число.
6. Количество кратных заданному числу бесконечно.
7. Все числа, кратные 2, являются четными числами.
8. Те кратные, которые являются общими среди кратных двух или более чисел, называются общими кратными этих чисел.
9. Мы не можем определить наибольшее кратное числа или группы чисел, но мы всегда можем перечислить первое кратное числа.
10. Наименьшее общее кратное ( LCM ) двух или более чисел определяется как наименьшее число (отличное от нуля), являющееся кратным этих чисел.
11. Существует два основных метода, с помощью которых мы можем найти LCM двух или более чисел — метод наименьшего общего (LCM) и метод общего деления.
12. Для нахождения LCM с использованием метода простой факторизации мы разлагаем каждое число как произведение его простых множителей. Затем мы находим произведение всех различных простых множителей с наибольшей степенью при разложении каждого числа на простые множители.
13. Чтобы найти L C M методом общего деления, мы делим числа, которые делятся на число, выбранное на предыдущем шаге, и записываем частные прямо под ними.

    No related posts.