y cosx модуль cosx
Вы искали y cosx модуль cosx? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и модуль y cosx, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «y cosx модуль cosx».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как y cosx модуль cosx,модуль y cosx. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и y cosx модуль cosx. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, y cosx модуль cosx).
Где можно решить любую задачу по математике, а так же y cosx модуль cosx Онлайн?
Решить задачу y cosx модуль cosx вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.
www.pocketteacher.ru
Модуль в тригонометрических уравнениях: найти и обезвредить
Достаточно часто в задачах повышенной сложности встречаются тригонометрические уравнения, содержащие модуль. Большинство из них требуют эвристического подхода к решению, который совсем не знаком большинству школьников.
Предлагаемые ниже задачи призваны познакомить вас с наиболее характерными приемами решения тригонометрических уравнений содержащих модуль.
Задача 1. Найти разность (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 1 + 2sin x · |cos x| = 0.
Решение.
Раскроем модуль:
1) Если cos x ≥ 0, то исходное уравнение примет вид 1 + 2sin x · cos x = 0.
Воспользуемся формулой синуса двойного угла, получим:
1 + sin 2x = 0; sin 2x = -1;
2x = -π/2 + 2πn, n € Z;
x = -π/4 + πn, n € Z. Так как cos x ≥ 0, то x = -π/4 + 2πk, k € Z.
2) Если cos x < 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. По формуле синуса двойного угла, имеем:
1 – sin 2x = 0; sin 2x = 1;
2x = π/2 + 2πn, n € Z;
x = π/4 + πn, n € Z. Так как cos x < 0, то x = 5π/4 + 2πk, k € Z.
3) Наибольший отрицательный корень уравнения: -π/4; наименьший положительный корень уравнения: 5π/4.
Искомая разность: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 · 180°/2 = 270°.
Ответ: 270°.
Задача 2. Найти (в градусах) наименьший положительный корень уравнения |tg x| + 1/cos x = tg x.
Решение.
Раскроем модуль:
1) Если tg x ≥ 0, тогда
tg x + 1/cos x = tg x;
1/cos x = 0.
В полученном уравнении корней нет.
2) Если tg x < 0, тогда
-tg x + 1/cos x = tg x;
1/cos x – 2tg x = 0;
1/cos x – 2sin x / cos x = 0;
(1 – 2sin x) / cos x = 0;
1 – 2sin x = 0 и cos x ≠ 0.С помощью рисунка 1 и условия tg x < 0 находим, что x = 5π/6 + 2πn, где n € Z.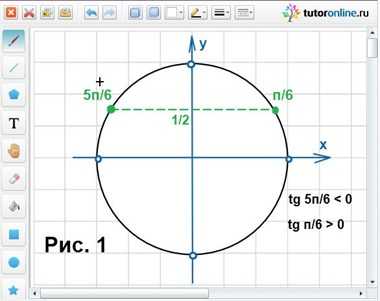
3) Наименьший положительный корень уравнения 5π/6. Переведем это значение в градусы:
5π/6 = 5 · 180°/6 = 5 · 30° = 150°.
Ответ: 150°.
Задача 3. Найти количество различных корней уравнения sin |2x| = cos 2x на промежутке [-π/2; π/2].
Решение.
Запишем уравнение в виде sin|2x| – cos 2x = 0 и рассмотрим функцию y = sin |2x| – cos 2x. Так как функция является четной, то найдем ее нули при x ≥ 0.
sin 2x – cos 2x = 0; разделим обе части уравнения на cos 2x ≠ 0, получим:
tg 2x – 1 = 0;
tg 2x = 1;
2x = π/4 + πn, n € Z;
x = π/8 + πn/2, n € Z.
Воспользовавшись четностью функции, получим, что корнями исходного уравнения являются числа вида
± (π/8 + πn/2), где n € Z.
Промежутку [-π/2; π/2] принадлежат числа: -π/8; π/8.
Итак, два корня уравнения принадлежат заданному промежутку.
Ответ: 2.
Данное уравнения можно было бы решить и раскрытием модуля.
Задача 4. Найти количество корней уравнения sin x – (|2cos x – 1|)/(2cos x – 1) · sin2 x = sin2 x на промежутке [-π; 2π].
Решение.
1) Рассмотрим случай, когда 2cos x – 1 > 0, т.е. cos x > 1/2, тогда уравнение принимает вид:
sin x – sin2 x = sin2 x;
sin x – 2sin2 x = 0;
sin x(1 – 2sin x) = 0;
sin x = 0 или 1 – 2sin x = 0;
sin x = 0 или sin x = 1/2.
Используя рисунок 2 и условие cos x > 1/2, найдем корни уравнения:
x = π/6 + 2πn или x = 2πn, n € Z.
2) Рассмотрим случай, когда 2cos x – 1 < 0, т.е. cos x < 1/2, тогда исходное уравнение принимает вид:
sin x + sin 2 x = sin2 x;
sin x = 0;
x = 2πn, n € Z.
Используя рисунок 2 и условие cos x < 1/2, находим, что x = π + 2πn, где n € Z.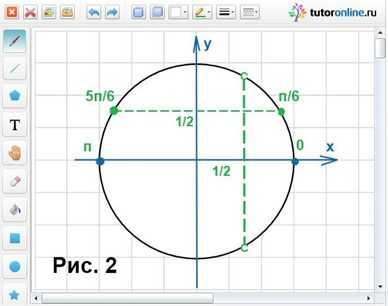
Объединим два случая, получим:
x = π/6 + 2πn или x = πn.
3) Промежутку [-π; 2π] принадлежат корни: π/6; -π; 0; π; 2π.
Таким образом, заданному промежутку принадлежат пять корней уравнения.
Ответ: 5.
Задача 5. Найти количество корней уравнения (x – 0,7)2 |sin x| + sin x = 0 на промежутке [-π; 2π].
Решение.
1) Если sin x ≥ 0, то исходное уравнение принимает вид (x – 0,7)2 sin x + sin x = 0. После вынесения общего множителя sin x за скобки, получим:
sin x((x – 0,7)2 + 1) = 0; так как (x – 0,7)2 + 1 > 0 при всех действительных x, то sinx = 0, т.е. x = πn, n € Z.
2) Если sin x < 0, то -(x – 0,7)
sin x((x – 0,7)2 – 1) = 0;
sinx = 0 или (x – 0,7)2 + 1 = 0. Так как sin x < 0, то (x – 0,7)2 = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:
x – 0,7 = 1 или x – 0,7 = -1, а значит x = 1,7 или x = -0,3.
С учетом условия sinx < 0 получим, что sin (-0,3) ≈ sin (-17,1°) < 0 и sin (1,7) ≈ sin (96,9°) > 0, значит только число -0,3 является корнем исходного уравнения.
3) Промежутку [-π; 2π] принадлежат числа: -π; 0; π; 2π; -0,3.
Таким образом, уравнение имеет пять корней на заданном промежутке.
Ответ: 5.
Заняться подготовкой к урокам или экзаменам можно при помощи различных образовательных ресурсов, которые есть в сети. В настоящее время любому человеку просто необходимо использовать новые информационные технологии, ведь правильное, а главное уместное их применение будет способствовать повышению мотивации в изучении предмета, повысит интерес и поможет лучше усвоить необходимый материал. Но не стоит забывать о том, что компьютер не учит думать, полученную информацию обязательно необходимо обрабатывать, понимать и запоминать. Поэтому вы можете обратиться за помощью к нашим онлайн репетиторам, которые помогут вам разобраться с решением интересующих вас задач.
Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Тригонометрические уравнения с модулем
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а < 0.
Согласно этому определению, в уравнениях модуль можно раскрывать следующим образом:
№1. Решить уравнение.
№2. Решить уравнение.
Решаем уравнение первой системы:
2sin2x-sinx=0
sinx(2sinx-1)=0
sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx<0,
получаем х =
Серии ответов можно записать объединяя
№3. Решить уравнение.
Решение. Раскрывая знак модуля, получаем системы:
Решая уравнение первой системы, получим Из значений нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это при n=0, 1, 2, 3…
Решая уравнение второй системы, получим Из этого множества значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это значения при m= -1, -2, -3…
Ответ: при n=0, 1, 2, 3…; при m = -1, -2, -3…и х = -3
№4 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, поэтому, раскрывая знак модуля, получим только одну систему
Решаем уравнение системы:
соsx=cosx(x+1,5)2
cosx(1-(x+1,5)2)=0
cosx=0 или x+1,5=1 или x-1,5 = -1
х= -0,5 х = -2,5
Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения на отрезке [0;4].
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии в нужном промежутке [0;4] лежат точки 0 и ; , а из серии
Решая вторую систему, получим систему , которая не имеет решений.
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений надо выбрать те, при которых sinx>0. На круге видно, что это точки вида
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Обратная замена:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
при причем, f(х)= -1 в точках 4 и 11.Левая часть cos при любых х, причем, в точках 4 и 11 не равна -1, значит, система решений не имеет.
При решении уравнения второй системы получается:
В промежутке только одно целое нечетное число 3, т.е
Ответ: 9
Другие способы раскрытия модулей.
Уравнения вида можно решать и следующим способом:
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx <0, тогда уравнение равносильно системе
Рассмотрим две системы:
Решая уравнение первой системы получим: cosx-2sinx=0
Учитывая, что cosx≤0, x = arctg Вторая система решений не имеет.
Ответ: x = arctg.
№11. Решить уравнение.
cosx
Решение.
№12. Решить уравнение.
Решение. Уравнение равносильно sinx = ± cosx
Ответ:
Задачи для самостоятельного решения:
21.02.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Ответы@Mail.Ru: как построить график y=cos|x|???
Это то же самое, что просто соs х, потому что косинус — чётная ф-ция и ей по фиг с каким знаком х. P.S. Многие отвечающие путают модуль функции и аргумента, поэтому дают неверные ответы.
имхо это косинусоида, части которой в отрицательной части оси оординат нужно зеркально отразить в положительную чать
cos x для x>0 отразить относительно оси oY
Косинусоида. Открой тетрадь. Выглядит как волна, начинается на у от 1, х размечается по тригонометрии- от 0 до 2пи
Если стоит знак модуля, то значит х не имеет отрицательных значений. Т. е. строишь график косинуса и тупо стираешь его ниже оси х. По моему так?
также как и просто косинус икс, подставляй икс, получай игрек, ну в общем получится та же самая косинусоида толь ко она будет находиться в 1 и 4 четвертях и симметрично положительной оси икс
Строишь график для х>0 и симметрично отражаешь относительно оси Oy. Построй на сайте введи свою функцию в виде y=cos(abs(x)) (abs — это модуль)
строишь косинусоиду.. . т. к. модуль, по игреку получается только больше или равно нулю.. симметрию из нижней полуплоскости в верхню..
touch.otvet.mail.ru
найдите множество значений функции y=2+3 модуль cosx
Ответ есть вот тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=373474″ target=»_blank»>vk.com/wiki-18832533-37373474236</a>
твет есть вот тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=216331″ target=»_blank»>vk.com/wiki-18832533-37216331236</a>
С такими заданиями Вам лучше на студенческий сайт: reshebnik.biz
<a rel=»nofollow» href=»http://v.ht/dGSl?0=34302″ target=»_blank»>настя посмотри здесь, страница 334</a>
твет есть вот тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=173110″ target=»_blank»>vk.com/wiki-18832533-37173110236</a>
Отет есть вот тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=16694″ target=»_blank»>vk.com/wiki-18832533-3716694236</a>
<a rel=»nofollow» href=»http://v.ht/wqSj?0=232047″ target=»_blank»>настя посмотри здесь, страница 223</a>
touch.otvet.mail.ru
