Как находить матрицу обратную: Как найти обратную матрицу: примеры решений

Обратная матрица схема вычисления обратной матрицы

Автор admin На чтение 6 мин Просмотров 1 Опубликовано 7 апреля 2023 Обновлено 7 апреля 2023

Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции вы научитесь находить обратную матрицу. Научитесь. Даже если с математикой туго.

Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число

. Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Однако обо всём по порядку – сначала решим важный практический вопрос, а именно, научимся эту самую обратную матрицу находить.

Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.

Есть? Тогда поехали дальше. А хотя… ехать могут все, если что-то не знаете, я буду ставить нужную ссылку по ходу объяснений.

Существует два основных метода нахождения обратной матрицы:
с помощью алгебраических дополнений и с помощью элементарных преобразований.

Сегодня мы изучим первый, более простой способ.

Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу

. Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом

Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.

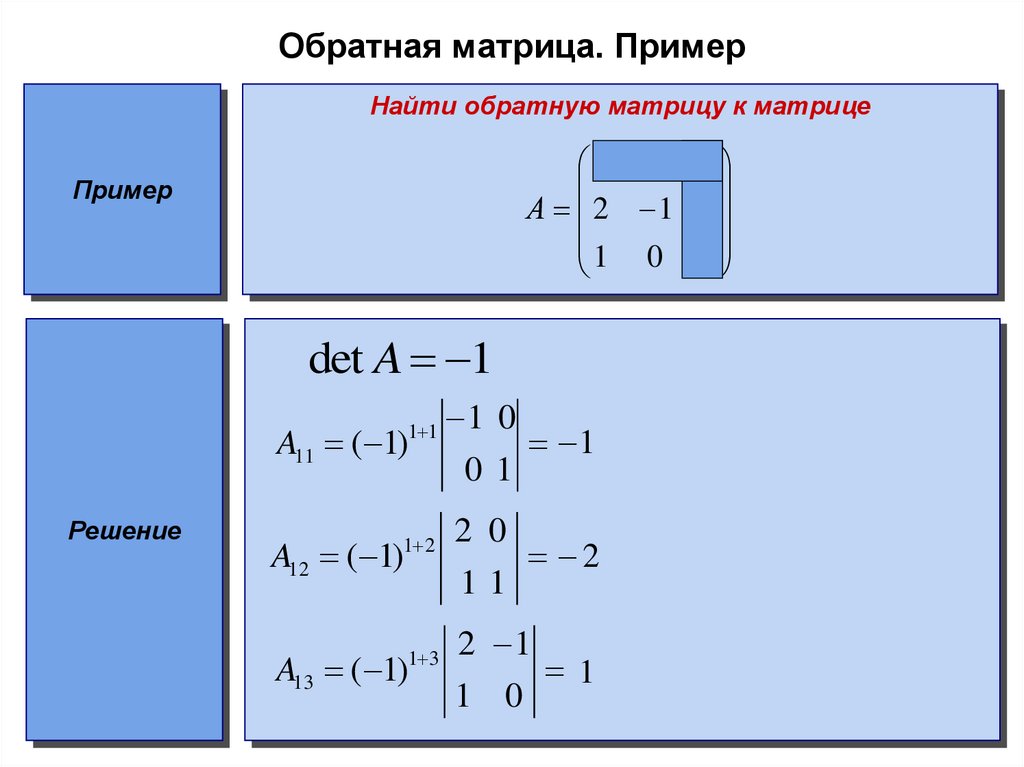
Найти обратную матрицу для матрицы

Решаем. Последовательность действий удобно разложить по пунктам.

1) Сначала находим определитель матрицы.

Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель?

Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.

В рассматриваемом примере, как выяснилось,

, а значит, всё в порядке.

2) Находим матрицу миноров

.

Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.

Матрица миноров имеет такие же размеры, как и матрица

, то есть в данном случае .
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.

Возвращаемся к нашей матрице

Сначала рассмотрим левый верхний элемент:

Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:

Рассматриваем следующий элемент матрицы :

Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:

То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:

Аналогично рассматриваем элементы второй строки и находим их миноры:


Готово.

– матрица миноров соответствующих элементов матрицы .

3) Находим матрицу алгебраических дополнений

.

Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:

Именно у этих чисел, которые я обвел в кружок!

– матрица алгебраических дополнений соответствующих элементов матрицы .

4) Находим транспонированную матрицу алгебраических дополнений .

Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Вспоминаем нашу формулу

Всё найдено!

Таким образом, обратная матрица:

Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статье Действия с матрицами.

Необходимо выполнить матричное умножение

либо

Проверка:

Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.

Таким образом, обратная матрица найдена правильно.

Если провести действие

, то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.

Переходим к более распространенному на практике случаю – матрице «три на три»:

Найти обратную матрицу для матрицы

Алгоритм точно такой же, как и для случая «два на два».

Обратную матрицу найдем по формуле:

, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

1) Находим определитель матрицы.

Здесь определитель раскрыт по первой строке.

Также не забываем, что

, а значит, всё нормально – обратная матрица существует.

2) Находим матрицу миноров

.

Матрица миноров имеет размерность «три на три»

, и нам нужно найти девять чисел.

Я подробно рассмотрю парочку миноров:

Рассмотрим следующий элемент матрицы:

МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:

Оставшиеся четыре числа записываем в определитель «два на два»

Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить:

Всё, минор найден, записываем его в нашу матрицу миноров:

Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.

Ну и для закрепления – нахождение еще одного минора в картинках:

Остальные миноры попробуйте вычислить самостоятельно.

Окончательный результат:

– матрица миноров соответствующих элементов матрицы .

То, что все миноры получились отрицательными – чистая случайность.

3) Находим матрицу алгебраических дополнений

.

В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов:

В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы .

4) Находим транспонированную матрицу алгебраических дополнений .

– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

Проверка:

Таким образом, обратная матрица найдена правильно.

Как оформить решение на чистовик? Примерный образец чистового оформления задания можно найти на странице Правило Крамера. Метод обратной матрицы в параграфе, где идет речь о матричном методе решения системы линейных уравнений. По существу, основная часть упомянутой задачи – и есть поиск обратной матрицы.

Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил один определитель «четыре на четыре» и 16 определителей «три на три»). В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).

В ряде учебников, методичек можно встретить несколько другой подход к нахождению обратной матрицы, однако я рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому что вероятность запутаться в вычислениях и знаках – гораздо меньше.

Иногда обратную матрицу требуется найти методом Гаусса-Жордана, но второй способ доступен для студентов с приличной техникой элементарных преобразований.

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Источник

Обратная матрица

Матрица размера n × n, A, обратима, если существует матрица размера n × n, A ^-1 , называемая обратной матрицей A, такая, что

A ^-1 A = AA ^{— 1} = I _n

, где I _n — единичная матрица размера n × n. В дальнейшем мы будем обозначать единичную матрицу просто I, так как будет понятно, какого размера I должен быть в контексте каждой задачи. Помните, что I особенный, потому что для любой другой матрицы A

IA = AI = A

Обратите внимание, что для обратимой матрицы A размера n × n следующие условия эквивалентны (либо все они истинны, либо все ложны):

1. rref(A) = I


2. дет(А) ≠ 0


3. x = 0 — единственное решение Ax = 0, где 0 — n-мерный 0-вектор

Матрица, имеющая обратную, называется обратимой или невырожденной.

Матрица, которая не является обратимой, называется сингулярной. Также стоит отметить, что только квадратные матрицы имеют обратные, но не все квадратные матрицы обратимы.

Обратная матрица 2 × 2

Обратная матрица 2 × 2 может быть рассчитана по формуле, как показано ниже. Если

, то

Чтобы подтвердить, что это верно,

и

Обратите внимание, что (ad — bc) также является определителем A, данной матрицы 2 × 2, поэтому формула для A ^-1 также может быть записано как:

Инверсия матрицы 3 × 3

Существует несколько методов определения инверсии матрицы 3 × 3 или более крупной матрицы.

Использование расширенных матриц

Одним из методов нахождения определителя матрицы A является использование ее расширенной матрицы [A|I]. Этот метод включает использование исключения Гаусса для нахождения сокращенной эшелонированной формы строки [A|I]. При необходимости обратитесь к странице матрицы для обзора метода исключения Гаусса. Процесс не будет показан в этом примере. Рассмотрим следующую матрицу

и ее расширенную матрицу [A|I]:

Чтобы найти обратную A, мы выполняем исключение Гаусса над ее расширенной матрицей, чтобы получить:

, где rref([A|I]) означает «уменьшенную эшелонированную форму строки [A|I]». Три левых столбца rref([A|I]) образуют rref(A), которая также является единичной матрицей, поэтому rref(A) = I. Поэтому мы утверждаем, что правые 3 столбца образуют обратную A ^{— 1} of A, поэтому:

Затем мы можем подтвердить это как

и

. , Топор ₂ = e ₂ и Ax ₃ = e ₃ , где e ₁ , e ₂ и e ₃ — стандартные базисные векторы одновременно. Когда rref(A) = I, векторы решений x ₁ , x ₂ и x ₃ однозначно определены и образуют новую матрицу [x ₁ x ₂ x ₃ ], которая появляется на правая половина rref([A|I]). [x ₁ x ₂ x ₃ ] удовлетворяет A[x ₁ x ₂ x ₃ ] = [e ₁ e ₂ e ₃ ]. Но с момента [E ₁ E ₂ E ₃ ] = I, A [x ₁ x ₂ x ₃ ] = [E ₁ E ₂ E ₃ ] = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =. I, и по определению обратного, [x ₁ x ₂ x ₃ ] = A ^-1 .

В качестве примера рассмотрим также случай сингулярной (необратимой) матрицы B:

Составим расширенную матрицу [B|I]:

Однако, когда мы вычисляем rref([B|I]), мы получаем:

Обратите внимание, что первые 3 столбца не образуют единичную матрицу. Вместо этого они образуют:

, в котором все 0 находятся в строке 3 ^rd . Следовательно, B необратима. Что бы мы ни делали, мы никогда не найдем матрицу B ^-1 , удовлетворяющую условию BB ^-1 = B ^-1 B = I. Необратимую матрицу обычно называют сингулярной.

Примечание. Форма rref(B) говорит о том, что 3 ^rd столбец B в 1 раз больше 1 ^st столбца B плюс -3 раза 2 ^nd ряд ​​B, как показано ниже.

Детерминанты и обратимость

Можно доказать, что если матрица A обратима, то det(A) ≠ 0. Верно и обратное: если det(A) ≠ 0, то A обратима. Доказательство связано с тем свойством, что каждая операция со строками, которую мы используем для получения от A до rref(A), может только умножать определитель на ненулевое число. Хотя доказательство здесь не приводится, мы можем видеть, что приведенное выше верно для наших предыдущих примеров.

В приведенных выше примерах мы обнаружили, что

обратимы, а

— в единственном числе. Если мы вычислим определители A и B, мы обнаружим, что

		=
		+
		=
		=
		=
		+
		=
		=

Использование сопряжения матрицы

Другой метод нахождения обратной матрицы большего размера заключается в использовании ее определителя вместе с сопряжением матрицы. Если A является обратимой матрицей размера n × n, кофактор C _ij для соответствующей записи в A равен

, где M _ij является определителем матрицы, полученной в результате удаления i 9Столбец 0315 th и j th A. M _ij называется минором для соответствующей записи в A. Матрица, образованная всеми кофакторами A, называется его матрицей кофакторов или матрицей кофакторов:

Транспонированная матрица кофакторов матрицы A называется сопряженной матрицей A или ее присоединенной матрицей. Таким образом:

Сопряженная матрица A может быть использована для нахождения ее обратной по следующей формуле:

Пример

Найдите обратную , если она существует, используя ее сопряженную.

Сначала определите, обратима ли матрица A, найдя ее определитель (напомним, что если det(A) = 0, матрица необратима). В этом примере мы используем расширение кофактора по второй строке A, чтобы найти определитель. Обратитесь к странице определителя, чтобы просмотреть расширение кофактора или другие методы вычисления определителя.

Так как det(A) ≠ 0, мы знаем, что у A есть обратный, и переходим к поиску его сопряженного. Найдя определитель, мы знаем C ₂₁ = 1, C ₂₂ = -1 и C ₂₃ = -½, поэтому нам нужно вычислить сомножители только для первой и третьей строк:

Таким образом,

,

2 и

,

Подставляем это в формулу:

,

Как найти обратную матрицу

В предыдущей статье вы узнали об обратной матрице и почему это важно. В этой статье вы узнаете, как найти обратную матрицу. Есть два основных метода нахождения обратной любой квадратной обратимой матрицы — Классический сопряженный метод и метод исключения Гаусса-Жордана.

Методы нахождения обратной матрицы

Основным методом нахождения обратной матрицы являются

1. Классический сопряженный метод в деталях.

   Классический метод сопряженных

   Если — обратимая матрица, то мы можем найти обратную матрицу с сопряженной матрицей.

   Но, прежде чем мы начнем, вы должны понять несколько терминов.

   Определитель – Это специальное число, полученное из квадратной матрицы, неквадратная матрица не имеет определителя. Если матрица квадратная, то есть несколько способов обозначить ее определитель.

    или или 

   Минор матрицы – Минор квадратной матрицы получается путем удаления строки и столбца из определителя большей квадратной матрицы. Обозначается for элемента, где i ^-й -й ряд и j ^-й -й столбец.

    Определитель матрицы 2 x 2
   
   Вы получаете следующую матрицу определителей
    

   Кофактор матрицы – Кофактор матрицы можно найти из определителя миноров, присвоив соответствующие отрицательные или положительные знаки. Каждый кофактор можно найти по следующему уравнению.

   Матрица кофакторов A
    

   Сопряженная матрица – Сопряженная матрица получается путем транспонирования матрицы кофакторов. Обозначается как .

   Нахождение обратной матрицы сопряженным методом

   Процесс нахождения обратной матрицы сопряженным методом выглядит следующим образом.

   1. Найти матрицу миноров
   2. Найти матрицу сомножителей
   3. Найти определитель det(A) путем умножения первой строки матрицы A на первую строку матрицы сомножителей A.
   4. Найти сопряженную матрицу Используйте матрицу кофакторов A.
   5. Умножьте 1/det(A) на сопряженную A (adj A), чтобы получить обратную матрицу A.

   Мы найдем обратную матрицу, используя сопряженную матрицу в следующем разделе. Сначала мы должны найти обратную матрицу, затем и, наконец, матрицу.

   Пример #1 : Найдите обратную матрицу с помощью сопряженного метода.

   Решение:

    Позвольте быть матрицей порядка 1 x 1.
   Шаг 1: Для матрицы 1x1 минор отсутствует.
   Шаг 2: Для матрицы 1x1 нет кофактора.
   Шаг 3: определитель A равен . (обратимый)
   Шаг 4: Сопряженная матрица A равна .
   Чтобы вычислить обратную матрицу A, используйте
    

   Пример #2 : Найдите обратную матрицу с помощью сопряженного метода.

   Решение:

   Позвольте быть квадратной и обратимой матрицей порядка .

   Шаг 1: Миноры матрицы равны

   Минорная матрица
   
   Шаг 2: Кофактор матрицы получается из минорной матрицы.
   
   Кофакторная матрица
   
   Шаг 3: Чтобы вычислить определитель, просто перемножьте соответствующие элементы верхней строки матрицы и второй строки кофактора и сложите их.
   Верхняя строка матрицы B = 2, 1
   Верхняя строка матрицы кофакторов = 7 -3
   
   Шаг 4: Найдите сопряженную матрицу, транспонируя матрицу кофакторов.
   
   Чтобы найти обратную матрицу, используйте следующее
   
   Проверьте обратную матрицу 

   Пример #3 : Найдите обратную матрицу 3 x 3, используя сопряженный метод.

   Решение:

   Дана матрица порядка.

   .

   Шаг 1: Найдите миноры матрицы .

   Имеем следующую матрицу миноров
    

   Шаг 2: Найдите сомножители матрицы .

    Мы можем использовать матрицу миноров, чтобы найти матрицу кофакторов.
   
   Мы получаем кофакторную матрицу 

   Шаг 3: Найдите определитель матрицы .

    Верхняя строка матрицы A = 1, -2, 1
   Верхний ряд коактора A = 5, -18, 2
    

   Шаг 4: Найдите сопряженную матрицу . Сопряженная матрица может быть получена транспонированием матрицы кофакторов.

   Шаг 5: Найдите обратную матрицу, используя следующее уравнение.

   Проверка результатов :

    Проверка правильности 

   Нахождение обратной матрицы с использованием метода исключения Гаусса-Жордана

   Метод исключения Гаусса-Жордана преобразует матрицу в эшелонированную форму с уменьшенными строками, чтобы найти значение вектора решения в , но здесь мы используем метод, чтобы найти обратную матрицу .

   Операции со строками

   Метод Гаусса-Жордана включает операции со строками над расширенной матрицей, полученной из системы линейных уравнений, которая преобразует матрицу в единичную матрицу, где порядок матрицы .

   Эти операции со строками

   • Умножить строку на скаляр где .
   • Поменять строку на строку .
   • Добавление времени от строки к строке .

   Пример №5: Операции со строками

    Позвольте быть матрицей порядка.
   
   Умножьте строку 1 на 3.
   
   Поменять местами 2-й ряд с 1-м.
   
   Прибавить 2 раза 1 ряд ко 2 ряду.
    

   Элементарная матрица

   Элементарная матрица — это матрица, полученная в результате выполнения однострочной операции над единичной матрицей.

   Предположим, что A — матрица порядка, тогда результат такой же, как при выполнении этой операции со строками над матрицей.

   Пример #6: Элементарная матрица

    Предположим, это матрица порядка.
     Позвольте быть строковой операцией порядка .
   Позволять
   Давайте выступим на .
    (1)
   Теперь найдем матрицу.
    (2)
   Следовательно, (1) и (2) совпадают. 

   Обратные операции

   Если матрица является результатом операции над строкой над единичной матрицей, то существует некоторая операция, если ее выполнить над возвратом. Такая операция называется Обратной операцией.

   Для каждой элементарной операции со строкой существует эквивалентная обратная операция. Проверьте таблицу ниже.

   Elementary Row Operation	Inverse Operation
   Multiply row i by c where c != 0	Multiply row i by 1/c
   Interchange row i with row j	Поменять строку j на строку i
   Добавить k раз строку i к строке j	Добавить -k раз строку i к строке j

   Обратные операции

   Пример #7 : Обратные операции

    Умножить строку на . 
   
   Умножить строку на где 

   Из вышесказанного можно сделать вывод, что

    1. Некоторые операции над дают элементарную матрицу .
   2. Обратная предыдущая операция над E даст обратно .
   3. Обратная операция над приведет к обратной матрице такой, что
   
   Обратите внимание, что это обратимая матрица, и ее определитель больше 0. 

   4 Необходимые утверждения для метода Гаусса-Жордана и обратные

   Прежде чем мы найдем обратную матрицу с помощью метода Гаусса-Жордана, необходимо выполнить 4 необходимых предлога относительно матрицы и ее обратной.

   Если матрица квадратная, эти 4 утверждения всегда должны быть истинными.

   • Матрица обратима, то есть определитель больше 0 и не имеет нулевой строки.
   • имеет только тривиальное решение.
   • Матрица приведена к ступенчатой ​​форме с уменьшенными строками, которая является единичной матрицей . Это потому, что имеет только тривиальное решение, что означает наличие одного решения для каждого .

     No related posts.