Как находить определенный интеграл: Как вычислить определенный интеграл, примеры решений

alexxlab / / Разное

Определенный интеграл. Примеры решений

И снова здравствуйте. На данном уроке мы подробно разберем такую замечательную вещь, как определенный интеграл. На этот раз вступление будет кратким. Всё. Потому что снежная метель за окном.

 Для того чтобы научиться решать определенные интегралы необходимо:

1) Уметь находить неопределенные интегралы.

2) Уметь вычислить определенный интеграл.

Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.

В общем виде определенный интеграл записывается так: Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой .

Верхний предел интегрирования стандартно обозначается буквой . Отрезок  называется отрезком интегрирования.

Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.

Что такое определенный интеграл? Я бы мог вам рассказать про диаметр разбиения отрезка, предел интегральных сумм и т.д., но урок носит практический характер. Поэтому я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.

Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:

Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию  (неопределенный интеграл). Обратите внимание, что константа  в определенном интеграле никогда не добавляется. Обозначение   является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ?  Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .

3) Подставляем значение нижнего предела в первообразную функцию: .

4) Рассчитываем (без ошибок!) разность , то есть, находим число.

Готово.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла  не существует, поскольку отрезок интегрирования  не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках ,  отрезка  не существует тангенса.

Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.  

Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так: ???! Нельзя подставлять отрицательные числа под корень! Изначальная невнимательность.

Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен  несуществующий интеграл вроде , то нужно дать ответ, что интеграла не существует и обосновать – почему.

Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.

 –  интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.

Урок 6. Определённый интеграл | Уроки математики и физики для школьников и родителей

ВИДЕО УРОК

Для того чтобы научиться решать определённые интегралы необходимо

1)  Уметь находить неопределённые интегралы.

2)  Уметь вычислить определённый интеграл.

В общем виде определённый интеграл записывается так:

По сравнению с неопределённым интегралом прибавились пределы интегрирования.

Нижний предел интегрирования обозначается буквой  а.

Верхний предел интегрирования обозначается буквой  b.

Отрезок  [a; b]  называется отрезком интегрирования.

Определённый интеграл – это число. Решить определённый интеграл это значит найти число.

Находится определённый интеграл с помощью формулы Ньютона-Лейбница.

Этапы решения определённого интеграла.

1)  Сначала находим первообразную функцию

(неопределённый интеграл). Константа  С  в определённом интеграле не добавляется.

Обозначение

является чисто техническим, и вертикальная палочка не несёт никакого математического смысла. Запись

нужна для подготовки применения формулы Ньютона-Лейбница.

2)  Подставляем значение верхнего предела в первообразную функцию

3)  Подставляем значение нижнего предела в первообразную функцию

4)  Находим разность (число)


F(b) – F(a).

Определённый интеграл существует не всегда.


ПРИМЕР:


Интеграла

не существует, поскольку отрезок интегрирования  


[–5; –2]  


не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными).


ПРИМЕР:


Интеграла

не существует, поскольку на отрезке интегрирования  [–2; 3]  тангенс терпит бесконечные разрывы в точках


х = –π/2,  х = π/2.


Для того чтобы определённый интеграл существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Поэтому перед тем, как приступить к решению любого определённого интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

Определённый интеграл может быть равен отрицательному числу или нулю.

Нижний предел интегрирования может быть больше верхнего предела интегрирования.


ПРИМЕР:

Интеграл вычисляется по формуле Ньютона-Лейбница.


Свойства определённого интеграла.

1)  В определённом интеграле можно переставить верхний и нижний предел, сменив при этом знак.

ПРИМЕР:

В определённом интеграле

перед интегрированием целесообразно поменять пределы интегрирования на <<привычный>> порядок:

В таком виде интегрировать значительно удобнее.

2)  Свойства линейности.

где   k = const.

Это справедливо не только для двух, но и для любого количества функций.


ПРИМЕР:


Вычислить определённый интеграл:

РЕШЕНИЕ:

Выносим константу за знак интеграла:

Интегрируем по таблице с помощью формулы

Используем формулу Ньютона-Лейбница.

Сначала подставляем в  х3  верхний предел, зптем нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

= 2/3 (23 – 13) = 2/3 (8 – 1) = 2/3 ∙ 7 = 14/3 = 42/3.


ПРИМЕР:


Вычислить определённый интеграл:

РЕШЕНИЕ:

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

Используем свойства линейности определённого интеграла.

Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница.

Рассмотрим второй способ решения этого интеграла.


ПРИМЕР:


Вычислить определённый интеграл:

РЕШЕНИЕ:

Сначала используем правило линейности и проинтегрируем по таблице. Получается одна скобка с отчёркиванием пределов.

В первообразную функцию сначала подставим  4, затем  –2. А затем найдём разность. Перед тем, как использовать формулу Ньютона-Лейбница, полезно провести проверку и убедиться, что первообразная функция найдена правильно.
 Так, применительно к рассматриваемому примеру, перед тем, как в первообразную функцию

подставлять верхний и нижний пределы, необходимо проверить правильно или нет, найден неопределённый интеграл. Дифференцируем:

Получена исходная подынтегральная функция, значит, неопределённый интеграл найден верно.

ПРИМЕР:

Вычислить определённый интеграл:

РЕШЕНИЕ:

Задания к уроку 6

Определенный интеграл

Начнем с простой задачи. Объект движется прямолинейно с постоянной скоростью 5 м/с в течение 10 с. На каком расстоянии от начальной точки находится объект?

Мы подходим к этой проблеме с помощью знакомого уравнения «Расстояние = Скорость × Время». В этом случае Расстояние = 5 футов/с × 10 с = 50 футов.

Интересно отметить, что это решение для 50 футов может быть представлено графически. Рассмотрим рисунок 5.2.1, где по осям нанесена постоянная скорость 5 футов/с. Затенение области под линией от \(t=0\) до \(t=10\) дает прямоугольник площадью 50 квадратных единиц; если принять во внимание единицы измерения осей, мы можем сказать, что эта площадь равна 50 футам.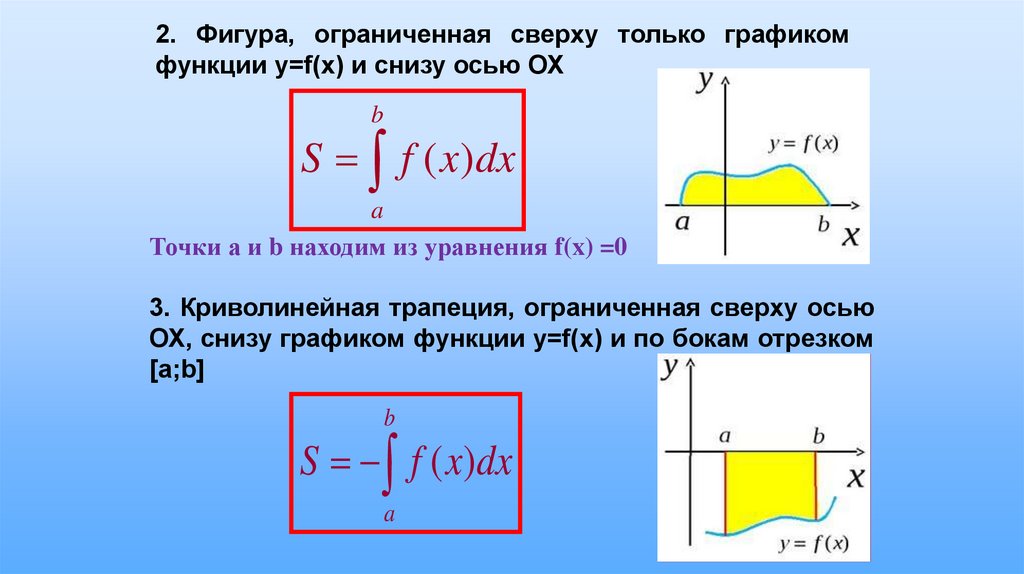 0003 Рисунок 5.2.1. Площадь под функцией постоянной скорости соответствует пройденному расстоянию.

Теперь рассмотрим немного более сложную ситуацию (и не очень реалистичную): объект движется по прямой линии с постоянной скоростью 5 футов/с в течение 10 секунд, затем мгновенно меняет курс со скоростью 2 фута/с в течение 4 секунд. (Поскольку при изменении курса объект движется в противоположном направлении, мы говорим, что скорость постоянна \(-2\) фут/с.) Как далеко от начальной точки находится объект — какова его скорость?0009 смещение ?

Здесь мы используем «Перемещение = Скорость\(_1\) × Время\(_1\) + Скорость\(_2\) × Время\(_2\текст{,}\)», что равно

\begin{уравнение*} \text{ Водоизмещение } \ = 5\cdot10 + (-2)\cdot 4 = 42\text{ футов } \end{уравнение*}

Следовательно, объект находится в 42 футах от своего начального положения.

Мы снова можем изобразить эту ситуацию графически. На рисунке 5.2.2 скорости изображены прямыми линиями на \([0,10]\) и \([10,14]\text{,}\) соответственно. Перемещение объекта

\begin{уравнение*} \text{Область над осью }t\text{-} -\text{Область под осью }t\text{-,} \end{уравнение*}

, что легко вычислить как \(50-8=42\) футов.

Рисунок 5.2.2. Полное смещение представляет собой площадь над осью \(t\) минус площадь под осью \(t\).

Теперь рассмотрим более сложную задачу.

Пример 5.2.3. Определение положения по скорости.

Скорость объекта, движущегося прямо вверх/вниз под действием ускорения свободного падения, определяется как \(v(t) = -32t+48\text{,}\), где время \(t\) указано в секундах, а скорость находится в футах/с. Когда \(t=0\text{,}\) объект имел высоту 0 футов.

  1. Какова была начальная скорость объекта?

  2. Какой была максимальная высота объекта?

  3. Какова была высота объекта в момент времени \(t=2\text{?}\)

Раствор.

Начальную скорость найти несложно; во время \(t=0\text{,}\)

\begin{align*} v(0) \амп =-32\cdot 0+48 \\ \амп = 48 \end{align*}

Начальная скорость была \(48\)ft/s.

Чтобы ответить на вопросы о высоте объекта, нам нужно найти функцию положения объекта \(s(t)\text{.}\) Это задача с начальными значениями, которую мы изучали в предыдущем разделе. Нам говорят, что начальная высота равна \(0\text{,}\), то есть \(s(0) = 0\text{.}\). Мы знаем, что \(s'(t) = v(t) = — 32t+48\text{.}\) Чтобы найти \(s\text{,}\), мы находим неопределенный интеграл от \(v(t)\text{:}\) 92+48t\text{.}\)

Чтобы найти максимальную высоту объекта, нам нужно найти максимум \(s\text{.}\) Вспоминая нашу работу по поиску экстремальных значений, мы находим критические точки \(s\), установив его производную (функцию скорости) равной \(0\) и решив для \(t\text{:}\)

\begin{align*} 0 \ампер = -32t+48\\ т\ампер=48/32\\ \амп = 1,5\текст{с} \end{выравнивание*}

.

(Обратите внимание, как мы в итоге нашли, когда скорость была 0 футов/с!) Проверка первой производной показывает, что это максимум, поэтому максимальная высота объекта находится на 92+48(2)\\ \ампер = 32 \end{выравнивание*}

. Высота составляет \(32\) футов через \(2\) секунд.

Хотя мы ответили на все три вопроса (используя производные и первообразные), давайте еще раз посмотрим на них графически, используя концепции площади, которые мы исследовали ранее.

На рис. 5.2.4 показан график \(v(t)\) на осях от \(t=0\) до \(t=3\text{.}\). Опять же, легко найти \(v (0)\text{.}\) Как мы можем использовать график, чтобы найти максимальную высоту объекта?

Рисунок 5.2.4. График \(v(t)=-32t+48\text{;}\) заштрихованных областей помогает определить смещение.

Вспомните, как в нашей предыдущей работе смещение объекта (в данном случае его высота) находилось как площадь под кривой скорости, как заштриховано на рисунке. Кроме того, площадь между кривой и осью \(t\), которая находится ниже оси \(t\), считается «отрицательной» площадью. То есть он представляет объект, возвращающийся к исходному положению. Итак, чтобы найти максимальное расстояние от начальной точки — максимальную высоту — находим площадь под линией скорости, которая находится над осью \(t\), т. е. от \(t=0\) до \(t= 1.5\text{.}\) Эта область представляет собой треугольник; его площадь

\begin{выравнивание*} \text{ Площадь } \amp = \frac12\text{ База } \times \text{ Высота }\\ \amp =\frac12\times 1.5\text{s} \times 48\text{ft/s}\\ \амп = 36\текст{футов} \end{align*}

, что соответствует нашему предыдущему расчету максимальной высоты.

Наконец, чтобы найти высоту объекта в момент времени \(t=2\), мы вычисляем общую площадь со знаком под функцией скорости от \(t=0\) до \(t=2\text{.}\ ) Эта площадь со знаком равна \(s(2)\text{,}\) смещению (т.е. расстоянию со знаком) от начальной позиции в \(t=0\) до позиции в момент времени \(t=2 \text{.}\) То есть

Смещение = Площадь над осью \(t\) \(-\) Площадь под осью \(t\).

Области представляют собой треугольники, и мы находим

\begin{align*} \text{ Водоизмещение} \amp = \frac12(1.5\text{s})(48\text{ ft/s}) — \frac12(.5\text{s})(16\text{ ft/s}) \\ \амп = 32\текст{ футов}. \end{align*}

Это также соответствует нашему предыдущему расчету высоты в \(t=2\text{. }\)

Обратите внимание, что мы ответили на каждый вопрос в этом примере двумя способами. Наш первый метод состоял в том, чтобы манипулировать уравнениями, используя наше понимание первообразных и производных. Второй наш метод был геометрическим: мы отвечали на вопросы, глядя на граф и находя площади определенных областей этого графа.

Приведенный выше пример не доказывает взаимосвязь между площадью под функцией скорости и перемещением, но подразумевает, что взаимосвязь существует. Раздел 5.4 полностью установит тот факт, что площадь под функцией скорости является смещением.

Имея график функции \(y=f(x)\text{,}\), мы обнаружим, что очень полезно вычислить площадь между кривой \(y=f(x)\) и \ (х\)-ось. В связи с этим нам необходимо определить некоторые термины.

Определение 5.2.5. Определенный интеграл, общая площадь со знаком. 9б f(x)\dx, \end{уравнение*}

, где \(a\) и \(b\) — границы интегрирования.

Согласно нашему определению, определенный интеграл дает «площадь со знаком под \(f\text{. }\)». Мы обычно опускаем слово «со знаком», когда говорим об определенном интеграле, и просто говорим, что определенный интеграл дает « площадь под \(f\)» или, чаще, «площадь под кривой».

В предыдущем разделе был введен неопределенный интеграл, относящийся к первообразным. Мы определили определенный интеграл, относящийся к площадям под функцией. Они очень тесно связаны, как мы увидим, когда изучим Фундаментальную теорему исчисления в разделе 5.4. Напомним, ранее мы говорили, что символ «\(\int\)» — это «удлиненная буква S», обозначающая нахождение «суммы». В контексте определенного интеграла это обозначение имеет немного больше смысла, так как мы складываем площади под функцией \(f\text{.}\) 91f(x)\ dx\) — площадь под \(f\) на «интервале» \([1,1]\text{.}\) Это описывает отрезок, а не область; у него нет ширины. Следовательно, площадь равна 0,

.

Этот пример иллюстрирует некоторые свойства определенного интеграла, приведенные здесь.

Теорема 5.2.9. Свойства определенного интеграла.

Пусть \(f\) и \(g\) заданы на замкнутом интервале \(I\), который содержит значения \(a\text{,}\) \(b\) и \(c\text{ ,}\) и пусть \(k\) — константа. Следующее удержание: 9bf(x)\dx\)

Здесь мы даем краткое обоснование теоремы 5.2.9.

  1. Как показано в примере 5.2.6, не существует «области под кривой», когда область не имеет ширины; следовательно, этот определенный интеграл равен 0.

  2. Указывает, что общая площадь представляет собой сумму площадей субрегионов. Это легко понять, если мы допустим \(a\lt b\lt c\text{.}\) Мы можем разбить интервал \([a,c]\) на два подинтервала, \([a,b]\) и \([b,c]\text{.}\) Общая площадь над \([a,c]\) равна площади над \([a,b]\) плюс площадь над \([b, c]\text{.}\) Важно отметить, что это остается верным, даже если \(a\lt b\lt c\) неверно. Мы обсудим это в следующем пункте. 9f(x)\dx\) терм; когда это сделано, уравнения (5.2.1) и (5.2.2) эквивалентны. Вывод таков: принимая соглашение о Свойстве (3), Свойство (2) выполняется независимо от порядка \(a\text{,}\) \(b\) и \(c\text{. }\ ) Опять же, в следующем разделе мы увидим другое обоснование этого свойства.

  3. 4,5..

    Каждый из них может быть неинтуитивным. Свойство (5) утверждает, что при масштабировании функции, например, в 7 раз, площадь замкнутой области также увеличивается в 7 раз. Оба свойства (4) и (5) можно доказать с помощью геометрии. Детали не сложны, но здесь не обсуждаются. 92}\ дх. \end{уравнение*}

    Решение.

    1. Полезно набросать функцию под интегралом, как показано на рисунке 5.2.13.(a). Мы видим, что нам нужно вычислить площади двух областей, которые мы пометили \(R_1\) и \(R_2\text{.}\). Оба являются треугольниками, поэтому вычисление площади простое:

      \begin{уравнение*} R_1: \frac12(4)(8) = 16 \qquad R_2: \frac12(3)6 = 9. \end{уравнение*}

      Область \(R_1\) лежит под осью \(x\), следовательно, она считается отрицательной площадью (мы можем считать высоту треугольника равной «\(-8\)»), поэтому 92}\) Рисунок 5. 2.13. Графики из примера 5.2.12

    Пример 5.2.14. Понимание движения с заданной скоростью.

    Рассмотрим график функции скорости объекта, движущегося по прямой линии, представленный на рисунке 5.2.15, где числа в заданных областях обозначают площадь этой области. Предположим, что определенный интеграл функции скорости дает перемещение. Найдите максимальную скорость тела и его максимальное перемещение от исходного положения.

    Рисунок 5.2.15. График скорости в примере 5.2.14.

    Решение.

    Поскольку на графике указана скорость, найти максимальную скорость несложно: она равна 15 футам/с.

    В момент времени \(t=0\text{,}\) смещение равно 0; объект находится в исходном положении. В момент времени \(t=a\text{,}\) объект переместился назад на 11 футов. Между моментами времени \(t=a\) и \(t=b\text{,}\) объект перемещается вперед на 38 футов, переводя его в положение на 27 футов вперед от исходного положения. От \(t=b\) до \(t=c\) объект снова движется назад, следовательно, его максимальное перемещение составляет 27 футов от исходного положения. 9b f(x)\ dx\text{,}\), где

    \(0\le a\le b\le 10\)

Ответ.

  1. \(\displaystyle 15\)

  2. \(\displaystyle 12\)

  3. \(\displaystyle 0\)

  4. \(\displaystyle 3(b-a)\)

Группа упражнений.

В упражнениях 11–14 дан график функции \(f(x)\); числа внутри заштрихованных областей дают площадь этой области. Оцените определенные интегралы, используя эту информацию о площади. 92+5\большое )\ дх\)

Ответ.

  1. \(\displaystyle 40/3\)

  2. \(\displaystyle 26/3\)

  3. \(\displaystyle 8/3\)

  4. \(\displaystyle 38/3\)

Группа упражнений.

В упражнениях 15–16 приведен график функции скорости объекта, движущегося по прямой линии. Ответьте на вопросы, опираясь на этот график.

15.

  1. Какова максимальная скорость объекта?

  2. Каково максимальное перемещение объекта?

  3. Каково полное перемещение объекта на \([0,3]\text{?}\)

Ответ.

  1. 2 фута/с

  2. 2 фута

  3. 1,5 фута

16.

  1. Какова максимальная скорость объекта?

  2. Каково максимальное перемещение объекта?

  3. Каково полное перемещение объекта на \([0,5]\text{?}\)

Ответ.

  1. 3 фута/с

  2. 9,5 футов

  3. 9,5 футов

17.

Объект брошен прямо вверх со скоростью в футах в секунду, определяемой выражением \(v(t) = -32t+64\text{,}\), где \(t\) в секундах, с высоты 48 футов.

  1. Какова максимальная скорость объекта?

  2. Каково максимальное перемещение объекта?

  3. Когда происходит максимальное смещение?

  4. Когда объект достигнет высоты 0? (Подсказка: найдите, когда водоизмещение равно \(-48\)ft.)

Ответ.

  1. 64 фута/с

  2. 64 фута

  3. \(\displaystyle t=2\)

  4. \(t=2+\sqrt{7}\примерно 4,65\) секунд

18.

Объект брошен прямо вверх со скоростью в футах в секунду, определяемой выражением \(v(t) = -32t+96\text{,}\), где \(t\) в секундах, с высоты 64 фута.

  1. Какова начальная скорость объекта?

  2. Когда смещение объекта равно 0?

  3. Сколько времени требуется объекту, чтобы вернуться к своей первоначальной высоте?

  4. Когда объект достигнет высоты 210 футов?

Ответ.

  1. 96 футов/с

  2. 6 секунд

  3. 6 секунд

  4. Никогда; максимальная высота 208 футов. 9т/\ln 2+C\)

    30.

    \(\displaystyle \int \left(\frac{1}{x} -\csc x\cot x\right)\ dx\)

    Ответ.

    \(\ln |x| + \csc x+C\)

    Введение в интегралы: определенный интеграл

    правые аппроксимации, рассмотренные в предыдущем разделе. f ( x ) dx означает площадь области, ограниченной f , у -оси и строки x = a и x = b . Запись f ( x ) dx эквивалентна записи

    f(x k ) Δx

    на интервале [ a , b ], но это гораздо более компактный способ сделать так. Обратите также внимание на сходство между двумя выражениями. Этот должны служить ясным напоминанием о том, что определенный интеграл есть лишь предел правой и левые аппроксимации.

    В отличие от неопределенного интеграла, представляющего функцию, определенный интеграл представляет число, а просто область со знаком под кривой f . Площадь считается «подписанным», поскольку согласно методике расчета площадей по подразделения, области, расположенные ниже оси x , будут считаться отрицательными, а регионы выше будут считаться положительными. Отрицательные области нейтрализуют положительные области, а определенный интеграл представляет собой общий баланс между ними по данному интервал. Например, найти

    sin( x ) dx

    Исходя из картины рассматриваемого региона, должно быть понятно, что ответ нуль. Здесь отрицательная область точно такого же размера, как и положительная область:

    Рисунок %: График f ( x ) = sin ( x ) на интервале [- Π , Π ]

    Свойства определенного интеграла

    Определенный интеграл обладает определенными свойствами, которые должны быть интуитивно понятны, учитывая его определение как область со знаком под кривой:

    1. cf ( x ) dx = c f ( x ) dx
    2. f ( x )+ g ( x ) dx = f ( x ) dx + g ( x ) dx
    3. Если c находится в интервале [ a , b ], то
      f ( x ) дх = f ( x ) дх + f ( x ) дх

      Это означает, что мы можем разбить граф на удобные единиц и найти определенный интеграл каждого сечения, а затем добавьте результаты, чтобы найти общую подписанную область для всего региона.

      Основная теорема исчисления

      Фундаментальная теорема исчисления, или «FTC», предлагает быстрый и мощный метод вычисления определенных интегралов. В нем говорится: если F является производным от f , тогда
      ф ( х ) дх = ф ( б ) — ф ( а )

      Например,
      x 2 дх = (1) 3 — (0) 3 =

      Часто используется сокращение, означающее то же самое, что написано выше:
      х 2 дх = х 3 =

      Одна из интерпретаций FTC состоит в том, что площадь под графиком производной равна полное изменение исходной функции.

      No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *