Как находить расстояние от точки до точки: формулы, примеры, решения, формула расстояния между двумя точками

Расстояния между фигурами — Умскул Учебник

На этой странице вы узнаете

• Как найти расстояние между мухой и столбом?
• Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости?
• Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом? 

Отправляясь в любое путешествие, мы проверяем, как далеко нам придется ехать. На пробежке мы смотрим, какое расстояние преодолели. А пробег на машине? Если мы с такой легкостью считаем расстояния в нашей жизни, неужели в математике должно быть что-то сложнее? 

Расстояния между фигурами

Когда нам нужно дойти от дома до магазина, мы можем точно сказать, какое расстояние нам нужно пройти. Например, магазин находится в 200 метрах от дома, следовательно, мы и должны пройти 200 метров, чтобы купить что-то вкусненькое. 

Таким образом, мы получаем расстояние между двумя точками.  

Расстояние между точками — это длина отрезка, заключенного между ними. 

Пока мы шли в магазин, мы заметили на столбе интересное объявление о продаже цветов. Как найти расстояние от нас до этого объявления? Разумеется, пройти определенное расстояние до столба. Допустим, это будет 5 метров. 

Заметим, что мы прошли по асфальту, то есть по горизонтальной поверхности. А мы и столб стоим вертикально, то есть перпендикулярны поверхности асфальта. Обратим внимание, что при этом мы со столбом будем параллельными прямыми. 

Следовательно, мы пришли к выводу, что: 

Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними. 

Иными словами, это отрезок, который мы прошли по асфальту. 

Но как только мы собрались дойти до столба и сорвать объявление, прямо мимо наших глаз пролетела муха. Она летела строго на одной высоте, долетела до столба и села на объявление. 

Как найти в этом случае расстояние между мухой и столбом? На самом деле, муха пролетела ровно такое же расстояние, которое нам необходимо было пройти до столба.  

Поскольку муха совсем маленькая, возьмем ее за точку. И таким образом, мы получаем расстояние между точкой и прямой.

Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую. 

Как найти расстояние между мухой и столбом? Для этого достаточно найти расстояние между точкой и прямой — длину перпендикуляра, опущенного из этой точки на прямую.

Пока мы злились на муху за то, что она опередила нас и добралась до объявления первой, мимо нас прошли грузчики, которые несли вешалку под углом к асфальту и столбу. Чему тогда будет равно расстояние между вешалкой и столбом?

Мы не можем точно сказать, что 5 метров, поскольку вешалка не параллельна столбу. Чтобы его найти, достаточно провести перпендикуляр и к столбу, и к вешалке. 

Так мы нашли расстояние между скрещивающимися прямыми. Подробнее о скрещивающихся прямых можно прочесть в статье «Аксиомы стереометрии.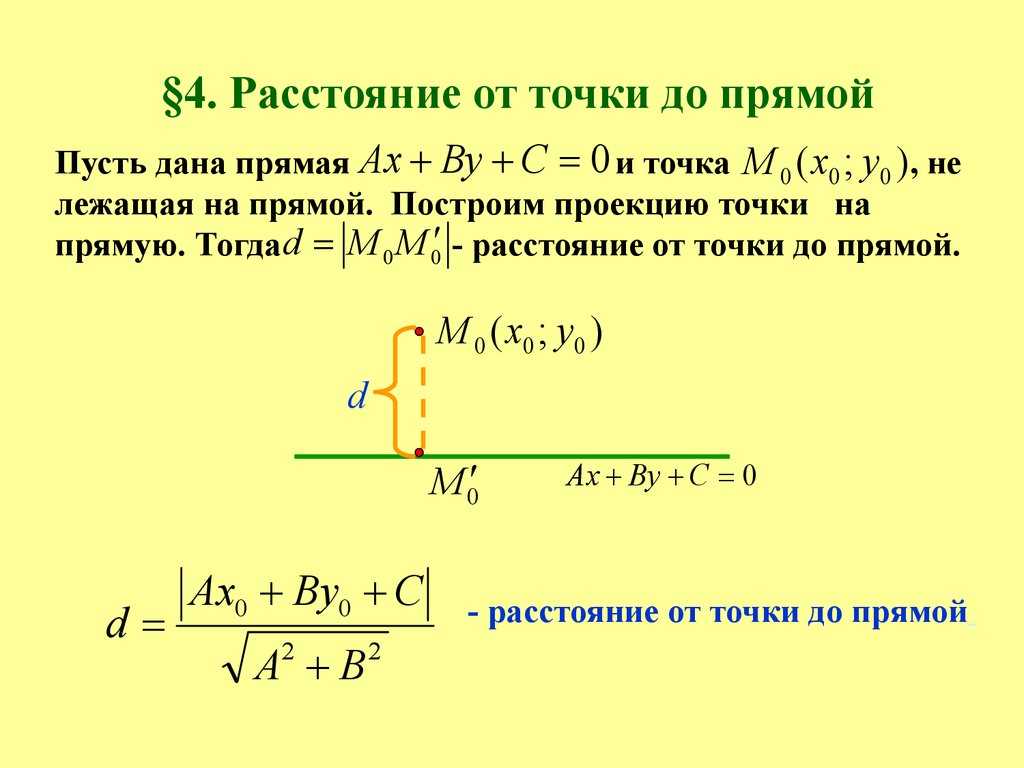 Прямые и плоскости в пространстве». 

Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра. 

Удивившись тому, как много всего может произойти только со столбом, мы все-таки дошли до магазина, купили тортик и рулетик и вернулись домой. Поставили покупки на стол и пошли готовить чай. 

В этот момент на стол запрыгнул наш кот и решил проверить, какое расстояние от тортика до пола. И для этого он скинул наш тортик со стола. 

Существует ли возможность измерить расстояние от тортика до пола, при этом не жертвовать этим самым тортиком? Представим, что пол — это плоскость, а тортик — точка. Тогда нам всего лишь нужно найти расстояние от точки до плоскости. 

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость. 

Так и есть: когда кот скинул тортик, он пролетел строго вертикально до пола. 

Наш кот посмотрел на упавший торт и тут резко заметил, что мы принесли еще и очень длинный рулетик! Теперь ему стало интересно, какое расстояние от рулетика до пола, поэтому он решил скинуть и его.  

Расстояние от рулетика до пола можно было найти и другим способом, а именно найти  расстояние от прямой до плоскости. Поскольку рулетик лежит на столе, то он параллелен полу. 

Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость. 

Заметим, что если прямая не параллельна плоскости, то рано или поздно она ее пересечет, а значит, точного расстояния между ними не будет. 

Как любопытный кот, скидывая вкусняшки со стола, нашел расстояния от точки до плоскости и от прямой до плоскости? Оказывается, наши вкусняшки пролетели строго вертикально вниз, то есть преодолели длину перпендикуляра, проведенного от них до пола! Таким образом, расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость. Расстояние между прямой, параллельной плоскости, и плоскостью — длина перпендикуляра, опущенного из любой точки этой прямой на плоскость.

Увидев, что он скинул все продукты питания, кот решил сбежать с места преступления. Но перед этим он задался вопросом, какое расстояние от плоскости столешницы до плоскости пола, чтобы рассчитать свой прыжок. 

Но и в этом ему на помощь могла прийти стереометрия. Как жаль, что кот ее не знает, поэтому все проверяет на практике. 

Теперь нам нужно найти расстояние между параллельными плоскостями. 

Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость. 

Внимание! Сложные расчеты! Как любопытному коту найти расстояние между плоскостью стола и полом?  Для этого ему также нужно найти, сколько он пролетит строго вниз. Или, иначе говоря, расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки этой плоскости на вторую плоскость.

Вот так, благодаря одной прогулке до магазина и любопытству кота, мы рассмотрели, как находятся расстояния между двумя фигурами.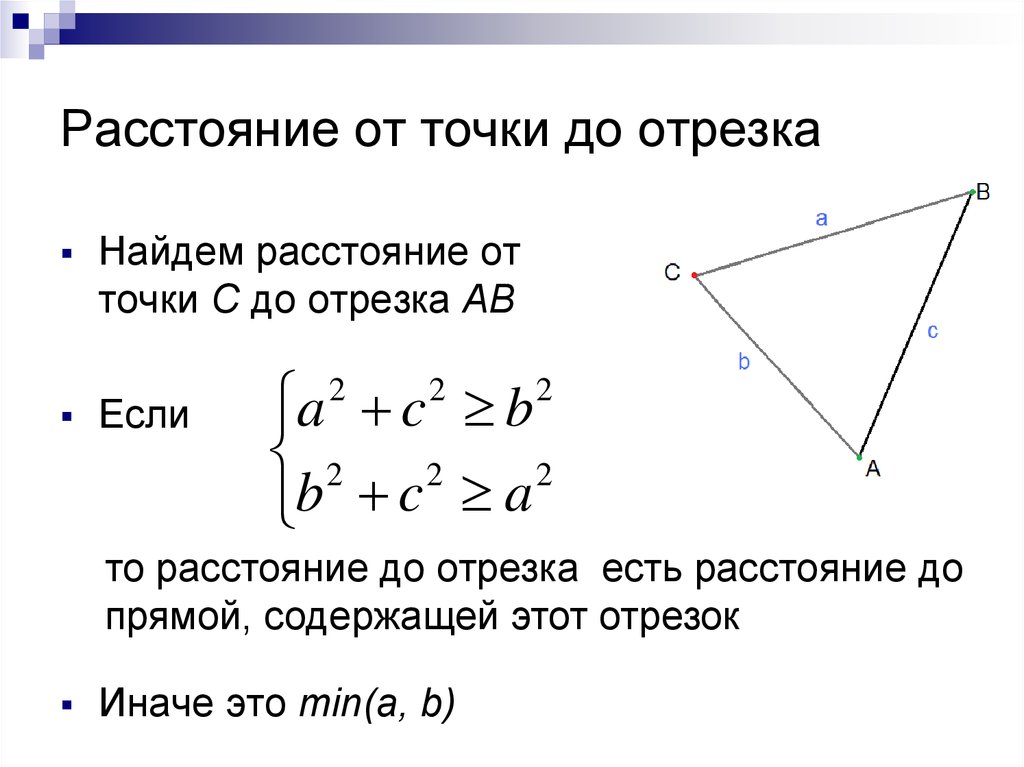 Ничего сложного, верно? 

При решении задач, конечно, в условии не встретишь любопытного кота или муху на объявлении, но кто мешает включать нам фантазию и представить условие задачи как жизненные ситуации.

Фактчек

• Расстояние между точками — это длина отрезка между ними. Расстояние между точкой и прямой — это длина перпендикуляра, опущенного из этой точки на прямую. 
• Расстояние между параллельными прямыми — это длина перпендикуляра, проведенного между ними.  Расстояние между скрещивающимися прямыми — длина их общего перпендикуляра. 
• Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на плоскость. 
• Расстояние между прямой, параллельной плоскости, и плоскостью — это длина перпендикуляра, опущенного из любой точки этой прямой на плоскость. 
• Расстояние между параллельными плоскостями — это длина перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.  

Проверь себя

Задание 1. 
Как найти расстояние между точкой и прямой?

1. Найти длину любой линии от этой точки до прямой.
2. Найти длину перпендикуляра, опущенного из этой точки на прямую.
3. Невозможно найти расстояние между точкой и прямой.
4. Ни один из вышеперечисленных вариантов. 

Задание 2. 
Как найти расстояние между скрещивающимися прямыми?

1. Найти длину произвольной прямой между ними.
2. Найти длину прямой, перпендикулярной одной из прямых и не перпендикулярной второй прямой.
3. Найти длину их общего перпендикуляра.
4. Невозможно найти расстояние между скрещивающимися прямыми. 

Задание 3. 
Как найти расстояние от точки до плоскости?

1. Найти длину перпендикуляра, опущенного из этой точки на плоскость.
2. Найти длину произвольной линии, проведенной из точки к плоскости.
3. Найти расстояние от точки до любой прямой, лежащей в плоскости.
4. Невозможно найти расстояние между точкой и плоскостью.

Задание 4. 
Как найти расстояние от прямой до плоскости?

1. Найти длину произвольной линии, проведенной из любой точки этой прямой до плоскости.
2. Найти длину отрезка, соединяющего любую точку на прямой и любую прямую в плоскости.
3. Найти длину перпендикуляра, опущенного из любой точки этой прямой на плоскость.
4. Невозможно найти расстояние между прямой и плоскостью. 

Задание 5. 
Как найти расстояние между параллельными плоскостями?

1. Невозможно найти расстояние между параллельными плоскостями.
2. Найти длину перпендикуляра, опущенного из любой точки одной плоскости на вторую плоскость.
3. Найти длину отрезка, соединяющего точку одной плоскости с произвольной точкой на второй плоскости.
4. Найти длину отрезка, соединяющего две произвольные прямые в плоскостях. 

Ответы: 1. — 2 2. — 3 3. — 1 4. — 3 5. — 2

Как найти расстояние от точки до прямой: формула, пример задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение расстояния от точки до прямой

В данной публикации мы рассмотрим, что такое расстояние от точки до прямой, и по какой формуле оно считается. Также разберем пример решения задачи по этой теме.

• Расчет расстояния от точки до прямой
• Пример задачи

Расчет расстояния от точки до прямой

Чтобы найти расстояние от произвольной точки для прямой, нужно от нее опустить перпендикуляр на эту прямую.

Длина перпендикуляра (d) и является искомым расстоянием.

Формула для расчета

Допустим, есть прямая, заданная уравнением Ax + By + C = 0. Расстояние от нее до точки L с координатами (L_x, L_y) считается следующим образом:

Пример задачи

Дана прямая 2x + 6y – 5 = 0. Найдем расстояние от нее до точки M (1, -3).

Решение:

Воспользуемся формулой выше, подставив в нее известные нам по условиям задачи данные:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

геометрия — Нахождение точки вдоль линии на определенном расстоянии от другой точки!

спросил 10 лет, 6 месяцев назад

Изменено 1 месяц назад

Просмотрено 194k раз

$\begingroup$

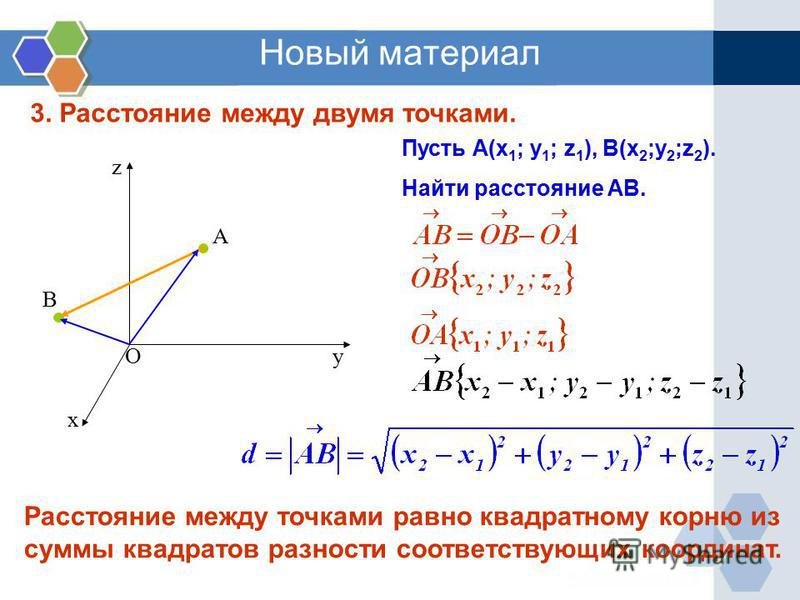
Допустим, у вас есть две точки: $(x_0, y_0)$ и $(x_1, y_1)$.

Градиент линии между ними:

$$m = (y_1 — y_0)/(x_1 — x_0)$$

Следовательно, уравнение линии между ними:

$$y = m (x — x_0) + y_0$$

Теперь, поскольку мне нужна еще одна точка на этой линии, но на расстоянии $d$ от $(x_0, y_0)$, я получу уравнение окружности с радиусом $d $ с центром $(x_0, y_0)$, затем найдите точку пересечения между уравнением окружности и уравнением прямой.

Уравнение окружности с радиусом $d$: 92}$$

Однако после проверки этого уравнения оказалось, что оно не работает! Есть ли очевидная ошибка, которую я допустил в своей теоретической части, или я просто распушил свои расчеты?

• геометрия

$\endgroup$

7

$\begingroup$

Поясню ответ простым языком.

Начальная точка — $(x_0, y_0)$

92}$

Пусть отношение расстояний, $t=d_t/d$

Тогда точка $(x_t, y_t) =(((1-t)x_0+tx_1), ((1-t)y_0+ ty_1))$

При $0

Когда $t<0$, точка находится вне линии рядом с $(x_0,y_0)$.

Когда $t>1$, точка находится вне линии рядом с $(x_1,y_1)$.

$\endgroup$

9

$\begingroup$

Другой способ с использованием векторов:

Пусть $\mathbf v = (x_1,y_1)-(x_0,y_0)$. Нормализуйте это к $\mathbf u = \frac{\mathbf v}{||\mathbf v||}$.

Точка вдоль вашей линии на расстоянии $d$ от $(x_0,y_0)$ тогда равна $(x_0,y_0)+d\mathbf u$, если вы хотите, чтобы она находилась в направлении $(x_1,y_1) $ или $(x_0,y_0)-d\mathbf u$, если вы хотите в обратном направлении. Одним из преимуществ выполнения вычислений таким образом является то, что вы не столкнетесь с проблемой деления на ноль в случае, когда $x_0 = x_1$.

$\endgroup$

11

$\begingroup$

Вы можете очень легко найти его с помощью тригонометрии!

Допустим, Xa и Xb — две точки вашей линии, а D — расстояние между ними. И вы ищете Xc , который находится на расстоянии D2 от Xa (как показано на диаграмме ниже):

You can easily find D :

The formulas that you can find Xa , Xb , Xc , D and D2 are:

But SIN a-b and SIN a-c имеют один и тот же угол, поэтому они равны:

Зная расстояние ( D2 ) между Xa и Xc , которое вы ищете, вы можете легко решить следующее :

В заключение, решив формулу для D и последнюю, вы сделали. (Вам также нужен один для Y , просто замените в последнем X на Y )

Надеюсь, это поможет!!

$\endgroup$

5

$\begingroup$

В прямоугольных системах координат проще всего использовать векторную формулу
P = D (B — A) + A
, где
A является отправной точкой (x ₀ , Y ₀ ) 5 из
из . из из . из из . конечная точка (x ₁ , y ₁ )
d — расстояние от начальной точки A до желаемой коллинеарной точки
P — желаемая коллинеарная точка 5 $\endgroup$

2

$\begingroup$

Думаю, ваш метод работает. Вот код Python для теста, а вывод теста связан ниже,

 import numpy as np
импортировать matplotlib.pyplot как plt
защита f(x, m, c):
    у = м * х + с
    вернуть у
защита X(x0,d,m):
    x1 = x0 + (d/np.sqrt(1+m**2))
    x2 = x0 - (d/np.sqrt(1+m**2))
    вернуть np.массив ([x1, x2])
х = np.arange (1,5,0,5)
м = 1
с = 0,5
plt.plot(x, f(x, m, c), "-")
х0 = 3
d = np.массив ([0,25, 0,5, 0,75, 1])
Х = Х (х0, д, м)
печать (тип (X))
plt.plot(X, f(X,m,c), "о")
plt.show()
 

Вывод приведенного выше кода: [1] https://i.stack.imgur.com/n0XJH. png

$\endgroup$

$\begingroup$

Я думаю, вам нужно проверить $x_0 > x_1$, когда вы пытаетесь вычислить $x$ (последнее уравнение в вашем расчете), тогда вы определите, что это будет $(+)$ или $(-)$ в вашем уравнении.

$\endgroup$

1

$\begingroup$ 92},$$, то довольно легко показать, что

$$|\rho(t) — \rho(s)| = D|t-s|$$

Итак, если вы хотите найти точки на расстоянии $d$ от $(x_0,y_0)$, вам нужно решить $$d = |\rho(t) — \ ро(0)| = D|t-0|$$

Вы получаете $ t = \pm \dfrac dD$. Следовательно, точки равны

$$\rho\left( \pm \dfrac dD \right) = \left\{ \begin{массив}{с} \left( 1-\dfrac dD \right)(x_0,y_0) + \dfrac dD (x_1,y_1) \\ \left( 1+\dfrac dD \right)(x_0,y_0) — \dfrac dD (x_1,y_1) \end{массив} \right. $$

$\endgroup$

Измерение расстояния на карте

Инструмент измерения расстояния — это простой способ определения расстояния между двумя или более точками на карте.

Как пользоваться инструментом «Измерить расстояние»

Просто нажмите один раз на одну точку, затем нажмите еще раз на вторую точку. Расстояние должно отображаться. Вы можете щелкнуть более двух точек, чтобы построить непрерывный маршрут.

Используйте переключатель миль/км/морских миль/ярдов для измерения расстояний в км, милях или морских милях. Опция Autopan будет перемещать карту по мере того, как вы нажимаете на точки.

Текстовое поле «Поиск местоположения» позволяет быстро добраться до нужной области, не тратя время на масштабирование и панорамирование, чтобы найти ее. Например, если вы хотите найти город Рим в Италии, введите «Рим, Италия» и нажмите «Поиск». Затем карта отправится прямо в Рим. Обратите внимание на формат «[город][запятая][пробел][округ]»

Маркеры-переключатели будут отображать или скрывать маркеры, если они мешают

Очистить последнее удалит последнюю точку с карты

Увеличить до нужного размера будет масштабировать и перемещать карту, чтобы получить наилучшее соответствие всем вашим точкам с максимально возможным увеличением

«Очистить карту» — это кнопка сброса, которая очистит все точки и позволит вам снова начать измерение расстояния. position

Вы также можете отрегулировать высоту карты, чтобы сделать ее большой, средней или маленькой по размеру

Вы можете удалить точку, нажав на узел

Будущие идеи и улучшения

• Автоматическое изменение маршрута для оптимального расстояния ( задача коммивояжера)
• Имеют другие скорости, такие как оптоволоконный кабель (~ 0,6 с) и число Маха
• Возможность добавить заголовок к маркеру, который затем появляется при наведении указателя мыши и экспорте данных
• Добавить байдарку в список видов транспорта

История версий

• 20 апреля 2022 г. — Улучшено поведение при нажатии кнопки «Маленький/Средний/Большой»
• 21 февраля 2021 г. — выбранные единицы измерения расстояния сохраняются и вызываются при следующем посещении
.
• 6 июля 2020 г. — Новая опция для экспорта ссылки на маршрут. Находится в разделе «Параметры экспорта» 9.0040
• 2 июня 2019 г. — исправлена ​​ошибка с неработающим выходом счетчиков
• 29 мая 2019 г.  – Реализованы карты листовок
• 20 мая 2019 г. — исправлена ​​ошибка в браузере IE
.
• 9 мая 2019 г. — исправлена ​​проблема, из-за которой расстояние не сбрасывалось до нуля при нажатии кнопки «Очистить карту»
• 14 сентября 2017 г. — расстояние теперь отображается на карте в полноэкранном режиме
• 4 августа 2017 г. — Обновлен селектор юнитов. Добавлены единицы футов
• 24 июля 2017 г. — Полноэкранный режим перемещен на карту. Теперь находится в правом верхнем углу
• 4 июля 2017 г. — Исправлена ​​проблема с экспортом CSV и XLSX
• 29 января 2017 г. — Возможность отображения карты высот и экспорта файла CSV с данными высот по маршруту
.
• 25 ноября 2016 г. — экспорт KML для отображения контактов на каждом узле маршрута
• 23 ноября 2016 г. — Добавлена ​​опция загрузки KML, CSV и XLSX
.
• 19 июля 2016 г. — Исправлены ошибки, связанные с изменением вида транспорта и расчетного времени в пути при изменении единиц измерения
• 5 июля 2016 г. — Добавлены метры в качестве единицы измерения расстояния
• 25 июня 2016 г. — Единицы скорости движения меняются в зависимости от единиц расстояния
• 20 июня 2016 г. — исправлена ​​ошибка, из-за которой при измерении количества дней в два раза отображалось фактическое значение
.
• 24 марта 2016 г. — точки маршрута теперь можно добавлять в середине пути. Точки также можно удалить, щелкнув правой кнопкой мыши
.
• 25 января 2016 г. — скорость теперь можно вводить вручную
• 28 декабря 2015 г. — добавлена ​​возможность переключения между минутами, часами и днями для оценки времени в пути
• 24 июня 2014 г. — добавлена ​​опция «Привязка к дорогам»
• 24 марта 2014 г. — добавлена ​​опция «Переместиться к моему местоположению»
• 11 января 2012 г. — реализован API Google Maps V3. Добавлен полноэкранный режим
• 12 октября 2010 г. — Маркеры теперь показывают свою широту и долготу, когда вы наводите на них курсор
• 15 октября 2009 г.

  No related posts.