Введение понятия «Угол. Построение углов»
Цель: создать условия для формирования у детей первичного представления “Угол” и научить их строить углы с помощью линейки.
Для достижения цели урока были поставлены следующие задачи:
- Совершенствовать навыки использования чертежных инструментов – линейки, карандаша;
- Способствовать развитию мышления учащихся с помощью проблемных ситуаций и использование заданий, формирующих параметры мыслительных операций: сравнение, анализ, синтез, обобщение, абстрагирование;
- Создать положительную психологическую обстановку в классе через использование игровых и информационных технологий. Посредством работы в парах воспитывать умение общаться друг с другом.
Оборудование: Геометрические фигуры:
квадраты, прямоугольники, треугольники, круги,
овалы, углы, макет угла, презентация, линейки,
карандаши.
Тип урока: Урок изучения и первичного закрепления новых знаний.
Ведущие технологии: компьютерные и игровые.
| 1. | Знакомство. Здравствуйте ребята. Сегодня на уроке моя помощница из мультфильма “Смешарики” будет помогать вести урок математики. Давайте посмотрим, что у вас лежит на парте (карандаши, линейки, фигуры, листочки). А сейчас поможем назвать хором правильно геометрические фигуры, с которыми вы знакомились на уроках математики. Наука, где изучают фигуры, работают с чертёжными инструментами называется – геометрия. Геометрия – одна из древнейших наук. |
|
| 2. | Наша героиня знает, что вы любите играть
и она приготовила вам Игру, которая называется
“Расшифруйте слово”. Если мы правильно даём
ответ на решение примера, то выходит буква Если мы правильно даём
ответ на решение примера, то выходит букваПрочитаем все вместе. (Угол) Итак, сегодня на уроке мы познакомимся с новой геометрической фигурой и научимся её строить. — Посмотрите внимательно вокруг и назовите предметы, у которых есть углы. (Доска, тетрадь, парта, окно и т.д.). |
|
| 3. | А сейчас предлагаем вам поработать в
парах. На парте у вас лежат геометрические фигуры
разделите их на группы. Значит, углы у нас встречаются и на известных нам геометрических фигурах. Посмотрите, как Нюша разбила фигуры на части (вправо, влево). |
|
| 4. | Перед вами лежит лист. Надо изобразить
отгадку на листе посередине. Надо изобразить
отгадку на листе посередине.
С помощью каких геометрических фигур изобразим солнышко?. Каким цветом? Давайте нарисуем его небольшим, так как знаем из учебников окружающий мир, что солнце это звезда, но не самая большая, и не обладает большим теплом, как другие. А что вы ещё знаете про солнышко? Нарисовали. Покажите своё солнышко друг другу, улыбнитесь ему. Помашите им. А сколько лучей у вашего солнышка? Посчитайте. Сколько лучей можно провести из одной точки-солнышка? (Много, множество) Молодцы. Действительно, из одной точки мы можем
провести любое количество лучей. Посмотрите, какое солнышко нарисовала Нюша. Дайте определение. Что такое луч? (Прямая линия, которая имеет начало, но не имеет конца) Показать модель. |
|
| 5. |
|
А, сейчас мы будем работать на
листочках. Для работы нам понадобится линейка и
карандаш цветной. У вас на листочке в клеточке
поместили точку. С помощью линейки и карандаша
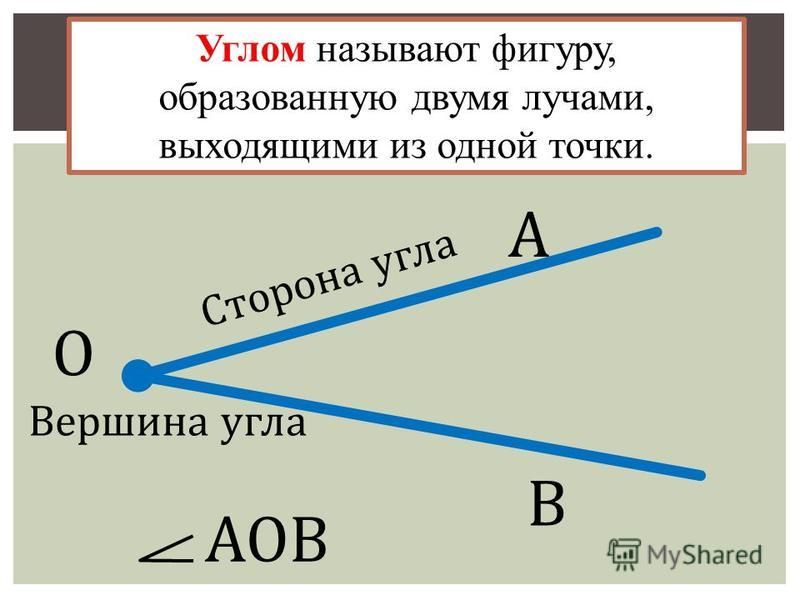
проведите аккуратно, не спеша от точки 2 луча. Какая у вас получилась фигура? Угол. Да, ребята мы с вами построили угол. Давайте посмотрим ваши углы. (Показать у доски). Что можно сказать про эти углы? Они все разные. Одни больше, другие меньше. Значит, углы можно сравнивать по величине. Дайте определение. Фигура, которая состоит из точки и двух лучей, выходящих из этой точки, называют углом. Физкультминутка. Вышли мышки как-то раз…Ребята, вы любите кататься с горки? И наши девочки любит. Сели подружки в санки и покатилась с горки. Катятся да и приговаривают:
Как называются лучи выходящие из точки? Стороны. Дайте определение и покажите стороны на рисунке. Лучи, образующие угол называются сторонами. |
| 6. | А сейчас самостоятельно попробуем
начертить угол. С чего начнём?. Где будем ставить
точку?. Показать угол учителю. Где будем ставить
точку?. Показать угол учителю.(Рассмотреть углы). |
|
| 7. | Кто умеет определять время? Посмотрим,
как 2 луча образуют угол на часах. Проговорим
углы. Постройте понравившийся вам угол. Порядок
построения вспомним. Начертите понравившийся
угол. А для чего мы строим и изучаем углы? Где они нам пригодятся? |
|
| 8.. | Как же различать такое количество
углов между собой? (Нужно дать углам имена) Каждый
угол так же как отрезок (показать рисунок)
имеет своё название, имя. Отрезок имеет имя из 2
букв, а сколько букв может содержать угол. Вспомним буквы, которые мы можем использовать из латинского алфавита? (А,О,М,К,Д Т,Е). Запишите название начерченного вами в тетради угла. |
|
| 9. | Как называется фигура, которая
состоит из точки и двух лучей выходящих из неё? (Угол). Сколько сторон имеет угол? (Две) Урок закончен. Примите улыбки от наших героинь. |
Приложение 1
Приложение 2
Краевой угол смачивания: понятие, методы измерения
Краевым углом смачивания называется угол между твердой поверхностью и каплей жидкости в точке контакта трех фаз – твердой, жидкой и газообразной.
Величина угла смачивания показывает степень межмолекулярного взаимодействия частиц жидкости и поверхности твердого тела.
Смачиванием называется такое взаимодействие твердого тела и жидкости, при котором последняя растекается по поверхности. Площадь контакта капли и тела при смачивании максимальна.
Это происходит из-за неравенства сил адгезии и когезии.
Адгезия действует на сцепление молекул разнородных материалов: жидкого и твердого. Она направлена противоположно когезии, которая действует на сцепление молекул внутри капли жидкости.
Когда адгезия превышает когезию, происходит растяжение капли по поверхности твердого тела. При этом угол смачивания оказывается острым.
Если угол равен или приближен к 0, то говорят о полном смачивании поверхности и ее супергидрофильности.
Менискообразные капли, соответствующие углу смачивания около 60 градусов, образуются на гидрофильных поверхностях. Такие капли формируются при попадании воды на стекло, ртути на цинковую поверхность.
Если когезионное взаимодействие молекул внутри капли жидкости превышает силы адгезии, то капля стремится приобрести шарообразную форму, а площадь ее контакта с твердым телом уменьшается.
Поверхности, при попадании на которые жидкости приобретают полукруглую форму, называются гидрофобными. Угол смачивания в таком случае равен или превышает 90 градусов.
На сверхгидрофобных поверхностях жидкость приобретает форму шара, краевой угол смачивания стремится к 180 градусам. В природе таких явлений не наблюдается.
Термины гидрофильность и гидрофобность применяются в случаях взаимодействия твердых поверхностей и воды. Смачиваемость или несмачиваемость другими жидкостями называются лиофильностью и лиофобностью.
Один из самых простых и распространенных способов измерения краевого узла смачивания – фотофиксация.
Капля воды или другой жидкости наносится на горизонтальную поверхность, после чего проводится фотосъемка.
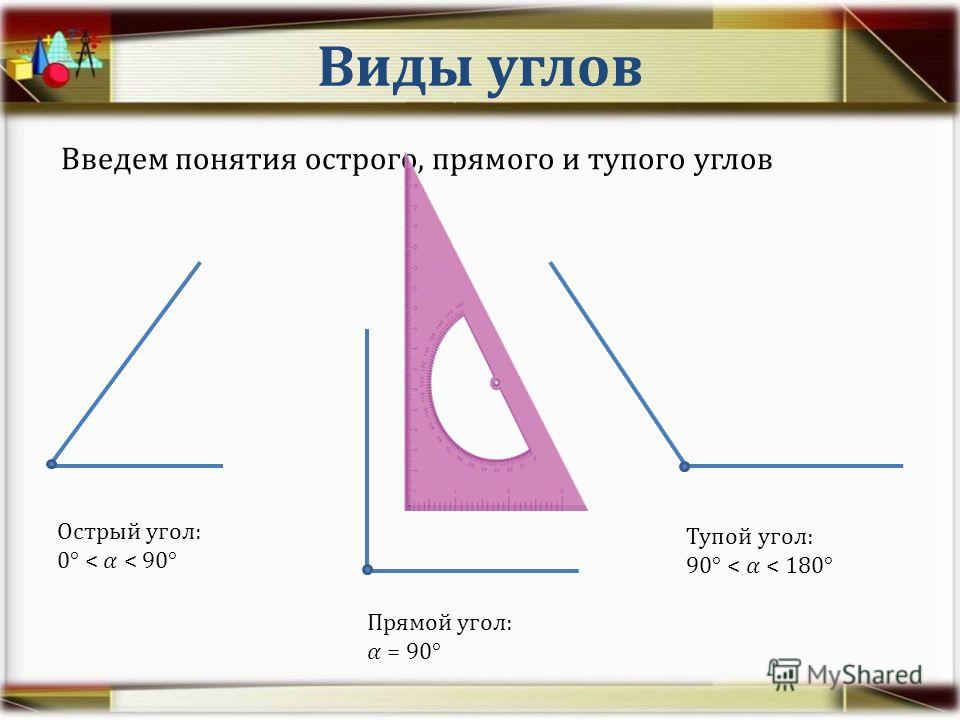 Угол определяют по полученному изображению.
Угол определяют по полученному изображению.
Данный способ измерения также называют методом «сидячей капли».
Для более профессионального и точного измерения угла смачивания используются специальные приборы.
Они состоят из нескольких камер, регистрирующих каплю с разных ракурсов, дозирующих систем, подающих жидкость, программного обеспечения для автоматического определения не только краевого угла смачивания, в том числе под давлением, но и расчета свободной энергии поверхности, поверхностного и межфазного натяжения.
Существуют устройства с измерением угла смачивания методом отраженного света. Они позволяют измерить краевой угол смачивания на поверхности со сложным рельефом, не разрушая ее.
Наблюдение за каплей в этом случае происходит сверху. Краевой угол рассчитывается на основании расстояния между двумя точками отраженного света с кривой поверхности капли. Фиксация осуществляется в формате видео. Камера передает отраженный свет на компьютер, где осуществляется расчет.
Фиксация осуществляется в формате видео. Камера передает отраженный свет на компьютер, где осуществляется расчет.
Такие приборы позволяют также выявить неоднородность смачивания за счет наблюдения сверху.
Измерение угла смачивания необходимо для создания и модернизации гидрофобных покрытий. Сегодня они находят очень широкое применение.
Гидрофобное покрытие – это материал, который наносится на поверхности для обеспечения их водонепроницаемости и несмачиваемости.
Они защищают поверхности от разрушающего воздействия влаги и намокания.
В быту такие материалы применяются на стеклах и частях корпусов автомобилей, обуви, тканях, экранах гаджетов для обеспечения стекания капель воды без удерживания на поверхности.
Более широкое использование они получили в промышленности.
При строительстве конструкций гидрофобные пропитки позволяют предотвратить разрушение пористых материалов под воздействием влаги и увеличить надежность и срок их эксплуатации.
На деталях оборудования они выполняют ряд важных функций: защита от коррозии, обледенения, увеличение срока службы.
Например, для узлов промышленного оборудования разработано гидрофобное покрытие MODENGY 1009.
В его состав включен политетрафторэтилен. Он обладает низкой адгезией к большинству материалов. Данное вещество также обеспечивает низкий коэффициент трения, благодаря чему сфера применения покрытия очень широка.
Например, покрытие MODENGY 1009 наносится на механизмы оборудования, работающего при отрицательных температурах. За счет предотвращения задерживания конденсата материал защищает от примерзания и обеспечивает штатное срабатывание устройств.
Также покрытие эффективно работает на механизмах, эксплуатируемых в агрессивных средах, таких как морской климат. Оно защищает обработанные поверхности от воздействия соляного тумана и предотвращает оседание капель соленой воды. Благодаря этому обеспечивается длительная защита от коррозионного разрушения.
Благодаря этому обеспечивается длительная защита от коррозионного разрушения.
Свойства гидрофобных покрытий полезны на производствах, оборудование которых работает с расплавленными полимерными материалами. Это станки по упаковке изделий в пленку, термоформовочные аппараты, экструзионные линии, форсунки для подачи расплавленного пластика, формообразующая оснастка.
Применение покрытия позволяет предотвратить прилипание и нагар разогретых полимеров, благодаря чему повышаются срок службы оборудования и качество продукции, ускоряется процесс производства.
Возврат к списку
Определение:Угол — ProofWiki
Содержание
- 1 Определение
- 1.1 Прямолинейный
- 1.2 Субстенд
- 1.3 Смежный
- 1.4 Защитная оболочка
- 1,5 Вершина
- 2 Измерение
- 2.1 Степень
- 2,2 минуты
- 2,3 секунды
- 2,4 Радиан
- 3 типа угла
- 3.
 1 Нулевой угол
1 Нулевой угол - 3.2 Острый угол
- 3.3 Прямоугольный
- 3.4 Тупой угол
- 3,5 Прямоугольный
- 3.6 Угол отражения
- 3,7 Полный угол
- 3.
- 4 Направленные и ненаправленные углы
- 5 См. также
- 6 источников
Определение
Даны две пересекающиеся прямые или отрезки, величина поворота вокруг пересечения, необходимая для приведения одного в соответствие с другим, называется углом между ними.
По словам Евклида:
- Плоский угол — это наклон друг к другу двух прямых на плоскости, которые пересекаются и не лежат на одной прямой.
( Элементы : Книга $\text{I}$: Определение $8$)
Прямолинейный
По словам Евклида:
- А когда линии, содержащие угол, прямые, угол называется прямолинейным .
( Элементы : Книга $\text{I}$: Определение $9$)
Таким образом, проводится различие между прямыми и изогнутыми углами.
В большинстве случаев тот факт, что углы прямолинейны, считается само собой разумеющимся.
Subtend
Пусть $AB$ — отрезок, а $C$ — точка:
Говорят, что отрезок $AB$ стягивает угол $\угол ACB$.
Смежные
Два угла смежные , если они имеют общую пересекающуюся линию:
Сдерживание
Говорят, что две линии, пересечение которых образует угол, содержат этот угол.
Вершина
Точка, в которой встречаются линии, содержащие угол, называется вершиной этого угла.
Обычные единицы измерения угла следующие:
Градус
градус (дуги) — это измерение плоских углов, обозначаемое $\градусами$.
| \(\дс\) | \(\) | \(\дс 1\) | степень | |||||||||||
| \(\дс\) | \(=\) | \(\дс 60\) | минуты | |||||||||||
| \(\дс\) | \(=\) | \(\ds 60 \умножить на 60 = 3600\) | секунды | |||||||||||
| \(\дс\) | \(=\) | \(\ds \dfrac 1 {360}\) | полный угол (по определению) |
Минута
минута (угловой) является измерением плоских углов, обозначенных $’$.
| \(\дс\) | \(\) | \(\дс 1\) | минута | |||||||||||
| \(\дс\) | \(=\) | \(\дс 60\) | секунды | |||||||||||
| \(\дс\) | \(=\) | \(\ds\dfrac 1 {60}\) | градуса дуги (по определению) |
Секунда
секунда (дуги) является измерением плоских углов, обозначенных символом $»$.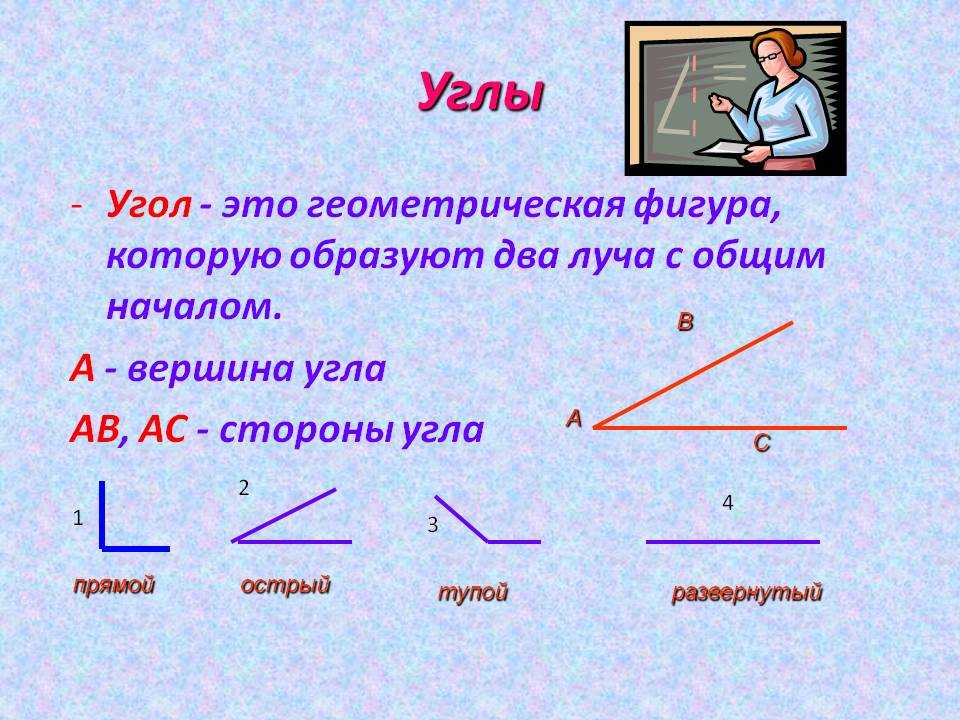
| \(\дс\) | \(\) | \(\дс 1\) | второй | |||||||||||
| \(\дс\) | \(=\) | \(\ds\dfrac 1 {60}\) | минуты дуги (по определению) | |||||||||||
| \(\дс\) | \(=\) | \(\ds \dfrac 1 {60 \times 60} = \dfrac 1 {3600}\) | градуса дуги |
Радиан
радиан — это мера плоских углов, обозначаемая либо словом $\radians$, либо без какой-либо единицы измерения.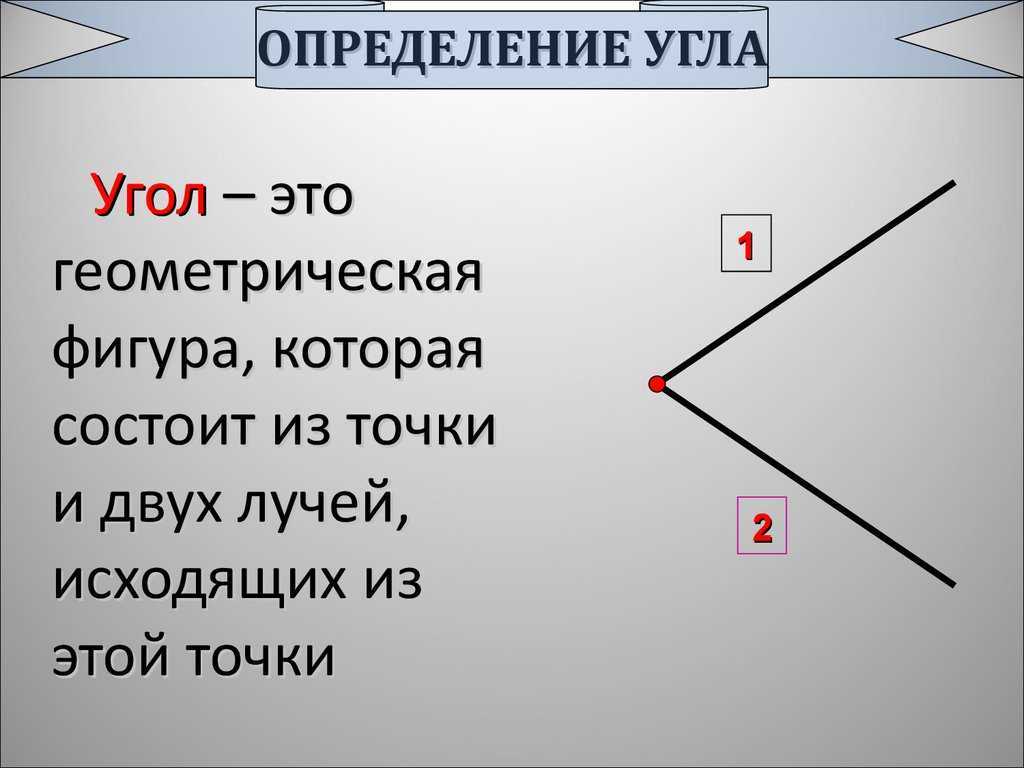
Радианы — это чистые числа, поскольку они являются отношением длин. Добавление $\radians$ просто для пояснения.
$1 \радианы$ — это угол, образуемый в центре окружности дугой, длина которой равна радиусу:
Уголки можно разделить на категории:
Нулевой угол
Нулевой угол — это угол, мера которого равна $0$ независимо от единицы измерения.
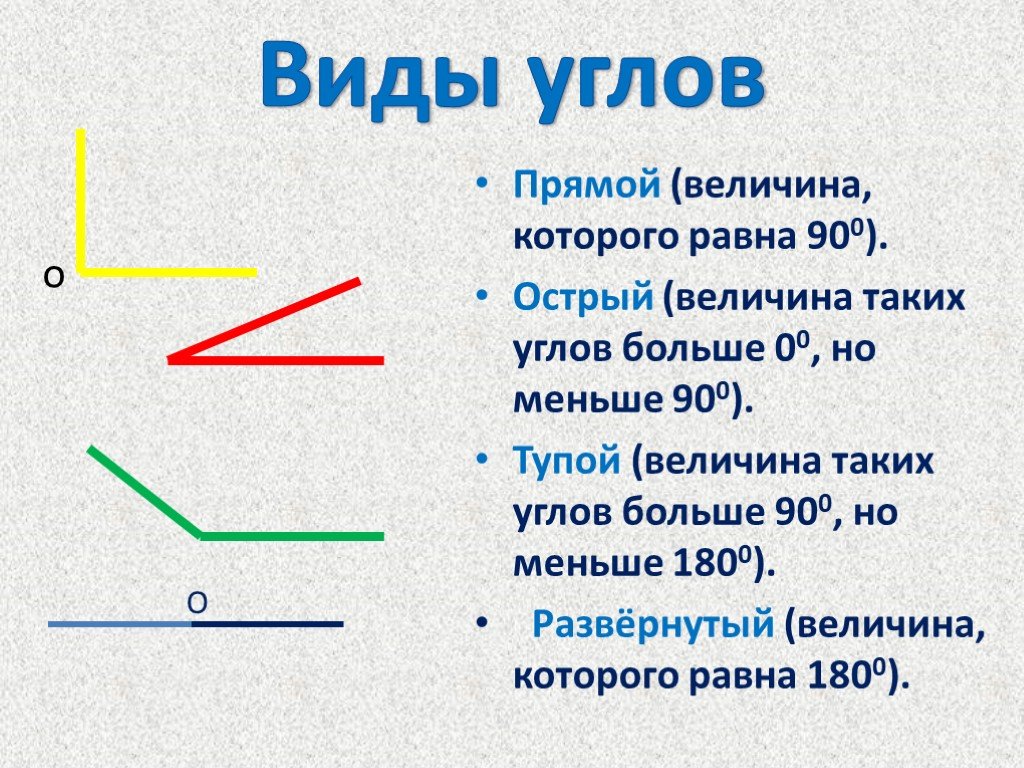
Острый угол
Острый угол — это угол, величина которого находится между прямым и нулевым углами.
Прямой угол
A Прямой угол — это угол, равный половине прямого угла.
Тупой угол
Тупой угол — это угол, величина которого находится между прямым и прямым углами.
Прямой угол
Прямой угол определяется как угол, образованный двумя частями прямой линии от точки на этой линии.
Угол рефлекса
A Угол рефлекса — это угол, который имеет меру между прямым углом и полным углом.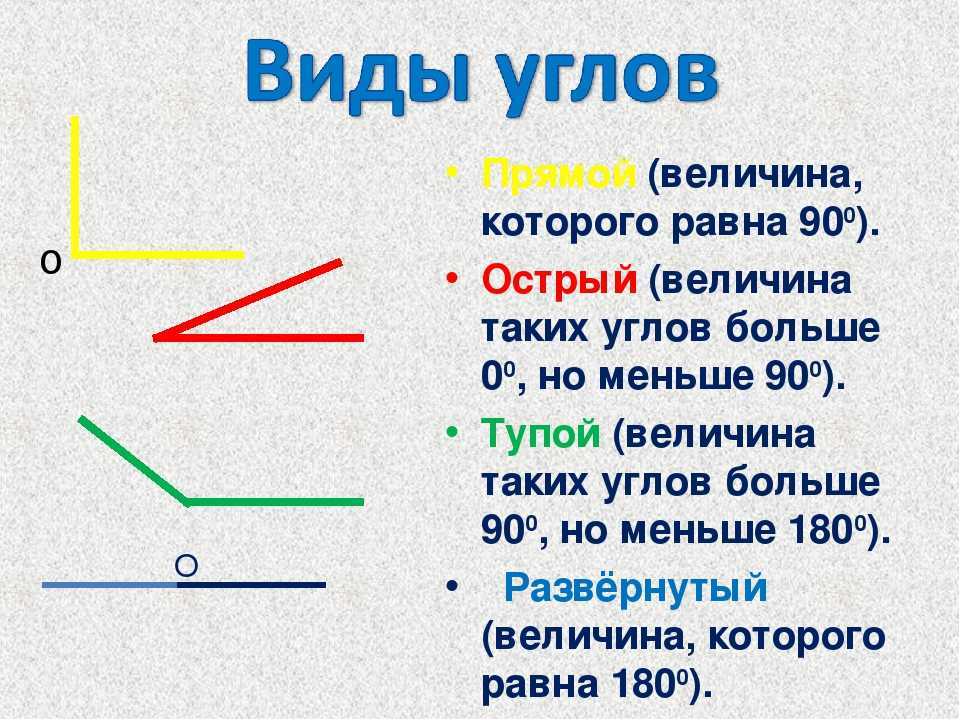
Полный угол
Полный угол — это угол, эквивалентный одному полному обороту.
Можно рассматривать углы вне диапазона $\closedint {0 \степени} {360 \градусов}$, то есть $\closedint 0 {2 \pi}$.
Однако в геометрическом контексте обычно предпочтительнее преобразовывать их в углы внутри этого диапазона, добавляя или вычитая кратные значения полного угла.
Самое основное определение угла — это ненаправленный угол на интервале $\closedint {0 \степеней} {180 \степеней}$ или $\closedint 0 \pi$.
Этого определения часто бывает недостаточно, например, для внешних углов многоугольника.
Таким образом, углы чаще всего определяются одним из двух способов:
- $(1): \quad$ Ненаправленные углы на отрезке $\closedint {0 \степеней} {360 \степеней}$ или $\closedint 0 {2 \pi}$.
- $(2): \quad$ Направленные углы с положительным направлением против часовой стрелки от данной линии (или, если линия не указана, от оси $x$).

- Это определение чаще встречается в прикладной математике, например, в геодезии, навигации или, говоря более просто, при вращении на 720 градусов в скейтборде, лыжах и т. д.
См. также
- Определение: Solid Angle
- Результаты по углам можно найти здесь .
Источники
- 1947: Уильям Х. МакКри: Аналитическая геометрия трех измерений (2-е изд.) … (предыдущее) … (следующее): Глава $\text {I}$: Система координат: Направления: $\S 1$. Введение: Метрическая геометрия
- 2014: Кристофер Клэпэм и Джеймс Николсон: Краткий Оксфордский математический словарь (5-е изд.) … (предыдущий) … (следующий): Ввод: угол (между строками в пространстве)
геометрия — Строгое определение понятия угла для старшеклассников
Во многих учебниках по геометрии для старших классов угол определяется просто как
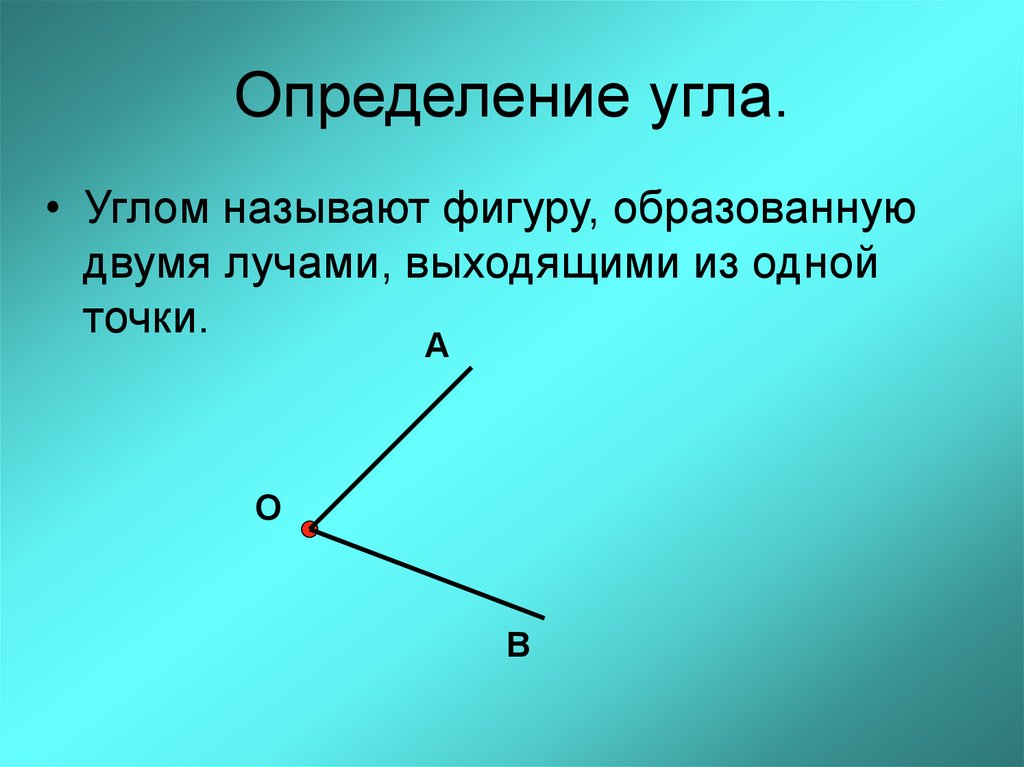
объединение двух лучей с общим концом
Преимуществом этого определения является его простота. Среди его недостатков:
Среди его недостатков:
- Он плохо улавливает идею «направления»: то есть невозможно отличить вращение по часовой стрелке от вращения против часовой стрелки.
- Это более или менее вынуждает вас определять «угловую меру» таким образом, чтобы она была ограничена между $0°$ и $180°$ (или между $0$ и $\pi$ радиан).
Однако второе возражение можно несколько устранить, введя понятие угловой области , определяемой как
часть плоскости, ограниченная углом
Таким образом, каждый угол делит плоскость на две угловые области. Если угол не является прямым углом, то эти области можно различить как «внутреннюю» и «внешнюю» часть угла (используя промежуточность в качестве критерия). Затем вы можете определить меру угловой области в соответствии с двумя случаями: внутренняя угловая область имеет ту же меру, что и ограничивающий ее угол, а внешняя угловая область имеет меру, равную $360°$ минус мера угла, который ее ограничивает.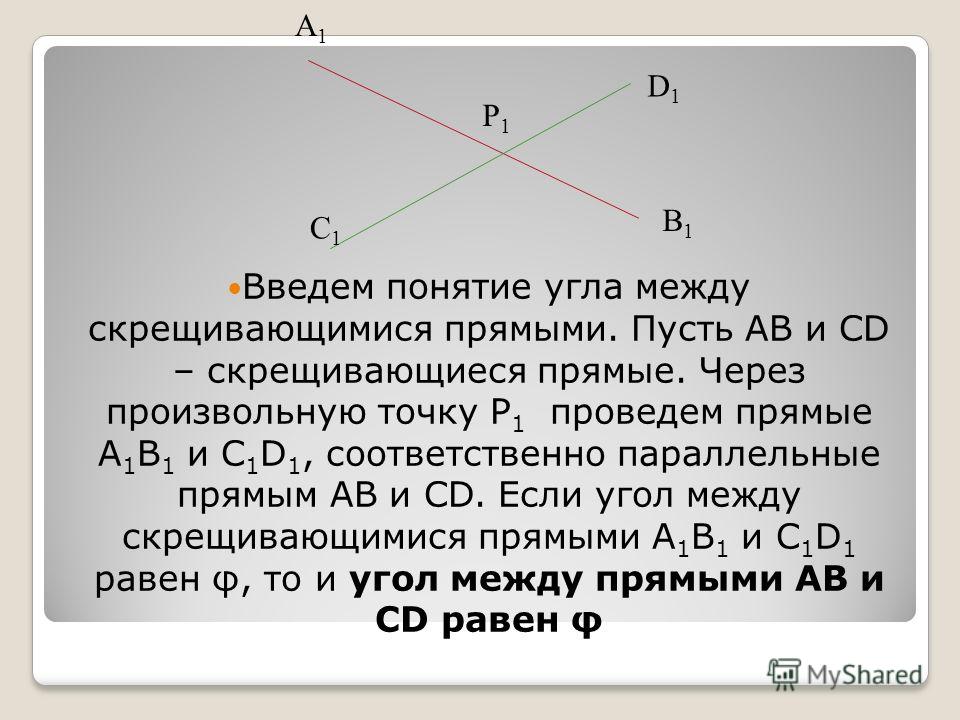 ограничивает его.
ограничивает его.
С помощью этого механизма вы можете различать угловые области $270°$ и $90°$. Но вы все еще не можете уловить идею направления. Вы также не можете обсуждать углы с отрицательной мерой или углы с мерой больше $360°$. «Угловые области» — это, по сути, 90 624 статических 90 625 объектов; если вы хотите уловить идею «ротации», они вам не подойдут.
( Отредактировано с добавлением : Принятый выше подход более или менее идентичен определению, приведенному в Geometry от Lang & Murrow, https://books.google.com/books?id=ntA5AlD3p4AC&printsec=frontcover#v=onepage&q&f=false. Спасибо пользователю @whatever за ссылку на него в комментариях.)
Сказав все это, я думаю, что стоит переосмыслить предпосылку этого вопроса. Я не знаю ваших учеников, но сильно сомневаюсь, что «строгость» является их главным критерием для принятия решения о том, как вам доверять и насколько быть мотивированным. Помните: Они еще не знают, что такое строгость , а они не ожидали . Вероятно, им нужен ясный и внимательный учитель, а не строгий и точный.
Вероятно, им нужен ясный и внимательный учитель, а не строгий и точный.
Обратите внимание: то, что я только что написал, не является аргументом против строгости . Я думаю, что есть веские причины быть строгим на уроках математики в старшей школе, но я не уверен, что вы назвали хоть одну.
Вы также можете рассмотреть утверждение, что «строгость» является не абсолютным критерием, а относительным. Некоторые определения более строгие, чем другие; как правило, чем более строгое, тем менее ясное определение. Вопрос, который вы должны задать себе, состоит не в том, «Что является строгим определением для старшеклассников?» но «Насколько я могу быть строгим, не жертвуя ясностью и не сбивая с толку мою аудиторию?»
Дополнение: Как указывает Бен Кроуэлл, приведенный выше ответ определяет «угол», но на самом деле не касается вопроса о измерении угла . В большинстве современных учебных программ по геометрии средней школы (по крайней мере, в Соединенных Штатах) это решается с помощью так называемого «постулата о транспортире», который утверждает (в немного более формальной терминологии, чем в средней школе) существование отображения который сопоставляет каждому углу $\angle ABC$ действительное число, обозначаемое $m\angle ABC$, с $0 \leq m\angle ABC \leq 180$ (если используются градусы). В зависимости от определения «угла» верхняя граница может составлять 360 долларов США; также, опять же, в зависимости от того, как определяется «угол», верхняя и нижняя границы могут быть или не быть строгими.
В зависимости от определения «угла» верхняя граница может составлять 360 долларов США; также, опять же, в зависимости от того, как определяется «угол», верхняя и нижняя границы могут быть или не быть строгими.
Свойства отображения $\angle ABC \mapsto m\angle ABC$ уточняются дополнительными постулатами и/или определениями. Нам нужно одно важное свойство:
.Два угла равны тогда и только тогда, когда они имеют одинаковую меру
Является ли вышеизложенное постулатом, определением или следствием, во многом зависит от того, как структурирована остальная часть теории — в частности, рассматривается ли «конгруэнтный угол» как неопределенное отношение или определяется в свободном от измерений отношении. пути, или же вышеприведенное принято как определение равных углов. Ради этого обсуждения давайте назовем его «Постулатом соответствия углов».
Еще одно свойство, которое нам нужно, это «Постулат сложения углов», который можно сформулировать так:
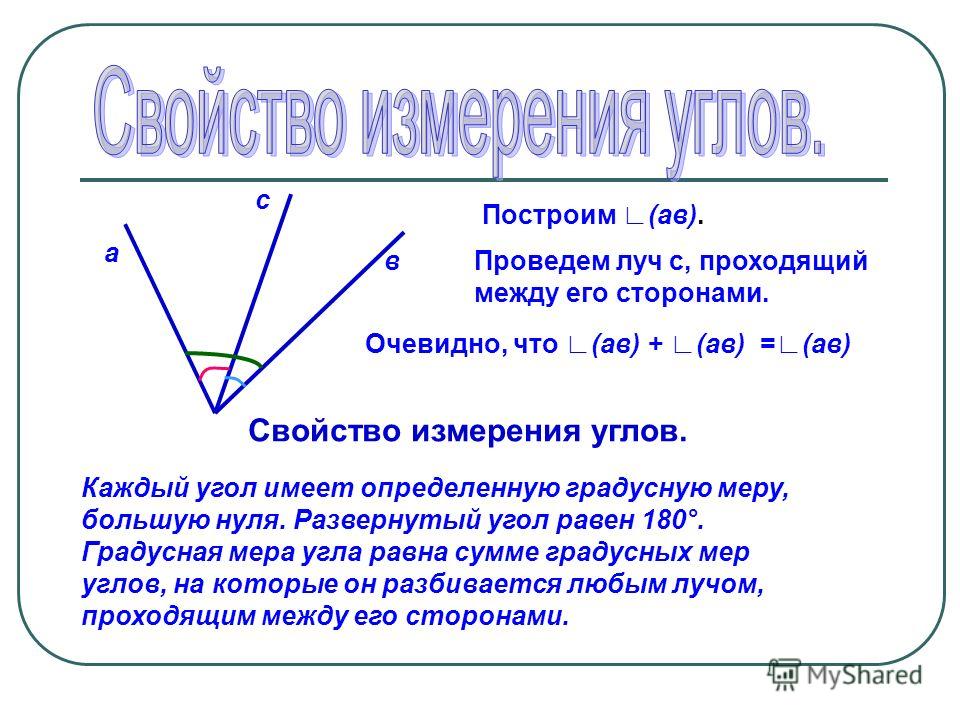
Пусть три различных луча имеют общую вершину.
Тогда любые два луча определяют две угловые области, причем третий луч лежит ровно в одной из этих областей и делит ее на две подобласти. В этой ситуации сумма мер двух подобластей равна мере полной угловой области.
Обратите внимание, что постулат транспортира, постулат равенства углов и постулат сложения углов фактически не определяют функцию измерения, но они характеризуют ее, по крайней мере, достаточно, чтобы сделать возможным все, что вам нужно для изучения геометрии в средней школе.
Историческая справка: насколько я знаю, описанный выше подход был впервые представлен Биркгоффом и Битли в Basic Geometry (1941), но в основном игнорировался в течение двадцати лет или около того, пока Школьная исследовательская группа по математике (SMSG) не приняла «Постулаты линейки и транспортира» как часть аксиоматической основы в учебниках по геометрии эпохи Новой математики, и с тех пор он остается стандартным подходом. Во введении к первому тому SMSG Геометрия текст, редакция написала:
Основная схема постулатов — это схема Г.

 1 Нулевой угол
1 Нулевой угол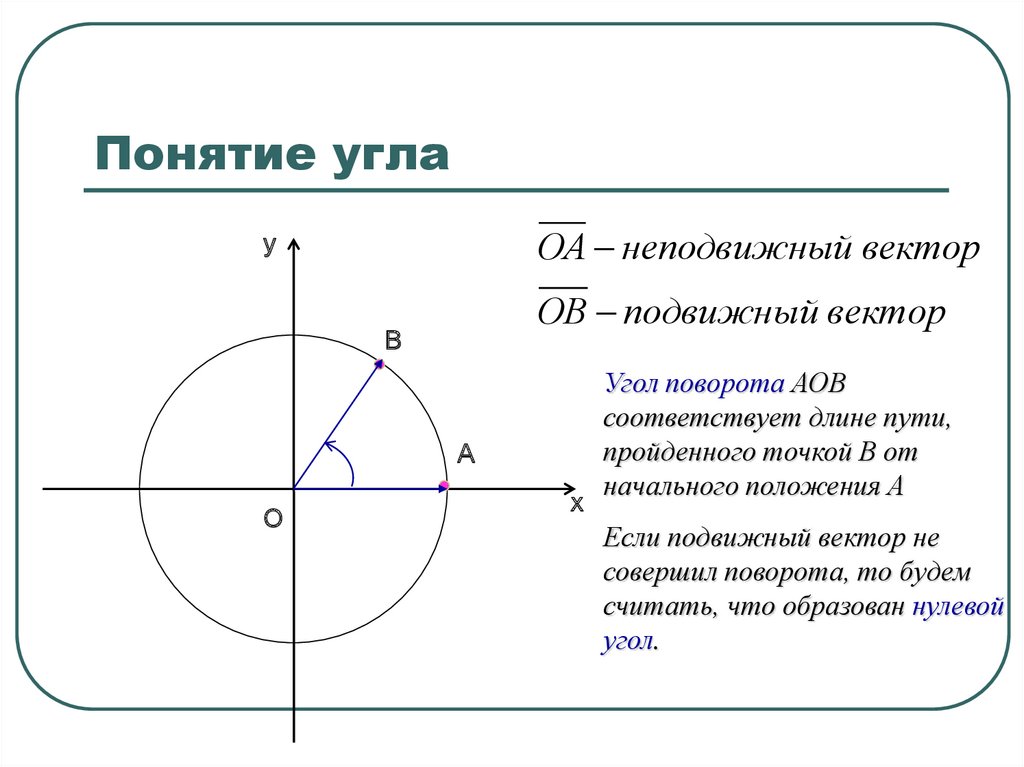
 Тогда любые два луча определяют две угловые области, причем третий луч лежит ровно в одной из этих областей и делит ее на две подобласти. В этой ситуации сумма мер двух подобластей равна мере полной угловой области.
Тогда любые два луча определяют две угловые области, причем третий луч лежит ровно в одной из этих областей и делит ее на две подобласти. В этой ситуации сумма мер двух подобластей равна мере полной угловой области.