Как найти асимптоту функции: Как найти асимптоты графика функции, примеры решений

3. Асимптоты графика функции

Асимптотой будем называть прямую, к которой график функции неограниченно близко приближается. Различают вертикальные и наклонные асимптоты.

Прямая х = х₀ называется вертикальной асимптотой графика функции f (х), если хотя бы один из пределов f (х₀ – 0) или f (х₀ + 0) равен бесконечности.

Пример 6. Найти вертикальные асимптоты функций:

а) б) в)

Решение. Вертикальными асимптотами функций будут прямые х = х₀, где х₀ – точки, в которых функция не определена.

а) х = 3 – вертикальная асимптота функции . Действительно, ;

б) х = 2, х = – 4 – вертикальные асимптоты функции .

Действительно, ,

;

в) х = 0 – вертикальная асимптота функции Действительно, .

Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f (х) при х  + или х  –, если f (х) = kx + b + α(х), , то есть если наклонная асимптота для графика функции f (х) существует, то разность ординат функции f (х) и прямой у = kx + b в точке х стремится к 0 при х  + или при х  – .

Теорема 6. Для того чтобы прямая у = kx + b являлась наклонной асимптотой графика функции f (х) при

х  + или х  – , необходимо и достаточно существование конечных пределов:

(4)

Следовательно, если хотя бы один из данных пределов не существует или равен бесконечности, то функция не имеет наклонных асимптот.

Пример 7. Найти наклонные асимптоты функции

Решение. Найдем пределы (4):

Следовательно, k = 1.

Следовательно, b = 0.

Таким образом, функция имеет наклонную асимптоту у = kx + b = 1 · х + 0 = х.

Ответ: у = х – наклонная асимптота.

Пример 8. Найти асимптоты функции .

Решение.

а) функция неопределенна в точках х₁ = –1, х₂ = 1. Следовательно, прямые х₁ = –1, х₂ = 1 – вертикальные асимптоты данной функции.

Действительно, .

;

б) у = kx + b.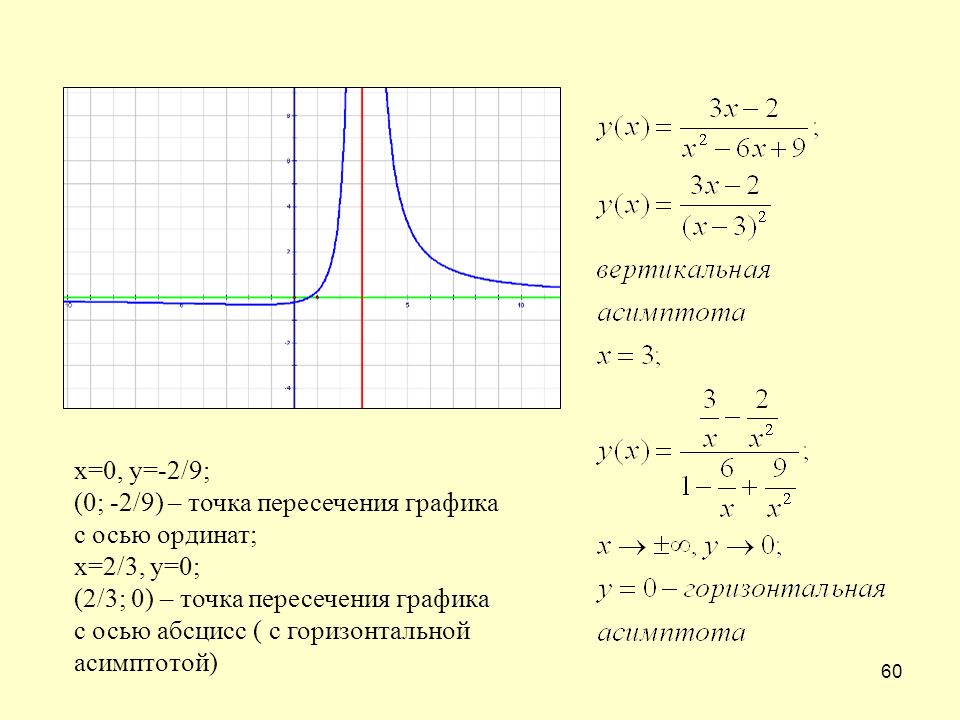

Следовательно, у = 2х + 1 – наклонная асимптота данной функции.

Ответ: х₁ = –1, х₂ = 1 – вертикальные, у = 2х + 1 – наклонная асимп- тоты.

1. Находим область определения функции.

2. Исследуем функцию на периодичность, четность или нечетность.

3. Исследуем функцию на монотонность и экстремум.

4. Находим промежутки выпуклости и точки перегиба.

5. Находим асимптоты графика функции.

6. Находим точки пересечения графика функции с осями координат.

7. Строим график.

Прежде чем перейти к примерам, напомним определения четности и нечетности функции.

Функция у = f (

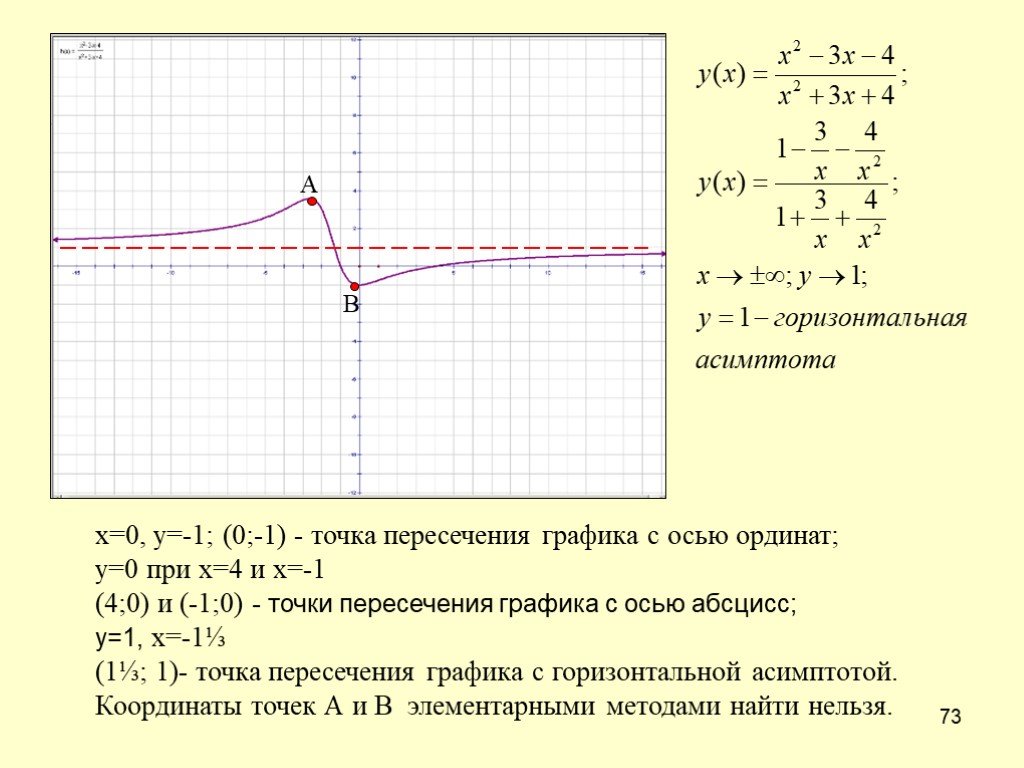х) называется четной, если для любого значения х, взятого из области определения функции, значение (–х) также принад-лежит области определения и выполняется равенство f (х) = f (–х). График четной функции симметричен относительно оси ординат.

Функция у = f (х) называется нечетной для любого значения х, взятого из области определения функции, значение (–х) также принадлежит об-ласти определения, и выполняется равенство f (–х) = –f (х). График не-четной функции симметричен относительно начала координат.

Пример 9. Построить график .

Решение. Мы используем данные, полученные для этой функции в других примерах.

1. D (у) = (–; 0)  (0; +).

2. Следовательно, функция нечетная. Ее график будет симметричен относительно начала координат.

3. (см. пример 2). Исследуем функцию на монотонность и экстремум:

х	(–; –1)	–1	(–1; 0)	0	(0; 1)	1	(1; +)
у’	+	0	–	–	–	0	+
у		–2		–		2

max min

4.

(см. пример 5). Исследуем функцию на выпуклость и найдем точки перегиба.

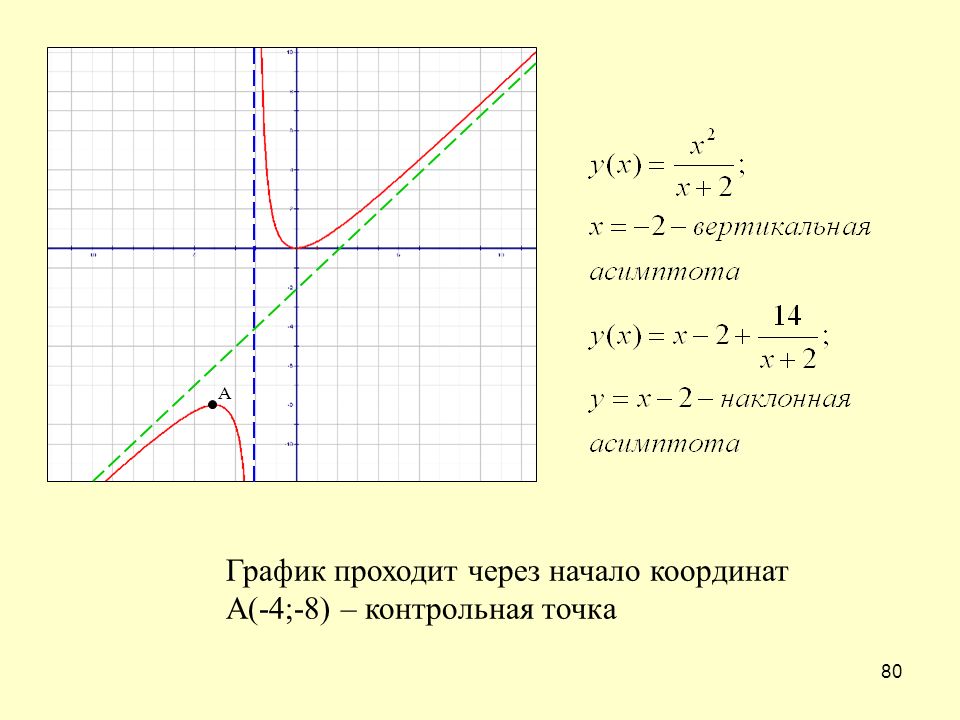
х	(–; 0)	0	(0; +)
у»	–	–	+
у	выпукла вверх	–	выпукла вниз
		функция не определена

Несмотря на то, что функция поменяла характер выпуклости при переходе через точку х = 0, но в ней нет перегиба, так как в этой точке функция не определена.

5. (см. примеры 6 и 7). Найдем асимптоты функции:

а) х = 0 – вертикальная асимптота;

б) у = х – наклонная асимптота.

6. Точек пересечения с осями координат у данной функции нет, так как , при любых х  , а х = 0  D(у).

7. По полученным данным строим график функции:

Пример 10. Построить график функции .

Решение.

1. D(у) = (–; –1)  (–1; 1)  (1; +).

2. – функция нечетная. Следовательно, график функции будет симметричен относительно начала координат.

3. Исследуем функцию на монотонность и экстремум:

3х² – х⁴ = 0, х² · (3 – х²) = 0,

х₁ = 0, х₂ = , х₃ = .

х	(–;)		(; 0)	–1	(–1; 0)	0	(0; 1)	1	(1; )		(; +)
у’	–	0	+	–	+	0	+	–	+	0	–
у		2,6		–		0		–		–2,6

4. Исследуем функцию на выпуклость и точки перегиба:

х = 0 – точка, подозрительная на перегиб.

х	(–; –1)	–1	(–1; 0)	0	(0; 1)	1	(0; +)
у»	+	–	–	0	+	–	–
у	выпукла вниз	–	выпукла вверх	0	выпукла вниз	–	выпукла вниз
			перегиб

5.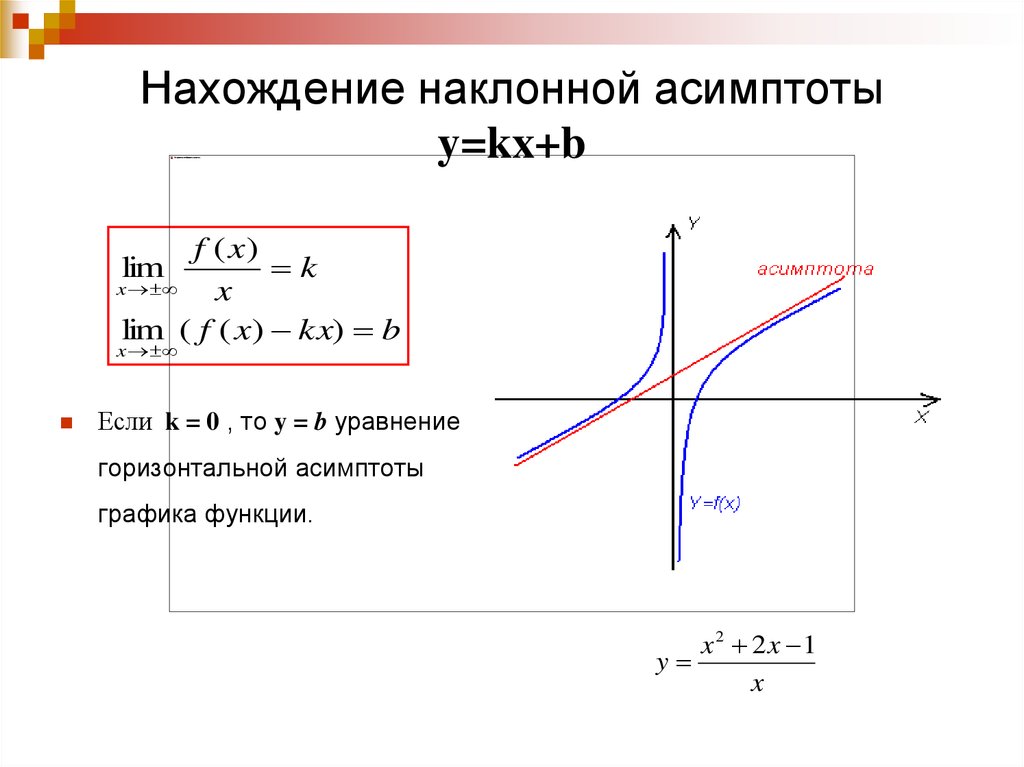 Найдем асимптоты функции:

а) х = –1, х = 1 – вертикальные асимптоты.

Действительно:

б) у = kx + b.

,

 у = –1х + 0 = – х – наклонная асимптота.

6. Найдем точки пересечения с осями координат:

х = 0  у = 0  (0; 0) – точка пересечения с осями координат.

7. Строим график:

ЗАДАЧИ И УПРАЖНЕНИЯ

Исследовать на монотонность и экстремум функции:

1.

2.

3.

Исследовать на выпуклость и точки перегиба функции:

4.

5.

6.

Найти асимптоты функции:

7.

8.

9.

Построить графики функций:

10.

11.

12.

13.

14.

15.

ОТВЕТЫ К ЗАДАЧАМ И УПРАЖНЕНИЯМ

1.

2. .

3.

4. – точки перегиба.

5. – точки перегиба.

6. – точки перегиба.

7. х = 0, у = х.

8. х = –1, у = х – 1.

9. у = 1.

ЛИТЕРАТУРА

Гусак А. А. Математический анализ и дифференциальные уравнения.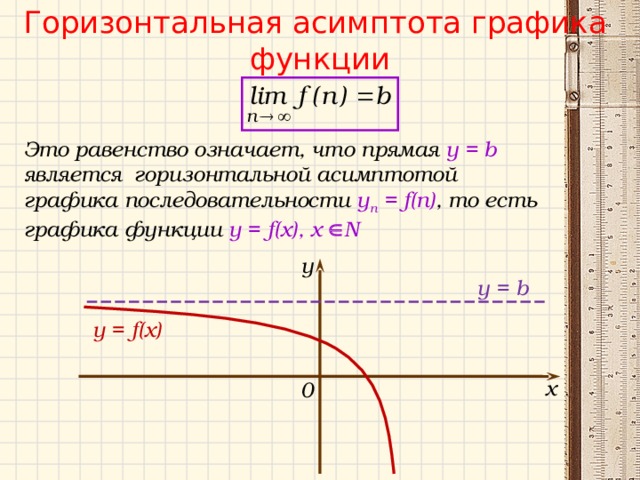 – Мн.: Тетрасистемс, 1998. – 415 с.

Минченков Ю. В. Высшая математика. Производная функции. Дифференциал функции: Учебно-методическое пособие.– Мн.: ЧИУиП, 2007.– 20 с.

СОДЕРЖАНИЕ

Лекция 1. Основные теоремы дифференциального исчисления 3

Асимптоты графика функции — интернет энциклопедия для студентов

ОПРЕДЕЛЕНИЕ

Асимптотой графика функции \(\ f(x) \) называется прямая такая, что расстояние от точки \(\ (x, f(x)) \) до этой прямой стремится к нулю при движении сколь угодно далеко от начала координат.

Вертикальные и наклонные асимптоты функции

Асимптоты бывают двух видов: вертикальные и наклонные (в частности, горизонтальные).

ОПРЕДЕЛЕНИЕ

Прямая \(\ x=a \) называется вертикальной асимптотой графика функции \(\ y=f(x) \) , если хотя бы один из пределов

\(\ \lim _{x \rightarrow a} f(x), \lim _{x \rightarrow a+0} f(x), \lim _{x \rightarrow a+0} f(x) \)

равен \(\ +\infty \) или \(\ -\infty \)

Вертикальные асимптоты ищут в точках разрыва функции.

ОПРЕДЕЛЕНИЕ

Прямая \(\ y=k x+b \) называется наклонной асимптотой графика функции \(\ y=f(x) \) , если существуют конечные пределы

\(\ k=\lim _{x \rightarrow \infty} \frac{f(x)}{x} ; b=\lim _{x \rightarrow \infty}[f(x)-k x] \)

Если при этом \(\ \mathrm{k}=0 \), то \(\ y=b \) — горизонтальная асимптота.

Примеры решения задач

ПРИМЕР 1

Задание

Найти асимптоты функции \(\ y=3 x-\frac{2}{x} \)

Решение

Область определения этой функции \(\ D(y)=(-\infty ; 0) \cup(0 ;+\infty) \) .При \(\ \mathrm{x}=\mathrm{O} \) функция имеет разрыв. Проверим, является ли прямая x=0 вертикальной асимптотой.

\(\ \lim _{x \rightarrow 0+0}\left(3 x-\frac{2}{x}\right)=-\infty ; \lim _{x \rightarrow 0-0}\left(3 x-\frac{2}{x}\right)=+\infty \)

Поскольку односторонние пределы в точке \(\ \mathrm{x}=0 \) бесконечны, то прямая \(\ \mathrm{x}=0 \) — вертикальная асимптота.

Проверим, имеет ли функция наклонную асимптоту \(\ y=k x+b \) .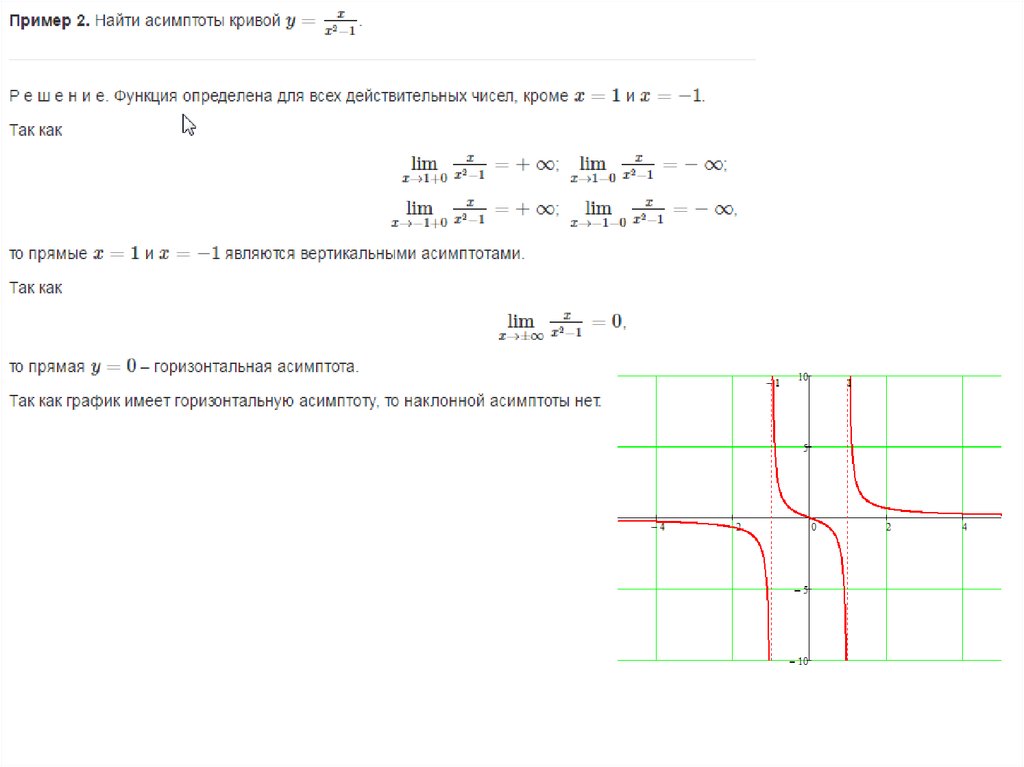 {2}} \) имеет вертикальную асимптоту — \(\ \mathrm{x}=\mathrm{O} \) и горизонтальную асимптоту — \(\ y=4 \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Четность и нечетность функции Область значений функции Область определения функции Квадратная матрица

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Как найти горизонтальную асимптоту функции

Горизонтальная асимптота:

Это горизонтальная линия , которая не является частью графика функции, но направляет ее для значений x «далеко» вправо и/или «далеко» Слева.

График может пересечь его, но в конце концов, для достаточно больших или малых достаточное количество значений x, то есть

x —> ±∞

Всегда график будет все ближе и ближе к горизонтальной асимптоте, не касаясь Это.

На приведенной выше диаграмме y = k является горизонтальной асимптотой. Потому что график становится все ближе и ближе к y = k, не касаясь его, поскольку x —> ±∞.

Мы можем найти горизонтальные асимптоты функции, только если это рациональная функция.

То есть функция должна быть в виде

f(x) = g(x)/h(x)

Рациональная функция. Пример:

Пусть f(x) — заданная рациональная функция . Сравните наибольший показатель степени числителя и знаменателя.

Случай 1 :

Если наибольшие показатели числителя и знаменателя равны, уравнение горизонтальной асимптоты равно

y = a/b

Здесь a и b – коэффициенты при наибольшем показателе степени в числителе и знаменателе соответственно.

Случай 2 :

Если наибольший показатель числителя меньше наибольшего показателя знаменателя, уравнение горизонтальной асимптоты имеет вид

y = o (или) ось x наибольший показатель числителя больше наибольшего показателя знаменателя горизонтальной асимптоты нет, а есть только наклонная асимптота или косая.

В каждом случае найдите уравнение горизонтальной асимптоты.

Пример 1:

f(x) = 1/(x + 6)

Решение:

Шаг 1:

В данной рациональной функции наибольший показатель числителя равен 0, а наибольший показатель знаменатель равен 1.

Шаг 2 :

Ясно, что наибольший показатель числителя меньше наибольшего показателя знаменателя.

Итак, уравнение горизонтальной асимптоты

y = 0 (или) ось x

Пример 2 :

f(x) = (x ² + 2x — 3)/(x ²  — 5x + 6)

Решение 5 :

Шаг 1 :

В заданной рациональной функции наибольший показатель числителя равен 2, а наибольший показатель знаменателя равен 2.

Шаг 2 :

Очевидно, что показатель степени числителя и знаменателя равны.

Шаг 3 :

Теперь, чтобы получить уравнение горизонтальной асимптоты, мы должны разделить коэффициенты при наибольшем члене степени числителя и знаменателя.

Итак, уравнение горизонтальной асимптоты:

y = 1/1

y = 1

Решение :

Шаг 1 :

В заданной рациональной функции наибольший показатель числителя равен 2, а наибольший показатель знаменателя равен 1.

Шаг 2 :

Очевидно, что наибольший показатель числителя равен больше наибольшего показателя знаменателя.

Шаг 3:

Поскольку наибольший показатель числителя больше, чем наибольший показатель знаменателя, горизонтальной асимптоты нет.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Видео-урок: Горизонтальные и вертикальные асимптоты функции

Стенограмма видео

Горизонтальные и вертикальные асимптоты функции

В этом видео мы научимся найти горизонтальную и вертикальную асимптоты функции. И мы рассмотрим разнообразие примеров того, как мы можем это сделать. Начнем с подведения итогов определение асимптоты.

Асимптота – это линия, которую кривая приближается и становится сколь угодно близкой, но не касается ее. Например, если мы рассмотрим график 𝑦 равен единице над 𝑥. Мы видим, что он имеет горизонтальную асимптота в точке 𝑦 равна нулю, а вертикальная асимптота в точке 𝑥 равна нуль.

Давайте теперь посмотрим на более строгий определение вертикальной и горизонтальной асимптоты. Мы можем определить вертикальную асимптоту в дальнейшем. Если по мере приближения 𝑥 к некоторой постоянной 𝑐, 𝑓 из 𝑥 приближается к положительному или отрицательному ∞, тогда 𝑥 равно 𝑐 является вертикальным асимптота. Другой способ думать о вертикальная асимптота — это любой вход, который не имеет определенного выхода.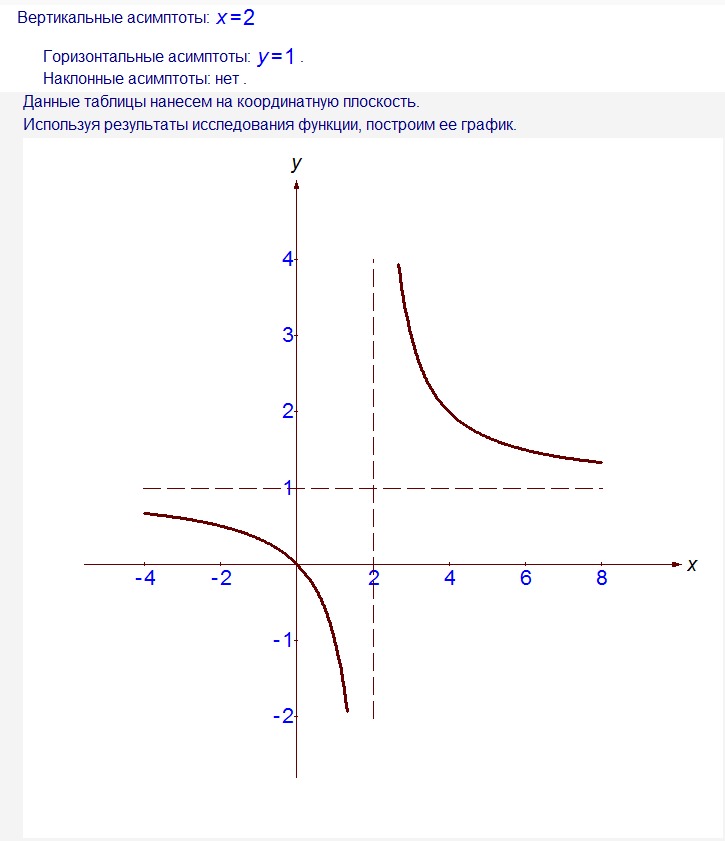

Мы можем определить горизонтальную асимптота следующим образом. Если по мере приближения 𝑥 к положительному или отрицательное ∞, 𝑓 из 𝑥 приближается к некоторой константе 𝑐, тогда 𝑦 равно 𝑐 является горизонтальным асимптота. Другой способ, которым мы можем думать о горизонтальных асимптотах — это любой выход, который не может быть достигнут из любого входа в область функций.

Однако мы должны быть осторожны при использовании эту линию рассуждений, поскольку это не всегда так. Иногда вывод может быть в состоянии быть достигнуто входом в область функций. И все же может быть асимптота в этой точке. При нахождении горизонтальных асимптот часто легче понять, что происходит, когда 𝑥 приближается к положительному или отрицательному значению ∞.

При определении и нахождении вертикали и горизонтальные асимптоты, мы много говорим о входах и выходах. И по этой причине они связывают довольно сильно в область и диапазон функций. Если мы знаем область и диапазон функции, часто проще найти горизонтальную и вертикальную асимптоты. И точно так же, если мы знаем горизонтальные и вертикальные асимптоты, часто проще найти область определения и диапазон этой функции. Давайте теперь продолжим и посмотрим на пример того, как мы можем найти вертикальные и горизонтальные асимптоты.

Определить вертикаль и горизонтальная асимптота функции 𝑓 от 𝑥 равна отрицательной единице плюс три больше 𝑥 минус четыре больше 𝑥 в квадрате.

Мы можем начать с поиска вертикальная асимптота этой функции. Теперь мы можем найти вертикаль асимптота путем нахождения любого входа, который не имеет определенного выхода. Когда мы смотрим на нашу функцию 𝑓 of 𝑥, мы замечаем, что оно имеет два рациональных члена. А это три больше 𝑥 и минус четыре больше 𝑥 в квадрате.

Теперь рациональный термин не определен когда его знаменатель равен нулю. Итак, на три больше 𝑥, это когда 𝑥 равно нулю. И для отрицательных четырех больше 𝑥 в квадрате, это когда 𝑥 в квадрате равно нулю. И когда 𝑥 в квадрате равно ноль, это, конечно, означает, что 𝑥 также равно нулю. Поскольку эти два термина появляются в 𝑓 из 𝑥, когда любой из этих терминов не определен, 𝑓 из 𝑥 также не определен.

Итак, следовательно, мы можем сказать, что когда 𝑥 равно нулю, 𝑓 из 𝑥 не имеет определенного выхода. Итак, мы нашли вертикаль асимптота 𝑓 из 𝑥. И это то, что 𝑥 равно нуль. Чтобы найти любую горизонталь асимптоты, нам нужно найти любое значение, которое не входит в диапазон их функция. А для этого можно рассмотреть что происходит, когда 𝑥 приближается к ∞.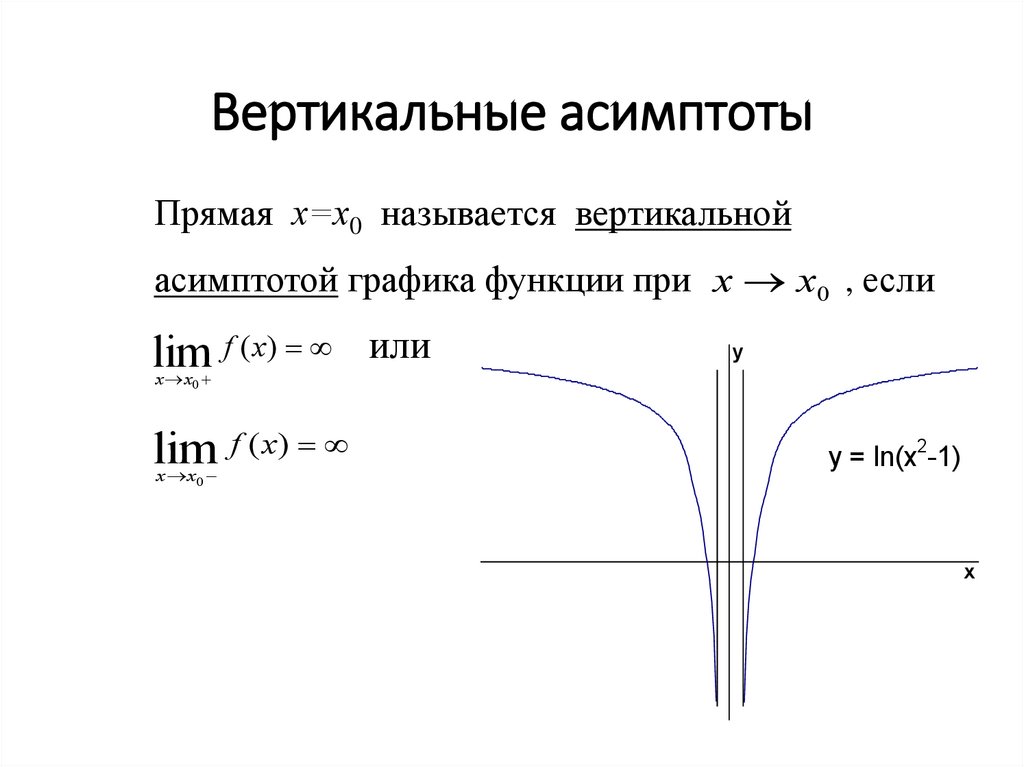

Ну, мы можем посмотреть на условия 𝑥 в 𝑓 из 𝑥. У нас три больше 𝑥 и минус четыре больше 𝑥 в квадрате. Когда 𝑥 приближается к ∞, мы имеем, что знаменатель обоих этих рациональных членов будет становиться все больше и больше и больше. Итак, оба этих рациональных термина будет приближаться к нулю. Однако ни один из этих терминов никогда не достигнет нуля. Они просто получат произвольно близко к нулю.

Поэтому, когда мы смотрим на 𝑓 из 𝑥 и у нас оба этих рациональных члена приближаются к нулю, мы можем видеть, что 𝑓 из 𝑥 приблизится к отрицательному. И мы можем сказать, что 𝑓 из 𝑥 будет получить произвольно близко к отрицательному, не достигая отрицательного. Таким образом, у нас получится горизонтальная асимптота в точке 𝑦 равна отрицательной.

Здесь мы нашли вертикаль и горизонтальные асимптоты нашей функции 𝑓 от 𝑥. Они при 𝑥 равны нулю и 𝑦 равно отрицательной единице. И это решение задачи вопрос. Однако этот вопрос хорошо пример того, почему мы должны быть осторожны, используя это рассуждение, чтобы найти горизонтальные асимптоты. Поскольку иногда значение может появляются в диапазоне функции. И все же может быть горизонталь асимптота в этой точке.

Мы можем увидеть это, установив 𝑓 из 𝑥 равен отрицательной единице. У нас отрицательный равен минус один плюс три больше 𝑥 минус четыре больше 𝑥 в квадрате. Мы можем добавить по одному с обеих сторон уравнение для получения нуля равно трем на 𝑥 минус четырем на 𝑥 в квадрате.

На следующем этапе мы добавляем четыре 𝑥 в квадрате с обеих сторон. Затем умножаем обе части уравнение на 𝑥 в квадрате. Затем делим обе части уравнение на три, чтобы получить 𝑥, равно четырем на три.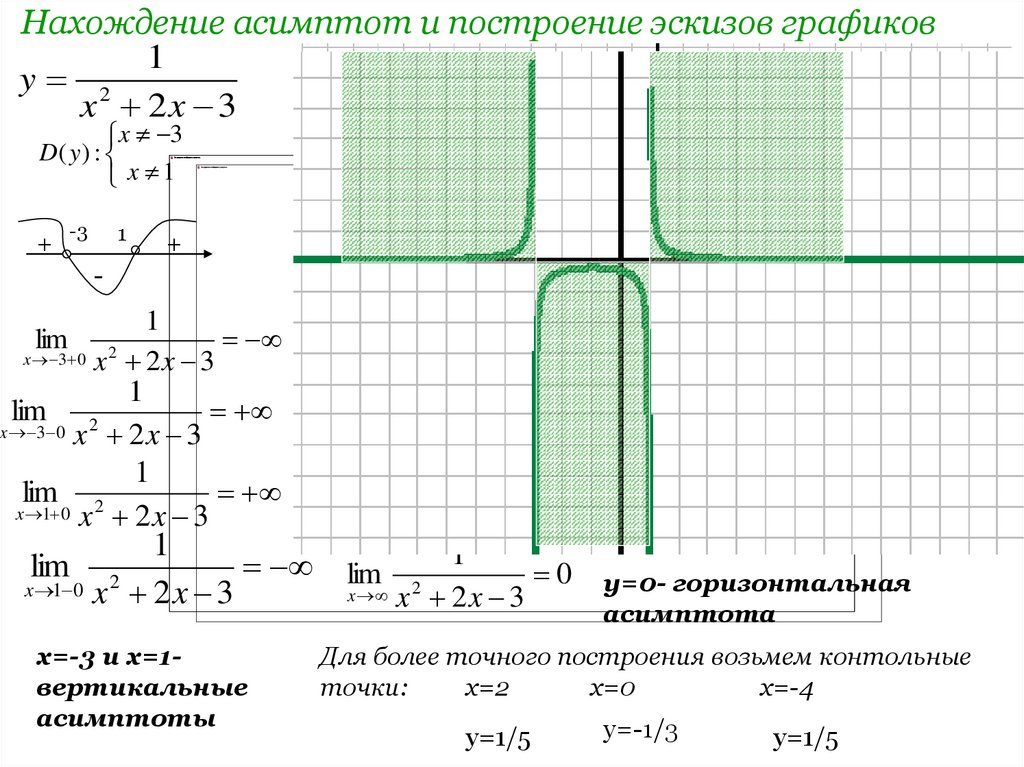 Итак, это говорит нам о том, что когда 𝑥 равно четырем на три, 𝑓 из 𝑥 равно отрицательной единице. Следовательно, отрицательная единица находится в диапазоне из 𝑓 из 𝑥.

Тем не менее, асимптота в точке 𝑦 равна отрицательной. Мы можем понять, почему это так, учитывая график 𝑓 of 𝑥. С помощью графического калькулятора или некоторое графическое программное обеспечение, мы можем видеть, что график 𝑓 of 𝑥 будет выглядеть как-то как это. Мы можем видеть, что асимптоты в 𝑥 равны равно нулю, а 𝑦 равно отрицательной единице. И мы можем видеть, где линия 𝑓 𝑥 пересекает асимптоту в 𝑦 равно отрицательной единице, а 𝑥 равно четырем более трех. Тогда мы увидим, как 𝑓 из 𝑥 продолжает демонстрировать асимптотическое поведение по отношению к прямой 𝑦 равно отрицательному один.

Так как если мы посмотрим вправо от 𝑥 равно четырем на три, мы можем видеть, что 𝑓 из 𝑥 становится сколь угодно близким до 𝑦 равно отрицательной единице, фактически не касаясь этой линии. И вот почему мы должны быть осторожны используя это рассуждение при нахождении горизонтальных асимптот. В следующем примере мы увидим, как мы можем найти асимптоту гиперболы. Гипербола – это тип рационального функция с двумя асимптотами.

Каковы асимптоты гипербола 𝑦 равна восьми на четыре 𝑥 минус три плюс пять на три?

Мы можем начать с поиска вертикальная асимптота этой гиперболы. Воспользуемся тем, что вертикаль асимптота может быть описана как любой вход без определенного выхода. Глядя на уравнение нашего гипербола, мы видим, что у нас есть рациональный член, который равен восьми на четыре 𝑥 минус три.

Теперь мы знаем, что любой рациональный термин не определено, когда знаменатель равен нулю. Так это когда четыре 𝑥 минус три равен нулю. Мы можем изменить это, чтобы найти 𝑥. Это дает нам, что 𝑥 равно три больше четырех.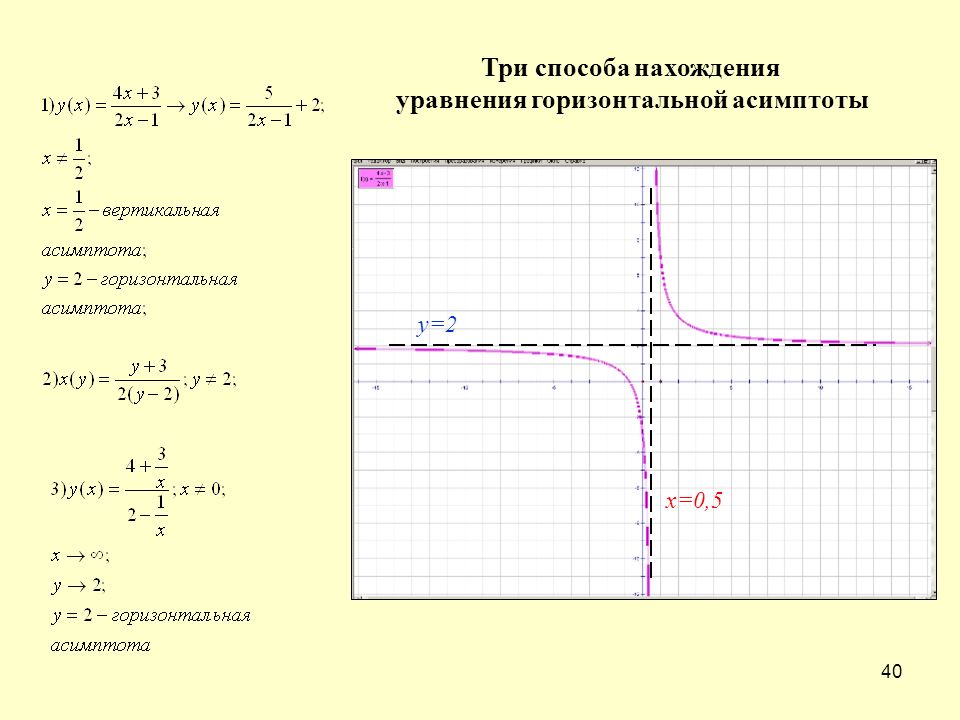 Теперь у нас есть это, когда 𝑥 равно на три на четыре, этот рациональный член восемь на четыре 𝑥 минус три не определенный.

Следовательно, когда мы вводим 𝑥 равно три на четыре в уравнение для нашей гиперболы, мы получим неопределенное выход. Поэтому наша гипербола будет иметь вертикальная асимптота в 𝑥 равна трем на четыре.

Теперь мы можем перейти к поиску горизонтальная асимптота. Горизонтальные асимптоты – это значения которые не входят в диапазон функции. Для того, чтобы найти такие значения, мы можно рассмотреть, что происходит, когда 𝑥 приближается к положительному или отрицательному ∞.

Теперь единственный 𝑥-зависимый член в наше уравнение восемь плюс четыре 𝑥 минус три. Теперь, когда 𝑥 приближается к положительному или отрицательный ∞, этот рациональный член стремится к нулю. А ведь получается произвольно близко к нулю. Поэтому, если мы оглянемся назад на уравнение гиперболы, мы можем видеть, что 𝑦 будет сколь угодно близко к пяти более трех, когда 𝑥 приближается к положительному или отрицательному ∞. Поскольку рациональный член в уравнение будет стремиться к нулю. Следовательно, наша гипербола имеет горизонтальная асимптота в 𝑦 равна пяти больше трех. И вот теперь мы нашли асимптоты нашей гиперболы, что и завершает решение этого вопроса.

Прежде чем мы перейдем к следующему Например, давайте быстро отметим, что на самом деле функция может иметь больше чем одна горизонтальная или вертикальная асимптота. Например, рассмотрим функцию 𝑓 из 𝑥 равно единице на 𝑥 в квадрате минус четыре. Мы можем разложить знаменатель эту функцию, чтобы получить единицу на 𝑥 минус два, умноженную на 𝑥 плюс два.

Теперь мы можем определить вертикальное асимптоты как любой вход без определенного выхода. Поскольку 𝑓 из 𝑥 является рациональным функции, это произойдет, когда знаменатель равен нулю. Итак, когда 𝑥 минус два умножить на 𝑥 плюс два равно нулю. Это дает нам два решения и, следовательно, две асимптоты. А это при 𝑥 равно двум а 𝑥 равно минус двум.

Используя эти асимптоты, мы могли бы попробуйте нарисовать график 𝑓 of 𝑥. Однако сначала нам необходимо рассмотреть то, что происходит с 𝑓 из 𝑥 вокруг значений 𝑥, равно двум, а 𝑥 равно минус два. Мы должны учитывать, когда 𝑥 меньше чем минус два, когда 𝑥 находится между минус двумя и двумя, и когда 𝑥 больше чем два.

Когда 𝑥 меньше минус двух и больше двух, 𝑥 в квадрате минус четыре больше нуля. Следовательно, 𝑓 из 𝑥 должно быть положительный. И когда 𝑥 находится между отрицательными двумя и два, 𝑥 в квадрате минус четыре меньше нуля. Следовательно, 𝑓 из 𝑥 отрицательно. Используя эту информацию, мы можем нарисовать график 𝑓 из 𝑥, примерно так. И, как мы видим, у него есть два вертикальные асимптоты. Нахождение этих асимптот действительно помог нам нарисовать этот график. Итак, мы видим, насколько полезны асимптоты может быть для рисования графиков.

В некоторых случаях мы должны быть очень осторожны, пытаясь найти асимптоты. И это те случаи, когда наши функция имеет коэффициент, который можно отменить. Рассмотрим следующий пример.

Найдите асимптоты функции 𝑓 из 𝑥 равно 𝑥 плюс два на 𝑥 в квадрате минус четыре.

Обычно мы начинаем с поиска для вертикальных асимптот этой функции. Однако, если мы внимательно посмотрим на нашей функции, мы замечаем, что знаменатель можно разложить на множители. Следовательно, мы можем записать 𝑓 из 𝑥 как 𝑥 плюс два на 𝑥 плюс два умножить на 𝑥 минус два. И мы замечаем, что можем отменить коэффициент 𝑥 плюс два.

Однако здесь надо быть осторожным так как, делая это, мы немного меняем функцию. После отмены фактора мы можем вызовите новую функцию 𝑔 из 𝑥. У нас есть, что 𝑔 из 𝑥 равно один больше 𝑥 минус два. Мы можем видеть, как эти две функции несколько различаются, учитывая области определения этих функций.

Мы видим, что если мы ввели 𝑥 равно минус двум в 𝑓 из 𝑥, мы получим неопределенный результат. Так как это дало бы 𝑓 a знаменатель нуля. Однако мы можем ввести 𝑥 равно минус двум в 𝑔 из 𝑥.

Теперь важно отметить, что хотя эти две функции немного отличаются, на самом деле они имеют одно и то же асимптоты. Таким образом, мы можем найти асимптоты 𝑓, найдя асимптоты 𝑔. Итак, давайте найдем эти асимптоты. Мы можем определить вертикальные асимптоты как любой вход без определенного выхода.

Так как 𝑔 из 𝑥 является рациональным функции, это происходит, когда знаменатель равен нулю или когда 𝑥 минус два равно равен нулю. Переставляя это, мы имеем 𝑥 is равен двум. Следовательно, 𝑔 из 𝑥 имеет вертикаль асимптота в 𝑥 равна двум. Мы можем определить горизонтальную асимптота как любое значение, которое не находится в диапазоне функции. Мы можем найти такие значения по учитывая, что происходит, когда 𝑥 приближается к положительному или отрицательному ∞.

Мы видим, что по мере того, как 𝑥 становится очень больше в положительном или отрицательном направлении, что знаменатель 𝑔 из 𝑥 становится очень большим как в положительном, так и в отрицательном направлении. Следовательно, 𝑔 из 𝑥 станет ближе и ближе к нулю. Итак, мы обнаружили, что 𝑔 из 𝑥 имеет горизонтальная асимптота в 𝑦 равна нулю.

Так как 𝑔 из 𝑥 и 𝑓 из 𝑥 делятся те же асимптоты, при нахождении вертикальной и горизонтальной асимптот 𝑔 мы получили нашел вертикальную и горизонтальную асимптоты 𝑓. И это завершает наше решение для этот вопрос.

Но прежде чем двигаться дальше, давайте быстро рассмотрите, чем отличаются 𝑔 и 𝑓 с помощью быстрого наброска. Здесь у нас есть эскизы 𝑓 из 𝑥 и 𝑔 из 𝑥. Мы можем видеть, что асимптоты в 𝑦 равны равно нулю, а 𝑥 равно двум. Теперь единственная разница между на этих двух графиках состоит в том, что 𝑓 из 𝑥 не определено, а 𝑥 равно отрицательному значению двух. И 𝑔 из 𝑥 определяется как 𝑥 равно минус двум. И несмотря на это, мы видим, что два графика по-прежнему имеют одинаковые асимптоты. В нашем последнем примере мы увидим, как мы можем использовать асимптоты, чтобы идентифицировать график функции.

Какой из следующих графиков представляет 𝑓 из 𝑥 равно одному больше 𝑥 плюс один?

Начнем с поиска вертикали асимптоты 𝑓 из 𝑥. Мы можем найти вертикальные асимптоты с помощью идентификация любого входа без определенного выхода. Поскольку 𝑓 из 𝑥 является рациональным функции, это происходит, когда ее знаменатель равен нулю, поэтому, когда 𝑥 плюс один равно нуль. Переставляя, мы видим, что это это когда 𝑥 равно отрицательной единице.

Отсюда мы можем сделать вывод, что 𝑓 из 𝑥 имеет вертикальную асимптоту в точке 𝑥, равную отрицательной единице. в) и г) являются единственными графики с вертикальными асимптотами в точке 𝑥 равна отрицательной единице. Поэтому мы можем исключить варианты а) и б). Когда мы смотрим на графики c) и d), мы можем видеть, что они оба имеют горизонтальную асимптоту в 𝑦 равна нуль. Следовательно, наша функция 𝑓 от 𝑥 должна имеют горизонтальную асимптоту в 𝑦 равна нулю.

Теперь давайте посмотрим, как графики c) и d) отличаются. Для графика c) мы видим, что когда 𝑥 меньше отрицательного, 𝑓 из 𝑥 отрицательно. И когда 𝑥 больше, чем отрицательный, 𝑓 из 𝑥 положительный. Однако для графика d), когда 𝑥 равно меньше отрицательного, 𝑓 из 𝑥 положительно. И когда 𝑥 больше, чем отрицательный, 𝑓 из 𝑥 отрицательный.

Теперь давайте посмотрим, что происходит с 𝑓 из 𝑥 дается в вопросе, когда 𝑥 меньше отрицательного и когда 𝑥 больше чем отрицательный. У нас есть это, когда 𝑥 меньше, чем минус один, 𝑥 плюс один минус. Следовательно, 𝑓 из 𝑥 также должно быть отрицательный. И когда 𝑥 больше, чем минус один, 𝑥 плюс один положительный. Следовательно, 𝑓 из 𝑥 также положительный. И эта информация о 𝑓 согласуется с тем, что мы показали для графика c). Поэтому наше решение состоит в том, что график c) представляет нашу функцию 𝑓 от 𝑥.

Мы рассмотрели множество примеры того, как мы можем найти асимптоты и насколько полезными могут быть асимптоты, особенно при идентификации или построении графиков.