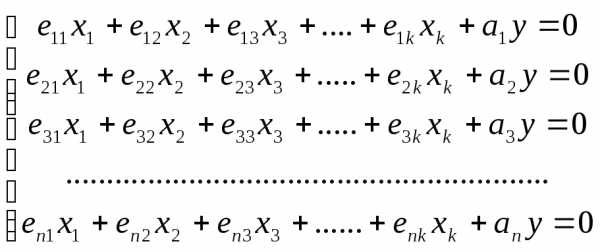2. Базис и размерность линейного пространства
Фундаментальным вопросом теории линейных пространств является вопрос о том, можно ли, а если можно, то как, произвольный вектор пространства представить в виде линейной комбинации фиксированного набора векторов из этого пространства. Далее мы получим ответ на этот вопрос.
Система
линейно независимых векторов
векторного пространства называетсябазисом этого пространства, если любой вектор
из
называетсябазисом этого пространства, если любой вектор
из  может быть представлен в виде линейной
комбинации векторов этой системы, т.е.
для каждого вектора
может быть представлен в виде линейной
комбинации векторов этой системы, т.е.
для каждого вектора существуют вещественные числатакие, что имеет место равенство
существуют вещественные числатакие, что имеет место равенство
.
 по базису
,
а числаназываютсякоординатами
вектора
по базису
,
а числаназываютсякоординатами
вектора  относительно базиса (или в базисе)
.
относительно базиса (или в базисе)
.Утверждение
Базисом линейного пространства решений однородной системы является ее фундаментальная система решений.
ТЕОРЕМА (о единственности разложения по базису). Каждый вектор  пространства
пространства может быть разложен по базису единственным
образом, т.е. координаты каждого вектора
может быть разложен по базису единственным
образом, т.е. координаты каждого вектора 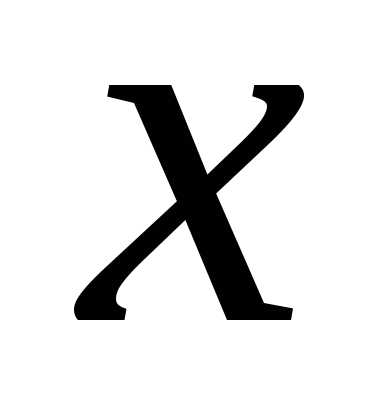 в базисе определяются однозначно.
в базисе определяются однозначно.
Главное значение базиса заключается в том, что операции сложения векторов и умножения их на числа при задании базиса превращаются в соответствующие операции над числами – координатами этих векторов. А именно, справедлива следующая
ТЕОРЕМА. При сложении
двух любых векторов линейного пространства 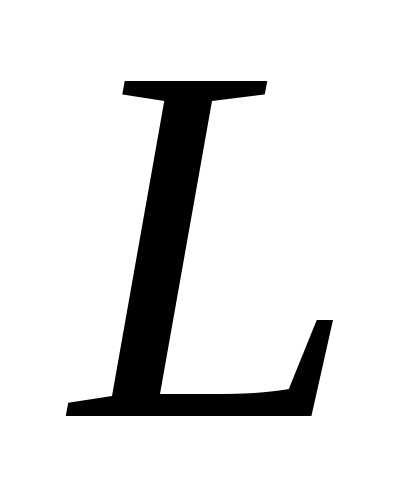 их координаты (относительно любого
базиса пространства) складываются; при
умножении произвольного вектора на любое число
их координаты (относительно любого
базиса пространства) складываются; при
умножении произвольного вектора на любое число  все координаты этого вектора умножаются
на
все координаты этого вектора умножаются
на .
.
Типовой пример
Исследуем
вопрос о базисе пространства 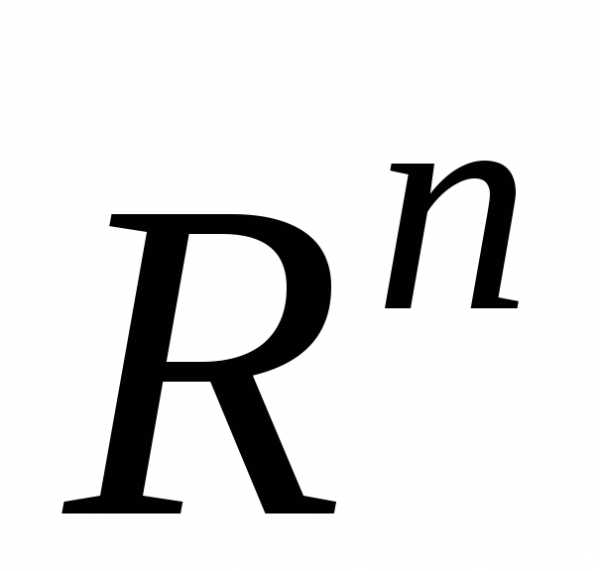 ,
введенного ранее при рассмотрении
Типовой примеров векторных пространств.
Покажем, что
,
введенного ранее при рассмотрении
Типовой примеров векторных пространств.
Покажем, что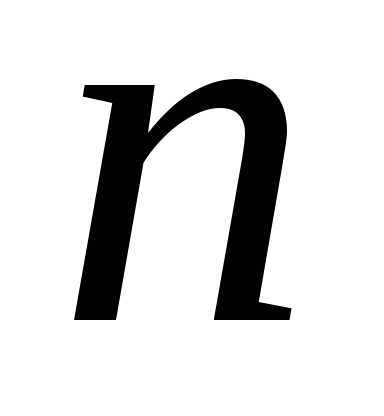
►Во-первых,
эти векторы линейно независимы. Проверка
линейной независимости набора  состоит в определении значений,
при которых возможно равенство
состоит в определении значений,
при которых возможно равенство
.
Но в силу только что доказанной теоремы
,
а
последний вектор является нулевым лишь
при условии
.
Во-вторых, всякий векторзаведомо представим в виде линейной
комбинации векторов :и, значит, набор
:и, значит, набор образует базис. ◄
образует базис. ◄
Векторное
пространство  называется
называется 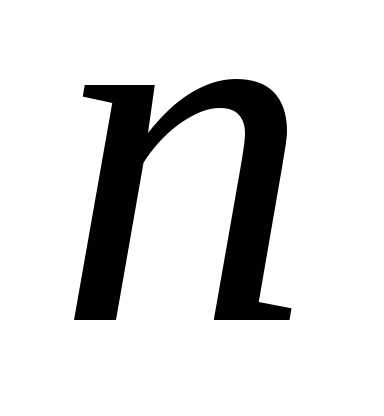 -мерным,
если в нем существуют
-мерным,
если в нем существуют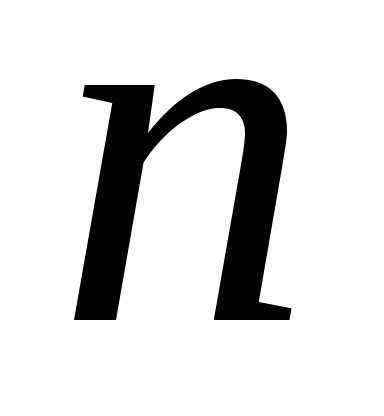
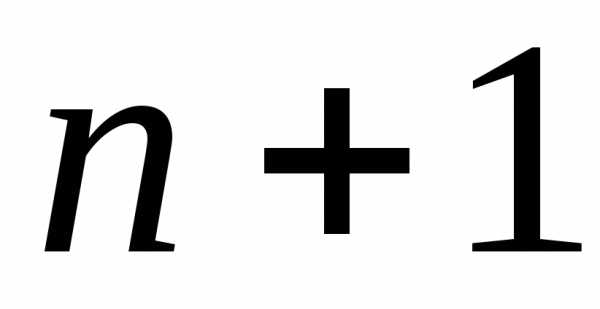 векторов уже являются линейно зависимыми.
При этом число
векторов уже являются линейно зависимыми.
При этом число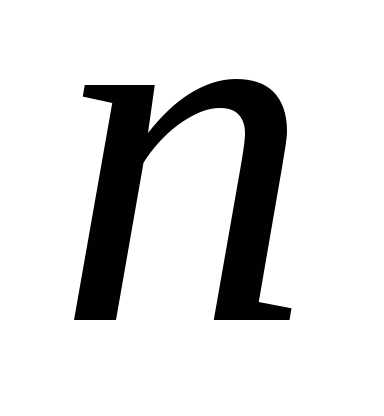 называетсяразмерностьюпространства
называетсяразмерностьюпространства .
.Размерность векторного пространства, состоящего из одного нулевого вектора, принимается равной нулю.
Размерность
пространства  обычно обозначают символом.
обычно обозначают символом.
Векторное
пространство  называетсябесконечномерным, если
в нем существует любое число линейно
независимых векторов. В этом случае
пишут.
называетсябесконечномерным, если
в нем существует любое число линейно
независимых векторов. В этом случае
пишут.
Выясним связь между понятиями базиса и размерности пространства.
ТЕОРЕМА.
 – векторное пространство размерности
– векторное пространство размерности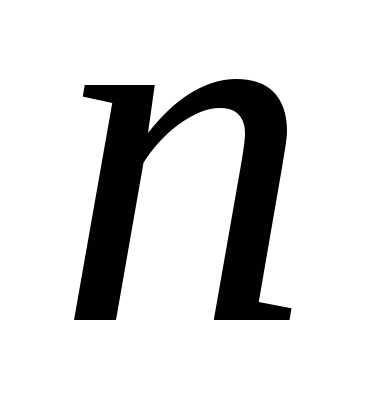 ,
то любые
,
то любые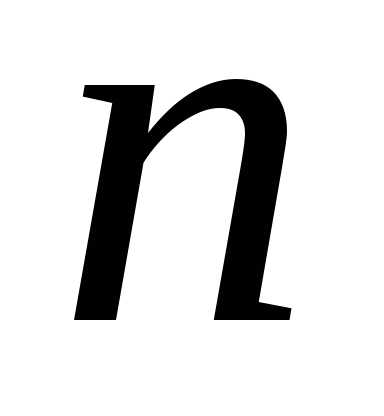 линейно независимых векторов этого
пространства образуют его базис.
линейно независимых векторов этого
пространства образуют его базис.ТЕОРЕМА.Если векторное пространство
имеет базис, состоящий из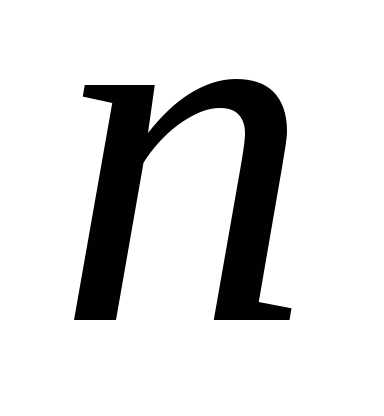 векторов, то.
векторов, то.
Утверждение
 Rn=n.
Rn=n.
Типовые примеры
Образуют ли базис в пространстве R3 векторы ?
►По определению базис составляют линейно независимые векторы. Линейная зависимость (или независимость) определяется исходя из анализа равенства нулю линейной комбинации этих векторов:
.
Последнее
векторное уравнение после записи его
по компонентам представляет собой
систему трёх однородных уравнений
относительно 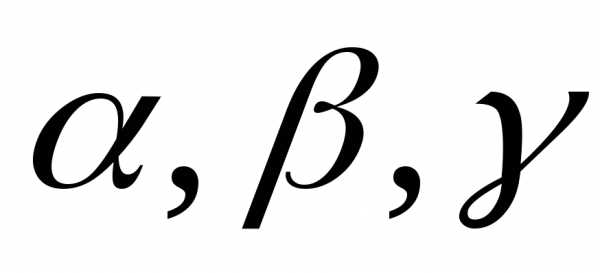 .
Согласно схеме исследования линейной
зависимости векторов вычислим
определитель матрицы, составленной из
координат векторов
.
Согласно схеме исследования линейной
зависимости векторов вычислим
определитель матрицы, составленной из
координат векторов
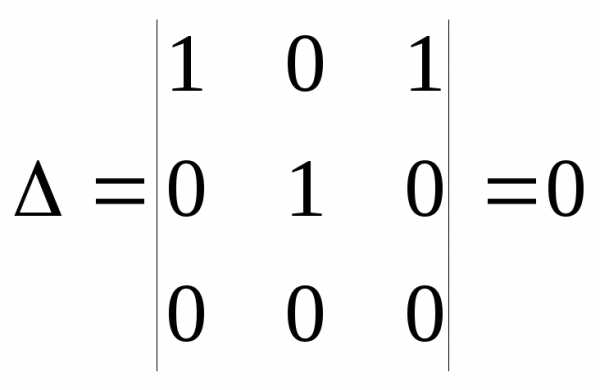
Определитель системы равен нулю, следовательно, она имеет нетривиальное решение и это означает, что исходная группа векторов линейно зависима и не образует базис в R3. ◄
2.Найти размерность и один из базисов линейного пространства решений однородной системы:
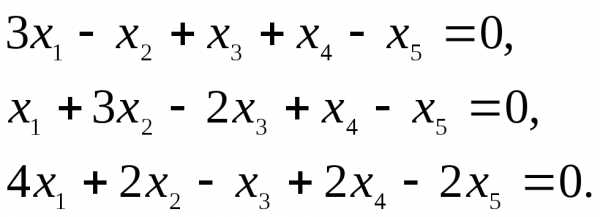
►Представленная система состоит из трёх уравнений и содержит 5 неизвестных. Выпишем матрицу системы и упростим её с помощью элементарных преобразований, сначала поменяв местами строки 1 и 2, а затем вычитая новую первую строку, умноженную на 3 и 4, соответственно из второй и третьей строк :
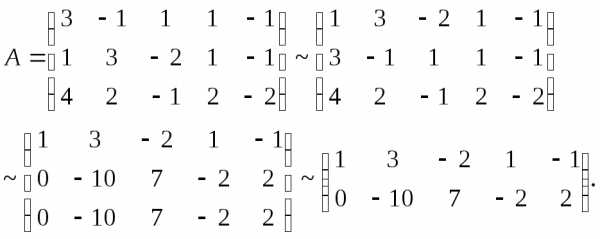
Видно,
что ранг матрицы  равен 2. Следовательно, две неизвестные
являются главными, а три — свободными.
Значит ФСР системы содержит 5-2=3 линейно
независимых решения. Выберем в качестве
главных
равен 2. Следовательно, две неизвестные
являются главными, а три — свободными.
Значит ФСР системы содержит 5-2=3 линейно
независимых решения. Выберем в качестве
главных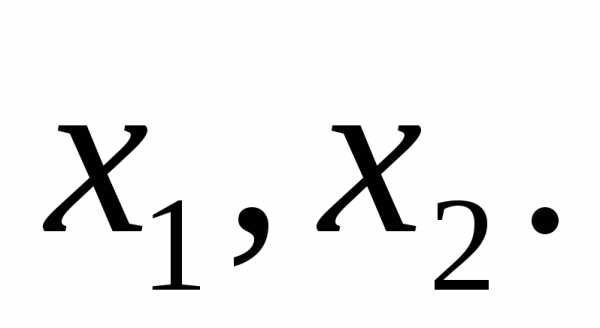 .
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид
.
Это можно сделать, т.к. минор 2-го порядка,
составленный из коэффициентов при этих
неизвестных, отличен от нуля. Система,
соответствующая преобразованной
матрице, имеет вид
Отсюда, выражая главные неизвестные через свободные, получим общее решение
Или иначе:
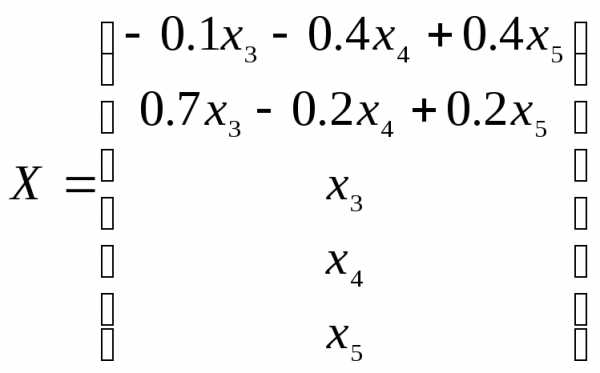 .
.
Фундаментальная совокупность решений является базисом линейного пространства решений исходной системы и в данном случае имеет вид
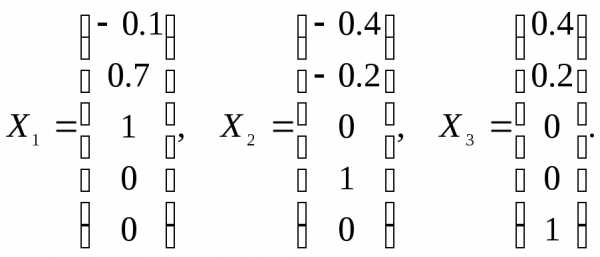
Размерность искомого пространства равна 3.◄
Матрицей
переходаот базиса к базису
к базису называется матрица вида
называется матрица вида
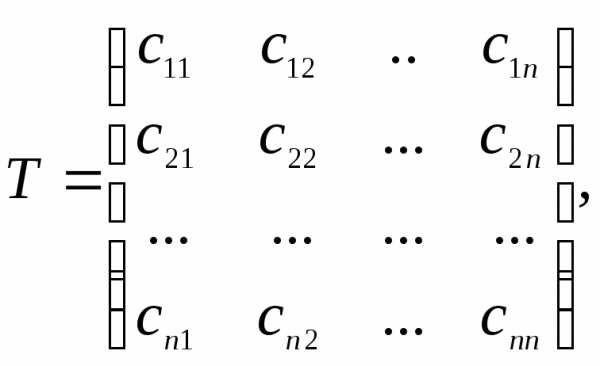
где
для каждого
в  -ом
столбце стоят координатывектора
-ом
столбце стоят координатывектора
 .
.Утверждение
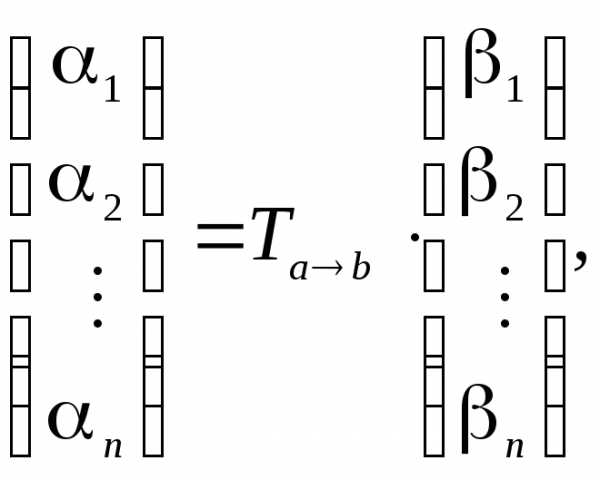
Координаты
вектора в базисе
в базисе и координатыэтого же вектора в базисе
и координатыэтого же вектора в базисе связаны равенством
связаны равенством
где 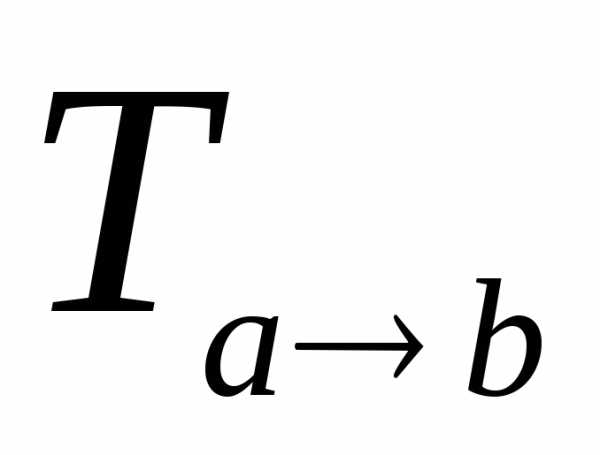 — матрица перехода от базиса
— матрица перехода от базиса к базису
к базису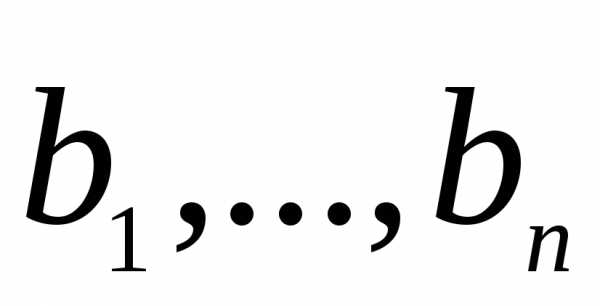 .
.
Утверждение. Матрица перехода 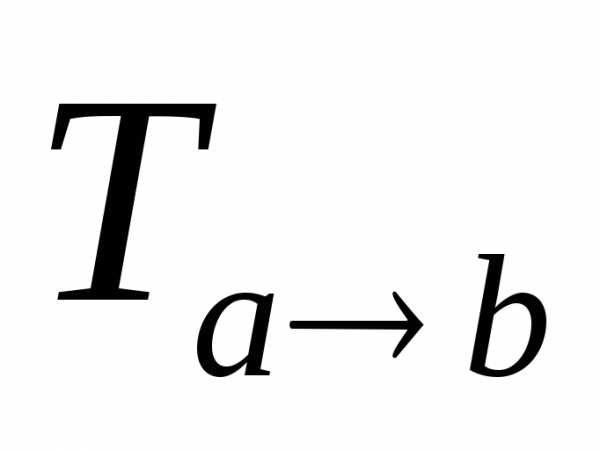 от базиса
от базиса к базису
к базису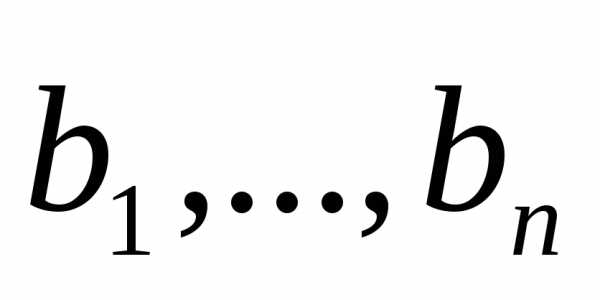 и матрица обратного перехода
и матрица обратного перехода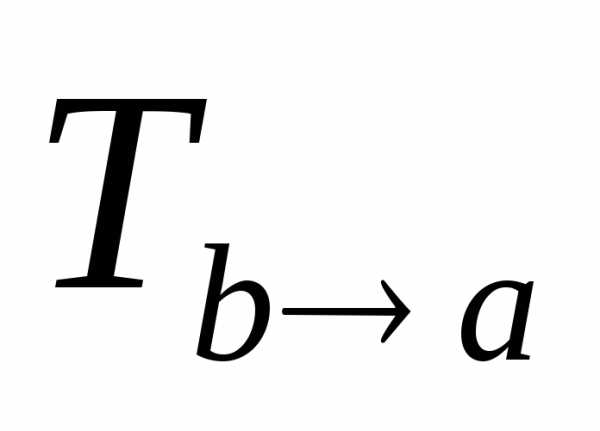 от базиса
от базиса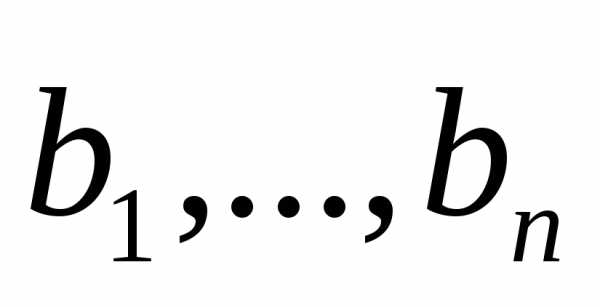 к базису
к базису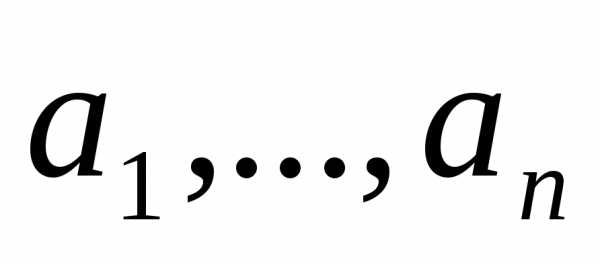 связаны равенством
связаны равенством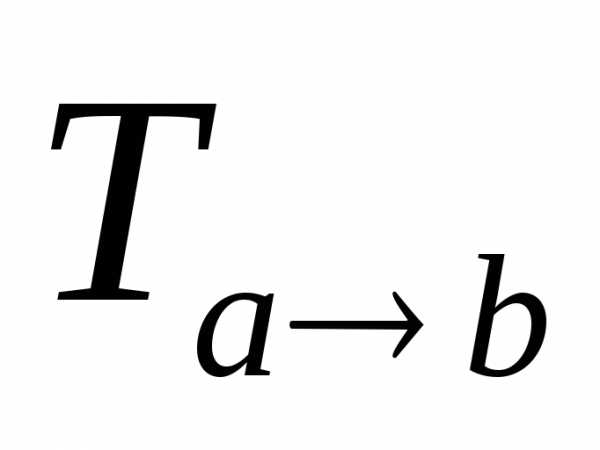 =
= .
.
Типовые примеры
1.Найти координаты вектора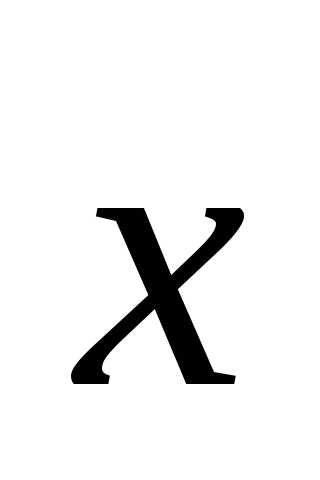 в базисе
в базисе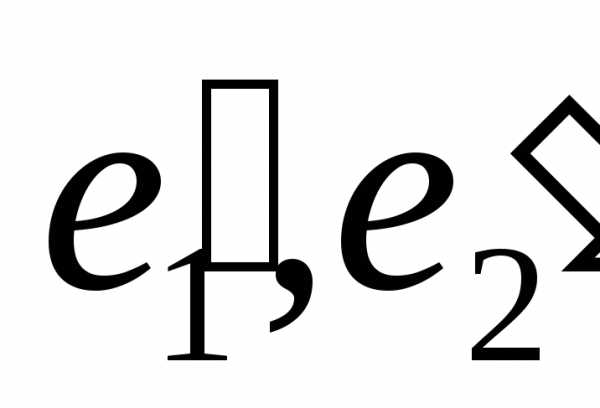 ,
если известно
,
если известно
►В
соответствии с определением матрица
перехода от базиса 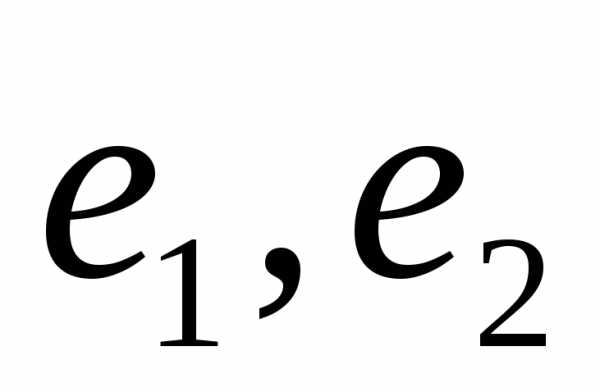
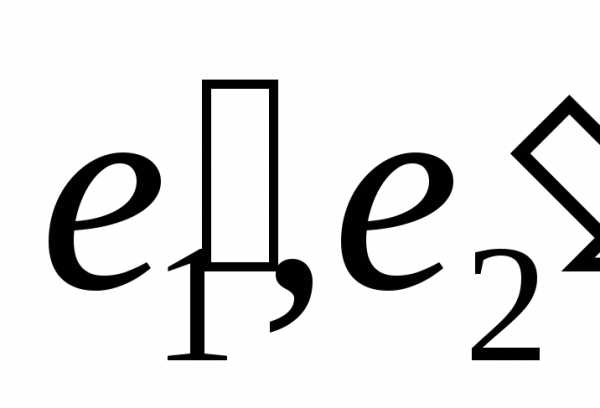 есть
есть 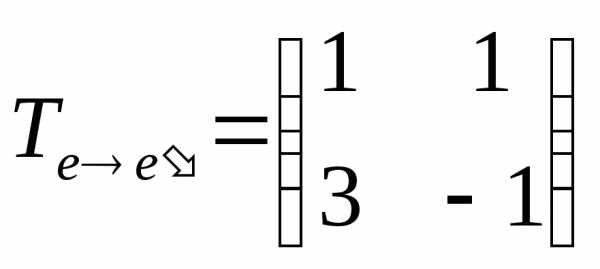 .
.
Обозначим
координаты вектора 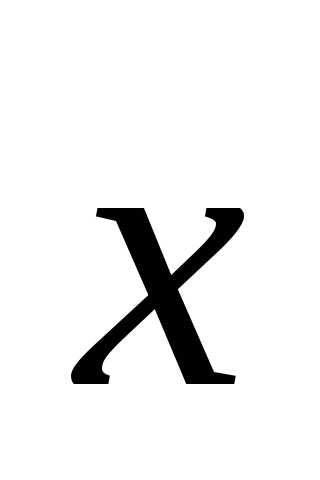 в базисе
в базисе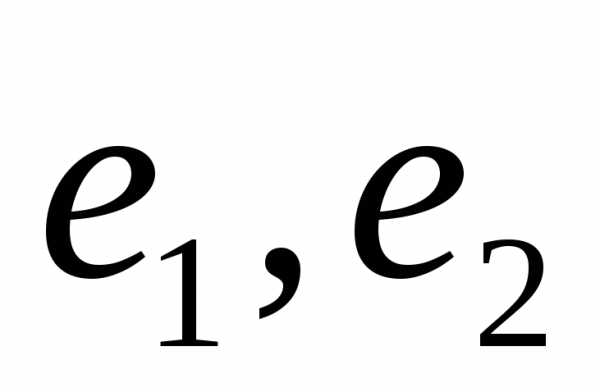 через
через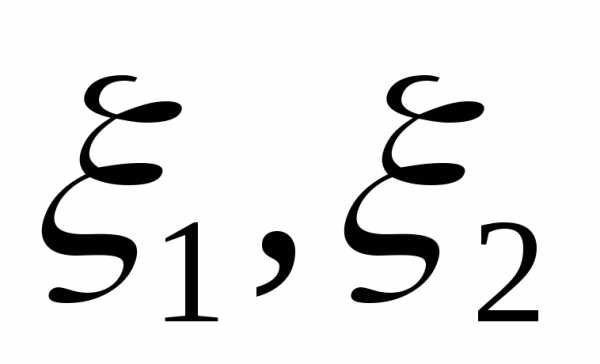 ,
а в базисе
,
а в базисе через
через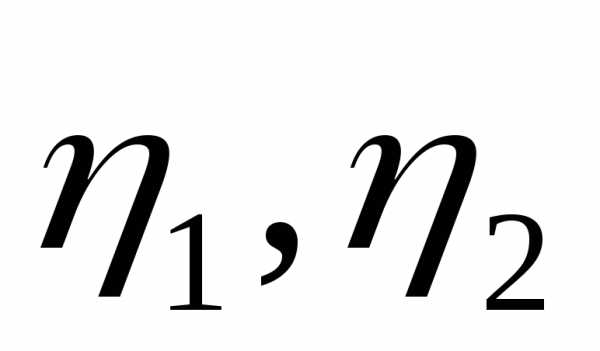 .
Искомые координаты
.
Искомые координаты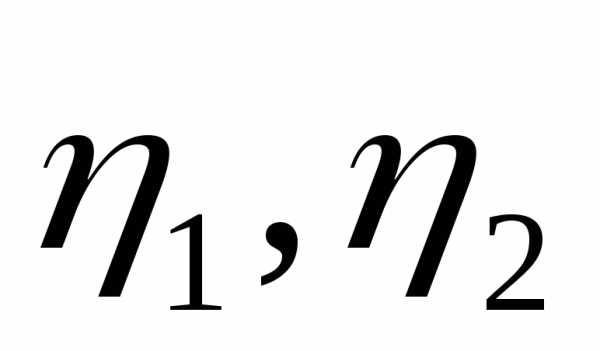 связаны с известными координатами
связаны с известными координатами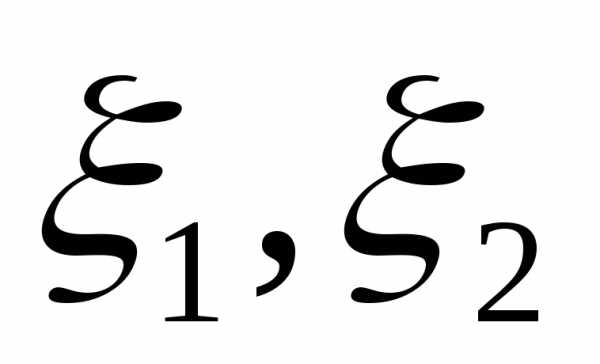 следующим соотношением:
следующим соотношением:
.
Видно,
что для получения координат 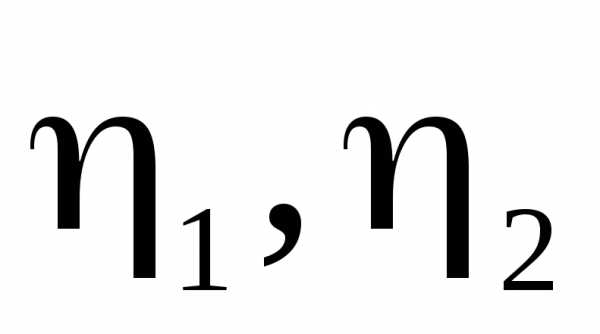 необходимо вычислить матрицу, обратную
необходимо вычислить матрицу, обратную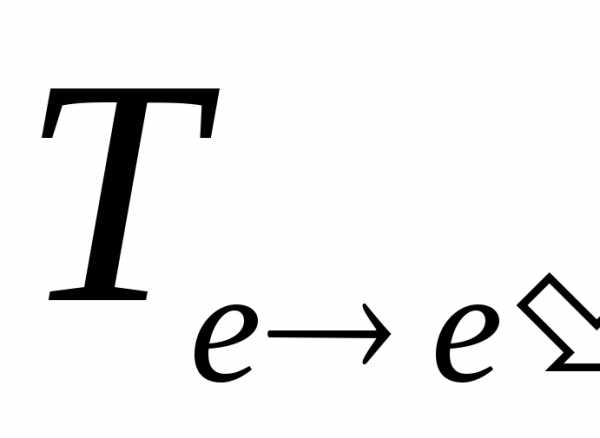 .
Используя стандартную процедуру, имеем
.
Используя стандартную процедуру, имеем
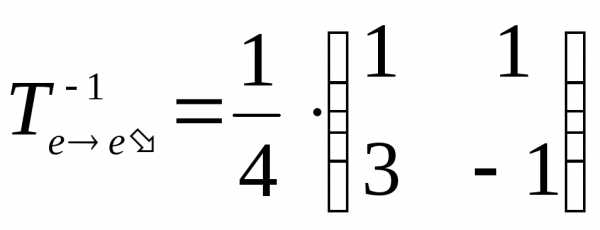 .
.
Вычислим теперь координаты 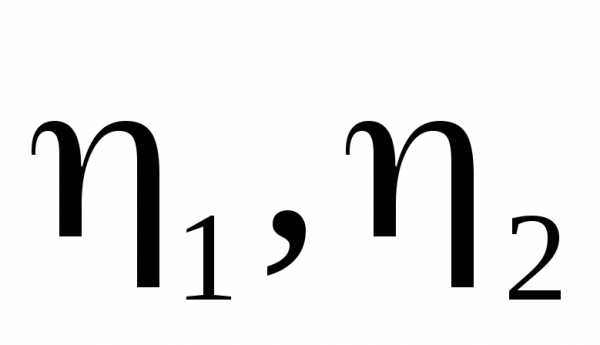 :
:
. ◄
Найти матрицу перехода от базиса
 к базису
к базису по данным разложениям этих векторов
в базисе
по данным разложениям этих векторов
в базисе :
:
.
►Чтобы
построить матрицу 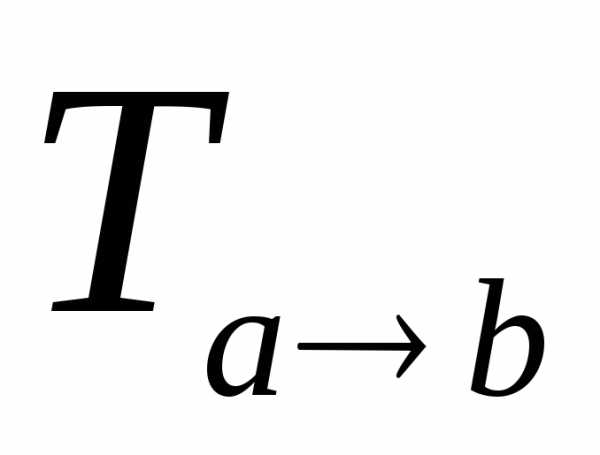 перехода
от базиса
перехода
от базиса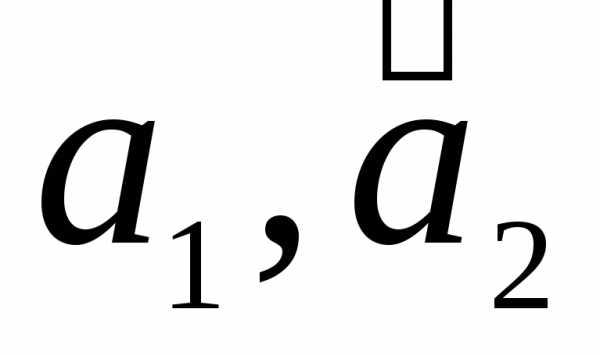 к базису
к базису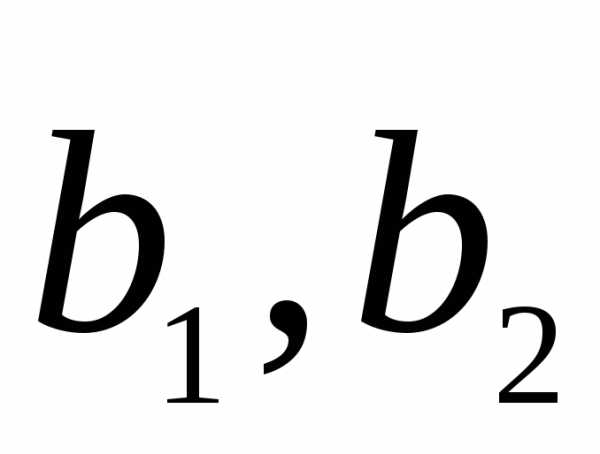 ,
необходимо найти разложение векторов
,
необходимо найти разложение векторов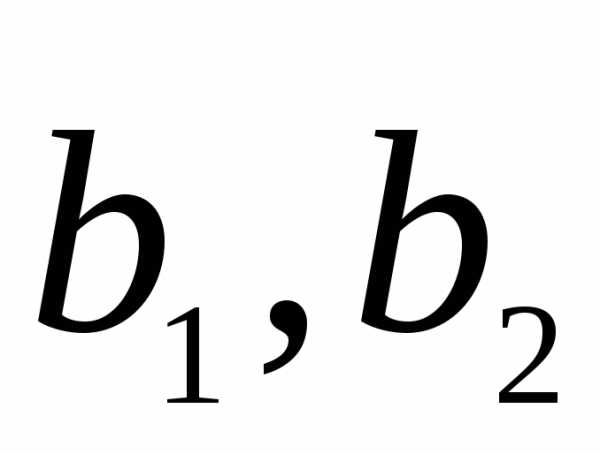 по базису
по базису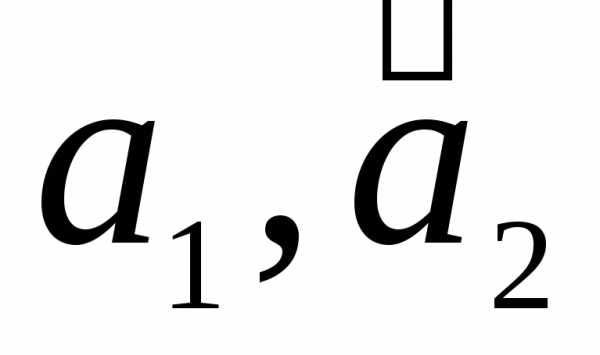 .
Сделаем это, представив
.
Сделаем это, представив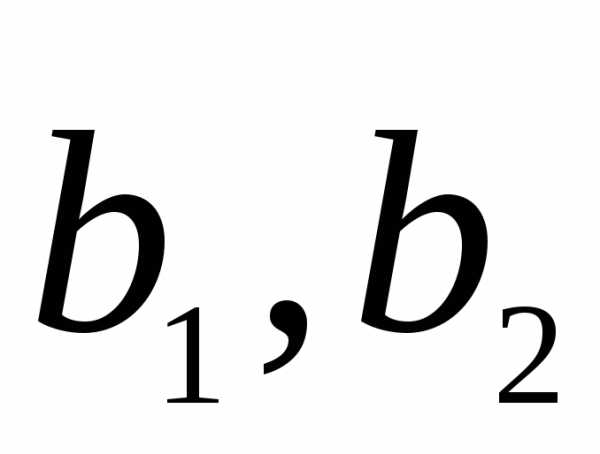 в виде разложения по
в виде разложения по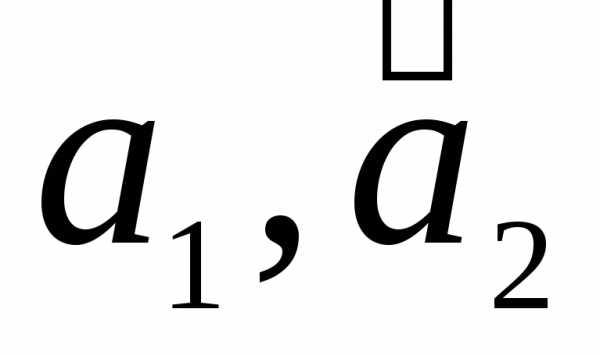 с неизвестными координатами, которые
требуется определить:
с неизвестными координатами, которые
требуется определить:
,
или с
учётом вида этих векторов в базисе 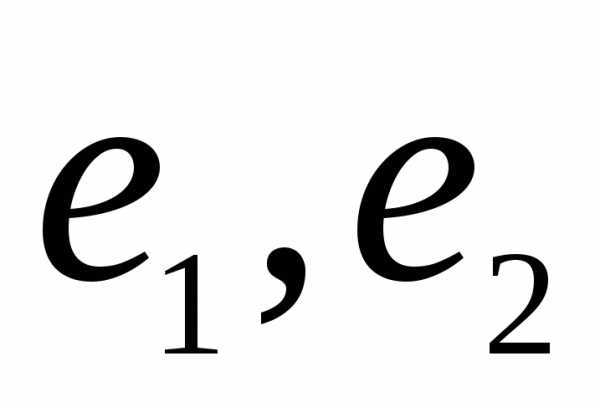
.
Откуда для координат имеем
Теперь,
зная разложение 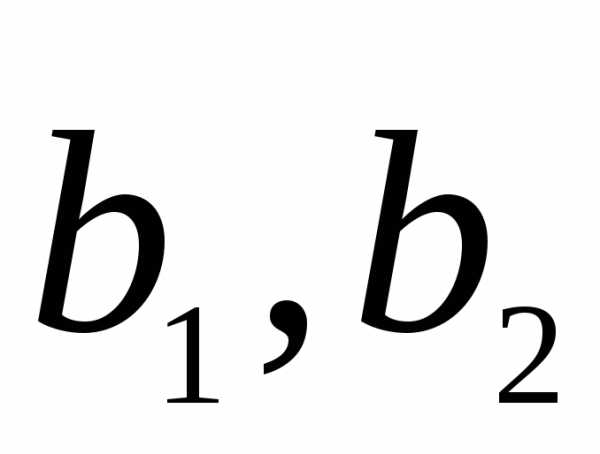 по
по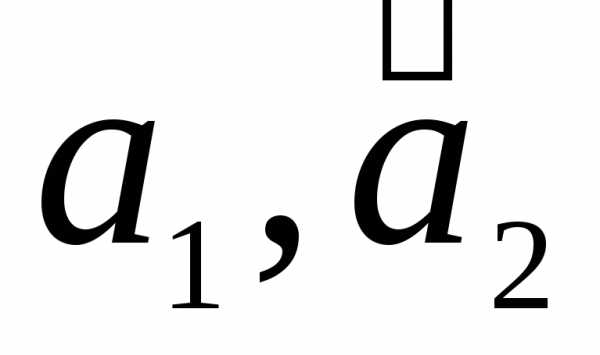 ,
выпишем матрицу
,
выпишем матрицу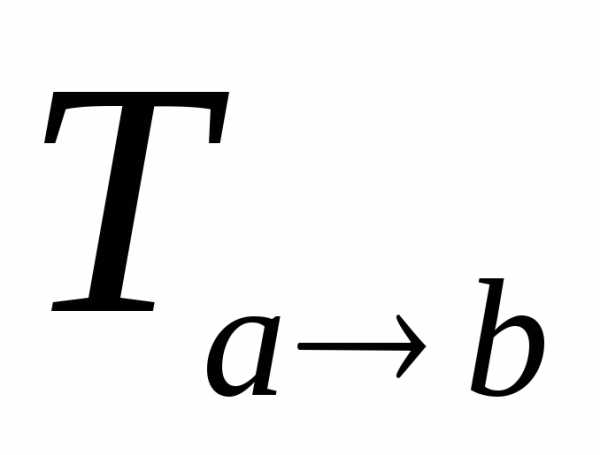 :
:
.◄
5. Линейные оболочки и подпространства
Подпространством 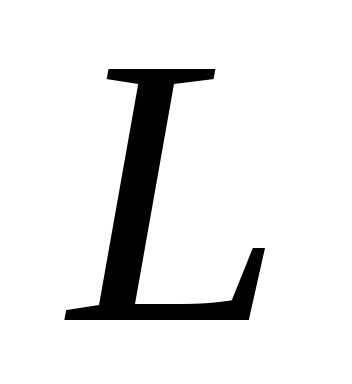 линейного пространства
линейного пространства называется множество векторов из
называется множество векторов из такое, что для любых двух векторов
такое, что для любых двух векторов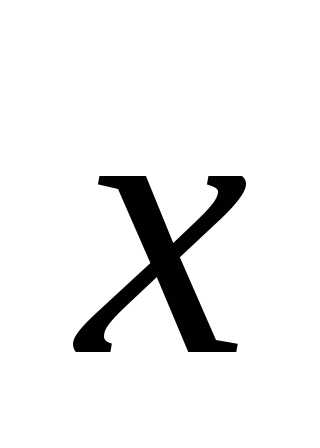 и
и из
из и любых двух вещественных чисел
и любых двух вещественных чисел и
и линейная комбинация
линейная комбинация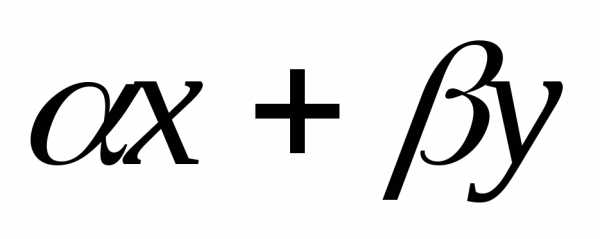 также принадлежит
также принадлежит .
.
Утверждение. Подпространство само является линейным пространством.
Линейной оболочкойсистемы векторов называется множество всех линейных
комбинаций векторов
называется множество всех линейных
комбинаций векторов .
Обозначается.
.
Обозначается.
Утверждение. Линейная оболочка системы векторов является подпространством.
Пересечениемдвух подпространств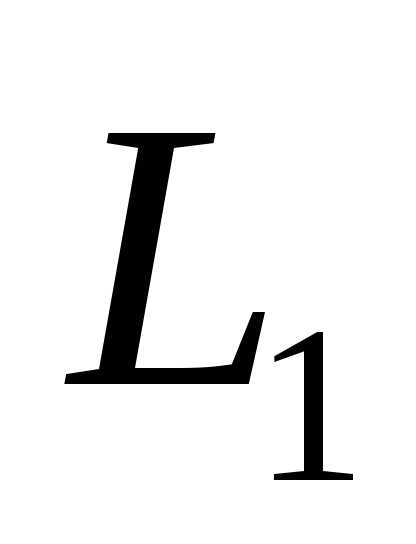 и
и 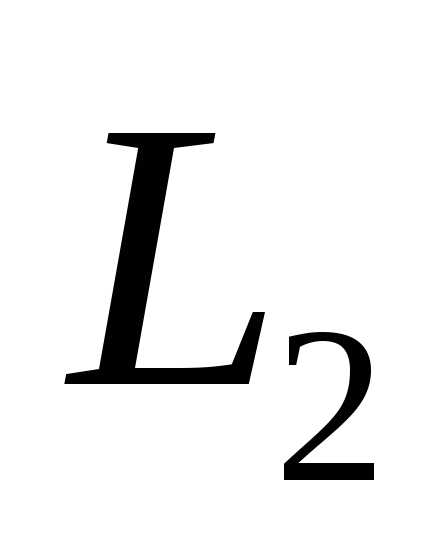 называется множество всех векторов,
принадлежащих одновременно и
называется множество всех векторов,
принадлежащих одновременно и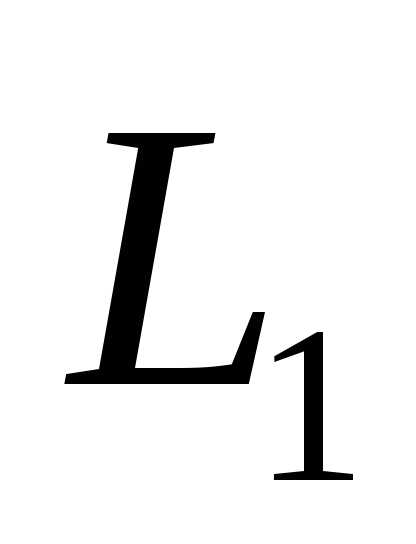 ,
и
,
и 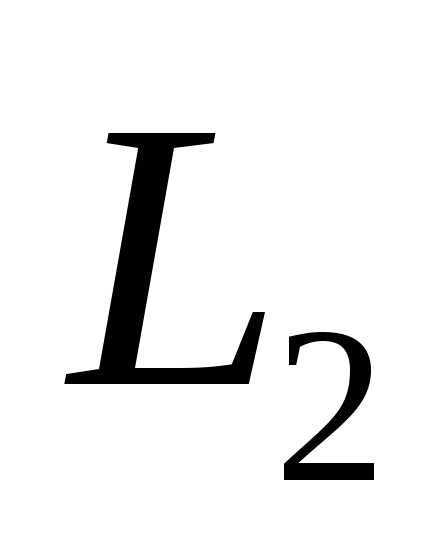 .
Обозначается
.
Обозначается 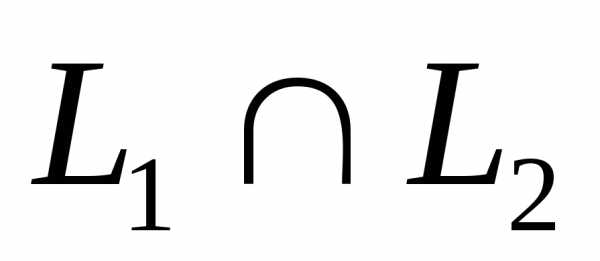 .
.
Суммой двух подпространств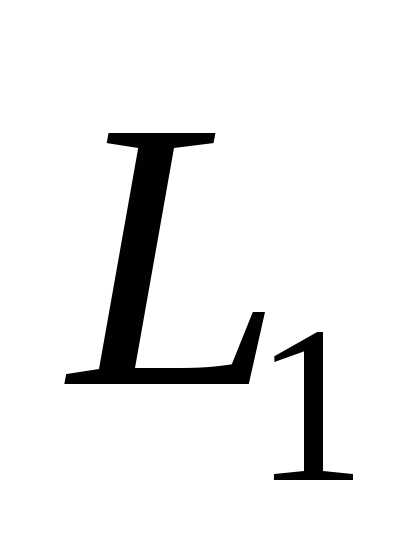 и
и 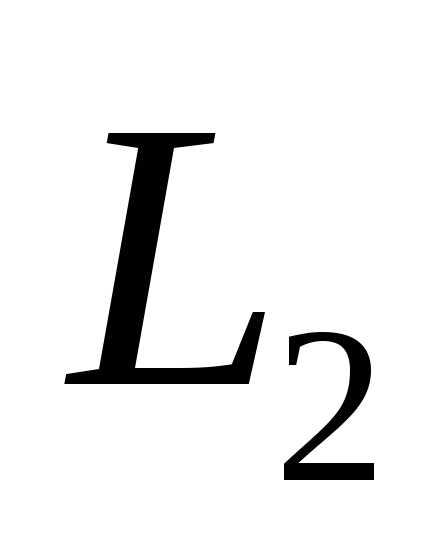 называется множество всех векторов
называется множество всех векторов ,
представимых в виде,
где
,
представимых в виде,
где
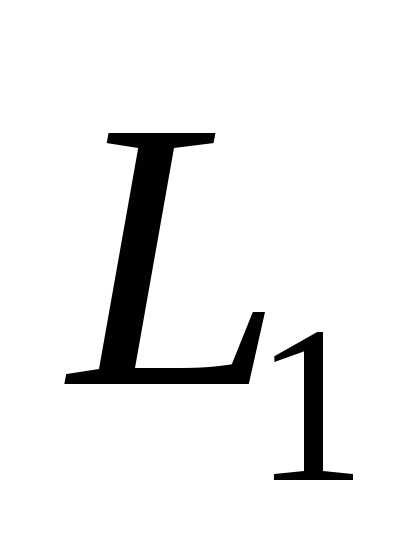 ,
, 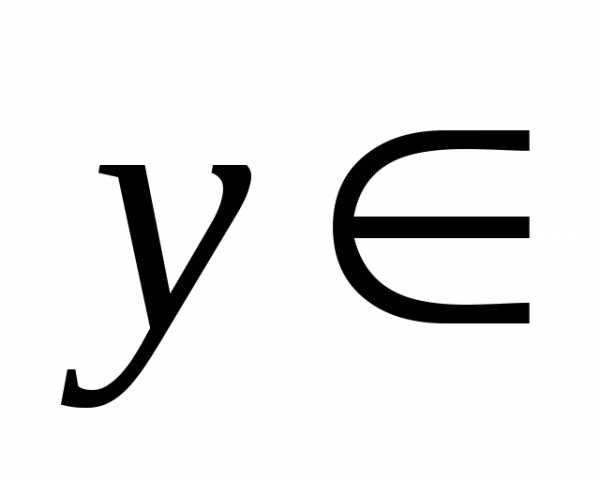
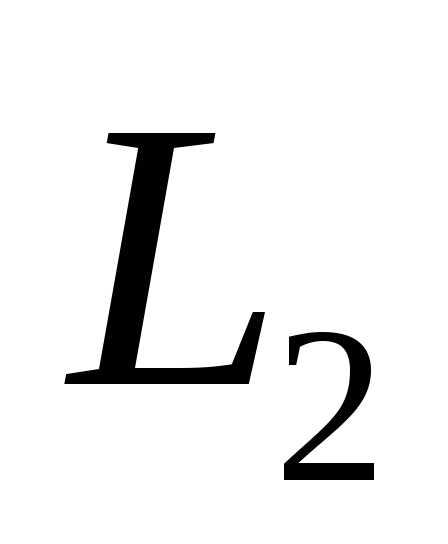 .
Обозначается
.
Обозначается 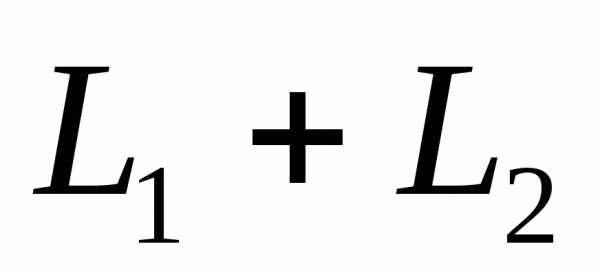 .
.
Утверждение. Сумма и пересечение
подпространств
и 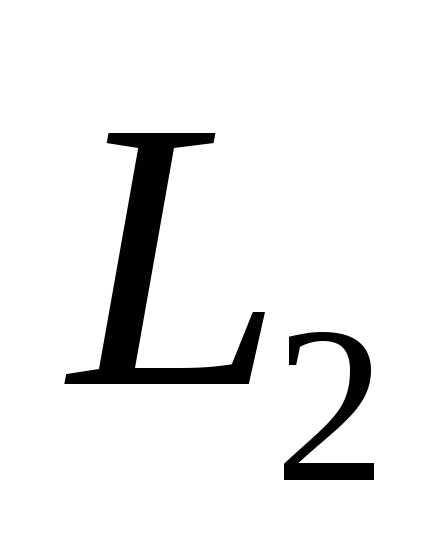 являются линейными пространствами, и
их размерности связаны равенством
являются линейными пространствами, и
их размерности связаны равенством

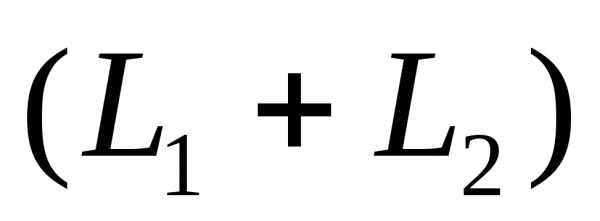 +
+
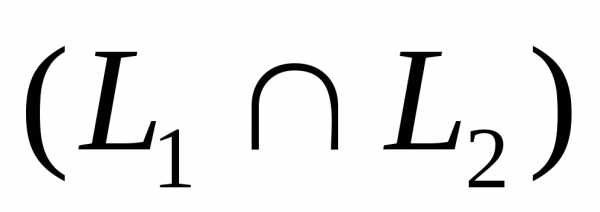 =
=
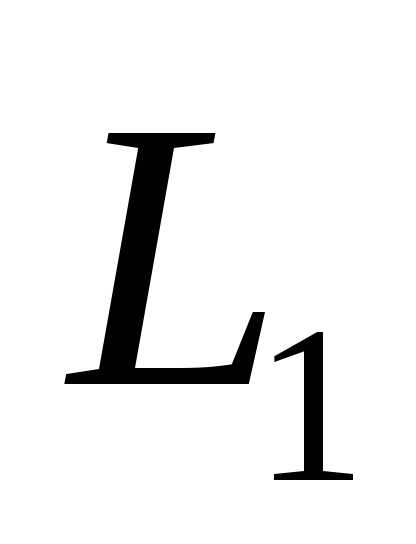 +
+
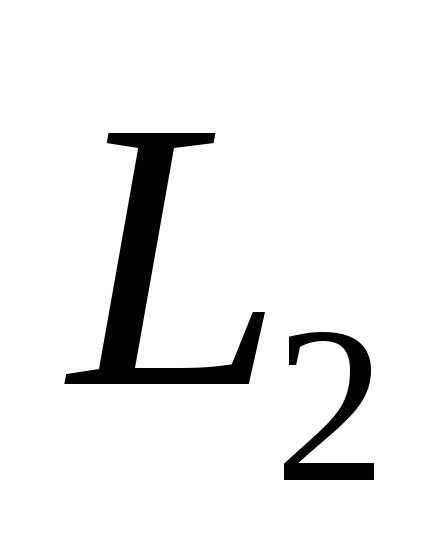 .
.
Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Типовой пример
Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами .
►Вычислим вначале размерность
подпространств. С этой целью установим,
являются ли линейно независимыми
векторы, порождающие данные подпространства.
Для подпространства 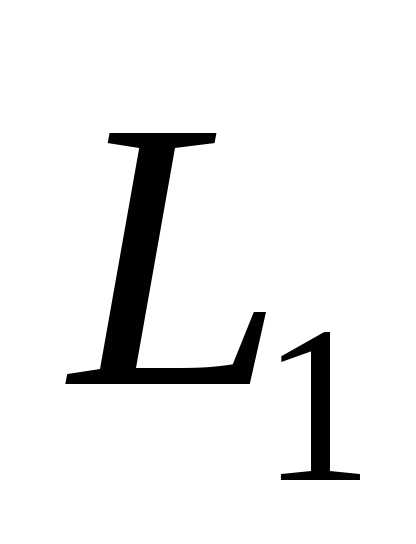 ,
порождённого векторами
,
порождённого векторами ,
равенство нулю линейной комбинации,
эквивалентное системе уравнений,
достигается лишь при условии.
Следовательно, векторы
,
равенство нулю линейной комбинации,
эквивалентное системе уравнений,
достигается лишь при условии.
Следовательно, векторы линейно независимы и размерность
подпространства
линейно независимы и размерность
подпространства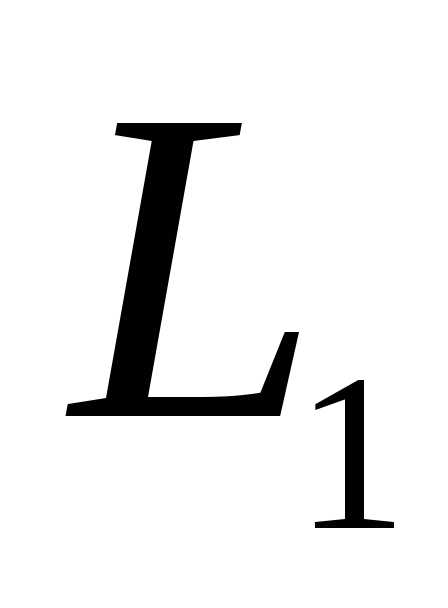 равна 2:.
Для подпространства
равна 2:.
Для подпространства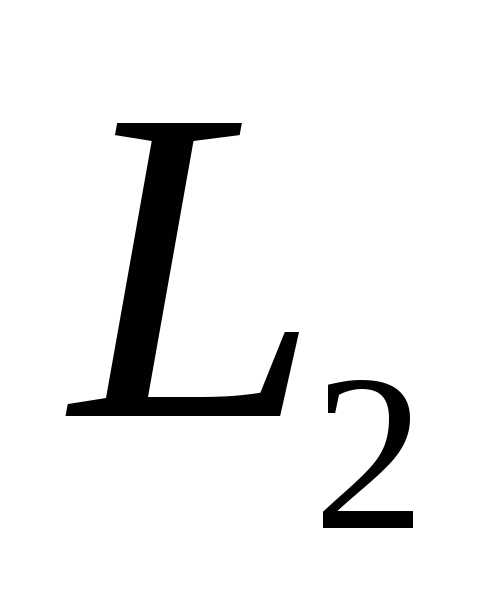 ,
порождённого векторами
,
порождённого векторами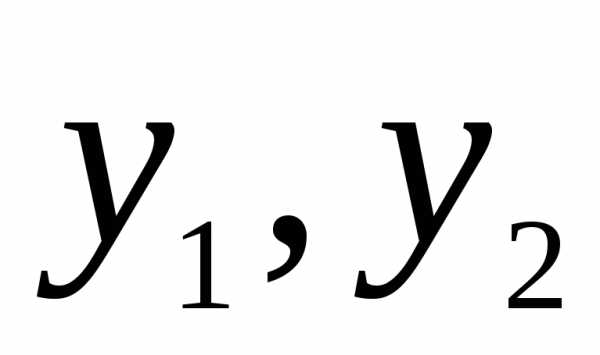 ,
проводя аналогичный анализ, получим.
,
проводя аналогичный анализ, получим.
Вычислим теперь размерность пересечения
подпространств 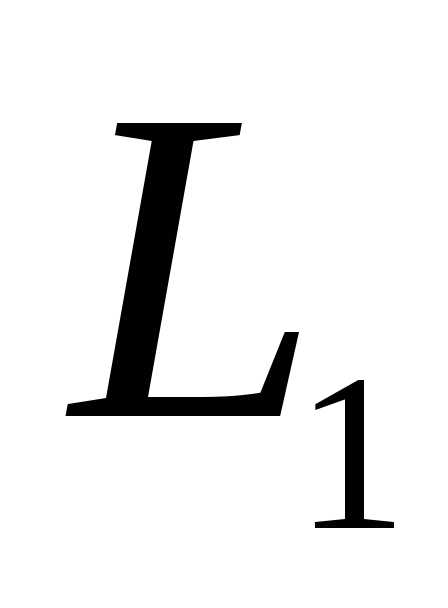 и
и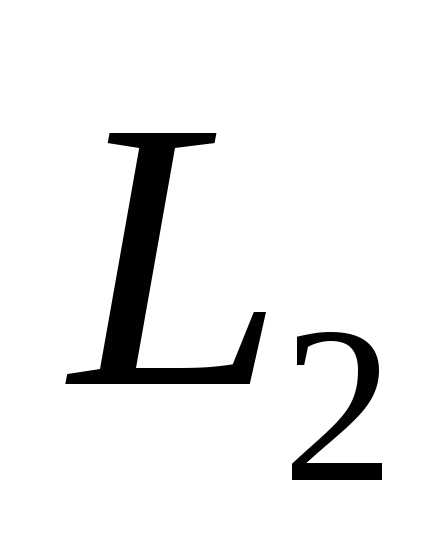 .
По определению векторы, составляющие
пересечение, принадлежат одновременно
обоим подпространствам. Произвольный
вектор
.
По определению векторы, составляющие
пересечение, принадлежат одновременно
обоим подпространствам. Произвольный
вектор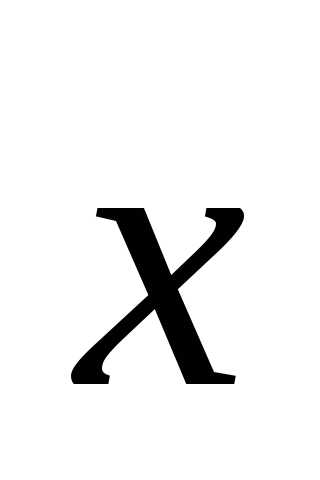 подпространства
подпространства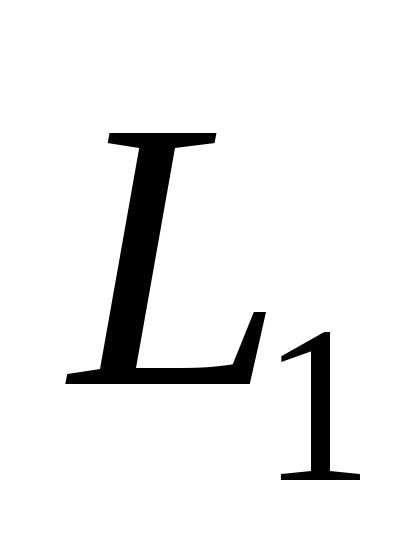 является линейной комбинацией базисных
векторов
является линейной комбинацией базисных
векторов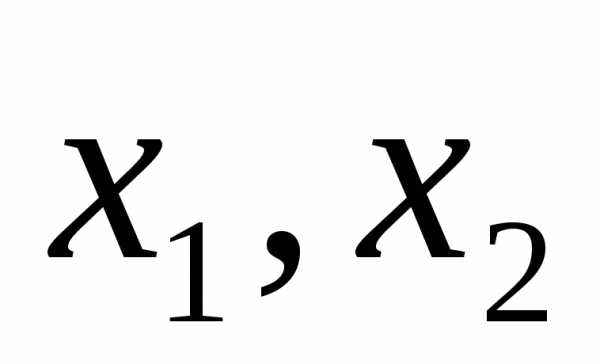 :.
Аналогично для подпространства
:.
Аналогично для подпространства имеем,
тогда условие принадлежности пересечению
естьили.
имеем,
тогда условие принадлежности пересечению
естьили.
Это условие представляет собой систему уравнений относительно коэффициентов . Составим матрицу системы и упростим её с помощью элементарных преобразований:
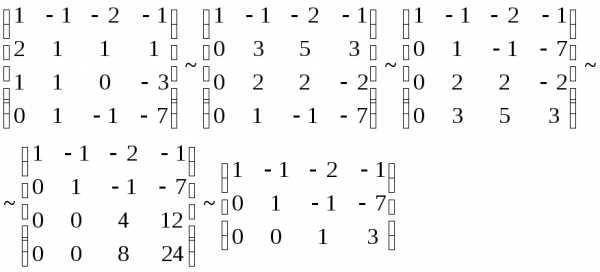
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим ,
откуда .
Полагая свободное неизвестное 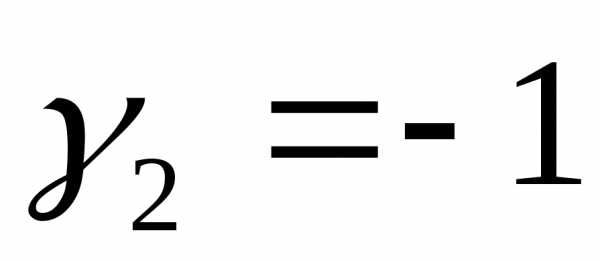 ,
для остальных имеем
,
для остальных имеем
.
Итак, пересечение подпространств имеет
один базисный вектор
имеет
один базисный вектор
.
Размерность пересечения . Следовательно, в соответствии с равенством

размерность суммы подпространств
.
В качестве базиса суммы подпространств
можно взять, например, векторы,
дополненные вектором .
В линейной независимости векторов
.
В линейной независимости векторов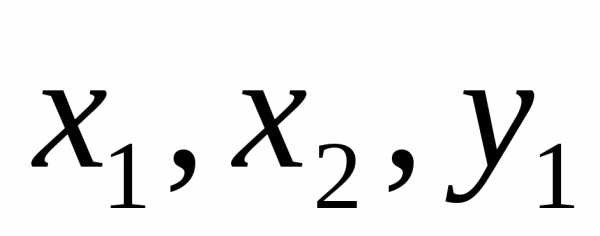 убедиться нетрудно.◄
убедиться нетрудно.◄
studfiles.net
размерность и базис, разложение вектора по базису, базис линейного пространства
В статье о n-мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n-мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Yandex.RTB R-A-339285-1Введем некоторые определения.
Определение 1Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Определение 2Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n-векторов. Размерность его соответственно равна n. Возьмем систему из n-единичных векторов:
e(1)=(1, 0,…,0)e(2)=(0, 1,…,0)e(n)=(0, 0,…,1)
Используем эти векторы в качестве составляющих матрицы A: она будет являться единичной с размерностью n на n. Ранг этой матрицы равен n. Следовательно, векторная система e(1), e(2),…, e(n) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n, то размерность пространства n-мерных векторов равна n, а единичные векторы e(1), e(2),…, e(n) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n-мерных векторов, в которой число векторов меньше n, не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e(2), e(1),…, e(n). Она также будет являться базисом n-мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n. Система e(2), e(1),…, e(n) линейно независима и является базисом
zaochnik.com
Базис и размерность линейного пространства. Переход к новому базису — ПриМат
Задача №1
Условие задачи
Векторы и заданы своими координатами в некотором базисе. Показать, что векторы сами образуют базис, и найти координаты вектора в этом базисе:
, , ; ; .
Эту задачу можно решить двумя способами.
Задача №2
Условие задачи
Доказать, что каждая из двух систем векторов является базисом, и найти связь координат одного и того же вектора в этих двух базисах:
, , ; , , .
Задача №3
Условие задачи
Найти размерность и базис линейных подпространств, натянутых на следующие системы векторов:
, , , , .
Литература:
- Белозёров Г.С. Конспект лекций.
- Проскуряков И.В. Сборник задач по линейной алгебре. М.:Наука, 1984 — стр.167-170.
- Воеводин В.В. Линейная алгебра. М.: Наука, 1980 — стр.52.
Тест на тему «Базис и размерность линейного пространства. Переход к новому базису»
Лимит времени: 0
Информация
Тест на знание темы «Базис и размерность линейного пространства. Переход к новому базису»
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 4
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
- С ответом
- С отметкой о просмотре
ib.mazurok.com
Лекция 3
1.6. Размерность линейного пространства
Эта важнейшая характеристика линейного пространства связана со свойствами систем векторов в этом пространстве.
Определение 1.5. Максимальное количество линейно независимых векторов в данном линейном пространстве называют размерностью линейного пространства.
Если размерность линейного пространства С равна n, т.е. существует линейно независимая система из п векторов, а любая система векторов, содержащая вектор или более, линейно зависима, то говорят, что это линейное пространство п-мерно. Размерность такого линейного пространства обозначают
Существуют линейные пространства, в которых можно выбрать линейно независимую систему, содержащую сколь угодно большое количество векторов. Такие линейные пространства называют бесконечномерными. В отличие от них, n-мерные линейные пространства называют конечномерными. Мы будем рассматривать конечномерные линейные пространства.
Пример 1.12. Линейное пространство функций, непрерывных на отрезке [0,1] (см. 1.1), является бесконечномерным, так как для любого натурального п система многочленов , являющихся элементами этого линейного пространства, линейно независима. В самом деле, линейная комбинация этих многочленов, отвечающая набору коэффициентов , есть многочлен
,
который является нулевым (т.е. равен постоянной функции 0), только если все его коэффициенты (они же коэффициенты линейной комбинации) равны нулю.
Оказывается, что размерность линейного пространства тесно связана с количеством векторов, которое может иметь базис линейного пространства.
Теорема 1.4. Если линейное пространство n-мерно, то любая линейно независимая система из п векторов является его базисом.
Пусть система векторов линейно независима. Тогда для любого вектора система векторов линейно зависима, так как она содержит вектор, т.е. количество большее, чем размерность линейного пространства. Это значит, что существуют такие коэффициенты , одновременно не равные нулю, что
(1.6)
Заметим, что , так как в противном случае равенство (1.6) сводится к равенству
причем среди коэффициентов есть хотя бы один ненулевой (так как ). Но это означало бы, что система векторов линейно зависима. Учитывая, что , из (1.6) находим
Так как вектор х был выбран произвольно, заключаем, что любой вектор в линейном пространстве можно представить в виде линейной комбинации системы векторов Поэтому эта система векторов, по предположению линейно независимая, является базисом в .
Теорема 1.5. Если в линейном пространстве существует базис из п векторов, то .
(Без доказательства)
Из теорем 1.4 и 1.5 следует, что в каждом линейном пространстве любые два базиса содержат одно и то же количество векторов, и это количество равно размерности линейного пространства.
Пример 1.13. В линейном арифметическом пространстве стандартный базис (1.5) состоит из п векторов, поэтому , что и отражено в обозначении этого линейного пространства.
Пример 1.14. Рассмотрим однородную СЛАУ
множество решений которой образует линейное пространство. Найдем размерность этого линейного пространства и какой-либо базис в нем.
Решим эту систему, определив ее фундаментальную систему решений. Для этого запишем матрицу системы и при помощи элементарных преобразований строк приведем ее к треугольному виду:
Из полученного находим, что в качестве свободных неизвестных можно взять и , а в качестве базисных неизвестных — и .Преобразованная система имеет вид
Полагая и , находим и , а при и имеем и . Записав найденные решения в виде столбцов, получим фундаментальную систему решений:
Согласно теории систем линейных алгебраических уравнений, эти два решения линейно независимы, а любое другое решение СЛАУ представляется в виде их линейной комбинации. Другими словами, столбцы и образуют базис в линейном пространстве решений рассматриваемой однородной СЛАУ. Размерность этого линейного пространства равна двум — количеству векторов в базисе.
1.7. Преобразование координат вектора при замене базиса
В линейном пространстве все базисы равноправны. Тот или иной базис выбирают исходя из конкретных обстоятельств, а может быть, и вообще произвольно. Иногда удобно использовать для представления элементов линейного пространства несколько базисов, но тогда естественным образом возникает задача преобразования координат векторов, которое связано с изменением базиса.
Пусть в n-мерном линейном пространстве заданы два базиса: старый и новый . Любой вектор можно разложить по базису b. В частности, каждый вектор из базиса с может быть представлен в виде линейной комбинации векторов базиса b:
Запишем эти представления в матричной форме:
или , где
(1.7)
Определение 1.6. Матрицу (1.7) называют матрицей перехода от старого базиса b к новому базису с.
Согласно данному определению, i-й столбец матрицы перехода есть столбец координат i-го вектора нового базиса в старом. Поэтому говорят, что матрица перехода состоит из координат векторов нового базиса в старом, записанных по столбцам.
Обсудим некоторые свойства матрицы перехода.
1°. Матрица перехода невырождена и всегда имеет обратную.
Действительно, столбцы матрицы перехода — это столбцы координат векторов нового базиса в старом. Следовательно, они, как и векторы базиса, линейно независимы. Значит, матрица U невырожденная и имеет обратную матрицу .
2°. Если в n-мерном линейном пространстве задан базис b, то для любой невырожденной квадратной матрицы U порядка п существует такой базис с в этом линейном пространстве, что U будет матрицей перехода от базиса b к базису с.
Из невырожденности матрицы U следует, что ее ранг равен n, и поэтому ее столбцы, будучи базисными, линейно независимы. Эти столбцы являются столбцами координат векторов системы . Линейная независимость столбцов матрицы U равносильна линейной независимости системы векторов с. Так как система с содержит п векторов, причем линейное пространство п-мерно, то, согласно теореме 1.4, эта система является базисом.
Пример 1.15. Пусть — базис линейного пространства. Тогда система векторов тоже является базисом в этом линейном пространстве. Это следует из того, что
,
где диагональная матрица невырождена.
3°. Если U — матрица перехода от старого базиса b к новому базису с линейного пространства, то — матрица перехода от базиса с к базису b.
Матрица невырождена, и поэтому из равенства следует, что . Последнее равенство означает, что столбцы матрицы являются столбцами координат векторов базиса b относительно базиса с, т.е., согласно определению 1.6, — это матрица перехода от базиса с к базису b.
4°. Если в линейном пространстве заданы базисы b, с и d, причем U — матрица перехода от базиса b к базису с, а V — матрица перехода от базиса с к базису d то произведение этих матриц — матрица перехода от базиса b к базису d.
Согласно определению 1.6 матрицы перехода, имеем равенства
,
откуда
,
т.е. — матрица перехода от базиса b к базису d.
Рассмотрим теперь, как преобразуются координаты произвольного вектора в линейном пространстве при переходе от старого базиса к новому. Выберем произвольный вектор и разложим его в старом базисе:
(1.8)
Разложение того же вектора в новом базисе имеет вид.
(1.8)
Найдем связь между старыми координатами х вектора х и новыми его координатами . Из соотношений (1.8), (1.9) следует, что . Учитывая, что , получаем или . Последнее равенство можно рассматривать как запись двух разложений одного и того же вектора х в данном базисе b. Разложениям соответствуют столбцы координат х и которые, согласно теореме 1.2 о единственности разложения вектора по базису, должны быть равны:
или .
Итак, чтобы получить координаты вектора в старом базисе, необходимо столбец координат этого вектора в новом базисе умножить слева на матрицу перехода из старого базиса в новый. Матрица перехода из старого базиса в новый позволяет пересчитывать новые координаты в старые.
cos^A sin<p y
Пример 1.16. Рассмотрим в ортонормированный базис из векторов осей координат. Обозначим через новый базис, который получается поворотом старого базиса b на заданный угол . Исходя из заданного угла поворота, мы можем найти координаты векторов нового базиса относительно старогоЭти разложения позволяют составить матрицу перехода U из старого базиса b в новый e, а также обратную матрицу:
Найденные матрицы перехода U (из старого базиса в новый) и (из нового базиса в старый) позволяют записать соотношения между старыми и новыми , координатами произвольного вектора х из :
Например, вектор в старом базисе имеет координаты , а в новом базисе — ,
Вопросы и задачи
1.1. Найдите координаты вектора х в базисе , если известны его координаты в базисе, а базисы связаны соотношениями
1.2. В линейном пространстве две системы векторов и заданы своими координатами в некотором базисе:
Докажите, что эти системы являются базисами. Найдите:
а) матрицу перехода от базиса b к базису е;
б) матрицу обратного перехода от базиса е к базису b;
в) координаты вектора в обоих базисах;
г) координаты вектора в базисе е.
1.3. Найдите размерность линейного пространства матриц типа с элементами из R.
1.4. Является ли матрица матрицей перехода от одного базиса трехмерного линейного пространства к его другому базису?
1.5. Какой вид имеет матрица перехода от старого базиса к новому, если матрица перехода от нового базиса к старому является:
а) треугольной; б) симметрической; в) кососимметрической?
1.5. Может ли в пространстве матрица перехода быть кососимметрической?
1.6. При каких условиях векторы в пространстве образуют базис?
1.7. Докажите, что в линейном пространстве многочлены
,
образуют базис. Найти координаты произвольно взятого многочлена в этом базисе.
studfiles.net
1.5. Базис линейного пространства
В линейном пространстве наибольший интерес представляют системы векторов, в виде линейной комбинации которых можно представить любой вектор, причем единственным образом. Если зафиксировать такую систему векторов, то любой вектор можно будет однозначно представить набором чисел, являющихся коэффициентами соответствующей линейной комбинации, а всевозможные векторные соотношения превратить в соотношения числовые.
Этот подход применялся уже в аналитической геометрии. В пространстве векторов на плоскости любые два неколлинеарных вектора образуют базис, так как через такую пару векторов любой вектор плоскости выражается однозначно в виде линейной комбинации. Аналогично в(множестве векторов в пространстве) базис образуют любые три некомпланарных вектора. Для матриц использовалось понятие базисных строк и базисных столбцов. По теореме о базисном миноре базисные строки (столбцы) линейно независимы, а любая строка (столбец) матрицы является линейной комбинацией базисных строк (столбцов).
Определение 1.3. Базисом линейного пространства называют любую упорядоченную систему векторов, для которой выполнены два условия:
1) эта система векторов линейно независима,
2) каждый вектор в линейном пространстве может быть представлен в виде линейной комбинации векторов этой системы.
Пусть — базис в . Определение 1.3 говорит о том, что любой векторможет быть записан следующим образом:
Такую запись называют разложением вектора х по базису .
Данное нами определение базиса согласовывается с понятием базиса в пространстве свободных векторов в , или . Например, вбазисом была названа любая тройка некомпланарных векторов. Такая тройка векторов является линейно независимой, так как представление одного ее вектора в виде линейной комбинации двух других равносильна компланарности трех векторов. Но, кроме того, из курса векторной алгебры мы знаем, что любой вектор в пространстве можно выразить через произвольные три некомпланараных вектора в виде их линейной комбинации. Три компланарных вектора не могут быть базисом в , так как любая линейная комбинация таких векторов даст вектор, им компланарный.
Теорема 1.2 (о единственности разложения). В линейном пространстве разложение любого вектора по данному базису единственно.
Выберем в линейном пространстве произвольный базис и предположим, что вектор х имеет в этом базисе два разложения
Воспользуемся тем, что аксиомы линейного пространства позволяют преобразовывать линейные комбинации так же, как и обычные алгебраические выражения. Вычитая записанные равенства почленно, получим
Так как базис — это линейно независимая система векторов, ее линейная комбинация равна 0, лишь, если она тривиальная (см. определение 1.2). Значит, все коэффициенты этой линейной комбинации равны нулю: . Таким образом,и два разложения векторах в базисе совпадают.
Замечание 1.3. Условие линейной независимости векторов базиса означает, что нулевой вектор имеет в этом базисе единственное разложение, а именно тривиальное: все коэффициенты этого разложения равны нулю. Из доказательства теоремы 1.2 следует, что из единственности разложения нулевого вектора по данной системе векторов вытекает единственность разложения любого другого вектора.
Согласно определению 1.3, базис является упорядоченной системой векторов. Это значит, что, изменив порядок векторов в системе, мы получим другой базис. Порядок векторов в базисе фиксируют для того, чтобы задать определенный порядок коэффициентов разложения произвольного вектора. Это позволяет заменить линейную комбинацию, представляющую вектор, упорядоченным набором ее коэффициентов и тем самым упростить запись. Порядок векторов в базисе определяется их нумерацией.
Определение 1.4. Коэффициенты разложения вектора по базису линейного пространства, записанные в соответствии с порядком векторов в базисе, называют координатами вектора в этом базисе.
Пример 1.8. В линейном пространстве многочленов переменного степени не выше 2 (см. пример 1.1) элементы и линейно независимы: их линейная комбинация есть многочлен, который равен нулю (нулевому многочлену) лишь при. В то же время пара этих элементов не образует базиса. Действительно, многочлен 1 нулевой степени, являющийся элементом, нельзя представить в виде линейной комбинации многочленов и .Дело в том, что линейная комбинация многочленов и есть либо многочлен второй степени (при ), либо многочлен первой степени(, ), либо нулевой многочлен(). Значит, равенство двух многочленов невозможно ни при каких значениях коэффициентов.
В то же время три многочлена 1, и образуют базис линейного пространства . Докажем это.
Во-первых, система многочленов 1, и линейно независима. Составим их линейную комбинацию с произвольными коэффициентами и приравняем нулю: . Это равенство есть равенство двух многочленов, и оно возможно только в случае, когда коэффициенты этих двух многочленов совпадают. Значит,.
Во-вторых, через многочлены 1, и можно выразить любой многочлен второй степени, т.е. любой элемент линейного пространства можно представить в виде линейной комбинации указанных трех элементов.
Итак, система трех многочленов 1, и линейно независима, а любой элемент линейного пространства является линейной комбинацией указанной системы. Согласно определению 1.3, система многочленов 1, и есть базис в .
Пример 1.10. В линейном арифметическом пространстве векторы
образуют базис , так как они линейно независимы (см. пример 1.5) и любой векторпредставим в виде
Такой базис (1.5) в пространстве называютстандартным. Отметим, что запись элементов арифметического пространства в виде столбца не противоречит определению арифметического пространства, понимаемого как множество упорядоченных совокупностей чисел. Порядок же элементов можно указывать как при помощи записи в строку, так и при помощи записи в столбец.
Пример 1.11. Покажем, что в система векторов образует базис и найдем в этом базисе координаты вектора
Для того чтобы доказать, что система векторов ,, образует базис, надо убедиться в линейной независимости этих векторов и в том, что любой вектор является их линейной комбинацией.
В стандартном базисе е в векторыимеют следующие столбцы координат:
Из стобцов координат векторов составим матрицу
и рассмотрим квадратную систему линейных алгебраических уравнений (СЛАУ) ,Так как, то матрицаневырожденная, ее ранг равен 3 и все ее столбцы являются базисными. Поэтому, во-первых, согласно теореме о базисном миноре, эти столбцы линейно независимы, значит, СЛАУ при любом столбце правых частей имеет решение
В частности, решив СЛАУ , которая в координатной форме имеет вид
находим координаты вектора в базисе:
.
studfiles.net
2.3. Линейные векторные пространства. Базис линейного пространства
Понятия одно- двух- и трехмерного арифметических векторов может быть естественным образом обобщено на векторы любой размерности.
Определение 2.4. n-мерным арифметическим вектором называют последовательность n чисел – координат вектора.
Множество
всех n-мерных арифметических векторов,
координатами которых являются
действительные числа, обозначают Rn  ,
Записывают n-мерные арифметические
векторы либо в виде строки:
,
Записывают n-мерные арифметические
векторы либо в виде строки:
| (2.18) |
либо в виде столбца:
| (2.19) |
Все основные понятия и все операции над одно-, двух- и трехмерными арифметическими векторами (разд. 2.2), за исключением векторного умножения, естественным образом обобщаются на векторы произвольной размерности. Однако в разд. 2.2 не был введен ряд важных понятий, характеризующих множества арифметических векторов любой размерности. Основным понятием векторной алгебры является понятие линейного векторного пространства, но прежде, чем ввести это понятие, дадим определение множества, замкнутого относительно операции.
Определение 2.5. Множество называют замкнутым относительно какой-либо операции, определенной в этом множестве, если в результате выполнения этой операции получают элемент этого же множества.
Примеры.
1. МножествоV2 геометрических векторов на плоскости замкнуто относительно операций умножения на число и сложения, так как, умножив вектор на любое число, сложив векторы или построив их линейную комбинацию, получим вектор, принадлежащий этой же плоскости. Однако относительно векторного умножения V2 не замкнуто, поскольку результат такой операции – вектор, перпендикулярный плоскости, в которой лежат векторы множители.
2. Пусть V0 — множество векторов на прямой, имеющих целочисленные координаты. (Например, ). V0 замкнуто относительно операции сложения: складывая или вычитая целые числа, вновь получают целое число. Однако V0 не замкнуто относительно умножения на число: умножив вектор на дробное или иррациональное число, целочисленной координаты получить нельзя.
Понятие замкнутости множества относительно какой-либо операции относится не только к множествам векторов, но и, например, к множествам чисел. Так множество всех целых чисел замкнуто относительно операций сложения, вычитания и умножения, но не замкнуто относительно деления: поделив одно целое число на другое, не всегда получают целое число, может получиться дробь. Множество всех действительных чисел замкнуто относительно деления, если из него исключить число нуль (на нуль делить нельзя).
Пусть L множество n-мерных арифметических векторов, координатами которых являются действительные числа. Определены операции умножения вектора на число и сложения векторов, обладающие свойствами 1-8 (см. разд. 1.3).
Определение 2.6. Множество векторов L называют линейным векторным пространством над полем действительных чисел6, если L замкнуто относительно операций умножения на число и сложения.
Пусть — n-мерные векторы.. Рассмотрим линейную комбинацию этих векторов:
, | (2.19) |
где
Пусть все векторы, участвующие в равенстве (2.19), – это векторы столбцы, то есть:
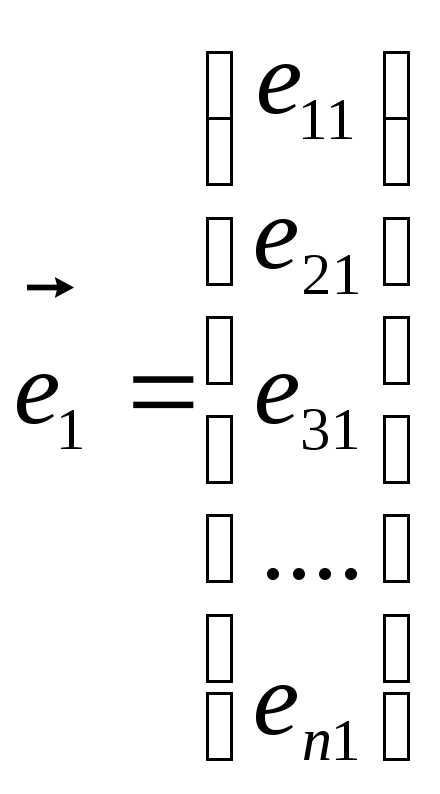 ,
, 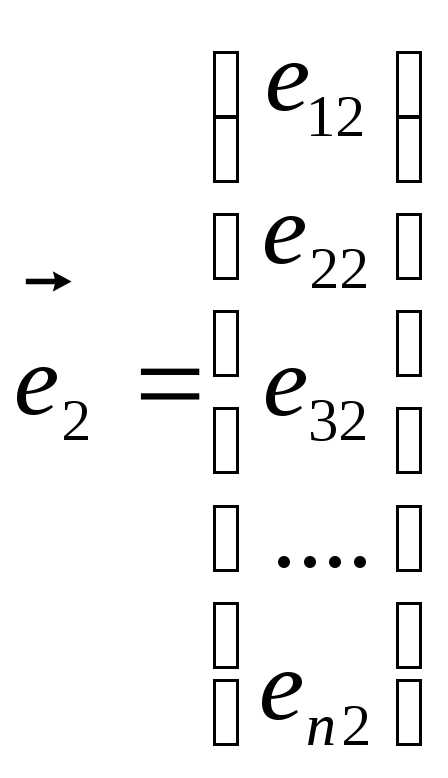 ,
,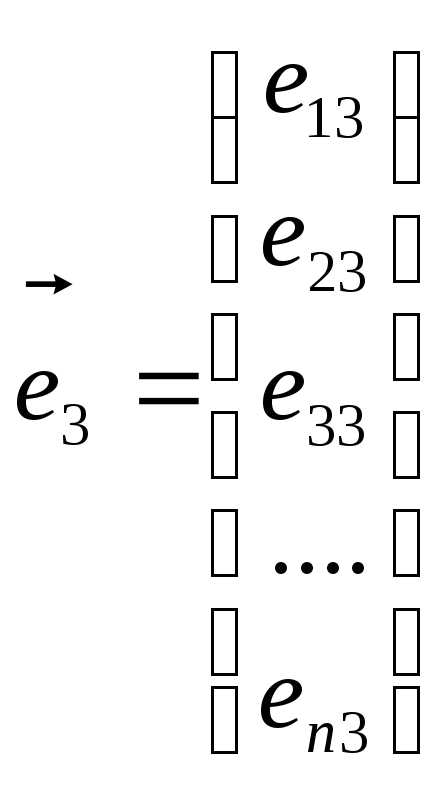 ,……
,……
Обратим внимание на двойную индексацию координат векторов: первый индекс – номер координаты, второй – номер вектора.
Перепишем равенство (2.19) в следующем виде:
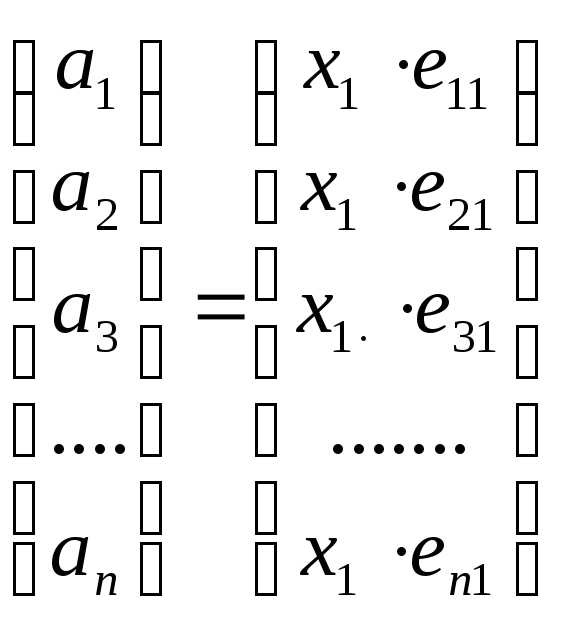 +
+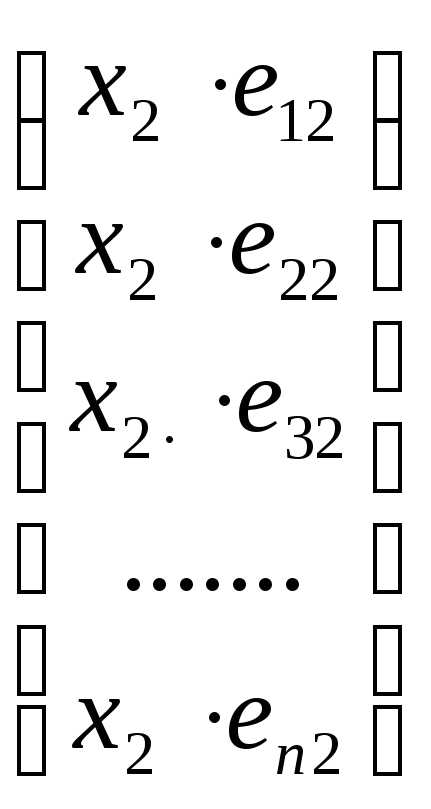 +
+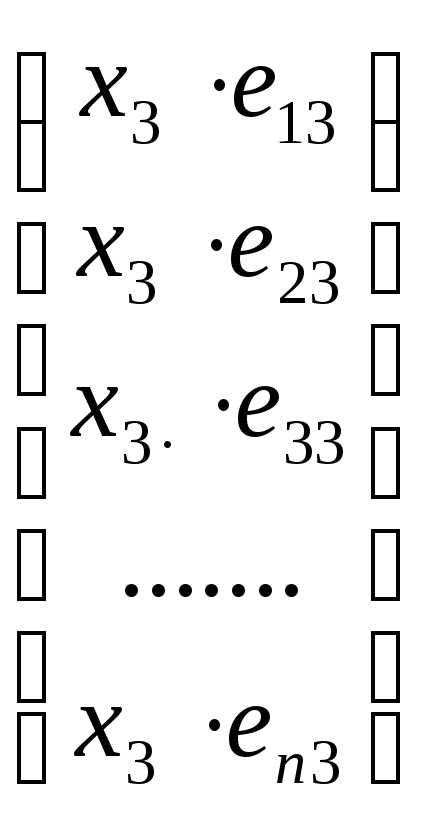 +…….+
+…….+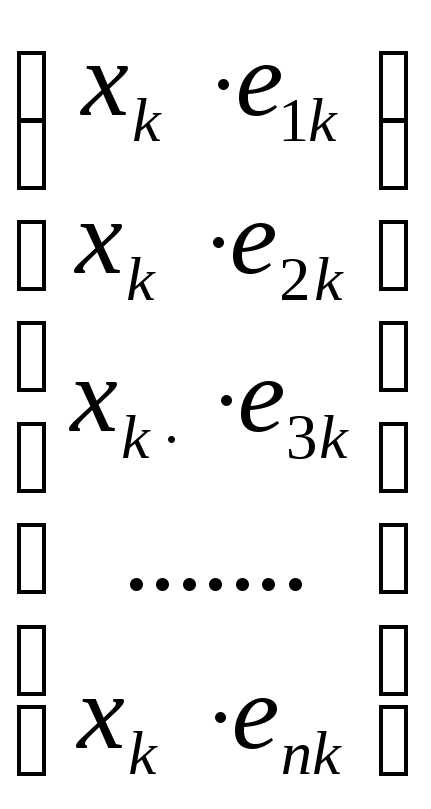
Учитывая определение равенства арифметических векторов, последнее равенство можно переписать следующим образом:
| (2.20) |
Систему равенств (2.20) можно рассматривать с различных точек зрения:
1.
Если заданы все векторы 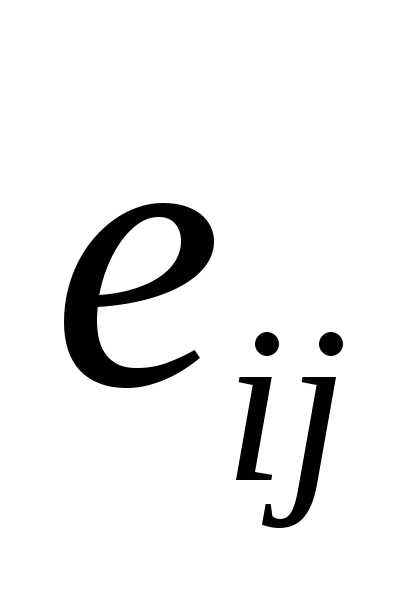 и все числа
и все числа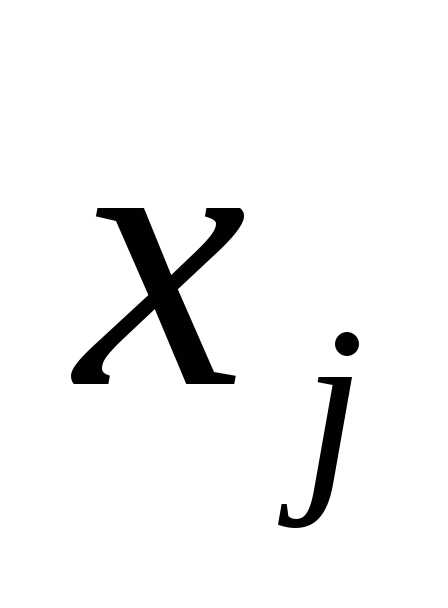 (i=1,2,3,…n;
j=1,2,3,…k),
то с помощью системы равенств (2.20)
вычисляются координаты вектора
(i=1,2,3,…n;
j=1,2,3,…k),
то с помощью системы равенств (2.20)
вычисляются координаты вектора  .
.
2.
Если заданы все векторы 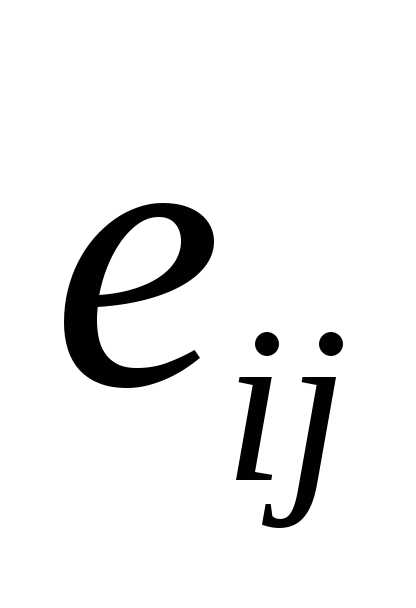 и вектор
и вектор  ,
то система (2.20) — это система n линейных алгебраических уравнений с k неизвестными x1,
x2,
x3,…..xk . Системы
такого вида и их решение рассмотрены в
разделе 4. Из школьного курса алгебры известно,
что при решении системы линейных
уравнений реализуется одна из следующих
возможностей: (а) система имеет единственное
решение, (б) система имеет бесконечно
много решений, (в) система не имеют ни
одного решения. В связи с этим решение
системы (2.19) позволяет ответить на
вопросы:
,
то система (2.20) — это система n линейных алгебраических уравнений с k неизвестными x1,
x2,
x3,…..xk . Системы
такого вида и их решение рассмотрены в
разделе 4. Из школьного курса алгебры известно,
что при решении системы линейных
уравнений реализуется одна из следующих
возможностей: (а) система имеет единственное
решение, (б) система имеет бесконечно
много решений, (в) система не имеют ни
одного решения. В связи с этим решение
системы (2.19) позволяет ответить на
вопросы:
может ли вектор
 быть представлен как линейная комбинация
векторов ?
быть представлен как линейная комбинация
векторов ?единственно ли такое представление?
3.
Если заданы векторы 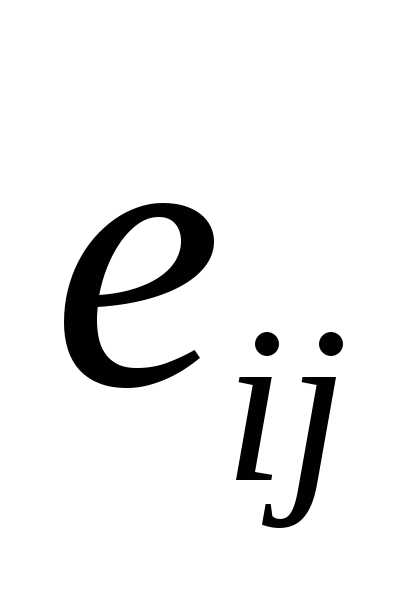 ,
то система (2.19) определяетлинейную
оболочку множества векторов ().
,
то система (2.19) определяетлинейную
оболочку множества векторов ().
Определение 2.5. Линейной оболочкой множества векторов называют множество всех линейных комбинаций этих векторов.
Линейную оболочку множества M принято обозначать [M].
Справедливо следующее утверждение:
Утверждение 1 Если M — какое-либо (любое) множество векторов из Rn , то линейная оболочка множества M замкнута относительно операций умножение на число и сложения векторов.
Доказательство.
Пусть M={}.
Векторы из [M]
– это векторы, координаты которых
определяются системой (1.19), если переменные
пробегают
все возможные значения из R. Возьмем два
любых вектора из [M]:  и
и .
.
Сумма этих векторов:
+=
=
является
вектором из [M],
так как
,
а значит, есть линейная комбинация векторов .
есть линейная комбинация векторов .
Аналогично доказывается, что, умножив вектор линейной оболочки множества M на любое действительное число, вновь получим линейную комбинацию векторов , то есть вектор из [M]. Это и означает, что [M] является замкнутым относительно операций сложения и умножения на число.
Обратим внимание на то, что в доказательстве использованы в неявном виде следующие свойства линейных операций над векторами: коммутативность сложения, ассоциативность сложения, дистрибутивность умножения относительно сложения чисел, смешанная ассоциативность.
Докажите
замкнутость линейной оболочки множества  ,
обосновывая переходы от одного равенства
к другому ссылками на соответствующие
свойства.
,
обосновывая переходы от одного равенства
к другому ссылками на соответствующие
свойства.
Какой бы n-мерный вектор мы ни взяли, это будет вектор из пространства Rn. Но как было показано, линейная оболочка системы векторов из Rn замкнута относительно операций сложения и умножения на число, а следовательно, сама является пространством. Любая система n-мерных векторов является подмножеством множества векторов Rn, а линейная оболочка такой системы – линейным подпространством пространства Rn.
Отметим,
что линейная оболочка системы векторов,
состоящая из одного нуль-вектора,
является подпространством Rn,
хотя и состоит из одного лишь вектора  .
Подпространство, состоящее из одного
нуль-вектора, называют вырожденным
подпространством.
.
Подпространство, состоящее из одного
нуль-вектора, называют вырожденным
подпространством.
Над линейными подпространствами определены операции сложения, пересечения и объединения.
Определение
2.6. Суммой
линейных подпространств L1 и L2 пространства Rn называют множество L1+L2 всех векторов из Rn вида:  ,
где.
,
где.
Определение
2.7. Пересечением
линейных подпространств L1 и L2 пространства Rn называют множество векторов 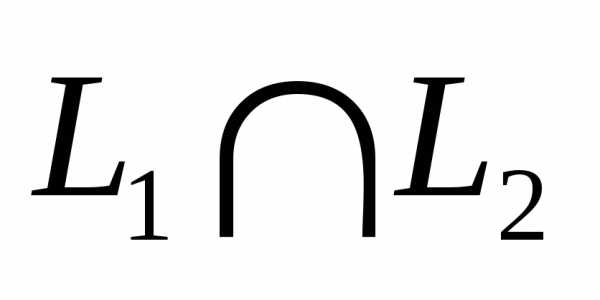 ,
состоящее из общих векторов пространствL1и L2.
,
состоящее из общих векторов пространствL1и L2.
Определение
2.8. Объединением
линейных подпространств L1 и L2 пространства Rn называют множество векторов 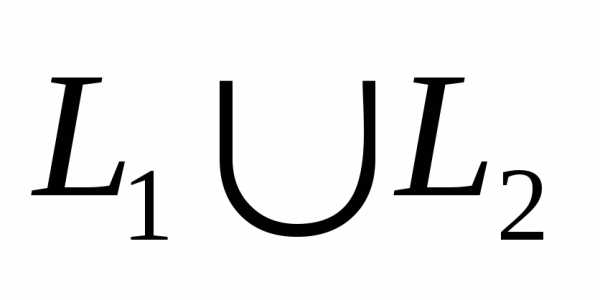 ,
состоящее из всех векторов, принадлежащих
,
состоящее из всех векторов, принадлежащих или
или .
.
Встает
вопрос о ранжировании подпространств.
В случае геометрических пространств
вопрос этот интуитивно ясен: прямая
«больше» точки, размерность пространства
V1 равна 1. Плоскость «больше» прямой,
размерность пространства V2 равна 2. Все геометрическое пространство
векторов «больше» плоскости, размерность
V3 равна 3. Все векторы на прямой есть
линейные комбинации единственного
базисного вектора, например, вектора  ,
на плоскости – системы двух базисных
векторов (
,
на плоскости – системы двух базисных
векторов ( ),
в пространстве – системы трех базисных
векторов (
),
в пространстве – системы трех базисных
векторов ( ).
).
Таким образом, размерность пространства равна числу базисных векторов. Определение базиса векторного пространства геометрических векторов было введено через понятие максимальной системы линейно независимых или свободных векторов (см. Определение 1.15). Аналогично можно ввести понятие базиса и размерности линейного векторного пространства в общем случае. Потребуются следующие понятия
Нулевая линейная комбинация системы векторов ():
(2.21) |
Вырожденная линейная комбинация системы векторов ():
(2.22) |
Очевидно, что вырожденная линейная комбинация всегда является нулевой, но, как и в случае геометрических векторов, обратное утверждение не всегда верно: существуют нулевые невырожденные линейные комбинации.
3. Линейная зависимость и линейная независимость системы векторов (): систему векторов () называют линейно независимой или свободной, если ни один из векторов системы не может быть представлен линейной комбинацией других ее векторов. В противном случае систему называют линейно зависимой.
Как и в случае систем геометрических векторов, справедливо следующая теорема.
Теорема 1. Если существует невырожденная нулевая линейная комбинация системы векторов () , то система векторов является линейно зависимой, если же единственной нулевой комбинацией векторов системы является вырожденная комбинация, то система является свободной.
Эта теорема, как и ее доказательство полностью повторяет соответствующую теорему в разделе 1.4. Для арифметических векторов, также, как и для геометрических, справедливы утверждения 1-4, вытекающие из этой теоремы (см. стр )
На основании Теоремы 1, вопрос о линейной зависимости или линейной независимости системы n-мерных арифметических векторов может быть решен с помощью системы уравнений:
Отметим, что в правой части системы (2.23) все числа –нули. Такая система называется однородной линейной системой алгебраических уравнений. Очевидно, что однородная система имеет по крайней мере одно решение — нулевое: . Таким образом, вопрос о линейной зависимости и линейной независимости системы векторов, сводится к вопросу о решении однородной системы уравнений: если (2.23) имеет только нулевое решение, то система векторов () свободна, если же имеются ненулевые решения, то система векторов линейно зависима.
4. Максимальная свободная система векторов.
Определение этого понятия для пространства арифметических векторов полностью совпадает с его определением для пространства геометрических векторов (см. определение 1.14, стр ). Однако следует помнить, что геометрический вектор не может иметь более трех измерений, поэтому в любом пространстве геометрических векторов максимальная свободная система содержит не более трех векторов. Размерность арифметического вектора может быть любой, а вопрос о числе векторов в максимальной свободной системе решается с помощью систем уравнений. Решение этого вопроса рассмотрено в разделе 4.
Согласно определению максимальной свободной системы векторов пространства, добавление в нее любого вектора пространства делает систему базисных векторов линейно зависимой.
Пусть
()
— максимальная свободная система
векторов линейного векторного пространства L и
,
но ().
В силу линейной независимости этих
векторов, однородная система уравнений
(2.23) имеет единственное решение –
нулевое.
().
В силу линейной независимости этих
векторов, однородная система уравнений
(2.23) имеет единственное решение –
нулевое.
Докажем справедливость утверждения:
Утверждение
1. Любой
вектор  можно представить как линейную комбинацию
векторов максимальной свободной системы
векторов этого пространства (),
или по-другому, разложить
его по векторам ().
можно представить как линейную комбинацию
векторов максимальной свободной системы
векторов этого пространства (),
или по-другому, разложить
его по векторам ().
Пусть
сначала  .
Система векторов ()
линейно зависима, то есть существует
их невырожденная нулевая линейная
комбинация:
,
в которой среди чиселесть
хотя бы одно число отличное от нуля, а
следовательно, система уравнений
.
Система векторов ()
линейно зависима, то есть существует
их невырожденная нулевая линейная
комбинация:
,
в которой среди чиселесть
хотя бы одно число отличное от нуля, а
следовательно, система уравнений
| (2.24) |
помимо
нулевого, имеет хотя бы одно ненулевое
решение. Пусть в ненулевом решении
системы (2.24) y=0.
В этом случае система (2.24) обращается в
систему (2.23), имеющую единственное
решение – нулевое, а значит все xi (i=1,2,3,…..k) в
этом решении также равны 0. Таким образом,
равенство y=0 возможно
лишь в случае нулевого решения системы
(2.24), а чтобы
решение было ненулевым необходимо
условие: 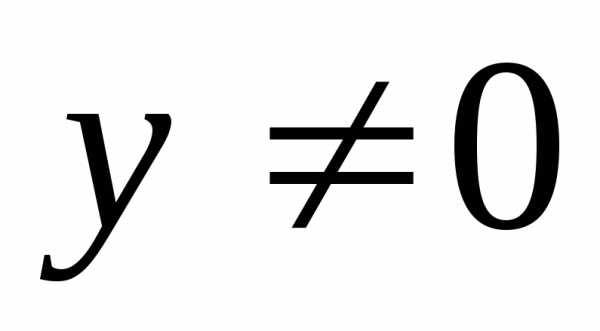 . Отсюда следует, что
. Отсюда следует, что  есть линейная
комбинация системы
векторов ():
есть линейная
комбинация системы
векторов ():
=, | (2.25) |
где .
Если  ,
то в системе (2.23)у может быть любым числом. Положив
,
то в системе (2.23)у может быть любым числом. Положив 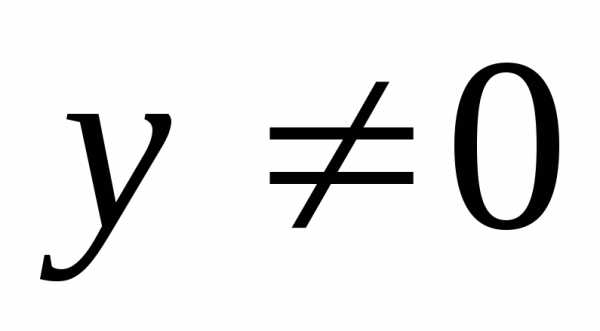 ,
вектор
,
вектор  также можно записать в виде (2.25).
также можно записать в виде (2.25).
Утверждение 1 доказано.
Утверждение
2. Разложение  =вектора
=вектора  по
векторам ()
является единственным.
по
векторам ()
является единственным.
(Другими словами, других чисел, помимо , не существует).
Докажем Утверждение 2 методом от противного. Предположим, что помимо набора чисел существует другой набор чисел, таких, что
 =.
=.
Получим:
 —
— =
= =()
— ()=
=()
— ()=
=(.
В силу линейной независимости системы векторов () , любая их нулевая линейная комбинация является вырожденной, следовательно:
.
Это и означает, что другого набора чисел, помимо не существует.
Определение 2.10. Базис линейного векторного пространства L – это любая максимальная свободная система векторов пространства L .
Определение 2.11. Число векторов в базисе линейного векторного пространства L называют размерностью пространства L.
Размерность пространства L обозначают: dimL.
Любой вектор из L можно единственным образом разложить по базисным векторам. Числовые коэффициенты в этом разложении называют координатами вектора в данном базисе.
Пусть
-n-мерный
вектор. Все векторы вида: 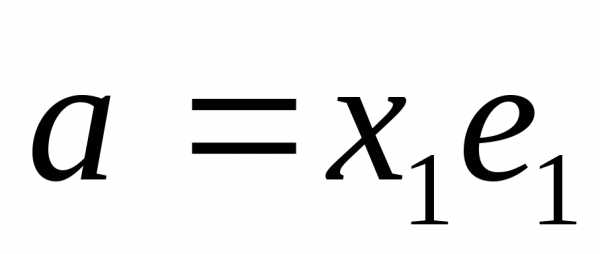 ,
где
,
где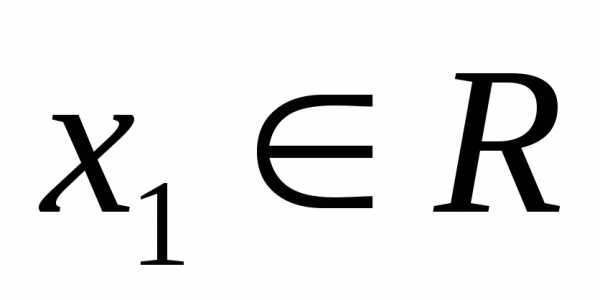 ,
образуют линейную оболочку вектора,
которая замкнута относительно операций
сложения и умножения на число, а
следовательно образует линейное
векторное пространствоL1 =[
,
образуют линейную оболочку вектора,
которая замкнута относительно операций
сложения и умножения на число, а
следовательно образует линейное
векторное пространствоL1 =[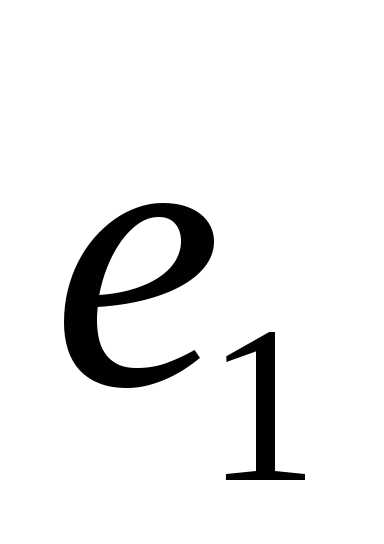 ].
Единственным базисным вектором этого
пространства является вектор
].
Единственным базисным вектором этого
пространства является вектор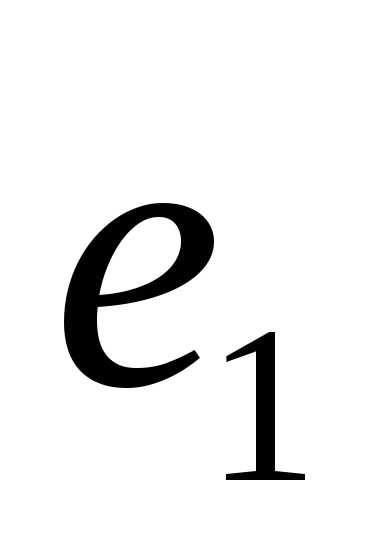 .СледовательноdimL1=1. С
геометрической точки зрения, L1 – это числовая прямая, и
.СледовательноdimL1=1. С
геометрической точки зрения, L1 – это числовая прямая, и 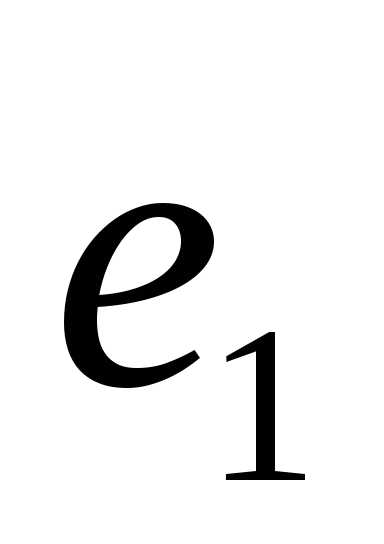 —
направленный отрезок единичной длины,
приложенный к точкеO. (См. стр. ).
—
направленный отрезок единичной длины,
приложенный к точкеO. (См. стр. ).
Пусть
и- два неколлинеарных вектора. Каждый из
них образует линейное пространство
размерности 1:L’1 =[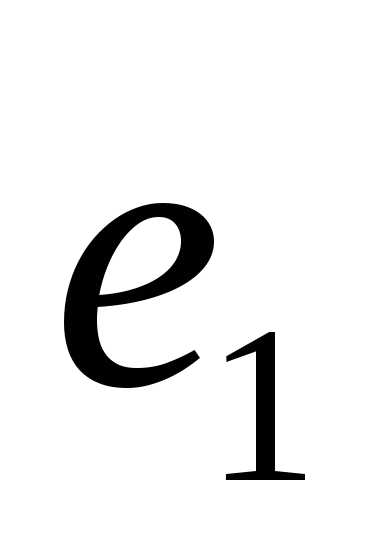 ]
иL’’1=[
]
иL’’1=[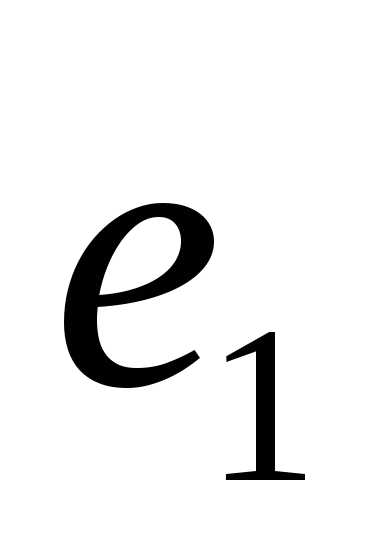 ],dimL’1 = dimL’’1=1. В геометрическом пространстве они
соответствуют двум непараллельным
прямым. Составляя
всевозможные линейные комбинации
системы векторов (
],dimL’1 = dimL’’1=1. В геометрическом пространстве они
соответствуют двум непараллельным
прямым. Составляя
всевозможные линейные комбинации
системы векторов (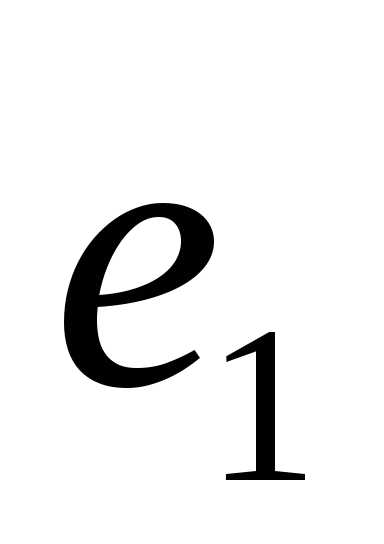 ,
,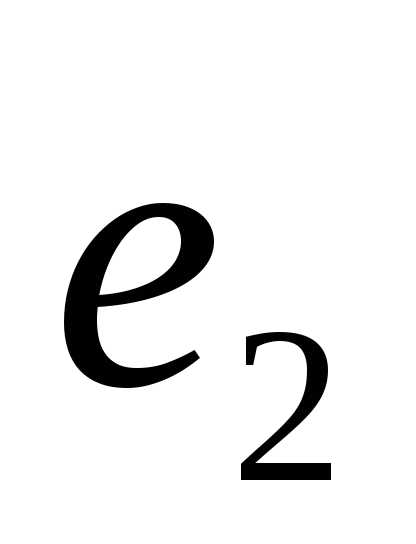 ):
):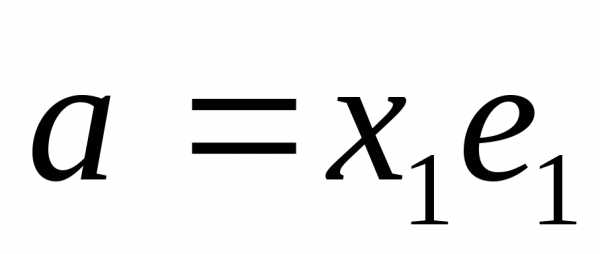
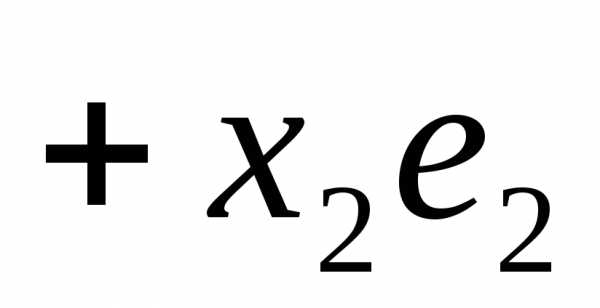 ,
получим линейную оболочкуL2 =[
,
получим линейную оболочкуL2 =[ ,
,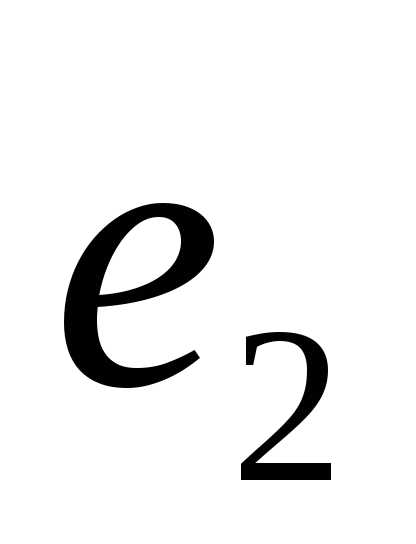 ],
которая является линейным пространством
размерности 2, аL’1 и L’’1 – его подпространствами. В геометрических
терминах L2 представляет
плоскость, проходящую через две
пересекающиеся прямые.
],
которая является линейным пространством
размерности 2, аL’1 и L’’1 – его подпространствами. В геометрических
терминах L2 представляет
плоскость, проходящую через две
пересекающиеся прямые.
Аналогично
строятся пространства  ,
,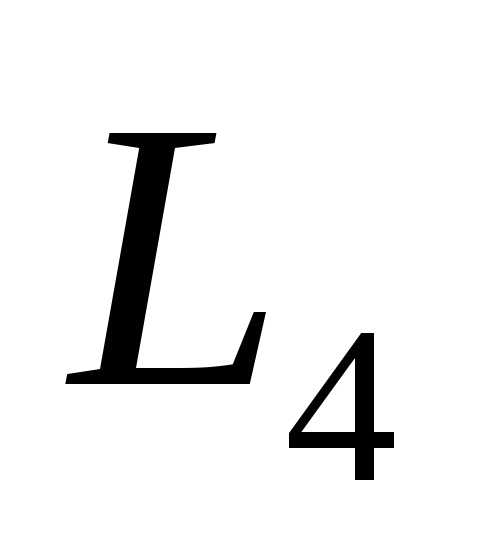 …..
…..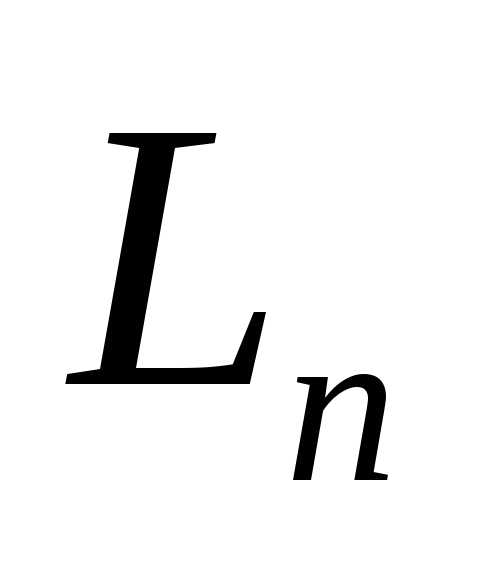 ,
размерности которых 3, 4,….n
соответственно. Отметим, что, начиная
с
,
размерности которых 3, 4,….n
соответственно. Отметим, что, начиная
с 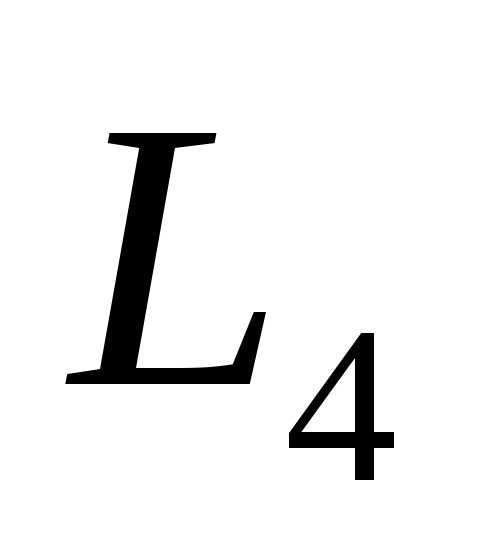 геометрическая
интерпретация неприменима. Математика,
наряду с конечномерными, занимается
изучением и бесконечномерных линейных
пространств, однако бесконечномерные
линейные пространства в нашем курсе не
рассматриваются.
геометрическая
интерпретация неприменима. Математика,
наряду с конечномерными, занимается
изучением и бесконечномерных линейных
пространств, однако бесконечномерные
линейные пространства в нашем курсе не
рассматриваются.
Справедлива Теорема, которую принимаем без доказательства.
Теорема о конечномерных пространствах. Пусть L – конечномерное пространство и () – его базис. Тогда:
(1) все базисы L конечны и состоят из k векторов;
(2) любая система векторов L, состоящая более, чем из k векторов, линейно зависима;
(3) всякая свободная система, состоящая из k векторов, является базисом пространства L;
(4) произвольную свободную систему векторов, состоящую из m векторов, где m<k, можно дополнить (k — m) векторами из () до базиса пространстваL.
В пространстве Rn часто используется ортонормированный базис, примером которого может служить последовательность векторов ():
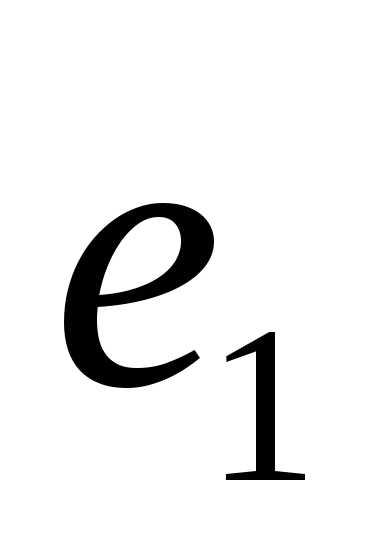 =
=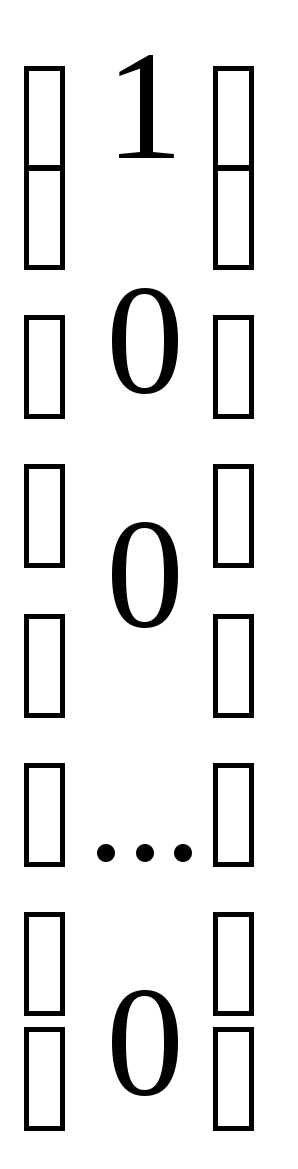 ,
, =
=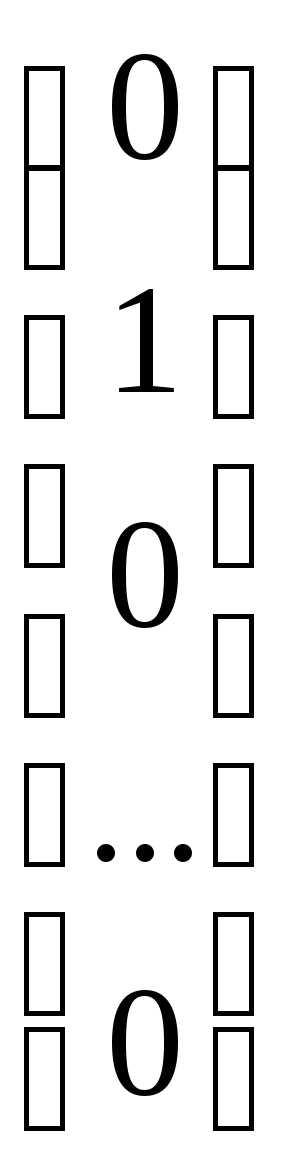 ,
,
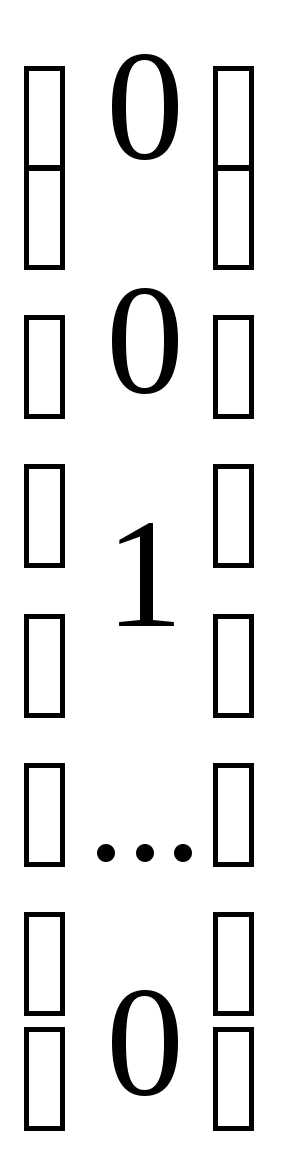 ….
….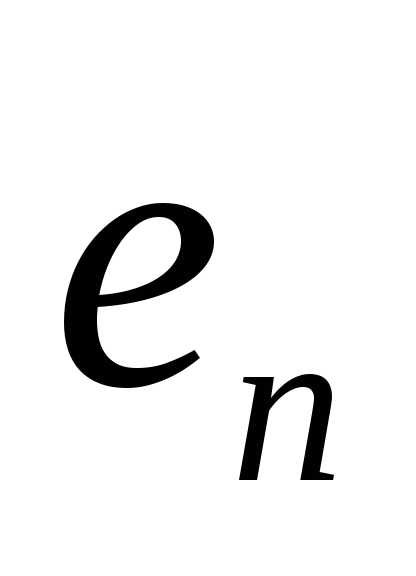 =
=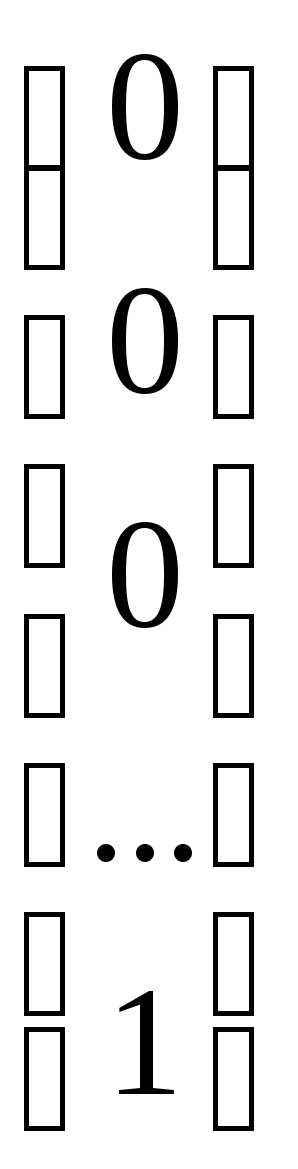 .
.
Норма каждого из этих векторов равна 1, а скалярное произведение любых двух векторов равна 0.
studfiles.net
Базис линейного пространства. Примеры базисов в конкретных пространствах.
Определение 2. Пусть — линейное пространство. Векторназывается линейной комбинацией векторов, если найдутся такие числа , что
.
Определение 3. Система векторов , принадлежащих линейному пространству, называется линейно зависимой, если найдутся такие числа, не все равные нулю одновременно, что выполняется равенство
.
Определение 3′. Система векторов , принадлежащих линейному пространству, называется линейно зависимой, если один из векторов является линейной комбинацией остальных.
Определение 4. Система векторов , принадлежащих линейному пространству, называется линейно независимой, если из равенства
следует, что .
Теорема 1. Всякая система векторов, содержащая нулевой вектор, линейно зависима.
Теорема 2. Всякая система векторов , содержащая линейно зависимую подсистему векторов, , линейно зависима.
Определение 5. Система векторов линейного пространстваназывается базисом в, если:
1) линейно независима;
2) (вещественные числа):
. (10.3)
Правая часть равенства (10.3) называется разложением вектора по базису, а числа — координатами векторав базисе.
Приведем примеры базисов в конкретных линейных пространствах.
Базис линейного пространства. Единственность разложения вектора по базису.
Теорема 3. Пусть — линейное пространство, — базис в, . Координатыотносительно базиса определены однозначно.
Базис линейного пространства. Координаы суммы векторов и произведения вектора на число.
Теорема 4. Пусть — линейное пространство, — базис в. При сложении любых двух векторов их соответствующие координаты складываются, при умножении вектора на число каждая координата умножается на это число.
Теорема 5. Пусть — линейное пространство, — базис в. Всякая система векторовпри линейно зависима.
Следствие. Все базисы линейного пространства состоят из одного и того же числа векторов.
Размерность линейного пространства.
Определение 6. Число векторов в любом базисе линейного пространства называется размерностью линейного пространства.
Для размерности линейного пространства принято обозначение.
В рассмотренных примерах:
если — линейное пространство всех геометрических векторов пространства, ;
если — линейное пространство всех многочленов степени ,;
если — линейное пространство всех квадратных матриц порядка 2, .
Связь между базисами линейного пространства.
Определение 1. Матрица называется матрицей перехода от базиса(I) к базису (II).
Замечание 1. Столбцы матрицы перехода , являются координатами в разложении векторовпо базису (I).
Замечание 2. Матрица перехода от базиса к базису является невырожденной матрицей.
Теорема 1. Пусть — линейное пространство, (I) и (II) — два базиса в ,- матрица перехода от(I) к (II), , и, тогда
Линейные подпространства. Примеры.
Определение 2. Пусть — линейное пространство. Непустое подмножестволинейного пространства() называется линейным подпространством в , если выполняются два условия:
1) ;
2) при любом вещественном числе .
Замечание. Если — линейное подпространство в , то само является линейным пространством относительно введенных в операций сложения и умножения на число.
Линейные операторы, определения и примеры.
Определение 1. Пусть — линейное пространство и каждому вектору, принадлежащему, поставлен в соответствие вектор , . Соответствиеназывается оператором, определенным в линейном пространстве .
Определение 2. Оператор , определенный в линейном пространстве , называется линейным, если:
1) ;
2) — вещественного числа.
Матрица линейного оператора. Связь координат образа и прообраза.
Определение 3. Пусть — линейное пространство, — базис в, — линейный оператор в. Матрицей линейного операторав базисеназывается матрица, ,такая, что
,
,
…………………………………….. (12.1)
.
Замечание 1. Столбцы матрицы являются координатами в разложении векторовпо базису.
Замечание 2. Пусть — линейное пространство,- линейный оператор в,(I) — базис в . Матрица оператора в базисе (I) определена однозначно.
Теорема 1. Пусть — линейное пространство, (I) — базис в , — линейный оператор в, — матрица линейного операторав базисе(I), , , ,. Тогда
.
Теорема 3. Пусть — линейное пространство, — базис в, . Координатыотносительно базиса определены однозначно.
studfiles.net

 к базису
к базису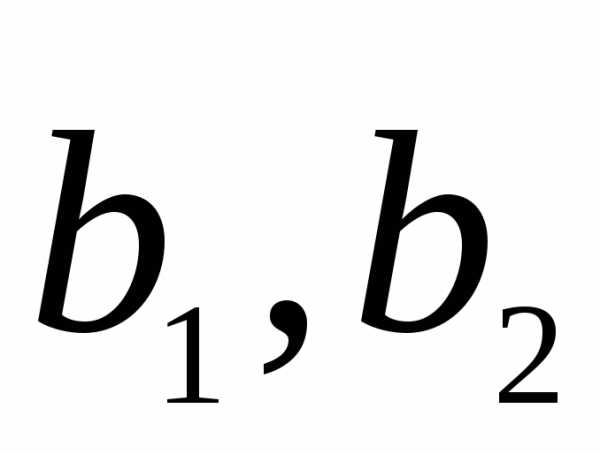 по данным разложениям этих векторов
в базисе
по данным разложениям этих векторов
в базисе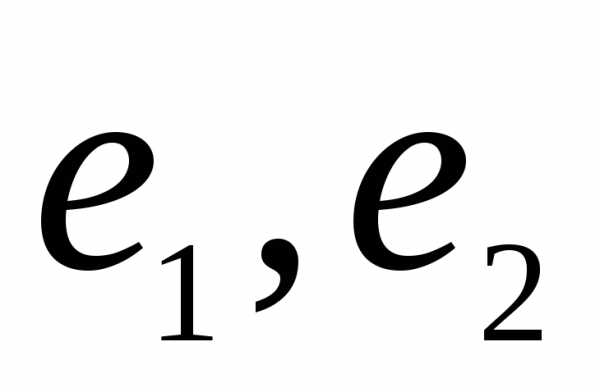 :
: =(- вектор строка,
=(- вектор строка, =
= 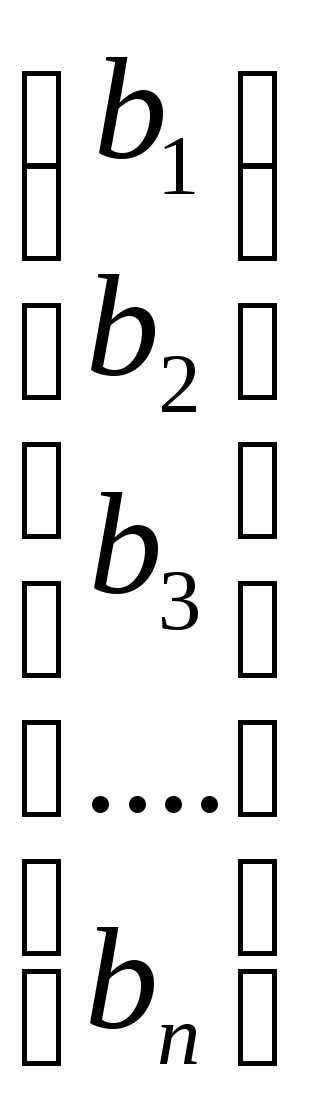 =- вектор столбец.
=- вектор столбец.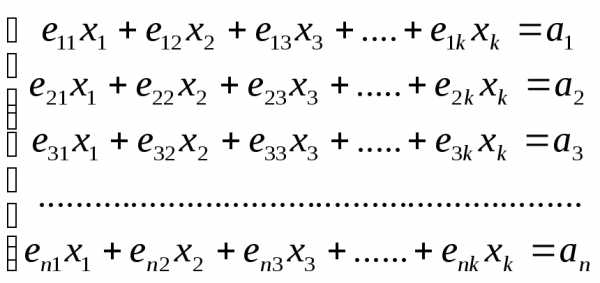
 быть представлен как линейная комбинация
векторов ?
быть представлен как линейная комбинация
векторов ?