Как найти синус, косинус и тангенс углов 15° и 75° (без использования идентификатора триггера)
СИНУС, КОсинус и тангенс углов 15° И 75°
Можно найти синус, косинус и тангенс 15°, а также 75° без использования тождества триггера (и без использования калькулятора).
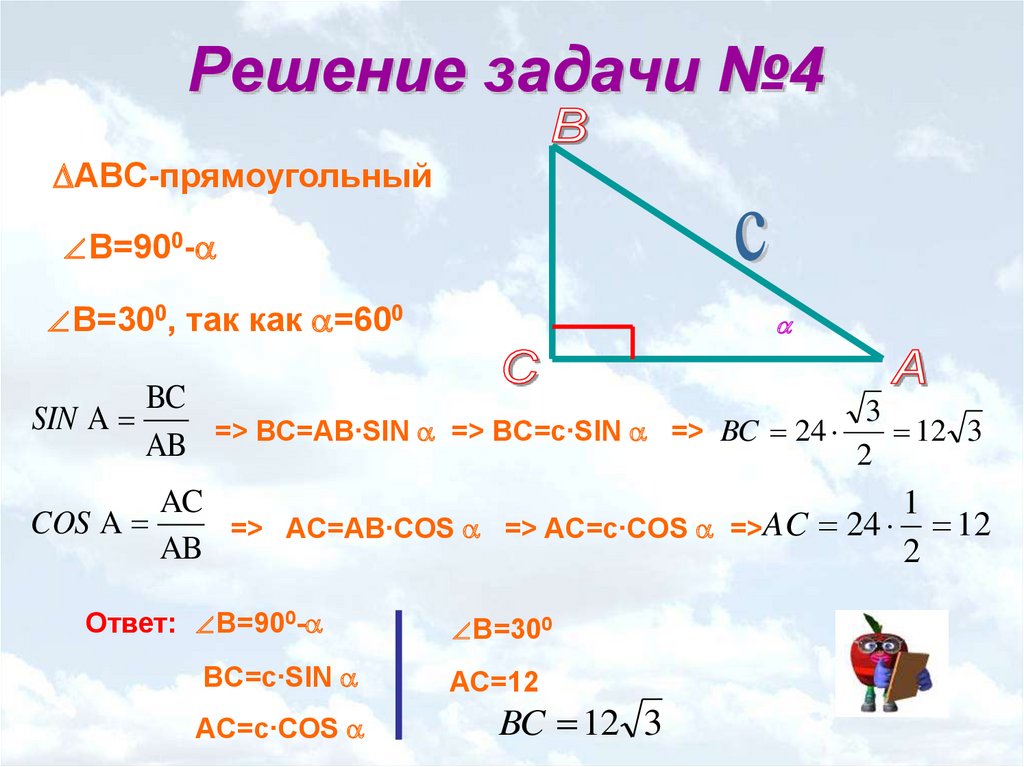
Хитрость заключается в том, чтобы начать с равнобедренного треугольника 75°-75°-30°, как показано выше. Пусть AB = AC = 2. Это стороны, противоположные углам 75°. Оставшаяся сторона, ВС, на данный момент неизвестна.
Используя сторону AB в качестве основания, проведите высоту вниз от точки C, как показано ниже. Это делит равнобедренный треугольник на два прямоугольных треугольника. Треугольник ACD — это треугольник с углами 30°-60°-90°, а треугольник BCD — треугольник с углами 75°-15°-90°.
Хорошо известно, что стороны треугольника 30°-60-°90° относятся как 1:sqrt(3):2, где 1 напротив 30°, sqrt(3) напротив 60°, и 2 как гипотенуза. Поскольку AC = 2 — гипотенуза, это означает, что CD = 1 и AD = sqrt(3).
Теперь мы знаем, что высота треугольника ABC равна CD = 1, что составляет одну сторону треугольника BCD. Мы можем найти сторону BD, вычитая AD из AB. Поскольку AB = 2 и AD = sqrt(3), мы получаем BD = 2 – sqrt(3).
Теорема Пифагора может быть использована для определения BC, которая является гипотенузой треугольника BCD.
Напомним, что BD = 2 – sqrt(3) и что CD = 1. После применения теоремы Пифагора применим метод «фольги» из алгебры: (x – y)² = x² – 2xy + y². Напомним, что (sqrt(3))² = sqrt(3) × sqrt(3) = 3,
Чтобы найти BC, возьмите квадратный корень из обеих частей уравнения. Вынесите 4 из них. Вспомните, что sqrt(ab) = sqrt(a) × sqrt(b). Обратите внимание, что sqrt(4) = 2.
Приведенный выше ответ содержит один квадратный корень внутри другого. Есть умный способ переписать это без использования вложенного квадратного корня. Перепишите 8 как 6 + 2. Причина этого в том, что (sqrt(6))² = 6 и (sqrt(2))² = 2.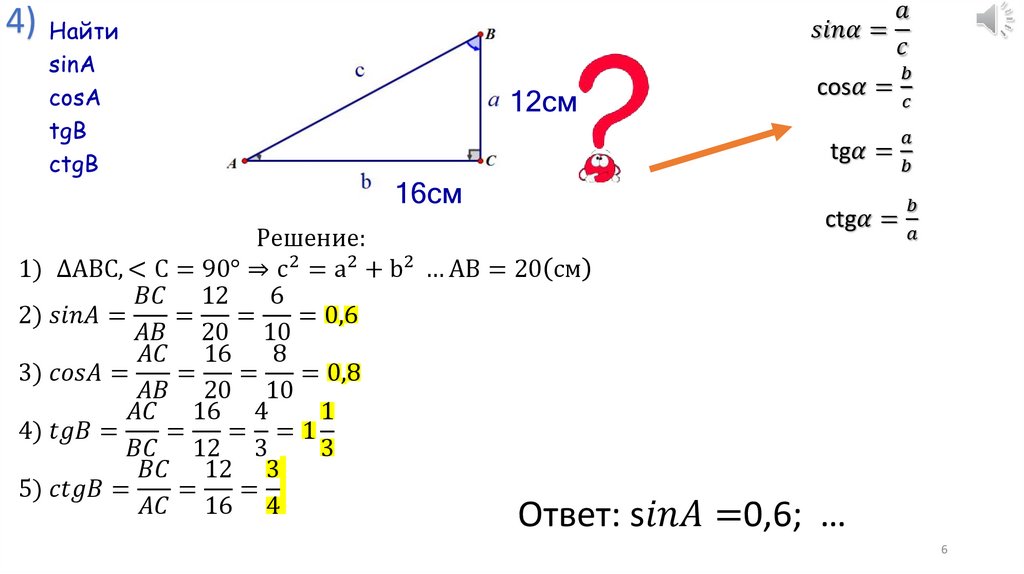
Если вы «свернете» (sqrt(6) – sqrt(2)) ², вы получаете 6 – 2sqrt(12) + 2 = 8 – 4sqrt(3), потому что sqrt(12) = sqrt(4) × sqrt(3) = 2 sqrt(3), так что 2sqrt(12) = 2(2 )кв.(3) = 4 кв.м(3). Если вы все еще не уверены, обратите внимание, что sqrt(8 – 4sqrt(3)) на калькуляторе составляет приблизительно 1,03527618, а sqrt(6) – sqrt(2) также приблизительно равен 1,03527618 на калькуляторе.
Так как BC = 2 sqrt(2 – sqrt(3)) и BC = sqrt(6) – sqrt(2), то из транзитивного свойства следует, что 2 sqrt(2 – sqrt(3)) = sqrt( 6) – квадрат(2). Разделите обе части на 2, чтобы получить следующее:
Следующие формы для BC эквивалентны, но правильное выражение считается «стандартной формой».
Теперь, когда мы знаем BC, BD и CD, мы можем легко найти синус, косинус и тангенс 15°. Обратите внимание, что в треугольнике BCD угол BD лежит против угла 15°, угол CD примыкает к углу 15°, а угол BC — гипотенуза. Для синуса 15° обратите внимание, что (2 – sqrt(3)) / sqrt(2 – sqrt(3)) = sqrt(2 – sqrt(3)) по той же причине, что x/sqrt(x) = sqrt (Икс).
Для косинуса 15° ответ 1/(sqrt(6) – sqrt(2)) эквивалентен ответу (sqrt(6) + sqrt(2))/4. Оба ответа примерно равны 0,965925826 на калькуляторе, но самое правое выражение считается «стандартной формой», потому что оно имеет рациональный знаменатель. Мы умножили числитель и знаменатель на (sqrt(6) + sqrt(2)) для рационализации знаменателя. Это называется «умножение на сопряженное». Сопряженное выражение sqrt(6) – sqrt(2) есть sqrt(6) + sqrt(2), потому что произведение этих двух сопряженных выражений рационально. При применении метода «фольги» иррациональные члены сокращаются.
Обратите внимание, что синус 15° эквивалентен косинусу 75°, а косинус 15° эквивалентен синусу 75°. То, что «противоположно» для 15°, является «смежным» для 75°, и наоборот. Для тангенса 75 ° мы снова умножили на сопряженную, чтобы рационализировать знаменатель.
Ниже приводится сводка наших окончательных ответов.
КРИС МАКМУЛЛЕН, PH.D.
Copyright © 2021 Крис МакМаллен, автор книги Улучшите беглость математики серия рабочих тетрадей по математике
Новейшие выпуски:
- Практическая рабочая тетрадь по плоской геометрии с ответами (тома 1 и 2)
- 101 задача по алгебре (включая полные решения)
- Рабочая тетрадь Trig Identities Practice с ответами
- Рабочая тетрадь по основным навыкам работы с логарифмами и экспонентами (с ответами)
- Практическая тетрадь Master Essential Skills Skills (с ответами)
- Словесные задачи с ответами
Нравится:
Нравится Загрузка.
..
Как найти тангенс с синусом и косинусом
Тангенс, котангенс, секанс и косеканс
Чтобы получить полный урок по синус-косинус-тангенсу, или SOHCATOA, перейдите на страницу — 1000+ онлайн-уроков по математике с персональным
398 Учителя
9/10 Звездный рейтинг
87859 Доставлено заказов
Синус Косинус Тангенс Объяснение
Чтобы найти sin, cos и tan, мы используем следующие формулы: sin = Противоположность/Гипотенуза cos = Смежность/Гипотенуза tan = Противоположность/Смежность. Для нахождения греха
Получить самое полезное объяснение домашнего задания
Если вы хотите получить лучшие ответы на домашнее задание, вам нужно задавать правильные вопросы.
Решить математическое уравнение
Чтобы решить математическое уравнение, вам нужно решить, какую операцию выполнить с каждой частью уравнения.
Определить математические вопросы
Чтобы определить, в чем заключается математическая задача, вам нужно будет просмотреть предоставленную информацию и выяснить, о чем ее спрашивают. Как только вы узнаете, в чем проблема, вы можете решить ее, используя предоставленную информацию.
Обучение шаг за шагом
Вы можете научиться чему угодно, если готовы потратить время и усилия. Просто найдите хороший учебник или курс и работайте с ним шаг за шагом.
Решение математических задач
Я могу помочь тебе с той математической задачей, над которой ты застрял.
Отслеживание прогресса
Вы можете отслеживать свои успехи в фитнес-путешествии, записывая свои тренировки, контролируя потребление пищи и отмечая любые изменения в своем теле.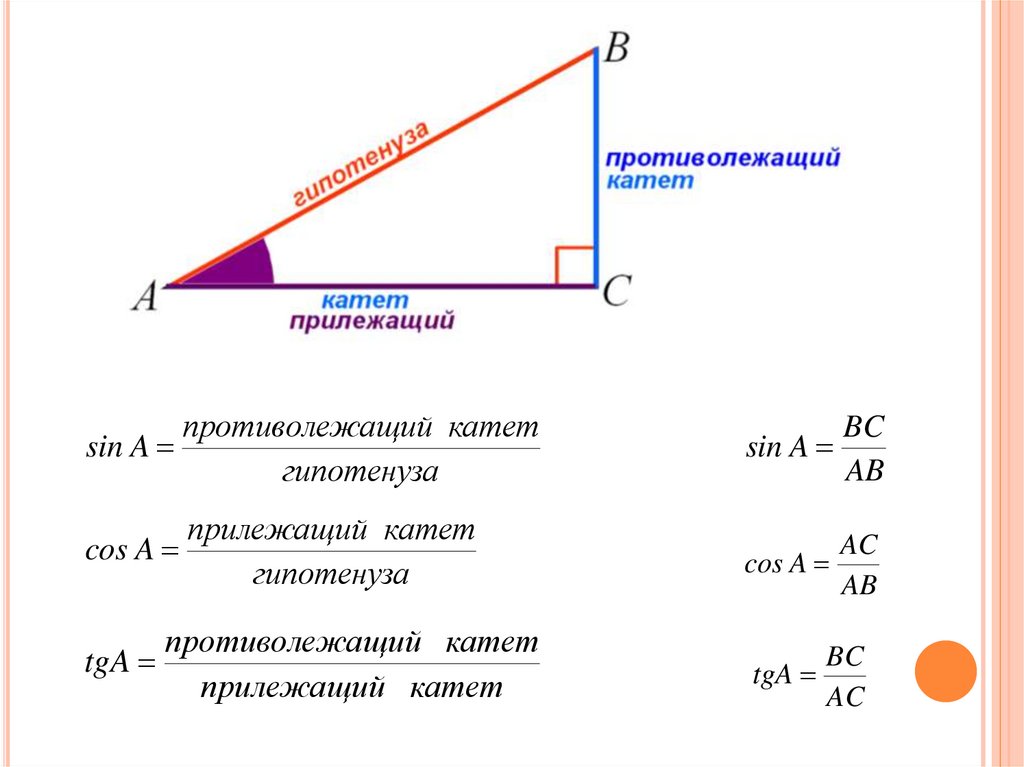
Значения Sin Cos Tan (формула, таблица и способы нахождения)
Объяснение синуса, косинуса, тангенса — основы тригонометрии прямоугольного треугольника Как найти точное значение шести тригонометрических функций 7.
Получить помощь
Если вам нужна помощь, наша служба поддержки клиентов будет рада помочь.
Получить помощь
Вы можете получить помощь по математике в Интернете, посетив такие веб-сайты, как Khan Academy или Mathway.
Решить математическую задачу
Решение математических задач может быть интересным и полезным занятием.
Фантастическое приложение, очень полезное для тех, кто привык проверять каждый ответ, правильный он или неправильный, все, что вам нужно сделать, это сделать снимок, и он не только решает его, используя любой метод, который вы хотите, но также показывает и ОБЪЯСНЯЕТ каждый один шаг, я дал 5 звезд для этого приложения.
Это было правильно, так что да, это совершенно нормально для меня прямо сейчас, и это может помочь вам всем более простым способом, но более информативные должны платить. Это замечательное приложение для решения ваших математических задач, оно хорошо показывает все шаги один за другим с подробным объяснением.
Если вы боретесь с проблемой, вы можете сделать фотографию, а затем бум! У вас есть ответ с шагами решения прямо перед вами. Замечательно, почти совсем не добавляет и может понять даже почерк моей сестры, он такой подробный, он говорит вам, в какой книге вы находитесь, и все проблемы, если бы я мог оценить это больше, я бы поставил 1000000000000/10.
