Вики тригонометрия: HTTP 429 — too many requests, слишком много запросов

Тригонометрия | это… Что такое Тригонометрия?

Тригономе́трия (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии^[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре.

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

В Школе СССР имела статус учебного предмета.

Содержание 1 Определение тригонометрических функций 2 История 2.1 Древняя Греция 2.2 Средневековая Индия 3 См. также 4 Примечания

Определение тригонометрических функций

Основная статья: Тригонометрические функции

Тригонометрические функции угла θ внутри единичной окружности

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим

A. Тогда:

• Синус угла определяется как ордината точки A.
• Косинус — абсцисса точки A.
• Тангенс — отношение синуса к косинусу.
• Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу).
• Секанс — величина, обратная косинусу.
• Косеканс — величина, обратная синусу.

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

История

Основная статья: История тригонометрии

Древняя Греция

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла, и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме.

Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sin α/ sin β < α/β < tan α/ tan β, где 0° < β < α < 90°, совместно с другими теоремами.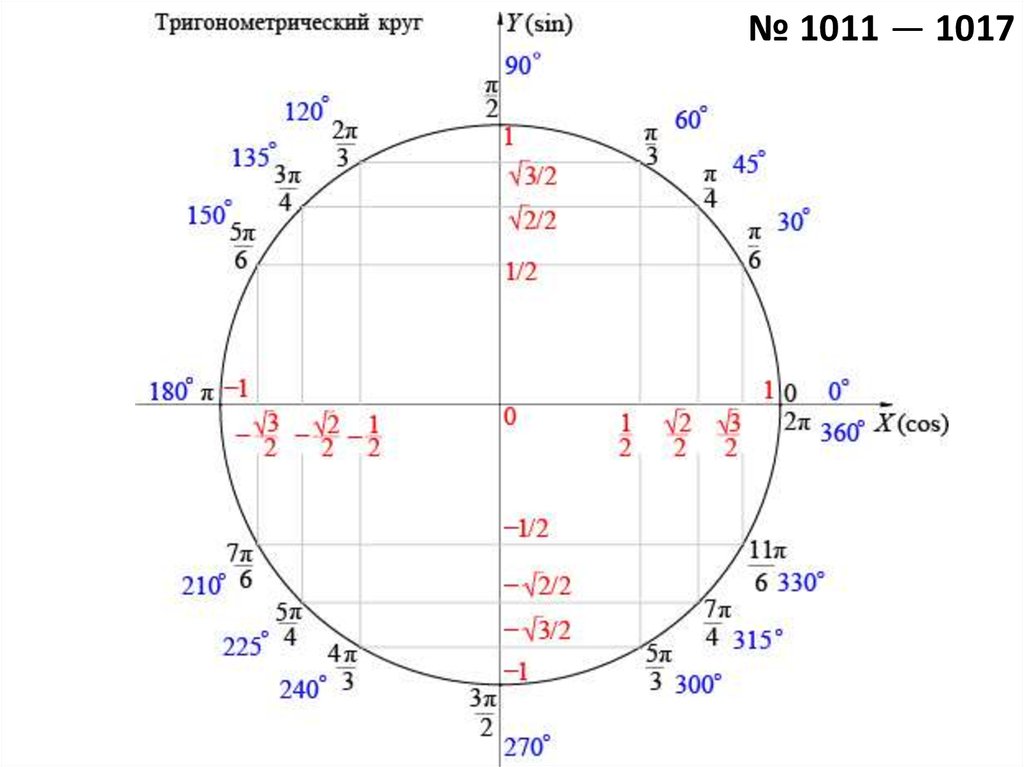

Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.

Менелай Александрийский (100 н. э.) написал «Сферику» в трёх книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».

Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93 предложение «Данных» Евклида.

Теорема Птолемея влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха. Ни таблицы Гиппарха, ни Птолемея не сохранились до настоящего дня, хотя свидетельства других древних авторов снимают сомнения об их существовании.

Средневековая Индия

Другие источники сообщают, что именно замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

Индийцы также знали формулы для кратных углов , , где .

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в 16 веке добивались больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π.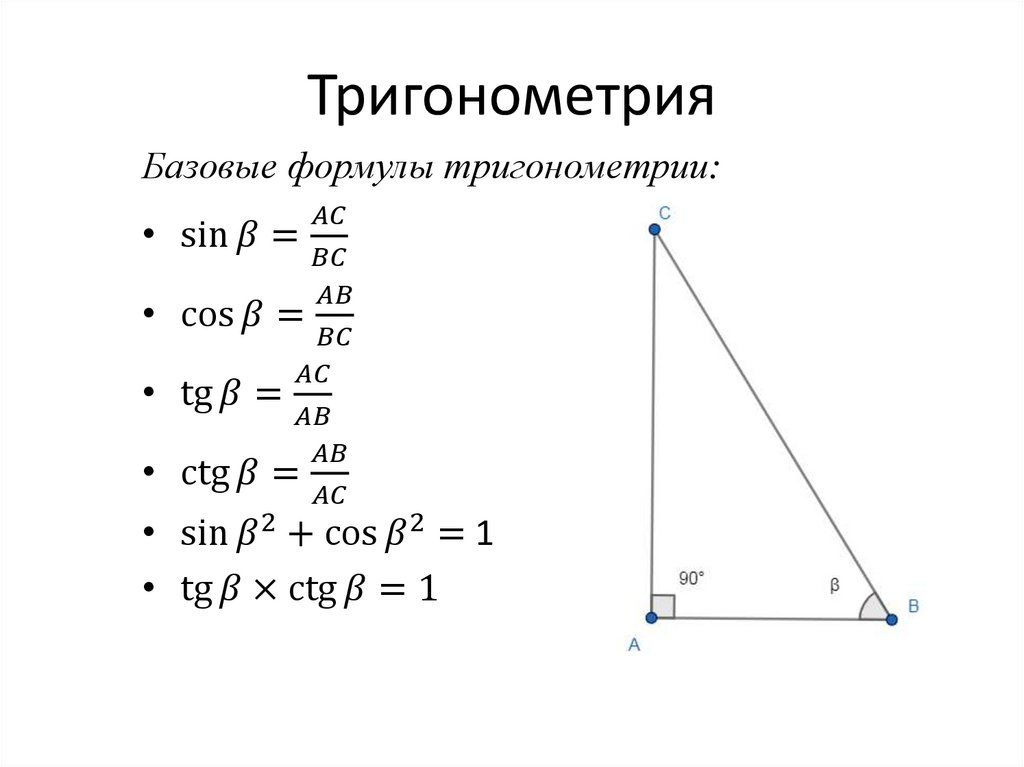 Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.

См. также

• Рациональная тригонометрия
• Сферическая тригонометрия
• Тригонометрические тождества
• Тригонометрические функции

Примечания

1. ↑ Советский энциклопедический словарь.
   М.: Советская энциклопедия, 1982.

ТРИГОНОМЕТРИЯ . Энциклопедический словарь юного математика

Тригонометрия — математическая дисциплина, изучающая зависимость между сторонами и углами треугольника.

Казалось бы, тригонометрию можно считать лишь частью геометрии, однако тригонометрические функции, с помощью которых связываются элементы треугольника, — это объект изучения математического анализа, а тригонометрические уравнения — уравнения, в которых неизвестные являются аргументами тригонометрических функций, — изучаются методами алгебры. Таким образом, тригонометрия — раздел математики, использующий достижения других важных ее разделов.

Основные формулы тригонометрии задаются теоремой синусов (см. Синусов теорема) и теоремой косинусов (см. Косинусов теорема). Кроме них часто применяются теорема тангенсов, открытая в XV в. немецким математиком И. Региомонтаном,

, , ,

и формулы К. Мольвейде (немецкого математика конца XVIII — начала XIX в. ):

, .

Здесь через a,b,c обозначены длины сторон треугольника, а через A,B,C — соответственно величины противоположных им углов.

Помимо теоремы косинусов углы треугольника могут быть также выражены через его стороны с помощью формул:

, , ,

где p — полупериметр треугольника.

Площадь треугольника помимо формулы Герона (см. Герона формула) может быть выражена с помощью тригонометрии через стороны и углы треугольника еще несколькими способами:

S = 1/2 ab sin C, , S = p² tg A/2 tg B/2 tg B/2.

Тригонометрия возникла из практических нужд человека. С ее помощью можно определить расстояние до недоступных предметов и, вообще, существенно упрощать процесс геодезической съемки местности для составления географических карт.

Зачатки тригонометрических познаний зародились в древности. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вспомогательным разделом.

Древнегреческие ученые разработали «тригонометрию хорд», изложенную выдающимся астрономом Птолемеем (II в.) в его работе «Альмагест». Птолемей вывел соотношения между хордами в круге (выражавшиеся словесно ввиду отсутствия в то время математической символики), которые равносильны современным формулам для синуса половинного и двойного угла, суммы и разности двух углов:

, sin 2α = 2 sin α cos α, sin (α±β) = sin α cosβ ± sin β cos α.

Важный шаг в развитии тригонометрии был сделан индийскими учеными, которые заменили хорды синусами. Это нововведение перешло в VIII в. в арабоязычную математику стран Ближнего и Среднего Востока, где тригонометрия постепенно превратилась из раздела астрономии в самостоятельную математическую дисциплину. Помимо синуса были введены и другие тригонометрические функции, и для них были составлены таблицы.

Общепринятые понятия тригонометрии, а также обозначения и определения тригонометрических функций сформировались в процессе долгого исторического развития. Если, например, при введении основных тригонометрических понятий представляется естественным принимать радиус тригонометрического круга (рис. 1) равным единице, то эта, казалось бы, простая идея была усвоена только в Х-XI вв. Если мы понимаем под синусом угла α в прямоугольном треугольнике OBC отношение катета BC (линия синуса) к гипотенузе OC (т.е. радиусу единичной окружности), то в средние века термином «синус» обозначали саму линию синуса BC. То же относится к косинусу, под которым понималась линия косинуса

OB, и другим тригонометрическим функциям.

Рис. 1

Лишь постепенно, благодаря введению новых понятий, а также в результате разработки и усовершенствования математической символики, тригонометрия приобрела современный вид, наиболее удобный для решения вычислительных задач. Окончательный вид она приобрела в XVIII в. в трудах Л. Эйлера.

Существует также сферическая тригонометрия, рассматривающая соотношения между сторонами и углами треугольников на сфере, образованных дугами больших кругов.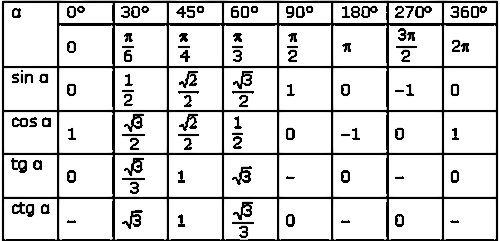 Она является частью сферической геометрии и возникла исторически раньше тригонометрии на плоскости из потребностей практической астроном

Простая английская Википедия, бесплатная энциклопедия

Из Простая английская Википедия, бесплатная энциклопедия

Тригонометрия (от греческого trigonon = три угла и метрон = мера) является частью элементарной математики, имеющей дело с углами, треугольников и тригонометрических функций , таких как синус (сокращенно sin), косинус (сокращенно cos) и тангенс (сокращенно tan). ^{[1] [2]} Он имеет некоторую связь с геометрией, хотя существуют разногласия по поводу того, какая именно это связь; для некоторых тригонометрия — это просто раздел геометрии.

Стандартный прямоугольный треугольник. C — прямой угол на этом рисунке.

Тригонометрия использует большое количество специальных слов для описания частей треугольника. Вот некоторые из определений тригонометрии:

• Прямоугольный треугольник — Прямоугольным треугольником называется треугольник, угол которого равен 90 градусов. (В треугольнике не может быть более одного прямого угла) Стандартные тригонометрические соотношения можно использовать только для прямоугольных треугольников.
• Гипотенуза — Гипотенуза треугольника — это самая длинная сторона и сторона, лежащая против прямого угла. Например, для треугольника справа гипотенуза равна стороне c .
• Противоположная угла — Противоположная сторона угла — это сторона, не пересекающаяся с вершиной угла. Например, сторона a противоположен углу A в треугольнике справа.
• Смежная угла — Смежной стороной угла называется сторона, пересекающая вершину угла, но не являющаяся гипотенузой. Например, сторона b примыкает к углу A в треугольнике справа.

Существуют три основных тригонометрических отношения для прямоугольных треугольников и три обратных значения этих отношений, что в сумме составляет 6 отношений. Их: ^[3]

• Синус (sin) — Синус угла равен Гипотенузе напротив {\ displaystyle \ textstyle {\ text {Противоположно}} \ over {\ text {Гипотенуза}}}.
• Косинус (cos) — косинус угла равен AdjacentHypotenuse{\displaystyle \textstyle {\text{Adjacent}} \over {\text{Гипотенуза}}}.
• Тангенс (тангенс) — Тангенс угла равен OppositeAdjacent{\displaystyle \textstyle {\text{Противоположный}} \over {\text{Смежный}}}.

Обратные величины этих соотношений:

Косеканс (косек) — Косеканс угла равен гипотенузеПротивоположный {\displaystyle \textstyle {\text{Гипотенуза}} \over {\text{Противоположный}}} или csc⁡θ=1sin⁡θ{ \displaystyle \csc \theta = {1 \over \sin \theta }}.

Секанс (сек) — Секанс угла равен HypotenuseAdjacent{\displaystyle {{\text{Гипотенуза}} \over {\text{Adjacent}}}} или sec⁡θ=1cos⁡θ{ \displaystyle \sec \theta = {1 \over \cos \theta }}.

Котангенс (cot) — Котангенс угла равен AdjacentOpposite{\displaystyle {{\text{Adjacent}} \over {\text{Opposite}}}} или cot⁡θ=1tan⁡θ{ \displaystyle \cot \theta = {1 \over \tan \theta }}.

Студенты часто используют мнемонику, чтобы запомнить эту связь. Отношения синуса , косинуса и тангенса в прямоугольном треугольнике можно запомнить, представив их в виде строк букв, таких как SOH-CAH-TOA:

S ine = O pposite ÷ H ypotenuse

C осин = A djacent ÷ H ypotenuse

T angent = O pposite ÷ A djacent

С синусами и косинусами можно ответить практически на все вопросы о треугольниках. Это называется «решением» треугольника. Остальные углы и стороны любого треугольника можно вычислить, если известны две стороны и угол, прилежащий к ним, или два угла и сторона, или три стороны. Эти законы полезны во всех разделах геометрии, начиная с каждый многоугольник может быть описан как комбинация треугольников .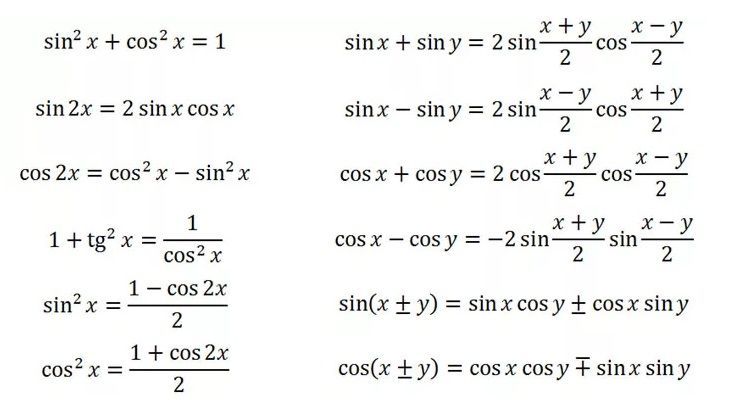

Тригонометрия также необходима при геодезии, векторном анализе и изучении периодических функций. Он возник из-за необходимости вычислять углы и расстояния в таких областях, как астрономия, картографирование, геодезия и дальномер артиллерийских орудий. ^[2]

Существует также такое понятие, как сферическая тригонометрия, которая занимается сферической геометрией. Это используется для расчетов в астрономии, геодезии и навигации. 9{2}-2bc\cos(A)}

Закон касательных[изменить | изменить источник]

a−ba+b=tan⁡(12(A−B))tan⁡(12(A+B)){\displaystyle {\frac {ab}{a+b}}={\frac {\ tan ({\ frac {1} {2}} (AB))} {\ tan ({\ frac {1} {2}} (A + B))}}}

• Радиан
• Полярная система координат
• Единичный круг

1. ↑ «Список символов геометрии и тригонометрии». Математическое хранилище . 2020-04-17. Проверено 24 сентября 2020 г. . {{цитировать в Интернете}} : CS1 maint: URL-статус (ссылка)
2. ↑ ^{2. 0 2.1} «тригонометрия | Определение, формулы, соотношения и тождества». Британская энциклопедия . Проверено 24 сентября 2020 г. .
3. ↑ Менц, Петра; Малберри, Никола (13 июля 2020 г.). «Раннее трансцендентальное исчисление: дифференциальное и многомерное исчисление для социальных наук (1.3 тригонометрия)». sfu.ca . Проверено 24 сентября 2020 г. {{cite web}} : CS1 maint: url-status (ссылка)

• Базовый курс тригонометрии в Академии Хана

Brilliant Math & Science Wiki

Содержание

• Элементарное определение и использование
• Единичный круг
• Свойства тригонометрических функций.
• Тригонометрические тождества
• Закон синусов и закон косинусов
• Тригонометрические функции на комплексной плоскости.
• Гиперболические тригонометрические функции
• Смотрите также

Рассмотрим знакомый пример 45-45-9\ обр. 90∘. По теореме Пифагора такой треугольник должен иметь гипотенузу, длина которой в 2 \sqrt{2} 2​ раза больше длины каждого из катетов:

В этом случае относительно одного из острых углов треугольника можно записать отношение сторон как

противолежащая сторона гипотенуза = 12, прилежащая сторона гипотенуза = 12, противолежащая сторона прилежащая сторона = 1. \frac{\text{противоположная сторона}}{\text{гипотенуза}} = \frac{1}{\sqrt{2}}, \quad \frac{\text{прилегающая сторона}}{\text{гипотенуза}} = \frac{1}{\sqrt{2}}, \quad \frac{\text{противоположная сторона}}{\text{прилежащая сторона}} = 1. гипотенузапротивоположная сторона=2​1​,гипотенузаприлежащая сторона​= 2​1​, соседняя сторона​противоположная​=1. 9\circ угол 30∘, отношение сторон можно записать как

противолежащая сторонагипотенуза=12,прилежащая сторонагипотенуза=32,противоположная сторонаприлежащая сторона=13. \frac{\text{противоположная сторона}}{\text{гипотенуза}} = \frac{1}{2}, \quad \frac{\text{прилегающая сторона}}{\text{гипотенуза}} = \frac{ \sqrt{3}}{2}, \quad \frac{\text{противоположная сторона}}{\text{прилегающая сторона}} = \frac{1}{\sqrt{3}}. гипотенуза противоположной стороны=21,гипотенуза соседней стороны=23​,прилежащая сторонапротивоположная сторона=3​1​.

В обоих случаях указание острых углов прямоугольного треугольника определяет относительные отношения между каждой из сторон. Когда один угол уменьшается, а другой увеличивается, сторона, противоположная большему углу, становится больше, а сторона, противоположная меньшему углу, уменьшается.

Нет никаких причин, по которым отношения нельзя указать для любого произвольного прямоугольного треугольника. В принципе, если задан один из острых углов прямоугольного треугольника, отношения между каждой парой сторон фиксированы.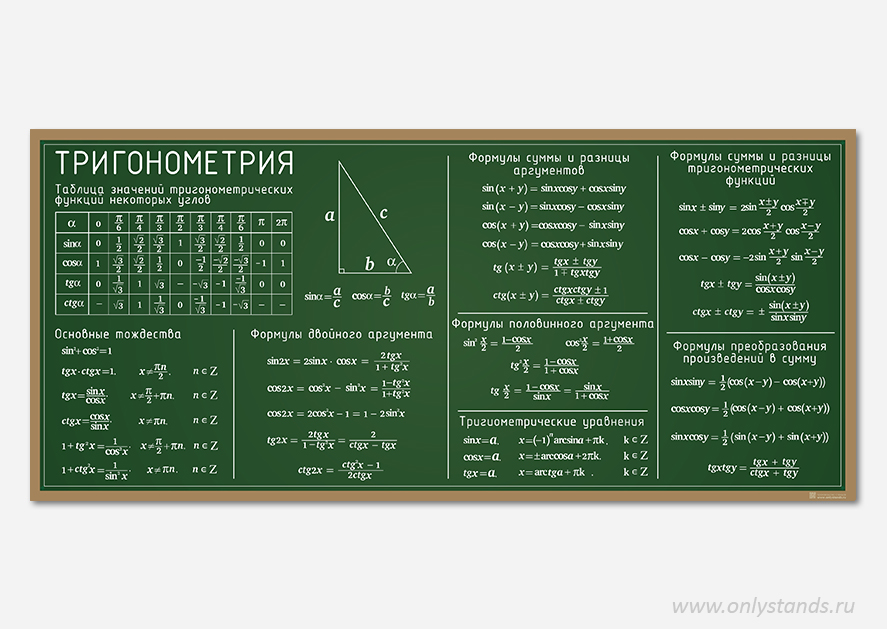 Другими словами, отношения сторон можно считать функциями меры острого угла. В тригонометрии три отношения составляют основу определения трех основных тригонометрических функций, называемых синус , косинус и касательной .

Дан острый угол θ \ тета θ, постройте прямоугольный треугольник, один (или оба) из которых острый угол равен θ \ тета θ:

• Синус θ \ тета θ записывается как sin ⁡ θ \ sin {\ theta} sin θ и определяется как отношение sin⁡θ=противоположная сторона гипотенузы. \sin{\theta} = \frac{\text{противоположная сторона}}{\text{гипотенуза}}. sinθ = гипотенуза, противоположная сторона​.

• Косинус θ \theta θ записывается как cos⁡θ \cos{\theta} cosθ и определяется как отношение cos⁡θ=прилегающая сторона-гипотенуза. \cos{\theta} = \frac{\text{прилежащая сторона}}{\text{гипотенуза}}. cosθ = гипотенуза, примыкающая сторона. 9\circ 90∘, синус изменяется от 0 0 0 до 1 1 1, а косинус изменяется от 1 1 1 до 0 0 0. При этом тангенс изменяется от 0 0 0 до ∞ \infty ∞.

  Кроме того, поскольку они часто используются, обратные величины синуса, косинуса и тангенса также имеют имена: это косеканс , секанс и котангенс .

  • Косеканс θ \theta θ записывается как csc⁡θ \csc{\theta} cscθ и определяется как csc⁡θ=1sin⁡θ. \csc{\theta} = \frac{1}{\sin{\theta}}. cscθ=sinθ1​.

  • секанс θ \theta θ записывается как sec⁡θ \sec{\theta} secθ и определяется как сек⁡θ=1cos⁡θ. \sec{\theta} = \frac{1}{\cos{\theta}}. секθ=cosθ1​.

  • Котангенс θ \theta θ записывается как cot⁡θ \cot{\theta} cotθ и определяется как детская кроватка⁡θ=1tan⁡θ. \cot{\theta} = \frac{1}{\tan{\theta}}. раскладушка θ = загар θ1​.

  Хотя значения тригонометрических функций для определенных углов могут быть вычислены как алгебраические числа (т. е. выражаемые только в терминах дробей и корней), в общем случае синус или косинус произвольного угла могут быть трансцендентными. Это доказывается теоремой Бейкера. 9\circ}} = \sqrt{3}.\ _\squarecsc30∘=sin30∘1​=2,sec30∘=cos30∘1​=3​2​,cot30∘=tan30∘1​=3​. □​

Напомним, что два угла и сторона между ними или две стороны и угол между ними задают уникальный треугольник. В конечном счете, тригонометрические функции позволяют указать все неизвестные стороны и углы для однозначно определенного треугольника.

Прямоугольный треугольник имеет гипотенузу длины L L L. Если меньший из двух углов в треугольнике равен θ \ тета θ, каковы длины двух катетов прямоугольного треугольника?

---

Длина более короткой стороны (сторона, противоположная θ \theta θ, должна быть равна Lsin⁡θ L \sin{\theta} Lsinθ из определения синуса. Отсюда следует, что длина более длинной стороны, которая равна сторона, примыкающая к θ \theta θ, должна быть Lcos⁡θ L \cos{\theta} Lcosθ. □_\square□​

Ничего из вышеперечисленного 1 2 0

(1cos⁡a−sin⁡acos⁡a)(1cos⁡a+sin⁡acos⁡a)= ?\left( \dfrac1{\cos a} — \dfrac{\sin a}{\cos a} \right) \left( \dfrac1{\cos a} + \dfrac{\sin a}{\cos a} \right) = \, ? (cosa1​−cosasina​)(cosa1​+cosasina​)=?

Предположим, что a≠2nπ±π2. a \neq 2n\pi \pm \dfrac{\pi}{2}.a​=2nπ±2π​.

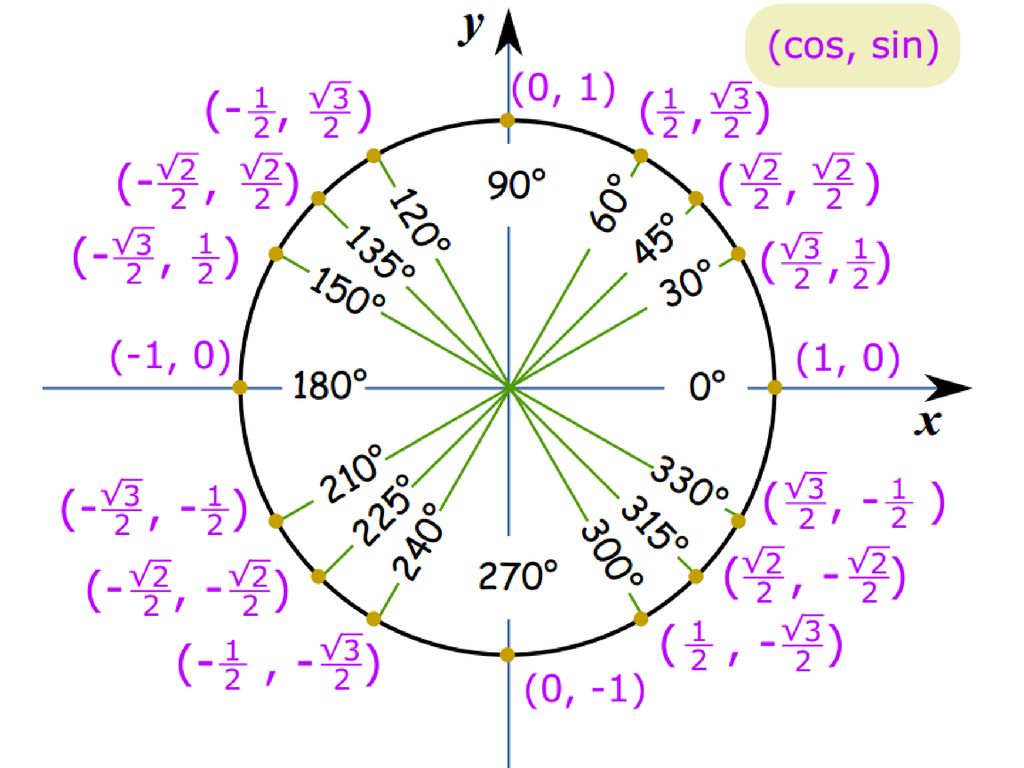
Чтобы расширить область определения тригонометрических функций на все углы, а не только на те, которые существуют как острый угол прямоугольного треугольника, можно рассмотреть координаты точки, расположенной на единичной окружности . Приведение радиуса окружности к точке на окружности дает прямоугольный треугольник, гипотенуза которого имеет единичную длину, а катеты полностью лежат на осях координат. Таким образом, можно определить тригонометрические функции в терминах координат x x x и y y y точки на единичной окружности. \circ 0∘ (представляющего поворот по часовой стрелке). вращение).

Дан угол θ \theta θ, пусть x x x и y y y будут координатами точки на единичной окружности, так что угол, образованный между радиусом и положительной осью x x x, равен θ \theta θ. Затем

sin⁡θ=y,cos⁡θ=x,tan⁡θ=yx. \sin{\theta} = y, \quad \cos{\theta} = x, \quad \tan{\theta} = \frac{y}{x}.sinθ=y,cosθ=x,tanθ=xy​ .

В расширенном определении тригонометрические функции могут принимать отрицательные значения:

• В первом квадранте (ось +x +x +x и ось +y +y +y) и синус, и косинус положительны.
• Во втором квадранте (оси −x — x −x и оси +y +y +y) синус положительный, а косинус отрицательный.
• В третьем квадранте (ось −x −x −x и ось −y − y −y) и синус, и косинус отрицательны.
• В четвертом квадранте (ось +x +x +x и ось −y-y−y) синус отрицательный, а косинус положительный.

Косинус переходит от 1 1 1 к 0 0 0, к −1 -1 −1, к 0 00 и, наконец, обратно к 1 1 1, тогда как синус делает обратное: сначала от 0 0 0 к 1 1 1, а затем к 0 0 0, за которым следует -1 -1 -1, а затем обратно к 0 0 0. \circ 360∘, или 2π 2 \pi 2π по радианному углу, при этом оба графика смещены на 9\ обр. 90∘.

3+3π 3 + 3\pi 3+3π 3+4π 3 + 4 \pi 3+4π 4+3π 4 + 3 \pi 4+3π 4+4π 4 + 4 \pi 4+4π

5 единичных кругов размещены центрами на квадратной сетке. Какова общая площадь зелени?

Примечание: Центры окружностей: (−1,1),(1,1),(0,0),(−1,−1),(1,−1) (-1, 1 ), (1,1), (0,0), (-1,-1), (1,-1) (-1,1),(1,1),(0,0),(-1 ,−1),(1,−1).

Тригонометрические функции обладают несколькими интересными аналитическими свойствами. Во-первых, как уже упоминалось, синус и косинус имеют период 2π: 2 \pi: 2π:

sin⁡θ=sin⁡(θ+2π)cos⁡θ=cos⁡(θ+2π)\begin{выровнено} \sin{\theta} &= \sin(\theta + 2 \pi) \\ \cos{\theta} &= \cos(\theta + 2 \pi) \end{выровнено}sinθcosθ​=sin(θ+2π)=cos(θ+2π)​

Тангенс, тем временем, имеет период только π \pi π, так как относительный знак синуса по сравнению с косинусом требует только периода π \pi π, чтобы совершить полный цикл (переключение с положительного на отрицательное и обратно на положительное) :

загар ⁡ θ = tan ⁡ (θ + π) \ tan {\ theta} = \ tan (\ theta + \ pi) tan θ = tan (θ + π)

Как видно из графика, косинус четен, а синус нечетен:

sin⁡(−θ)=−sin⁡θcos⁡(−θ)=cos⁡θ \begin{выровнено} \sin(-\theta) &= -\sin{\theta} \\ \cos(-\theta) &= \cos{\theta} \end{выровнено} sin(-θ)cos(-θ)​=-sinθ=cosθ​

Свойство, связывающее синус с косинусом, заключается в том, что синус представляет собой просто косинус, сдвинутый на сдвиг на π2. \фракция{\пи}2. 2π​. Ясно, что это должно быть так, потому что синус угла должен быть равен косинусу его дополнения; противолежащая сторона одного угла прямоугольного треугольника равна прилежащей стороне дополнительного угла:

sin⁡θ=cos⁡(θ−π2) \sin{\theta} = \cos\left(\theta — \frac{\pi}2\right) sinθ=cos(θ−2π​)

Те, кто знаком с вычислениями, знают, что производные синуса и косинуса тесно связаны между собой:

Для θ \ тета θ измеряется в радианах ,

ddθsin⁡θ=cos⁡θ,ddθcos⁡θ=−sin⁡θ. \ frac {d} {d \ theta} \ sin {\ theta} = \ cos {\ theta}, \ quad \ frac {d} {d \ theta} \ cos {\ theta} = — \ sin {\ theta} . dθd​sinθ=cosθ, dθd​cosθ=-sinθ.

Аналогичные свойства применимы и к другим тригонометрическим функциям. 9{-1} х = \, ? грех-1x+cos-1x=?

На практике выражения, содержащие тригонометрические функции, могут быть довольно сложными. Одним из средств их упрощения является использование различных тождеств. Среди наиболее известных из них формулы суммы и разности . Эти тождества позволяют разложить тригонометрическую функцию, аргументом которой является сумма или разность двух углов. Эти тождества могут быть доказаны с помощью довольно простых геометрических аргументов среди других методов.

96\тета.sin6θ+cos6θ.

Особого упоминания заслуживают две теоремы о синусе и косинусе треугольников. Закон синусов связывает длины сторон треугольника (не обязательно прямоугольного треугольника) с их противоположными углами, а закон косинусов обобщает теорему Пифагора.

Закон синусов

Пусть A,B,C A, B, C A,B,C обозначают меры углов при соответствующих вершинах, а a,b,c a, b, c a,b,c обозначают длины противоположных сторон соответствующие углы.

Считается, что

asin⁡A=bsin⁡B=csin⁡C. \frac{a}{\sin{A}} = \frac{b}{\sin{B}} = \frac{c}{\sin{C}}. sinAa​=sinBb​=sinCc​. 2 — 2ab \cos{C}. \end{выровнено} a2b2c2​=b2+c2−2bccosA=a2+c2−2accosB=a2+b2−2abcosC.​ 9{ix} &= 2\pm \sqrt{3} \\ x &= -i \ln\big(2\pm \sqrt{3}\big).\ _\квадрат \end{выровнено} eix+e−ix(eix)2−4eix+1eixx​=4=0=2±3​=−iln(2±3​). □​​

π2±iln⁡(2+3) \frac\pi2 \pm i \ln\big(2 + \sqrt{3}\big) 2π​±iln(2+3

​) −π4±iln⁡(2+3) — \frac\pi4 \pm i \ln\big(2 + \sqrt{3}\big) −4π​±iln(2+3

​) π4±iln⁡(2+3) \frac\pi4 \pm i \ln\big(2 + \sqrt{3}\big) 4π±iln(2+3 9{\pm iy} \\ &= (\cos{x} + i\sin{x})(\cos{y} \pm i \sin{y}) \\ &= \cos{x} \cos{y} \mp \sin{x} \sin{y} + i(\sin{x} \cos{y} \pm \cos{x} \sin{y}) . \end{aligned} ei(x±y)​=eixe±iy=(cosx+isinx)(cosy±isiny)=cosxcosy∓sinxsiny+i(sinxcosy±cosxsiny).​

Приравнивание действительной и мнимой частей соответственно , дает известные формулы суммы и разности

cos⁡(x±y)=cos⁡xcos⁡y∓sin⁡xsin⁡y \cos(x \pm y) = \cos{x} \cos{y} \mp \sin{x} \sin{y} cos(x±y)=cosxcosy∓sinxsiny

и 9{-x}}{2}coshx=2ex+e−x​

sech x=1cosh⁡x\text{sech} x = \frac{1}{\cosh x}sech x=coshx1​

csch x=1sinh⁡x\text{csch} x = \frac{1}{\sinh x}csch x=sinhx1​

tanh⁡x=sin⁡xcosh⁡x\tanh x = \frac{\sinxx}{\coshx}tanhx=coshxsinhx​

coth⁡x=1tanh⁡x\coth x = \frac{1}{\tanh x}cothx=tanhx1​.

Они так называются из-за схожих свойств, которые они разделяют с их тригонометрическими аналогами.

Это можно увидеть в некоторых соотношениях гиперболических тригонометрических функций: 92 х = 1coth3x−csch3x=1

sinh⁡(x+y)=sinh⁡xcosh⁡y+cosh⁡xsinh⁡y\sinh (x + y) = \sinh x \cosh y + \cosh x \sinh ysinh(x+y)=sinhxcoshy+coshxsinhy

sinh⁡(x−y)=sinh⁡xcosh⁡y−cosh⁡xsinh⁡y\sinh (x — y) = \sinh x \ch y — \cosh x \sinh ysinh(x−y)=sinhxcoshy-chxsinhy

ch⁡(x+y)=ch⁡xcosh⁡y+sinh⁡xsinh⁡y\ch (x + y) = \ch x \ch y + \sinh x \sinh ycosh(x+y)=chxcoshy+sinhxsinhy

ch⁡(x−y) = ch⁡xcosh⁡y−sinh⁡xsinh⁡y\ch (x — y) = \ ch x \ ch y — \ sinh x \ sinh ycosh(x−y) = chxcoshy-sinhxsinhy . 9{-1}\left(\frac{v_2}{c}\right).tanh−1(cv​)=tanh−1(cv1​​)+tanh−1(cv2​​).

y=sech x y=\text{sech}\, xy=sechx y=csch x y=\text{csch}\, xy=cschx у = шиш⁡х у = \ шиш ху = шишх y=tanh⁡xy=\tanhxy=tanhx y = sinh⁡x y = \ sinh xy = sinhx y=coth⁡xy=\coth xy=cothx

Какой из следующих гиперболических тригнометрических графиков лучше всего «аппроксимируется» с помощью y=1x?y = \frac{1}{x}?y=x1​?

• Графическое преобразование тригонометрических функций
• Доказательство тригонометрических тождеств
• Обратные тригонометрические функции
• Симметрия в тригонометрических графах
• Основные фигуры, многоугольники и тригонометрия

Цитировать как: Тригонометрия.

No related posts.