Урок математики по теме «Решение систем неравенств с двумя переменными». 11-й класс
Тип урока: комбинированный.
Цели урока.
Оборудование урока: компьютерный класс, мультимедийный проектор, презентации, программа “Графер”, Открытая Математика 2.6. Функции и Графики.
Структура урока.
- Вводная часть.
- Устные упражнения.
- Основной практикум.
- Зарядка для глаз.
- Повторение теоретического материала.

- Самостоятельная работа с самопроверкой на компьютере.
- Подведение итогов урока.
- Задание на дом.
Ход урока
1. Вводная часть:
- Эпиграф: “Разумеется, хорошая математика красива”. Коэн П.Д.
- Знакомство с ходом и целью урока.
2. Устные упражнения. (Приложение 1)
1) Решите неравенство:
а) 2х – 6 > 0
б) 10 – 5х < 0
в) | х| < 3
г) | у | > 8
д) |х — 7| < -5
е) |у + 2| > -11
2) Какая функция и что является графиком?
у = 12х – 7; у = -4х; у =; у = -2х2; у = 8 – 2х;
у =; у = х2 — 10х +5; у = 125х; у =;
3) Что можно найти по этой формуле?
S = a2 S = p r2 S = ab C = 2p r P = a + b + c S = P = (a + b) ·2
3. Основной практикум.
1. Построить множество точек, координаты х и у которых удовлетворяют системе:
Решение: (Слайд 1-2)
х2+у2-2х; (х-1)2+у21. Имеем множество точек, лежащих вне окружности и на самой окружности с R=1 и с центром в точке А(1;0). Имеем множество точек, лежащих внутри окружности и на самой окружности с R=2 и с центром в точке В(2;0). Искомое множество точек есть общая часть этих двух множеств.
2. Найдите периметр фигуры, точки которой на координатной плоскости удовлетворяют системе:
Решение: (Слайд 3-4),
Длина границы фигуры (заштрихованной) равна
Сокр+ОА+ОВ=. 2+2=
3. Найти площадь фигуры, задаваемой на плоскости множеством решений неравенства:
|х – 2| + |у| < 2.
Решение: (Слайд 5-6),
ОДЗ:
S=d1d2; S=.
4. Найти периметр и площадь плоской фигуры, заданной на координатной плоскости условиями:
Решение: (Слайд 7-8),
или
решений не
имеет.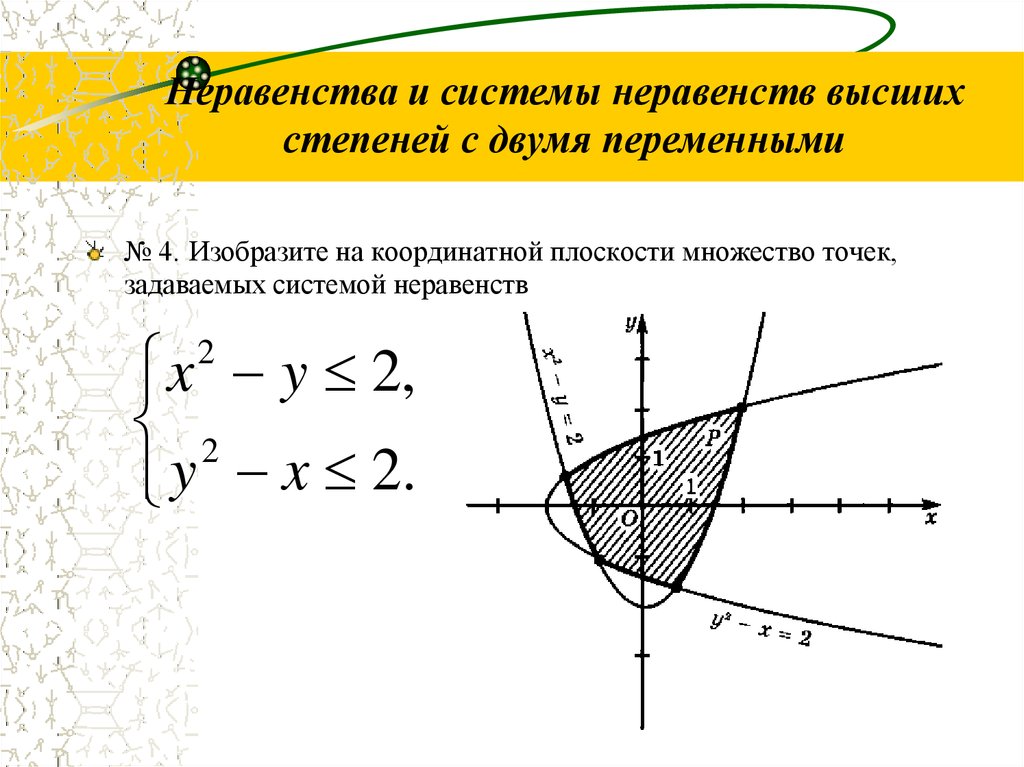
Р=АВ+ВС+СD+DE+EA=
S=Sкв+2Sтр=
5. Построить множество точек, координаты х и у которых удовлетворяют системе неравенств:
Найти все значения а, при которых точка М принадлежит этому множеству.
Решение: (Слайд 9-10),
1) Строим графики функций и Штрихуем соответствующее множество точек. Получаем фигуру ABCD.
2) Найдем все значения a, при которых точка М принадлежит заштрихованному множеству точек. Точка М(а+1;2а) принадлежит множеству, если ее координаты
удовлетворяют системет.е.
Таким образом, точка Мпринадлежит множеству точек, если .
6. Дополнительно: изобразить на плоскости множество решений системы неравенств. При каком значении r площадь получившейся фигуры ?
Ответ:
4. Зарядка для глаз.
5. Повторение.
На уроке с использованием ЭОР организуется
работа для обучающихся, учитывая их знания и
умения, индивидуальный стиль усвоения.
По второй части курса “ Открытая Математика 2.6. Функции и графики”, глава 2.5.3 “Элементарные функции и их графики” обучающиеся повторяют базовые сведения о функциях и графиках, графические методы решения уравнений и неравенств.
| 1 группа учащихся | 2 группа учащихся | |
| Самостоятельно, без подсказок (со стороны учителя и минимум подсказок с помощью компьютера) решают задачи раздела. | Для решения задачи используют подсказки с помощью компьютера | Обращаются к готовым решениям и отвечают на вопросы, используя справочный материал |
6. Самостоятельная работа. (Самопроверка на
компьютере). (Приложение 3)
Самостоятельная работа. (Самопроверка на
компьютере). (Приложение 3)
1. Найти площадь и периметр фигуры, задаваемой на плоскости множеством решений системы неравенств:
1 вариант:
2 вариант:
Решение:
1 вариант: (Слайд 3),
Sф=SАВСD-. . Рф=ВС+СD+DA+C окр
Рф=4+4+4+.
2 вариант: (Слайд 4),
Sф=SABCD — . Рф=ВС+СD+DA+ВЕ+АF+C окр.
Рф=1+4+1+1+1+
2. Учащиеся с помощью компьютера строят фигуру, задаваемую на плоскости множеством решений системы неравенств, и определяют все точки пересечения.
7. Подведение итогов урока.
- Анализ хода урока и его основных моментов.
- Оценивание деятельности каждого ученика на уроке.
- Результаты самостоятельной работы.
8. Задание на дом.
- Учащимся предлагается изобразить пословицу,
поговорку, цитату с помощью графика, установив
при этом функциональную зависимость.
 Например:
много будешь знать — скоро состаришься (аргумент -
знания, функция-возраст). (Приложение 4)
Например:
много будешь знать — скоро состаришься (аргумент -
знания, функция-возраст). (Приложение 4) - Изобразите на координатной плоскости множество решений системы неравенств и найдите площадь полученной фигуры: Составить презентацию по решению задания (по желанию). (Приложение 5)
- Найти задачи прикладного характера, приводящие к понятию функция.
- Выполнить задания учебных модулей “Систематизация и обобщение сведений о неравенствах. Основные методы решения неравенств.П1” и “Решение комбинированных неравенств. Неравенства с параметром. К1”.
ftp://85.142.23.53/packages/cm/7723F82D-B9B5-574F-1F94- 66E58C3AF724/0.0.0.0/A11_042_k01.oms
A11_042_k01.oms
A11_042_p01.oms
Методические комментарии к уроку
Чтобы успешно сдать итоговую аттестацию по
математике, следует в первую очередь
совершенствовать навыки решения практических
заданий, т.
В перспективе для организации работы используется учебно-методический комплекс “Функции и графики” из Единой коллекции цифровых образовательных ресурсов. Данный комплекс обеспечивает демонстрационные функции, возможность практикума и проверки знаний обучающихся, а также набор готовых задач для проверки.
Использование ЭОР в обычных и профильных
классах, в дополнительном образовании
(элективных и факультативных курсах, подготовке
к экзаменам, исследовательской и проектной
деятельности обучающихся) позволяет
комбинировать различные формы организации
учебной деятельности.
Возможно проводить современный многоуровневый контроль знаний и получать полную информацию о работе обучаемого и уровне усвоения им учебного материала, учитывать потребности контингента обучаемых, предлагать им нетривиальные творческие задания.
Использование ЭОР в образовательном процессе позволяет нацелить обучающихся на приобретение опыта поиска информации по предлагаемым вопросам, совершенствование своих умений в переработке и представлении информации.
Методические и учебные материалы
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П., Ивлев Б.М., Шварцбурд С.И. Алгебра начала анализа: Учебник для 10-11 классов общеобразовательных учреждений. — М.: Просвещение, 2006.
- Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа для 10-11 классов. — М.: Просвещение, 2005.
- Шахмейстер А.Х. Построение графиков функций
элементарными методами.
 — С. -Петербург, Москва,
2008.
— С. -Петербург, Москва,
2008. - Шахмейстер А.Х. Задачи с параметрами на экзамене.- С.-Петербург, Москва, 2008 .
- Федеральный центр информационных образовательных ресурсов (ФЦИОР, http://eor.edu.ru/).
- Единая коллекция цифровых образовательных ресурсов (Единая коллекция ЦОР, http://school-collection.edu.ru/).
- Информационная система «Единое окно доступа к образовательным ресурсам» (ИС «Единое окно», http://window.edu.ru/), а также ресурсов, описания которых находятся на Федеральном портале «Российское образование» (http://www.edu.ru/).
- Учебное наглядное пособие: Открытая Математика 2.6. Функции и Графики, ООО “Физикон”.
Урок 14. Система неравенств с двумя переменными
ВИДЕО УРОК
ПРИМЕР:
Найти все такие пары целых чисел х, у, которые удовлетворяют системе неравенств:
РЕШЕНИЕ:
Запишем данную систему в следующем виде:
Так как
|х2 – 2х| ≥ 0,
|х –1| ≥ 0,
то из неравенств
у + 1/2 ˃ |х2 – 2х|,
у < 2 – |х –1|.
следует, что
–1/2 < у < 2.
Целыми числами, удовлетворяющими этому неравенству, являются лишь 0 и 1, поэтому системаможет иметь целые решения только при
у = 0 и у = 1.
1) Если у = 0, то система примет следующий вид:
Второму из этих неравенств удовлетворяют целые числа 0, 1 и 2.
Проверка показывает, что первому неравенству удовлетворяют
лишь 0 и 2. Следовательно, пары чисел
х1 = 0, у1 = 0
и
х2 = 2, у2 = 0
образуют решения исходной системы неравенств.
2) Если у = 1, то система примет следующий вид:
Второму неравенству данной
системы удовлетворяет единственное целое число х = 1,
которое является также и решением первого неравенства.
ОТВЕТ:
х1 = 0, у1 = 0,
х2 = 2, у2 = 0,
х3 = 1, у3 = 1.
Графический метод решения систем неравенств с двумя переменными.
Суть метода решений системы неравенств с двумя переменными проста. Находим решение каждого неравенства в отдельности, изображаем решения на одной координатной плоскости и ищем пересечение этих решений.
ПРИМЕР:
Решить графически систему неравенство
РЕШЕНИЕ:
Сначала решим графически первое неравенство.
у ≥ 0.
Затем второе.
х ≤ 0
Объединим эти решения в одной координатной плоскости.Системой неравенствзадаётся второй координатный угол.
ПРИМЕР:
Решить графически систему неравенств:
РЕШЕНИЕ:
Сначала решим графически первое
неравенство.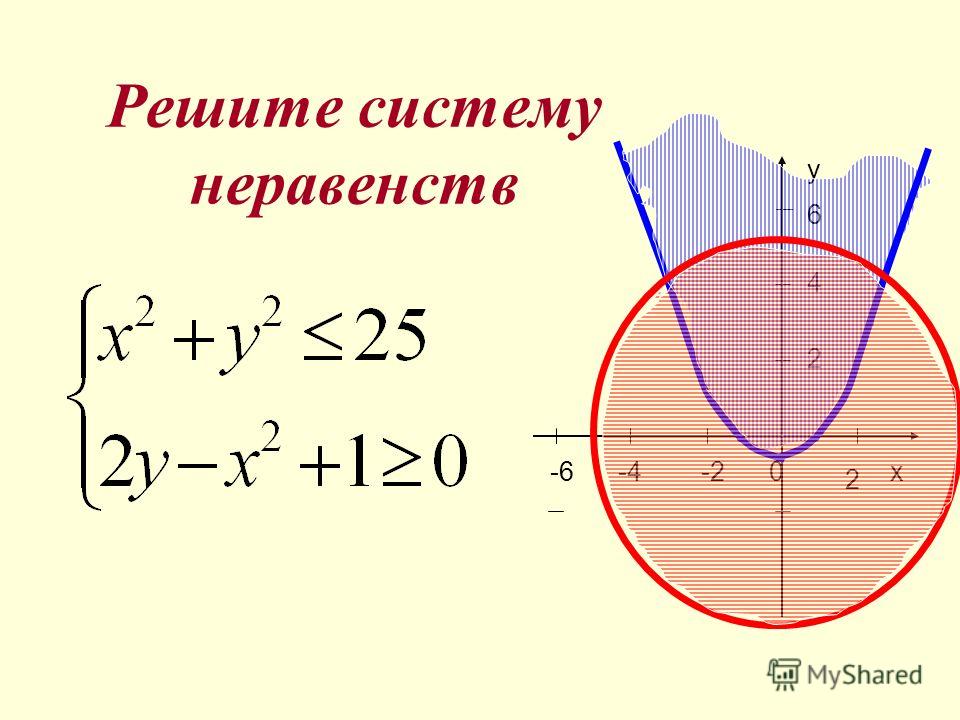
у ≥ 2х – 3.
Затем второе.
у ≤ 2х + 2.
Объединим эти решения в одной координатной плоскости.Системой неравенствзадаётся полоса, ограниченная прямыми
у = 2х – 3,
у = 2х + 2.
ПРИМЕР:
Решить систему неравенств:
РЕШЕНИЕ:
Найдём решение каждого неравенства в отдельности.
Для неравенства
у ≥ х2 – 6х + 2,
множество всех точек расположено выше или “внутри” параболы.
Решения неравенства
у ≤ х + 5
расположены ниже прямой
у = х + 5.
Изобразим оба графика на одной плоскости и найдём пересечение областей.
ПРИМЕР:
Изобразите на координатной плоскости множество решений системы неравенств:
РЕШЕНИЕ:
Множество решений этой системы есть пересечение множеств решений входящих в неё неравенств.
Выясним, что представляет собой множество точек плоскости, координаты которых являются решениями рассматриваемой системы.
Множество точек, координаты которых удовлетворяют неравенству
у ≥ х,
Есть объединение множества точек прямой
и открытой полуплоскости, расположенной выше этой прямой. Множество точек, координаты которых удовлетворяют неравенству
х2 + у2 ≤ 9,
есть круг с центром в начале
координат и радиусом 3.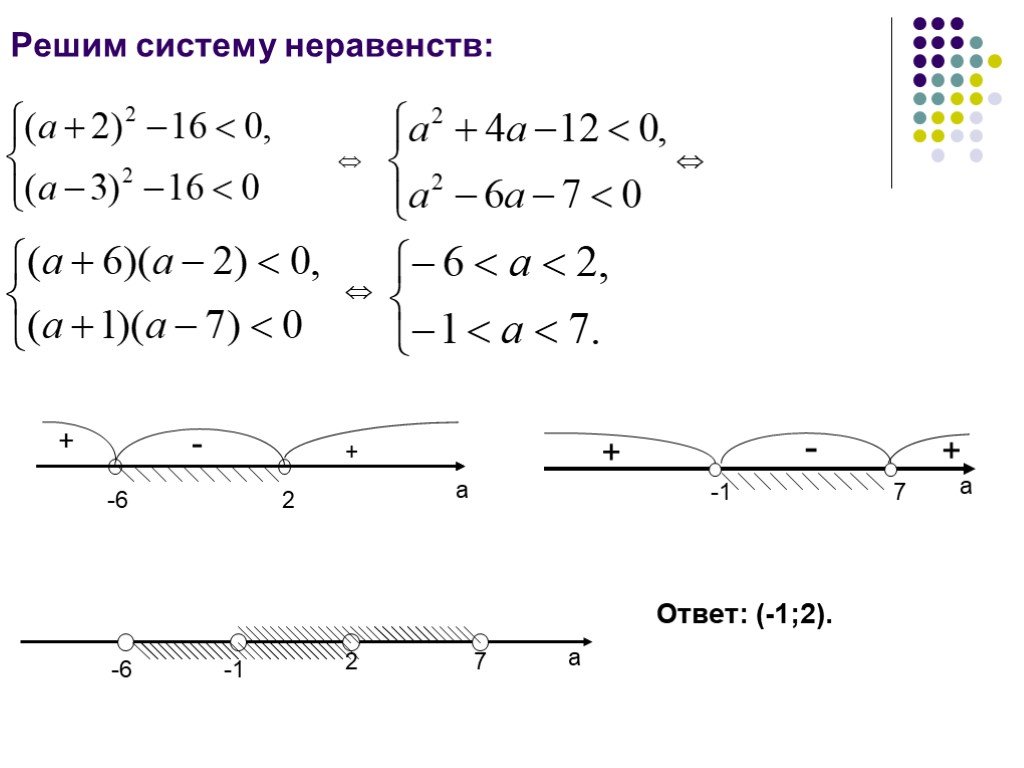 Очевидно, что системе
удовлетворяют координаты тех и только тех точек, которые принадлежат
пересечению множеств точек, задаваемых каждым из неравенств системы (на рисунке ему соответствует та область, где штриховки накладываются
одна на другую). Значит,
рассматриваемой системой неравенств задаётся полукруг.
Очевидно, что системе
удовлетворяют координаты тех и только тех точек, которые принадлежат
пересечению множеств точек, задаваемых каждым из неравенств системы (на рисунке ему соответствует та область, где штриховки накладываются
одна на другую). Значит,
рассматриваемой системой неравенств задаётся полукруг.
ПРИМЕР:
Изобразите на координатной плоскости множество решений системы неравенств:
РЕШЕНИЕ:
Построим прямые
х + у = 3,
4х – 5у = 20.
Множество решений первого неравенства показано горизонтальной штриховкой, а множество решений второго неравенства – вертикальной штриховкой.
Двойная штриховка – множество решений системы. Система задаёт плоский угол.
ПРИМЕР:
Изобразите на координатной плоскости множество решений системы неравенств:
РЕШЕНИЕ:
Построим прямые
х + у = 3,
4х – 5у = 20,
5х + у = –5.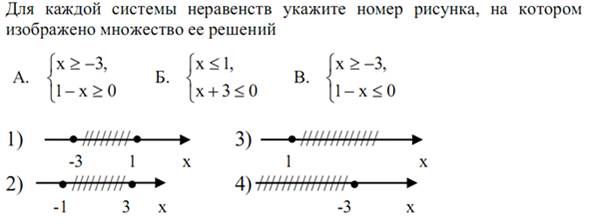
Этой системой задаётся треугольник.
ПРИМЕР:
Изобразите на координатной плоскости множество решений системы неравенств:
РЕШЕНИЕ:
Геометрическим изображением решений системы неравенствявляется множество точек первого координатного угла.
Геометрическим изображением решений неравенства
х + у < 5 или
у < 5 – х
является множество точек, лежащих ниже прямой, служащей графиком функции
у = 5 – х.
Геометрическим изображением решений неравенства ху ˃ 4, или, поскольку х ˃ 0, неравенства
у ˃ 4/х
является множество точек, лежащих выше ветви гиперболы, служащей графиком функции
у = 4/х.
В итоге получаем множество точек координатной плоскости, лежащих в первом координатном углу ниже прямой, служащей графиком функции
у = 5 – х,
и выше гиперболы, служащей графиком функции
у = 4/х.
ПРИМЕР:
Изобразить на координатной плоскости Оху фигуру Ф, координаты точек которой удовлетворяют системе неравенств:
РЕШЕНИЕ:
Построим графики функций
у = |х|,
у = 3 – |х –1|,
Решив систему уравненийнаходим общую точку А(2;2) этих
графиков, лежащую в I квадранте.
Аналогично, решив систему уравненийнаходим общую точку В(–1;1) графиков
функций
у = |х| и
у = 3 – |х –1|,
лежащую в II квадранте.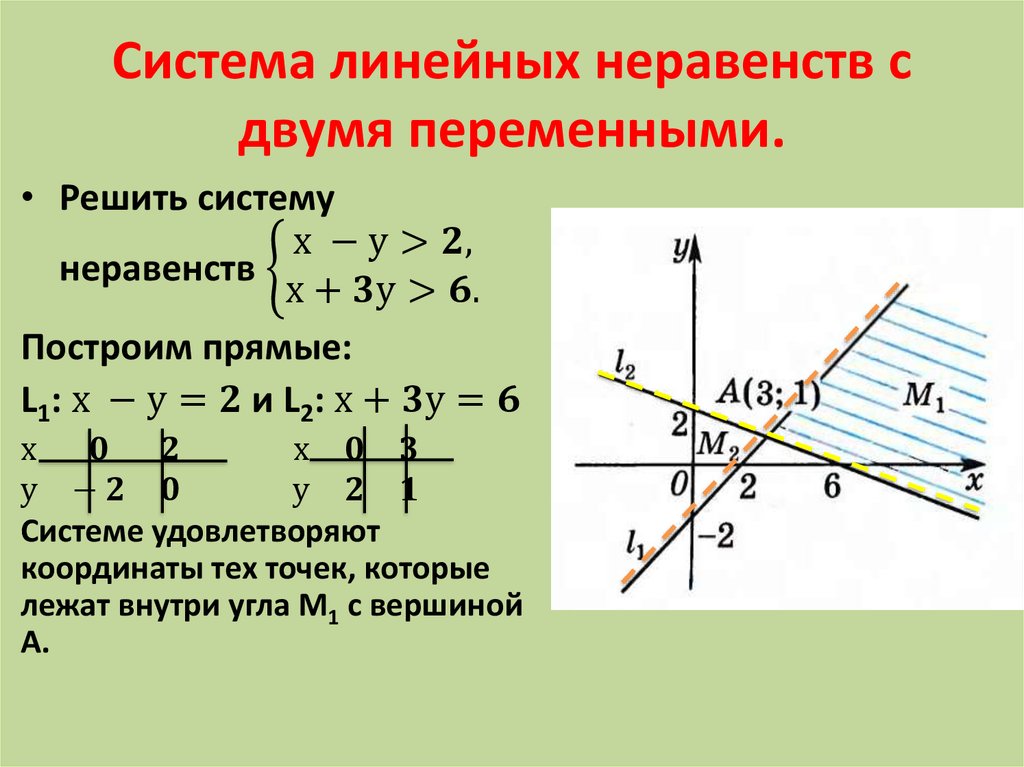
Неравенству
у ˃ |х|
удовлетворяют все точки координатной плоскости, расположенные выше графика функции
у = |х|,
а неравенству
у < 3 – |х –1|
все точки координатной плоскости, лежащие ниже графика функции
у = 3 – |х –1|.
Следовательно, исходной системе удовлетворяют все точки, лежащие внутри прямоугольника ОАСВ, полученного при пересечении графиков функций:
у = |х|,
у = 3 – |х –1|.
Задания к уроку 14
Видео-урок: Приложения к системам неравенств
Стенограмма видео
В этом видео мы научимся
решать приложения систем неравенств, переводя каждое условие в
неравенство. Система линейных неравенств
набор из двух или более линейных неравенств с несколькими переменными. Они часто используются, когда проблема
требует ряда решений, и существует более одного ограничения на
решения, например, магазин пытается купить акции с заданным бюджетом. Начнем с более подробного изучения
подробно, как мы можем представить их.
Они часто используются, когда проблема
требует ряда решений, и существует более одного ограничения на
решения, например, магазин пытается купить акции с заданным бюджетом. Начнем с более подробного изучения
подробно, как мы можем представить их.
Например, если бы у нас была система неравенств 𝑥 больше или равно двум, 𝑦 больше или равно четыре и два 𝑥 плюс три 𝑦 меньше или равно 24, мы можем представить это на двумерная координатная плоскость. Уравнение 𝑥 равно двум может быть представлен вертикальной линией, проходящей через две на оси 𝑥. Поскольку данное неравенство 𝑥 равно больше или равно двум, область, которая нам нужна, находится справа от этого линия. Таким образом, мы можем заштриховать что угодно слева от этой строки.
Важно отметить, что если бы мы
имело строгое неравенство, например, 𝑥 больше двух, то это было бы
представлена пунктирной линией. Уравнение 𝑦 равно четырем
представлен горизонтальной линией, проходящей через ось 𝑦 в точке четыре. Так как неравенство было 𝑦 больше
больше или равно четырем, требуемая площадь находится выше этой линии. И снова мы можем заштриховать
область ниже. Наконец, нам нужно нарисовать
прямая два 𝑥 плюс три 𝑦 равняется 24. Это пересечет ось 𝑦
когда 𝑥 равно нулю, и это происходит, когда 𝑦 равно восьми. Точно так же линия будет пересекаться
𝑥-ось, когда 𝑦 равно нулю, и это происходит, когда 𝑥 равно 12. Уравнение два 𝑥 плюс три 𝑦
равно 24, можно представить на графике, как показано.
Уравнение 𝑦 равно четырем
представлен горизонтальной линией, проходящей через ось 𝑦 в точке четыре. Так как неравенство было 𝑦 больше
больше или равно четырем, требуемая площадь находится выше этой линии. И снова мы можем заштриховать
область ниже. Наконец, нам нужно нарисовать
прямая два 𝑥 плюс три 𝑦 равняется 24. Это пересечет ось 𝑦
когда 𝑥 равно нулю, и это происходит, когда 𝑦 равно восьми. Точно так же линия будет пересекаться
𝑥-ось, когда 𝑦 равно нулю, и это происходит, когда 𝑥 равно 12. Уравнение два 𝑥 плюс три 𝑦
равно 24, можно представить на графике, как показано.
Чтобы выяснить, с какой стороны этой линии
мы требуем, мы можем изменить наше неравенство, чтобы сделать 𝑦 субъектом. Во-первых, мы можем вычесть два 𝑥
с обеих сторон. Тогда мы можем разделить на три
так что 𝑦 меньше или равно отрицательным двум третям 𝑥 плюс восемь. Поскольку 𝑦 меньше или равно
отрицательные две трети 𝑥 плюс восемь, требуемая площадь находится под чертой. Поэтому мы можем заштриховать область
выше этой линии. Это оставляет нас с треугольным
область, удовлетворяющая системе неравенств.
Поскольку 𝑦 меньше или равно
отрицательные две трети 𝑥 плюс восемь, требуемая площадь находится под чертой. Поэтому мы можем заштриховать область
выше этой линии. Это оставляет нас с треугольным
область, удовлетворяющая системе неравенств.
Еще раз важно отметить что мы включаем только значения на краях пересечения областей, если есть сплошная линия на обоих. Это потому, что все необходимо выполнение неравенств, а строгое неравенство исключает его из набор решений.
Теперь рассмотрим несколько примеров где мы получаем систему неравенств из текстовой задачи.
Пастух хочет построить
прямоугольный сарай для овец. Длина сарая должна быть больше
88 метров, а его периметр должен быть меньше 253 метров. Выведите систему неравенств
который описывает ситуацию, обозначая длину сарая через 𝑥 и его ширину через
𝑦.
В этом вопросе нам говорят, что пастух хочет построить прямоугольный сарай для овец длиной 𝑥 метров и шириной 𝑦 метров. Нам нужно сформулировать систему неравенства, удовлетворяющие заданным условиям. Нам говорят, что длина сарай должен быть более 88 метров. Следовательно, 𝑥 должно быть больше, чем 88. Так как ширина амбара не может быть отрицательным значением, мы имеем 𝑦 больше или равно нулю.
Нам также сказали, что периметр
сарая должна быть менее 253 метров. Вспоминая, что периметр любого
двумерная форма — это расстояние вокруг внешней стороны, тогда оно равно 𝑥
плюс 𝑦 плюс 𝑥 плюс 𝑦. Это упрощается до двух 𝑥 плюс два
𝑦. И, разложив два, мы имеем
периметр сарая равен двум, умноженным на 𝑥 плюс 𝑦. Этот периметр должен быть меньше
253 метра. Следовательно, два умножить на 𝑥
плюс 𝑦 меньше 253. Теперь у нас есть система из трех
неравенства, описывающие ситуацию. Длина 𝑥 должна быть больше, чем
88. Ширина 𝑦 должна быть больше, чем
или равным нулю. И два, умноженные на 𝑥 плюс 𝑦, это
менее 253,
Теперь у нас есть система из трех
неравенства, описывающие ситуацию. Длина 𝑥 должна быть больше, чем
88. Ширина 𝑦 должна быть больше, чем
или равным нулю. И два, умноженные на 𝑥 плюс 𝑦, это
менее 253,
Хотя в данном случае это не требуется вопрос или даже это видео, мы могли бы изобразить это графически. Мы можем провести сплошную линию в 𝑦 равно нулю, а пунктирные линии на 𝑥 равны 88, а два, умноженные на 𝑥 плюс 𝑦, равны 253. Поскольку 𝑥 больше 88, мы можем заштрихуйте область слева от нее, так как нам нужна область справа. Поскольку 𝑦 больше или равно ноль, требуемая область находится выше оси 𝑥. И, наконец, как два умножить на 𝑥 плюс 𝑦 меньше 253, нам нужна область ниже этой строки. Это дает нам треугольную область которая удовлетворяет всем трем неравенствам.
Теперь рассмотрим другой пример.
в контексте.
Плотник хочет купить два типа ногтей. Первый тип стоит шесть фунтов за штуку. килограмм, а второй тип стоит девять фунтов за килограмм. Ему нужно не менее пяти килограммов первого типа и не менее семи килограммов второго. Он может потратить менее 55 фунтов стерлингов. Использование 𝑥 для представления количества первый тип и 𝑦 для представления второго типа, сформулируйте систему неравенств который представляет эту ситуацию.
В этом вопросе нужно указать
система неравенств, удовлетворяющая условиям для плотника, желающего
купите два типа гвоздей. Пусть 𝑥 представляет собой сумму
первого типа, а 𝑦 представляет количество второго типа. Это будет количество гвоздей в
килограммы. Так как ему нужно как минимум пять
килограммов первого типа, мы знаем, что 𝑥 больше или равно пяти. Ему также нужно как минимум семь
килограммов второго типа, поэтому 𝑦 больше или равно семи.
Другим ограничением является расходы. Нам говорят, что первый тип стоит шесть фунтов за килограмм. Это эквивалентно шести 𝑥. Второй тип гвоздя стоит девять фунтов за килограмм, что эквивалентно девяти 𝑦. Как общая сумма, которую он может потратить должно быть меньше 55 фунтов, мы знаем, что их сумма должна быть меньше 55. Система неравенств, которая представляет ситуацию, когда 𝑥 больше или равно пяти, 𝑦 больше чем или равно семи, а шесть 𝑥 плюс девять 𝑦 меньше 55,
В следующих двух вопросах мы посмотрите на более сложные проблемы, где есть больше ограничений.
Учитель дал своим ученикам 100
минут на решение теста, состоящего из двух разделов: раздела A и раздела B. Студенты должны были ответить не менее
четыре вопроса из раздела А и не менее шести вопросов из раздела Б и ответ
всего не менее 11 вопросов. Если девушка ответила на каждый вопрос в
раздел А за три минуты и каждый вопрос раздела Б за шесть минут, выведите
система неравенств, которая помогла бы узнать, сколько вопросов она пыталась решить
в каждом разделе. Используйте 𝑥 для представления количества
ответы на вопросы из раздела A и 𝑦 для представления числа из раздела B.
Если девушка ответила на каждый вопрос в
раздел А за три минуты и каждый вопрос раздела Б за шесть минут, выведите
система неравенств, которая помогла бы узнать, сколько вопросов она пыталась решить
в каждом разделе. Используйте 𝑥 для представления количества
ответы на вопросы из раздела A и 𝑦 для представления числа из раздела B.
Нам говорят, что тест имеет два
сечения A и B. И пусть 𝑥 будет количеством
ответы на вопросы из раздела A и 𝑦 число ответов из раздела B. Нам говорят, что студент должен
ответьте не менее чем на четыре вопроса из раздела A. Следовательно, 𝑥 должно быть больше, чем
или равно четырем. Они также должны ответить как минимум на шесть
вопросы из раздела B. Значит, 𝑦 должно быть больше или равно
до шести. Поскольку любой студент также должен ответить на
всего не менее 11 вопросов, 𝑥 плюс 𝑦 должно быть больше или равно 11.
Также существует ограничение по времени 100 минут. А нам говорят, что девушка ответил на каждый вопрос в разделе А за три минуты. Она также ответила на каждый вопрос в раздел B за шесть минут. Это означает, что общее время, которое она потраченные на ответы на вопросы, можно записать как выражение три 𝑥 плюс шесть 𝑦. А так же общее время на тест было 100 минут, это должно быть меньше или равно 100. Система неравенств, которая помогло бы узнать, сколько вопросов девушка пыталась решить в каждом разделе 𝑥 больше или равно четырем, 𝑦 больше или равно шести, 𝑥 плюс 𝑦 больше или равно 11, а три 𝑥 плюс шесть 𝑦 меньше или равно 100.
Сейчас мы рассмотрим один последний вопрос в этом видео.
Фабрика детского питания производит два
виды детского питания. Первый тип содержит две единицы
витамина А и три единицы витамина В на грамм. Второй тип содержит три
единиц витамина А и двух единиц витамина В на грамм. Если ребенку необходимо не менее 100 ЕД
витамина А и 120 единиц витамина В в сутки, сформулируйте систему неравенств
который описывает пищу, которую ребенок должен есть каждый день, чтобы удовлетворить эти
требования. Используйте 𝑥 для представления массы
первого типа детского питания в граммах и 𝑦 для обозначения массы второго типа
детское питание в граммах.
Второй тип содержит три
единиц витамина А и двух единиц витамина В на грамм. Если ребенку необходимо не менее 100 ЕД
витамина А и 120 единиц витамина В в сутки, сформулируйте систему неравенств
который описывает пищу, которую ребенок должен есть каждый день, чтобы удовлетворить эти
требования. Используйте 𝑥 для представления массы
первого типа детского питания в граммах и 𝑦 для обозначения массы второго типа
детское питание в граммах.
В этом вопросе нам говорят, что
фабрика выпускает два вида детского питания. Мы позволим 𝑥 представлять массу
первого вида детского питания, а 𝑦 представляют собой массу второго вида. Так как это массы, заданные в
граммов, мы знаем, что и 𝑥, и 𝑦 должны быть неотрицательны. Следовательно, 𝑥 больше или
равно нулю, а 𝑦 больше или равно нулю. Мы знаем, что первый тип ребенка
пища содержит две единицы витамина А на грамм, а второй тип содержит три
единиц витамина А на грамм. Как нам также говорят, что ребенок
нужно не менее 100 единиц витамина А в день, мы знаем, что два 𝑥 плюс три 𝑦
должно быть больше или равно 100.
Как нам также говорят, что ребенок
нужно не менее 100 единиц витамина А в день, мы знаем, что два 𝑥 плюс три 𝑦
должно быть больше или равно 100.
Аналогичное неравенство можно найти на витамин В. Первый вид детского питания содержит три единицы, а второй тип содержит две единицы. В младенчестве требуется 120 единиц витамина B в день, у нас есть три 𝑥 плюс два 𝑦 больше или равно 120. Таким образом, мы можем сделать вывод, что мы есть система из четырех неравенств, описывающая пищу, которую ребенок должен есть каждый день. 𝑥 больше или равно ноль, 𝑦 больше или равно нулю, два 𝑥 плюс три 𝑦 больше или равно 100, а три 𝑥 плюс два 𝑦 больше или равно 120.
Теперь мы суммируем ключ
очки из этого видео. В той или иной ситуации для того, чтобы
сформулировать систему неравенств, мы должны обозначить каждую из величин 𝑥 или
𝑦. Если количества являются величинами, которые
никогда не может быть отрицательным, тогда мы всегда начинаем с 𝑥 больше или равно нулю
и 𝑦 больше или равно нулю. Нам также могут быть предоставлены другие
ограничения для количества, такие как минимальное или максимальное значение для каждого. Например, 𝑥 больше или
равно 10 или 𝑦 меньше или равно 15. Эти неравенства также могут быть
строгие неравенства, такие как 𝑥 больше 10 и 𝑦 меньше 15.
Если количества являются величинами, которые
никогда не может быть отрицательным, тогда мы всегда начинаем с 𝑥 больше или равно нулю
и 𝑦 больше или равно нулю. Нам также могут быть предоставлены другие
ограничения для количества, такие как минимальное или максимальное значение для каждого. Например, 𝑥 больше или
равно 10 или 𝑦 меньше или равно 15. Эти неравенства также могут быть
строгие неравенства, такие как 𝑥 больше 10 и 𝑦 меньше 15.
Дополнительные линейные неравенства могут быть переведено из ограничений, заданных для полной комбинации величин, таких как время так и стоимость. Их можно записать в виде два 𝑥 плюс три 𝑦 больше или равно 15. Мы можем представить любой из этих системы неравенств графически. И пока он находится за пределами охват этого видео, мы могли бы также решить их, чтобы найти оптимальные решения.
Видео-урок: Решение систем линейных неравенств
Расшифровка видео
В этом видео мы узнаем, как
решать системы линейных неравенств, изображая их в виде графиков и определяя области
представляющий решение. Нам уже должно быть удобно
с использованием и интерпретацией обозначений неравенства, построением прямолинейных графиков, заданных
их уравнения и построение графиков отдельных линейных неравенств.
Нам уже должно быть удобно
с использованием и интерпретацией обозначений неравенства, построением прямолинейных графиков, заданных
их уравнения и построение графиков отдельных линейных неравенств.
Система линейных неравенств набор из двух или более линейных неравенств с несколькими переменными. Например, 𝑦 больше или равно единице, 𝑥 больше нуля, а 𝑥 плюс 𝑦 меньше или равно четырем представляет собой систему линейных неравенств относительно двух переменных 𝑥 и 𝑦. Такие системы используются на практике. контекстах, когда одна проблема требует ряда решений, и существует более одного ограничения на эти решения.
Начнем с того, что вспомним некоторые
основы того, как мы представляем линейные неравенства графически. Рассмотрим неравенства 𝑦
меньше пяти, а 𝑥 больше или равно трем. Напомним, что при представлении
неравенства на графе, сначала нужно определить уравнение границы
линия области. И для этого меняем местами
знак неравенства вместо знака равенства. Таким образом, пограничная линия для
неравенство 𝑦 меньше пяти, если 𝑦 равно пяти. Затем мы проводим эту линию, вспоминая
что линии вида 𝑦 равны некоторой константе, являются горизонтальными линиями. Мы также должны помнить, что мы используем
сплошная линия, если у нас есть слабое неравенство, и мы используем пунктирную линию, если у нас есть
строгое неравенство. Здесь неравенство строгое. Это 𝑦 строго меньше пяти,
поэтому мы рисуем линию 𝑦, равную пяти, в виде пунктирной линии.
И для этого меняем местами
знак неравенства вместо знака равенства. Таким образом, пограничная линия для
неравенство 𝑦 меньше пяти, если 𝑦 равно пяти. Затем мы проводим эту линию, вспоминая
что линии вида 𝑦 равны некоторой константе, являются горизонтальными линиями. Мы также должны помнить, что мы используем
сплошная линия, если у нас есть слабое неравенство, и мы используем пунктирную линию, если у нас есть
строгое неравенство. Здесь неравенство строгое. Это 𝑦 строго меньше пяти,
поэтому мы рисуем линию 𝑦, равную пяти, в виде пунктирной линии.
Теперь у нас есть граница для
графическое решение этого неравенства. И нам нужно решить, с какой стороны
линия для затенения. Если мы хотим, чтобы 𝑦 было меньше пяти,
то нам нужно включить в координатную плоскость все точки, для которых
𝑦-координата меньше пяти. Это все пункты ниже
граничная линия, поэтому мы заштриховываем эту сторону линии.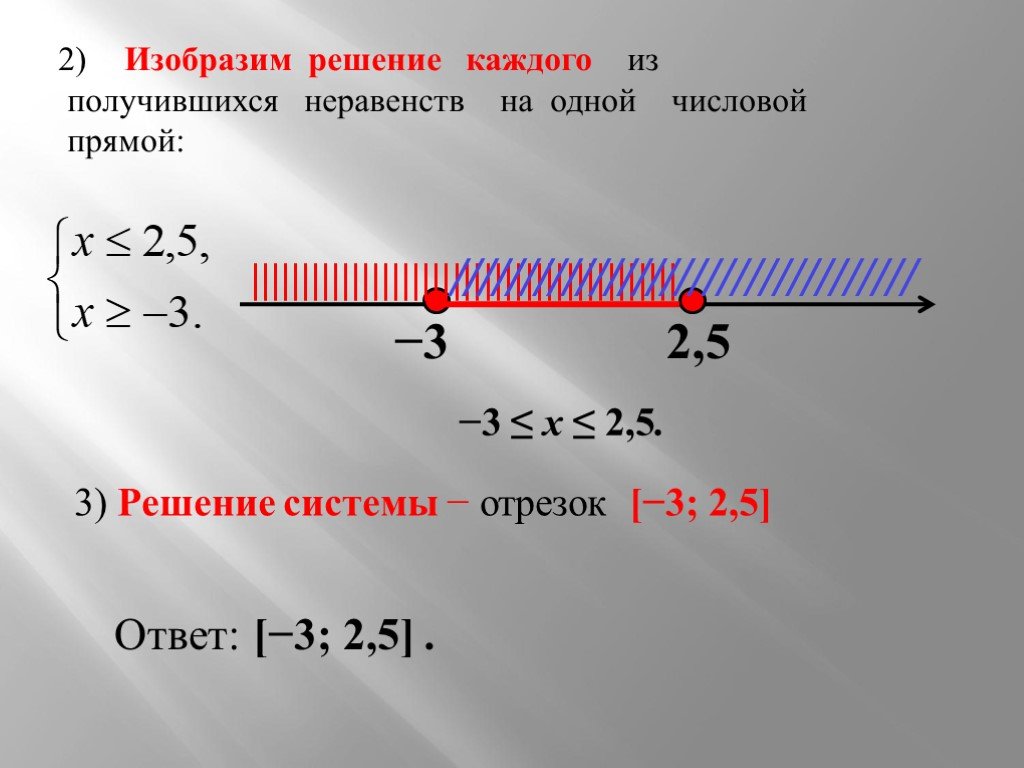
Теперь мы представили решение к первому неравенству графически. Итак, давайте теперь рассмотрим второй неравенство: 𝑥 больше или равно трем. В очередной раз заменяем неравенство со знаком равенства, чтобы найти уравнение граничной линии. Уравнение границы 𝑥 равно трем, которое, как мы помним, представляет собой вертикальную линию, проходящую через значение три на 𝑥-ось.
Поскольку у нас есть слабое неравенство, 𝑥 равно
больше или равно трем, мы изображаем эту границу сплошной линией. Затем нам нужно решить, с какой стороны
линии, чтобы заштриховать. И как мы хотим, чтобы 𝑥 было больше
больше или равно трем, нам нужно заштриховать область справа от
граница. Помните, что сплошная линия
указывает, что точки на самой граничной линии включены в решение задачи
это неравенство. Итак, мы представили решение
к каждому неравенству графически.
Если мы хотим рассматривать это как системы линейных неравенств, то это означает, что нам нужно найти область, которая удовлетворяет обоим неравенствам одновременно, что является пересечением двух области, которые мы заштриховали. Область ниже оранжевой линии и справа от розовой линии представляет собой решение этой системы неравенств. Он содержит все точки в координатная плоскость такая, что 𝑦 меньше пяти, а 𝑥 больше или равно три. Теперь рассмотрим некоторые Примеры.
Укажите систему неравенства, решение которых представлено следующим графиком.
На схеме видно
что заштрихованная область является первым квадрантом координатной плоскости, которая
содержит все точки такие, что и 𝑥, и 𝑦 положительны. Пограничные линии для
области, которые являются положительными 𝑥- и 𝑦-осями, нарисованы сплошными линиями. Так точки вдоль границ
также включены. Это означает, что нулевые значения
оба 𝑥 и 𝑦 включены в регион. Используя немного логики, мы можем
поэтому выразите эту область с помощью неравенств 𝑥 больше или равно
равно нулю, а 𝑦 больше или равно нулю.
Так точки вдоль границ
также включены. Это означает, что нулевые значения
оба 𝑥 и 𝑦 включены в регион. Используя немного логики, мы можем
поэтому выразите эту область с помощью неравенств 𝑥 больше или равно
равно нулю, а 𝑦 больше или равно нулю.
Давайте подтвердим это
представим каждое из этих неравенств графически сами. Неравенство 𝑥 больше
больше или равно нулю, представлено осью 𝑦, где 𝑥 равно нулю,
и все точки справа от оси 𝑦. Неравенство 𝑦 больше
больше или равно нулю, представлено осью 𝑥, где 𝑦 равно нулю, и
все точки выше оси 𝑥. Пересечение этих двух
Regions — это часть, которая закрашена оранжевым и розовым цветом. Вот и все первое
квадрант, включая положительные 𝑥- и 𝑦-оси, что совпадает с
график нам дали. Таким образом, мы можем сделать вывод, что
система неравенств, представленная данным графом, 𝑥 больше или
равно нулю, а 𝑦 больше или равно нулю.
Давайте теперь рассмотрим немного больше сложный пример.
Указать систему неравенства, решение которых представлено следующим графиком.
Мы видим, что эта система неравенства содержат горизонтальные, вертикальные и диагональные граничные линии, все для которых нам нужно найти уравнения. Сначала мы определяем, что заштрихованная область находится в первом квадранте, который содержит все неотрицательные значения 𝑥 и 𝑦. Это может быть представлено неравенства 𝑥 больше или равно нулю и 𝑦 больше или равно до нуля.
Далее рассмотрим
вертикальные линии. Уравнения этих линий
𝑥 равно трем, а 𝑥 равно шести. Область между этими линиями
заштриховано, так что это соответствует 𝑥 между тремя и шестью. Но мы должны четко понимать
какие знаки неравенства использовать на каждом конце интервала. Поскольку линия, проведенная в 𝑥, равна
три — сплошная линия, это соответствует слабому неравенству. Итак, у нас есть 𝑥 больше, чем
или равно трем. Поскольку линия, проведенная в 𝑥, равна
шесть — штриховая линия, это соответствует строгому неравенству. Итак, у нас есть 𝑥 меньше, чем
шесть. Это можно объединить в
двустороннее неравенство 𝑥 больше или равно трем и меньше
шесть.
Поскольку линия, проведенная в 𝑥, равна
три — сплошная линия, это соответствует слабому неравенству. Итак, у нас есть 𝑥 больше, чем
или равно трем. Поскольку линия, проведенная в 𝑥, равна
шесть — штриховая линия, это соответствует строгому неравенству. Итак, у нас есть 𝑥 меньше, чем
шесть. Это можно объединить в
двустороннее неравенство 𝑥 больше или равно трем и меньше
шесть.
Далее рассмотрим
горизонтальные линии. Все горизонтальные линии имеют
уравнения вида 𝑦 равно некоторой константе. Итак, уравнения этих прямых
𝑦 равно двум, а 𝑦 равно шести. Синяя область находится между
две строки, поэтому 𝑦 находится между двумя и шестью. Поскольку эти линии сплошные, обе
неравенства являются слабыми неравенствами. Таким образом, этот регион может быть
представленный как 𝑦, больше или равен двум и меньше или равен
шесть.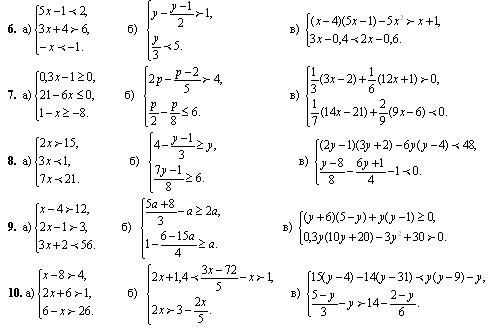
Наконец, мы рассматриваем апельсин области ниже диагональной линии. Эта линия проходит через восемь по оси 𝑥 и восемь по оси 𝑦. Мы не будем вдаваться в подробности как найти его уравнение здесь, но его уравнение можно записать как 𝑦 равно восемь минус 𝑥. Поскольку заштрихованная область ниже линия и сама линия сплошная, это соответствует неравенству 𝑦 is меньше или равно восьми минус 𝑥. Мы могли бы оставить это неравенство в этой форме, или мы можем изменить его, добавив 𝑥 к обеим сторонам, чтобы получить 𝑥 плюс 𝑦 меньше или равно восьми.
Итак, мы нашли систему
неравенства, решение которых изображено на графике. Их набор решений
пересечение отдельных заштрихованных областей, которое представляет собой зеленый треугольник
область, край. Система неравенств
𝑥 больше или равно нулю. 𝑦 больше или равно
нуль. 𝑥 больше или равно
три и меньше шести. 𝑦 больше или равно
два и меньше или равно шести. И 𝑥 плюс 𝑦 меньше или
равно восьми.
𝑦 больше или равно
нуль. 𝑥 больше или равно
три и меньше шести. 𝑦 больше или равно
два и меньше или равно шести. И 𝑥 плюс 𝑦 меньше или
равно восьми.
Теперь рассмотрим другой пример.
Какой из пунктов ниже принадлежит множеству решений системы линейных неравенств, представленной показанная фигура? а) один, три; б) шесть, восемь; в) четыре, три; или (г) три, шесть.
Важно понимать, что
нас не просят найти систему линейных неравенств, представленную
показанной фигуре, а определить, какая из четырех заданных точек лежит в
множество их решений. Из рисунка мы видим
что есть по существу три типа линейных неравенств, которые были
графически. Есть две вертикальные линии,
и область между этими линиями заштрихована красным. Есть две горизонтальные линии,
и область между этими линиями заштрихована синим цветом. Наконец, диагональ
линия, а область под этой линией заштрихована оранжевым цветом. Район, удовлетворяющий каждому
этих неравенств одновременно является пересечением трех заштрихованных
регионы, которые представляют собой треугольник, заштрихованный зеленым цветом.
Есть две горизонтальные линии,
и область между этими линиями заштрихована синим цветом. Наконец, диагональ
линия, а область под этой линией заштрихована оранжевым цветом. Район, удовлетворяющий каждому
этих неравенств одновременно является пересечением трех заштрихованных
регионы, которые представляют собой треугольник, заштрихованный зеленым цветом.
Чтобы определить, какой из четырех заданных точек лежит в множестве решений системы неравенств, мы просто необходимо нанести каждую из этих точек на график и определить любые точки, которые внутри или на твердых границах этой области. Когда мы это делаем, мы обнаруживаем, что единственная точка, которая лежит в заштрихованной области и, следовательно, принадлежит решению множеством системы линейных неравенств являются точки четыре, три.
Вот еще один пример.
Найдите набор решений линейные неравенства, показанные ниже.
Значит есть два линейных неравенства, нанесенные на одну и ту же координатную плоскость. И нас просят найти множество решений этой пары линейных неравенств. Это означает, что нам нужно найти область, удовлетворяющая обоим неравенствам одновременно, т. пересечение двух отдельных регионов. Но это понятно, глядя на график, что эти две области не перекрываются. Две диагональные линии параллельно, поэтому они никогда не встречаются. Красная область находится над выше диагональной линии, а синяя область находится ниже нижней линии. В результате нет пересечение этих двух регионов. Итак, набор решений этого пара линейных неравенств — это пустое множество, 𝜙.
Рассмотрим один финал
пример.
Какой регион на графике содержит решения множества неравенств 𝑦 больше двух, 𝑦 равно больше или равно отрицательному 𝑥, а 𝑥 меньше единицы?
Эти неравенства уже
были построены для нас на графике, и наша задача состоит в том, чтобы определить, какая из областей, отмеченных
буквы представляют решение всех трех неравенств одновременно. Мы сделаем это сначала
определение набора решений для каждого неравенства в отдельности. Пограничная линия для
неравенство 𝑦 больше двух, если 𝑦 равно двум, что является горизонтальным
линия через значение два на оси 𝑦. Это пунктирная линия, нарисованная
синий. Это пунктирная линия, потому что
неравенство 𝑦 строго больше двух. Поскольку неравенство 𝑦 равно
больше двух, набор решений этого неравенства будет областью выше
пунктирная линия. Таким образом, это сразу сужает
варианты до G, D и F.
Таким образом, это сразу сужает
варианты до G, D и F.
Граница для неравенство 𝑦 больше или равно отрицательному 𝑥 равна ли линия 𝑦 отрицательный 𝑥, который представляет собой диагональную линию, проходящую через начало координат с наклоном отрицательный. Это сплошная линия, нарисованная зеленый, и здесь использована сплошная линия, потому что это слабое неравенство. Поскольку неравенство 𝑦 равно больше или равно отрицательному 𝑥, набор решений этого неравенства является области на линии и над ней. Поэтому мы можем исключить район Г.
Для окончательного неравенства
граничная линия 𝑥 равна единице, которая представляет собой вертикальную линию, проходящую через единицу на
𝑥-ось. это конечно финал
линия, нарисованная на координатной сетке, вертикальная пунктирная линия, нарисованная красным цветом. Поскольку неравенство 𝑥 меньше
чем единица, область, удовлетворяющая этому неравенству, находится левее границы
линия. Это исключает вариант F. Таким образом, мы можем сделать вывод, что
область, содержащая решения системы всех трех неравенств,
которая является пересечением трех отдельных областей, является областью D.
Поскольку неравенство 𝑥 меньше
чем единица, область, удовлетворяющая этому неравенству, находится левее границы
линия. Это исключает вариант F. Таким образом, мы можем сделать вывод, что
область, содержащая решения системы всех трех неравенств,
которая является пересечением трех отдельных областей, является областью D.
Давайте теперь суммируем ключевые моменты
из этого видео. Для вертикальной линии, параллельной
𝑦-ось формы 𝑥 равна некоторой константе 𝑘, области справа от прямой
содержит все точки, для которых 𝑥 больше 𝑘 и область слева
прямой содержит все точки такие, что 𝑥 меньше 𝑘. Для горизонтальной линии формы
𝑦 равно 𝑘, область над линией соответствует 𝑦 больше, чем 𝑘 и
область под линией соответствует 𝑦 меньше 𝑘. Для диагональной линии вида 𝑦
равно 𝑚𝑥 плюс 𝑏, область над чертой соответствует тому, где 𝑦 больше
чем 𝑚𝑥 плюс 𝑏, а область под линией соответствует тому, где 𝑦 меньше
𝑚𝑥 плюс 𝑏.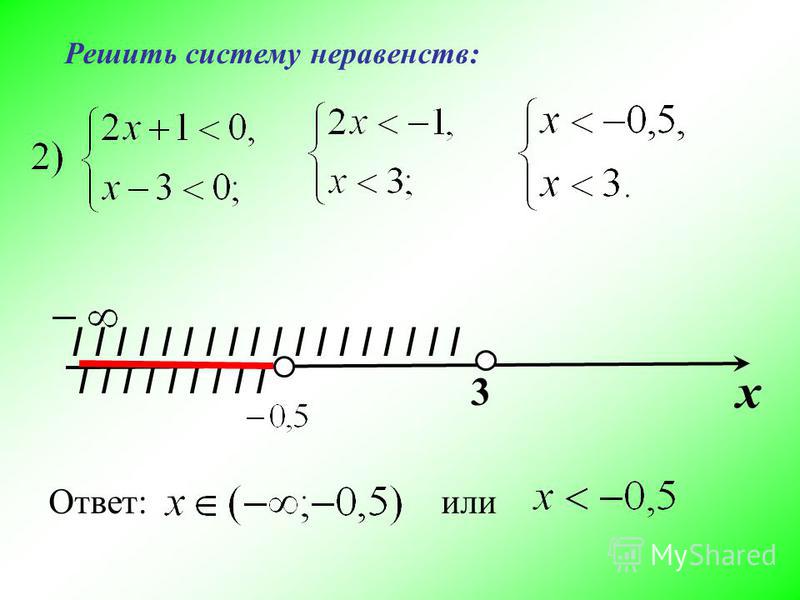


 Например:
много будешь знать — скоро состаришься (аргумент -
знания, функция-возраст). (Приложение 4)
Например:
много будешь знать — скоро состаришься (аргумент -
знания, функция-возраст). (Приложение 4)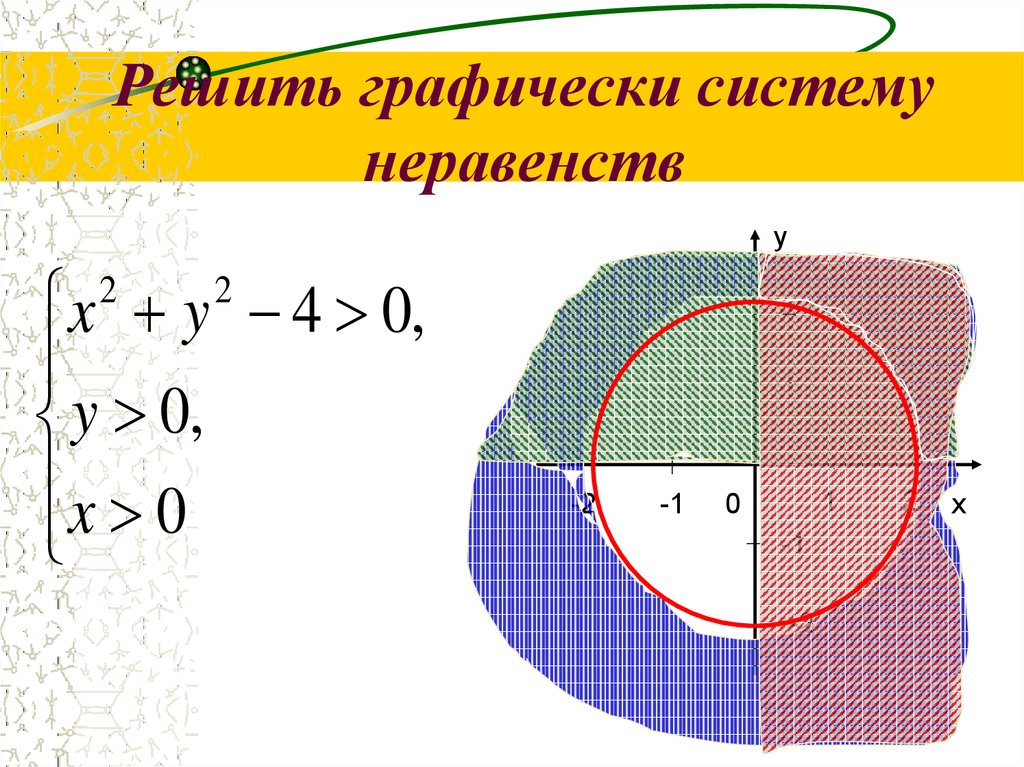 — С. -Петербург, Москва,
2008.
— С. -Петербург, Москва,
2008.