Даны вектора: а) |а + b|; б) |а| + |b|; в) |а| — |b|; г) |а — b|; д) |3с|; е) √14|c|; ж) |2а —Зс|.

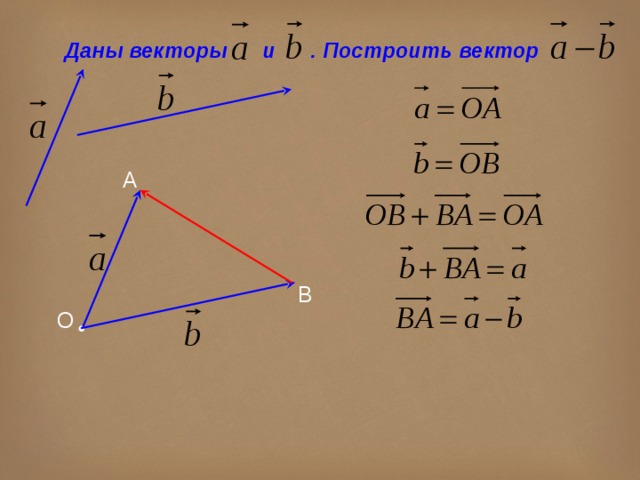
§4.Скалярное произведение векторов.

2.53 Найти скалярное произведение коллинеарных и противопо-ложно направленных векторов , если

2.54 Вычислить: а); б)

если , , .

2.55 Найти модуль вектора где единичные векторы, угол между которыми равен .

2.56 Определить, при каком значении векторы и будут перпендикулярны, если

2.57 Какой угол образуют единичные векторы , если известно, что векторы взаимно перпендикулярны?

2.58 Вычислить длину диагоналей параллелограмма, построен-ного на векторах если известно, что

2.59 Определить угол между векторами и , если известно, что , , .

2.60 Вычислить .

2.61 Даны векторы и . Вычислить:

а) ; б); в) ; г) ;

д) ; е) ; ж) .

2.62 Даны три вектора: Вычислить: а) ; б) .

2.63 Даны векторы: . При каком значении векторы и будут перпендикулярны.

2.64 Найти угол между диагоналями параллелограмма, построенного на векторах

2.65 Даны точки .На оси абсцисс найти такую точку М, чтобы

2.66 Даны три вектора: Найти вектор , удовлетворяющий одновременно уравнениям: , , .

2.67 Найти координаты вектора , коллинеарного вектору и удовлетворяющего условию .

2.68 Вычислить работу силы при перемещении материальной точки из положения в положение

2.69 Даны два вектора: и Найти вектор перпендикулярный , равный ему по длине, компланарный с векторами и образующий с вектором острый угол.

2.70 В треугольнике : . Вычислить длину его высоты , если известно, что — взаимно перпендикулярные орты.

2.71 Вычислить:

а); б),

если

2.72 Упростить выражения:

а)б)

2.73 Вычислить площадь параллелограмма, построенного на векторах единичные векторы, величина угла между которыми равна 60°.

2.74 Вычислить площадь параллелограмма, диагоналями которого служат векторы и , где — единич-ные векторы и

2.75 Даны векторы:

a) б)

Найти координаты вектора

2.76 Даны векторы . Найти координаты вектора: а) б)

2.77 Определить, при каких значениях вектор будет коллинеарен вектору если

а) ; б) .

2.78 Найти вектор ,

если .

2.79 Вычислить площадь треугольника с вершинами в точках ,, .

2.80 В треугольнике с вершинами в точках найти высоту

2.81 Даны два вектора: Найти

вектор единичной длины, перпендикулярный к векторам и направленный так, чтобы упорядоченная тройка векторов имела положительную ориентацию.

2.82 Вектор , перпендикулярный оси Oz и вектору образует острый угол с осью Ox. Зная, что , найти его координаты.

2.83 Найти координаты вектора , если известно, что он перпендикулярен векторам и , образует с ортом тупой угол и .

2.84. Найти координаты вектора , если он перпендикулярен векторам и , а также удовлетворяет условию .

2.85 Сила приложена к точке . Определить момент этой силы относительно начала координат.

2. 86 Сила приложена к точке . Определить момент этой силы относительно точки .

2.87 Даны три силы приложенные к точке . Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки .

Даны векторы a -5; 5; 0 и c 1; -2; -3. найдите координаты вектора а) 3b-3a+3c b)-0,1с+0,8а-0,5b. c объяснением пожалуйста. — Школьные Знания.net

• Все предметы

• Математика

• Литература

• Алгебра

• Русский язык

• Геометрия

• Английский язык

• Физика

• Биология

• Другие предметы

• История

• Обществознание

• Окружающий мир

• География

• Українська мова

• Информатика

• Українська література

• Қазақ тiлi

• Экономика

• Музыка

• Беларуская мова

• Французский язык

• Немецкий язык

• Психология

• Оʻzbek tili

• Кыргыз тили

• Астрономия

• Физкультура и спорт

Ответ дан

xxxeol

Объяснение:

Для вычисления математического вектора надо произвести вычисления для  каждой из трёх координат отдельно.  В задаче не задан вектор b.

По данному ответу получается, что вектор b(-7;10;-5).

m(x)  = 3*b(x) — 3*a(x) + 3*c(x) = 3*(-7) — 3*(-5) + 3*1 = -3

m(y)  = 3*b(y) — 3*a(y) + 3*c(y) = 3*10- 3*5 + 3*(-2) = 30 — 15 — 6 = 9

m(z)  = 3*b(z) — 3*a(z) + 3*c(z) = 3*(-5) — 3*0 + 3*(-3) = -24

ОТВЕТ: m(-3; 9;-24))

Поскольку вектора b не дано, то в этом решении только объяснение задачи.

Геометрическое решение задачи про вектора на рисунке в приложении.

Введение в векторные данные – Введение в геопространственные концепции

Обзор

Обучение: 10 мин.
Упражнения: 5 минут

Вопросы

Цели

О векторных данных

Векторные структуры данных представляют определенные особенности на поверхности Земли, и назначать атрибуты этим функциям. Векторы состоят из дискретных геометрических местоположения (значения x, y), известные как вершины, которые определяют форму пространственного объект. Организация вершин определяет тип вектора, который мы работают с: точкой, линией или полигоном.

Источник изображения: Национальная сеть экологических обсерваторий (NEON)

• Точки: Каждая точка определяется одной координатой x, y. Может быть много точек в векторном файле точек. Примеры точечных данных включают в себя: выборку мест, местонахождение отдельных деревьев или местонахождение учетных площадок.

• Линии: Линии состоят из множества (минимум 2) соединенных точек. Например, дорога или ручей могут быть представлены линией. Эта линия состоит из серии сегментов, каждый «изгиб» дороги или ручья представляет собой вершина, которая определила местоположение x, y.

• Многоугольники: Многоугольник состоит из 3 или более вершин, которые соединены и закрыто. Очертания границ съемочных площадок, озер, океанов и штатов или страны часто изображаются полигонами.

Подсказка данных

Иногда пограничные слои, такие как штаты и страны, сохраняются в виде линий а не многоугольники. Однако эти границы, представленные в виде линии, не создаст замкнутый объект с определенной областью, которую можно заполнить.

Определение типов векторов

График ниже включает примеры двух из трех типов векторов объекты. Используйте приведенные выше определения, чтобы определить, какие функции представлены типом вектора.

Решение

Государственные границы являются многоугольниками. Расположение Фишер Тауэр точка. Не отображаются линейные объекты.

Векторные данные имеют ряд важных преимуществ:

• Сама геометрия содержит информацию о том, что создатель набора данных считает важным
• Геометрические структуры содержат информацию сами по себе — зачем, например, выбирать точку вместо многоугольника?
• Каждый элемент геометрии может иметь несколько атрибутов вместо одного, например. база данных городов может иметь атрибуты имени, страны, населения и т. д.
• Хранение данных может быть очень эффективным по сравнению с растрами

К недостаткам векторных данных относятся:

• потенциальная потеря детализации по сравнению с растром
• потенциальное смещение в наборах данных — что не было записано?
• Расчеты с использованием нескольких векторных слоев должны выполнять математические операции на геометрия, а также атрибуты, поэтому может быть медленным по сравнению с растровой математикой.

Наборы векторных данных используются во многих отраслях помимо геопространственных полей. За Например, компьютерная графика в основном основана на векторах, хотя данные используемые структуры имеют тенденцию соединять точки, используя дуги и сложные кривые, а не прямые линии. Компьютерное проектирование (САПР) также основано на векторах. разница в том, что наборы геопространственных данных сопровождаются привязкой информации их функции в реальных местах.

Формат векторных данных для этого семинара

Как и растровые данные, векторные данные также могут иметь различные форматы. За это Workshop мы будем использовать формат Shapefile с расширением .shp . А В файле .shp хранятся географические координаты каждой вершины вектора, как а также метаданные, включая:

• Extent — пространственная протяженность шейп-файла (т. е. географическая область, обложки шейп-файла). Пространственный экстент шейп-файла представляет собой комбинированный экстент для всех пространственных объектов в шейп-файле.
• Тип объекта — содержит ли шейп-файл точки, линии или полигоны.
• Система координат (CRS)
• Другие атрибуты — например, шейп-файл линии, содержащий местоположения потоков, может содержать имя каждого потока.

Поскольку структура точек, линий и многоугольников различна, каждый отдельный шейп-файл может содержать только один тип вектора (все точки, все линии или все полигоны). Вы не найдете смесь точки, линии и многоугольника объектов в одном шейп-файле.

Дополнительные ресурсы

Подробнее о шейп-файлах можно узнать на Википедия

Почему не оба?

Очень немногие форматы могут содержать как растровые, так и векторные данные. даже более ограничительным, чем это. Наборы векторных данных обычно привязаны к одному тип геометрии, например. только баллы. Наборы растровых данных обычно могут кодировать только один типа данных, например, у вас не может быть многоканального GeoTIFF, где один слой целочисленные данные, а другой — с плавающей запятой. На то есть веские причины — стандарты форматов легче определить и поддерживать, как и метаданные. последствия определенных манипуляций с данными более предсказуемы, если вы уверены, что все ваши входные данные имеют одинаковые характеристики.

Ключевые моменты

• Векторные структуры данных представляют определенные объекты на поверхности Земли вместе с атрибутами этих объектов.

• Векторные объекты могут быть точками, линиями или полигонами.

Векторные данные

	Цели:	Понимание моделей векторных данных, используемых в ГИС.
	Ключевые слова:	Вектор, Точка, Ломаная, Многоугольник, Вершина, Геометрия, Масштаб, Качество данных, Символика, Источники данных

Обзор

Векторные данные обеспечивают способ представления объектов реального мира в ГИС среда. Особенность — это все, что вы можете увидеть на ландшафте. Представьте, что вы стоя на вершине холма. Глядя вниз, можно увидеть дома, дороги, деревья, реки и т. д. (см. figure_landscape). Каждая из этих вещей была бы функция , когда мы представляем их в приложении ГИС. Векторные объекты имеют атрибуты , состоящие из текстовой или числовой информации, которые описывают особенности.

Рисунок Ландшафт 1:

Глядя на ландшафт, вы можете увидеть основные элементы, такие как дороги, дома и деревья.

Форма векторного объекта представлена ​​с использованием геометрии . Геометрия состоит из одной или нескольких соединенных между собой вершин . Вершина описывает положение в космосе с использованием осей X , Y и опционально z . Геометрии, которые вершины с осью Z часто называют 2.5D , так как они описывают высота или глубина в каждой вершине, но не в обеих одновременно.

Когда геометрия объекта состоит только из одной вершины, это называется объект точек (см. иллюстрацию figure_geometry_point). Где геометрия состоит из двух или более вершин, причем первая и последняя вершины не равны, 9Полилиния 0006 Формируется элемент (см. рисунок figure_geometry_polyline). Где присутствуют три или более вершин, и последняя вершина равна первой, т. е. вложенный полигон объект сформирован (см. иллюстрацию figure_geometry_polygon).

Фигура Векторная геометрия 1:

Точечный объект описывается его координатами X, Y и, возможно, Z. Точка атрибуты описывают точку, например. если это дерево или фонарный столб.

Фигура Векторная геометрия 2:

Полилиния — это последовательность соединенных вершин. Каждая вершина имеет X, Y (и опционально Z) координата. Атрибуты описывают полилинию.

Фигура Векторная геометрия 3:

Многоугольник, как и ломаная, представляет собой последовательность вершин. Однако в многоугольнике первая и последняя вершины всегда находятся в одном и том же положении.

Оглядываясь назад на изображение пейзажа, которое мы показывали вам выше, вы должны иметь возможность видеть различные типы объектов так, как их представляет ГИС их сейчас (см. иллюстрацию figure_geometry_landscape).

Рисунок Ландшафт 2:

Ландшафтные особенности, как мы бы представили их в ГИС.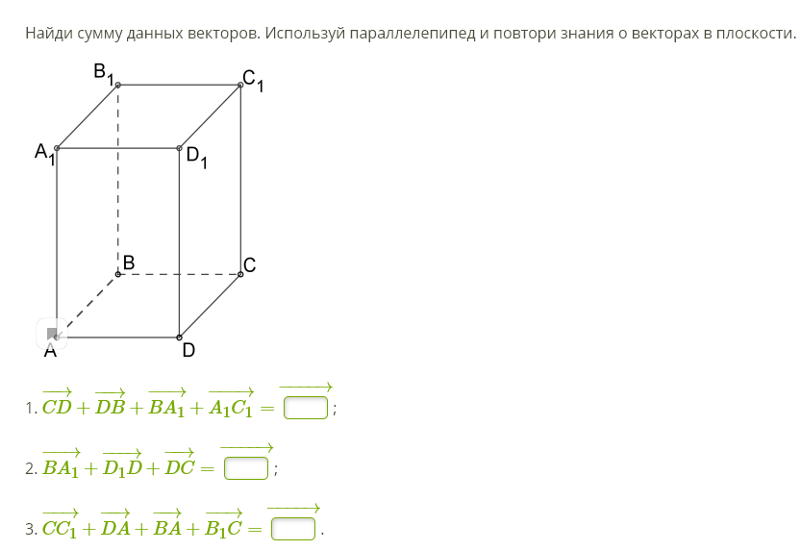 Реки (синие) и дороги (зеленый) можно представить в виде линий, деревья в виде точек (красный) и дома в виде полигоны (белые).

Точечные объекты в деталях

Первое, что нам нужно понять, говоря о точечных объектах, это то, что мы описываем как точку в ГИС, является вопросом мнения и часто зависит от шкала. давайте посмотрим, например, на города. Если у вас есть карта мелкого масштаба (которая охватывает большую территорию), может иметь смысл представить город с помощью точечного объекта. Однако по мере приближения к карте, двигаясь к более крупному масштабу, становится больше смысл показывать границы города в виде многоугольника.

Когда вы решите использовать точки для представления объекта, в основном это вопрос масштаба. (насколько далеко вы находитесь от объекта), удобство (это занимает меньше времени и усилия по созданию точечных объектов, а не полигональных), и тип объекта (некоторые вещи, такие как телефонные столбы, просто не имеют смысла хранить в виде полигонов).

Как показано на рисунке figure_geometry_point, точечный объект имеет X, Y и, необязательно, значение Z. Значения X и Y будут зависеть от координаты . Справочная система (CRS). Мы собираемся более подробно остановиться на Координатные системы отсчета в более позднем руководстве. А пока просто скажем, что CRS — это способ точного описания того, где находится конкретное место на Земле. поверхность. Одной из самых распространенных систем отсчета является долгота и широта . Линии долготы проходят от Северного полюса к Южному полюсу. Линии широты бежать с востока на запад. Вы можете точно описать, где вы находитесь в любом месте на земле, сообщив кому-нибудь свою долготу (X) и широту (Y). Если вы сделаете аналогичный размер для дерева или телефонного столба и отметить его на карте, вы будет создан точечный объект.

Поскольку мы знаем, что Земля не плоская, часто бывает полезно добавить значение Z к точечная особенность. Это описывает, как высоко над уровнем моря вы находитесь.

Полилинейные объекты в деталях

Если точечный объект представляет собой одну вершину, полилиния имеет две или более вершин . Ломаная линия представляет собой непрерывный путь, проведенный через каждую вершину, как показано на рис. фигура_геометрия_полилиния. При соединении двух вершин создается линия. Когда соединены более двух, они образуют «линию линий» или полилиния .

Ломаная линия используется для отображения геометрии линейных объектов , таких как дороги, реки, контуры, пешеходные дорожки, траектории полета и так далее. Иногда у нас есть спец. правила для полилиний в дополнение к их базовой геометрии. например контур линии могут соприкасаться (например, на скале), но никогда не должны пересекаться друг с другом. Точно так же полилинии, используемые для хранения дорожной сети, должны быть соединены в точках. перекрестки. В некоторых ГИС-приложениях вы можете установить эти специальные правила для тип объекта (например, дороги) и ГИС гарантируют, что эти полилинии всегда соблюдать эти правила.

Если изогнутая полилиния имеет очень большие расстояния между вершинами, она может выглядеть угловатый или зазубренный, в зависимости от масштаба, в котором он рассматривается (см. Figure_polyline_jagged). Поэтому важно, чтобы полилинии были оцифрованы (захвачены в компьютер) с расстояниями между вершинами, которые достаточно малы для масштаба, в котором вы хотите использовать данные.

Рисунок Полилиния 1:

Полилинии, рассматриваемые в меньшем масштабе (1:20 000 влево), могут казаться гладкими и изогнутый. При увеличении масштаба (1:500 вправо) полилинии может выглядеть очень угловатым.

Атрибуты полилинии описывают ее свойства или характеристики. За Например, полилиния дороги может иметь атрибуты, описывающие, имеет ли она покрытие. с гравием или гудроном, сколько у него полос движения, является ли это улицей с односторонним движением и скоро. ГИС может использовать эти атрибуты для обозначения полилинейного объекта с подходящий цвет или стиль линии.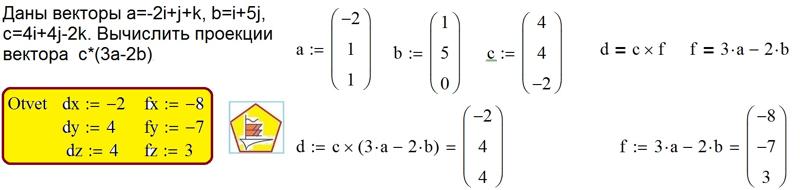

Полигональные объекты в деталях

Полигональные объекты представляют собой замкнутых областей , таких как плотины, острова, границы страны и так далее. Как и полилинейные объекты, полигоны создаются из набора вершин. которые соединены непрерывной линией. Однако, поскольку многоугольник всегда описывает замкнутую область, первая и последняя вершины всегда должны быть на то же место! Полигоны часто имеют общая геометрия – границы, находящиеся в общий с соседним полигоном. Многие ГИС-приложения имеют возможность убедиться, что границы соседних полигонов точно совпадают. Мы будем изучите это в разделе Топология далее в этом учебнике.

Как и точки и полилинии, многоугольники имеют атрибутов . Атрибуты описать каждый многоугольник. Например, плотина может иметь атрибуты глубины и воды. качество.

Векторные данные в слоях

Теперь, когда мы описали, что такое векторные данные, давайте посмотрим, что такое векторные данные. управляться и использоваться в среде ГИС. Большинство приложений ГИС группируют векторные объекты на слоев . Объекты в слое имеют одинаковый тип геометрии (например, они все будут точками) и одни и те же атрибуты (например, информация о том, что вид дерево для слоя деревьев). Например, если вы записали позиции всех пешеходных дорожек в вашей школе, они обычно сохраняются вместе на жестком диске компьютера и отображаются в ГИС как единый слой. Этот удобен тем, что позволяет скрыть или показать все функции для этого слоя в вашем ГИС-приложении одним щелчком мыши.

Редактирование векторных данных

ГИС-приложение позволит вам создавать и изменять геометрические данные в слой — процесс, называемый оцифровкой — который мы рассмотрим более подробно в более позднем учебнике. Если слой содержит полигоны (например, плотины фермы), ГИС приложение позволит вам создавать новые полигоны только в этом слое. Сходным образом если вы хотите изменить форму объекта, приложение позволит вам только сделать это, если измененная форма правильная. Например, он не позволит вам редактировать линию таким образом, что она имеет только одну вершину – помните в нашем обсуждении линий выше этой все линии должны иметь по крайней мере две вершины.

Создание и редактирование векторных данных — важная функция ГИС, поскольку она один из основных способов, с помощью которых вы можете создавать личные данные для вещей, которые вы интересует. Скажем, например, вы следите за загрязнением реки. Вы могли бы использовать ГИС для оцифровки всех выпусков ливневых стоков (как точечные объекты). Вы также можете оцифровать саму реку (как полилинейный объект). Наконец ты могли снимать показания уровня pH по течению реки и оцифровывать места, где вы сделали эти показания (как точечный слой).

Помимо создания собственных данных, существует множество бесплатных векторных данных, которые вы можете можно получить и использовать. Например, вы можете получить векторные данные, которые появляются на Картографические листы масштаба 1:50 000 из Главного управления: съемки и картографии.

Масштаб и векторные данные

Карта Масштаб — важный вопрос, который следует учитывать при работе с векторными данными в ГИС. Когда данные собираются, они обычно оцифровываются с существующих карт или получение информации из геодезических записей и устройств глобальной системы позиционирования. Карты имеют разный масштаб, поэтому при импорте векторных данных с карты в ГИС среды (например, путем оцифровки бумажных карт), цифровые векторные данные будут имеют те же проблемы с масштабом, что и исходная карта. Этот эффект можно увидеть в иллюстрации figure_vector_small_scale и figure_vector_large_scale. Многие Проблемы могут возникнуть из-за неправильного выбора масштаба карты. Например, с помощью векторные данные на иллюстрации figure_vector_small_scale для планирования водно-болотных угодий заповедная зона может привести к тому, что важные части водно-болотных угодий будут оставлены без внимания из резерва! С другой стороны, если вы пытаетесь создать карту региона, использование данных, захваченных в масштабе 1:1000 000, может быть вполне приемлемым и сэкономит вам много времени. время и усилия для сбора данных.

Масштаб вектора рисунка 1:

Векторные данные (красные линии), оцифрованные с карты мелкого масштаба (1:1000 000).

Масштаб вектора рисунка 2:

Векторные данные (зеленые линии), оцифрованные с крупномасштабной (1:50 000) карты.

Символы

Когда вы добавляете векторные слои в представление карты в ГИС-приложении, они будут нарисованы случайными цветами и основными символами. Одно из больших преимуществ использования ГИС заключается в том, что вы можете очень легко создавать персонализированные карты. Программа ГИС будет позволяет вам выбирать цвета в соответствии с типом объекта (например, вы можете сказать, чтобы он рисовал векторный слой водоемов (синий). ГИС также позволит вам настроить символ использовал. Итак, если у вас есть точечный слой деревьев, вы можете показать положение каждого дерева с помощью маленькое изображение дерева, а не основной круговой маркер, который использует ГИС при первой загрузке слоя (см. иллюстрации figure_vector_symbology, «figure_generic_symbology» и «figure_custom_symbology»).

Символы вектора рисунка 1:

В ГИС вы можете использовать панель (подобную приведенной выше) для настройки того, как объекты в вашем слое должно быть нарисовано.

Символы вектора рисунка 2:

Когда слой (например, слой деревьев выше) загружается впервые, ГИС приложение даст ему общий символ.

Символы вектора рисунка 3:

После внесения корректировок гораздо легче увидеть, что наши точки представляют деревья.

Символы — это мощная функция, позволяющая оживить карты и данные в вашем ГИС проще для понимания. В следующем разделе ( Данные атрибутов вектора ) мы более глубоко изучим, как символы могут помочь пользователю понять вектор данные.

Что мы можем делать с векторными данными в ГИС?

На самом простом уровне мы можем использовать векторные данные в ГИС-приложении во многих так же, как вы бы использовали обычную топографическую карту.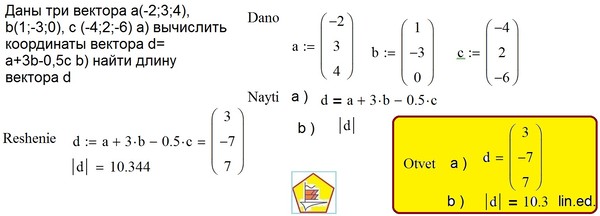 Настоящая мощь ГИС начинает проявляться проявляется, когда вы начинаете задавать вопросы типа «какие дома находятся в пределах 100 уровень разлива реки в год?’; где лучше всего поставить больницу, чтобы он легко доступен как можно большему количеству людей?»; «в которых живут учащиеся конкретный пригород?». ГИС — отличный инструмент для ответа на эти типы вопросы с помощью векторных данных. Обычно мы имеем в виду процесс отвечая на такие вопросы как пространственный анализ . В более поздних темах В этом уроке мы более подробно рассмотрим пространственный анализ.

Общие проблемы с векторными данными

Работа с векторными данными имеет некоторые проблемы. Мы уже упоминали о проблемах которые могут возникать с векторами, захваченными в разных масштабах. Векторные данные также нужны много работы и обслуживания, чтобы гарантировать, что это точно и надежно. Неточные векторные данные могут возникать, когда инструменты, используемые для захвата данных, неправильно настроены, когда люди, собирающие данные, не проявляют осторожности, когда время или деньги не позволяют в достаточной степени детализировать процесс сбора, и скоро.

Если у вас векторные данные плохого качества, это часто можно обнаружить при просмотре данные в ГИС. Например, осколков могут возникнуть, когда ребра двух полигонов области не сходятся должным образом (см. figure_vector_slivers).

Проблемы с вектором фигуры 1:

Осколки возникают, когда вершины двух полигонов не совпадают границы. В мелком масштабе (например, 1 слева) вы можете не увидеть эти ошибки. В крупном масштабе они видны как тонкие полоски между двумя полигонами. (2 справа).

Перерегулирование может произойти, когда линейный объект, такой как дорога, не пересекается с другим дорога ровно на перекрестке. Недостаток может произойти, когда линейный объект (например, река) точно не соответствует другому признаку, которому она должна соответствовать. связано. На рисунке figure_vector_overshoots показано, что перегибы выглядят.

Проблемы вектора рисунка 2:

Недостаток (1) возникает при оцифровке векторных линий, которые должны соединяться с каждым другие не совсем трогают. Перерегулирование (2) происходит, если линия заканчивается за линией он должен подключаться к.

Из-за этих типов ошибок очень важно тщательно оцифровывать данные и точно. В следующем разделе по топологии мы рассмотрим некоторые из эти типы ошибок более подробно.

Чему мы научились?

Давайте завершим то, что мы рассмотрели на этом листе:

• Векторные данные используются для представления объектов реального мира в ГИС.
• Векторный объект может иметь тип геометрии точка , строка или полигон .
• Каждый векторный объект имеет атрибутивных данных , которые его описывают.
• Геометрия элемента описывается в терминах вершин.
Геометрия
• Point состоит из одной вершины (X, Y и, возможно, Z).
• Ломаные геометрии состоят из двух или более вершин, образующих связанную линия.
• Полигональная геометрия состоит из минимум четырех вершин формирование закрытого область. Первая и последняя вершины всегда находятся в одном и том же месте.
• Выбор используемого типа геометрии зависит от масштаба, удобства и ваших потребностей. хотите делать с данными в ГИС.
• Большинство ГИС-приложений не позволяют смешивать более одного типа геометрии в одном Одиночный слой.
• Оцифровка — это процесс создания цифровых векторных данных путем их рисования в ГИС-приложение.
• Векторные данные могут иметь проблемы с качеством, такие как недоборов , превышает и осколков о которых вам нужно знать.
• Векторные данные можно использовать для пространственного анализа в приложении ГИС, для пример, чтобы найти ближайшую больницу к школе.

Мы обобщили концепцию векторных данных ГИС на рисунке figure_vector_summary.

Рисунок Сводка векторов 1:

На этой диаграмме показано, как приложения ГИС работают с векторными данными.

А теперь попробуй!

Вот несколько идей, которые вы можете попробовать со своими учащимися:

• Использование копии топографической карты вашего региона (подобной той, что показана на Figure_sample_map), посмотрите, смогут ли ваши учащиеся назвать примеры различных типы векторных данных, выделяя их на карте.
• Подумайте, как бы вы создали векторные объекты в ГИС для представления реального мира особенности на территории вашей школы. Создайте таблицу различных функций в и вокруг вашей школы, а затем поручите своим учащимся решить, будут ли они лучше всего представить в ГИС в виде точки, линии или полигона. См. table_vector_1 для примера.

Рисунок Образец карты 1:

Можете ли вы определить на этой карте два точечных объекта и один полигональный объект?

Функция реального мира	Подходящий тип геометрии
Школьный флагшток
Футбольное поле
Пешеходные дорожки в школе и вокруг нее
Места, где расположены краны
И т. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт