детерминант матрицы 3 на 3
Вы искали детерминант матрицы 3 на 3? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как в матрице найти определитель, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «детерминант матрицы 3 на 3».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как детерминант матрицы 3 на 3,как в матрице найти определитель,как вычислить определитель в матрице,как вычислить определитель матрицы 3 на 3,как вычислять матрицы,как искать определитель матрицы,как найти в матрице определитель,как найти детерминант матрицы 3 на 3,как находить определитель матрицы,как посчитать определитель матрицы 3 на 3,как решать матрицу 3 на 3,как решать матрицы 3х3,как решить матрицу 3 на 3,как считать определитель матрицы 3 на 3,матрица 3 на 3 пример,матрицы 3 на 3,матрицы определитель формула,нахождение определителя матрицы формула,определители,определитель в матрице как найти,определитель как решать,определитель матрицы 2х2,определитель матрицы как вычислить,определитель матрицы как найти,определитель матрицы примеры,правило треугольника матрица,формула нахождение определителя матрицы,формула определитель матрицы,формула определителя матрицы.
Где можно решить любую задачу по математике, а так же детерминант матрицы 3 на 3 Онлайн?
Решить задачу детерминант матрицы 3 на 3 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Найти определитель (детерминант) матрицы онлайн
При решении сложных систем уравнения большую роль играет определитель матрицы или детерминант матрицы.
| det (A) = | Σ | (-1)N (α1,α2,…,αn)·aα11·aα22·…·aαnn |
| (α1,α2,…,αn) |
В данном выражении а1,а2,…,аn — перестановка чисел от 1 до n, N (а1,а2,…,аn) — количество инверсий при перестановке. Суммирование производится по всем перестановкам порядка n.
Свойства определителей:
- Определитель матрицы с двумя равными или пропорциональными строками (столбцами), с нулевой строкой (столбцом), с двумя или несколькими линейно зависимыми строками (столбцами) равняется нулю.

- Определитель единичной матрицы равняется единице: det (E) = 1.
- Определитель матрицы не меняется при транспонировании.
Способы вычисления определителя матрицы:
1. Значение определителя матрицы 1×1 равняется значению ее элемента:
∆ = |a11| = a112. Значение определителя матрицы 2×2 равняется разности между произведениями элементов главной диагонали и побочной.
| ∆ = | = a11·a22 — a12·a21 |
3. Определитель матрицы 3×3 равен разности между суммой произведений элементов главной диагонали плюс произведение элементов лежащих на треугольниках, грань которых параллельна главной диагонали, и суммой произведений элементов побочной диагонали и элементов, лежащих на треугольниках с параллельной побочной диагонали гранью.
| ∆ = |
| = a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33 |
Значение определителя матрицы 3-го порядка (3×3) можно рассчитать, используя правило Саррюса.
4. Определитель матрицы произвольного размера рассчитывается как сумма произведений элементов строки определителя на их алгебраические дополнения.
| n | |||
| det (A) = | Σ | aij·Aij | — разложение по i-той строке |
| j = 1 |
5. Определитель матрицы произвольного размера можно расчитать как суииу произведений элементов столбца определителя на их алгебраические дополнения:
| n | |||
| det (A) = | Σ | aij·Aij | — разложение по j-тому столбцу |
| i = 1 |

| Размер матрицы: 2×23×34×45×56×67×7 Введите значения Матрицы: |
Вычисление определителей. Миноры, алгебраические дополнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$
Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$
— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число
$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}.
$D=25-16=9$
$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$
Ответ: $x_1=-4;\,\,\, x_2=-1.$
{jumi[*4]}
3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$
Решение.
$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$
$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$
Ответ: $0.$
3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$
Решение.
$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$
$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$
$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha). T=\det A.$
T=\det A.$
2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.
3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.
4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.
6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).
Примеры:
3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. $
$
Доказательство.
$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$
$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$
$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$
$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$
$=8a+15b+12c-19d.$
Ответ: $8a+15b+12c-19d.$
{jumi[*4]}
3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью приведения определителя к треугольному виду:
$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два
$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394. 2.$
2.$
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$
Ответ: $-14.$
3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$
Ответ: $4.$
3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$
Ответ: $2a-8b+c+5d.$
3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$
Ответ: $665.$
{jumi[*4]}
Как найти определитель матрицы 3 порядка
Матрицы существуют для отображения и решения систем линейных уравнений. Одним из шагов в алгоритме поиска решения является нахождение определителя, или детерминанта. Матрица 3 порядка – это квадратная матрица размерностью 3х3.
Одним из шагов в алгоритме поиска решения является нахождение определителя, или детерминанта. Матрица 3 порядка – это квадратная матрица размерностью 3х3.Диагональ от левого верхнего элемента к правому нижнему называется главной диагональю квадратной матрицы. От правого верхнего элемента к нижнему левому – побочной. Сама матрица 3 порядка имеет вид:a11 a12 a13a21 a22 a23a31 a32 a33
Для нахождения определителя матрицы третьего порядка существует четкий алгоритм. Сначала просуммируйте элементы главной диагонали: a11+a22+a33. Затем – нижний левый элемент a31 со средними элементами первой строки и третьего столбца: a31+a12+a23 (визуально получается треугольник). Еще один треугольник – правый верхний элемент a13 и срединные элементы третьей строки и первого столбца: a13+a21+a32. Все данные слагаемые перейдут в детерминант со знаком «плюс».
Теперь можно перейти к слагаемым со знаком «минус». Во-первых, это побочная диагональ: a13+a22+a31. Во-вторых, два треугольника: a11+a23+a32 и a33+a12+a21. Конечная формула для поиска определителя выглядит так: Δ=a11+a22+a33+a31+a12+a23+a13+a21+a32-(a13+a22+a31)-(a11+a23+a32)-(a33+a12+a21). Формула довольно громоздкая, но после некоторого времени практики она становится привычной и «срабатывает» на автомате.
Конечная формула для поиска определителя выглядит так: Δ=a11+a22+a33+a31+a12+a23+a13+a21+a32-(a13+a22+a31)-(a11+a23+a32)-(a33+a12+a21). Формула довольно громоздкая, но после некоторого времени практики она становится привычной и «срабатывает» на автомате.
В ряде случаев нетрудно сразу увидеть, что определитель матрицы равен нулю. Детерминант нулевой, если какие-либо две строки или два столбца совпадают, пропорциональны или линейно зависимы. Если хотя бы одна из строк или один из столбцов полностью состоит из нулей, определитель всей матрицы равен нулю.
Иногда, чтобы найти определитель матрицы, удобнее и проще использовать преобразования матриц: алгебраическое сложение строк и столбцов между собой, вынесение общего множителя строки (столбца) за знак детерминанта, домножение всех элементов строки или столбца на одно и то же число. Для преобразования матриц важно знать их основные свойства.
Функция МОПРЕД — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование MDETERM
в Microsoft Excel.
Описание
Возвращает определитель матрицы (матрица хранится в массиве).
Синтаксис
МОПРЕД(массив)
Аргументы функции МОПРЕД описаны ниже.
Замечания
-
Массив может быть задан как интервал ячеек, например A1:C3, как массив констант, например {1;2;3:4;5;6:7;8;9}, как имя для интервала или массива.
-
Функция МОПРЕД возвращает значение ошибки #ЗНАЧ! в случаях, указанных ниже.

-
Если какая-либо ячейка в массиве пуста или содержит текст.
-
Если количество строк в массиве не равно количеству столбцов.
-
-
Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех строк и трех столбцов, определитель вычисляется следующим образом:
МОПРЕД(A1:C3)
равно A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)
-
Определители матриц обычно используются при решении систем уравнений с несколькими неизвестными.

-
Функция МОПРЕД производит вычисления с точностью примерно 16 значащих цифр, что может в некоторых случаях приводить к незначительным ошибкам. Например, определитель сингулярной матрицы отличается от нуля на 1E-16.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Данные | Данные | Данные | Данные |
|---|---|---|---|
|
1 |
3 |
8 |
5 |
|
1 |
3 |
6 |
1 |
|
1 |
1 |
1 |
0 |
|
7 |
3 |
10 |
2 |
|
Формула |
Описание |
Результат |
|
|
=МОПРЕД(A2:D5) |
Определитель приведенной выше матрицы. |
88 |
|
|
=МОПРЕД({3;6;1:1;1;0:3;10;2}) |
Определитель матрицы, представленной в виде массива констант. |
1 |
|
|
=МОПРЕД({3;6:1;1}) |
Определитель матрицы в массиве констант. |
-3 |
|
|
=МОПРЕД({1;3;8;5:1;3;6;1}) |
Возвращает сообщение об ошибке, так как массив имеет разное количество строк и столбцов. |
#ЗНАЧ! |
Вычисляем определитель матрицы на Хаскелле / Хабр
Решил выложить код вычисления определителей. Код рабочий, хотя и не претендует на виртуозность. Просто было интересно решить эту задачу именно на Хаскелле. Рассмотрены два подхода к решению задачи: простая рекурсия и метод Гаусса.
Код рабочий, хотя и не претендует на виртуозность. Просто было интересно решить эту задачу именно на Хаскелле. Рассмотрены два подхода к решению задачи: простая рекурсия и метод Гаусса.Немного теории
Как известно, определитель квадратной матрицы n*n — это сумма n! слагаемых, каждое из которых есть произведение, содержащее ровно по одному элементу матрицы из каждого столбца и ровно по одному из каждой строки. Знак очередного произведения:
определяется чётностью подстановки:
\begin{pmatrix}1 & 2 &… & n \\ {i}_{1} & {i}_{2} &… & {i}_{n} \end{pmatrix}
Прямой метод вычисления определителя состоит в разложении его по элементам строки или столбца в сумму произведений элементов какой-либо строки или столбца на их алгебраические дополнения. В свою очередь, алгебраическое дополнение элемента матрицы есть при этом — есть минор элемента (i,j), т.е. определитель, получающийся из исходного определителя вычеркиванием i-й строки и j-го столбца.

Такой метод порождает рекурсивный процесс, позволяющий вычислить любой определитель. Но производительность этого алгоритма оставляет желать лучшего — O(n!). Поэтому применяется такое прямое вычисление разве что при символьных выкладках (и с определителями не слишком высокого порядка).
Гораздо производительнее оказывается метод Гаусса. Его суть основывается на следующих положениях:
1. Определитель верхней треугольной матрицы \begin{pmatrix}{a}_{1,1} & {a}_{1,2} &… & {a}_{1,n} \\ 0 & {a}_{2,2} &… & {a}_{2,n} \\ 0 & 0 &… & …\\ 0 & 0 &… & {a}_{n,n} \\\end{pmatrix} равен произведению ее диагональных элементов. Этот факт сразу же следует из разложения определителя по элементам первой строки или первого столбца.
2. Если в матрице к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, то значение определителя не изменится.
3. Если в матрице поменять местами две строки (или два столбца), то значение определителя изменит знак на противоположный.
Мы можем, подбирая коэффициенты, складывать первую строку матрицы со всеми остальными и получать в первом столбце нули во всех позициях, кроме первой. Для получения нуля во второй строке, нужно прибавить ко второй строке первую, умноженную на
Для получения нуля в третьей строке, нужно к третьей строке прибавить первую строку, умноженную на и т.д. В конечном итоге, матрица приведется к виду, в котором все элементы при n>1 будут равны нулю.Если же в матрице элемент
оказался равным нулю, то можно найти в первом столбце ненулевой элемент (предположим, он оказался на k-м месте) и обменять местами первую и k-ю строки. При этом преобразовании определитель просто поменяет знак, что можно учесть. Если же в первом столбце нет ненулевых элементов, то определитель равен нулю.Далее, действуя аналогично, можно получить нули во втором столбце, затем в третьем и т.п. Важно, что при сложении строк полученные ранее нули не изменятся. Если для какой-либо строки не удастся найти ненулевой элемент для знаменателя, то определитель равен нулю и процесс можно остановить. Нормальное завершение процесса Гаусса порождает матрицу, у которой все элементы, расположенные ниже главной диагонали, равны нулю. Как говорилось выше, определитель такой матрицы равен произведению диагональных элементов.
Нормальное завершение процесса Гаусса порождает матрицу, у которой все элементы, расположенные ниже главной диагонали, равны нулю. Как говорилось выше, определитель такой матрицы равен произведению диагональных элементов.
Перейдем к программированию.
Мы работаем с данными с плавающей точкой. Матрицы представляем списками строк. Для начала определим два типа:
type Row = [Double]
type Matrix = [Row]
Простая рекурсия
Ничтоже сумняшеся, мы будем раскладывать определитель по элементам первой (т.е. нулевой) строки. Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца.
-- Удаление k-го элемента изо всех строк матрицы
deln :: Matrix -> Int -> Matrix
deln matrix k = map (\ r -> (take (k) r)++(drop (k+1) r)) matrix
А вот и минор:
-- Минор k-го элемента нулевой строки
minor :: Matrix -> Int -> Double
minor matrix k = det $ deln (drop 1 matrix) k
Обратите внимание: минор — это определитель.
 Мы вызываем функцию det, которую еще не реализовали. Для реализации det, нам придется сформировать знакочередующуюся сумму произведений очередного элемента первой строки на определитель очередного минора. Чтобы избежать громоздких выражений, создадим для формирования знака суммы отдельную функцию:
Мы вызываем функцию det, которую еще не реализовали. Для реализации det, нам придется сформировать знакочередующуюся сумму произведений очередного элемента первой строки на определитель очередного минора. Чтобы избежать громоздких выражений, создадим для формирования знака суммы отдельную функцию:sgn :: Int -> Double
sgn n = if n `rem` 2 == 0 then 1.0 else (-1.0)
Теперь можно вычислить определитель:
-- Определитель квадратной матрицы
det :: Matrix -> Double
det [[a,b],[c,d]] = a*d-b*c
det matrix = sum $ map (\c -> ((matrix !! 0)!!c)*(sgn c)*(minor matrix c)) [0..n]
where n = length matrix - 1
Код очень прост и не требует особых комментариев. Чтобы проверить работоспособность наших функций, напишем функцию main:
main = print $ det [[1,2,3],[4,5,6],[7,8,(-9)]]Значение этого определителя равно 54, в чем можно убедиться.
Метод Гаусса
Нам понадобится несколько служебных функций (которые можно будет использовать и в других местах).
 Первая из них — взаимный обмен двух строк в матрице:
Первая из них — взаимный обмен двух строк в матрице:-- Обмен двух строк матрицы
swap :: Matrix -> Int -> Int -> Matrix
swap matrix n1 n2 = map row [0..n]
where n=length matrix - 1
row k | k==n1 = matrix !! n2
| k==n2 = matrix !! n1
| otherwise = matrix !! k
Как можно понять по приведенному выше коду, функция проходит строку за строкой. При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте.
Следующая функция вычисляет строку r1 сложенную со строкой r2, умноженной поэлементно на число f:
-- Вычислить строку r1+f*r2
comb :: Row -> Row -> Double -> Row
comb r1 r2 f = zipWith (\ x y -> x+f*y) r1 r2
Здесь все предельно прозрачно: действия выполняются над строками матрицы (т.е. над списками [Double]). А вот следующая функция выполняет это преобразование над матрицей (и, естественно, получает новую матрицу):
-- прибавить к строке r1 строку r2, умноженную на f
trans :: Matrix -> Int -> Int -> Double -> Matrix
trans matrix n1 n2 f = map row [0. .n]
where n=length matrix - 1
row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
| otherwise = matrix !! k
.n]
where n=length matrix - 1
row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
| otherwise = matrix !! k
Функция getNz ищет номер первого ненулевого элемента в списке. Она нужна в случае, когда очередной диагональный элемент оказался равным нулю.
-- Номер первого ненулевого в списке
getNz :: Row -> Int
getNz xs = if length tmp == 0 then (-1) else snd $ head tmp
where tmp=dropWhile (\ (x,k) -> (abs x) <= 1.0e-10) $ zip xs [0..]
Если все элементы списка равны нулю, функция вернет -1.
Функция search проверяет, подходит ли матрица для очередного преобразования (у нее должен быть ненулевым очередной диагональный элемент). Если это не так, матрица преобразовывается перестановкой строк.
-- Поиск ведущего элемента и перестановка строк при необходимости
search :: Matrix -> Int -> Matrix
search matrix k | (abs ((matrix !! k) !! k)) > 1. 0e-10 = matrix
| nz < 0 = matrix -- матрица вырождена
| otherwise = swap matrix k p
where n = length matrix
lst = map (\ r -> r !! k) $ drop k matrix
nz = getNz lst
p = k + nz
0e-10 = matrix
| nz < 0 = matrix -- матрица вырождена
| otherwise = swap matrix k p
where n = length matrix
lst = map (\ r -> r !! k) $ drop k matrix
nz = getNz lst
p = k + nz
Если ведущий (ненулевой) элемент найти невозможно (матрица вырождена), то функция вернет ее без изменений. Функция mkzero формирует нули в очередном столбце матрицы:
-- получение нулей в нужном столбце
mkzero :: Matrix -> Int -> Int -> Matrix
mkzero matrix k p | p>n-1 = matrix
| otherwise = mkzero (trans matrix p k (-f)) k (p+1)
where n = length matrix
f = ((matrix !! p) !! k)/((matrix !! k) !! k)
Функция triangle формирует верхнюю треугольную форму матрицы:
-- Получение верхней треугольной формы матрицы
triangle :: Matrix -> Int -> Matrix
triangle matrix k | k>=n = matrix
| (abs v) <= 1. 0e-10 = [[0.0]] -- матрица вырождена
| otherwise = triangle (mkzero tmp k k1) k1
where n = length matrix
tmp = search matrix k
v = (tmp !! k) !! k -- диагональный элемент
k1 = k+1
0e-10 = [[0.0]] -- матрица вырождена
| otherwise = triangle (mkzero tmp k k1) k1
where n = length matrix
tmp = search matrix k
v = (tmp !! k) !! k -- диагональный элемент
k1 = k+1
Если на очередном этапе не удалось найти ведущий элемент, функция возвращает нулевую матрицу 1-го порядка. Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:
-- Парадная функция
gauss :: Matrix -> Matrix
gauss matrix = triangle matrix 0
Для вычисления определителя нам нужно перемножить диагональные элементы. Для этого составим отдельную функцию:
-- Произведение диагональных элементов
proddiag :: Matrix -> Double
proddiag matrix = product $ map (\ (r,k) -> r !!k) $ zip matrix [0,1..]
Ну, и «бантик» — собственно вычисление определителя:
-- Вычисление определителя
det :: Matrix -> Double
det matrix = proddiag $ triangle matrix 0
Проверим, как работает эта функция:
main = print $ det [[1,2,3],[4,5,6],[7,8,-9]]
[1 of 1] Compiling Main ( main. hs, main.o )
Linking a.out ...
54.0
hs, main.o )
Linking a.out ...
54.0
Спасибо тем, кто дочитал до конца!
Код можно скачать здесь
Код для решения детерминанта с использованием Python без использования scipy.linalg.det
Описание (это вопрос hwk):
Я не знаю, с чего начать. Я планирую использовать расширение Лапласа, но не знаю, как его реализовать для матриц nxn. Любая помощь будет оценена по достоинству.
Примечание: у меня уже есть функция для генерации случайных матриц для матрицы nxn. Кроме того, время расчета не является проблемой. Единственное, что у меня есть проблема, — это как вычислить определитель.
Пришлось удалить описание вопроса b / c из моей классовой политики.
python matrix numerical determinantsПоделиться Источник theAngryPhysicist 29 сентября 2010 в 07:16
3 ответа
3
Ладно, вот тебе подсказка.
- напишите функцию для вычисления младших матриц. (подсказка, используйте ломтики)
- напишите функцию для вычисления кофакторов (это должно вызвать первую функцию и детерминированную функцию)
- детерминированная функция вызывает функцию на втором шаге и суммирует результаты. (подсказка: используйте
sum)
Виола, у тебя есть определитель.
Кроме того, не забывайте, что из-за того, как мы пишем списки в python, индексы меняются местами. То есть если
M = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
тогда m 0,1 равно 2, а не 4, как это было бы в обычной нотации. вы можете думать об этом как о транспонировании или использовать zip
Поделиться aaronasterling 29 сентября 2010 в 07:32
3
Вот рекурсивный код python для метода adjucate для нахождения определителя матрицы.
def getMatrixMinor(m,i,j):
return [row[:j] + row[j+1:] for row in (m[:i]+m[i+1:])]
def getMatrixDeternminant(m):
#base case for 2x2 matrix
if len(m) == 2:
return m[0][0]*m[1][1]-m[0][1]*m[1][0]
determinant = 0
for c in range(len(m)):
determinant += ((-1)**c)*m[0][c]*getMatrixDeternminant(getMatrixMinor(m,0,c))
return determinant
Обратите внимание, что входные данные представляют собой массив массивов, представляющих матрицу nxn
Поделиться stackPusher 05 октября 2016 в 18:31
0
def minor(array,i,j):
c = array
c = c[:i] + c[i+1:]
for k in range(0,len(c)):
c[k] = c[k][:j]+c[k][j+1:]
return c
def det(array,n):
if n == 1 :return array[0][0]
if n == 2 :return array[0][0]*array[1][1] - array[0][1]*array[1][0]
sum = 0
for i in range(0,n):
m = minor(array,0,i)
sum =sum + ((-1)**i)*array[0][i] * det(m,n-1)
return sum
Поделиться Peyman Naseri 22 декабря 2019 в 19:53
- Python код для решения классического P(n, r): вывести все перестановки n объектов, взятых r за один раз без повторения
Python код для решения классической задачи P(n, r) Задача: вывести все перестановки n объектов, взятых r за один раз, без повторения.
 Я ученик Python, ищущий элегантное решение, а не пытающийся решить проблему кодирования на работе. Интересно посмотреть код для решения классической проблемы…
Я ученик Python, ищущий элегантное решение, а не пытающийся решить проблему кодирования на работе. Интересно посмотреть код для решения классической проблемы… - Вычисления квадратов решения квадратного уравнения без использования корень
Я пытаюсь написать алгоритм обнаружения столкновений circle-to-line-segment, который включает в себя определение точки пересечения окружности и отрезка прямой. Отрезок линии представляет собой траекторию полета пули над последним кадром, что означает, что она попадет в первый круг, Даже если есть…
Похожие вопросы:
Можно ли получить байт-код python без использования co_code?
Скажем, я нахожусь в интерпретаторе python и определяю функцию следующим образом: def h(a): return a Если я хочу посмотреть на байт-код (а не на разборку с помощью dis), я обычно могу использовать…
Python вычисление детерминанта(без использования внешних библиотек)
Я создаю небольшую библиотеку матричных операций в качестве задачи программирования для себя(и для того, чтобы научиться кодировать с помощью Python), и я столкнулся с задачей вычисления.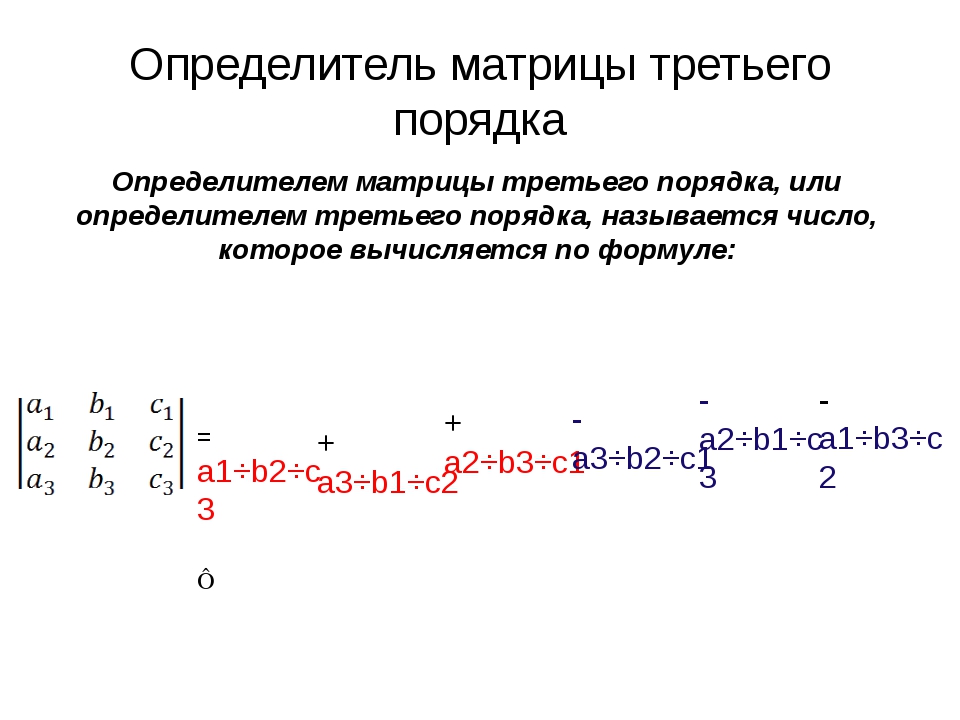 ..
..
построение границы решения кривой в python с использованием matplotlib
Я новичок в машинном обучении с python. Мне удалось нарисовать прямую границу принятия решений для логистической регрессии, используя matplotlib. Однако я столкнулся с некоторыми трудностями при…
Можно ли загрузить файл решения OpenFOAM с помощью ParaView Python Shell без использования графического интерфейса?
У меня есть файл решения OpenFOAM, полученный на HPC (кластерная компьютерная система), в котором у меня нет доступа GUI. У меня есть код Python, который работает на Python Shell из ParaView без…
Как найти определитель матрицы с помощью python
Новый в python и ржавый на линейной алгебре. Однако я ищу руководство по правильному способу создания детерминанта из Матрицы в python без использования Numpy. Пожалуйста, смотрите фрагмент кода…
Python код для решения классического P(n, r): вывести все перестановки n объектов, взятых r за один раз без повторения
Python код для решения классической задачи P(n, r) Задача: вывести все перестановки n объектов, взятых r за один раз, без повторения. Я ученик Python, ищущий элегантное решение, а не пытающийся…
Я ученик Python, ищущий элегантное решение, а не пытающийся…
Вычисления квадратов решения квадратного уравнения без использования корень
Я пытаюсь написать алгоритм обнаружения столкновений circle-to-line-segment, который включает в себя определение точки пересечения окружности и отрезка прямой. Отрезок линии представляет собой…
Есть ли какая-либо польза для детерминанта матрицы 4×4 в компьютерной графике?
В большинстве графических библиотек, которые я видел, есть какая-то функция, которая возвращает определитель из матриц 3×3 и 4×4, но я понятия не имею, когда вам действительно нужно будет…
Запустите код Python без использования python name.py и ./name
У меня есть основная проблема, когда я не знаю, как запустить скрипт Python из командной строки в Ubuntu без использования ключевого слова python. Итак, я поместил shebang в свой скрипт Python,…
Python: поиск всех встречающихся подстрок в строке без использования regex
У меня есть струна : b = ‘Can you can a can as a canner can can a can?’ Мне нужно найти все возможные начальные и конечные позиции подстроки can в строке b, независимо от случая. Я могу сделать это…
Я могу сделать это…
Определитель матрицы 3×3 — ChiliMath
Стандартная формула для определения определителя матрицы 3 × 3 представляет собой разбиение меньших задач определителя 2 × 2 , с которыми очень легко справиться. Если вам нужно напомнить что-то новое, посмотрите мой другой урок о том, как найти определитель 2 × 2. Предположим, нам дана квадратная матрица A, где,
Определитель матрицы A вычисляется как
Вот ключевые моменты:
- Обратите внимание, что элементы верхней строки, а именно a, b и c, служат скалярными умножителями для соответствующей матрицы 2 на 2.
- Скаляр a умножается на матрицу 2 × 2 оставшихся элементов, созданную, когда сегменты вертикальной и горизонтальной линии проходят через a.
- Тот же процесс применяется для построения матриц 2 × 2 для скалярных множителей b и c.
Определитель матрицы 3 x 3 (анимированный)
Примеры определения определителя матрицы 3 × 3
Пример 1: Найдите определитель матрицы 3 × 3 ниже.
Приведенная ниже настройка поможет вам найти соответствие между общими элементами формулы и элементами реальной проблемы.
Применяя формулу,
Пример 2: Вычислите определитель матрицы 3 × 3 ниже.
Будьте очень осторожны при замене значений в правильные места в формуле. Распространенные ошибки возникают, когда ученики становятся небрежными на начальном этапе подстановки значений.
Вдобавок убедитесь, что ваша арифметика верна.В противном случае одна ошибка в вычислении приведет к неверному ответу.
С,
наше вычисление определителя становится…
Пример 3: Найдите определитель матрицы 3 × 3 ниже.
Наличие нуля (0) в первой строке должно значительно упростить наши вычисления. Помните, что эти элементы в первой строке действуют как скалярные множители. Следовательно, умножение нуля на что-либо приведет к исчезновению всего выражения.
Вот снова настройка, показывающая соответствующее числовое значение каждой переменной в формуле.
По формуле имеем…
Практика с рабочими листами
Возможно, вас заинтересует:
Детерминанты матрицы 2 × 2
Определитель матрицы 3×3 (общий и сокращенный метод)
Определитель матрицы 3×3 (общий и сокращенный метод)
Как мы видели в прошлых уроках, чтобы определить, что является определителем матрицы, нам нужно вернуться к нашему определению матрицы.Помните, что мы узнали, что матрица — это упорядоченный список чисел, заключенный в прямоугольную скобку. Этот список также можно назвать прямоугольным массивом, и он обеспечивает упорядоченный способ отображения «списка» информационных элементов. Если вы хотите более подробно ознакомиться с определением матрицы, вы можете вернуться к нашему уроку о нотации матриц.
Матрица описывает линейное преобразование или линейную карту, которая является своего рода транскрипцией между двумя типами алгебраических структур, такими как векторные поля.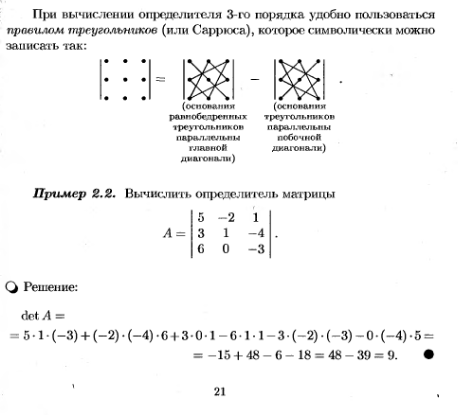 Таким образом, мы можем разрешить системы линейных уравнений, представив линейную систему в виде матрицы. Матричное представление линейной системы создается с использованием всех переменных коэффициентов, найденных в системе, и использования их в качестве элементов для построения прямоугольного массива расширенной матрицы соответствующего размера. В такой матрице результаты каждого уравнения из системы будут помещены справа от вертикальной линии, которая представляет знак равенства.
Таким образом, мы можем разрешить системы линейных уравнений, представив линейную систему в виде матрицы. Матричное представление линейной системы создается с использованием всех переменных коэффициентов, найденных в системе, и использования их в качестве элементов для построения прямоугольного массива расширенной матрицы соответствующего размера. В такой матрице результаты каждого уравнения из системы будут помещены справа от вертикальной линии, которая представляет знак равенства.
Зная это, в этом уроке основное внимание будет уделено процессу оценки определителя матрицы 3×3 и двум возможным методам, которые можно использовать.
Какой определитель матрицы
Используя знание того, что матрица представляет собой массив, содержащий информацию о линейном преобразовании, и что этот массив может быть согласован с коэффициентами каждой переменной в системе уравнений, мы можем описать функцию определителя: определитель будет масштабироваться линейное преобразование из матрицы, это позволит нам получить обратную матрицу (если она есть) и поможет в решении систем линейных уравнений, создав условия, при которых мы можем ожидать определенных результатов или характеристик от система (в зависимости от определителя и типа линейной системы, мы можем знать, можем ли мы ожидать уникального решения, более одного решения или вообще ни одного решения для системы).
Но есть условие для получения определителя матрицы, матрица должна быть квадратной матрицей, чтобы ее можно было вычислить. Следовательно, упрощенное определение состоит в том, что определитель — это значение, которое может быть вычислено из квадратной матрицы, чтобы помочь в разрешении систем линейных уравнений, связанных с такой матрицей. Определителя неквадратной матрицы не существует, математически определены только определители квадратных матриц.
Определитель матрицы можно обозначить просто как det A, det (A) или | A |.Это последнее обозначение происходит от обозначения, которое мы непосредственно применяем к матрице, определитель которой мы получаем. Другими словами, мы обычно записываем матрицы и их определители очень похожим образом:
Уравнение 1: Разница между обозначениями матрицы и определителяОбратите внимание на разницу: матрица записана в прямоугольных скобках, а компоненты определителя матрицы окружены двумя прямыми линиями.
Сегодняшний урок будет сосредоточен на процессе вычисления определителя матрицы 3×3, используя подход свойств определителя матрицы, которые были кратко рассмотрены на прошлых уроках. Помните, что мы рассмотрим эту полную тему на следующем уроке, который называется: свойства детерминантов. Тем не менее, важно помнить об этих свойствах при выполнении расчетов упражнений в последнем разделе этого урока.
Помните, что мы рассмотрим эту полную тему на следующем уроке, который называется: свойства детерминантов. Тем не менее, важно помнить об этих свойствах при выполнении расчетов упражнений в последнем разделе этого урока.
Как найти определитель матрицы 3×3
Существует два метода нахождения определителя матрицы 3×3: общий метод и сокращенный метод. Так же, как звучат названия каждого из них, общий метод является «формальным» методом для математического использования, следуя всем правилам и производя некоторые второстепенные вычисления определителя матрицы по пути нахождения окончательного решения.Хотя метод быстрого доступа — это более хитрый трюк, который мы можем использовать для упрощения вычислений, при этом стараясь не забыть числа, порядок, в котором они должны быть умножены, и некоторые перестановки элементов в матрице.
После того, как вы взглянете на оба метода, чтобы найти определитель матрицы 3×3, вы всегда можете выбрать тот, который вам больше всего подходит, и использовать его для своих исследований, но помните, что важно знать оба из них, на случай, если вас когда-нибудь спросят. сравнить результаты с ними.
сравнить результаты с ними.
Итак, без дальнейших задержек, давайте определим определитель матрицы 3×3 A, как показано ниже, чтобы мы могли наблюдать, как его можно вычислить обоими методами:
Уравнение 2: Определитель матрицы A- Общий метод
Общий метод получения определителя матрицы 3×3 состоит из разбиения матрицы на вторичные матрицы меньших размеров в процессе, называемом «расширением первой строки». Этот процесс использует элементы из первой строки матрицы 3×3 и использует их как множители в сумме умножений, при которой большая матрица перераспределяется.
Давайте шаг за шагом рассмотрим, как вычислить определитель матрицы 3×3:
- Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому принадлежит ваш первый выбранный элемент.
Взяв в качестве ссылки определитель матрицы 3×3, показанный в уравнении 2, мы строим первую часть результата этой операции, выбирая первый элемент первой строки и столбца (который является константой «a»), а затем умножаем его на матрица, созданная из четырех элементов, которые не принадлежат ни одной строке столбца, в котором находится «a».
 Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения.
Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения. - Второй член начинается со второго элемента в верхней строке (константа «b»), сопровождаемого отрицательным знаком, который теперь умножает вторичную матрицу 2×2, которая снова получается из четырех элементов в матрице, которые не принадлежат в любой столбец строки, в которой находится «b».
- Повторяем первый шаг, но уже с третьим элементом из верхней строки матрицы.
Итак, определитель матричной формулы 3×3 для общего метода:
Уравнение 3: Уравнение для определителя матрицы 3×3 посредством общего методаПроцесс называется расширением первой строки, потому что, как вы можете видеть в уравнении 3, все элементы из первой строки исходной матрицы 3×3 остаются основными факторами в расширении, для которого необходимо решить. Все матрицы 2×2 в раскрытии — это то, что мы называем «вторичными матрицами», и их можно легко разрешить, используя уравнение, изученное на определителе на уроке по матрице 2×2.

Итак, принимая во внимание формулу для определителя квадратной матрицы размером 2×2, мы видим, что уравнение 3 дает:
Уравнение 4: Уравнение для определителя матрицы 3×3 посредством общего метода (часть 2)На этом этапе вы, возможно, заметили, что поиск определителя матрицы, превышающей 2×2, становится долгим испытанием, но логика процесса остается той же, и поэтому сложность аналогична, единственный ключевой момент — отслеживать операции вы прорабатываете даже больше с матрицами даже большего размера, чем 3×3.
- Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому принадлежит ваш первый выбранный элемент.
- Сокращенный метод
Определитель метода быстрого доступа к матрице 3×3 — это хитрый трюк, который упрощает вычисление определителя большой матрицы путем прямого умножения и добавления (или вычитания) всех элементов в их необходимом виде, без необходимости пройти через матричное расширение первой строки и без необходимости оценивать детерминанты вторичных матриц.
Весь процесс того, как оценить определитель матрицы 3×3, используя сокращенный метод, можно увидеть в уравнении ниже:
Уравнение 5: Быстрый метод получения определителя матрицы 3×3Теперь давайте поясним метод быстрого доступа:
При вычислении определителя матрицы размера nxn (в данном случае матрицы 3×3), как показано выше, обратите внимание, что мы сначала переписываем матрицу, сопровождаемую повторением двух первых столбцов, которые теперь записываются снаружи с правой стороны.

Тогда значение определителя будет результатом вычитания между сложением произведений всех умножений вниз-вправо и умножений вниз-влево. Сказано более ясно, в общей сложности будет три полных диагонали, идущих от верхнего левого угла до нижнего правого, и еще один набор из трех полных диагоналей, идущих от верхнего правого угла до нижнего левого угла.
Мы умножим элементы каждой диагонали вместе, а затем сложим их с результатами, полученными на других диагоналях.Есть кое-что, что нужно иметь в виду, все умножения диагоналей, идущие от верхнего левого угла к нижнему правому, имеют внутренний положительный знак, умноженный на них, в то время как все умножения диагоналей, идущие сверху справа налево, имеют внутренний отрицательный знак умножения. к ним, и поэтому при сложении результатов всех умножений будет получено вычитание, подобное тому, которое показано в уравнении 5.
Хотя этот метод проще в применении, чем общий метод, его немного сложно объяснить из-за того, что все операции умножения и сложения выполняются одновременно, поэтому мы рекомендуем вам использовать уравнение 5 в качестве руководства и уделять пристальное внимание к видео, где демонстрируются примеры этого метода.

В последнем разделе этого урока мы проработаем набор из трех различных матриц 3×3 и их детерминанты. Мы рекомендуем вам сравнить процессы для обоих методов, чтобы лучше понять их.
Определитель большой матрицы
Процесс оценки определителя матрицы большей размерности, чем 3×3, следует той же логике, что и то, что мы видели до сих пор. Используя общий метод на матрице A 4×4, где ее первая (верхняя) строка соответствует элементам a, b, c и d, мы вычисляем определитель матрицы следующим образом:
Уравнение 6: Определитель матрицы 4×4 Мы еще раз расширили определитель на его первую строку и получили вторичные матрицы, которые в данном случае являются матрицами 3×3, каждая из которых может быть расширена и разбита на матрицы 2×2.Шаблон в процессе повторяется, вы можете продолжать работать таким образом с еще более крупными квадратными матрицами, и он всегда будет работать, но если вам больше нравится метод ярлыков, то вас ждет удовольствие, поскольку метод работает точно так же как и в случае с матрицами 3×3, он просто увеличивает количество элементов, с которыми вы работаете, но логика и перестановка точно такие же (умножение сверху слева вниз справа имеет положительный знак, умножения от верхнего правого угла до нижнего левого угла имеют внутренний отрицательный знак).
Вы взволнованы, увидев, как сокращенный метод работает с матрицами большего размера? Мы рекомендуем вам попробовать это самостоятельно, чтобы вы могли увидеть весь процесс. Вы всегда можете вернуться и решить ту же матрицу, используя общий метод, и доказать, что ваш результат верен.
Упражнения по вычислению определителя матрицы 3×3
В следующих упражнениях мы решим определитель матрицы 3×3, предоставленной в каждом случае, с помощью соответствующего метода, а в конце мы сравним полученные результаты.
Обратите внимание, что матрицы A, B и C, представленные в обоих разделах упражнений выше, абсолютно одинаковы. Это было сделано специально, чтобы вы могли сравнить результаты обоих методов и посмотреть, как они дают одинаковые значения.
Чтобы завершить этот урок, мы хотели бы порекомендовать вам эту статью о том, как вычислить определители, и другую статью о определителе квадратной матрицы, где вы найдете гораздо больше примеров, чем приведенные здесь.
Надеемся, этот урок был интересным и полезным, до встречи в следующем!
Детерминанты: 33 Детерминанты (стр. 2 из 2) Ячейки: 22 детерминанты, 33 детерминанты Расчеты для 33 детерминанты более беспорядочные, чем для 22-х.Могут использоваться различные методы, но самый простой, вероятно, следующий: Авторские права Элизабет Stapel 2004-2011 Все права защищены
Затем я складываю диагонали вниз, вычтите диагонали вверх и упростите, чтобы получить окончательный ответ: Есть и другие способы
для упрощения определителей вручную, и эти другие методы требуются
при оценке больших детерминант вручную, но эти методы
возможно, можно подождать позже. Но обязательно, даже если у вас есть графический калькулятор, с помощью которого вы можете вычислить 22 и 33 детерминанты, потому что вы, вероятно, скажете проблемы, где детерминанты содержат переменные, с которыми ваш калькулятор не может справиться. << Предыдущая Вверх | 1 | 2 | Вернуться к индексу
|
Определитель квадратной матрицы
6.4 — Определитель квадратной матрицыОпределитель — это действительное число, связанное с каждой квадратной матрицей. Я еще не нашел хорошего Английское определение детерминанта. Все, что я могу найти, определяет это с точки зрения математическая формула или предлагает некоторые из ее использования. Есть даже определение определитель, который определяет его в терминах самого себя.
Определитель квадратной матрицы A обозначается как «det A» или | А |, Теперь последний выглядит как абсолютное значение A, но вам придется применить контекст.Если вертикальные линии находятся вокруг матрица, то есть определитель.
В строке ниже показаны два способа записи определителя.
| 3 | 1 | = | дет | 3 | 1 | ||
| 5 | 2 | 5 | 2 |
Определитель матрицы 2 × 2
Определитель матрицы 2 × 2 находится во многом как операция поворота.Это произведение элементов на главной диагонали за вычетом произведение элементов от главной диагонали.
Свойства детерминантов
- Определитель — действительное число, а не матрица.
- Определитель может быть отрицательным числом.
- Он вообще не связан с абсолютным значением, за исключением того, что они оба используют вертикальные линии.
- Определитель существует только для квадратных матриц (2 × 2, 3 × 3,
… n × n). Определитель матрицы 1 × 1 — это единственное значение
в определителе.

- Обратная матрица будет существовать, только если определитель не равен нулю.
Расширение с использованием младших и сомножителей
Определение определителя, которое у нас есть до сих пор, относится только к матрице 2 × 2. Есть ярлык для матрица 3 × 3, но я твердо верю, что вам следует изучить способ, который будет работать для всех размеров, а не только для частный случай для матрицы 3 × 3.
Метод называется расширением с использованием миноров и сомножителей. Прежде чем мы сможем использовать их, нам нужно их определить.
Несовершеннолетние
Второстепенным для любого элемента является определитель, который получается, когда строка и столбец что элементы удалены.
Обозначение M ij используется для обозначения минорной части элемента. в строке i и столбце j. Таким образом, M 21 будет означать второстепенное значение для элемента. в строке 2, столбце 1.
Рассмотрим определитель 3 × 3, показанный ниже. Я включил заголовки, чтобы
вы можете держать строки и столбцы ровными, но обычно вы не включаете
те.Мы собираемся найти нескольких несовершеннолетних.
Я включил заголовки, чтобы
вы можете держать строки и столбцы ровными, но обычно вы не включаете
те.Мы собираемся найти нескольких несовершеннолетних.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | 1 | 3 | 2 |
| R 2 | 4 | 1 | 3 |
| R 3 | 2 | 5 | 2 |
Поиск второстепенного для R
2 C 1 Младший — это определитель, который остается при удалении строки и столбца.
элемента, для которого вы пытаетесь найти второстепенное.Это означает, что мы должны удалить
строка 2 и столбец 1, а затем найдите определитель.
| С 2 | С 3 | ||
|---|---|---|---|
| R 1 | 3 | 2 | = 3 (2) — 5 (2) = 6-10 = -4 |
| R 3 | 5 | 2 |
Как видите, второстепенное значение для строки 2 и столбца 1 — M 21 = -4.
Попробуем еще.
Поиск второстепенного для R
3 C 2На этот раз мы удалим строку 3 и столбец 2.
| С 1 | С 3 | ||
|---|---|---|---|
| R 1 | 1 | 2 | = 1 (3) — 4 (2) = 3-8 = -5 |
| R 2 | 4 | 3 |
Таким образом, второстепенное значение для строки 3, столбца 2 — M 32 = -5.
Матрица несовершеннолетних
Когда вы просто пытаетесь найти определитель матрицы, это перебор. Но для него есть одно чрезвычайно полезное приложение, которое даст нам практику. поиск несовершеннолетних.
Матрица миноров — это квадратная матрица, в которой каждый элемент является второстепенным. для номера в этой позиции.
Вот общая матрица миноров для определителя 3 × 3.
| С 1 | С 2 | С 3 | |||
|---|---|---|---|---|---|
| R 1 | M 11 | M 12 | M 13 | ||
| R 2 | M 21 | M 22 | M 23 | ||
| R 3 | M 31 | M 32 | M 33 |
Найдем матрицу миноров для нашего исходного определителя. Здесь
определитель.
Здесь
определитель.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | 1 | 3 | 2 |
| R 2 | 4 | 1 | 3 |
| R 3 | 2 | 5 | 2 |
Вот работа по поиску каждого минора в матрице миноров.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | = 2-15 = -13 | = 8-6 = 2 | = 20-2 = 18 |
| R 2 | = 6-10 = -4 | = 2 — 4 = -2 | = 5-6 = -1 |
| R 3 | = 9 — 2 = 7 | = 3-8 = -5 | = 1–12 = -11 |
И, наконец, матрица миноров. Опять же, метки ставить не нужно
для строки и столбцов, но это может вам помочь.
Опять же, метки ставить не нужно
для строки и столбцов, но это может вам помочь.
| С 1 | С 2 | С 3 | |||
|---|---|---|---|---|---|
| R 1 | -13 | 2 | 18 | ||
| R 2 | -4 | -2 | –1 | ||
| R 3 | 7 | -5 | -11 |
Кофакторы
Кофактор для любого элемента является второстепенным или противоположным второстепенным,
в зависимости от того, где находится элемент в исходном определителе.Если строка и
столбец элемента суммируется до четного числа, тогда сомножитель — это
так же, как и несовершеннолетний. Если сумма строки и столбца элемента получается нечетной
число, то сомножитель — это
противоположность несовершеннолетнему.
Если сумма строки и столбца элемента получается нечетной
число, то сомножитель — это
противоположность несовершеннолетнему.
О, ты понял? Нечетное меняет знаки, четное — тот же знак. Дежавю. Мы говорим об этом с момента раздела 3.2 о многочленах.
Знаковая диаграмма
Вместо того, чтобы складывать строку и столбец элемента, чтобы проверить, является четным или нечетным, многие люди предпочитают использовать знаковую диаграмму.Знаковая диаграмма — это либо a + или — для каждого элемента в матрице. Первый элемент (строка 1, столбец 1) является всегда а + и чередуется оттуда.
Примечание. Знак «+» не означает «положительный», а «-» — отрицательный. + Означает то же самое знак как несовершеннолетний и — означает противоположность несовершеннолетнему. Подумайте об этом дополнении и вычитание, а не положительное или отрицательное.
Вот знаковая диаграмма для определителя 2 × 2.
Вот знаковая диаграмма для определителя 3 × 3.
| С 1 | С 2 | С 3 | |
|---|---|---|---|
| R 1 | + | – | + |
| R 2 | – | + | – |
| R 3 | + | – | + |
Матрица сомножителей
Опять же, если все, что вы пытаетесь сделать, это найти определитель, вам не нужно проделать такую большую работу.
Матрица сомножителей — это матрица, найденная заменой каждого элемента матрицу ее сомножителем. Это матрица несовершеннолетних с измененными знаками по элементам в позициях -.
| С 1 | С 2 | С 3 | |||
|---|---|---|---|---|---|
| R 1 | -13 | -2 | 18 | ||
| R 2 | 4 | -2 | 1 | ||
| R 3 | 7 | 5 | -11 |
Расширение для поиска определителя
Вот шаги, которые необходимо выполнить, чтобы найти определитель.
- Выберите любую строку или столбец в матрице. Неважно, какая строка или какая столбец, который вы используете, ответ будет одинаковым для любой строки. Есть несколько строк или столбцы, которые проще, чем другие, но мы вернемся к этому позже.
- Умножить каждые элемент в этой строке или столбце по его кофактору и добавьте. В результате определитель.
Разложим нашу матрицу по первой строке.
Из диаграммы знаков мы видим, что 1 находится в положительном положении, 3 — в отрицательном положение, а 2 находится в положительном положении.Поставив + или — перед элемент, он заботится о корректировке знака при переходе от второстепенного к кофактору.
| + 1 | 1 | 3 | — 3 | 4 | 3 | + 2 | 4 | 1 |
| 5 | 2 | 2 | 2 | 2 | 5 |
= 1 (2-15) — 3 (8-6) + 2 (20-2)
= 1 (-13) — 3 (2) + 2 (18)
= -13-6
+ 36
= 17
Определитель этой матрицы равен 17.
Как я сказал ранее, на самом деле не имеет значения, какую строку или столбец вы используете.
Давайте попробуем еще раз, но на этот раз расширим вторые столбцы. Как усилие для экономии времени миноры для этого столбца (из матрицы миноров) были 2, -2 и -5. Исходные элементы были 3, 1 и 5. 3 и 5 отрицательны. позиции.
Определитель= — 3 (2) + 1 (-2) — 5 (-5) = -6-2 + 25 = 17
Раскройте любую строку или любой столбец, вы получите 17.
Но диагонали делать нельзя.Если попробовать по главной диагонали, получится
+ 1 (-13) + 1 (-2) + 2 (-11) = -13-2-22 = -37
Некоторые строки или столбцы лучше других
- Выберите строку или столбец с наибольшим количеством нулей.
Поскольку каждый младший или сомножитель умножается на элемент в матрице, выбор строки или столбца с большим количеством нулей означает, что вы будете умножение на множество нулей. Умножение на ноль совсем не занимает много времени. Фактически, если элемент равен нулю, вы не
нужно даже найти несовершеннолетнего
или кофактор.
Фактически, если элемент равен нулю, вы не
нужно даже найти несовершеннолетнего
или кофактор. - Выберите строку или столбец с наибольшими числами (или переменными) в нем.
Элементы в строке или столбце, по которым вы разворачиваете, не используются для поиска несовершеннолетние. Единственное место, где они умножаются, — это один раз в расширении. Если вы выберете строку или столбец с наименьшие числа, то каждое младшее число будет произведением большего числа.
Если вы выберете строку или столбец, в котором есть переменные, то вы только имеют умножить на переменные один раз, во время раскрытия.
Обратная матрица (пересмотренная)
Давайте на этот раз рассмотрим наш исходный определитель как матрицу.
| 1 | 3 | 2 | ||
| 4 | 1 | 3 | ||
| 2 | 5 | 2 |
Найдите матрицу миноров , как описано выше.
| -13 | 2 | 18 | ||
| -4 | -2 | –1 | ||
| 7 | -5 | -11 |
Превратите его в матрицу сомножителей , изменив знаки на соответствующих элементы на основе знаковой диаграммы.
| -13 | -2 | 18 | ||
| 4 | -2 | 1 | ||
| 7 | 5 | -11 |
Найдите , присоединенное к , транспонировав матрицу сомножителей.
Чтобы транспонировать матрицу, вы переключаете строки и столбцы. То есть строки
стать столбцами и
столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82.
или калькулятор TI-83, введя имя матрицы и выбрав Матрица,
Math, а затем вариант 2 с надстрочным символом T, например [A] T .
То есть строки
стать столбцами и
столбцы становятся строками. Транспонирование матрицы можно найти с помощью TI-82.
или калькулятор TI-83, введя имя матрицы и выбрав Матрица,
Math, а затем вариант 2 с надстрочным символом T, например [A] T .
| -13 | 4 | 7 | ||
| -2 | -2 | 5 | ||
| 18 | 1 | -11 |
Наконец разделите сопряженную матрицу на определитель матрицы.В этой задаче определитель равен 17, поэтому мы разделим каждый элемент на 17. Результирующая матрица — , обратная исходной матрицы.
| -13/17 | 17.04. | 17.07 | ||
| -2/17 | -2/17 | 17. 05 05 | ||
| 18/17 | 1/17 | -11/17 |
Матрица, обратная матрице, находится путем деления сопряженной матрица по определителю матрицы.Не пытайтесь это сделать на своем калькулятор, поскольку калькулятор не позволяет разделить матрицу на скаляр. Вместо этого вам придется умножить на обратное значение определителя.
Если вы проверите это с помощью своего калькулятора, вы можете убедиться, что на самом деле обратное — это сопряженное, деленное на определитель.
Поскольку обратная величина — это присоединенный элемент, деленный на детерминант, мы можем понять, почему обратное не существует, если определитель равен нулю. Это приведет к делению на ноль, что не определено.
Детерминанты более крупного порядка
Найдем определитель системы 4х4.
| С 1 | С 2 | С 3 | С 4 | |
|---|---|---|---|---|
| R 1 | 3 | 2 | 0 | 1 |
| R 2 | 4 | 0 | 1 | 2 |
| R 3 | 3 | 0 | 2 | 1 |
| R 4 | 9 | 2 | 3 | 1 |
Выберите строку или столбец с наибольшим количеством нулей. В данном случае это
второй столбец.
В данном случае это
второй столбец.
Для каждого элемента исходной матрицы свой минор будет определителем 3 × 3. Придется расширить каждый из них на с использованием трех определителей 2 × 2.
Вот почему мы хотим развернуть второй столбец. Несовершеннолетние умножаются по их элементам, поэтому, если элемент в исходной матрице равен 0, он не действительно имеет значение, что такое несовершеннолетний, и мы можем сэкономить много времени, не имея найти это. Во втором столбце вам не нужно будет искать двух несовершеннолетних. потому что их соответствующий элемент во втором столбце равен нулю.
| — 2 | 4 | 1 | 2 | + 0 | — 0 | + 2 | 3 | 0 | 1 | ||||||
| 3 | 2 | 1 | ? | ? | 4 | 1 | 2 | ||||||||
| 9 | 3 | 1 | 3 | 2 | 1 |
Мы действительно могли бы заполнить эти два средних младших, но поскольку они умножаются
на 0, неважно, какие они. Фактически, вы могли бы так же легко
пропустить их.
Фактически, вы могли бы так же легко
пропустить их.
Теперь осталось найти два определителя 3×3.
В первом определителе 3×3, нулей нет, поэтому выберите строку или столбец с наибольшими числами. Что будет столбцом 1, поэтому разверните его по первому столбцу.
Уведомление 4 находится в положительном положении. Таблицы знаков начинаются заново с каждого новый определитель. Положение числа в исходной матрице не имеет значение, только его положение в текущей матрице.
| 4 | 1 | 2 | ||||||||||
| 3 | 2 | 1 | = | + 4 | 2 | 1 | — 3 | 1 | 2 | + 9 | 1 | 2 |
| 9 | 3 | 1 | 3 | 1 | 3 | 1 | 2 | 1 |
= 4 (2-3) — 3 (1-6) + 9 (1-4) = 4 (-1) — 3 (-5) + 9 (-3 ) = -4 + 15 — 27 = -16
Рассмотрим другую матрицу 3 × 3. В этом в строке стоит 0
1 и столбец 2. Любой из них будет хорошим выбором для расширения, но
поскольку в строке 1 числа немного больше, мы расширим первую строку.
В этом в строке стоит 0
1 и столбец 2. Любой из них будет хорошим выбором для расширения, но
поскольку в строке 1 числа немного больше, мы расширим первую строку.
| 3 | 0 | 1 | ||||||||||
| 4 | 1 | 2 | = | + 3 | 1 | 2 | — 0 | ? | ? | + 1 | 4 | 1 |
| 3 | 2 | 1 | 2 | 1 | ? | ? | 3 | 2 |
= 3 (1-4) — 0 (не имеет значения) + 1 (8-3) = 3 (-3) + 1 (5) = -9 + 5 = -4
Когда вы идете искать определитель, помните, что были элементы из
исходная матрица 4 × 4, умноженная на каждый из этих определителей 3 × 3. Первый — -2, второй — +2.
Первый — -2, второй — +2.
Определитель = -2 (-16) + 2 (-4) = 32 — 8 = 24
Худший сценарий
Чтобы найти определитель 3×3 без нулей, вы должны найти три определителя 2×2.
Чтобы найти определитель 4×4 без нулей, вам нужно найти четыре определителя 3×3, каждый из которых затем становится тремя определителями 2×2, что в сумме дает двенадцать определителей 2×2.
Чтобы найти определитель 5×5 без нулей, вам нужно найти пять определителей 4×4, каждый из которых затем становится четырьмя детерминантами 3×3, каждый из которых становится тремя детерминантами 2×2, в сумме шестидесяти определителей 2×2.
Использование калькулятора
После этой последней проблемы вы должны спросить себя, нет ли более простого пути. Ну да, есть, если в определителе нет никаких переменных. Вы можете воспользоваться калькулятором.
Обозначение, которое использует калькулятор TI-82 или TI-83, — это обозначение Det A. Итак, после входа в
матрицу в одну из доступных матриц на калькуляторе, введите DET, выбрав Матрица, Математика и
выбор варианта 1. Затем введите название матрицы, которую вы используете.
Затем введите название матрицы, которую вы используете.
Вам не нужно использовать круглые скобки (если у вас нет TI-83), но вы можете, если ты хочешь найти определитель продукта «det ([A] * [B])» или определитель транспонирования «det ([A] T ) «как в отличие от транспонирования определителя «(det [A]) T» . Кстати, калькулятор не найдет транспонирование определителя, потому что в детерминант является скаляром (действительным числом) и калькулятор знает только, как найти транспонирование матрицы. Транспонирование скаляр — это то, что скаляр.
Треугольные матрицы
Вам действительно понравится находить определители этих матриц.
- Верхняя треугольная матрица
- Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо над ней. То есть все ненулевые значения находятся в верхнем треугольнике. Все, что ниже диагонали это ноль.
- Нижняя треугольная матрица
- Матрица, в которой все ненулевые элементы находятся либо на главной диагонали, либо ниже нее.

- То есть все ненулевые значения находятся в нижнем треугольнике. Все выше диагонали равно нулю.
- Диагональная матрица
- Матрица, в которой все ненулевые элементы находятся на главной диагонали. Все выключено главная диагональ — ноль.
Определителем треугольной или диагональной матрицы является произведение элементов по главной диагонали.
Операции с элементарными строками
Существовали три элементарные операции со строками, которые могли быть выполнены, которые возвращали бы эквивалентная система.С определителями, поскольку определитель транспонирования такой же, как и у Определитель матрицы, элементарные операции со строками также могут применяться к столбцам.
Выполняя сокращение строк (используя поворот на 1, если хотите), вы можете поместить матрицу в
треугольная форма. Как только он приобретет треугольную форму, все, что вам нужно сделать, это умножить на элементы
на главной диагонали, и у вас есть определитель.
Давайте рассмотрим каждую из трех элементарных операций со строками.
- Если вы поменяете местами две строки или два столбца в определителе, результирующий определитель будет отличаются только знаком.То есть, если вы меняете местами строки или столбцы, результирующий определитель будет противоположно исходному определителю.
- Если вы умножаете строку или столбец на ненулевую константу, определитель умножается на эту та же ненулевая константа.
- Если вы умножите строку или столбец на ненулевую константу и добавите ее к другой строке или столбцу, при замене этой строки или столбца определитель не изменяется.
Последняя операция эквивалентна повороту на единицу!
Предупреждение, если ваша точка поворота — это число, отличное от единицы, то вы умножаете каждую строку, которую вы
изменение поворотным элементом.Итак, если вы повернетесь к 3 и измените две строки, то полученный
определитель будет в 3 * 3 = 9 раз больше, чем исходный определитель.
Пока вы выбираете единицу, все будет в порядке.
Вам не нужно помещать матрицу в сокращенную форму строки-эшелон или даже форму строки-эшелона. Вы можете в любой момент остановить сокращение и расширить, используя миноры и кофакторы. Что я Предлагаю это стержень там, где он есть, а затем разверните.
Нулевые детерминанты
Определитель матрицы будет равен нулю, если
- Вся строка нулевая.
- Две строки или столбцы равны.
- Строка или столбец является постоянным кратным другой строке или столбцу.
Помните, что матрица обратима и невырождена тогда и только тогда, когда определитель не равен нулю. Итак, если определитель равен нулю, матрица сингулярна и не имеет обратной.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее.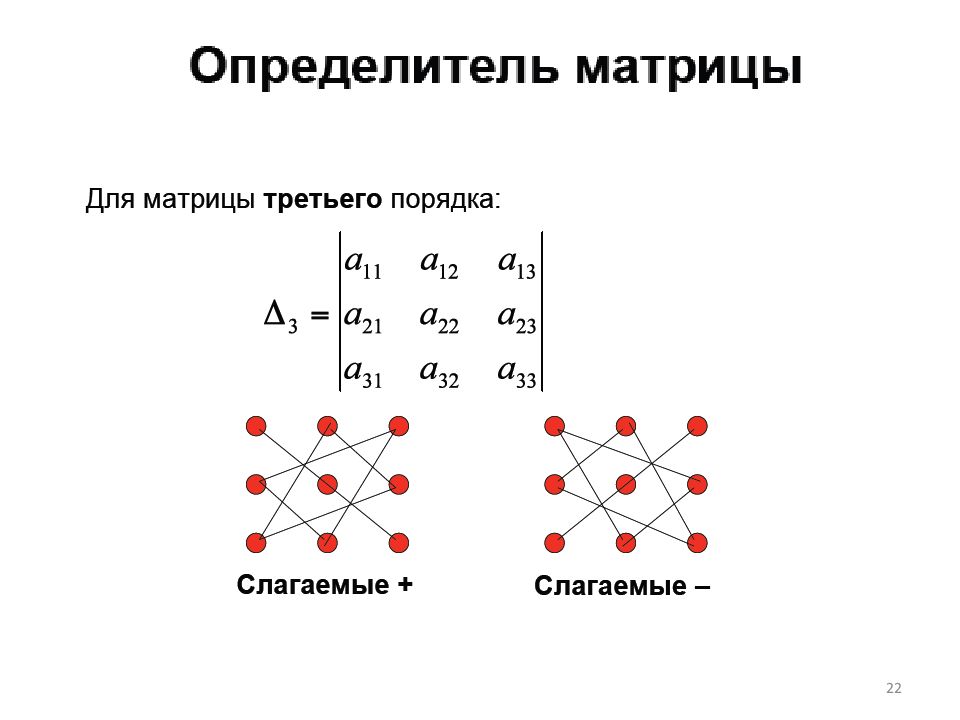 Один из способов — увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.
Один из способов — увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на каждой из трех диагоналей (нижний левый верхний правый). Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
[латекс] A = \ left [\ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \\ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} \ right] [/ латекс]
- Дополните [латекс] A [/ латекс] первыми двумя столбцами.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \ \ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ конец {массив} | \ begin {массив} {c} {a} _ {1} \\ {a} _ {2} \\ {a} _ {3} \ end {array} \ begin {array} {c } {b} _ {1} \\ {b} _ {2} \\ {b} _ {3} \ end {array} | [/ latex]
- С верхнего левого угла в нижний правый: умножение значений по первой диагонали.
 Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали. - От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали. Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Рисунок 2
Алгебра выглядит следующим образом:
[латекс] | A | = {a} _ {1} {b} _ {2} {c} _ {3} + {b} _ {1} {c} _ {2} {a} _ {3 } + {c} _ {1} {a} _ {2} {b} _ {3} — {a} _ {3} {b} _ {2} {c} _ {1} — {b} _ {3} {c} _ {2} {a} _ {1} — {c} _ {3} {a} _ {2} {b} _ {1} [/ latex]
Пример 3: Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 для данного
[латекс] A = \ left [\ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \ right] [/ latex]
Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле. Таким образом,
Таким образом,
[латекс] \ begin {array} {l} | A | = | \ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} | \ begin {array} {c} 0 \\ 3 \\ 4 \ end {array} \ begin {array} {c} 2 \\ -1 \\ 0 \ end {array} | \ hfill \\ = 0 \ left (-1 \ right ) \ влево (1 \ вправо) +2 \ влево (1 \ вправо) \ влево (4 \ вправо) +1 \ влево (3 \ вправо) \ влево (0 \ вправо) -4 \ влево (-1 \ вправо) \ left (1 \ right) -0 \ left (1 \ right) \ left (0 \ right) -1 \ left (3 \ right) \ left (2 \ right) \ hfill \\ = 0 + 8 + 0 + 4 — 0-6 \ hfill \\ = 6 \ hfill \ end {array} [/ latex]
Попробуй 2
Найдите определитель матрицы 3 × 3.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} 1 & -3 & 7 \\ 1 & 1 & 1 \\ 1 & -2 & 3 \ end {array} | [/ latex ]
Вопросы и ответы
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и [latex] \ text {3} \ text {} \ times \ text {} 3 [/ латексные] матрицы.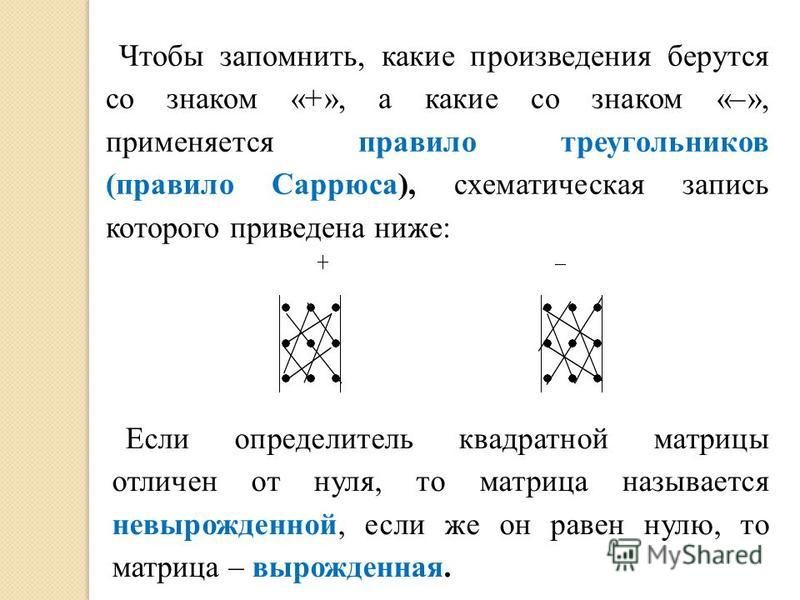 Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить Правило Крамера для решения системы трех уравнений с тремя переменными .Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что определитель равен нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или есть бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений 3 × 3.
Рисунок 3
[латекс] x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z} } {D}, D \ ne 0 [/ латекс]
где
Рисунок 4
Если мы записываем определитель [latex] {D} _ {x} [/ latex], мы заменяем столбец [latex] x [/ latex] на столбец констант. Если мы пишем определитель [latex] {D} _ {y} [/ latex], мы заменяем столбец [latex] y [/ latex] постоянным столбцом. Если мы пишем определитель [latex] {D} _ {z} [/ latex], мы заменяем столбец [latex] z [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Если мы пишем определитель [latex] {D} _ {y} [/ latex], мы заменяем столбец [latex] y [/ latex] постоянным столбцом. Если мы пишем определитель [latex] {D} _ {z} [/ latex], мы заменяем столбец [latex] z [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Пример 4: Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
[латекс] \ begin {array} {c} x + y-z = 6 \\ 3x — 2y + z = -5 \\ x + 3y — 2z = 14 \ end {array} [/ latex]
Решение
Используйте правило Крамера.
[латекс] D = | \ begin {array} {ccc} 1 & 1 & -1 \\ 3 & -2 & 1 \\ 1 & 3 & -2 \ end {array} |, {D} _ {x} = | \ begin { array} {ccc} 6 & 1 & -1 \\ -5 & -2 & 1 \\ 14 & 3 & -2 \ end {array} |, {D} _ {y} = | \ begin {array} {ccc} 1 & 6 & -1 \\ 3 & -5 & 1 \\ 1 & 14 & -2 \ end {array} |, {D} _ {z} = | \ begin {array} {ccc} 1 & 1 & 6 \\ 3 & -2 & -5 \\ 1 & 3 & 14 \ end {array} | [/ latex]
Затем,
[латекс] \ begin {array} {l} x = \ frac {{D} _ {x}} {D} = \ frac {-3} {- 3} = 1 \ hfill \\ y = \ frac { {D} _ {y}} {D} = \ frac {-9} {- 3} = 3 \ hfill \\ z = \ frac {{D} _ {z}} {D} = \ frac {6} {-3} = — 2 \ hfill \ end {array} [/ latex]
Решение [латекс] \ left (1,3, -2 \ right) [/ latex].
Попробовать 3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
[латекс] \ begin {array} {r} \ hfill x — 3y + 7z = 13 \\ \ hfill x + y + z = 1 \\ \ hfill x — 2y + 3z = 4 \ end {array} [/ латекс]
Пример 5: Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
[латекс] \ begin {array} {l} 3x — 2y = 4 \ text {} \ left (1 \ right) \\ 6x — 4y = 0 \ text {} \ left (2 \ right) \ end {массив } [/ latex]
Решение
Начнем с нахождения определителей [латекс] D, {D} _ {x}, \ text {и} {D} _ {y} [/ latex].
[латекс] D = | \ begin {array} {cc} 3 & -2 \\ 6 & -4 \ end {array} | = 3 \ left (-4 \ right) -6 \ left (-2 \ right) = 0 [/ латекс]
Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс].
- Добавьте результат в уравнение [латекс] \ left (2 \ right) [/ latex].
[латекс] \ begin {array} \ text {} \ hfill − 6x + 4y = −8 \\ \ hfill6x − 4y = 0 \\ \ hfill \ text {_____________} \\ \ hfill 0 = 8 \ end { array} [/ latex]
Получаем уравнение [латекс] 0 = -8 [/ латекс], которое неверно.Следовательно, у системы нет решения. График системы показывает две параллельные линии.
Рисунок 5
Пример 6. Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
[латекс] \ begin {array} {rr} \ hfill x — 2y + 3z = 0 & \ hfill \ left (1 \ right) \\ \ hfill 3x + y — 2z = 0 & \ hfill \ left (2 \ right) \\ \ hfill 2x — 4y + 6z = 0 & \ hfill \ left (3 \ right) \ end {array} [/ latex]
Решение
Давайте сначала найдем определитель.Создайте матрицу, дополненную первыми двумя столбцами.
[латекс] | \ begin {array} {rrr} \ hfill 1 & \ hfill -2 & \ hfill 3 \\ \ hfill 3 & \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -4 & \ hfill 6 \ end { array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 3 & \ hfill 1 \\ \ hfill 2 & \ hfill -4 \ end {array} | [ / латекс]
Затем,
[латекс] 1 \ влево (1 \ вправо) \ влево (6 \ вправо) + \ влево (-2 \ вправо) \ влево (-2 \ вправо) \ влево (2 \ вправо) +3 \ влево (3 \ вправо) \ влево (-4 \ вправо) -2 \ влево (1 \ вправо) \ влево (3 \ вправо) — \ влево (-4 \ вправо) \ влево (-2 \ вправо) \ влево (1 \ вправо) -6 \ влево (3 \ вправо) \ влево (-2 \ вправо) = 0 [/ латекс]
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс] и добавьте результат к уравнению (3):
[латекс] \ frac {\ begin {array} {r} \ hfill -2x + 4y — 6x = 0 \\ \ hfill 2x — 4y + 6z = 0 \ end {array}} {0 = 0} [/ latex ]
- Получение ответа [latex] 0 = 0 [/ latex], утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений.
 Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.
Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.
Фиг.6
Определители (алгебра 2, матрицы) — Mathplanet
Определитель det (A) или | A | квадратной матрицы A — это число, кодирующее определенные свойства матрицы. Детерминанты названы по размеру матриц. В следующем примере мы покажем, как определить детерминанты второго порядка.
Пример
$$ A = \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} $$
Определитель A (определитель второго порядка) равен
$$ det (A) = \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} = ad-bc $$
Определители матриц 3 × 3 называются определителями третьего порядка.Один из методов оценки детерминант третьего порядка называется разложением по минорам. Младший элемент — это определитель, формируемый при удалении строки и столбца, содержащих этот элемент.
$$ \ begin {vmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {vmatrix} = a \ begin {vmatrix} e & f \\ h & i \ end { vmatrix} -b \ begin {vmatrix} d & f \\ g & i \ end {vmatrix} + c \ begin {vmatrix} d & e \\ g & h \ end {vmatrix} $$
Определители могут использоваться для определения площади треугольника, если известны координаты вершин.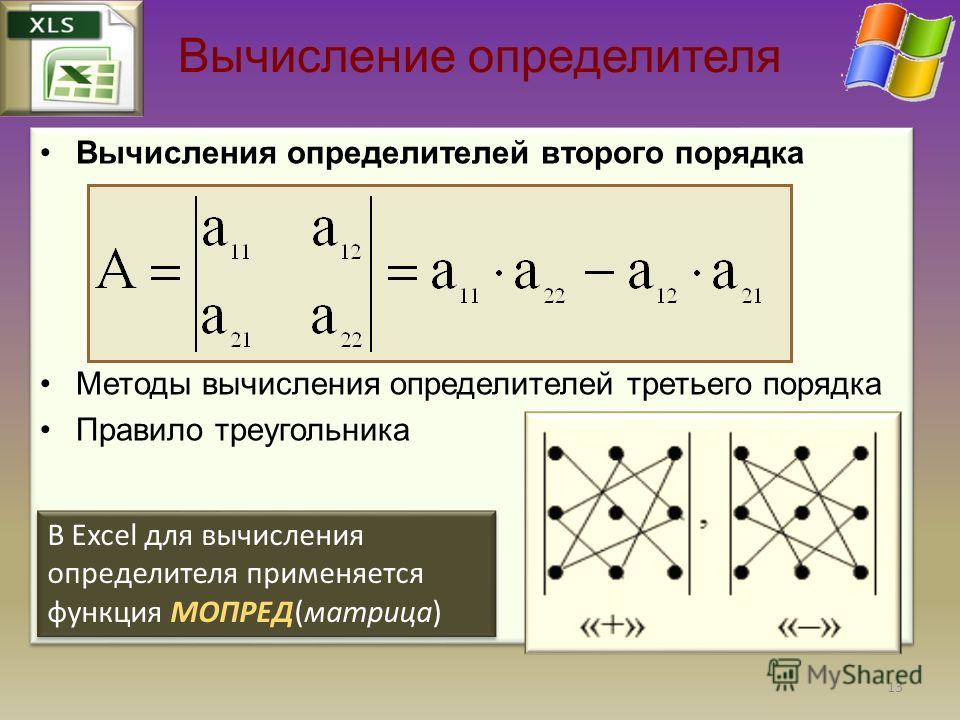 Если вершинами треугольников являются (a, b), (c, d) и (e, f), площадь равна
Если вершинами треугольников являются (a, b), (c, d) и (e, f), площадь равна
$$ A = \ frac {1} {2} \ begin {vmatrix} a & b & 1 \\ c & d & 1 \ e & f & 1 \ end {vmatrix} $$
Если A оказывается отрицательным, мы должны использовать абсолютное значение для A, чтобы иметь неотрицательное значение для нашей области.
Пример
Найдите площадь треугольника с вершинами, расположенными в точках (-2,2), (1,3) и (3,0) (этот пример также показан в нашем видео-уроке).
Подставляем координаты вершин в формулу площади
$$ A = \ frac {1} {2} \ begin {vmatrix} -2 & 2 & 1 \\ 1 & 3 & 1 \\ 3 & 0 & 1 \ end {vmatrix} $$
и продолжается с
$$ = \ frac {1} {2} (- 2 \ begin {vmatrix} 3 & 1 \\ 0 & 1 \ end {vmatrix} -2 \ begin {vmatrix} 1 & 1 \\ 3 & 1 \ end {vmatrix} +1 \ begin {vmatrix} 1 & 3 \\ 3 & 0 \ end {vmatrix}) = \\ \\ = \ frac {1} {2} (- 2 (3 \ cdot1-1 \ cdot 0 ) -2 (1 \ cdot 1-1 \ cdot 3) +1 (1 \ cdot 0-3 \ cdot 3)) = \\ \\ = \ frac {1} {2} (- 6 + 4-9) = \ frac {-11} {2} = — 5. 5 $$
5 $$
Мы получили отрицательное значение для A, и площадь не может быть отрицательной, поэтому мы должны взять абсолютное значение для A:
$$ \ mid A \ mid = \ mid -5.5 \ mid = 5.5 \; $$
Итак, площадь треугольников составляет 5,5 квадратных единиц.
Видеоурок
Найдите область из приведенного выше примера.
Детерминанты и правило Крамера
Линейные системы двух переменных и правило Крамера
Напомним, что матрица — это прямоугольный массив чисел, состоящий из строк и столбцов.Мы классифицируем матрицы по количеству строк n и количеству столбцов m . Например, матрица 3 × 4, читаемая как «матрица 3 на 4», состоит из 3 строк и 4 столбцов. Квадратная матрица Матрица с одинаковым количеством строк и столбцов. — матрица, в которой количество строк совпадает с количеством столбцов. В этом разделе мы обрисовываем еще один метод решения линейных систем с использованием специальных свойств квадратных матриц. Начнем с рассмотрения следующей матрицы коэффициентов 2 × 2 A ,
В этом разделе мы обрисовываем еще один метод решения линейных систем с использованием специальных свойств квадратных матриц. Начнем с рассмотрения следующей матрицы коэффициентов 2 × 2 A ,
A = [a1b1a2b2]
Определитель Действительное число, связанное с квадратной матрицей.матрицы 2 × 2, обозначенной вертикальными линиями | A |, или более компактно как det ( A ), определяется следующим образом:
Определитель — это действительное число, которое получается вычитанием произведений значений на диагонали.
Пример 1
Вычислить: | 3−52−2 |.
Решение:
Вертикальные линии по обе стороны от матрицы показывают, что нам нужно вычислить определитель.
| 3−52−2 | = 3 (−2) −2 (−5) = — 6 + 10 = 4
Ответ: 4
Пример 2
Вычислить: | −6403 |.
Решение:
Обратите внимание, что матрица представлена в виде верхнего треугольника.
| −6403 | = −6 (3) −4 (0) = — 18−0 = −18
Ответ: −18
Мы можем решать линейные системы с двумя переменными, используя определители.Начнем с общей линейной системы 2 × 2 и решим относительно y . Чтобы исключить переменную x , умножьте первое уравнение на −a2, а второе уравнение на a1.
{a1x + b1y = c1 a2x + b2y = c2 ⇒ × (−a2) ⇒ × a1 {−a1a2x − a2b1y = −a2c1a1a2x + a1b2y = a1c2
Это приводит к эквивалентной линейной системе, в которой переменная x выстроена в линию для исключения. Теперь складывая уравнения, мы получаем
И числитель, и знаменатель очень похожи на определитель матрицы 2 × 2.На самом деле это так. Знаменатель — это определитель матрицы коэффициентов. А числитель является определителем матрицы, образованной заменой столбца, представляющего коэффициенты y , на соответствующий столбец констант. Эта специальная матрица обозначается Dy.
Эта специальная матрица обозначается Dy.
y = DyD = | a1c1a2c2 | | a1b1a2b2 | = a1c2 − a2c1a1b2 − a2b1
Аналогичным образом может быть получено значение x .
x = DxD = | c1b1c2b2 | | a1b1a2b2 | = c1b2 − c2b1a1b2 − a2b1
В целом, мы можем сформировать расширенную матрицу следующим образом:
{a1x + b1y = c1a2x + b2y = c2 ⇔ [a1b1 | c1a2b2 | c2]
, а затем определите D, Dx и Dy, вычислив следующие детерминанты.
D = | a1b1a2b2 | Dx = | c1b1c2b2 | Dy = | a1c1a2c2 |
Решение системы в терминах определителей, описанных выше, когда D ≠ 0, называется правилом Крамера Решение независимой системы линейных уравнений, выраженное в терминах определителей ..
Правило Крамера (x, y) = (DxD, DyD)
Эта теорема названа в честь Габриэля Крамера (1704 — 1752).
Рисунок 3.2
Габриэль Крамер
Шаги решения линейной системы с двумя переменными с использованием определителей (правило Крамера) описаны в следующем примере.
Пример 3
Решите, используя правило Крамера: {2x + y = 7 3x − 2y = −7.
Решение:
Перед началом этого процесса убедитесь, что линейная система имеет стандартную форму.
Шаг 1 : Постройте расширенную матрицу и сформируйте матрицы, используемые в правиле Крамера.
{2x + y = 7 3x − 2y = −7 ⇒ [21 | 73−2 | −7]
В квадратной матрице, используемой для определения Dx, замените первый столбец матрицы коэффициентов константами.В квадратной матрице, используемой для определения Dy, замените второй столбец константами.
D = | 213−2 | Dx = | 71−7−2 | Dy = | 273−7 |
Шаг 2 : Рассчитайте детерминанты.
Dx = | 71−7−2 | = 7 (−2) — (- 7) (1) = — 14 + 7 = −7Dy = | 273−7 | = 2 (−7) −3 (7) = −14−21 = −35D = | 213−2 | = 2 (−2) −3 (1) = — 4−3 = −7
Шаг 3 : Используйте правило Крамера для вычисления x и y .
x = DxD = -7-7 = 1 и y = DyD = -35-7 = 5
Следовательно, одновременное решение (x, y) = (1,5).
Шаг 4 : Проверка необязательна; однако мы делаем это здесь для полноты картины.
Чек: (1,5) | |
|---|---|
Уравнение 1 | Уравнение 2 |
2x + y = 72 (1) + (5) = 72 + 5 = 77 = 7 ✓ | 3x − 2y = −73 (1) −2 (5) = — 73−10 = −7−7 = −7 ✓ |
Ответ: (1, 5)
Пример 4
Решите, используя правило Крамера: {3x − y = −26x + 4y = 2.
Решение:
Соответствующая расширенная матрица коэффициентов следует.
{3x − y = −26x + 4y = 2 ⇒ [3−1 | −264 | 2]
А у нас,
Dx = | −2−124 | = −8 — (- 2) = — 8 + 2 = −6Dy = | 3−262 | = 6 — (- 12) = 6 + 12 = 18D = | 3−164 | = 12 — (- 6) = 12 + 6 = 18
Используйте правило Крамера, чтобы найти решение.
x = DxD = -618 = -13 и y = DyD = 1818 = 1
Ответ: (−13,1)
Попробуй! Решите, используя правило Крамера: {5x − 3y = −7−7x + 6y = 11.
Ответ: (−1, 23)
Когда определитель матрицы коэффициентов D равен нулю, формулы правила Крамера не определены. В этом случае система либо зависима, либо несовместима в зависимости от значений Dx и Dy. Когда D = 0 и оба Dx = 0 и Dy = 0, система является зависимой. Когда D = 0 и либо Dx, либо Dy отличны от нуля, система несовместима.
Когда D = 0 и либо Dx, либо Dy отличны от нуля, система несовместима.
Когда D = 0, Dx = 0 и Dy = 0 ⇒ Зависимая система Dx ≠ 0 или Dy ≠ 0 ⇒ Несогласованная система
Пример 5
Решите, используя правило Крамера: {x + 15y = 3 5x + y = 15.
Решение:
Соответствующая расширенная матрица следует.
{x + 15y = 3 5x + y = 15 ⇒ [115 | 351 | 15]
А имеем следующее.
Dx = | 315151 | = 3−3 = 0Dy = | 13515 | = 15−15 = 0D = | 11551 | = 1−1 = 0
Если мы попытаемся использовать правило Крамера, мы получим
x = DxD = 00 и y = DyD = 00
, оба из которых являются неопределенными количествами.Поскольку D = 0 и как Dx = 0, так и Dy = 0, мы знаем, что это зависимая система. Фактически, мы можем увидеть, что оба уравнения представляют одну и ту же линию, если мы решим относительно y .
{x + 15y = 3 5x + y = 15 ⇒ {y = −5x + 15 y = −5x + 15
Следовательно, мы можем представить все решения (x, −5x + 15), где x — действительное число.
Ответ: (x, −5x + 15)
Попробуй! Решите, используя правило Крамера: {3x − 2y = 10 6x − 4y = 12.
Ответ: Ø
Линейные системы трех переменных и правило Крамера
Рассмотрим следующую матрицу коэффициентов 3 × 3 A ,
A = [a1b1c1a2b2c2a3b3c3]
Определитель этой матрицы определяется следующим образом:
det (A) = | a1b1c1a2b2c2a3b3c3 | = a1 | b2c2b3c3 | −b1 | a2c2a3c3 | + c1 | a2b2a3b3 | = a1 (b2c3 − b3c2) −b1 (a2c3 − 9 −3 ab2) +
Здесь каждый определитель 2 × 2 называется второстепенным определителем матрицы, которая получается после удаления строки и столбца квадратной матрицы. предыдущего фактора. Обратите внимание, что факторы — это элементы в первой строке матрицы, и что они меняют знак (+ — +).
предыдущего фактора. Обратите внимание, что факторы — это элементы в первой строке матрицы, и что они меняют знак (+ — +).
Пример 6
Рассчитать: | 1322−1305−1 |.
Решение:
Чтобы легко определить второстепенное значение каждого фактора в первой строке, мы выстраиваем первую строку и соответствующий столбец. Определитель матрицы оставшихся элементов определяет соответствующий минор.
Позаботьтесь о том, чтобы поменять знак множителей в первой строке. Далее следует разложение несовершеннолетними о первом ряду:
| 1322−1305−1 | = 1 | −135−1 | −3 | 230−1 | +2 | 2−105 | = 1 (1−15) −3 (−2−0) +2 (10−0) = 1 (−14) −3 (−2) +2 (10) = — 14 + 6 + 20 = 12
Ответ: 12
Расширение по несовершеннолетним может производиться по любой строке или любому столбцу. Знак коэффициентов, определяемый выбранной строкой или столбцом, будет чередоваться в соответствии со следующим массивом знаков.
[+ — + — + — + — +]
Поэтому, чтобы расширить второй ряд, мы будем чередовать знаки, начиная с противоположного первого элемента. Мы можем расширить предыдущий пример о второй строке, чтобы показать, что получен такой же ответ для определителя.
А можно написать,
| 1322−1305−1 | = — (2) | 325−1 | + (- 1) | 120−1 | — (3) | 1305 | = −2 (−3−10) −1 (−1−0) −3 (5−0) = — 2 (−13) −1 (−1) −3 (5) = 26 + 1−15 = 12
Обратите внимание, что мы получаем тот же ответ 12.
Пример 7
Рассчитать: | 4306122410 |.
Решение:
Расчеты упрощаются, если мы расширим третий столбец, потому что он содержит два нуля.
Далее следует расширение несовершеннолетними по поводу третьего столбца:
| 4306122410 | = 0 | 61241 | −2 | 4341 | +0 | 43612 | = 0−2 (4−12) + 0 = −2 (−8) = 16
Ответ: 16
Следует отметить, что существуют и другие методы, используемые для запоминания того, как вычислить определитель матрицы 3 × 3.Кроме того, многие современные калькуляторы и системы компьютерной алгебры могут найти определитель матриц. Предлагаем вам изучить эту обширную тему.
Мы можем решить линейные системы с тремя переменными, используя определители. Для этого мы начнем с расширенной матрицы коэффициентов,
{a1x + b1y + c1z = d1a2x + b2y + c2z = d2a3x + b3y + c3z = d3 ⇔ [a1b1c1 | d1a2b2c2 | d2a3b3c3 | d3]
Пусть D представляет определитель матрицы коэффициентов,
D = | a1b1c1a2b2c2a3b3c3 |
Затем определите Dx, Dy и Dz, вычислив следующие определители.
Dx = | d1b1c1d2b2c2d3b3c3 | Dy = | a1d1c1a2d2c2a3d3c3 | Dz = | a1b1d1a2b2d2a3b3d3 |
Когда D ≠ 0, решение системы в терминах детерминантов, описанных выше, может быть вычислено с использованием правила Крамера:
Правило Крамера (x, y, z) = (DxD, DyD, DzD)
Используйте это для эффективного решения систем с тремя переменными.
Пример 8
Решите, используя правило Крамера: {3x + 7y − 4z = 02x + 5y − 3z = 1−5x + 2y + 4z = 8.
Решение:
Начните с определения соответствующей расширенной матрицы.
{3x + 7y − 4z = 02x + 5y − 3z = 1−5x + 2y + 4z = 8 ⇔ [37−4 | 025−3 | 1−524 | 8]
Затем вычислите определитель матрицы коэффициентов.
D = | 37−425−3−524 | = 3 | 5−324 | −7 | 2−3−54 | + (- 4) | 25−52 | = 3 (20 — (- 6)) — 7 (8−15) −4 (4 — (- 25)) = 3 (26) −7 (−7) −4 (29) = 78 + 49−116 = 11
Аналогичным образом мы можем вычислить Dx, Dy и Dz.Это оставлено как упражнение.
Dx = | 07−415−3824 | = −44Dy = | 30−421−3−584 | = 0Dz = | 370251−528 | = −33
Используя правило Крамера, мы имеем,
x = DxD = −4411 = −4 y = DyD = 011 = 0 z = DzD = −3311 = −3
Ответ: (−4,0, −3)
Если определитель матрицы коэффициентов D = 0, то система либо зависимая, либо противоречивая. Это будет зависеть от Dx, Dy и Dz. Если все они равны нулю, то система зависима.Если хотя бы один из них отличен от нуля, то он несовместим.
Когда D = 0, Dx = 0 и Dy = 0 и Dz = 0 ⇒ Зависимая система Dx ≠ 0 или Dy ≠ 0 или Dz ≠ 0 ⇒ Несогласованная система
Пример 9
Решите, используя правило Крамера: {4x − y + 3z = 521x − 4y + 18z = 7−9x + y − 9z = −8.
Решение:
Начните с определения соответствующей расширенной матрицы.
{4x − y + 3z = 521x − 4y + 18z = 7−9x + y − 9z = −8 ⇔ [4−13 | 521−418 | 7−91−9 | −8]
Затем определите определитель матрицы коэффициентов.
D = | 4−1321−418−91−9 | = 4 | −4181−9 | — (- 1) | 2118−9−9 | +3 | 21−4−91 | = 4 (36−18) +1 (−189 — (- 162)) + 3 (21−36) = 4 (18) +1 (−27) +3 (−15) = 72−27−45 = 0
Поскольку D = 0, система является либо зависимой, либо несовместимой.
Dx = | 5−137−418−81−9 | = 96
Однако, поскольку Dx отличен от нуля, мы заключаем, что система несовместима. Одновременного решения нет.
Ответ: Ø
Попробуй! Решите, используя правило Крамера: {2x + 6y + 7z = 4−3x − 4y + 5z = 125x + 10y − 3z = −13.
Ответ: (−3,12,1)
Основные выводы
- Определитель матрицы — действительное число.
- Определитель матрицы 2 × 2 получается вычитанием произведения значений на диагоналях.
- Определитель матрицы 3 × 3 получается путем расширения матрицы с использованием миноров в любой строке или столбце. При этом позаботьтесь об использовании массива знаков для определения знака коэффициентов.
- Используйте правило Крамера для эффективного определения решений линейных систем.
- Когда определитель матрицы коэффициентов равен 0, правило Крамера не применяется; система будет либо зависимой, либо непоследовательной.
Тематические упражнения
| 1234 |
| 5324 |
| −13−3−2 |
| 743−2 |
| −41−30 |
| 95−10 |
| 1050 |
| 0350 |
| 04−13 |
| 102102 |
| a1b10b2 |
| 0b1a2b2 |
{3x − 5y = 82x − 7y = 9
{2x + 3y = −13x + 4y = −2
{2x − y = −34x + 3y = 4
{x + 3y = 15x − 6y = −9
{х + у = 16х + 3у = 2
{x − y = −15x + 10y = 4
{5x − 7y = 144x − 3y = 6
{9x + 5y = −97x + 2y = −7
{6x − 9y = 3−2x + 3y = 1
{3x − 9y = 32x − 6y = 2
{4x − 5y = 203y = −9
{x − y = 02x − 3y = 0
{2x + y = ax + y = Ь
{ax + y = 0by = 1
Часть A: Линейные системы с двумя переменными
Вычислить определитель.
Решите, используя правило Крамера.
| 123213132 |
| 251124323 |
| −31−13−1−2−251 |
| 1−15−45−1−12−3 |
| 3−1223−1521 |
| 40−33−100−52 |
| 0−34−30602−3 |
| 6−1−325284−1 |
| 257035004 |
| 210004 |
| a1b1c10b2c200c3 |
| a100a2b20a3b3c3 |
{x − y + 2z = −33x + 2y − z = 13−4x − 3y + z = −18
{3x + 4y − z = 104x + 6y + 7z = 92x + 3y + 5z = 3
{5x + y − z = 02x − 2y + z = −9−6x − 5y + 3z = −13
{−4x + 5y + 2z = 123x − y − z = −25x + 3y − 2z = 5
{x − y + z = −1−2x + 4y − 3z = 43x − 3y − 2z = 2
{2x + y − 4z = 72x − 3y + 2z = −44x − 5y + 2z = −5
{4x + 3y − 2z = 22x + 5y + 8z = −1x − y − 5z = 3
{x − y + z = 7x + 2y + z = 1x − 2y − 2z = 9
{3x − 6y + 2z = 12−5x − 2y + 3z = 47x + 3y − 4z = −6
{2x − y − 5z = 23x + 2y − 4z = −35x + y − 9z = 4
{4x + 3y − 4z = −132x + 6y − 5z = −2−2x − 3y + 3z = 5
{x − 2y + z = −14y − 3z = 03y − 2z = 1
{2x + 3y − z = −5x + 2y = 03x + 10y = 4
{2x − 3y − 2y = 9−3x + 4y + 4z = −13x − y − 2z = 4
{2x + y − 2z = −1x − y + 3z = 23x + y − z = 1
{3x − 8y + 9z = −2 − x + 5y − 10z = 3x − 3y + 4z = −1
{5x − 6y + 3z = 23x − 4y + 2z = 02x − 2y + z = 0
{5x + 10y − 4z = 122x + 5y + 4z = 0x + 5y − 8z = 6
{5x + 6y + 7z = 22y + 3z = 34z = 4
{x + 2z = −1−5y + 3z = 104x − 3y = 2
{x + y + z = ax + 2y + 2z = a + bx + 2y + 3z = a + b + c
{x + y + z = a + b + cx + 2y + 2z = a + 2b + 2cx + y + 2z = a + b + 2c
Часть B: Линейные системы с тремя переменными
Вычислить определитель.
Решите, используя правило Крамера.
Изучите и обсудите историю детерминанта.Кто первым ввел обозначение определителя?
Изучите другие способы вычисления определителя матрицы 3 × 3. Привести пример.
Часть C: Обсуждение
Ответы
(-12,2)
(-13,43)
(54, −3)
(12,12, −1)
(12z − 4,23z + 1, z)
(-12,5,52)


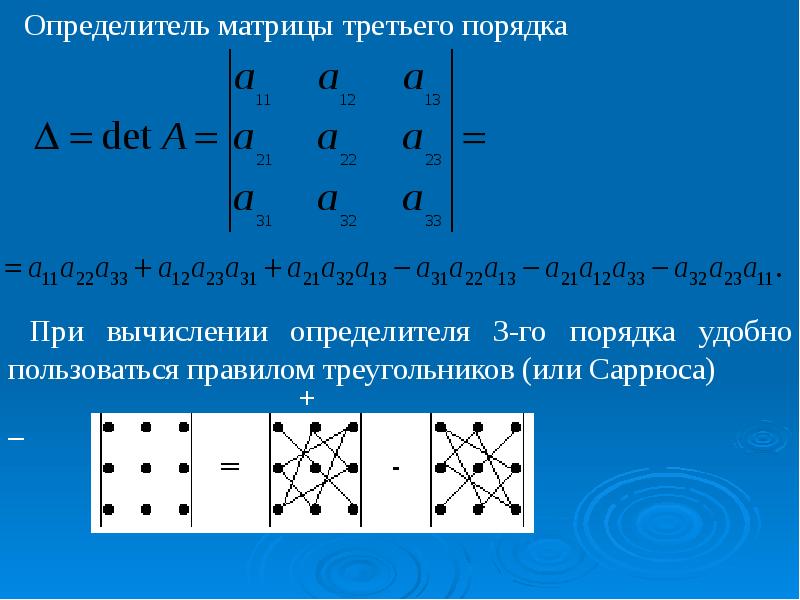


 .n]
where n=length matrix - 1
row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
| otherwise = matrix !! k
.n]
where n=length matrix - 1
row k | k==n1 = comb (matrix !! n1) (matrix !! n2) f
| otherwise = matrix !! k
 0e-10 = matrix
| nz < 0 = matrix -- матрица вырождена
| otherwise = swap matrix k p
where n = length matrix
lst = map (\ r -> r !! k) $ drop k matrix
nz = getNz lst
p = k + nz
0e-10 = matrix
| nz < 0 = matrix -- матрица вырождена
| otherwise = swap matrix k p
where n = length matrix
lst = map (\ r -> r !! k) $ drop k matrix
nz = getNz lst
p = k + nz
 0e-10 = [[0.0]] -- матрица вырождена
| otherwise = triangle (mkzero tmp k k1) k1
where n = length matrix
tmp = search matrix k
v = (tmp !! k) !! k -- диагональный элемент
k1 = k+1
0e-10 = [[0.0]] -- матрица вырождена
| otherwise = triangle (mkzero tmp k k1) k1
where n = length matrix
tmp = search matrix k
v = (tmp !! k) !! k -- диагональный элемент
k1 = k+1
 hs, main.o )
Linking a.out ...
54.0
hs, main.o )
Linking a.out ...
54.0
 Я ученик Python, ищущий элегантное решение, а не пытающийся решить проблему кодирования на работе. Интересно посмотреть код для решения классической проблемы…
Я ученик Python, ищущий элегантное решение, а не пытающийся решить проблему кодирования на работе. Интересно посмотреть код для решения классической проблемы… Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения.
Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения.

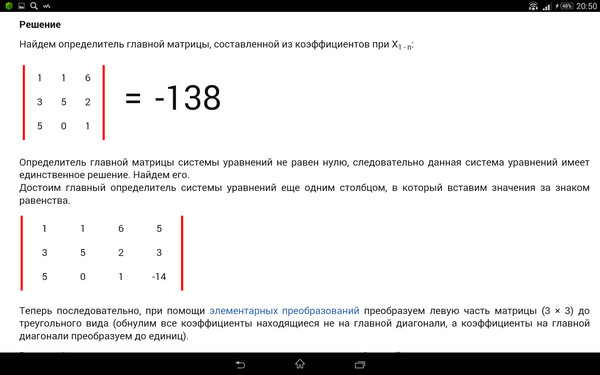 ..и вдоль
диагонали вверх
..и вдоль
диагонали вверх А пока обратите внимание, что ваши графики
калькулятор должен уметь вычислять определитель любого (квадрата)
матрица, которую вы вводите. Например:
А пока обратите внимание, что ваши графики
калькулятор должен уметь вычислять определитель любого (квадрата)
матрица, которую вы вводите. Например: com/modules/determs2.htm .
Дата обращения [Дата] [Месяц] 2016 г.
com/modules/determs2.htm .
Дата обращения [Дата] [Месяц] 2016 г. 
 Фактически, если элемент равен нулю, вы не
нужно даже найти несовершеннолетнего
или кофактор.
Фактически, если элемент равен нулю, вы не
нужно даже найти несовершеннолетнего
или кофактор.
 Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали. Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.
Изобразив систему, мы можем увидеть, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.