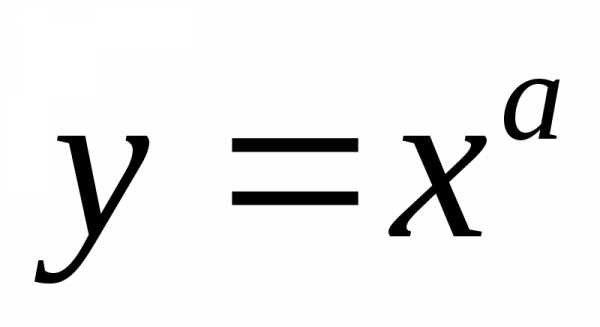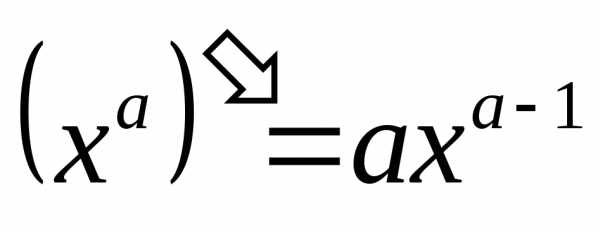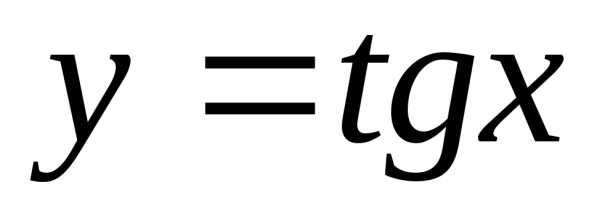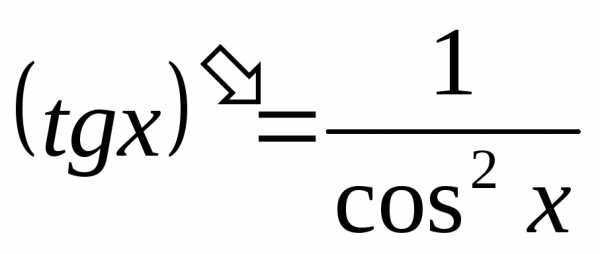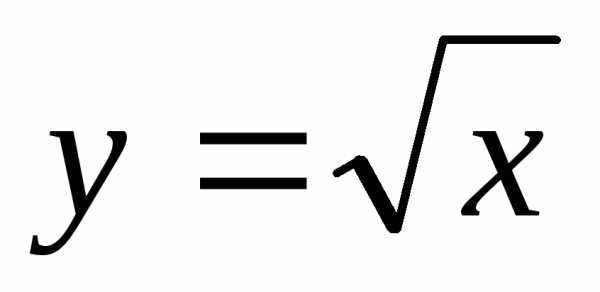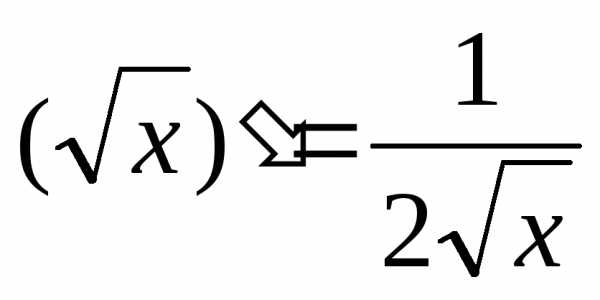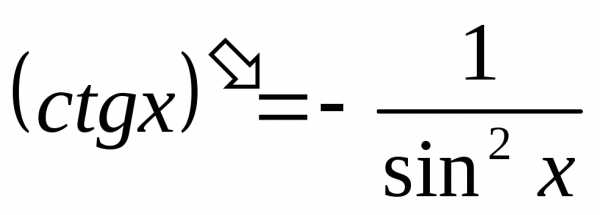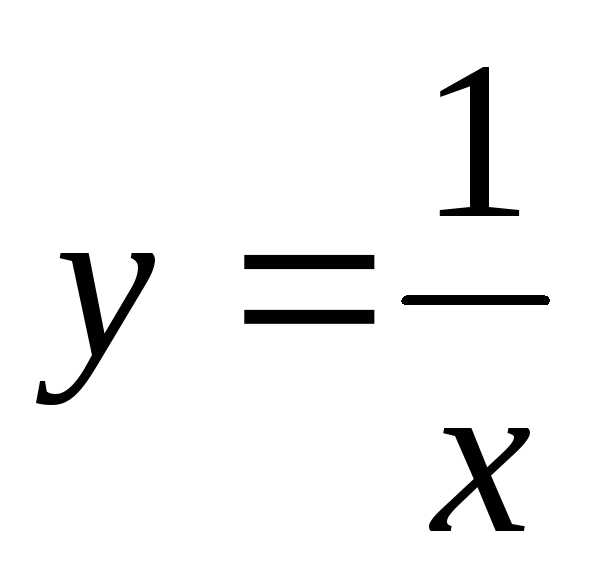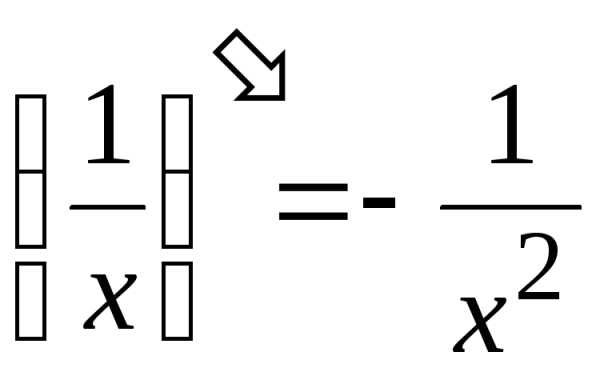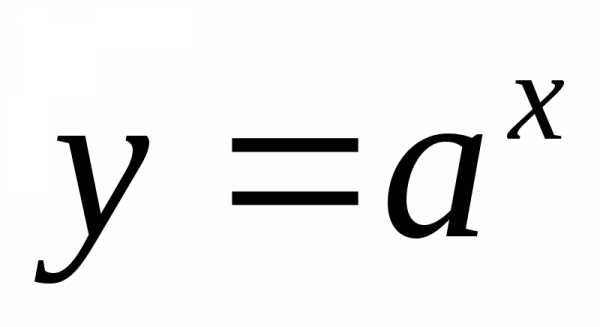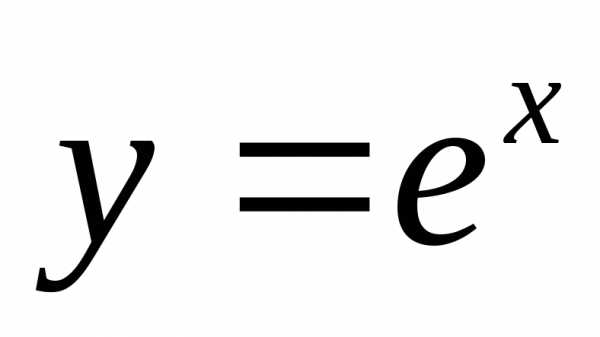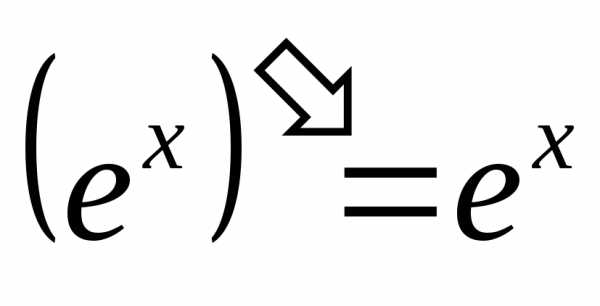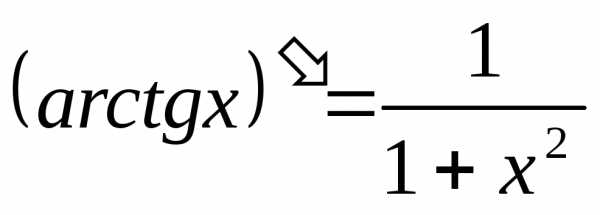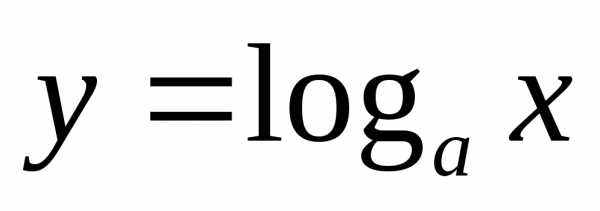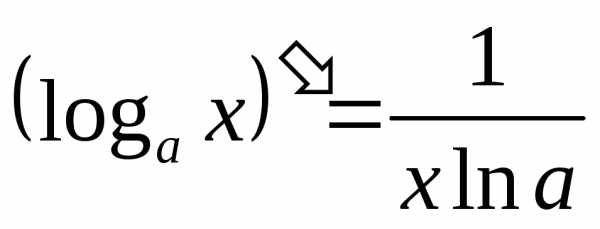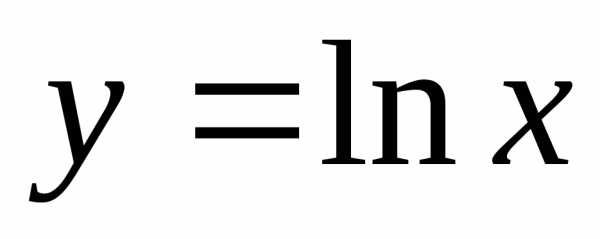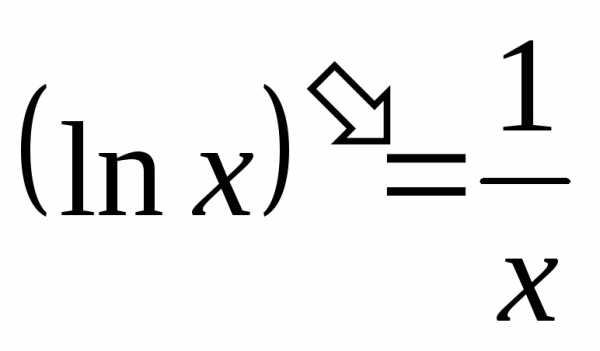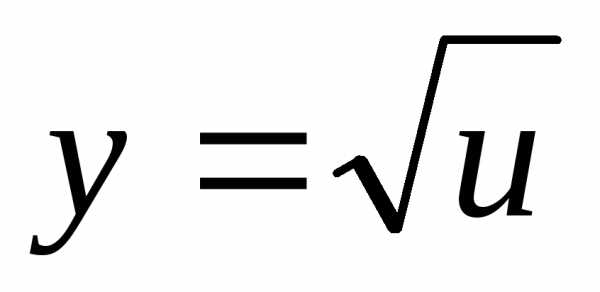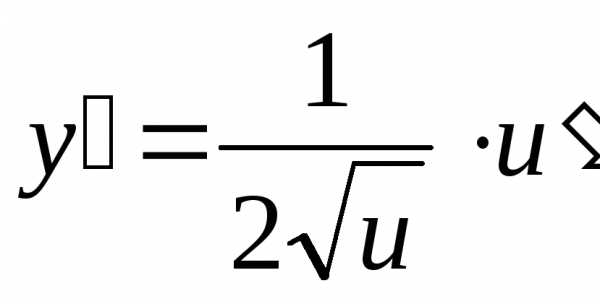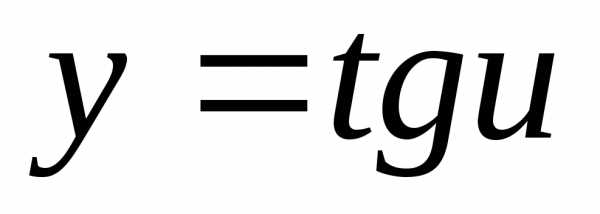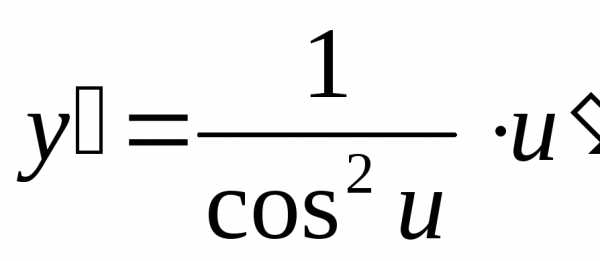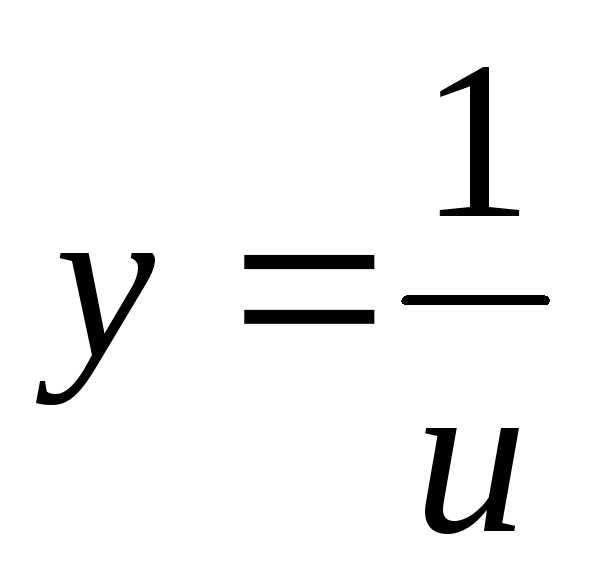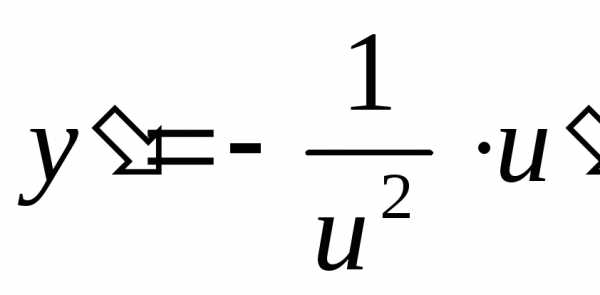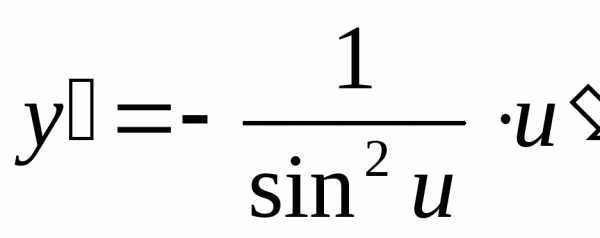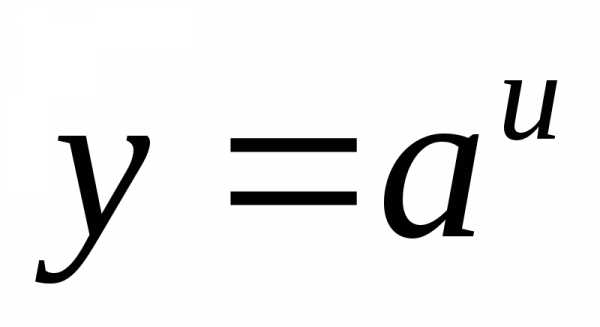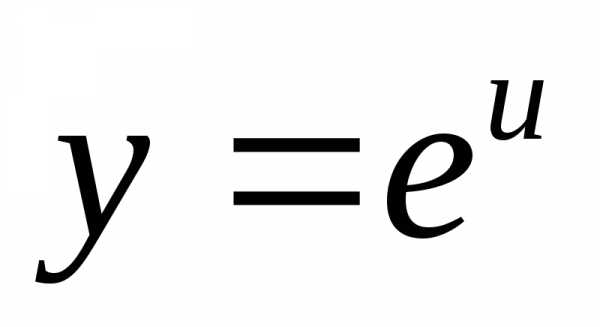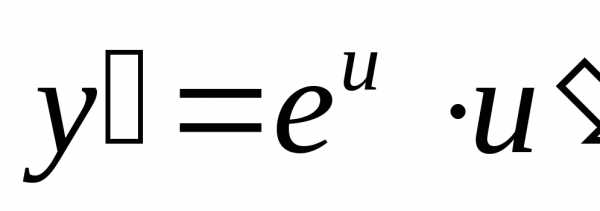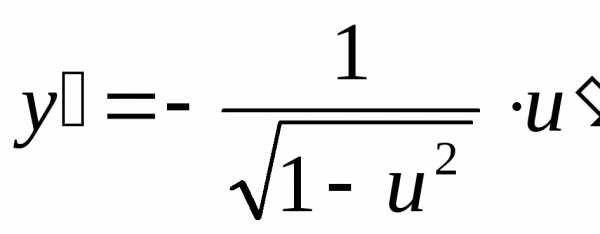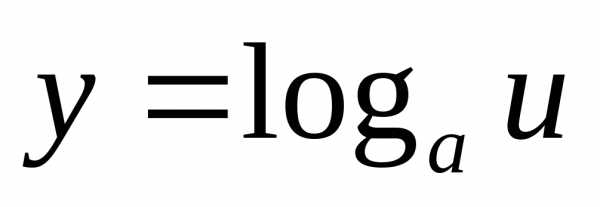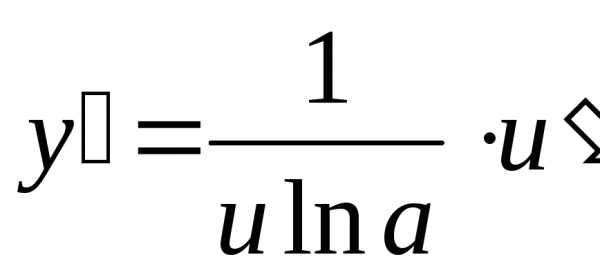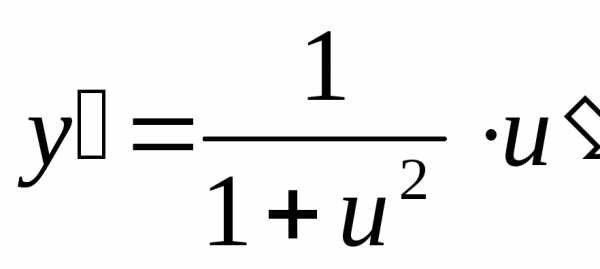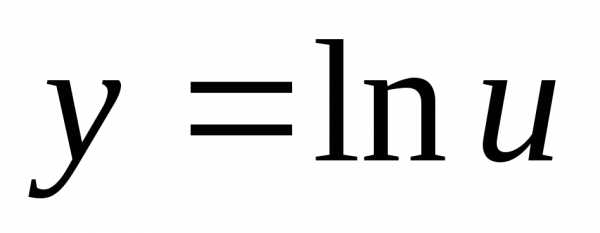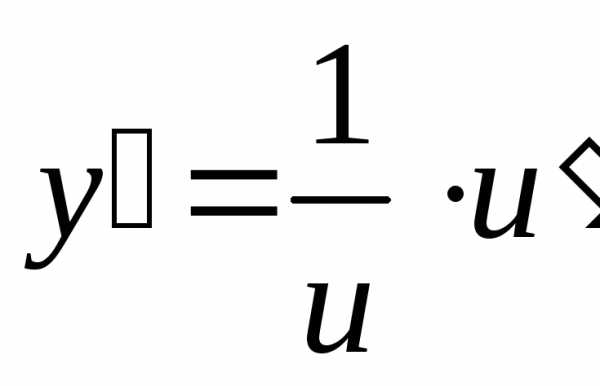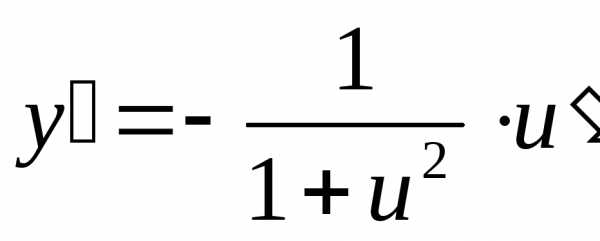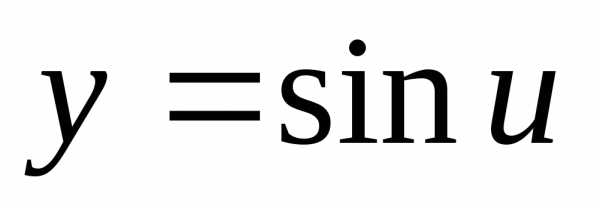Дифференциальные и производные 2019
Чтобы лучше понять разницу между дифференциалом и производной функции, вам нужно сначала понять концепцию функции.
Функция является одной из основных концепций математики, которая определяет взаимосвязь между набором входов и множеством возможных выходов, где каждый вход связан с одним выходом. Одной переменной является независимая переменная, а другая переменная — зависимая переменная.
Концепция функции является одной из самых недооцененных тем в математике, но имеет важное значение для определения физических отношений. Возьмем, к примеру: утверждение «y является функцией x» означает, что что-то, связанное с y, напрямую связано с x по какой-либо формуле. Скажем, если входной сигнал равен 6, а функция — добавить 5 к входу 6. Результат будет 6 + 5 = 11, что является вашим выходом.
В математике есть несколько исключений, или вы можете сказать о проблемах, которые не могут быть решены обычными методами геометрии и алгебры. Для решения этих проблем используется новая ветвь математики, известная как исчисление.
Исчисление принципиально отличается от математики, которая не только использует идеи из геометрии, арифметики и алгебры, но также имеет дело с изменением и движением.
Исчисление как инструмент определяет производную функции как предел определенного вида. Понятие производной функции отличает исчисление от других отраслей математики. Дифференциал — это подполе исчисления, которое относится к бесконечно малой разности в некоторой переменной величине и является одним из двух фундаментальных делений исчисления. Другая ветвь называется интегральным исчислением.
Что такое Дифференциал?
Дифференциал — одно из фундаментальных делений исчисления, а также интегральное исчисление. Это подполе исчисления, которое имеет дело с бесконечно малым изменением в некоторой переменной величине. Мир, в котором мы живем, наполнен взаимосвязанными количествами, которые меняются периодически.
Например, площадь кругового тела, которая изменяется при изменении радиуса или снаряд, который изменяется со скоростью. Эти изменяющиеся сущности в математических терминах называются переменными, а скорость изменения одной переменной по отношению к другой является производной. И уравнение, представляющее связь между этими переменными, называется дифференциальным уравнением.
Дифференциальные уравнения — это уравнения, содержащие неизвест
ru.esdifferent.com
Производная и дифференциал
Дифференциальное исчисление – это раздел математики, который исследует свойства функций, которые заданы на интервалах (сплошных множествах), с помощью определения предела функций.
Свойство непрерывности свидетельствует о том, что точке х 0 при малом отклонении аргумента Δx от х0 функция отклоняется мало. В связи с этим, непрерывную функцию в окрестности точки х0, приближенно можно заменить константой, значением в х0. В таком случае, при Δx?0 к нулю стремится абсолютная ошибка приближения. Однако данная аппроксимация не отражает изменения функции при переходе переменной х в точке 0 – убывая или возрастая, медленно или быстро. Для того, чтобы это выяснить и введены производная и дифференциал, которые и дают более точную аппроксимацию функции в окрестности х0 линейной функцией, а не константой. Производная и дифференциал отражает величину и тенденцию изменения в точке х0 функции.
Производная и дифференциал на наглядном примере выглядит так. Возьмем функцию y = f ( x), которая имеет действительные значения и задана на оси R. Внутреннюю точку x0 ε I фиксируем и берем еще любую точку xεI . Приращением независимой переменной в точке х
Функция, для которой возможно разложение, называется дифференцируемой в точке х0. Дифференциалом функции f в точке х0 называется слагаемое f’ (х0)(х-х0). Таким образом, наличие в точке производной эквивалентно и дифференцируемости в этой же точке.
Дифференциал также имеет и специальное обозначение:
df(x0)=dy(x0)= f’ (х0)(х-х0)
Создано дифференциальное исчисление одновременно, а также независимо друг от друга Готфиридом Вильгельмом Лейбницем и Исааком Ньютоном.
Производная и дифференциал | |||||||||||||
| Приращение функции y = f(x), соответствующее приращению Δx аргумента x | |||||||||||||
| Δy = f(x + Δx) — f(x) | |||||||||||||
Определение производной | |||||||||||||
| |||||||||||||
| Геометрически y’ = f'(x) — угловой коэффициент касательной к графику функции y = f(x) в точке с абсциссой x | |||||||||||||
Правила дифференцирования | |||||||||||||
| c’ = 0 (cu)’ = cu’ (u + v)’ = u’ + v’ (u — v)’ = u’ — v’ (uv)’ = u’v + uv’ | |||||||||||||
| где y = f(z) и z = φ(x), т.е y = f(φ(x)). | |||||||||||||
| |||||||||||||
Производные элементарных функций | |||||||||||||
| |||||||||||||
| |||||||||||||
| (sinx)’ = cosx | |||||||||||||
| (cosx)’ = — sinx | |||||||||||||
| |||||||||||||
| |||||||||||||
| (secx)’ = secx * tgx | |||||||||||||
| (cosecx)’ = -cosecx * ctgx | |||||||||||||
| |||||||||||||
| |||||||||||||
Свойства дифференциала | |||||||||||||
| d(af(x)) = a * df(x) | |||||||||||||
| |||||||||||||
| da = 0 (a = const) | |||||||||||||
| d(ax + b) = Δ(ax + b) = a Δx | |||||||||||||
Дифференциал второго порядка функции y = f(x), | |||||||||||||
| |||||||||||||
Производные высших порядков некоторых функций | |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
| если правый предел существует | |||||||||||||
Формула Тэйлора с остаточным членом в форме Лагранжа | |||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||
Формула Маклорена | |||||||||||||
| |||||||||||||
| где ξ — такое число, что 0 |
mateshka.ru
Лекция 13. Производная и дифференциал
Производная и дифференциал. Лекция 13.
Производная и дифференциал.
Производная функции и ее геометрический смысл.
Пусть функция определена на некотором интервале и.
Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.
называют приращением функции и обозначают .
Пример 43. Найти производную функции .
Решение. По определению производной
.
Геометрический смысл производной.
Пусть задана функция , непрерывная в некоторой окрестности точки(рис. 58). Построим на осях координат точкии. Тогда длина,,. Приточкастремится к точкеи в пределе совпадает с ней. Уголстремится к углу наклона касательнойи в пределе совпадает с ним. Секущаяпревращается в касательную к графику функциив точке. Таким образом,
Производная функции в точкеесть тангенс угла наклона к осикасательной к графику функции в этой точке. Это является геометрическим смыслом производной.
Так как общее уравнение касательной в точке имеет вид,,, то окончательно уравнение касательной (рис. 59) можно записать в виде
Пример 44. Написать уравнение касательной к графику функции в точке
Решение. Так как , то вычислим значения ,,. Окончательно получим или .
Связь между непрерывностью и дифференцируемостью функций.
Теорема 19. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Доказательство. Пусть функция дифференцируема в некоторой точке. Тогда существует предел
По теореме 8 о связи предела и бесконечно малой, имеем
где при. Отсюда Тогда
Это означает, что
Теорема доказана.
Обратная теорема неверна. Непрерывная функция может не иметь производной, что показывает следующий пример.
Пример 45. Пусть . Тогда в точкефункция непрерывна, но не имеет производной. Действительно
Пределы справа и слева не совпадают, следовательно, производной в точке не существует.
Основные формулы и правила дифференцирования функций.
Пусть функции идифференцируемы в некотором интервале.
Теорема 20. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций, т. е.
Доказательство.
Теорема 21. Числовой множитель (константу) можно выносить за знак производной, т. е.
Доказательство.
Теорема 22. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т. е.
Доказательство.
Теорема 23. Производная частного двух функций , если, равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя, т. е
Доказательство.
Теорема 24. Производная константы равна нулю, т. е. .
Доказательство. Пусть , тогда
Таблица основных производных.
Степенные функции.
Показательные функции.
1) ; 2).
Логарифмические функции.
Тригонометрические функции.
Дифференциал и его геометрический смысл.
Основные понятия.
Пусть функция имеет в точкеотличную от нуля производную
Тогда по теореме 8 о связи функции, ее предела и бесконечно малой, ее можно представить в виде суммы
где , при, отсюдаТаким образом,является суммой двух бесконечно малыхи. Величинуназываютглавной частью приращения функции .
Дифференциалом функции в точкеназывается главная часть ее приращения в этой точке. Обозначаетсяили,. Так как для функциисправедливы равенства
то иОтсюда следует выражение производной через дифференциалы
Пример 46. Найти дифференциалы функций и.
Решение. Для первой функции , для второй
Геометрический смысл дифференциала.
Пусть дана некоторая дифференцируемая в точке функция(рис. 60). По построениюТогда из прямоугольного треугольникаследует
Отсюда
Таким образом, дифференциал функции в точке равен приращению ординаты касательной к графику функции в этой точке при приращении аргумента. В этом заключается геометрический смысл дифференциала.
Применение дифференциала к приближенным вычислениям.
Пусть дана функция . Тогда, где, при. Отсюда, и. В итоге получаем формулу приближенного вычисления функции
Пример 47. Вычислить приближенное значение .
Решение. Рассмотрим функцию . ПустьТак как
то
Производная сложной функции.
Пусть некоторая функция, гдетак же функция, тогда выражениеявляется функцией, которая называетсясложной функцией от переменной . Переменная в этом случае называется промежуточной.
Теорема 25. Если функция имеет производнуюв точке, а функцияимеет производнуюв точке, то сложная функцияимеет производнуюв точке, которая находится по формуле.
Доказательство. Пусть
Отсюда по теореме 8 о связи функции, ее предела и бесконечно малой, имеем , или, гдепри. Функцияимеет производную в точке
поэтому или, гдепри. Отсюда
. Разделим обе части на
где и, при. По теореме 9 (обратной к теореме 8) о связи функции, ее предела и бесконечно малой, имеем
Рассмотрим примеры на применение теоремы 25.
Пример 48. Найти производную функции .
Решение. В нашем случае , . По теореме 25 имеем
.
Пример 49. Найти производную функции
Решение. В нашем случае , . По теореме 25 имеем
Пример 50. Найти производную функции .
Решение. В нашем случае , , . По теореме 25 имеем
Производная обратной функции.
Теорема 26. Если функция строго монотонна на интервалеи имеет неравную нулю производнуюв произвольной точке этого интервала, то обратная ей функциятак же имеет производнуюв соответствующей точке и
Доказательство. Пусть для функции и ее обратнойвыполнены все условия теоремы. Дадим аргументуобратной функции приращение. В силу монотонности исходной функции, соответствующее приращение будет так же не равно нулю, т. е.. Тогда справедливо равенство
Если , то в силу непрерывности обратной функции, так жеи так как
то имеем
Пример 51. Рассмотрим функцию . Ее обратная. Тогда по теореме 26
78
studfiles.net
Производная и дифференциал
Определение. Пусть функция 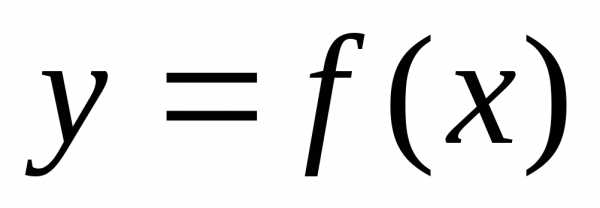 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки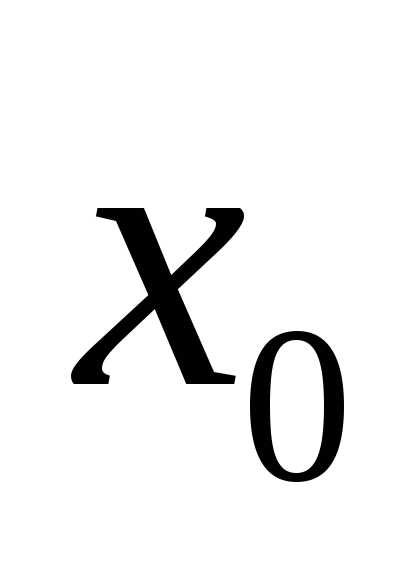 .Приращением этой функции в точке
.Приращением этой функции в точке 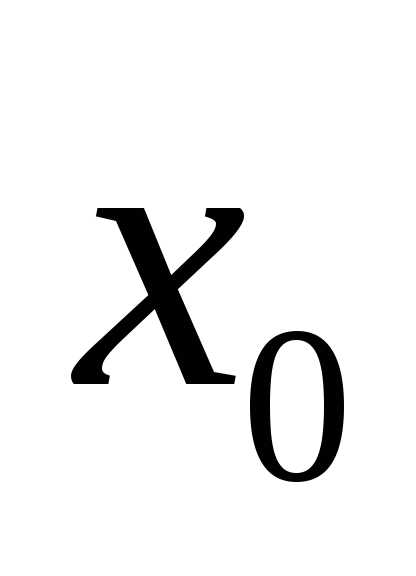 называется функция аргументаПроизводной функции
называется функция аргументаПроизводной функции 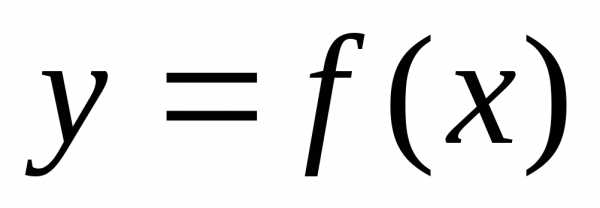 в
точке
в
точке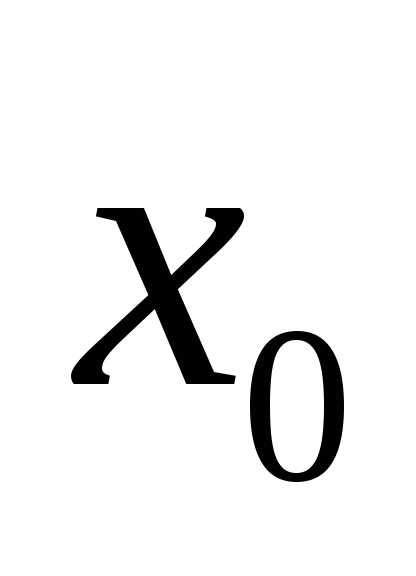 называется
называется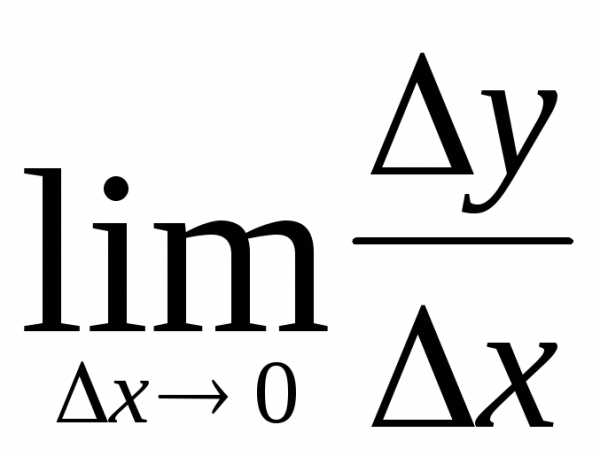 . Производная
функции в точке
. Производная
функции в точке 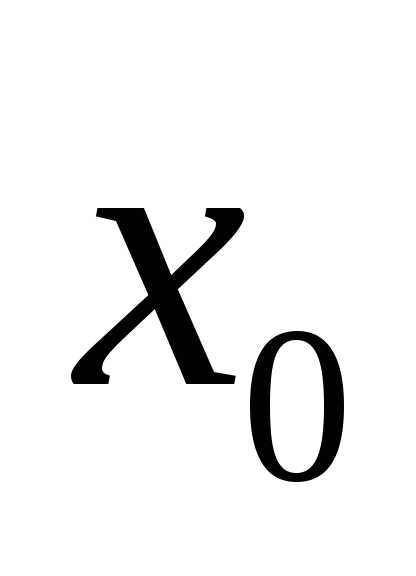 обозначается
обозначается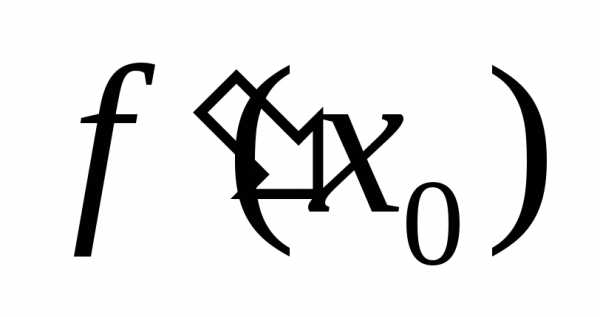 или
или .
Операция нахождения производной
называетсядифференцированием.
.
Операция нахождения производной
называетсядифференцированием.
Таблица производных простейших элементарных функций
1. 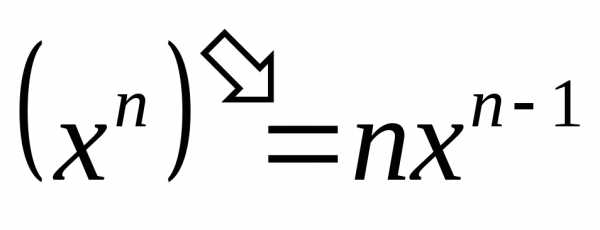 8.
8.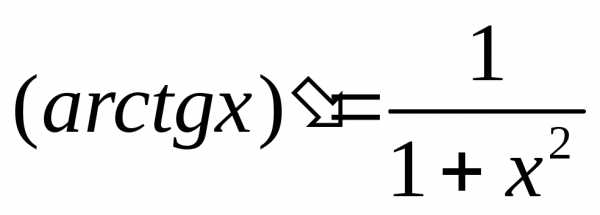
2. 9.
3.
10.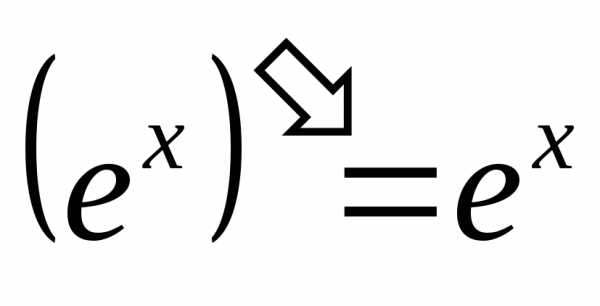
4. 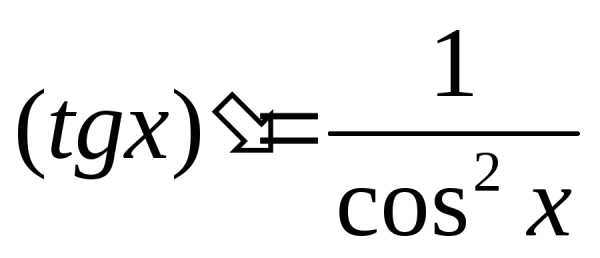 11.
11.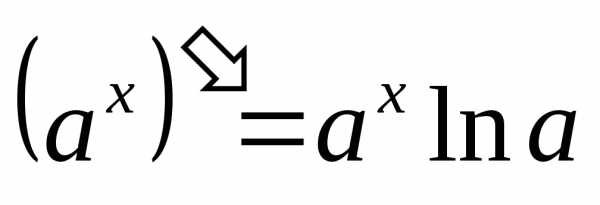
5.  12.
12.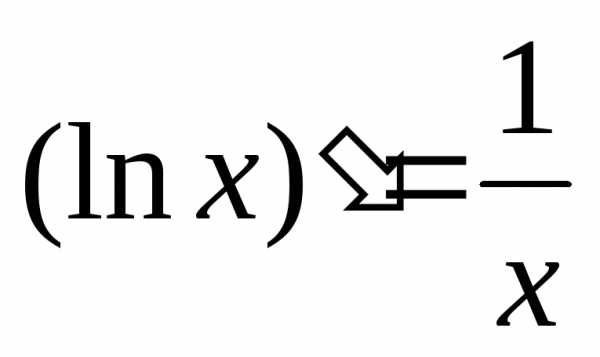
6. 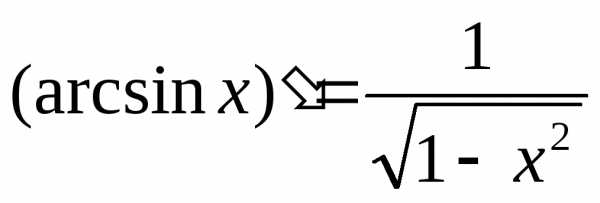 13.
13.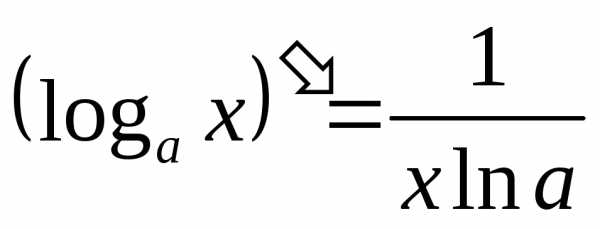
7.
Физический смысл производной
Производная  —
скорость изменения зависимой переменной
—
скорость изменения зависимой переменной по отношению к изменению независимой
переменной
по отношению к изменению независимой
переменной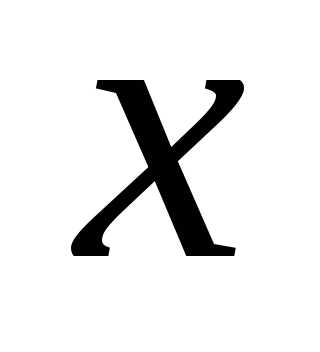 в точке
в точке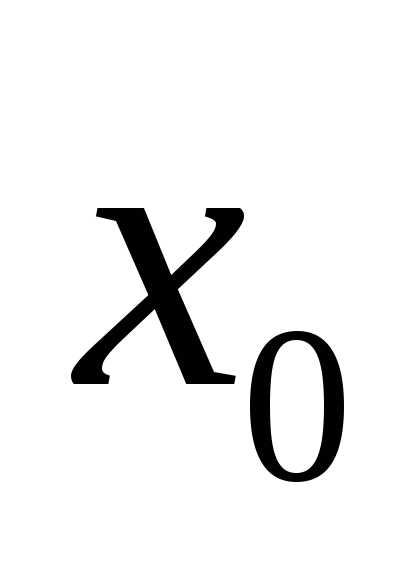 .
В частности, если
.
В частности, если —
время,
—
время,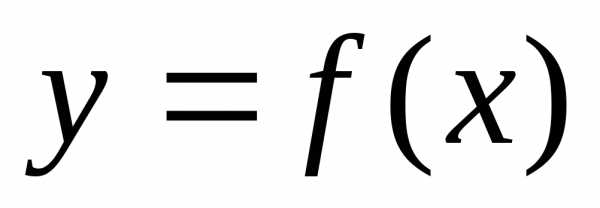 —
координата точки, движущейся по прямой,
то
—
координата точки, движущейся по прямой,
то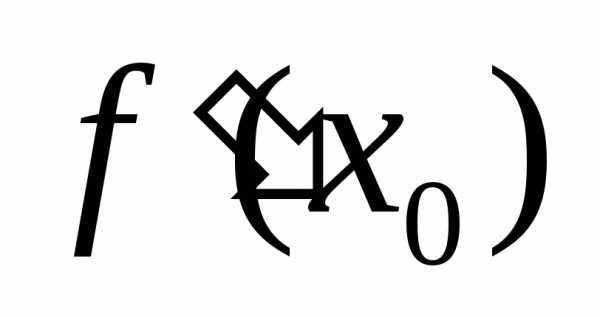 —
мгновенная скорость точки в момент
—
мгновенная скорость точки в момент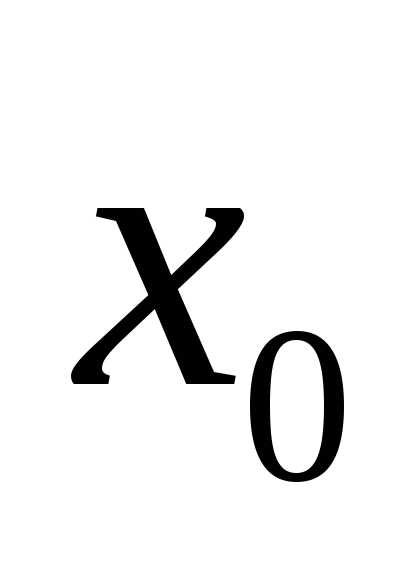 .
.
Геометрический смысл производной
Рассмотрим график
функции 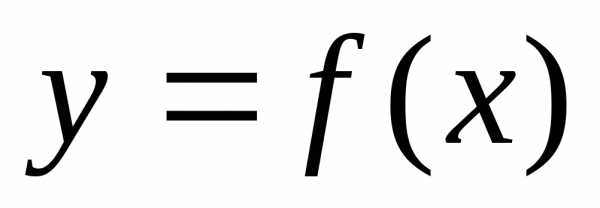 .
.
y
N
l
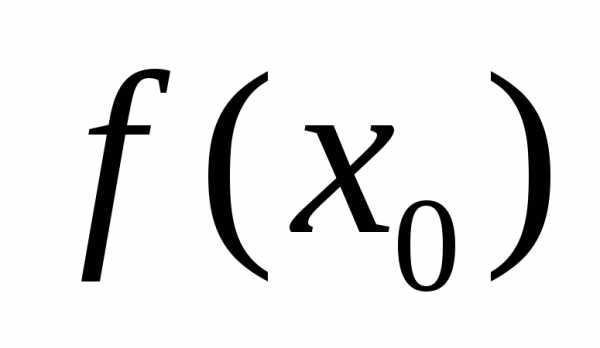 M
M

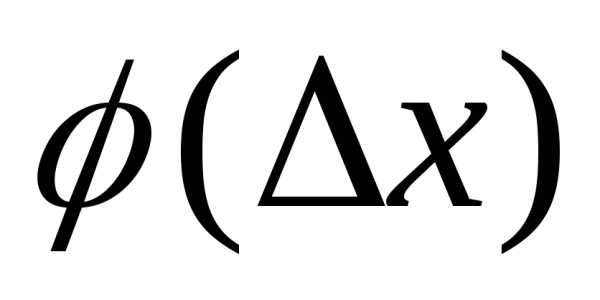
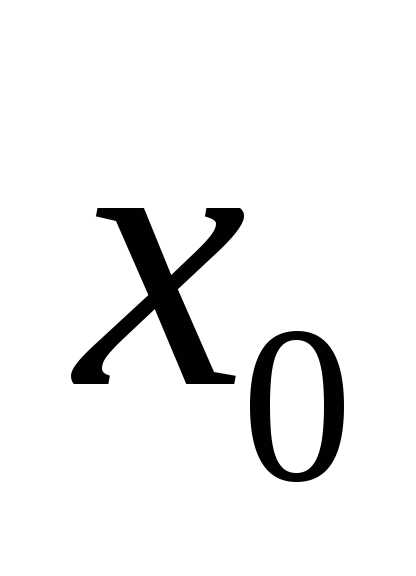
 x
x
MN — секущая к графику функции. При 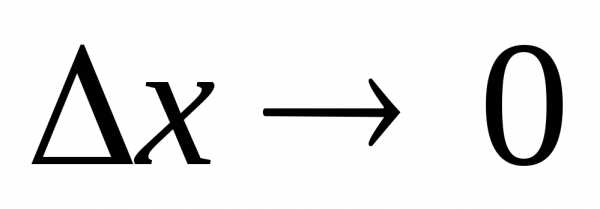 ,
угол
,
угол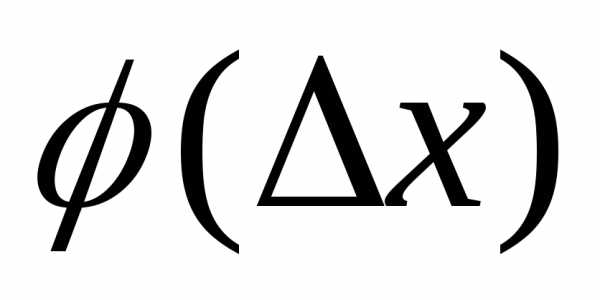 стремится к некоторому пределу
стремится к некоторому пределу ,
а секущая, поворачиваясь вокруг точкиM, становится
касательной.
,
а секущая, поворачиваясь вокруг точкиM, становится
касательной.
Уравнение касательной к графику функции:
.
Уравнение нормали, проведённой в той же точке:
.
Правила дифференцирования
Если 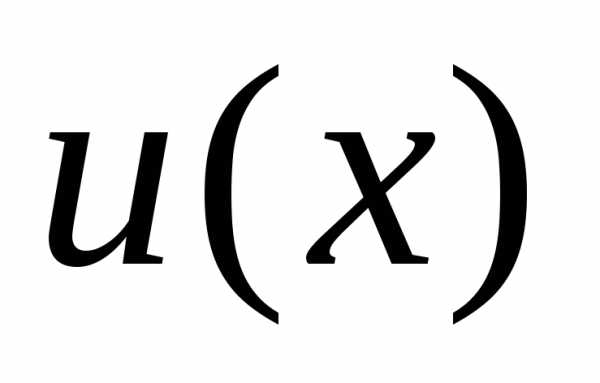 и
и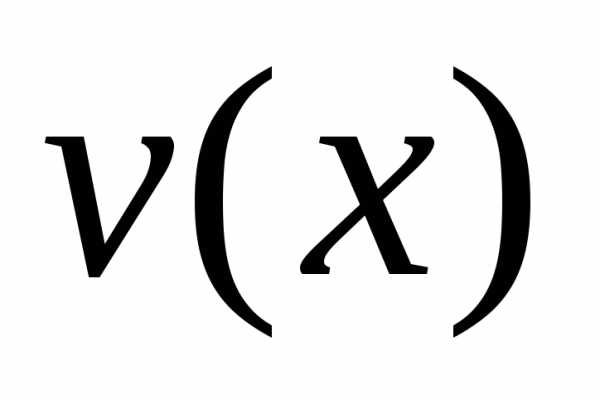 —
дифференцируемые функции, то справедливы
равенства
—
дифференцируемые функции, то справедливы
равенства
;
Производная сложной функции
Если функция 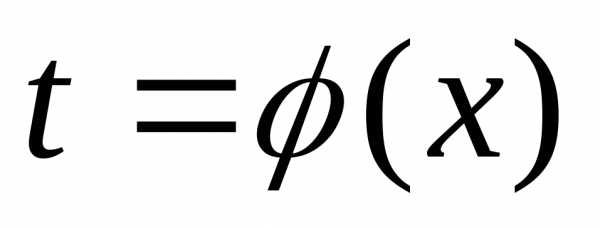 имеет в точке
имеет в точке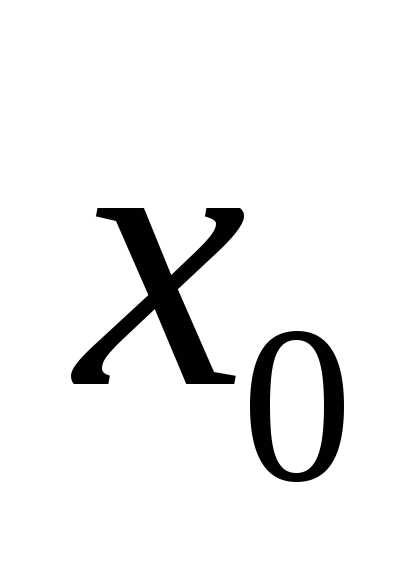 производную
производную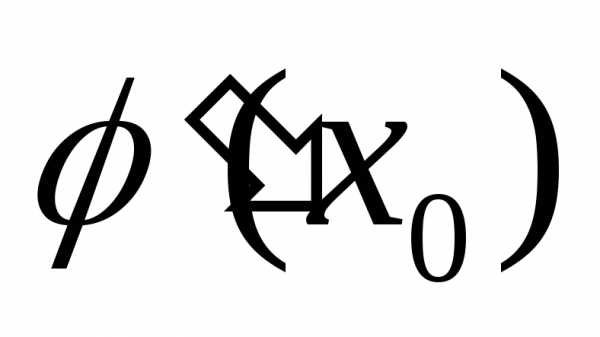 ,
а функция
,
а функция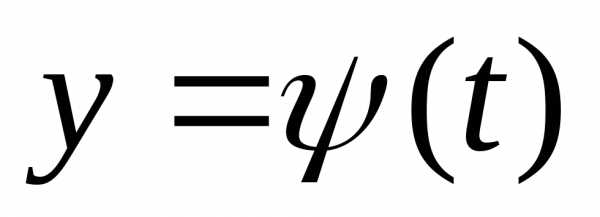 имеет в точкепроизводную
имеет в точкепроизводную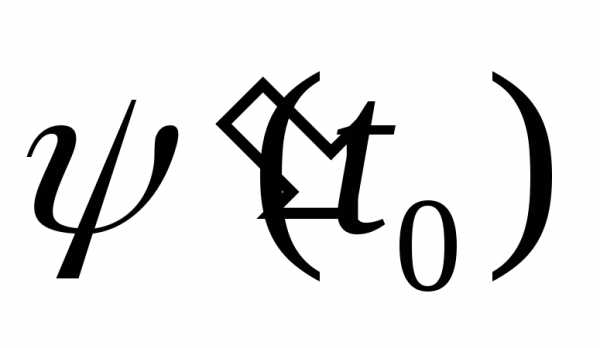 ,
то сложная функцияимеет производную в точке
,
то сложная функцияимеет производную в точке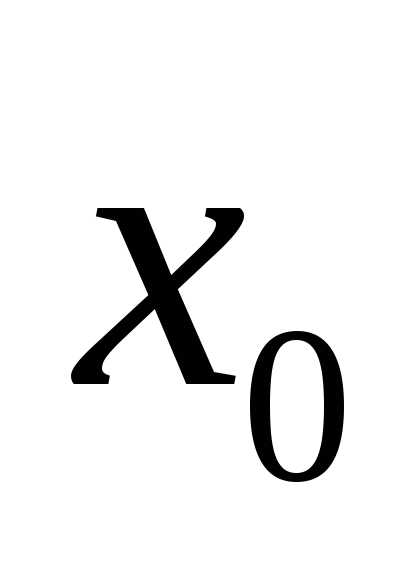 ,
причём
,
причём
. (1)
Физическая
интерпретация формулы (1): производная 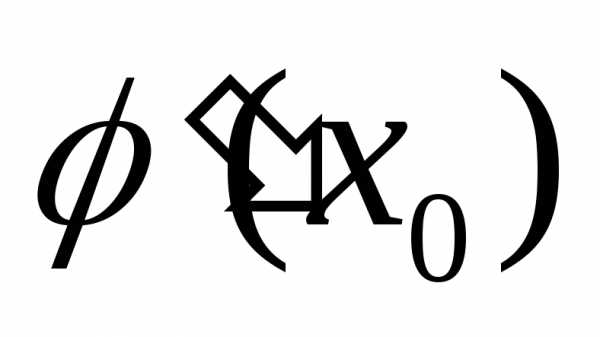 —
скорость изменения
—
скорость изменения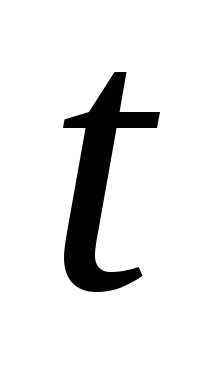 по отношению к
по отношению к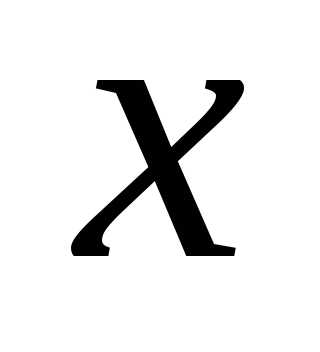 ,
производная
,
производная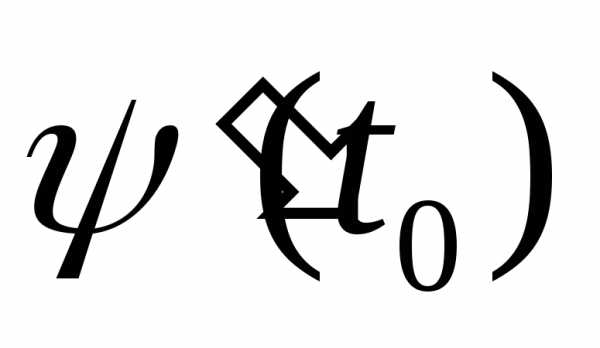 —
скорость изменения
—
скорость изменения по отношению к
по отношению к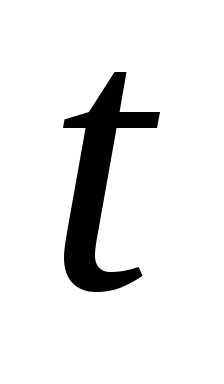 .
Очевидно, что скорость
.
Очевидно, что скорость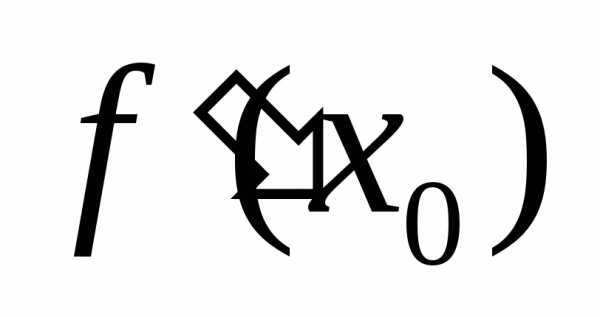 равна произведению скоростей
равна произведению скоростей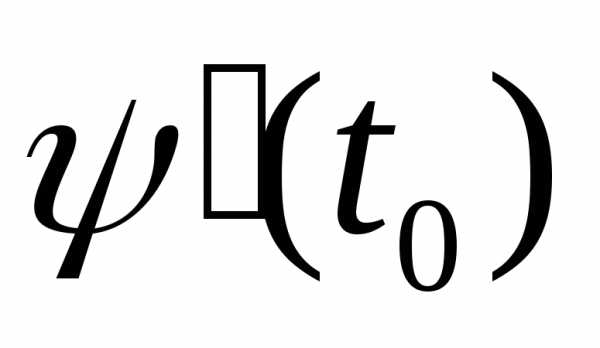 и
и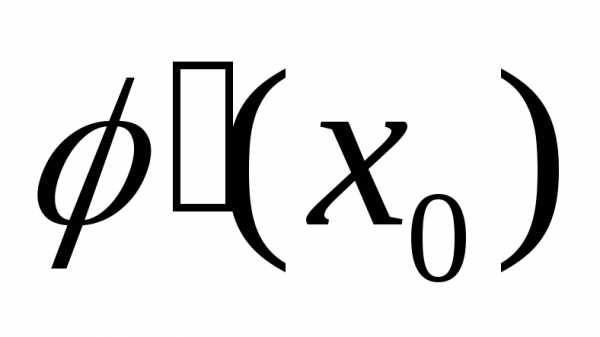 .
(Если
.
(Если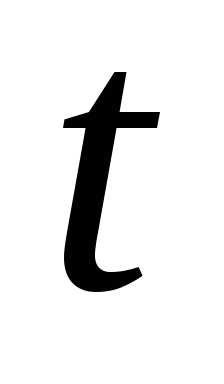 движется быстрее
движется быстрее в
в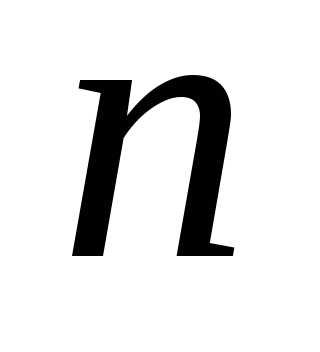 раз,
раз, —
быстрее
—
быстрее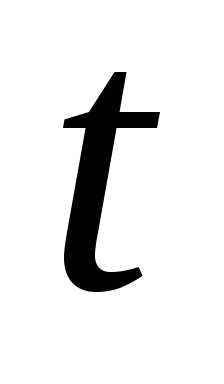 в
в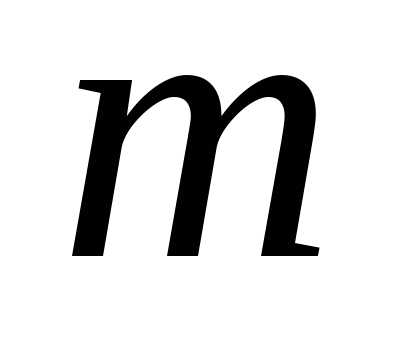 раз, то
раз, то движется быстрее
движется быстрее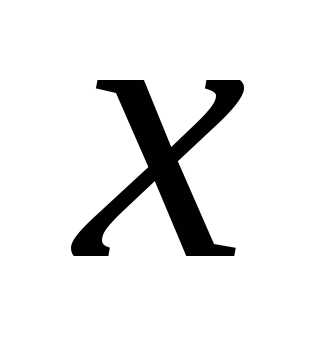 в
в раз).
раз).
Производная функции, заданной параметрически
Пусть функции 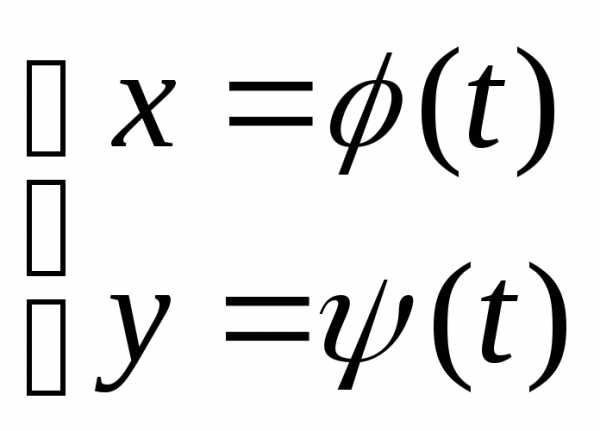 (2)
(2)
определены на
некотором промежутке изменения переменной  ,
которую назовёмпараметром. Пусть функция
,
которую назовёмпараметром. Пусть функция 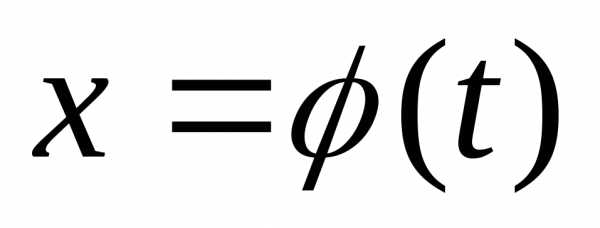 является строго монотонной на этом
промежутке. Тогда существует обратная
функция
является строго монотонной на этом
промежутке. Тогда существует обратная
функция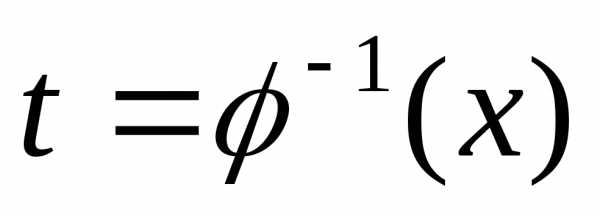 ,
подставляя которую в уравнение
,
подставляя которую в уравнение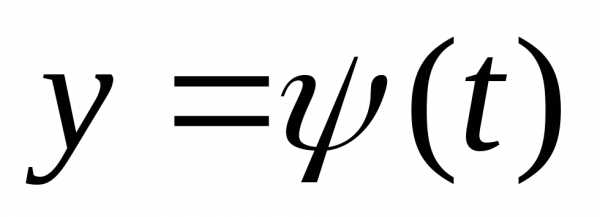 получим.
Таким образом, переменная
получим.
Таким образом, переменная является сложной функцией переменной
является сложной функцией переменной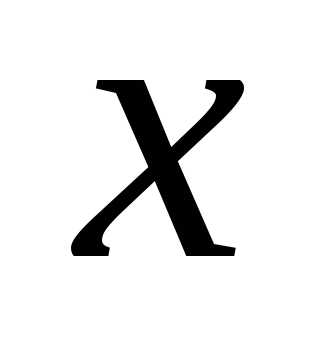 .
Задание функции
.
Задание функции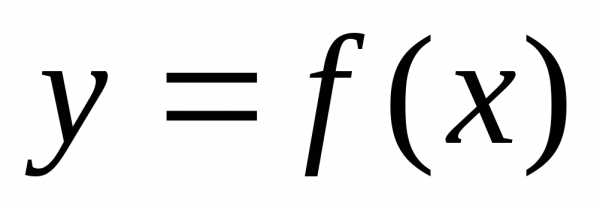 с помощью уравнений (2) называетсяпараметрическим. Если функции
имеют производные, причём
с помощью уравнений (2) называетсяпараметрическим. Если функции
имеют производные, причём ,
то
,
то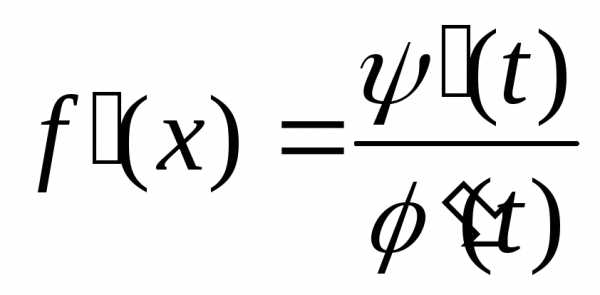 .
.
Дифференциалом функции 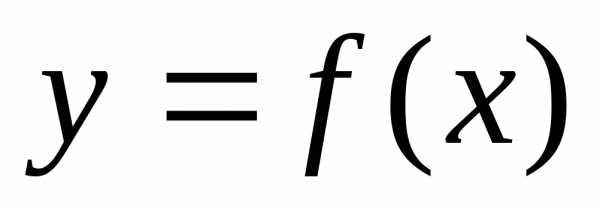 в точке
в точке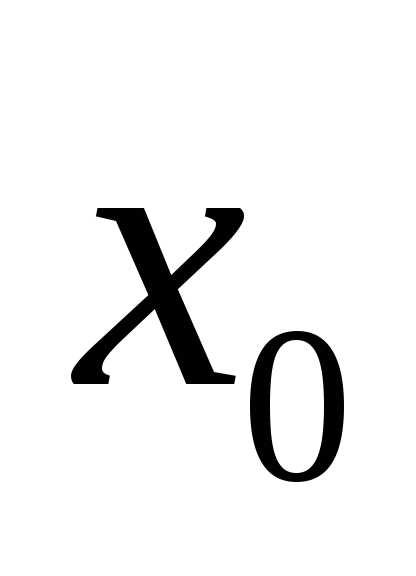 называется функция аргумента.
Дифференциалом независимой переменной
называется функция аргумента.
Дифференциалом независимой переменной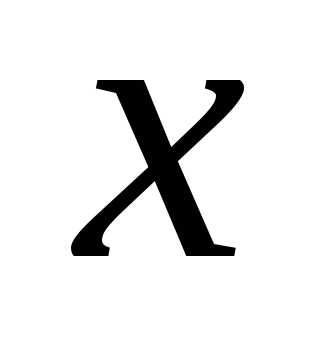 называется приращение этой переменной:
называется приращение этой переменной: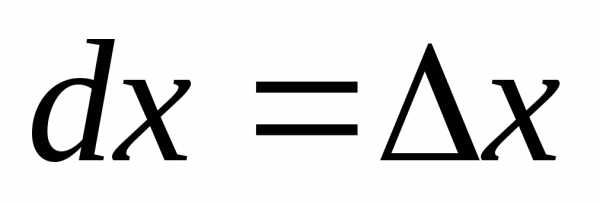 .
Таким образом, дифференциал функции
.
Таким образом, дифференциал функции в точке
в точке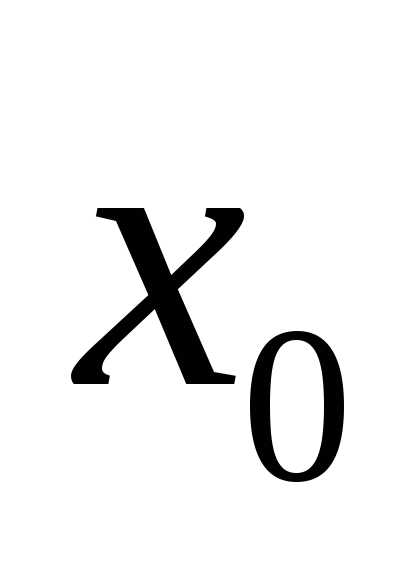 имеет вид
имеет вид
, (3)
откуда 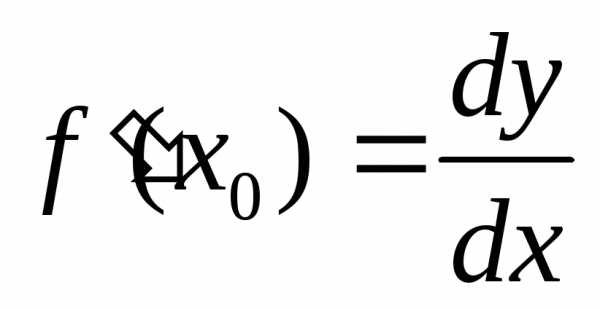 .
.
Геометрический и физический смысл дифференциала
y
N
 P
P
dy
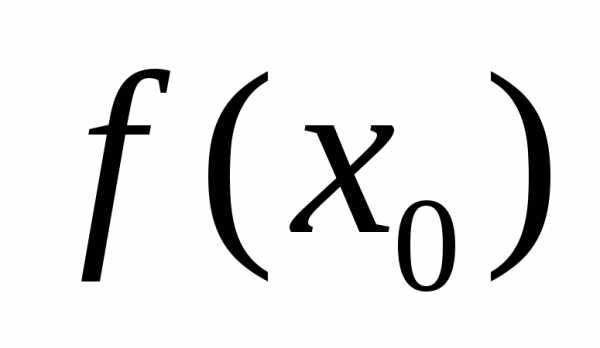 M
M 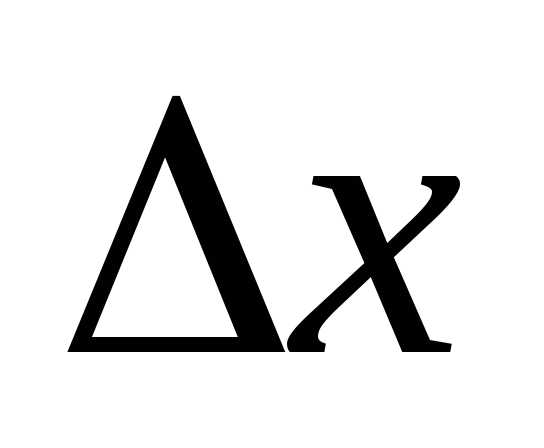
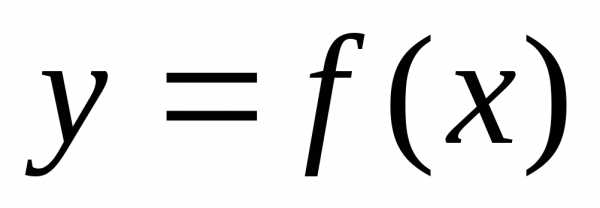

0 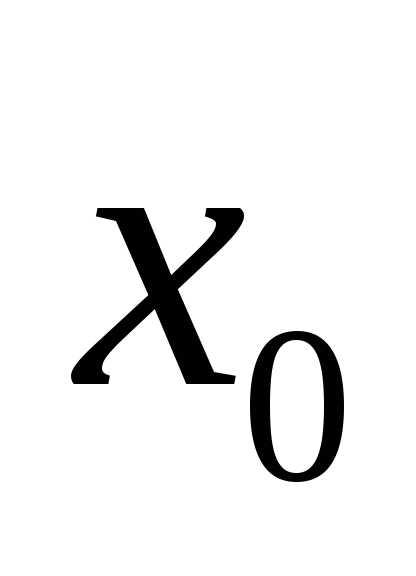
 x
x
Рассмотрим график
функции 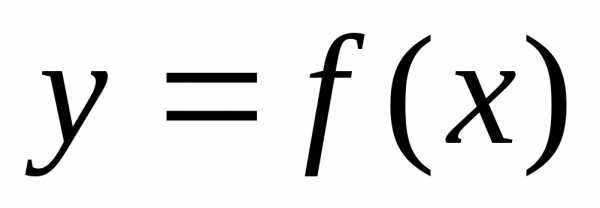 .
МР- касательная к графику функции в
точке М.
Дифференциалравен приращению ординаты касательной.
.
МР- касательная к графику функции в
точке М.
Дифференциалравен приращению ординаты касательной.
Если 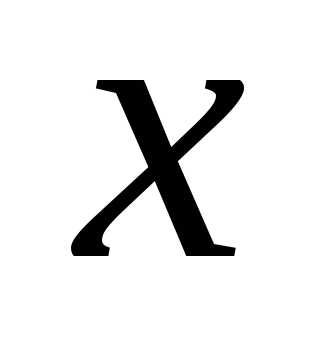 —
время,
—
время,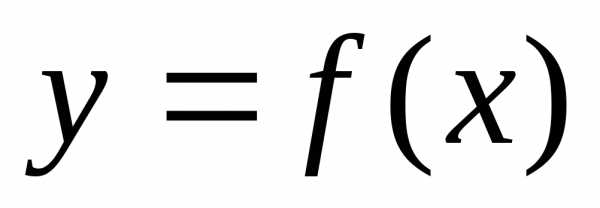 —
координата точки на прямой в момент
—
координата точки на прямой в момент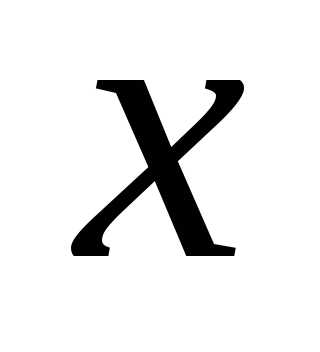 ,
то дифференциалравен тому изменению координаты, которое
получила бы точка за время
,
то дифференциалравен тому изменению координаты, которое
получила бы точка за время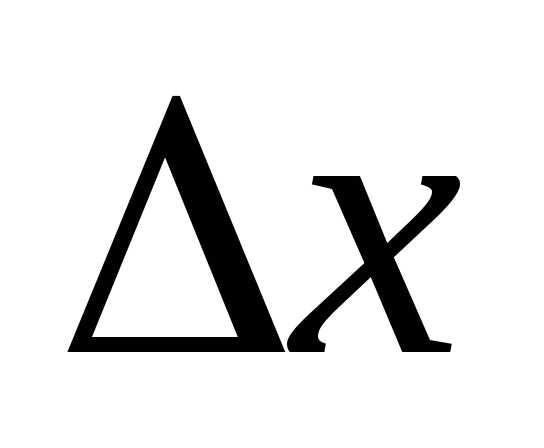 ,
если бы скорость точки на отрезкебыла постоянной и равной
,
если бы скорость точки на отрезкебыла постоянной и равной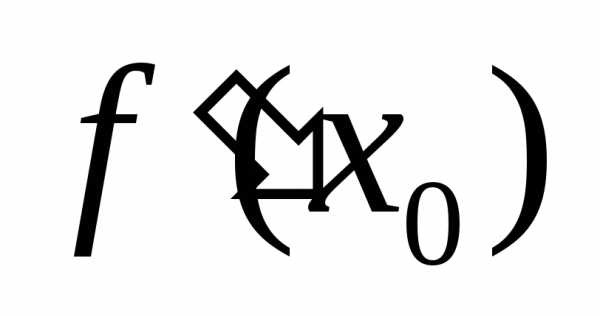 .
Изменение скорости на этом отрезке
приводит к тому, что
.
Изменение скорости на этом отрезке
приводит к тому, что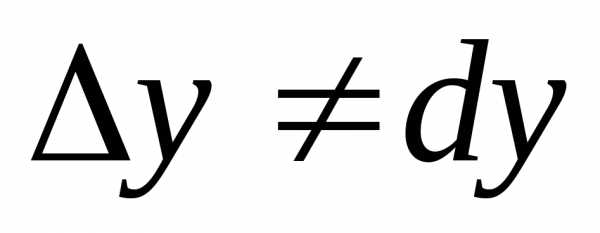 .
Однако на малых промежутках времени
.
Однако на малых промежутках времени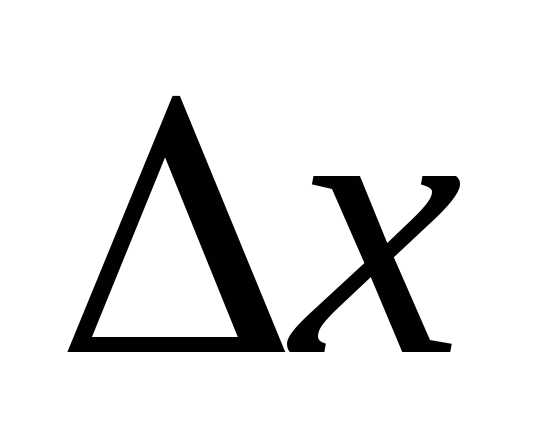 изменение скорости незначительно и.
изменение скорости незначительно и.
Инвариантность формы первого дифференциала
Пусть аргумент  функции
функции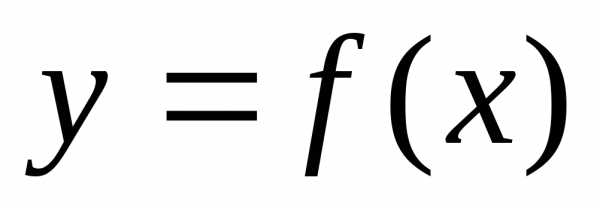 является функцией от,
тогда дифференциал функциипо-прежнему имеет вид (3), но теперь
является функцией от,
тогда дифференциал функциипо-прежнему имеет вид (3), но теперь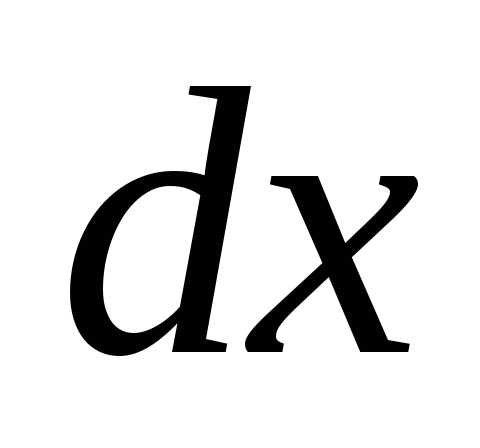 является не произвольным приращением
аргумента
является не произвольным приращением
аргумента ,
а дифференциалом функции
,
а дифференциалом функции ,
т.е..
Это свойство – сохранение формы и в том
случае, когда
,
т.е..
Это свойство – сохранение формы и в том
случае, когда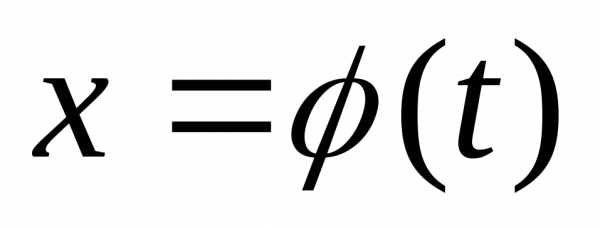 называется инвариантностью формы
первого дифференциала.
называется инвариантностью формы
первого дифференциала.
Применение дифференциала в приближённых вычислениях
Так как  при малых
при малых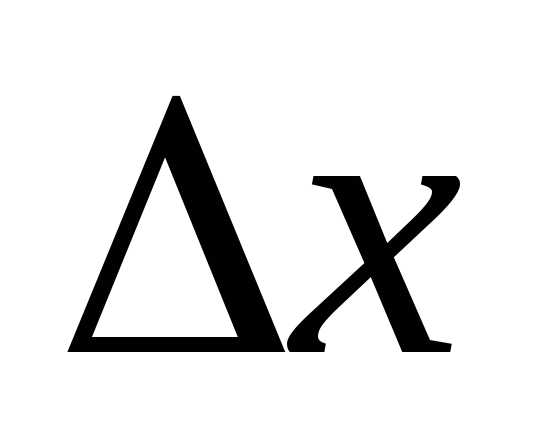 ,
т.е.,
то.
,
т.е.,
то.
Эта формула
позволяет находить приближённые значения
при малых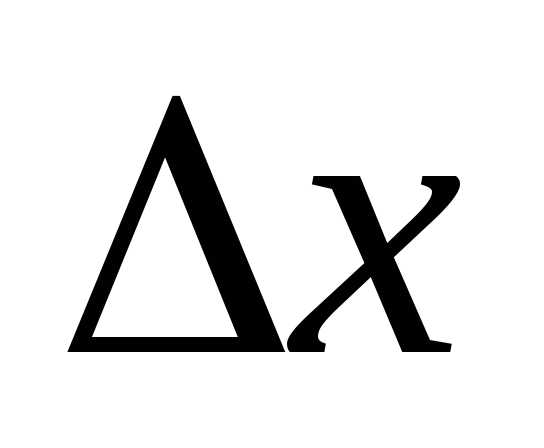 ,
если известны.
При этом погрешность при такой замене
при
,
если известны.
При этом погрешность при такой замене
при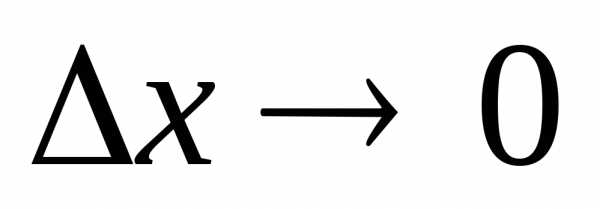 является бесконечно малой, более высокого
порядка, чем
является бесконечно малой, более высокого
порядка, чем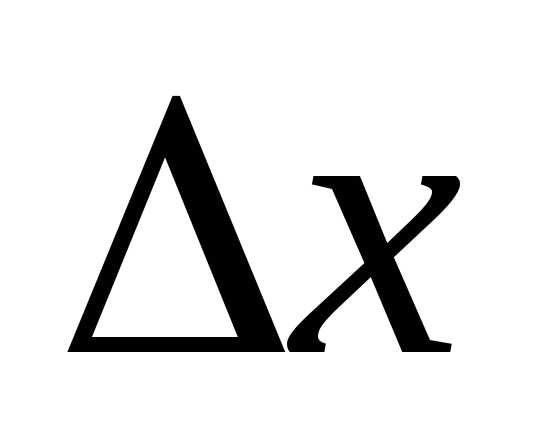 .
.
Производные высших порядков
Если производная 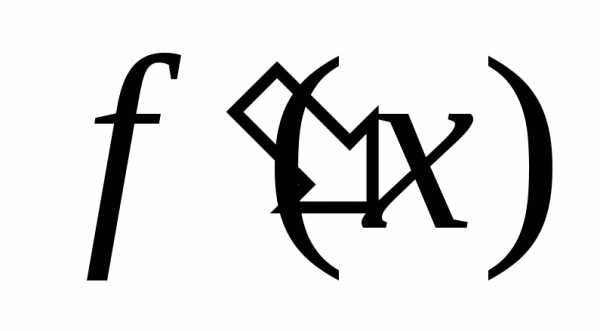 функции
функции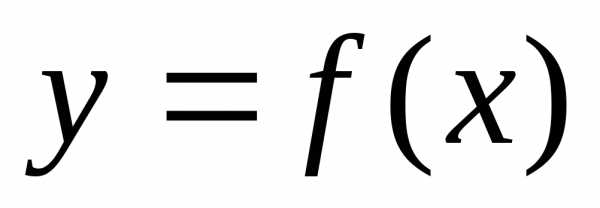 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки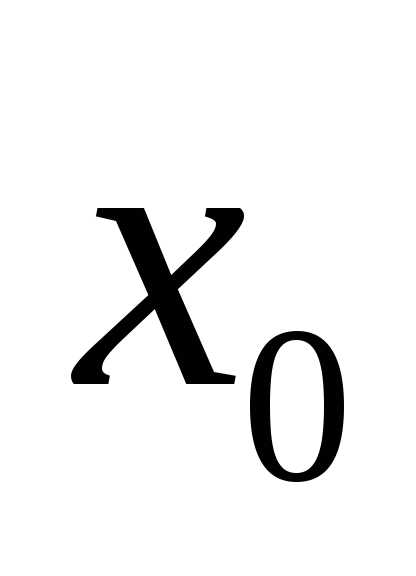 и имеет в этой точке производную, то эта
производная от
и имеет в этой точке производную, то эта
производная от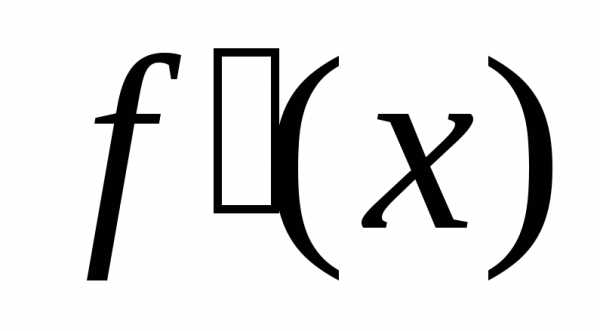 называется второй производной и
обозначается
называется второй производной и
обозначается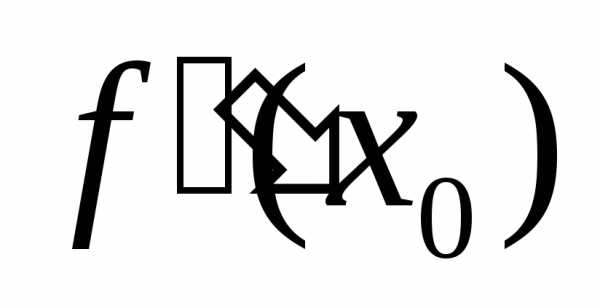 .
Третья производная является производной
от
.
Третья производная является производной
от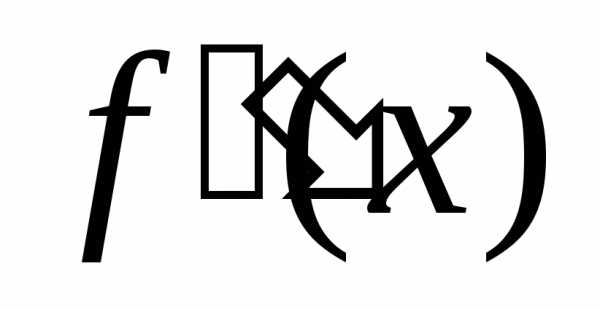 и т.д. Таким образом, производные высших
порядков определяются индуктивно по
формуле
и т.д. Таким образом, производные высших
порядков определяются индуктивно по
формуле
.
Основные формулы вычисления n-х производных
1.
2. Формула Лейбница
,
где 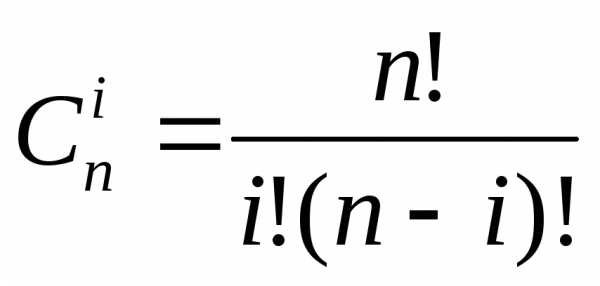
3.
4.
5. Если 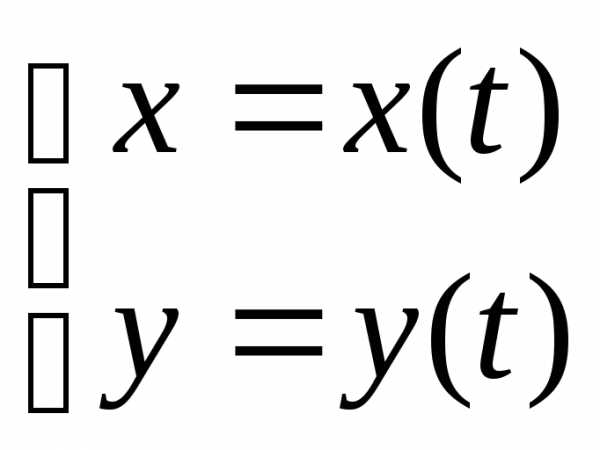 , то
, то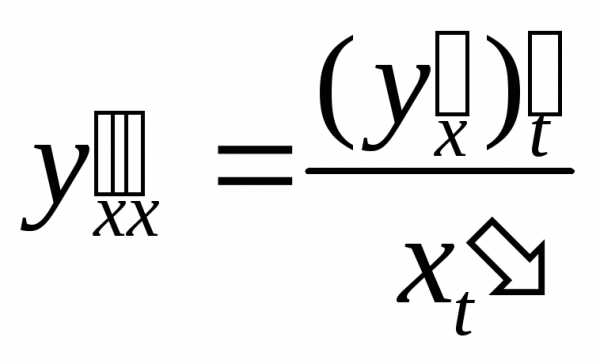 ,
или
,
или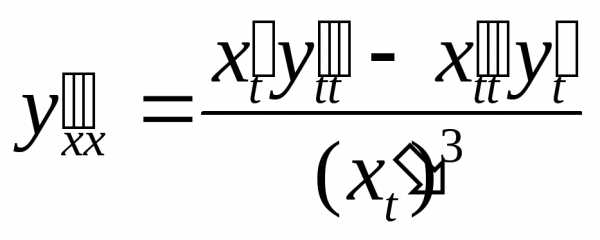
Общая схема исследования функции
и построения её графика
I. Элементарное исследование.
1. Найти область определения функции.
2. Исследовать функцию на чётность/нечётность, периодичность.
3. Вычислить предельные значения функции в граничных точках области определения.
4. Выяснить существование асимптот.
5. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.
6. Сделать эскиз графика функции, используя полученные результаты.
II. Исследование графика функции по первой производной.
1. Найти решения
уравнений 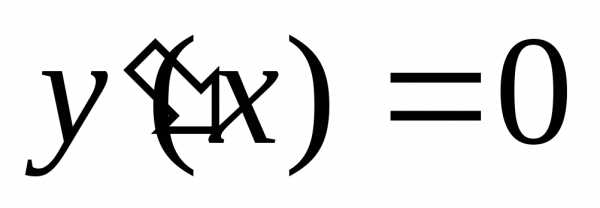 и выяснить, в каких точках производная
не существует.
и выяснить, в каких точках производная
не существует.
2. Точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия, определить вид экстремума.
3. Найти интервалы монотонности.
III. Исследование графика функции по второй производной.
1. Найти решения
уравнения 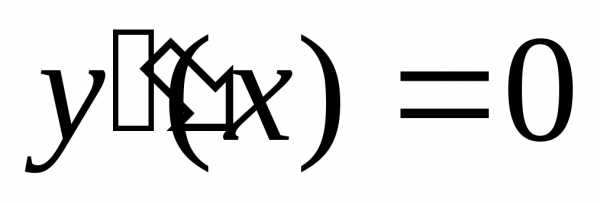 и выяснить, в каких точках производная
не существует.
и выяснить, в каких точках производная
не существует.
2. Точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия.
3. Вычислить значения функции в точках перегиба.
4. Найти интервалы выпуклости и вогнутости.
IV. Построить график функции.
Если в некоторой
окрестности точки 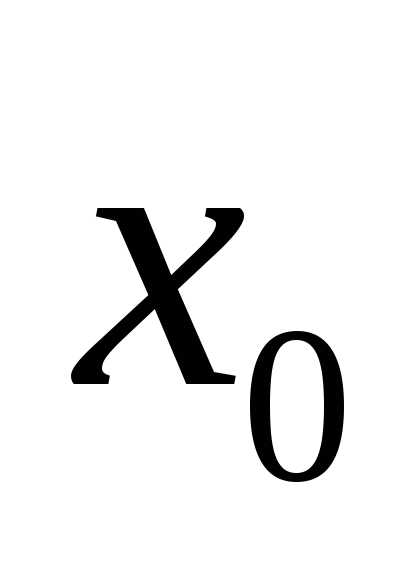 выполняется неравенствоили,
то точка
выполняется неравенствоили,
то точка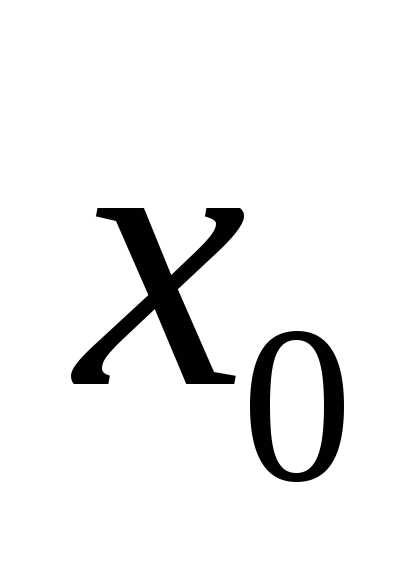 называется точкой экстремума функции
называется точкой экстремума функции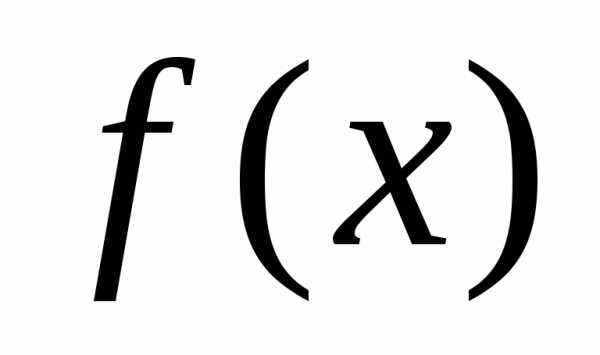 (соответственно точкой максимума или
минимума).
(соответственно точкой максимума или
минимума).
Необходимое условие
экстремума: если  —
точка экстремума, то
—
точка экстремума, то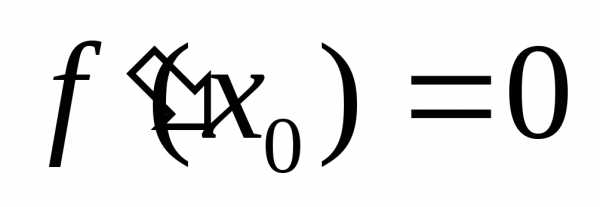 .
.
Достаточное условие
экстремума: точка 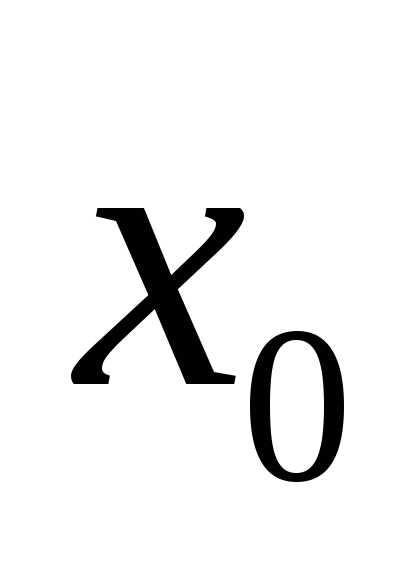 является точкой экстремума, если её
производная
является точкой экстремума, если её
производная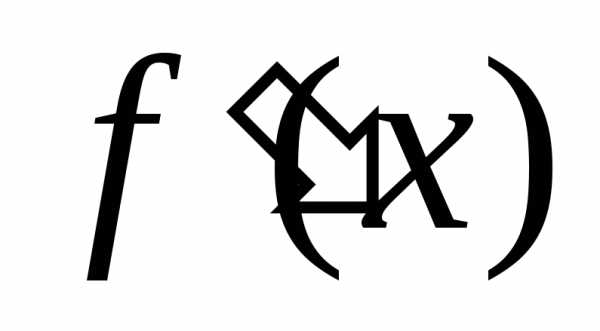 меняет знак при переходе через точку
меняет знак при переходе через точку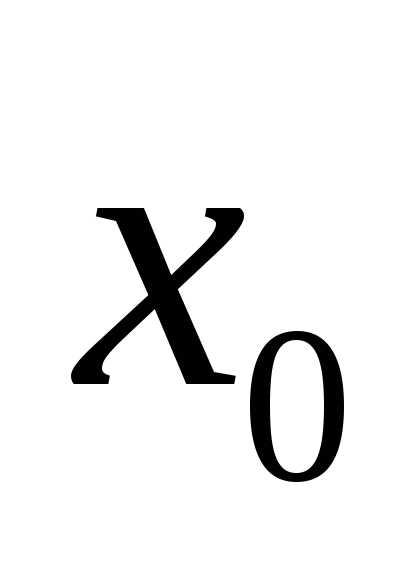 ,
с + на – при максимуме, с – на + при
минимуме.
,
с + на – при максимуме, с – на + при
минимуме.
Точка 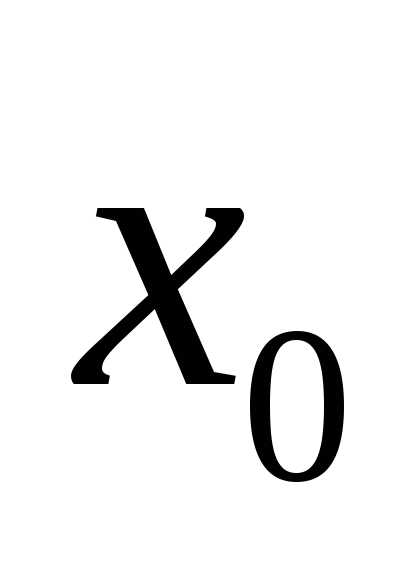 называется точкой перегиба кривой
называется точкой перегиба кривой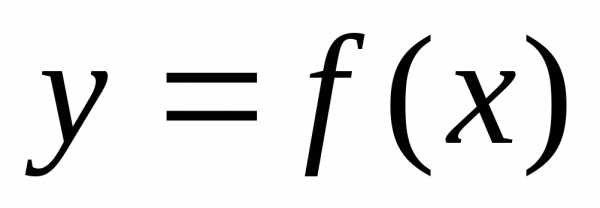 ,
если при переходе через точку
,
если при переходе через точку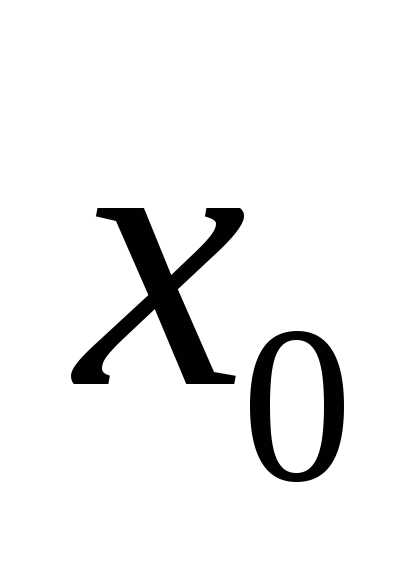 меняется направление выпуклости.
меняется направление выпуклости.
Необходимое условие
точки перегиба: если 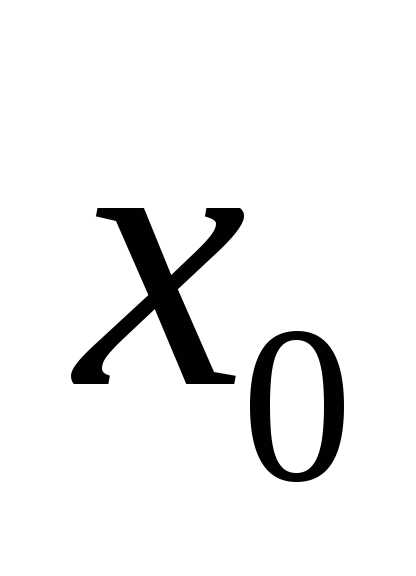 — точка перегиба, то
— точка перегиба, то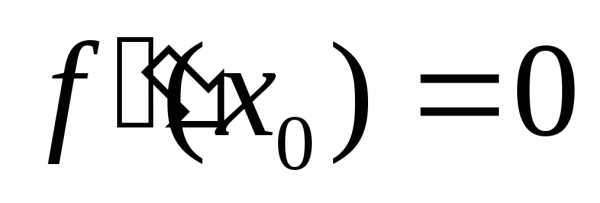 .
.
Достаточное условие
точки перегиба: 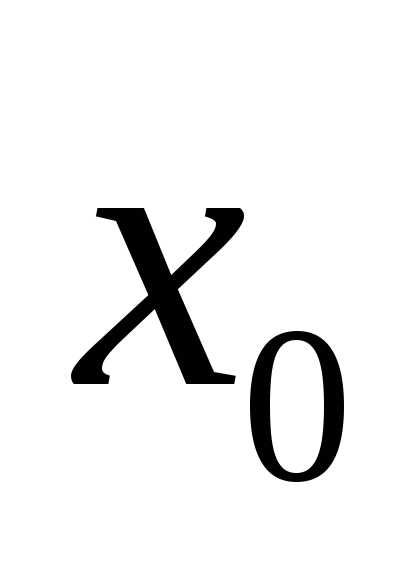 является точкой перегиба кривой
является точкой перегиба кривой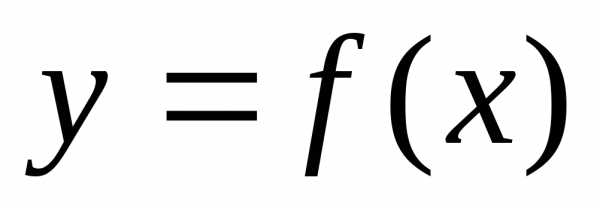 ,
если при переходе через точку
,
если при переходе через точку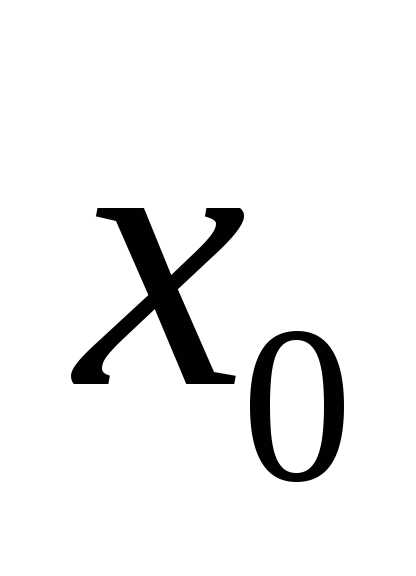 вторая производная меняет знак.
вторая производная меняет знак.
Прямая
называется наклонной асимптотой кривой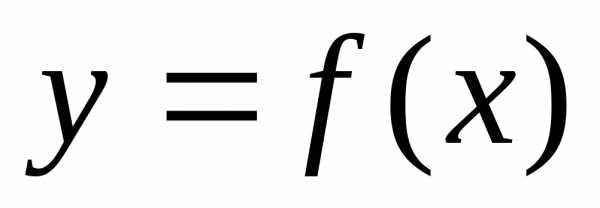 ,
если расстояние от точек кривой до
асимптоты стремится к нулю при.
,
если расстояние от точек кривой до
асимптоты стремится к нулю при.
При этом
.
При 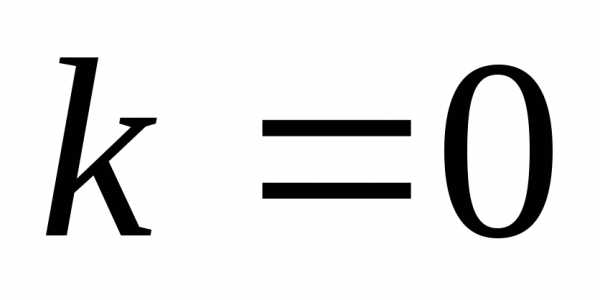 имеем горизонтальную асимптоту
имеем горизонтальную асимптоту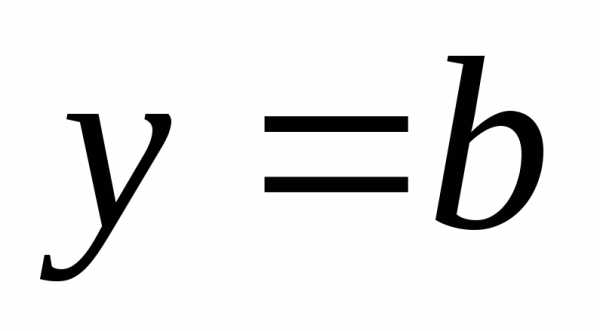 .
.
Если
или,
то прямая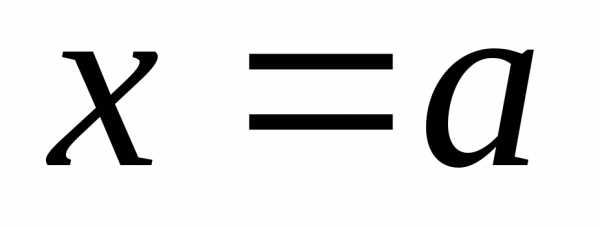 называется вертикальной асимптотой.
называется вертикальной асимптотой.
Примеры
1. Пользуясь формулами дифференцирования, найти производные следующих функций:
1)
2)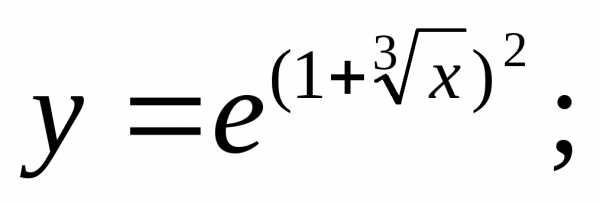
3) 4)
Решение:
1) есть сложная функция.
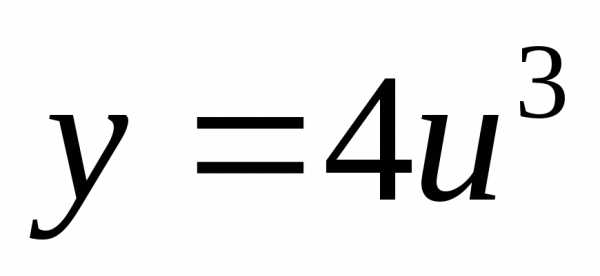 ,
где
,
где
Производная сложной функции имеет вид
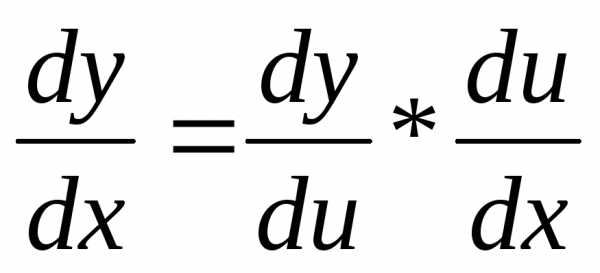 или
,
или
,
следовательно,
2) 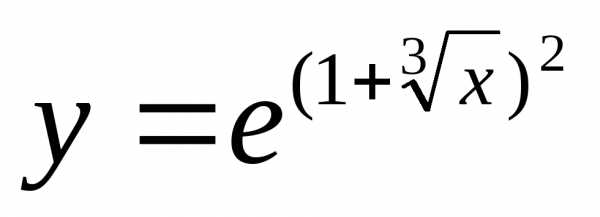 — сложная функция.
— сложная функция.
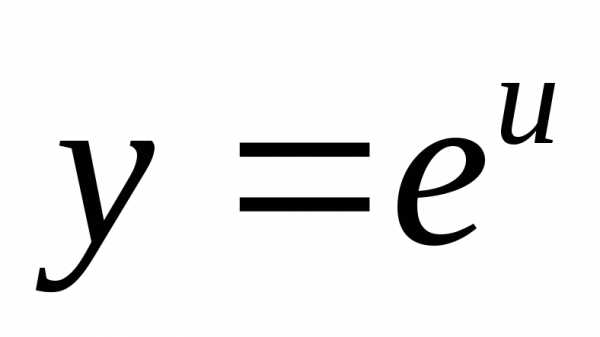 ,
где
,
где 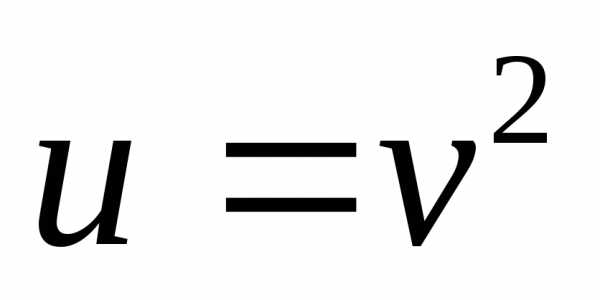 ,
а
,
а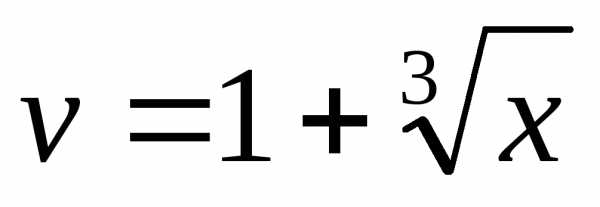 ,
,
;
3) применяя логарифмическое дифференцирование, последовательно находим
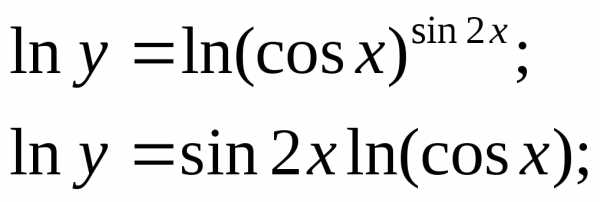
=
4) 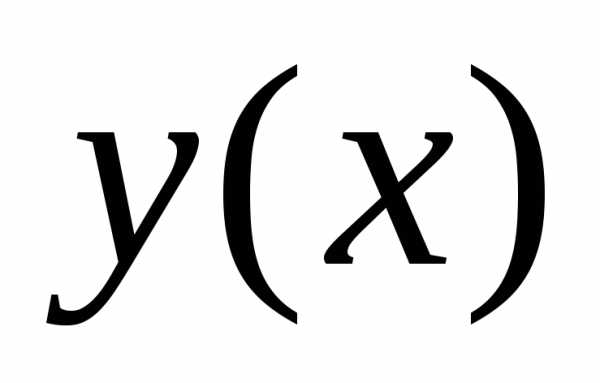 есть неявная функция, т.е. задана
уравнением,
не разрешенным
относительно у.
Для нахождения
производной
есть неявная функция, т.е. задана
уравнением,
не разрешенным
относительно у.
Для нахождения
производной 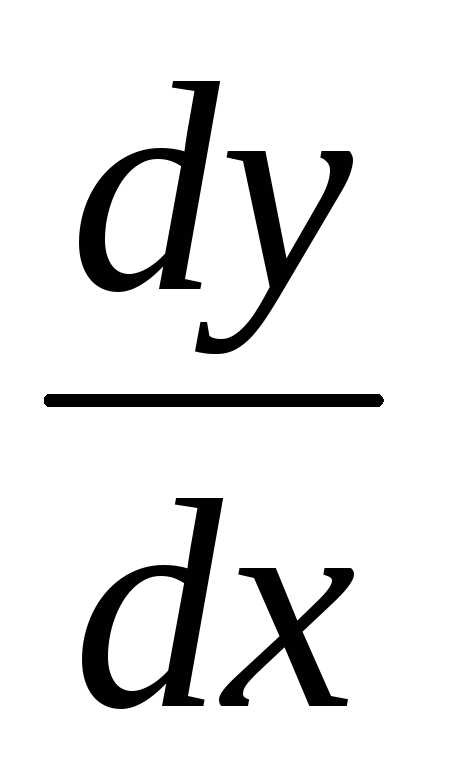 нужно продифференцировать пох обе части равенства, помня, что у есть функция
от х,
и затем разрешить полученное равенство
относительно искомой производной. Как
правило, она будет зависеть от х и у:
нужно продифференцировать пох обе части равенства, помня, что у есть функция
от х,
и затем разрешить полученное равенство
относительно искомой производной. Как
правило, она будет зависеть от х и у:
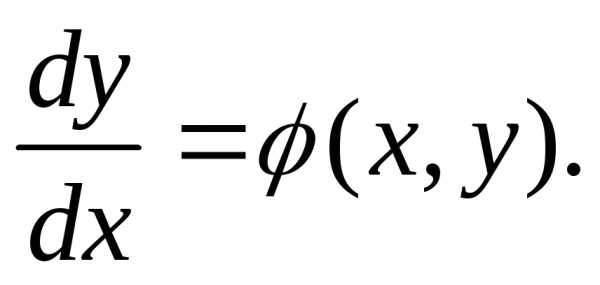
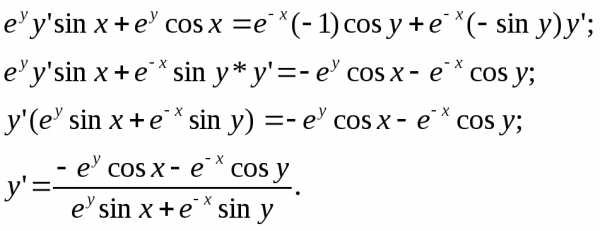
2. Найти производную
первого и второго порядка  и
и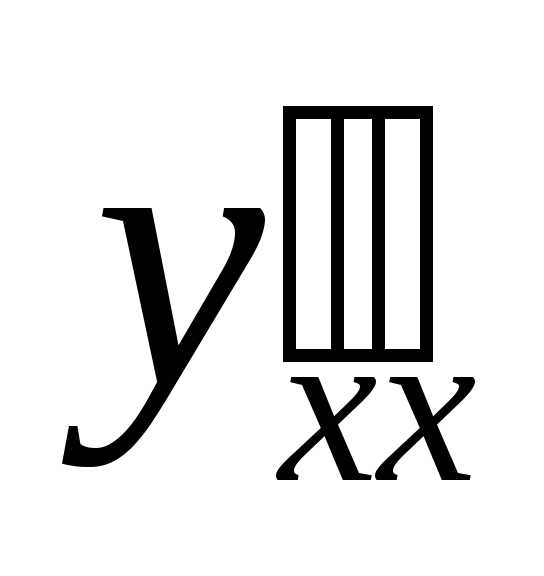 для параметрически заданной функции
для параметрически заданной функции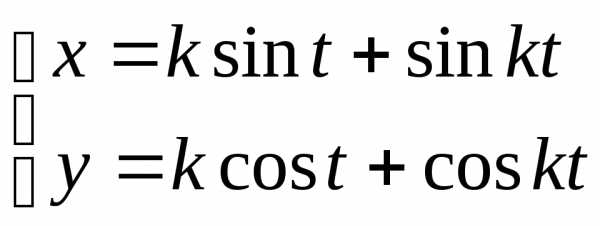 .
.
Функция у от независимой переменной х задана через посредство вспомогательной переменной (параметра t). Производная от у по х определяется формулой
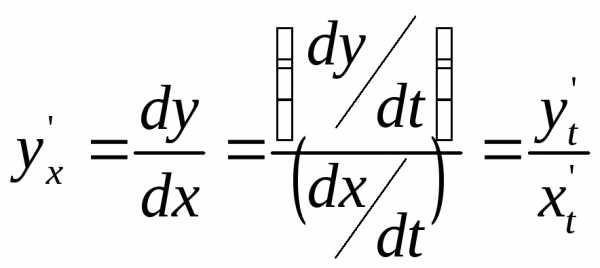 .
.
Находим производные от у и х по параметру t:
Находим производную второго порядка от y по х:
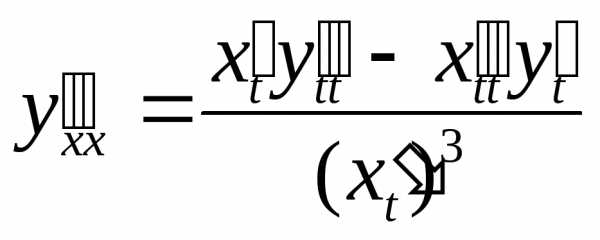 ,
или
,
или  .
.
Находим
;
.
3. Составить уравнение касательной и нормали к кривой у = х2 — 4х в точке, где х = 1.
Решение. Уравнение касательной к кривой в точке М(х0, у0)
х0 = 1,
Для определения
углового коэффициента касательной 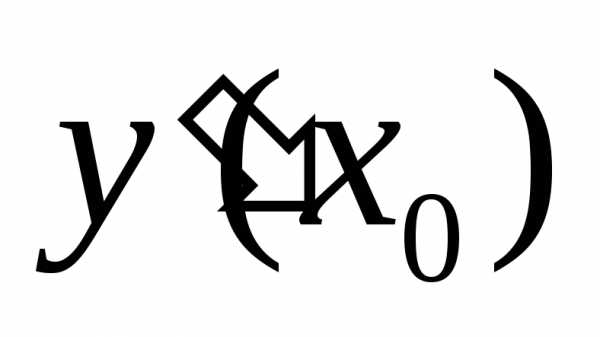 находим производную
находим производную
Подставляя значения х0, у0, у'(х0) в уравнение, получим
у+3 = -2(х-1) или 2х+у+1 = 0
Уравнение нормали —
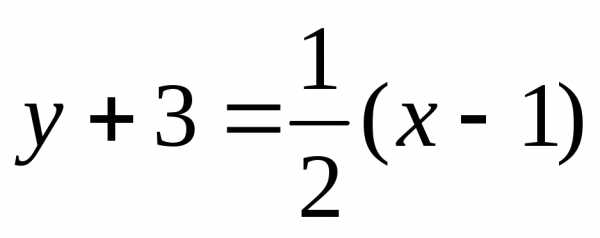 или
.
или
.
4. Найти дифференциалы функций:
1)  2)
2)
вычислить 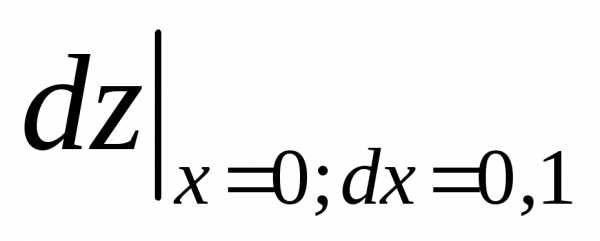 .
.
Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:
1)
2) .
Полагая х
= 0 и dx = 0,1, получим 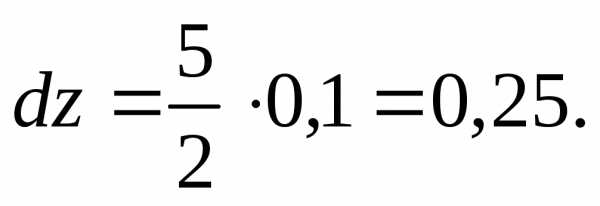
5. Вычислить приближенное значение:
studfiles.net
Лекция 4. Производная и дифференциал функции одной переменной
Лекция 4. Производная и дифференциал функции одной переменной
Задача о скорости движущейся точки
Пусть – закон прямолинейного движения материальной точки. Обозначим через путь, пройденный точкой за время , а через путь, пройденный за время . Тогда за время точка пройдет путь , равный: . Отношение называется средней скоростью точки за время от до . Чем меньше , т.е. чем короче промежуток времени от до , тем лучше средняя скорость характеризует движение точки в момент времени . Поэтому естественно ввести понятие скорости в данный момент , определив ее как предел средней скорости за промежуток от до , когда :
.
Величина называется мгновенной скоростью точки в данный момент .
Задача о касательной к данной кривой
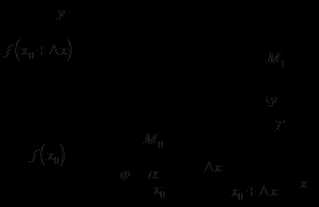 |
Пусть на плоскости задана непрерывная кривая уравнением . Требуется провести невертикальную касательную к данной кривой в точке . Так как точка касания дана, то для решения задачи требуется найти угловой коэффициент касательной. Из геометрии известно, что , где – угол наклона касательной к положительному направлению оси (см. рис.). Через точки и проведем секущую , где – угол, образованный секущей с положительным направлением оси . Из рисунка видно, что , где . Угловой коэффициент касательной к данной кривой в точке может быть найден на основании следующего определения.
Касательной к кривой в точке называется предельное положение секущей , когда точка стремится к точке . Отсюда следует, что .
Определение производной
Математическая операция, требуемая для решения рассмотренных выше задач, одна и та же. Выясним аналитическую сущность этой операции, отвлекаясь от вызвавших ее конкретных вопросов.
Пусть функция определена на некотором промежутке. Возьмем значение из этого промежутка. Придадим какое-нибудь приращение (положительное или отрицательное). Этому новому значению аргумента соответствует и новое значение функции , где .
Составим отношение , оно является функцией от .
Производной функции по переменной в точке называется предел отношения приращения функции в этой точке к вызвавшему его приращению аргумента , когда произвольным образом:
.
Замечание. Считается, что производная функции в точке существует, если предел в правой части формулы существует и конечен и не зависит от того, как приращение переменной стремится к 0 (слева или справа).
Процесс нахождения производной функции называется ее дифференцированием.
Нахождение производных некоторых функций по определению
а) Производная постоянной.
Пусть , где – постоянная, т.к. значения этой функции при всех одинаковы, то ее приращение равно нулю и, следовательно,
.
Итак, производная постоянной равна нулю, т.е. .
б) Производная функции .
Составим приращение функции:
.
При нахождении производной использовали свойство предела произведения функций, первый замечательный предел и непрерывность функции .
Таким образом, .
Связь между дифференцируемостью функции и ее непрерывностью
Функция, имеющая производную в точке , называется дифференцируемой в этой точке. Функция, имеющая производную во всех точках некоторого промежутка, называется дифференцируемой на этом промежутке.
Теорема. Если функция дифференцируема в точке , то она непрерывна в этой точке.
Доказательство. Придадим аргументу произвольное приращение . Тогда функция получит приращение . Запишем равенство и перейдем к пределу в левой и правой частях при :
Поскольку у непрерывной функции бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то теорему можно считать доказанной.
Замечание. Обратное утверждение не имеет места, т.е. из непрерывности функции в точке, вообще говоря, не следует дифференцируемость в этой точке. Например, функция непрерывна при всех , но она не дифференцируема в точке . Действительно:
Предел бесконечен, значит, функция не дифференцируема в точке .
Таблица производных элементарных функций
Замечание. Напомним свойства степеней и корней, используемые при дифференцировании функций:
Приведем примеры нахождения производных.
1) .
2)
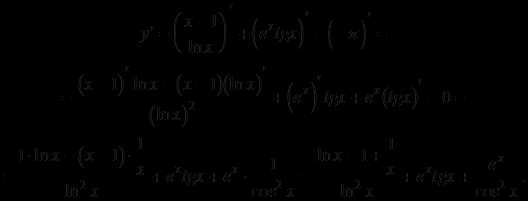
Производная сложной функции
Пусть . Тогда функция будет сложной функцией от x.
Если функция дифференцируема в точке x, а функция дифференцируема в точке u, то тоже дифференцируема в точке x, причем
.
Примеры.
1.
Полагаем , тогда . Следовательно
.
При достаточном навыке промежуточную переменную u не пишут, вводя ее лишь мысленно.
2.
.
Дифференциал
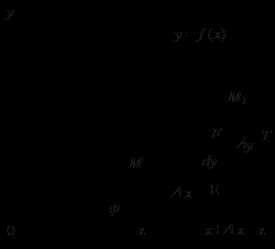 |
К графику непрерывной функции в точке проведем касательную MT, обозначив через j ее угол наклона к положительному направлению оси Ох. Так как , то из треугольника MEF следует, что
.
Введем обозначение
.
Это выражение называется дифференциалом функции . Итак
.
Замечая, что , т.е. что дифференциал независимой переменной равен ее приращению, получим
.
Таким образом, дифференциал функции равен произведению ее производной на дифференциал (или приращение) независимой переменной.
Из последней формулы следует, что , т.е. производная функции равна отношению дифференциала этой функции к дифференциалу аргумента.
Дифференциал функции dy геометрически представляет собой приращение ординаты касательной, соответствующее приращению аргумента Dх.
Из рисунка видно, что при достаточно малом Dх по абсолютной величине можно взять приращение функции приближенно равным ее дифференциалу, т.е.
.
Рассмотрим сложную функцию , где , причем дифференцируема по u, а – по х. По правилу дифференцирования сложной функции
.
Умножим это равенство на dx:
Так как (по определению дифференциала), то
или
Таким образом, дифференциал сложной функции имеет тот же вид, если бы переменная u была не промежуточным аргументом, а независимой переменной.
Это свойство дифференциала называется инвариантностью (неизменяемостью) формы дифференциала.
Пример. .
Все правила дифференцирования можно записать для дифференциалов.
Пусть – дифференцируемы в точке х. Тогда
Докажем второе правило.
Производная неявной функции
Пусть дано уравнение вида , связывающее переменные и . Если нельзя явно выразить через , (разрешить относительно ) то такая функция называется неявно заданной. Чтобы найти производную от такой функции, нужно обе части уравнения продифференцировать по , считая функцией от . Из полученного нового уравнения найти .
Пример. .
Дифференцируем обе части уравнения по , помня, что есть функция от
Лекция 4. Производная и дифференциал функции одной переменной
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Тема 2. Производная и дифференциал функции
Произво́дная (функции в точке) – основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется какпределотношения приращения функции к приращению ееаргументапри стремлении приращения аргумента кнулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс нахождения производной называетсядифференци́рованием.
Обозначения: 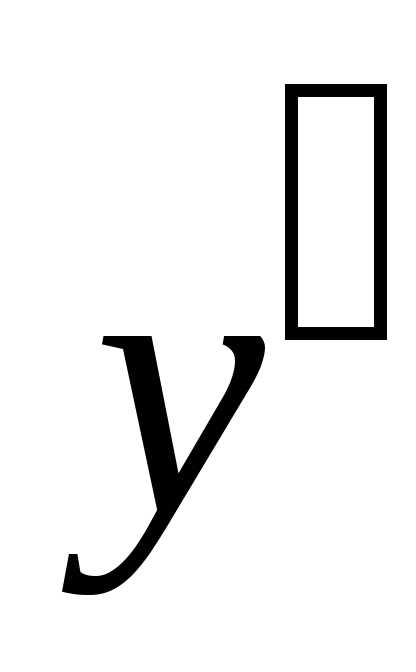 или
или 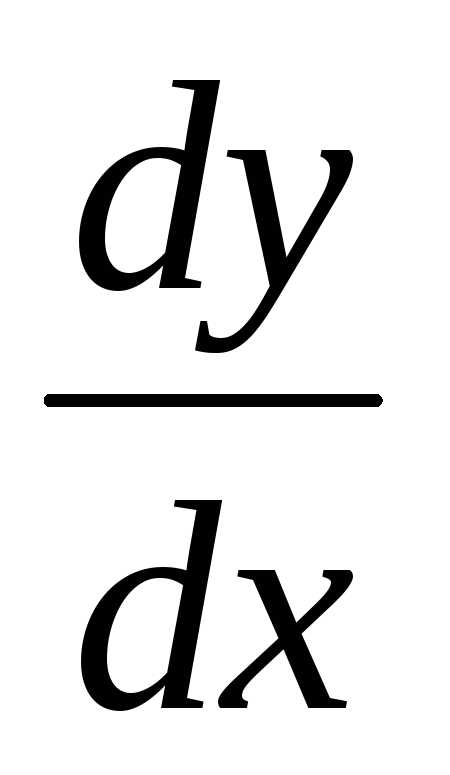 .
.
При вычислении производных используют таблицу производных и правила дифференцирования.
Правила дифференцирования
Пусть u = u(x)иv = v(х)– дифференцируемые функции в точкех = х0, тогда существуют производные от суммы, разности, произведения, частного этих функций в заданнойх0.
Замечание: производная постоянной равна нулю С = 0
Таблица производных основных элементарных функций
№ | y = f(х) | y = f(x) | № | y = f(х) | y = f(x) | |
1 |
|
| 10 |
| ||
2 |
| 11 | ||||
3 |
|
| 12 |
|
| |
4 |
| | 13 |
| ||
5 | | | 14 |
| ||
6 |
| 15 | ||||
7 |
|
| 16 |
| ||
8 |
|
| 17 | |||
9 |
|
| ||||
Задача 1.Найти
производную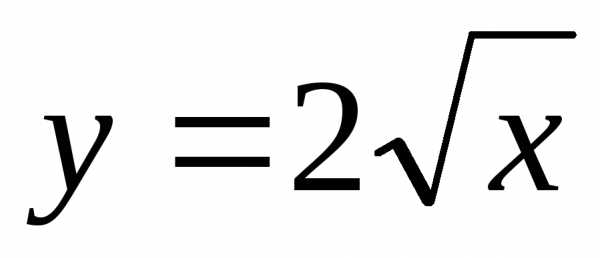 .
.
Решение.
.
В данном решении используем правило дифференцирования Ви формулу 4.
Задача 2. Найти производную функции.
Решение.
В данном решении используем правила дифференцирования А,Ви формулы 3, 7 и 11.
Задача 3. Найти
производную функции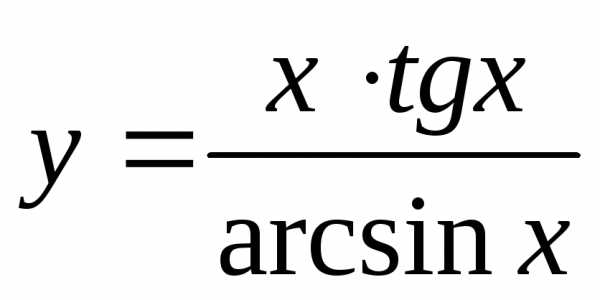 .
.
Решение.
В данном решении используем правила дифференцирования Б,Ги формулы 2, 12, 14.
В задаче 3 видно, что производная функции может получиться достаточно громоздкой и не всегда целесообразно упрощать полученный результат.
Производная сложной функции
Пусть у = f(u),аu = (х),тогдау = f((х))– сложная функция, ее производная находится по правилу дифференцирования сложной функции. Если каждая из функцийу = f(u)иu = (х)дифференцируема по своему аргументу, то
Правило дифференцирования сложной функции: Е.
Обратите внимание
на запись 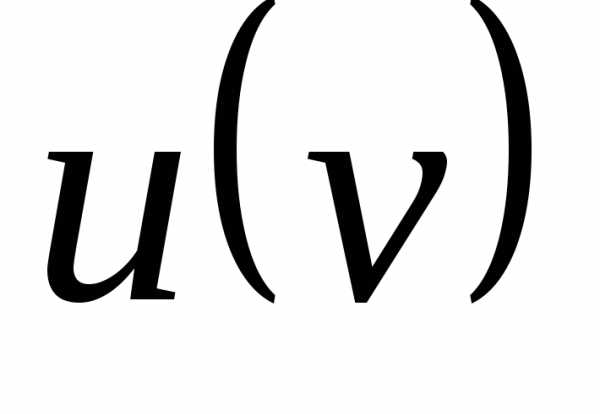 .
Здесь у нас две функции
.
Здесь у нас две функции и
и ,
причем функция
,
причем функция ,
образно говоря, вложена в функцию
,
образно говоря, вложена в функцию .
Функция такого вида (когда одна функция
вложена в другую) и называется сложной
функцией.
.
Функция такого вида (когда одна функция
вложена в другую) и называется сложной
функцией.
Задача 4. Найти производную функции
Решение:
Под косинусом у
нас находится не просто буква «икс», а
целое выражение 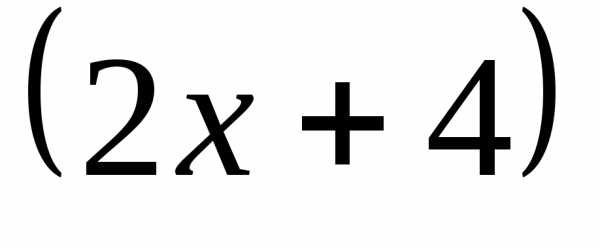 ,
поэтому найти производную сразу по
таблицепроизводных основных
элементарных функцийне получится.
,
поэтому найти производную сразу по
таблицепроизводных основных
элементарных функцийне получится.
В данном примере
функция
– это сложная функция, причем многочлен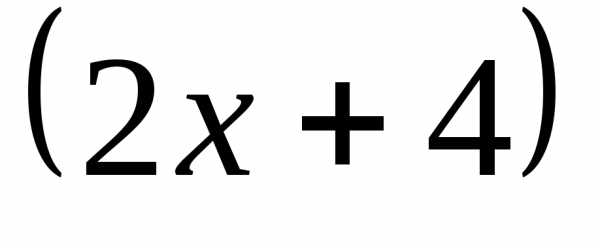 является внутренней функцией (вложением),
а– внешней функцией.
является внутренней функцией (вложением),
а– внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобыразобраться, какая функция является внутренней, а какая – внешней. После этого необходимо применить правило дифференцирования сложной функции (правилоЕ).
Начинаем решать:
Сначаланаходим производную внешней функции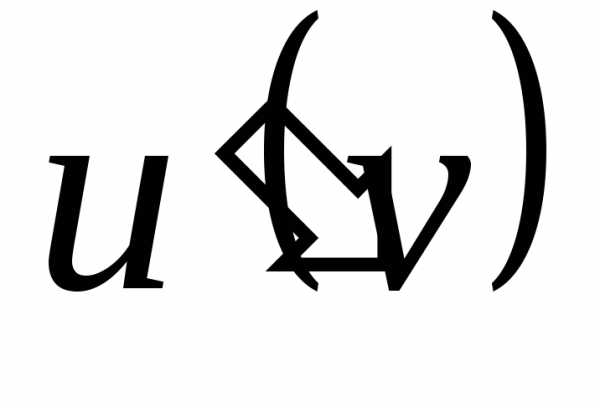 (косинуса), смотрим на таблицу производных
элементарных функций правило №11 и
замечаем, что
.Все табличные формулы
применимы и в том, случае, если «икс»
заменить сложным выражением, в
данном случае:
(косинуса), смотрим на таблицу производных
элементарных функций правило №11 и
замечаем, что
.Все табличные формулы
применимы и в том, случае, если «икс»
заменить сложным выражением, в
данном случае:
Обратите внимание,
что внутренняя функция 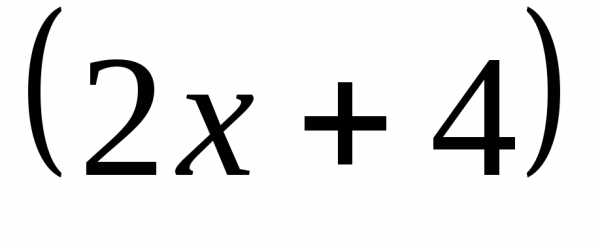 не изменилась, её мы не трогаем.
не изменилась, её мы не трогаем.
Ну и совершенно
очевидно, что 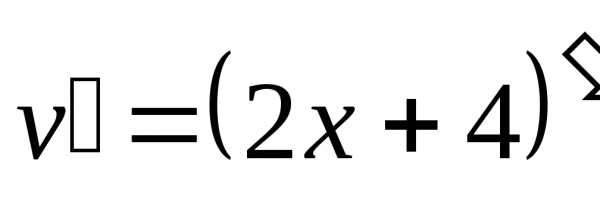 .
.
Результат применения формулы в чистовом оформлении выглядит так:
Далее мы берем производную внутренней функции, она очень простая:
Таблица производных основных сложных функций
№ | y = f(u), u = (х) | у = f(u)u | № | y = f(u), u = (х) | у = f(u)u | |
| ||||||
| | | | |||
| | | ||||
| | |||||
| | | ||||
| | | ||||
| | | ||||
| ||||||
studfiles.net
Производная и дифференциал — Мегаобучалка
Определение 1. Пусть функция определена на множестве , точки и . Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при (при условии, что этот предел существует): .
Определение 2.Функция называется дифференцируемой в точке , если её приращение в этой точке можно представить в виде , где – вещественное число, .
Теорема 1.Для того чтобы функция являлась дифференцируемой в точке , необходимо и достаточно, чтобы .
Определение 3. Дифференциалом функции в точке называется главная линейная относительно часть приращения функции в этой точке: .
Определение 4. Дифференциалом независимой переменной называется приращение этой переменной: .
Основные правила вычисления производных
1. Если функции , дифференцируемы в точке , то сумма (разность), произведение и частное (при условии ) этих функций также дифференцируемы в точке , причем справедливы следующие формулы:
, , .
2. Если функция дифференцируема в точке, а – число, то .
3. Пусть функция имеет производную в точке , а функция имеет производную в точке . Тогда сложная функция имеет производную в точке и справедлива формула: .
4. Если функция определена, непрерывна и строго монотонна на отрезке , то у нее существует обратная функция , производная которой вычисляется по формуле: .
Таблица производных элементарных функций
Основные правила вычисления дифференциалов
1. Если функции , дифференцируемы в точке , принадлежащей их общей области определения, то сумма (разность), произведение и частное (при условии ) этих функций также дифференцируемы в этой точке, причем справедливы следующие формулы:
, , .
2. Если функция дифференцируема в точке , а , то .
3. Пусть функция дифференцируема в точке , а функция дифференцируема в точке . Тогда сложная функция дифференцируема в точке и справедлива формула: .
Таблица дифференциалов элементарных функций
Пример 1.Вычислить производную функции .
Решение. .
Пример 2.Найти первый дифференциал функции в точке .
Решение. 1) Вычислим производную функции : .
2) Вычислим значение производной функции в точке : .
3) Тогда .
Уравнение касательной к графику функции в точке :
.
Геометрический смысл производной: значение производной функции в точке равно тангенсу угла наклона к положительному направлению оси касательной к графику этой функции в точке .
Пример 3. Составить уравнение касательной к графику функции в точке .
Решение. 1) Вычислим при : .
2) Вычислим значение производной функции в точке : .
3) Составим уравнение касательной: или .
Экономический смысл производной: производная объёма произведенной продукции по времени есть производительность труда в момент .
megaobuchalka.ru