Как найти длину средней линии в треугольнике: Средняя линия треугольника на клетчатой бумаге

Основные определения. Линии в треугольнике

Треугольником называется фигура, которая состоит из трехточек, не лежащих на одной прямой, и трех отрезков, соединяющих этиточки попарно. Точки называются вершинами, а отрезки — сторонами треугольника.

Треугольник называется разносторонним, если любые две стороны его не равны друг другу.

Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

Треугольник, все стороны которого равны, называется равносторонним.
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один из его углов тупой.

Внешним углом треугольника на­зывается угол, смежный с каким-нибудь углом этого треугольника.

 

 

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

---

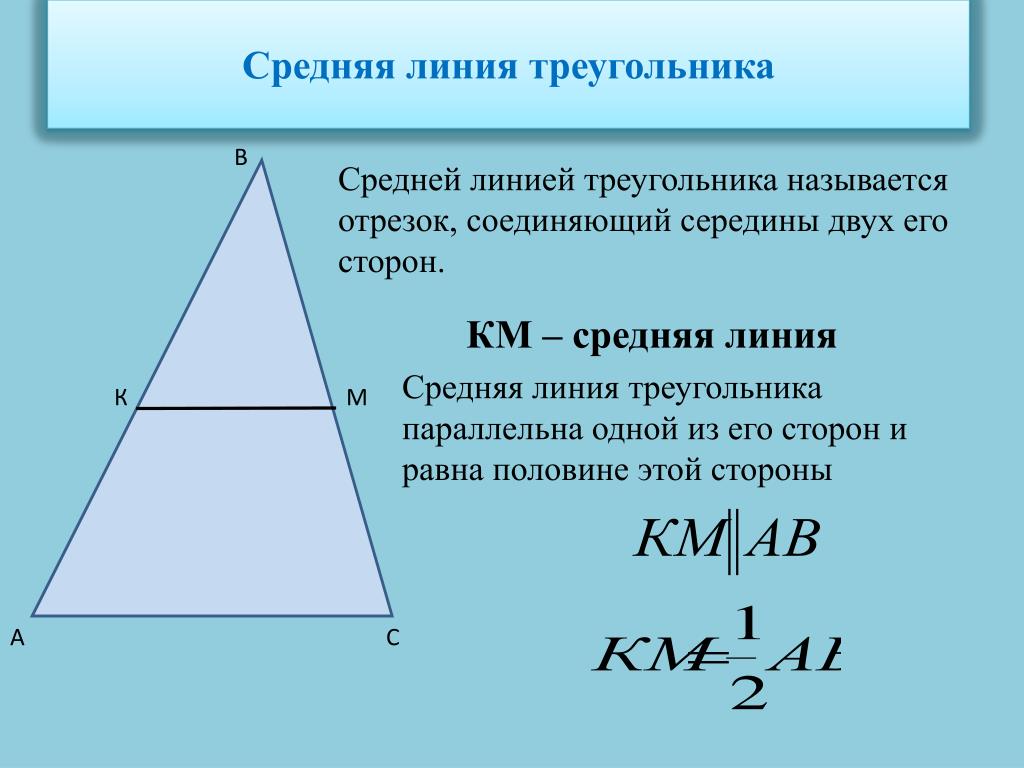
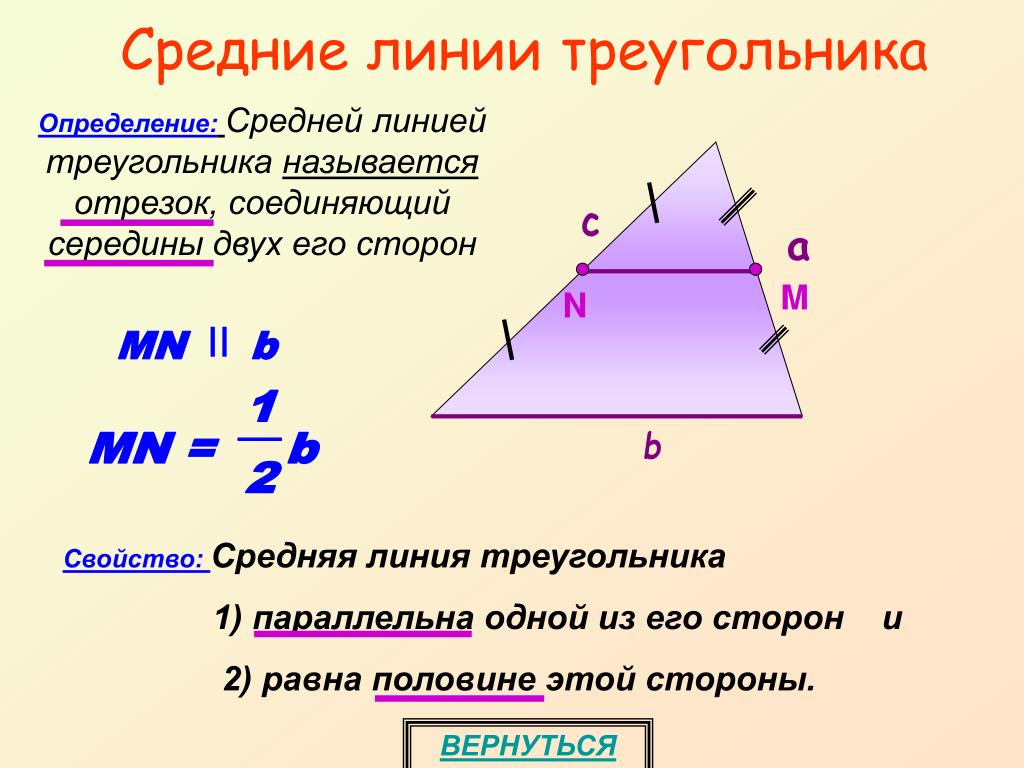
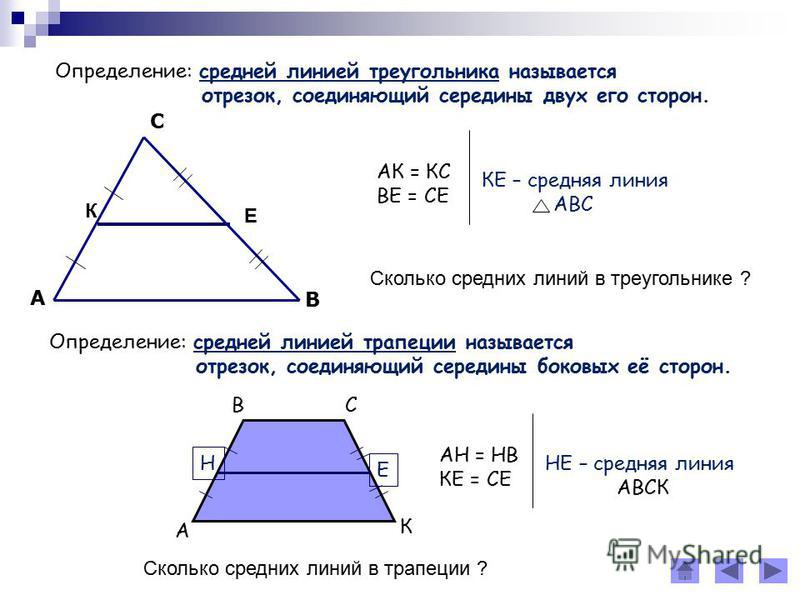
Средняя линия треугольника — отрезок, соединяющий середины двух сторон.

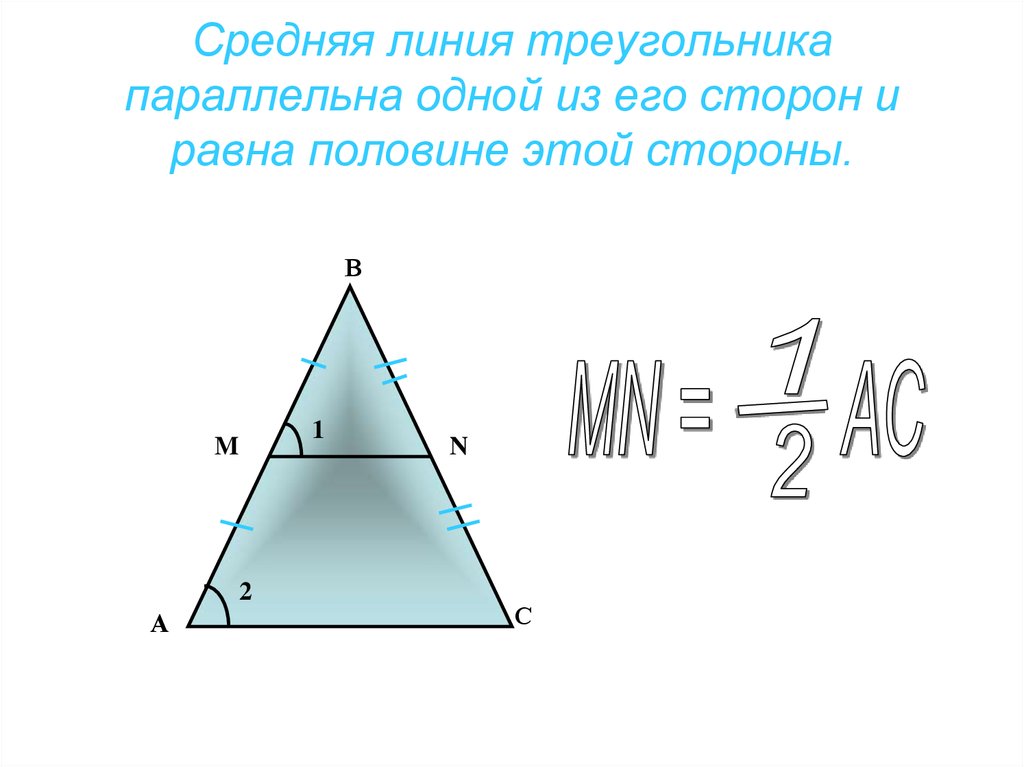
1. Средняя линия треугольника параллельна третьей стороне и равна половине этой стороны.
2. Средняя линия отсекает от треугольника треугольник подобный исходному, коэффициент подобия равен 1/2.

---

Медиана треугольника, проведенная из данной вершины, — отрезок прямой, соединяющий данную вершину с серединой противоположной стороны.

1. Во всяком треугольнике медианы пересекаются в одной точке и делятся этой точкой в отношении 2:, считая от вершины.
2. Медиана есть геометрическое место точек, являющихся серединами отрезков прямых, заключенных внутри треугольника и параллельных той стороне, к которой проведена медиана.

Точку пересечения медиан называют центроидом треугольника. Эта точка является центром тяжести (центром масс) треугольника, если:

• система состоит из трех одинаковых точечных масс, сосредоточенных в вершинах треугольника;
• масса системы равномерно распределена по периметру треугольника;
• масса системы равномерно распределена по всему треугольнику.

Центроид является точкой, для которой сумма квадратов расстоянний ее от вершин треугольника принимает наименьшее значение.

---

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противоположныю сторону (или ее продолжение).

1. Высоты треугольника пересекаются в одной точке.

 

---

Бисектриса внутреннего угла треугольника — отрезок прямой, делящей данный угол на две равные части, соединяющий вершину угла с точкой на противоположной стороне.

 

1. Бисектриса есть множество точек, равноудаленных от сторон угла.
2. Во всяком треугольнике бисектрисы пересекаются в одной точке, являющейся центром вписанной в треугольник окружности.
3. Бисектриса любого внутреннего ула делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
4. Бисектриса лежит между соответствующими медианой и высотой, и ее длина заключена между длиной медианы и длиной высоты h_a< l_a< m_a.
5. Бисектрисы смежных углов перпендикулярны.

---

Срединный перпендикуляр к стороне треугольника — прямая, перпендикулярная стороне треугольника и проходящая через ее середину.

1. Все три срединных перпендикуляра пересекаются в одной точке, являющейся центром описанной вокруг треугольника окружности. Эта точка лежит внутри треугольника, если треугольник остроугольный; на середине гипотенузы, если треугольник прямоугольный; вне треугольника, если треугольник тупоугольный.

---

Чему равна длина средней линии в треугольнике?

Чему равна длина средней линии в треугольнике?

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей стороне, а ее длина равна половине длины этой стороны. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Теорема.

Как доказать теорему о средней линии треугольника?

Если отрезок параллелен стороне треугольника и равен его половине, то отрезок является средней линией. Средняя линия треугольника делит пополам любой отрезок (хорду), соединяющую вершину треугольника с точкой на стороне, параллельной средней линии.

Чему равна средняя линия в параллелограмме?

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Что делает средняя линия?

Свойства средняя линия треугольника параллельна основанию и равна его половине. средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника. три средние линии делят исходный треугольник на четыре равных треугольника.

Чему равна средней линии трапеции?

Средняя линия трапеции парал- лельна основаниям и равна их полусумме. ⊳ Признак средней линии трапеции. Если отрезок с концами на боковых сторонах трапеции выходит из середины одной боковой стороны и параллелен основаниям, то этот отрезок средняя линия трапеции.

Как доказать теорему о средней линии трапеции?

Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям. Теорема: Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Что такое диагонали в трапеции?

Диагонали трапеции – это отрезки, соединяющие противоположные вершины трапеции.

Чему равны углы в равнобедренной трапеции?

Углы В равнобедренной трапеции углы при основаниях попарно равны. На рисунке ниже углы ∠ABC и ∠DCB являются одинаковыми тупыми углами, а углы ∠BAD и ∠CDA являются одинаковыми острыми углами.

Как найти высоту у равнобедренной трапеции?

Примечание: если диагонали равнобедренной трапеции взаимно перпендикулярны, то ее высота равняется половине суммы оснований или, другими словами, средней линии.

Как найти высоту трапеции если известны ее основания?

Зная площадь трапеции и ее среднюю линию (или два основания, среднее арифметическое которых дает среднюю линию), можно вычислить высоту трапеции, разделив одно на другое: Более изощренным является вычисление высоты трапеции через все ее стороны.

Средняя линия треугольника – формула, теорема, доказательство, примеры

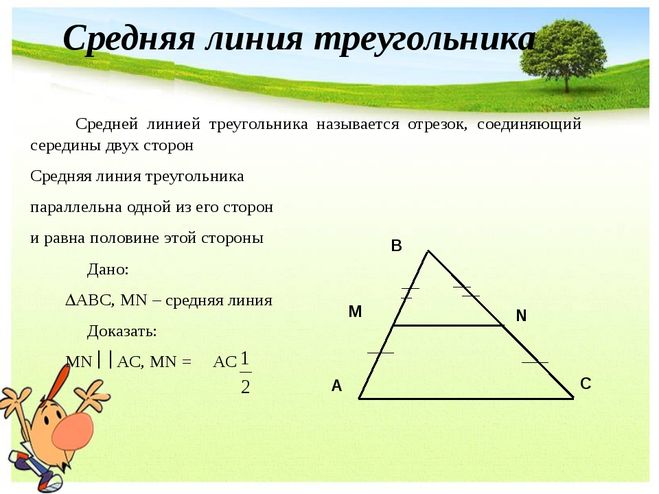
Что такое средняя линия треугольника

Средняя линия треугольника – это линия, соединяющая середины или центры любых двух (соседних или противоположных) сторон треугольника. Она параллельна третьей стороне и составляет половину длины третьей стороны.

Сколько средних сегментов у треугольника

Поскольку у треугольника три стороны, каждый треугольник имеет 3 средние сегмента.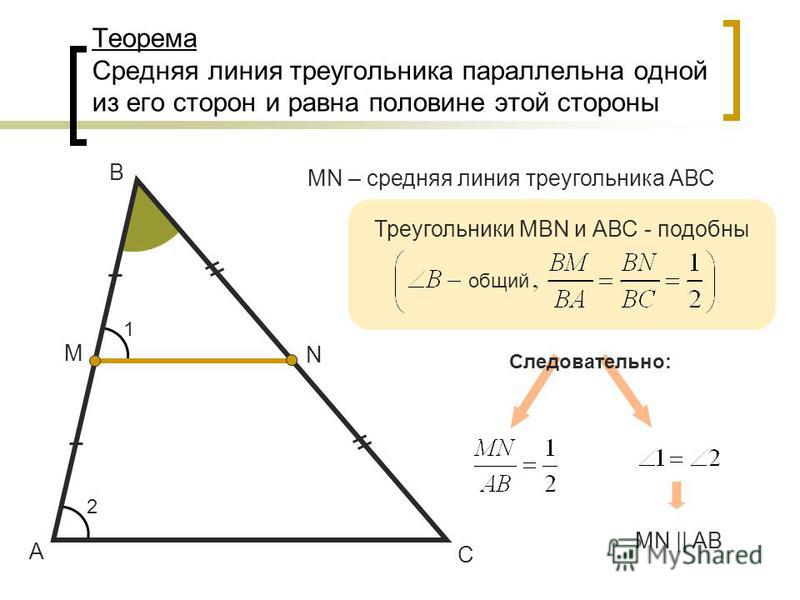 В заданном ∆ABC DE, EF и DF являются тремя средними сегментами. 3 средних сегмента образуют меньший треугольник, похожий на главный треугольник. Таким образом, ∆ABC ~ ∆FED

Средняя линия треугольника

Свойства

Свойства средних частей треугольника

1. Соединяет середины двух сторон треугольника; в ∆ABC D — середина AB, E — середина AC и F — середина BC
2. Треугольник имеет 3 возможных середины сегмента; DE, EF и DF — три средние линии
3. Средняя линия всегда параллельна третьей стороне треугольника; так, DE ∥ BC, EF ∥ AB и DF ∥ AC
4. Средний отрезок всегда равен 1/2 длины третьей стороны; таким образом, DE =1/2 до н.э., EF =1/2 AB и DF =1/2 AC

Формула

Как найти среднюю линию треугольника

Формула для определения средней линии треугольника приведена ниже:

Средняя линия треугольника Формула

Теорема о середине треугольника

Теорема о середине треугольника Теорема

Доказать: DE ∥ до н.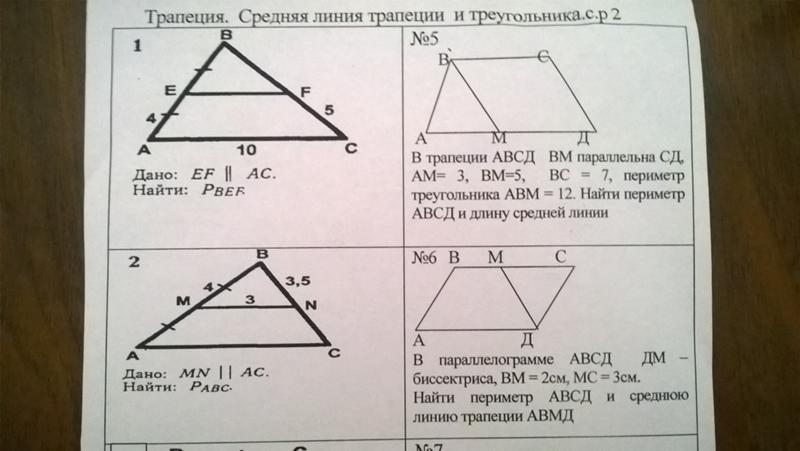 э.; DE = ½ BC

Доказательство : Прямая проведена параллельно AB так, что когда средний отрезок DE пересекается с параллельной линией в точке F

Given: D is the midpoint of AB

E is the midpoint of AC

F is the midpoint of BC

69969969969969969969969969969969969969969969969969.69.69

Steps	Statement	Reason
1.	In ∆ADE and ∆CFE AE = EC ∠AED  = ∠CEF ∠DAE  = ∠ECF	E is the midpoint of AC Vertically opposite angle Alternate angles
2.	∆ADE ≅ ∆CFE	By AAS congruency of triangle
3.	DE = FE AD = CF	Corresponding parts of Congruent triangles (CPCTC)  are congruent
4.	AD = BD BD = CF	D — средняя точка AB
5.	DF ∥ BC и DF = BC DE ∥ BC и DF = BC DE = ½ DF	DBCF — Paralleogram
9969969969969699.	. DE = 1/2 BC	DF = BC Отсюда доказано

Обратная теорема о средней линии треугольника

Обратная теорема о средней линии треугольника

Обратная теорема о средней линии треугольника Доказательство

Чтобы доказать : DE является средней линией ∆ABC

AD

9000; AE = EC

Доказательство :

Дано: D — средняя точка AB

E — средняя точка AC

DE ∥ BC

DE = 1/2 до н.э.

ШАГИ

9009,9,707069.70707069.7070707069.70707069.70707069.70707069.70707069.707069.707069. ∥ CF

. Заявление	Разум
1.	г. н.э. = дБ AB = AD + DB = DB + DB = 2DB	D — средняя точка
DBCF — это параллелограмм
3.	BD = CF DA = CF	противоположные стороны параллелограммы равны
4.	in y
4.	in y n. n.cfe
4.	in o o o o o o o o o o o o o o o o o o o o o o o o y n. n. n. n.	∠AED  = ∠CEF (вертикально противоположный угол) ↑DAE = ↑ECF (альтернативные углы)
5.	∆ADE ≅ ∆CFE	по AAS Congruency of Triangle
6.	AE
6.	AE eae
. AC) Аналогично, AD = DB (D — середина AB) DE — середина отрезка ∆ABC	Соответствующие части конгруэнтных треугольников (CPCTC) конгруэнтны

Решенные примеры

4

7 Найти 9 in данный треугольник. Дано BC = 22 см, а M, N — середины AB и AC.

Решение:

Как мы знаем, по теореме о серединах
MN = ½ BC, здесь BC = 22см
 = ½ x 22 = 11см

. Найдите ФГ.

Решение:

Как мы знаем, по теореме о средней точке
HI = ½ FG, здесь HI = 17 м
FG = 2 HI = 2 x 17 = 34 м данный треугольник. Учитывая, что D и E являются средними точками.

Решение:

Как мы знаем, по теореме о средней точке
DE = ½ XZ, здесь XZ = 32 единицы
3x -2 = ½ x 32
3x = 16 + 2 x = 6

Автор Анна Щепанек, доктор философии

Отзыв от Davide Borchia

Последнее обновление: 11 октября 2022 г.

Содержание:

• Что такое средняя линия треугольника?
• Как найти среднюю линию треугольника?
• Как использовать этот средний сегмент калькулятора треугольника?
• Другие калькуляторы треугольников от Omni
• Часто задаваемые вопросы

Добро пожаловать в средний сегмент калькулятора треугольников Omni ! Независимо от того, являетесь ли вы:

• Не знаете, что такое середина треугольника;
• Не знаете, как найти середину треугольника с помощью циркуля и линейки ; или
• Пытаюсь понять, что такое теорема о середине отрезка .

С помощью этого калькулятора среднего сегмента треугольника вы быстро станете экспертом по средним сегментам! Начнем наше путешествие с

определение середины треугольника, давайте?

Что такое средняя линия треугольника?

В треугольнике середина представляет собой линию, которая соединяет середины двух сторон этого треугольника . А середина стороны — это точка, которая находится на равном расстоянии от любой вершины. Поскольку у треугольника три стороны и мы можем соединить середины любых двух сторон, каждый треугольник имеет три середины .

Теорема о середине отрезка

Наиболее важным свойством отрезка является следующее: средний отрезок параллелен стороне, которую мы не использовали, чтобы провести этот средний отрезок (называется основанием ), и его длина равна половине длины этого основания.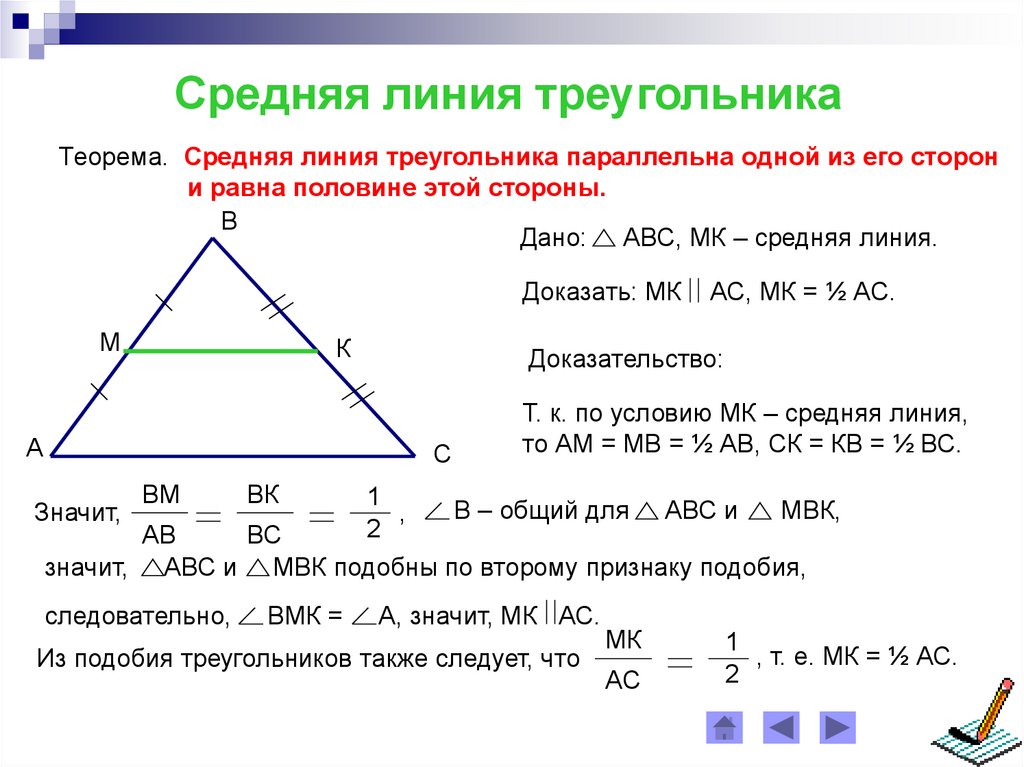 Этот результат известен под названием теоремы о середине треугольника .

Как найти среднюю линию треугольника?

Из определения середины треугольника непосредственно следует, что для нахождения середины нужно соедините середины двух сторон. Для найдите середины с помощью циркуля:

1. Поместите иглу в вершину и начертите дугу с радиусом больше половины стороны.
2. Повторите для другой вершины. Убедитесь, что дуги имеют две точки пересечения .
3. Соединить точки пересечения . Точка, в которой вы пересекаете сторону, является ровно серединой этой стороны .

Как использовать эту среднюю часть калькулятора треугольника?

Вот краткое руководство по эффективному использованию этого инструмента:

1. Выберите режим . Наш средний сегмент калькулятора треугольников может решить два типа задач:
   • Найдите длину среднего сегмента
     , зная длину основания и
   • Найти концы и длину середины по вершинам треугольника (их координаты).
2. Введите необходимые данные в калькулятор.
3. Наслаждайтесь результатом !

Другие калькуляторы треугольников от Omni

Для всех любителей треугольников вот подборка других инструментов треугольников, которые вы можете посетить:

• Площадь треугольника;
• Остроугольный треугольник;
• Центр окружности треугольника;
• Конгруэнтность треугольника;
• Тупоугольный треугольник;
• Косой треугольник;
• Основание треугольника;
• треугольник ААА;
• треугольник ААС;
• треугольник SAS;
• SSS треугольник; и
• Треугольник ASA.

Часто задаваемые вопросы

Какой длины средняя линия треугольника?

Теорема треугольника о среднем отрезке утверждает, что длина среднего отрезка всегда равна половине длины основания , т. е. стороны треугольника, которой не касается средний отрезок.