Как найти длину вектора аб: Найдите длину вектора АВ ,если а А(3;-6,),В(-4;-7).

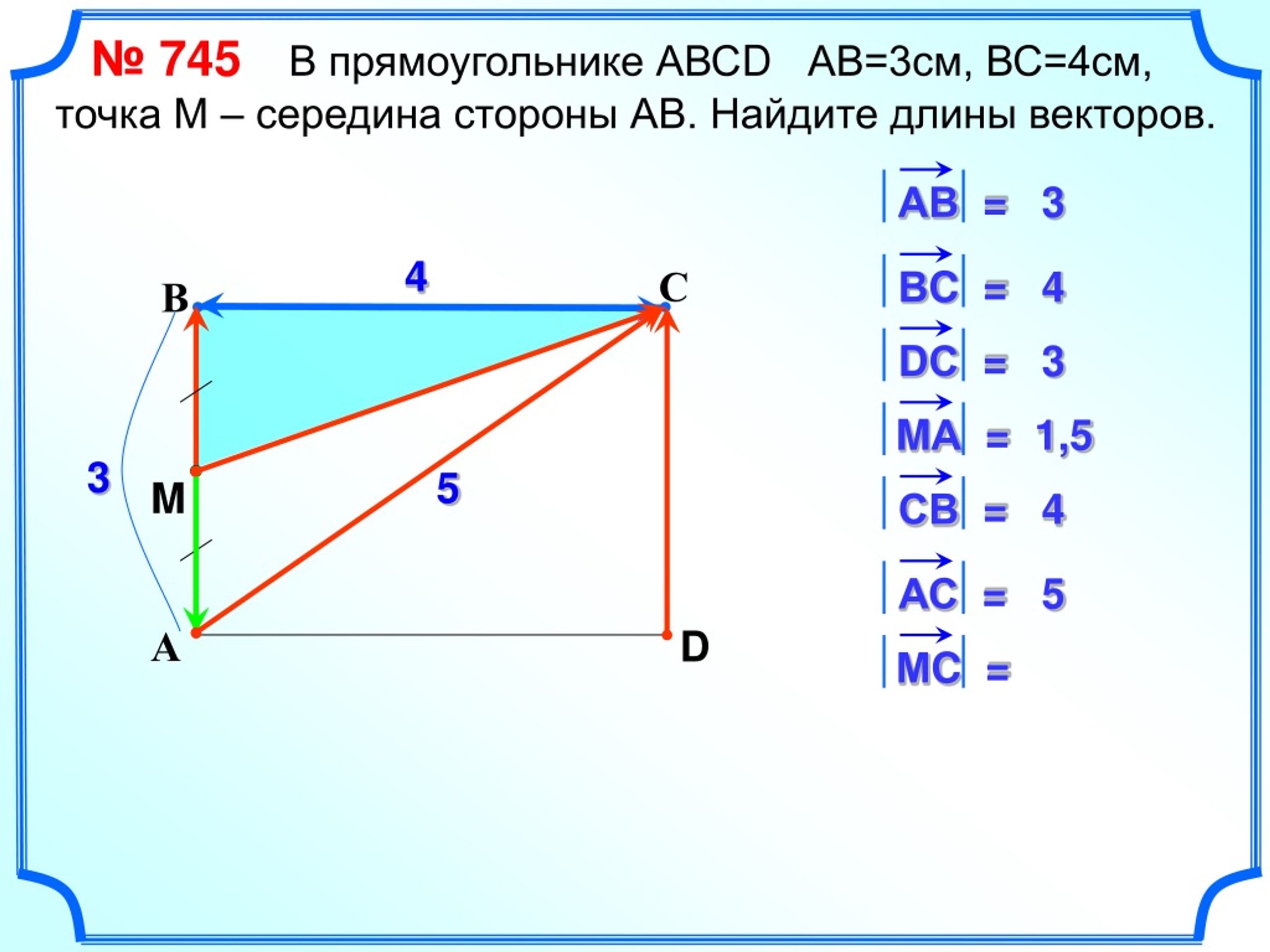
Нахождение длины вектора, примеры и решения. Векторы на ЕГЭ по математике. Действия над векторами Как проверить какой вектор длиннее

6.4. Некоторые приложения скалярного произведения

11. Выражение скалярного произведения вектора через координаты сомножителей. Теорема.

12. Длина вектора, длина отрезка, угол между векторами, условие перпендикулярности векторов.

13. Векторное произведение векторов, его свойства. Площадь параллелограмма.

14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.

15. Способы задания прямой на плоскости.

16. Нормальное уравнение прямой на плоскости (вывод). Геометрический смысл коэффициентов.

17. Уравнение прямой на плоскости в отрезках (вывод).

Приведение общего уравнения плоскости к уравнению плоскости в отрезках.

18. Уравнение прямой на плоскости с угловым коэффициентом (вывод).

19. Уравнение прямой на плоскости, проходящей через две точки (вывод).

20. Угол между прямыми на плоскости (вывод).

21. Расстояние от точки до прямой на плоскости (вывод).

22. Условия параллельности и перпендикулярности прямых на плоскости (вывод).

23. Уравнение плоскости. Нормальное уравнение плоскости (вывод). Геометрический смысл коэффициентов.

24. Уравнение плоскости в отрезках (вывод).

25. Уравнение плоскости, проходящей через три точки (вывод).

26. Угол между плоскостями (вывод).

27. Расстояние от точки до плоскости (вывод).

28. Условия параллельности и перпендикулярности плоскостей (вывод).

29. Уравнения прямой в r3. Уравнения прямой, проходящей через две фиксированные точки (вывод).

30. Канонические уравнения прямой в пространстве (вывод).

Составление канонических уравнений прямой в пространстве.

Частные случаи канонических уравнений прямой в пространстве.

Канонические уравнения прямой проходящей через две заданные точки пространства.

Переход от канонических уравнений прямой в пространстве к другим видам уравнений прямой.

31. Угол между прямыми (вывод).

32. Расстояние от точки до прямой на плоскости (вывод).

Расстояние от точки до прямой на плоскости – теория, примеры, решения.

Первый способ нахождения расстояния от заданной точки до заданной прямой на плоскости.

Второй способ, позволяющий найти расстояние от заданной точки до заданной прямой на плоскости.

Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости.

Расстояние от точки до прямой в пространстве – теория, примеры, решения.

Первый способ нахождения расстояния от точки до прямойaв пространстве.

Второй способ, позволяющий находить расстояние от точки до прямойaв пространстве.

33. Условия параллельности и перпендикулярности прямых в пространстве.

34. Взаимное расположение прямых в пространстве и прямой с плоскостью.

35. Классическое уравнение эллипса (вывод) и его построение. Каноническое уравнение эллипса имеет вид, где– положительные действительные числа, причём.Как построить эллипс?

36. Классическое уравнение гиперболы (вывод) и его построение. Асимптоты.

37. Каноническое уравнение параболы (вывод) и построение.

38. Функция. Основные определения. Графики основных элементарных функций.

39. Числовые последовательности. Предел числовой последовательности.

40. Бесконечно малые и бесконечно большие величины. Теорема о связи между ними, свойства.

41. Теоремы о действиях над переменными величинами, имеющими конечные пределы.

42. Число e.

Содержание

Способы определения

Свойства

История

Приближения

43. Определение предела функции. Раскрытие неопределённостей.

44. Замечательные пределы, их вывод. Эквивалентные бесконечно малые величины.

Содержание

Первый замечательный предел

Второй замечательный предел

45. Односторонние пределы. Непрерывность и разрывы функции. Односторонние пределы

Левый и правый пределы функции

Точка разрыва первого рода

Точка разрыва второго рода

Точка устранимого разрыва

46. Определение производной. Геометрический смысл, механический смысл производной. Уравнения касательной и нормали к кривой и точке.

47. Теоремы о производной обратной, сложной функций.

48. Производные простейших элементарных функций.

49. Дифференцирование параметрических, неявных и степенно-показательных функций.

21. Дифференцирование неявных и параметрически заданных функций

21.1. Неявно заданная функция

21.2. Функция, заданная параметрически

50. Производные высших порядков. Формула Тейлора.

51. Дифференциал. Применение дифференциала к приближенным вычислениям.

52. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.

53. Теорема о необходимом и достаточном условиях монотонности функции.

54. Определение максимума, минимума функции. Теоремы о необходимом и достаточном условиях существования экстремума функции.

Теорема (необходимое условие экстремума)

55. Выпуклость и вогнутость кривых. Точки перегиба. Теоремы о необходимом и достаточном условиях существования точек перегиба.

Доказательство

57. Определители n-ого порядка, их свойства.

58. Матрицы и действия над ними. Ранг матрицы.

Определение

Связанные определения

Свойства

Линейное преобразование и ранг матрицы

59. Обратная матрица. Теорема о существовании обратной матрицы.

60. Системы линейных уравнений. Матричное решение систем линейных уравнений. Правило Крамера. Метод Гаусса. Теорема Кронекера-Капелли.

Решение систем линейных алгебраических уравнений, методы решения, примеры.

Определения, понятия, обозначения.

Решение элементарных систем линейных алгебраических уравнений.

Решение систем линейных уравнений методом Крамера.

Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).

Решение систем линейных уравнений методом Гаусса.

Решение систем линейных алгебраических уравнений общего вида.

Теорема Кронекера – Капелли.

Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.

Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.

Решение систем уравнений, сводящихся к слау.

Примеры задач, сводящихся к решению систем линейных алгебраических уравнений.

Вектором называется направленный отрезок. Длиной или модулем вектора называется длина соответствующего направленного отрезка.

Модуль вектора a обозначается . Векторa называется единичным, если . Векторы называются коллинеарными, если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.

2. Умножение вектора на число. Свойства операции.

Умножение вектора на число, даёт противоположно направленный вектор в длиной враз больше. Умножение вектора на число в координатной форме производится умножением всех координат на это число:

Исходя из определения получается выражение для модуля вектора, умноженного на число:

Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:

А вычитание векторов можно переписать через сложение и умножение:

Исходя из того, что умножение на не меняет длины вектора, а меняет только направление и учитывая определение вектора, получаем:

3. Сложение векторов, вычитание векторов.

В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

Для геометрического построения вектора суммы используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов инекоторой точки будет тем же, что применение сразу одного переноса, соответствующего этому правилу. Для сложения двух векторовипо правилутреугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной :

Правило многоугольника

Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом-го (то есть изображается направленным отрезком, замыкающим ломаную).

Так же называется правилом ломаной.

Правило параллелограмма

Для сложения двух векторов ипо правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. (Легко видеть, что эта диагональ совпадает с третьей стороной треугольника при использовании правила треугольника).

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Модуль суммы векторов

Модуль суммы двух векторов можно вычислить, использую

теорему косинусов :

Где — косинус угла между векторамии.

Если векторы изображены в соответствии с правилом треугольника и берется угол по рисунку — между сторонами треугольника — что не совпадает с обычным определением угла между векторами, а значит и с углом в приведенной формуле, то последний член приобретает знак минус, что соответствует теореме косинусов в ее прямой формулировке.

Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:

Вычитание векторов

Два вектора и вектор их разности

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

Для получения вектора разности начала векторов соединяются и началом векторабудет конец, а концом — конец. Если записать, используя точки векторов, то.

Модуль разности векторов

Три вектора , как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным:

где — косинус угла между векторамии

Отличие от формулы модуля суммы в знаке перед косинусом, при этом надо хорошо следить, какой именно угол берется (вариант формулы модуля суммы с углом между сторонами треугольника при суммировании по правилу треугольника по виду не отличается от данной формулы для модуля разности, но надо иметь в виду, что для тут берутся разные углы: в случае суммы берётся угол, когда вектор переносится к концу вектора, когда же ищется модель разности, берётся угол между векторами, приложенными к одной точке; выражение для модуля суммы с использованием того же угла, что в данном выражении для модуля разности, отличается знаком перед косинусом).

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a x и a y , то длину вектора можно найти по формуле

В случае вектора в пространстве добавляется третья координата

В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9 , см. файл примера ).

Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9 .

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)) .

2. Нахождение длины вектора через координаты точек

Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() в озвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ() ).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание : для наглядности в ячейке со значением угла в градусах можно применить , см. например, статью

На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).

Формула определения координат вектора для двухмерных задач.

В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:

= (x 2 — x 1 ; y 2 — y 1).

Формула определения координат вектора для пространственных задач.

В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:

= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).

Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора . (Свойство 3, приведенное ниже).

Свойства координат вектора.

1. Любые равные векторы в единой системе координат имеют равные координаты .

2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.

3. Квадрат длины любого вектора равен сумме квадратов его координат .

4.При операции умножения вектора на действительное число каждая его координата умножается на это число.

5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .

6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок .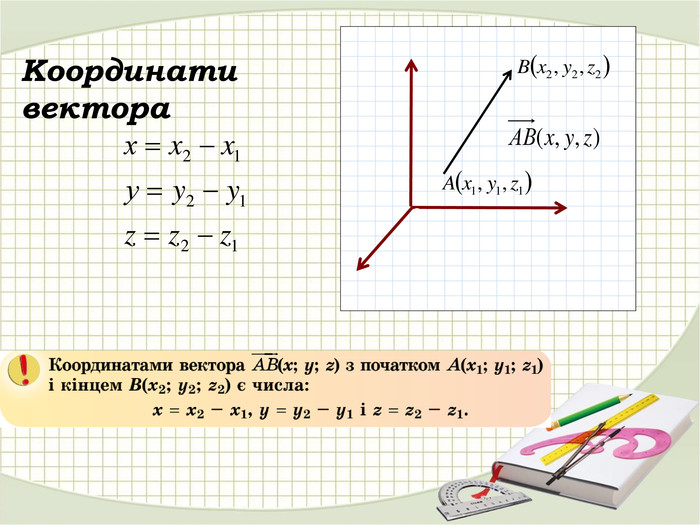 Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. 2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

Прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок . Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$=x$, $[ OA_2]=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=^2+^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.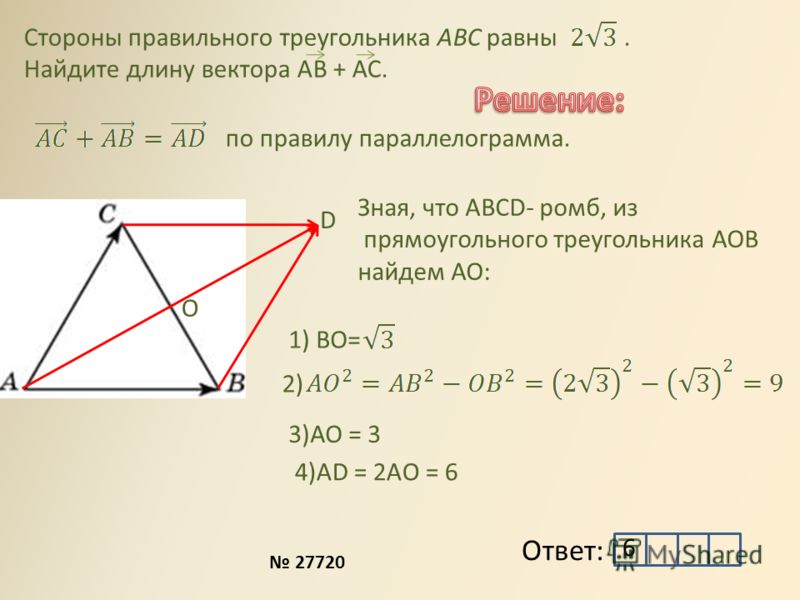

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

3.Координаты вектора

1.вектор — это элемент векторного пространства (или иначе: линейного пространства). геометрический объект, характеризуемый направлением ( т.е. заданной с точностью до параллельности прямой и направлением на ней) и длиной. Векторы можно складывать и умножать на число. Вектор также можно представить в виде линейной комбинации других векторов. 

Модулем (длиной) вектора называется длина соответствующего направленногоотрезка AB и обозначается как/АВ/

Дваненулевых вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м, но не рекомендуется, синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.Необходимым и достаточным условием компланарности 3-х векторов.есть условие abc=0

Понятие вектор в геометрии отлично от определяемого в алгебре. Различают понятие свободного и связанного (приложенного, закреплённого) вектора.

Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства.

Свободный вектор — класс эквивалентности направленных отрезков.При этом два направленных отрезка считаются эквивалентными, если они:

1. коллинеарны

2. равны по длине

3. одинаково направлены (сонаправлены)

Существует естественный изоморфизм свободных векторов и параллельных переносов пространства (каждый перенос взаимно однозначно соответствует какому-то свободному вектору). На этом также строят геометрическое определение свободного вектора, просто отождествляя его с соответственным переносом.

Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.

2.Действия над векторами

Сумма. Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и bслужат сторонами параллелограмма, а вектор c — его диагональю 

Приизведение.Произведением вектора a на вещественное число  называется вектор b, определяемый условием

1)    и, если   , то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если   , и противоположно, если   .  Разность. Разностью векторов a и b называется сумма   .  Разность обозначается а-в, то есть а-в=а+(-в)

Правило параллелограмма

Сложение векторных величин производится по правилу параллелограмма: сумма двух векторов   и  , приведенных к общему началу, есть третий вектор  , длина которого равна длине параллелограмма, построенного на векторах   и  , а направлен он от точки A к точке B

Правило многоугольника

Правило многоугольника применяется, если нужно найти сумму трех или большего числа векторов.  Сумма нескольких векторов не зависит от того, в каком порядке они складываются. От произвольной точки О отложен вектор   затем от точки А отложен вектор   и, наконец, от точки В отложен вектор   В результате получается вектор 

Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.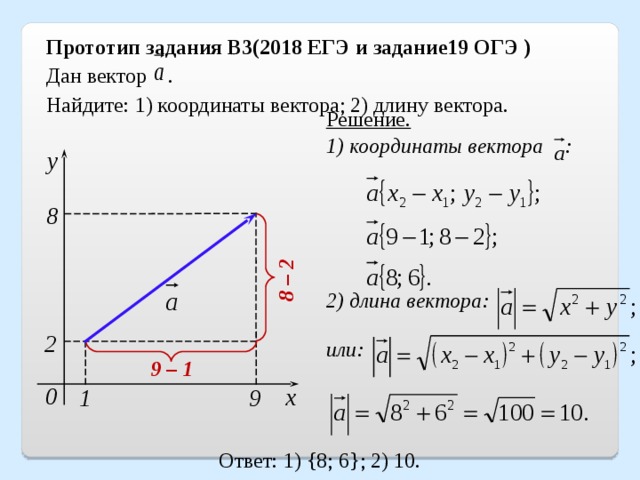

где   — координаты вектора

Свойства

Равные векторы в единой системе координат имеют равные координаты

Координаты коллинеарных векторов пропорциональны:

Подразумевается, что координаты вектора b не равны нулю.

При умножении вектора на действительное число каждая его координата умножается на это число:

При сложении векторов соответствующие координаты векторов складываются:

Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:

Векторное произведение двух векторов можно вычислить с помощью определителя матрицы

где

Аналогично, смешанное произведение трех векторов можно найти через определитель

4.

Скалярное произведение. Угол между векторами

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

 т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

  Угол между векторами 

5.Условие параллельности и перпендикулярности векторов

Условия параллельности

КОЛЛИНЕАРНЫЕ ВЕКТОРЫ

— векторы, параллельные одной плоскости. Необходимым и достаточным условием компланарности трех векторов

является равенство:

Условия перпендикулярности

Векторы перпендикулярны при к1= -1/к2

6.Уравнение прямой на плоскости Уравнение прямой с угловым коэффициентом

у = kx + b

Уравнение прямой в отрезках

Общее уравнение прямой

Уравнение прямой с данным вектором нормали

и проходящей через данную точку

Уравнение с данным направляющим вектором и проходящей через данную точку

7. Векторное параметрическое уравнение прямой в пространстве:

2

где  — радиус-вектор некоторой фиксированной точки M₀, лежащей на прямой,  — ненулевой вектор, коллинеарный этой прямой,  — радиус-вектор произвольной точки прямой.

Параметрическое уравнение прямой в пространстве:

где  — координаты некоторой фиксированной точки M₀, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.

Каноническое уравнение прямой в пространстве:

где  — координаты некоторой фиксированной точки M₀, лежащей на прямой;  — координаты вектора, коллинеарного этой прямой.

Общее векторное уравнение прямой в пространстве:

Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:

и

то уравнение прямой можно задать системой этих уравнений:

8. Прямые  линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися.

Найдите длину вектора A+B, зная длину вектора A, длину вектора B и угол между ними

Исчисление

Джон Г.

спросил 12.02.20

Предположим, что длина вектора A, [[A]] = 4, длина вектора B, [[B]] =√3, угол между ними равен Pi/6. Найдите длину A+B, [[A+B]]

Подписаться І 1

Подробнее

Отчет

1 ответ эксперта

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Йосеф Т. ответил 12.02.20

Репетитор

4.9 (62)

РПИ к. т.н. Репетитор по математике/физике со страстью к обучению

Об этом репетиторе ›

Об этом репетиторе ›

Есть два способа решить эту проблему. Один разлагает векторы на их горизонтальные и вертикальные компоненты, а затем использует теорему Пифагора, чтобы найти длину суммы. Другой использует закон косинусов. Я представлю здесь оба метода.

Разложение векторов на компоненты:

Задача никогда не говорила, в каких направлениях обращены векторы, только то, что они были разделены углом 30 градусов. (На самом деле в задаче указано число пи/6 радиан, но мы знаем, что число пи/6 радиан составляет 30 градусов.) Хорошая новость заключается в том, что мы можем принять любое направление для первого вектора и всегда получать один и тот же ответ.

Я предполагаю, что первый вектор совершенно горизонтален, а второй вектор указывает на 30 градусов вверх от горизонтали.

Мы хотим найти горизонтальную и вертикальную составляющие каждого из двух векторов, затем сложить эти компоненты, чтобы получить горизонтальную и вертикальную составляющие суммы (называемой результирующей ), и, наконец, вычислить ее длину, используя пифагорову формулу. теорема.

Первый вектор прост, потому что он горизонтальный. В задаче сказано, что длина равна 4. Получаем 9.0003

A _Horizontal = 4.

A _{Вертикальный} = 0.

Далее, мы делаем то же самое для вектора. используйте тригонометрию, чтобы найти его горизонтальную и вертикальную составляющие. Поскольку он имеет длину √(3) и направлен под углом 30 градусов, мы получаем следующие уравнения:

B _{по горизонтали} = √3 cos (30) = 1,5 .

B _{вертикально} = √3 sin (30) = √3/2 .

Now we add the vectors to get the components of the resultant:

(A+B) _horizontal = A _horizontal + B _Horizontal = 4 + 1,5 = 5,5

(А+В) _{по вертикали} = A _{по вертикали} + B _{по вертикали} = 0 + √3/2 = √3/2 = .

Наконец, мы используем теорему Пифагора, чтобы найти общую длину результирующего вектора A+B.

||А+В|| = √ (( (A+B) _{Горизонтальный} ) ² + ( (A+B) .0055 Vertical ) ² ) = √ (5,5 ² + (40165 2 + (4040165 2 + (40165 2 + ( ² + ( ² + ( ² . 31)

Закон косинусов:

На первый взгляд, вы можете подумать: «Зачем здесь может быть полезен закон косинусов. Закон косинусов используется для треугольников. Это не треугольник, это сумма двух векторов». Вспомним, как сложить два вектора. Если вы рисуете один вектор, затем другой вектор, который начинается там, где заканчивается первый, то сумма или результирующий из двух векторов — это вектор, который начинается в начале первого и движется по прямой линии, заканчиваясь в конце второго вектора. Эти три вектора (A, B и результирующий) образуют треугольник.

Обратите внимание, что у нас есть длины двух векторов и угол между ними. Есть еще одна деталь, которую легко испортить. Два вектора встречаются под углом , равным пи/6 радиан (или 30 градусов), когда они начинаются в одной и той же точке . Если вместо этого вектор B переместить в начало, где заканчивается вектор A, они фактически образуют угол 150 градусов. (Нарисовал бы картинку для демонстрации, но формат не позволяет. Может позже добавлю видео.)

Теперь, когда у нас есть длины двух векторов и угол между ними, мы можем использовать закон косинусов:

||A+B|| ² = ||А|| ² + ||В|| ² — 2||А|| ||Б|| cos(150)

||А+В|| ² = 4 ² + √3 ² — 2 x 9 √3 x 9 x 9 x 0047 — 20040

||А+В|| ² = 16 + 3 — (-12)

||A+B|| ² = 31

||A+B|| = √31

Голосовать за 1 голос против

Подробнее

Отчет

Все еще ищете помощь? Получите правильный ответ, быстро.

Задайте вопрос бесплатно

Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.

ИЛИ

Найдите онлайн-репетитора сейчас

Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.

Как найти длину и направление вектора \\[2

Дата последнего обновления: 31 января 2023

•

Всего просмотров: 218.7k

•

Просмотров сегодня: 6.11k

Проверено

218,7 тыс.+ просмотров

Подсказка: Квадратный корень из суммы квадратов горизонтальной и вертикальной составляющих дает длину вектора и угол \[\theta \] в стандартном положении конечной стороны хотя начало координат с координатами определяет направление вектора.