Лучший ответ по мнению автора
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.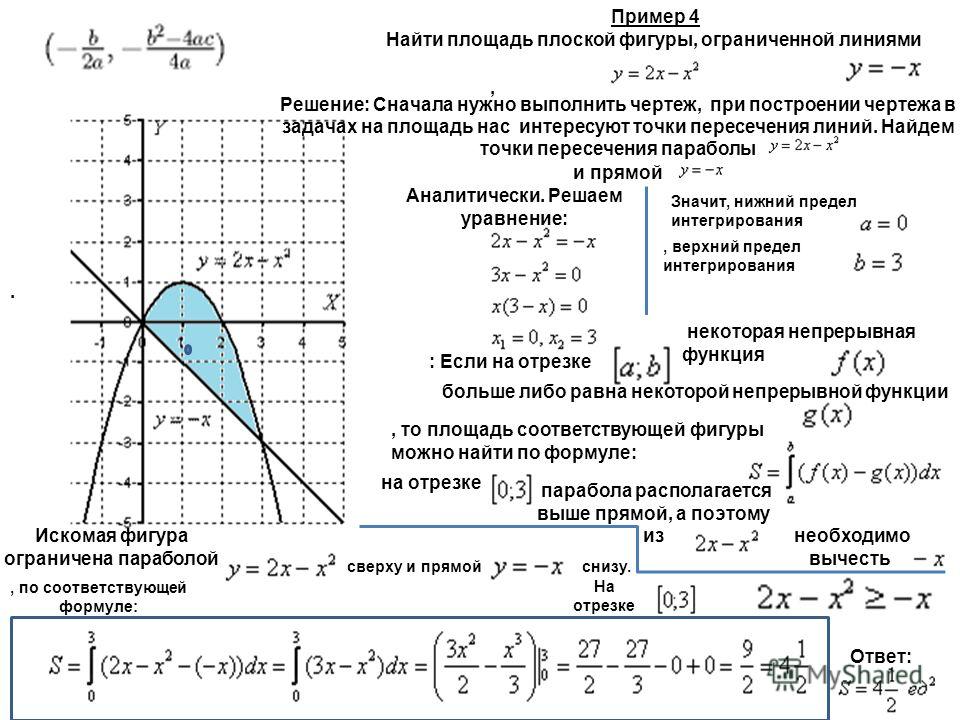 2. Найдите площадь полной поверхности цилиндра.
2. Найдите площадь полной поверхности цилиндра.
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
Вычислить площадь фигуры, ограниченной линиями y = 4 — х2 , y = 0
Угол при вершине осевого сечения конуса с высотой 1м равен 60 градусов. Чему равна площадь сечения конуса проведено через две образующие угол между которыми равен 45 градусов.
Пользуйтесь нашим приложением
2}$, вращаясь вокруг оси $x$, между $x=0$ и $x=4$.(9) Найдите объем, полученный с помощью синусоиды вращающийся вокруг оси $x$. Найдите также площадь его поверхность.
(10) Найти площадь участка кривой $xy=a$ находится между $x=1$ и $x = a$. Найди средняя ордината между этими пределами.
(11) Показать, что среднее квадратичное значение функции
$y=\sin x$ в пределах от $0$ до $\pi$ радиан равно $\dfrac{\sqrt2}{2}$. Найдите также среднее арифметическое того же
функционировать в одних и тех же пределах; и показать, что
форм-фактор $=1.11$.
9{0,21x}$.
Найдите площадь, заключенную между кривой и
ось $x$, от ординаты в точке $x=2$ до ординаты
при $x = 8$. Найдите также высоту средней ординаты
кривой между этими точками.
Найдите также среднее арифметическое того же
функционировать в одних и тех же пределах; и показать, что
форм-фактор $=1.11$.
9{0,21x}$.
Найдите площадь, заключенную между кривой и
ось $x$, от ординаты в точке $x=2$ до ординаты
при $x = 8$. Найдите также высоту средней ординаты
кривой между этими точками.
(15) Показать, что радиус круга, площадь что в два раза больше площади полярной диаграммы, равно квадратичному среднему всех значений $r$ для этого полярная диаграмма.
(16) Найдите объем, образованный кривой $y=±\dfrac{x}{6}\sqrt{x(10-x)}$, вращающийся вокруг оси $x$. 92 \пи$. И, следовательно, следует ответ.
(14) Площадь $62,6$ кв. Средняя ордината $10,42$.
(16) 436,3$. (Это твердое тело имеет грушевидную форму.)
Площадь, ограниченная данной осью и орнатами
Пример 1:
Найдите площадь области, ограниченная линией
x -y = 1
x — x = 2 и 2 и 2 и 2 и 2 x = 4
Решение :
В пределе x = 2 и x = 4 находим площадь под заданной кривой x — y = 1,
Площадь лежит над осью x, поэтому требуемая площадь равна
= интеграл от a до y dx
= 4 квадратных единицы.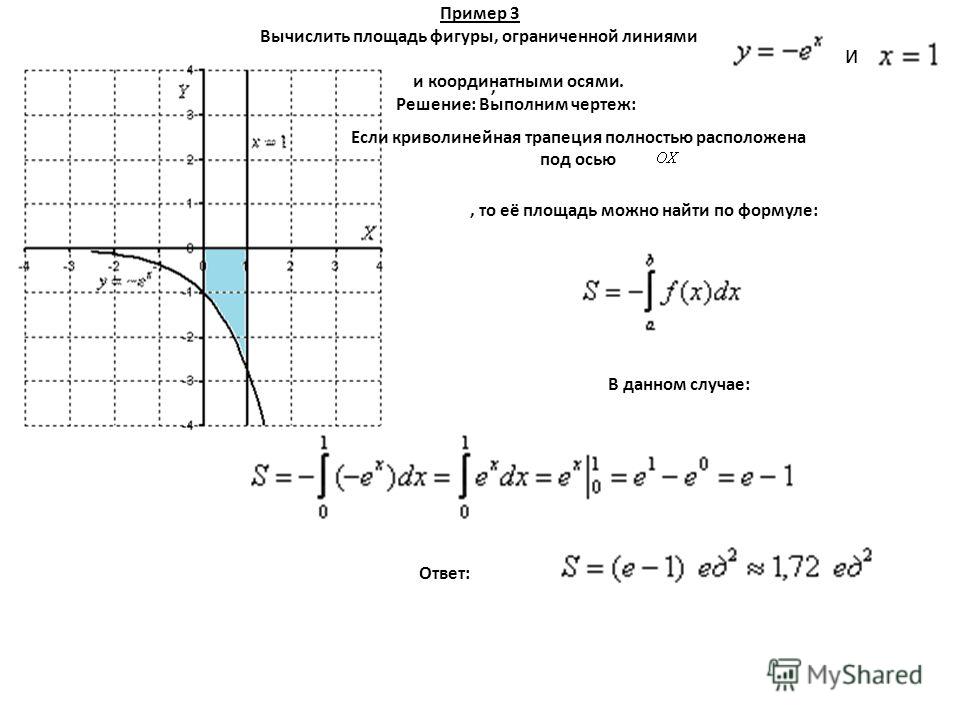
Пример 2:
Найдите площадь области, ограниченная строкой
x -y = 1
x — ось, x = — 2 и x = 0
Решение:
. = интеграл от a до b ∫-y dx
Итак, требуемая площадь равна 4 квадратным единицам.
Пример 3 :
Найдите площадь области по прямой ось Y. Итак,
= (25+60) — (4+24)
= 85-28
= 57
Итак, искомая площадь 57 квадратных единиц.
Пример 4 :
Найдите площадь области, ограниченной линией
y = x — 5
и осью x между ординатами x = 3 и x = 7.
Решение:
= [-(25/2) + 25] + [(9/2)-15] + [(49/2)-35] — [(25/2)-25]
= -12,5+25+4,5-15+24,5-35-12,5+25
= -12,5-15-35-12,5+25+4,5+24,5+25
= -75+54
= 21 кв. .
Пример 5:
Найдите площадь области, ограниченная
x 2 = 36y
Y — оси, y = 2 и y = 4
Решение:
Итак, область, область, область, область, область, область, область, область, область.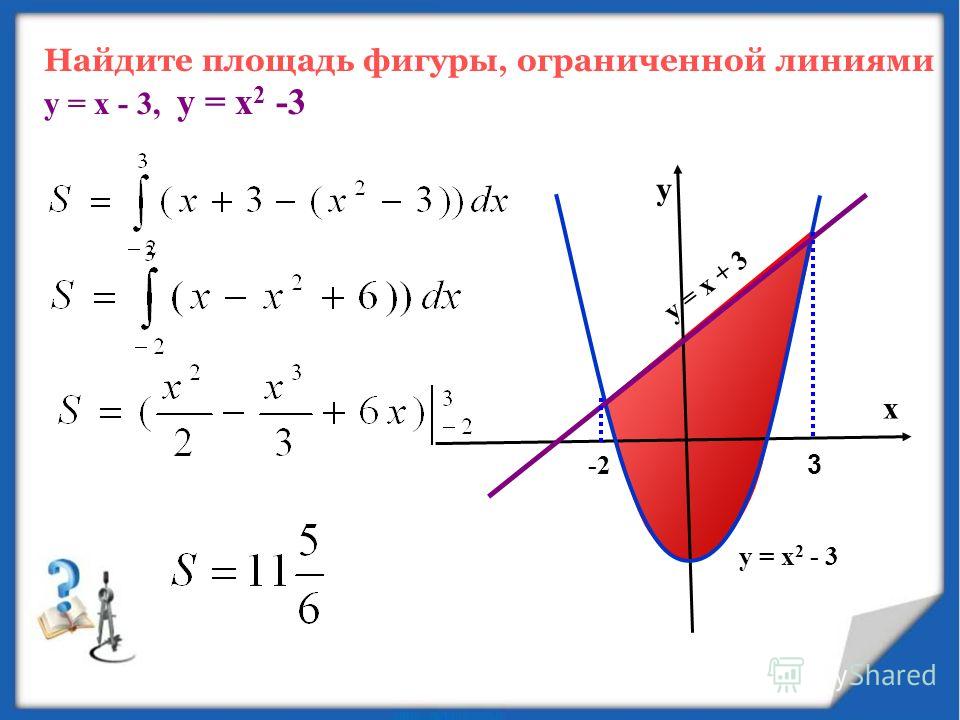 заштрихованная область составляет 8(4-√2) квадратных единиц.
заштрихованная область составляет 8(4-√2) квадратных единиц.
Пример 6 :
Найдите площадь, заключенную между параболой
y 2 = 4ax
и ее широкой прямой кишкой.
Решение:
Пример 7:
Найдите площадь области, ограниченной эллипсом
(x 2 /9) + (Y 2 /5) = 1
между. две латуса прямой кишки.
Решение:
а 2 = 9, б 2 = 5
e = √[1-(b 2 /a 2 )]
e = √[1-(5/9)]
= √[(9-5)/9 ]
= √(4/9)
e = 2/3
Уравнение широкой прямой кишки x = ± ae
a = 3, e = 2/3
ae = 2 (2/3
) ae = 2
Уравнение широкой прямой кишки x = ± 2
Требуемая площадь = интеграл от a до b ∫ y dx
(x 2 /9) + (y 2 /5) = 3 1
2 /5) = 1 — (x 2 /9)Y 2 /5 = (9 — x 2 ) /
Y 2 = (5/9) (9 -X 2 )
y = √ √ 2 )
y = √ (5/9) (9-x 2 )
y = √5/3 √(9-x 2 )
Используя пределы x = 0 и x = 2, мы можем найти площадь над ось х.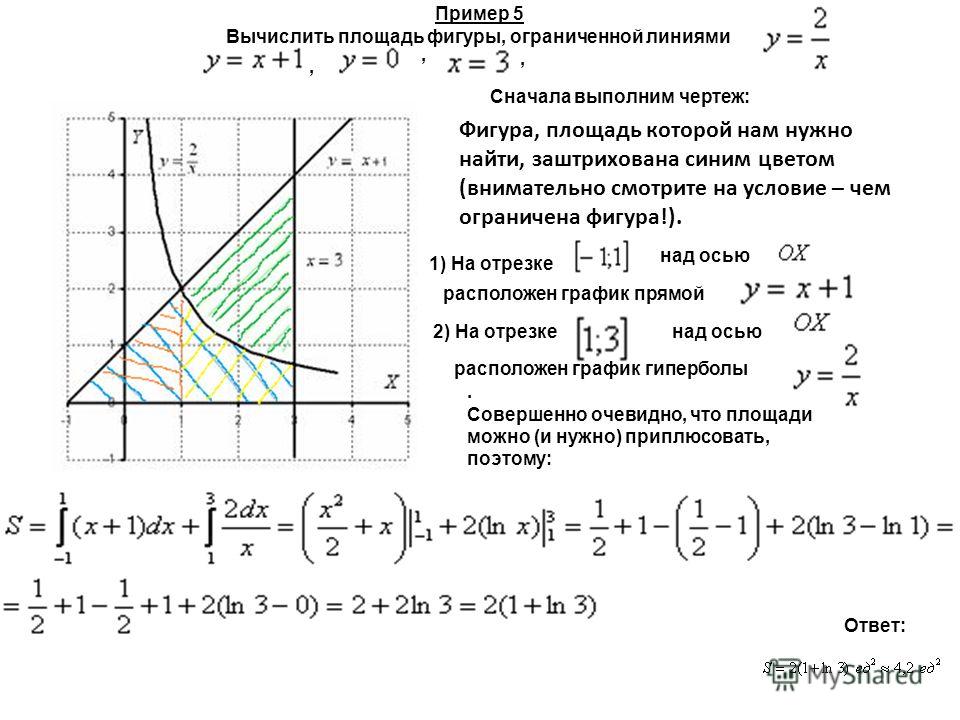

 06.17
06.17