Нормальные формы: ДНФ, КНФ, СДНФ, СКНФ
Нормальные формы формул алгебры высказываний бывают двух типов: дизъюктивные и конъюктивные, в каждом из этих типов выделен класс совершенных форм.
Алгоритм построения ДНФ:
1. Перейти к булевым операциям.
2. Перейти к формуле с тесными отрицаниями, т.е. к формуле, в которой отрицания находятся не выше, чем над переменными.
3. Раскрыть скобки.
4. Повторяющейся слагаемые взять по одному разу.
5. Применить законы поглощения и полупоглощения.
Пример.Найти ДНФ формулы
►
◄
Конъюнктивная нормальная форма (КНФ) – двойственное для ДНФ понятие, поэтому ее легко построить по схеме:
.
► ~ ~
.◄
Совершенную дизъюнктивную нормальную форму СДНФ можно строить, используя следующий алгоритм:
1. = 1. алгоритма ДНФ
2. = 2. алгоритма ДНФ
3. = 3. алгоритма ДНФ
4. = 4. алгоритма ДНФ
5. Опустить тождественно ложные слагаемые, т. е. слагаемые вида
.
6. Пополнить оставшиеся слагаемые недостающими переменными
7. Повторить пункт 4.
Пример.Найти СДНФ формулы.
► ~
.◄
Для построения СКНФ можно пользоваться следующей схемой:
Пример.Найти СДНФ формулы.
► ~
.◄
Известно (теоремы 2.11, 2.12), что СДНФ и СКНФ определены формулой однозначно и, значит, их можно строить по таблице истинности формулы [1].
►Схема построения СДНФ и СКНФ по таблице истинности приведена ниже, для формулы ~ :
2.2. Задание.
2.2.1 Ниже приведены логические выражения. Максимально упростите выражения своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
2.2.2. Выяснить вопрос о равносильности f1 и f 2 путем сведения их к СДНФ (табл. 1).
2.2.3. Найти двойственную функцию для f3 по обобщенному и булевому принципу (табл.1). Сравнить полученные результаты.
2.3. Контрольные вопросы.
2.3.1. Дайте определение высказывания.
2.3.2. Перечислите основные операции над высказыванием.
2.3.3. Что такое таблица истинности?
2.3.4. Составить таблицы истинности для следующих формул:
~ ~ ;
~ ;
~ ~ ~ ;
~ ~ ~ ~ .
2.3.5. Учитывая соглашения о порядке выполнения операций, опустить «лишние» скобки и знак « » в формулах:
;
;
;
;
~ .
2.3.6. Применяя равносильные преобразования, доказать тождественную истинность формул:
;
;
;
.
2.3.7.Найти двойственные формулы:
)
.
2.3.8. Привести к совершенной ДНФ (СДНФ) форме следующие формулы:
~
2.3.9. Привести к совершенной КНФ (СКНФ) форме следующие формулы:
~
~
Лабораторная работа № 3
Тема: «Минимизация булевых функций. Логические схемы»
Цель: Приобретение практических навыков работы с методами минимизации булевых функций.
3.1. Теоретические сведения [1].
Минимальные формы
Как было показано в [1], любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению. В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получается на основе принципа двойственности [1].
Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. При каноническом синтезе предполагается, что на входы схемы подаются как сигналы , так и их инверсий .
Формула, представленная в дизъюнктивной нормальной форме, упрощается многократными применением операции склеивания и операции поглощения и (дуальные тождества для конъюнктивной нормальной формы имеют вид: и ). Здесь под и можно понимать любую формулу булевой алгебры. В результате приходим к такому аналитическому выражению, когда дальнейшие преобразования оказываются уже невозможными, т.е. получаем тупиковую форму.
Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв.
Пусть, например, функция задана в совершенной нормальной дизъюнктивной форме:
.
Группируя члены и применяя операцию склеивания, имеем .
При другом способе группировки получим:
.
Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как ). В первом случае таким членом может быть . Тогда . Добавив член , получим: . Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными.
Работа с формулами на таком уровне подобна блужданию в потемках. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать некоторые графические и аналитические представления и специально разработанную для этой цели символику.
Многомерный куб
Каждой вершине -мерного куба можно поставить в соответствие конституенту единицы. Следовательно, подмножество отмеченных вершин является отображением на -мерном кубе булевой функции от переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показано такое отображение для функции из п.3.7.
Рис.3.1 Отображение на трехмерном кубе функции, представленной в СДНФ
Для отображения функции от переменных, представленной в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами и элементами -мерного куба.
Минитерм ( -1)-го ранга можно рассматривать как результат склеивания двух минитермов -го ранга (конституент единицы), т.е. , На -мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координаты , соединяющим эти вершины, ребром (говорят, что ребро покрывает инцидентные ему вершины). Таким образом, минитермам ( -1)-го порядка соответствуют ребра -мерного куба. Аналогично устанавливается соответствие минитермов ( -2)-го порядка — граням -мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы -мерного куба, характеризующиеся измерениями, называют -кубами. Так, вершины являются 0-кубами, ребра – 1-кубами, грани – 2-кубами и т.д. Обобщая приведенные рассуждения, можно считать, что минитерм ( )-го ранга в дизъюнктивной нормальной форме для функции переменных отображается -кубом, причем каждый -куб покрывает все те -кубы низшей размерности, которые связаны с его вершинами. В качестве примера на рис. 3.2 дано отображение функции трех переменных. Здесь минитермы и соответствуют 1-кубам ( ), а минитерм отображается 2-кубом ( ).
Рис.3.2 Покрытие функции
Итак, любая дизъюнктивная нормальная форма отображается на -мерном кубе совокупностью -кубов, которые покрывают все вершины, соответствующие конституентам единицы (0-кубы). Справедливо и обратное утверждение: если некоторая совокупность -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим -кубам минитермов является выражение данной функции в дизъюнктивной нормальной форме. Говорят, что такая совокупность -кубов (или соответствующих им минитермов) образует покрытие функции.
Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число -кубов которого было бы поменьше, а их размерность — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием. Например, для функции покрытие на рис. 3.3 соответствует минимальным формам и .
Рис. 3.3 Покрытия функции .
слева – ; справа –
Отображение функции на -мерном кубе наглядно и просто при . Четырехмерный куб можно изобразить, как показано на рис. 3.4, где отображены функция четырех переменных и ее минимальное покрытие, соответствующее выражению . Использование этого метода при требует настолько сложных построений, что теряется все его преимущества.
Рис. 3.4 Отображение функции на четырехмерном кубе
Карты Карно
В другом методе графического отображения булевых функций используются карты Карно, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис. 3.5 показаны карты Карно для двух, трех, четырех переменных.
Рис. 3.5 Карты Карно для двух, трех и четырех переменных
Как и в обычных таблицах истинности, клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки). Например, на рис. 3.6, а показана карта Карно для функции, отображение которой на четырехмерном кубе дано на рис. 3.4. Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
а б
Рис. 3.6 Отображение на карте Карно функции четырех переменных
(а) и ее минимального покрытия (б)
Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно s-кубу соответствует совокупность 2 соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Поэтому все положения, изложенные в выше (см. п. многомерный куб), справедливы для карт Карно. Так, на рис. 3.6, б показано покрытие единиц карты, соответствующее минимальной дизъюнктивной форме рассматриваемой функции.
Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие s-куб, дают минитер (n–s)-го ранга, в который входят те (n–s) переменные, которые сохраняют одинаковые значения на этом s-кубе, причем значении 1 соответствуют сами переменные, а значениям 0 – их отрицания. Переменные, которые не сохраняют свои значения на s-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в дизъюнктивной нормальной форме (крайняя правая является минимальной) (рис. 3.7).
Рис. 3.7 Способы считывания с карты Карно дизъюнктивной нормальной формы булевой функции (слева направо: ; ;
Пример.Получить минимальные формы для функции
Пример.Получить минимальную форму для функции, заданной на карте.
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используется две карты Карно на четыре переменные, а для функции шести переменных – четыре таких карты. При дальнейшем увеличении числа переменных карты Карно становятся практически непригодными.
Известные в литературе карты Вейча отличаются только другим порядком следования наборов значений переменных и обладают теми же свойствами, что и карты Карно.
Комплекс кубов
Несостоятельность графических методов при большом числе переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов, использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.
Комплекс кубов К(у) функции определяется как объединение множеств Кs(у) всех ее s-кубов (s=0.1,…,n), т. е. , причем некоторые из Кs(у) могут быть пустыми. Для записи s-кубов и минитермов функции от n переменных используются слова длины n, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для и 0 для ). Не входящие в минитерм переменные являются свободными и обозначаются через . Например, 2-куб функции пяти переменных, соответствующий минитерму запишем как ( ). 0-кубы, соответствующие конституентам единицы, представляются наборами значений переменных, на которых функция равна единице. Очевидно, в записи s-куба всегда имеется s свободных переменных. Если все n переменных свободны, что соответствует n-кубу, то это означает тождественность единице рассматриваемой функции. Таким образом, для функций, не равных тождественно единице Ø.
Множество всех s-кубов записывается как совокупность слов, соответствующих каждому s-кубу. Для удобства будем располагать слова s-кубов в столбцы, а их совокупность заключать в фигурные скобки. Например, комплекс кубов, соответствующий представлению функции на трехмерном кубе (рис. 3,10а), выражается как , где
; ; .
Для сравнения на рис. 3.8 изображен комплекс кубов в принятых обозначениях.
Рис. 3.8 Комплекс кубов функции трех переменных (а) и его символическое представление (б)
Комплекс кубов образует максимальное покрытие функции. Исключая из него все те s-кубы, которые покрываются кубами высшей размерности, получаем покрытия, соответствующие тупиковым формам. Так, для рассматриваемого примера (рис. 3.8) имеем тупиковое покрытие
,
которое соответствует функции . В данном случае это покрытие является и минимальным.
Для двух булевых функций операция дизъюнкции соответствует объединению их комплексов кубов , а операция конъюнкции — пересечению комплексов кубов . Отрицанию функции соответствует дополнение комплекса кубов, т. е. , причем определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, имеет место взаимно-однозначное соответствие (изоморфизм) между алгеброй булевых функций и булевых множеств, представляющих комплексы кубов.
Представление функции в виде комплексов кубов менее наглядно, однако его важнейшие достоинства состоят в том, что снимаются ограничения по числу переменных и облегчается кодирование информации при использовании вычислительных машин.
Минимизация булевых функций
Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия , где — число — кубов, образующих покрытие данной функции от п переменных. Минимальное покрытие характеризуется наименьшим значением его цены.
Обычно задача минимизации решается в два шага. Сначала ищут сокращенное покрытие, которое включает все -кубы максимальной размерности, но не содержит ни одного куба, покрывающегося каким-либо кубом этого покрытия. Соответствующею дизъюнктивную нормальную форму называют сокращенной, а ее минитермы — простыми импликантами. Для данной функции сокращенное покрытие является единственным, но оно может быть избыточным вследствие того, что некоторые из кубов покрываются совокупностями других кубов.
На втором шаге осуществляется переход от сокращенной к тупиковым дизъюнктивным нормальным формам, из которых выбираются минимальные формы. Тупиковые формы образуются путем исключения из сокращенного покрытия всех избыточных кубов, без которых оставшаяся совокупность кубов еще образует покрытие данной функции, но при дальнейшем исключении любого из кубов она уже не покрывает множества всех вершин, соответствующих единичным значениям функции, т. е. перестает быть покрытием.
Куб сокращенного покрытия, который покрывает вершины данной функции, не покрываемые никакими другими кубами, не может оказаться избыточным и всегда войдет в минимальное покрытие. Такой куб, как и соответствующая ему импликанта, называют экстремалью (существенной импликантой), а покрываемые им вершины — отмененными вершинами. Множество экстремалей образует ядро покрытия, ясно, что при переходе от сокращенного покрытия к минимальному прежде всего следует выделить все экстремали. Если множество экстремалей не образует покрытия, то оно дополняется до покрытия кубами из сокращенного покрытия.
Приведенные определения иллюстрируются на рис. 3.9, где сокращенное покрытие (см. рис. 3.9а,) и минимальные покрытия (рис. 3.9б) и (см. рис. 3.9, б) выражаются следующим образом:
Рис. 3.9 Сокращенное ( ) и минимальные покрытия ( , ) функции (а – сокращенное, б, в — минимальные)
Сокращенная форма представляет собой дизъюнкцию четырех простых импликант, т. е. Экстремалями являются простые импликанты и ,которым соответствуют 1-кубы (
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Алгоритм построения днф
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
A→B= ךAvB A⇔B=(A^B)v(ךAvךB)
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
ך(AvB)= ךA^ךB ך(A^B)= ךAvךB
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения днф
Приведем к ДНФ формулу :F=((X→Y)↓ ך(Y→Z))
Выразим логические операции → и ↓ через :v ^ ך
F=(( ךXvY)↓ ך(ךYvZ))= ך ((ךXvY)v ך (ךYvZ))
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
F= ך ((ךXvY)v ך (ךYvZ))=( ך ךX^ ךY)^( ךYvZ)=(X^ ךY)^( ךYvZ)
Используя закон дистрибутивности, приводим формулу к ДНФ:
F=(X^ ךY^ ךY)v(X^ ךY^Z)
Конъюнктивная нормальная форма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкцийлитералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ. Для этого можно использовать: Закон двойного отрицания, Закон де Моргана, Дистрибутивность.
Примеры и контр примеры
Формулы в КНФ:
ך A^(BvC) (AvB)^( ך BvCv ך D)^(Dv ך E)A^B
Формулы не в КНФ:
ך (BvC) (A^B)vC A^(Bv(D^E))
Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:
ך B^ ך C (AvC)^(BvC) A^(BvD)^(BvE)
Построение КНФ
Алгоритм построения КНФ
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:
A→B= ך AvB A↔B=(A^B)v(ך A^ ך B)
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:
ך (AvB)= ך A^ ך B ך (A^B)= ך Av ך B
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Пример построения КНФ
Приведем к КНФ формулу
F=(X→Y)^(( ך Y→Z) → ך X)
Преобразуем формулу F к формуле не содержащей → :
F=( ך XvY)^( ך (ך Y→Z)v ך X)=( ך XvY)^( ך (ך ך YvZ)v ך X)
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
F=( ך XvY)^(( ך Y^ ך Zv ך X)=( ך XvY)^(( ך Y^ ך Z)v ך X)
По закону дистрибутивности получим КНФ:
F=( ך XvY)^( ך Xv ך Y)^( ך Xv ך Z)
k-конъюнктивной нормальной формой называют конъюнктивную нормальную форму, в которой каждая дизъюнкция содержит ровно kлитералов.
Например, следующая формула записана в 2-КНФ:
(AvB)^( ך BvC)^(Bv ך C)
Переход от КНФ к СКНФ
Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение : (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:
(XvY)^(Xv ך Yv ך Z)=(XvYv(Z^ ך Z))^(Xv ך Yv ך Z)=(XvYvZ)^(XvY vך Z)^(Xv ךYv ךZ)
Таким образом, из КНФ получена СКНФ.
Переход от КНФ к СКНФ
Если в простой дизъюнкции не хватает какой-то переменной (например, z), то добавляем в нее выражение :Z^ ך Z=0 (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона:
(XvY)^(Xv ךY ךZ)=(XvYv(Zv ךZ))^(Xv ךYv ךZ)=(XvYvZ)^(XvYv ךZ)^(Xv ךYv ךZ) Таким образом, из КНФ получена СКНФ.
25. Совершенные дизъюнктивные и конъюнктивные нормальные формы и алгоритмы приведения к ним. Примеры.
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая конъюнктивная нормальная форма, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных дизъюнкций
в каждой дизъюнкции нет одинаковых пропозициональных переменных
каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
k-конъюнктивной нормальной формой называют конъюнктивную нормальную форму, в которой каждая дизъюнкция содержит ровно k литералов.
Например, следующая формула записана в 2-КНФ:
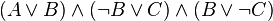
Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:
в ней нет одинаковых элементарных конъюнкций
в каждой конъюнкции нет одинаковых пропозициональных букв
каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.
Для любой функции алгебры логики существует своя СДНФ, причём единственная.
Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:
|
|
|
|
0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
Совершенная ДНФэтой функции:
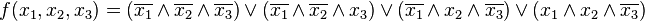
Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).
Например, является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Например, выражение является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том жепорядке.
Например, выражение является ДНФ, но не СДНФ. Выражение является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например, выражение – простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение – КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд. 5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
— если среди дизъюнктных слагаемых в ДНФ имеются слагаемые , то ко всей дизъюнкции добавляем слагаемое К1К2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
— если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем). Например:
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
ДНФ
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая конъюнкция
- полная, если в неё каждая переменная { или её отрицание } входит ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
ДНФ { Дизъюнктивная Нормальная Форма } — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
Пример ДНФ: $f(x,y,z) = (x \land y) \lor (y \land \neg { z } )$
СДНФ
СДНФ { Совершенная Дизъюнктивная Нормальная Форма } — это такая ДНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых конъюнкций
- каждая простая конъюнкция полная
Пример СДНФ: $f(x,y,z) = (x \land \neg { y } \land z) \lor (x \land y \land \neg { z } )$
Теорема: Для любой булевой функции $f(\vec { x } )$, не равной тождественному нулю (), существует СДНФ, ее задающая.
Доказательство:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
$f(\vec { x } ) = \neg x_i \wedge f(x_1, \dots ,x_ { i-1 } ,0,x_ { i+1 } , \dots ,x_n) \vee x_i \wedge f(x_1, \dots ,x_ { i-1 } ,1,x_ { i+1 } , \dots ,x_n)$
Данное соотношение легко проверить подстановкой всевозможных значений $x_i$ { $0$ и $1$ } . Эта формула позволяет выносить $x_i$ за знак функции. Последовательно вынося $x_1$, $x_2$,.., $x_n$ за знак $f(\vec { x } )$, получаем следующую формулу :
$ f(\vec { x } ) = \neg x_1 \wedge \neg x_2 \wedge …\wedge \neg x_ { n-1 } \wedge \neg x_n \wedge f(0,0,…,0,0)~\vee~$
$\neg x_1 \wedge \neg x_2 \wedge … \wedge \neg x_ { n-1 } \wedge x_n \wedge f(0,0,…,0,1) ~\vee~ $ $\dots $ $~\vee~ x_1 \wedge x_2 \wedge … \wedge x_ { n-1 } \wedge \neg x_n \wedge f(1,1,…,1,0) ~\vee~ $ $x_1 \wedge x_2 \wedge … \wedge x_ { n-1 } \wedge x_n \wedge f(1,1,…,1) $
Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от $n$ переменных мы имеем { { { $2^ { n } $ } } } конъюнктов. Каждый из них соответствует значению функции на одном из { { { $2^ { n } $ } } } возможных наборов значений $n$ переменных. Если на некотором наборе $f(\vec { x } )=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(\vec { x } )=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
x y z $\langle x,y,z \rangle$ 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
x y z $ \langle x,y,z \rangle $ 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 $(\neg { x } \land y \land z)$ 1 0 0 0 1 0 1 1 $(x \land \neg { y } \land z)$ 1 1 0 1 $(x \land y \land \neg { z } )$ 1 1 1 1 $(x \land y \land z)$ Все полученные конъюнкции связываем операциями дизъюнкции. $ \langle x,y,z \rangle = (x \land y \land z) \lor (\neg { x } \land y \land z) \lor (x \land \neg { y } \land z) \lor (x \land y \land \neg { z } )$
Примеры СДНФ для некоторых функций
Стрелка Пирса: $x \downarrow y = (\neg { x } \land \neg { y } )$
Исключающее или: $x \oplus y \oplus z = (\overline { x } \land \overline { y } \land z) \lor (\overline { x } \land y \land \overline { z } ) \lor (x \land \overline { y } \land \overline { z } ) \lor (x \land y \land z)$
Совершенной дизъюнктивной нормальной формой формулы $A(x_1,x_2,…,x_n)$ называется ДНФ, обладающая следующими свойствами:
а } в ней нет одинаковых дизъюнктивных элементов;
б } ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в } ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
г } в каждой элементарной конъюнкции содержится либо $X_i$, либо $\overline { X } _i$, где $i = 1, n$.
Условие а } – г } являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
1) если какая-нибудь элементарная конъюнкция не содержит высказывание $X_i$, то заменим выражением $B\wedge (X_i\vee \overline { X } _i) \equiv (B\wedge X_i)\vee (B\wedge \overline { X } _i)$;
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Формула называется дизъюнктивной нормальной формой { ДНФ } , если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: $A_1\vee A_2\vee …\vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
Формула $A$ от $k$ переменных называется совершенной дизъюнктивной нормальной формой { СДНФ } , если:
$A$ является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция $k$ переменных $x_1,x_2,…,x_k$, причем на $i$-м месте этой конъюнкции стоит либо переменная $x_i$ либо ее отрицание;
Все элементарные конъюнкции в такой ДНФ попарно различны.
Например: $A = x_1 \wedge$ НЕ $x_2 \vee x_1 \wedge x_2$
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций { дизъюнктивных членов } в ней.
Она является примером однозначного представления булевой функции в виде формульной { алгебраической } записи.
Теорема о СДНФ: Пусть $f(x_1 x_2, …, x_n)$ – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Алгоритм построения СДНФ по таблице истинности:
- В таблице истинности отмечаем наборы переменных, на которых значение функции $f = 1$.
- Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
6.1 Сокращенная и тупиковая днф.
В теме 3 было показано, что любая булева функция может быть представлена дизъюнктивной нормальной формой. Следует отметить, что дизъюнктивная нормальная форма часто допускает упрощение. При этом путем различных тождественных преобразований получится дизъюнктивная нормальная форма, эквивалентная исходной, но содержащая меньшее число вхождений символов.
Дизъюнктивная нормальная форма называется минимальной, если она включает минимальное число символов по сравнению со всеми другими эквивалентами ей дизъюнктивными нормальными формами.
Заметим, что если
некоторый символ в формуле, скажем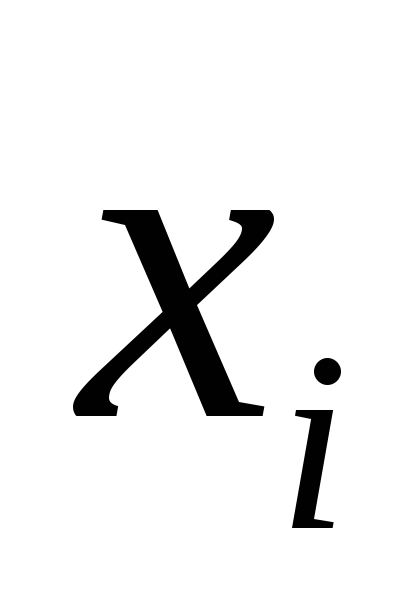 
,
встречается, например, два раза, то при
подсчете числа символов в формуле он
учитывается два раза.
Основной вопрос данного параграфа – как для произвольной булевой функции построить ей минимальную дизъюнктивную нормальную форму. Эта задача называется проблемой минимизации булевых функций.
Существует
тривиальный алгоритм построения
минимальной ДНФ для произвольной булевой
функции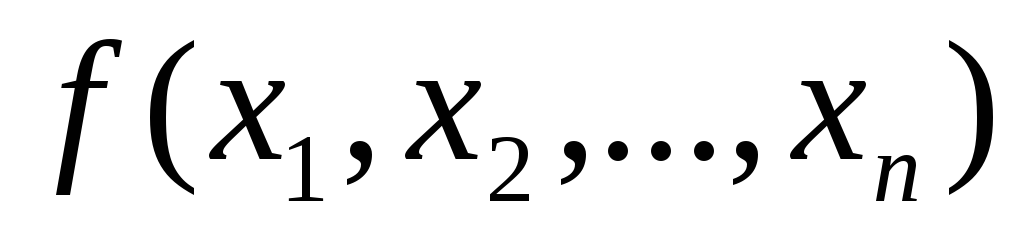 
.
Для этого все ДНФ, составленные из
символов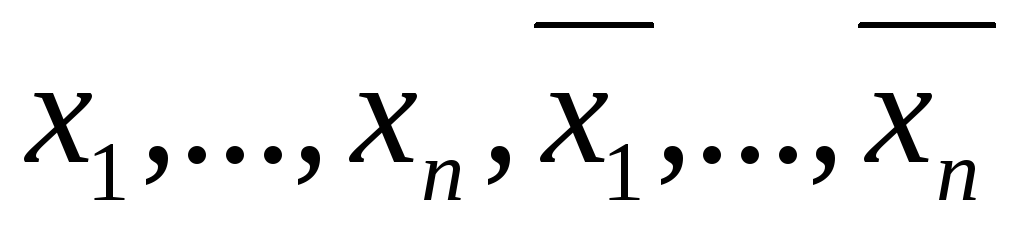
упорядочиваются по числу букв и по
порядку для каждой ДНФ Д проверяется
соотношение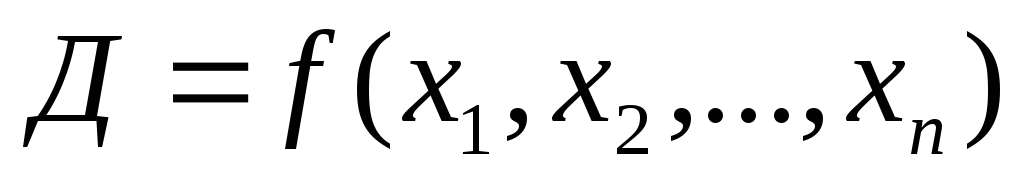
.
Первая по порядку ДНФ, для которой это
соотношение выполняется, есть, очевидно,
минимальная ДНФ функции
.
Число различных
ДНФ, составленных из переменных 
,
равно
.
Прежде чем доказать данное утверждение, приведем следующее определение.
Конъюнкция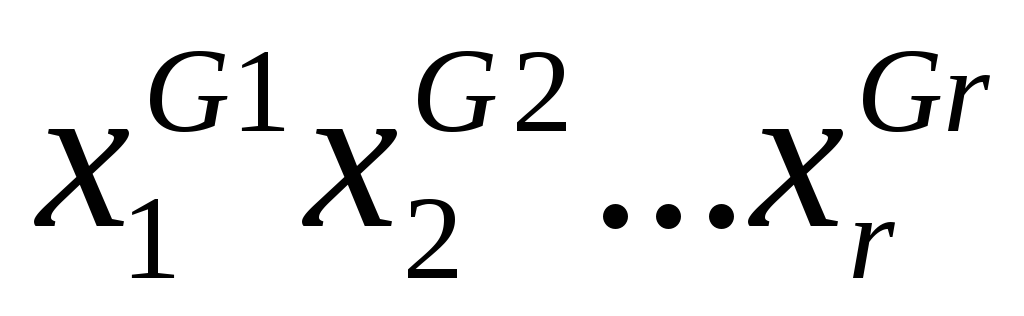 
называетсяэлементарной, если
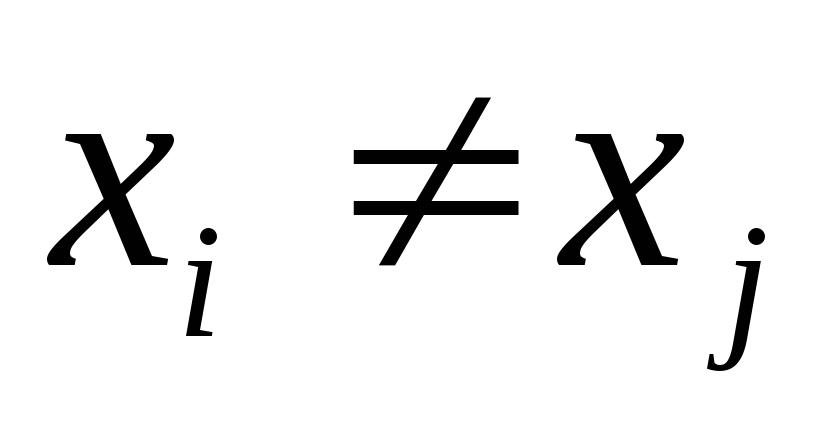при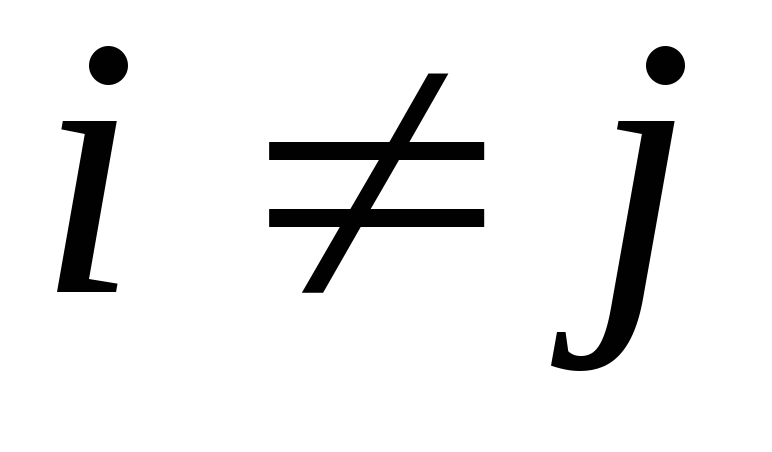
.
Число rназываетсярангом элементарной конъюнкции.В случаеr= 0 конъюнкция называетсяпустойиполагается равной 1.
Так как каждая из nпеременных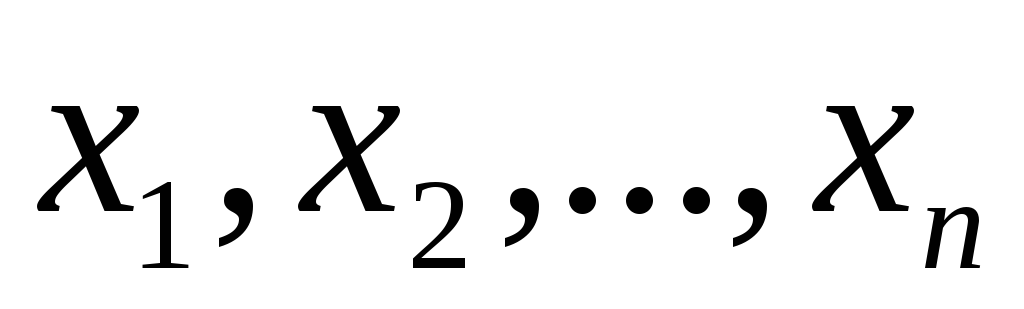 
либо не входит в элементарную, либо
входит в нее с отрицанием, или без
отрицания, то число элементарных
конъюнкций, составленных из 
равно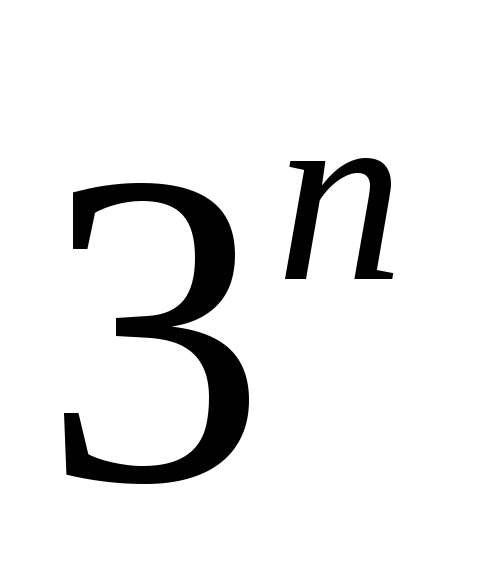
.
Ясно, что число различных ДНФ, составленных
из переменной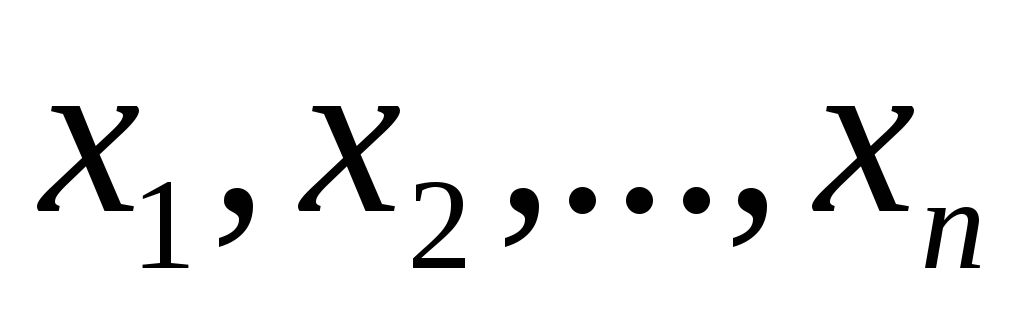 
,
равно числу подмножеств множества, из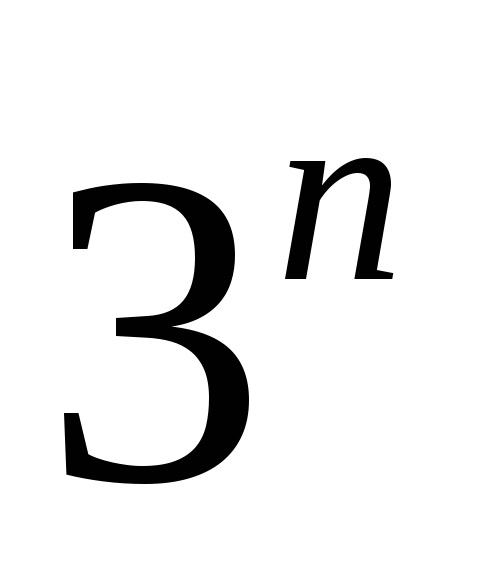
элементов, т.е.
.
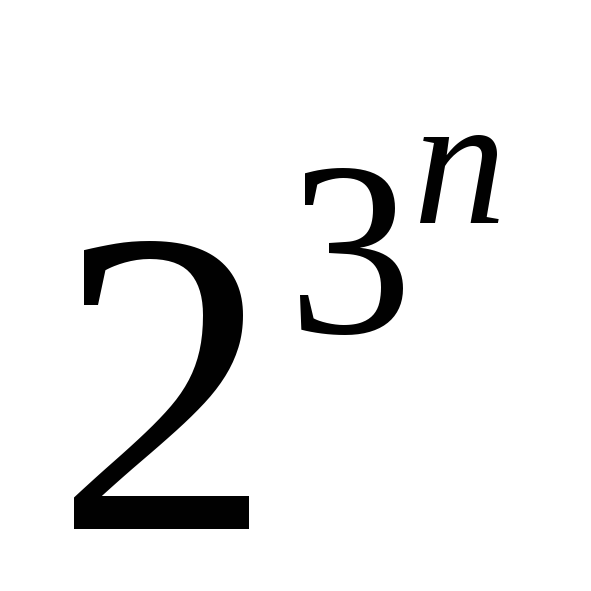Рассмотрим геометрическую интерпретацию задачи минимизации булевых функций.
Обозначим через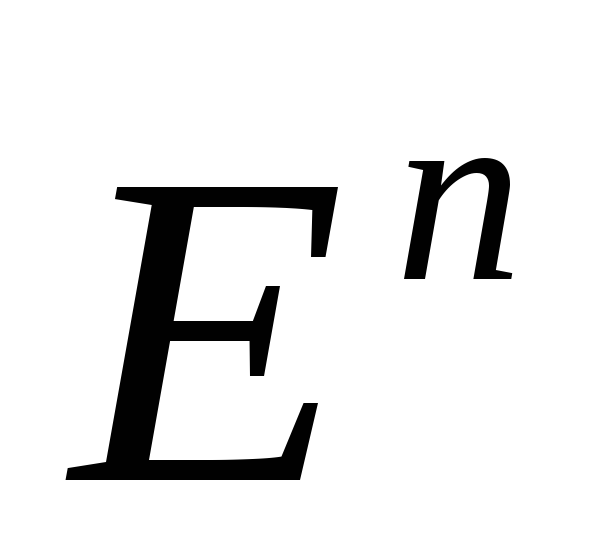 
множество всех точек
,
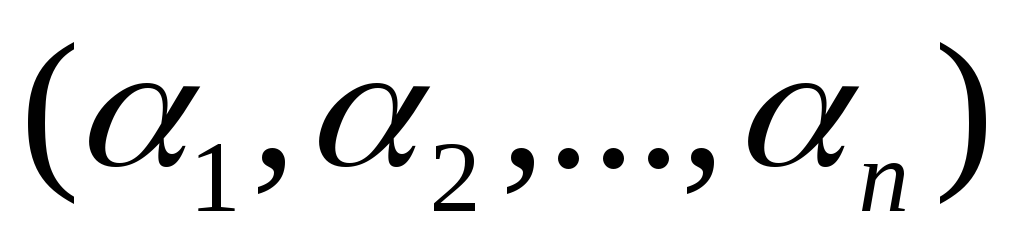где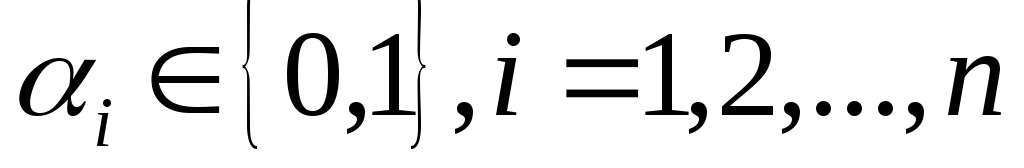
.
Ясно, что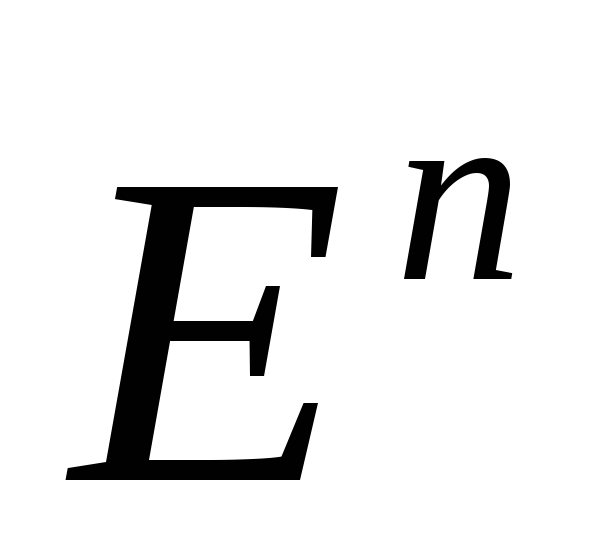
– множество всех вершин единичногоn-мерного куба.
Сопоставим каждой
булевой функции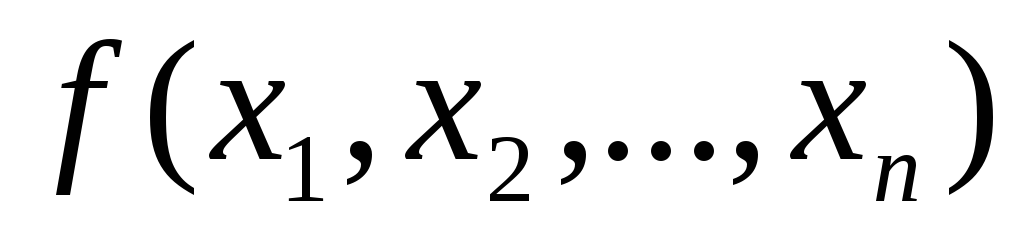 
подмножество
из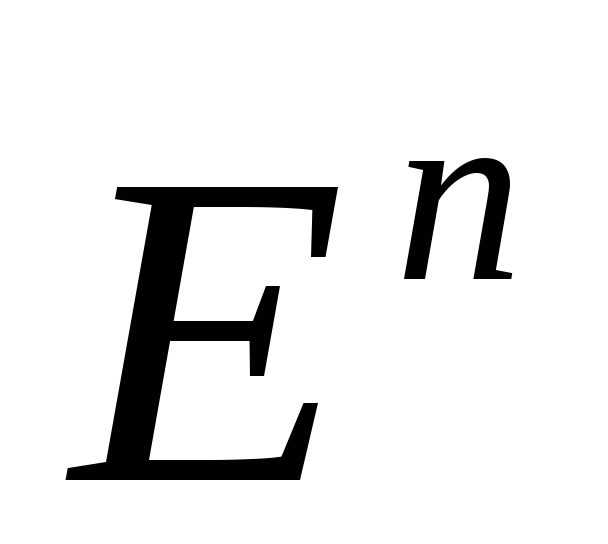
,
определенное следующим образом:
.
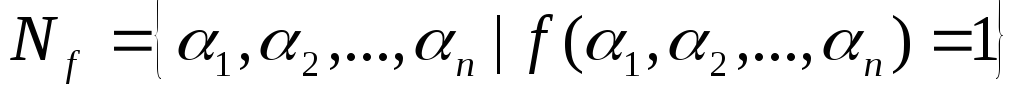Например, функции, заданной следующей таблицей истинности:
x
y
z
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
соответствует
подмножество 
вершин трехмерного единичного куба
Данное соответствие является взаимно однозначным и обладает следующими свойствами:
1) булевой функции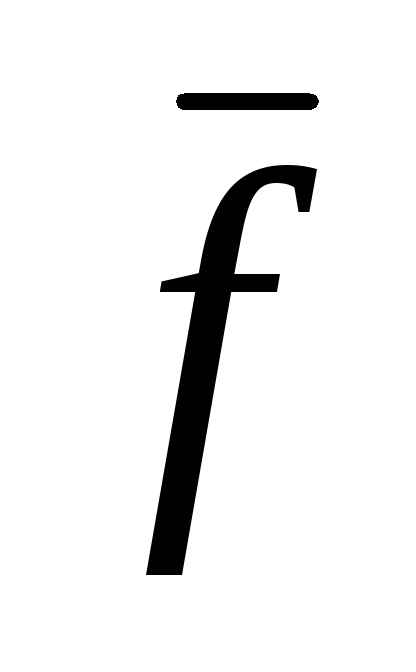 
соответствует
подмножество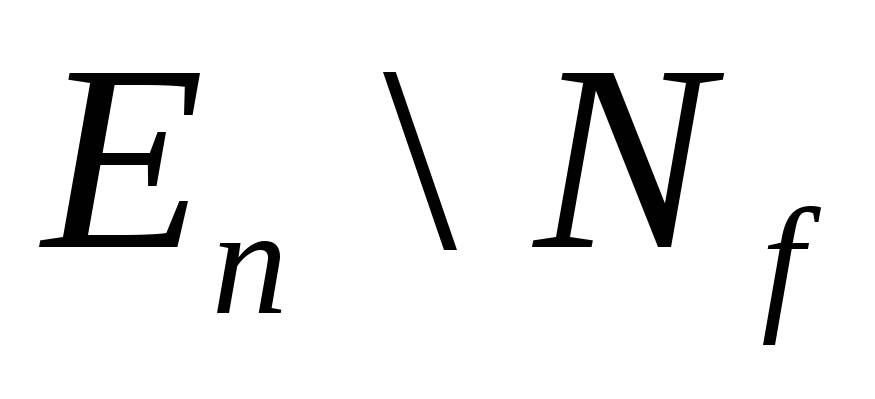
;
2) булевой функции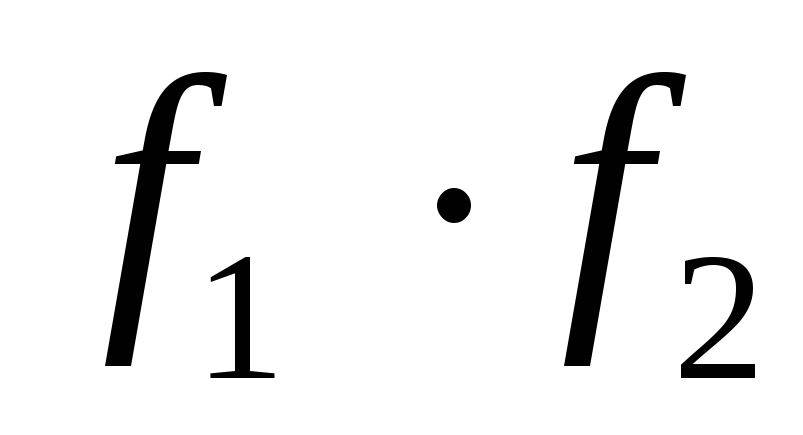 
соответствует подмножество
;
3) булевой функции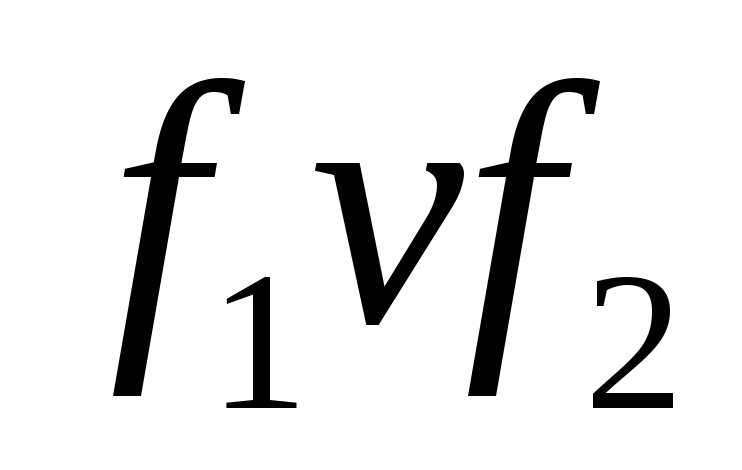 
соответствует подмножество
.
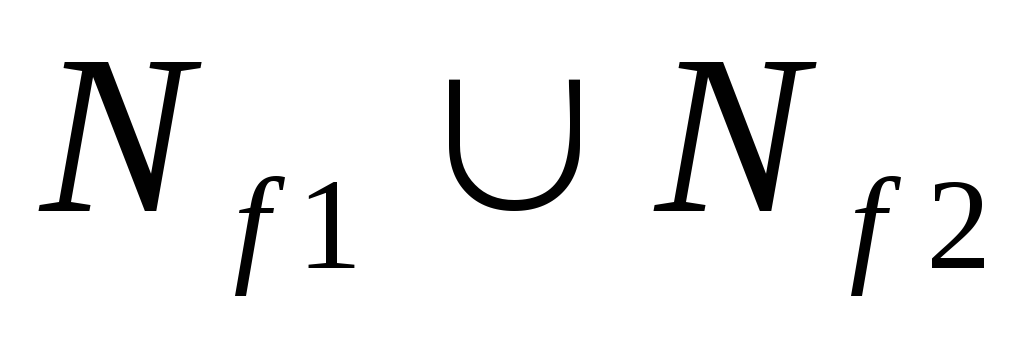Докажем свойство
2. Пусть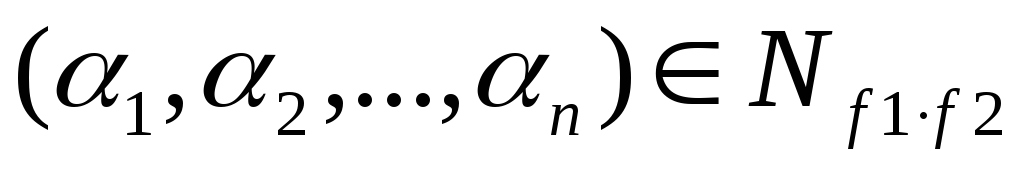 
Отсюда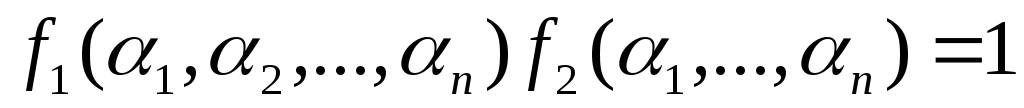 
.
Тогда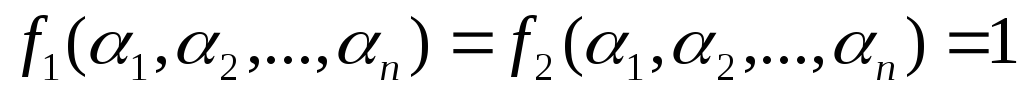 
.
А это значит, что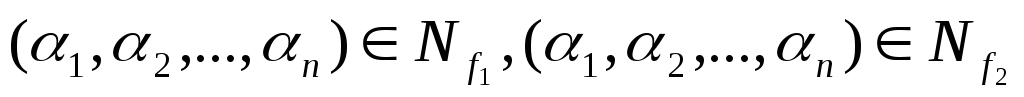 
.
Отсюда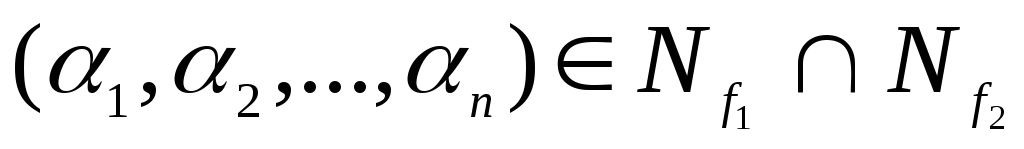 
.
Пусть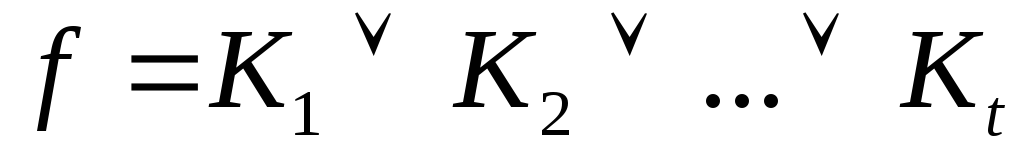 
ДНФ, где
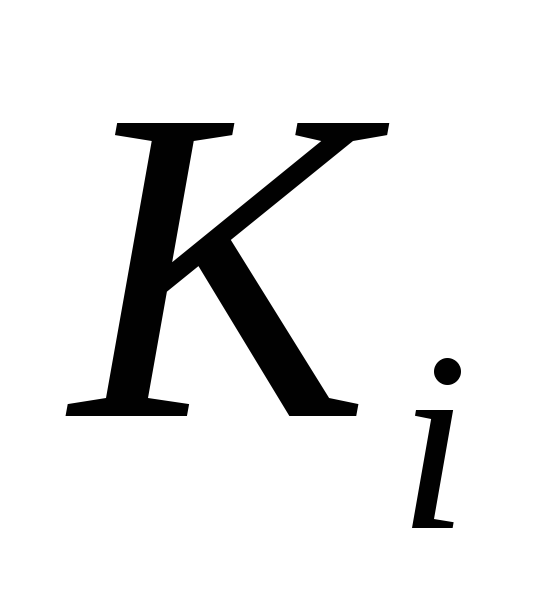– элементарные конъюнкции. Подмножество
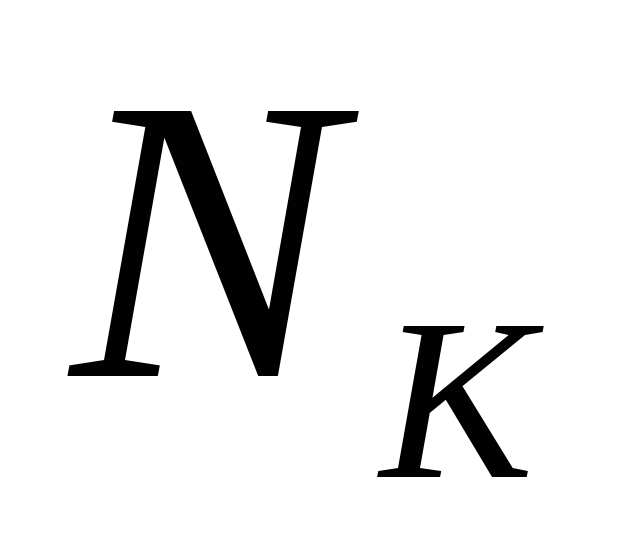называется интерваломr-го
ранга, если оно соответствует элементарной
конъюнкцииК r-го
ранга. Как показано выше,
.
Итак, с каждой ДНФ функцииfсвязано покрытие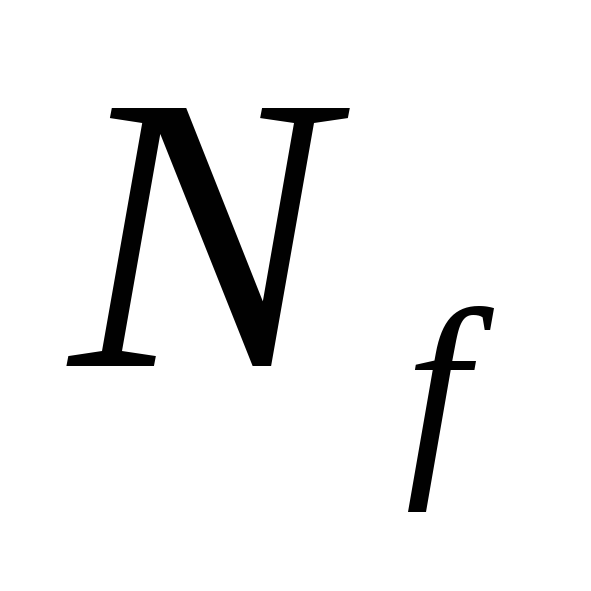
такими интервалами
,
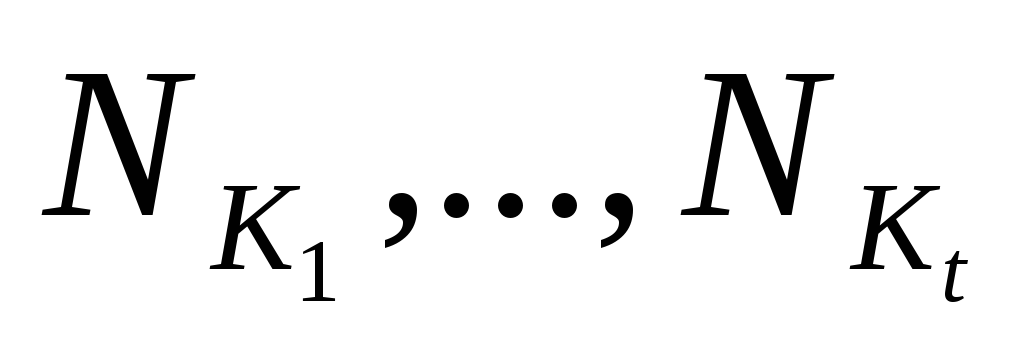что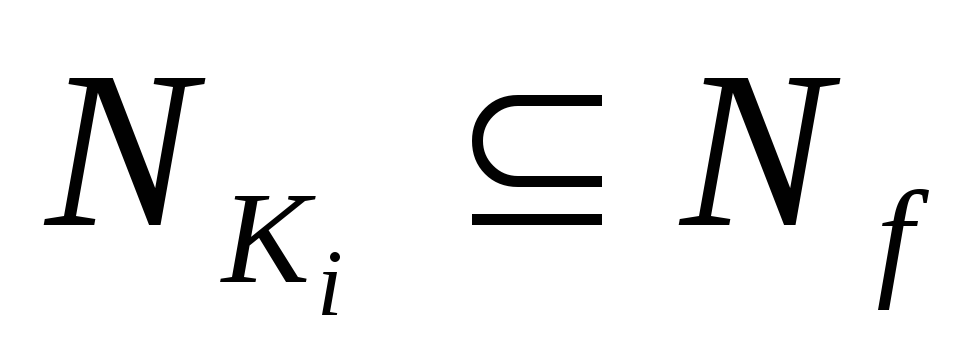
.
Пусть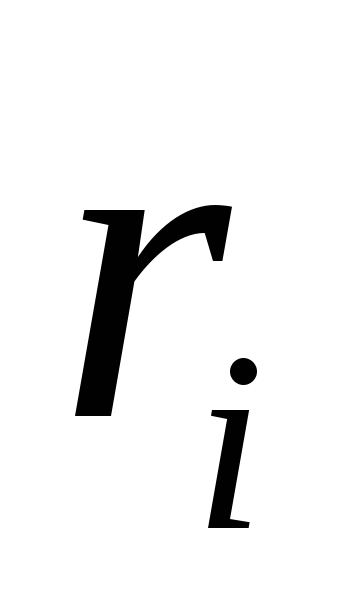 
– ранг интервала
.
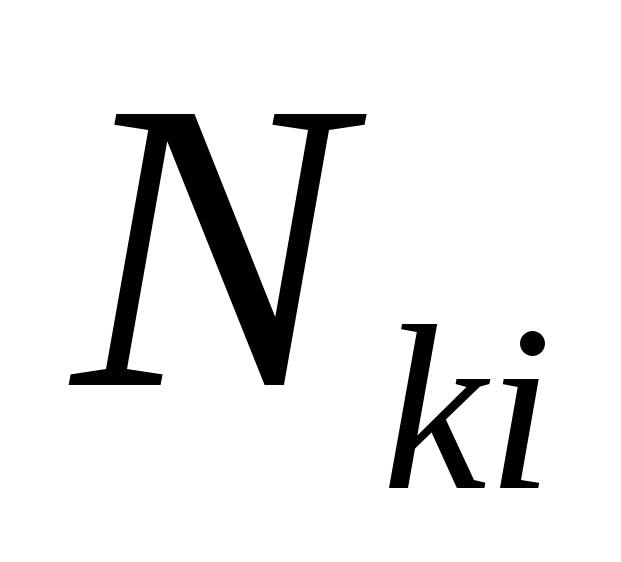Тогда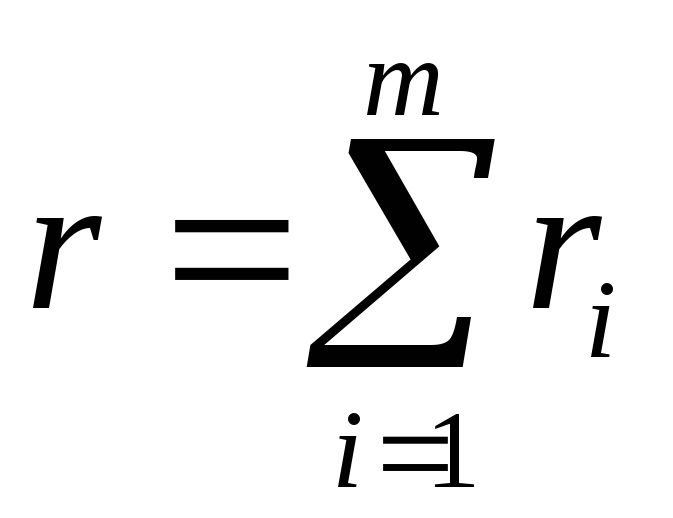
совпадает с числом букв в ДНФ
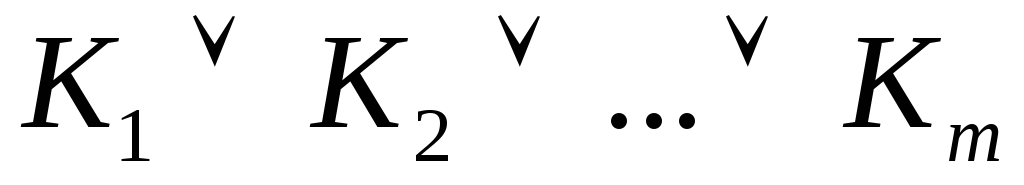функции
.
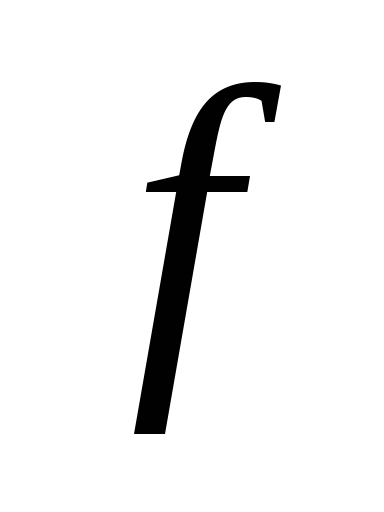Теперь ясно, что
задача построения минимальной ДНФ
сводится к отысканию такого покрытия
подмножества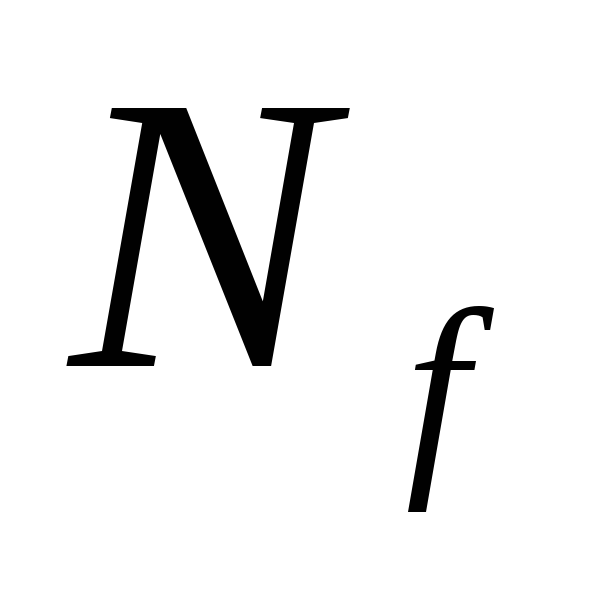 
интервалами
,
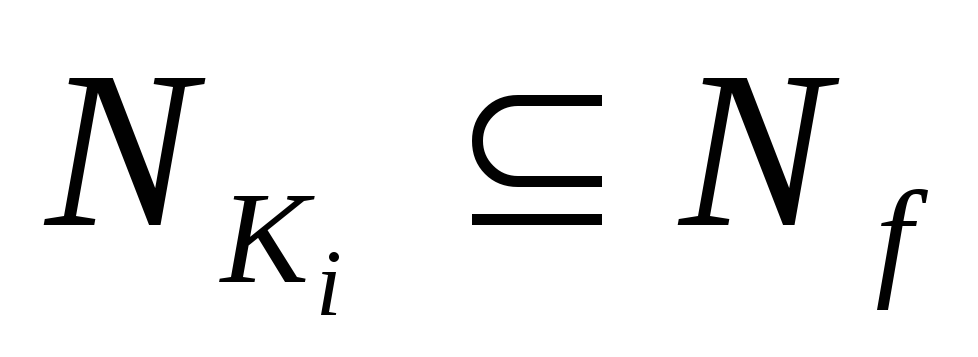чтобы число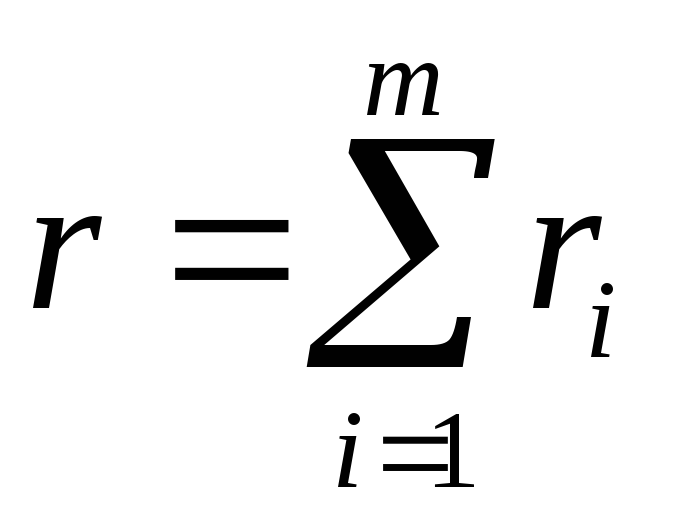
было наименьшим.
Интервал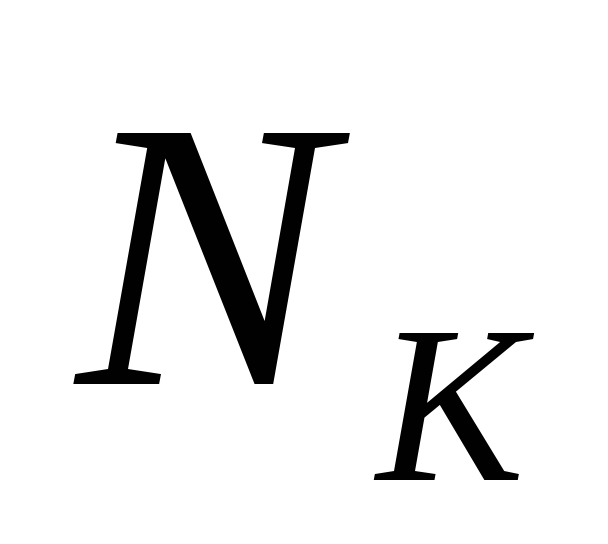 
,
содержащий
,
называетсямаксимальным для булевой
функции, если не существует интервала
,
такого, что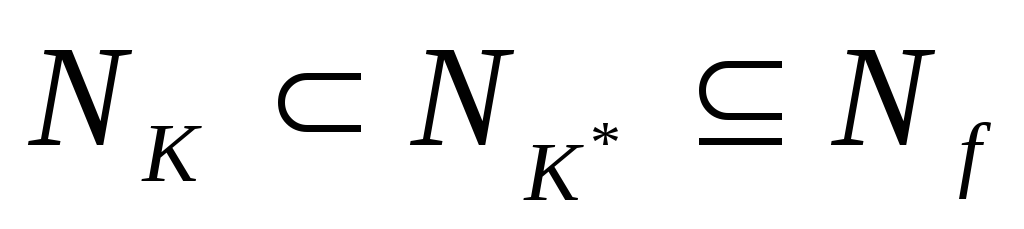
.
Заметим, что
соотношение 
выполняется тогда и только тогда, когда
элементарная конъюнкция
получается из элементарной конъюнкции
К путем вычеркивания непустого числа
сомножителей.
Очевидно, что
каждый интервал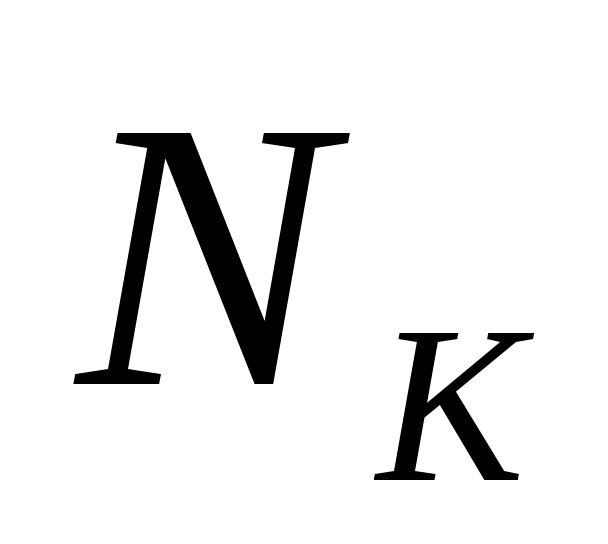 
из
содержится в некотором максимальном
интервале. Если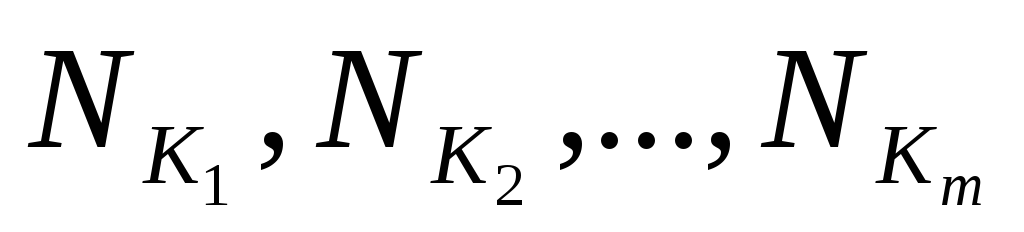
– список всех максимальных интервалов
подмножества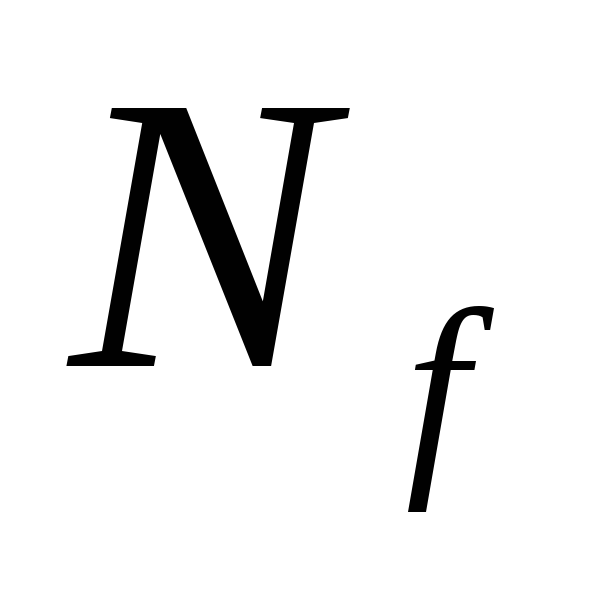
,
то нетрудно видеть, что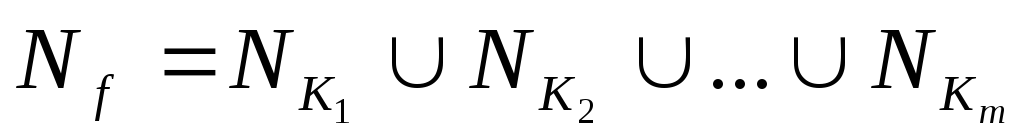
.
ДНФ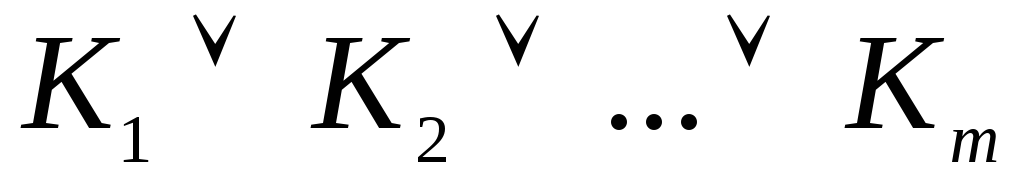 
булевой функцииf,
соответствующая покрытию
подмножества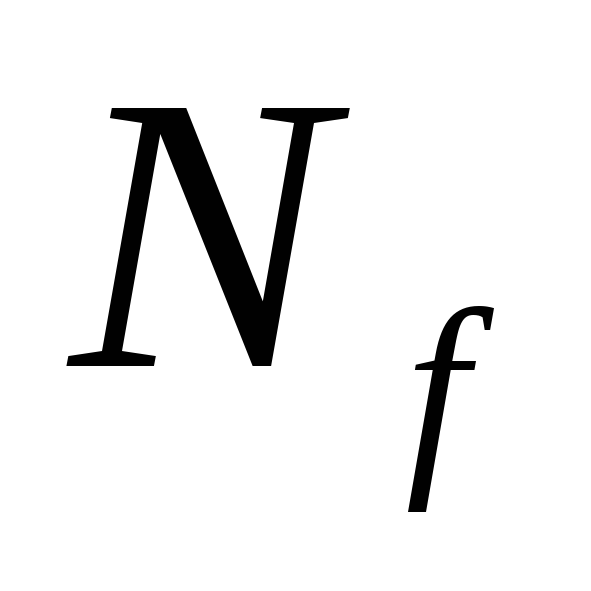 
всеми максимальными интервалами,
называетсясокра-
щенной ДНФ функции f.
Ясно, что сокращенная ДНФ для любой булевой функции f определяется однозначно.
Пример 1Пусть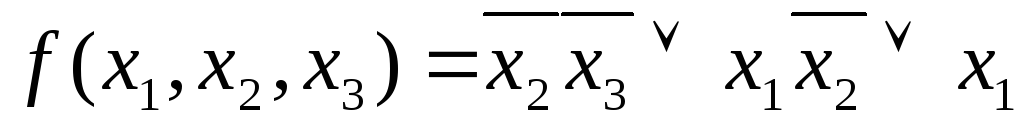
.
Обозначим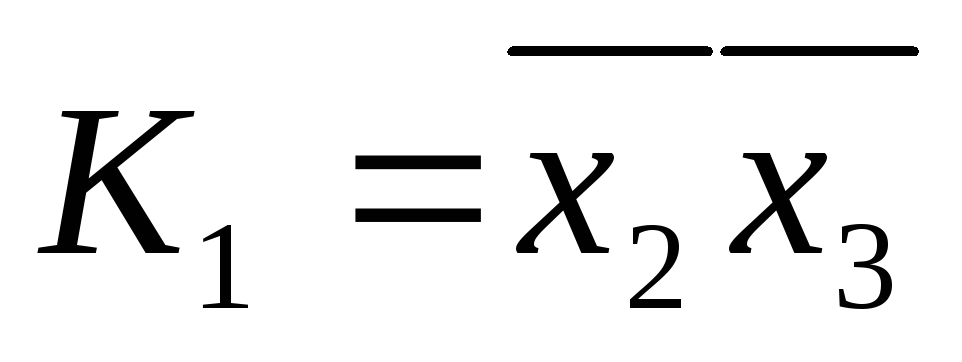
,
,
.
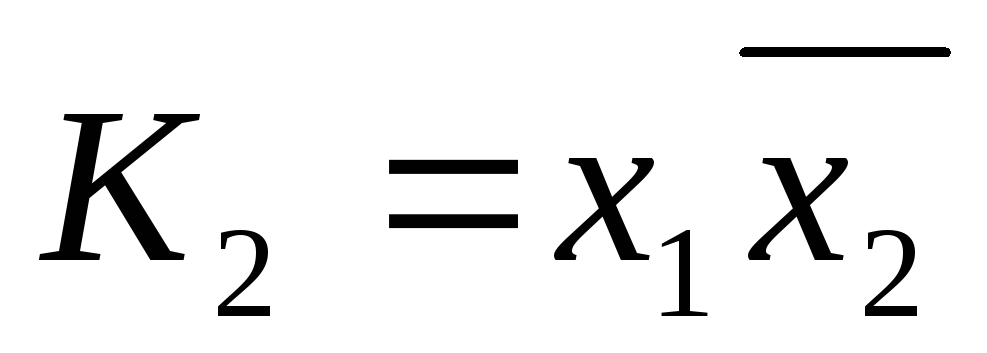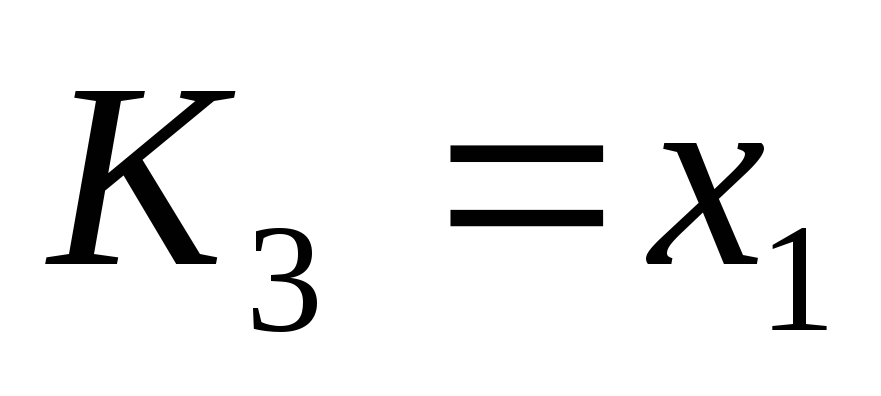Найдем соответствующие этим конъюнкциям
интервалы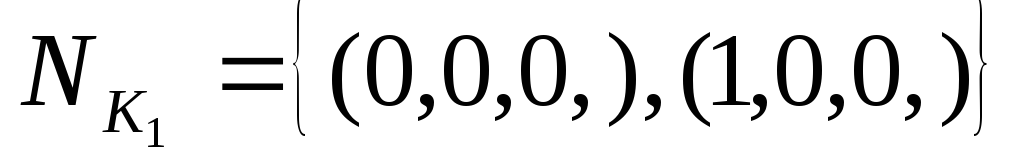
,
,
.
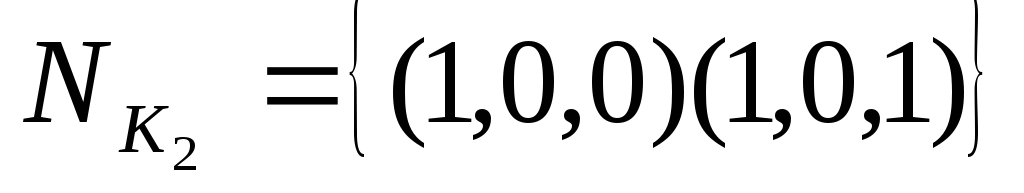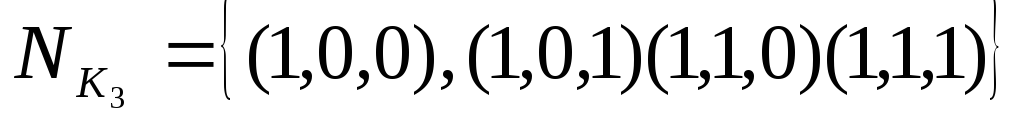Изобразим эти интервалы
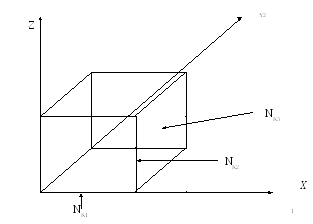
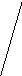
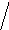
Очевидно, что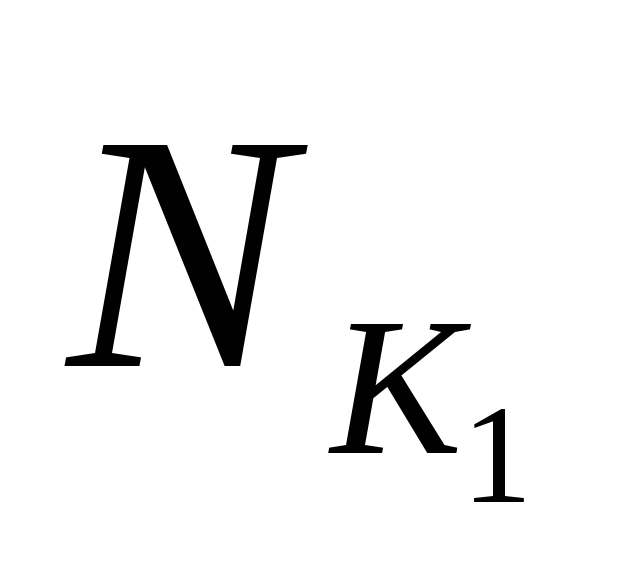 
и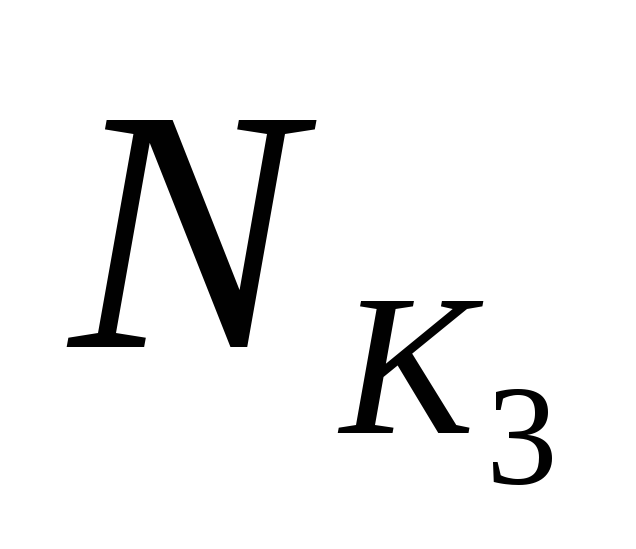
– все максимальные интервалы. Интервал
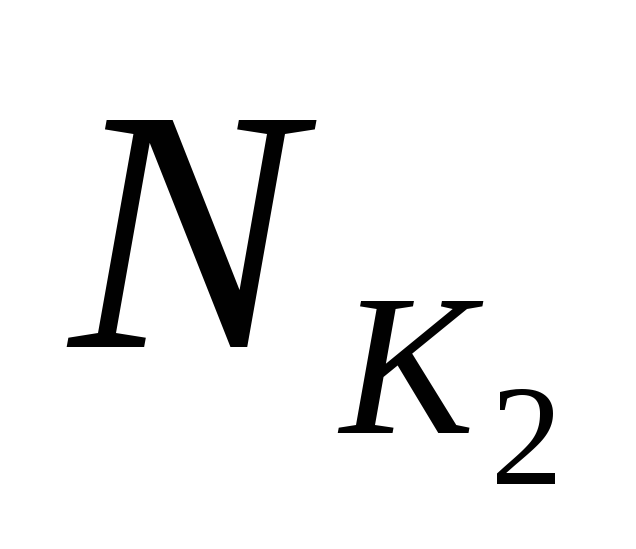не является максимальным, ибо
.
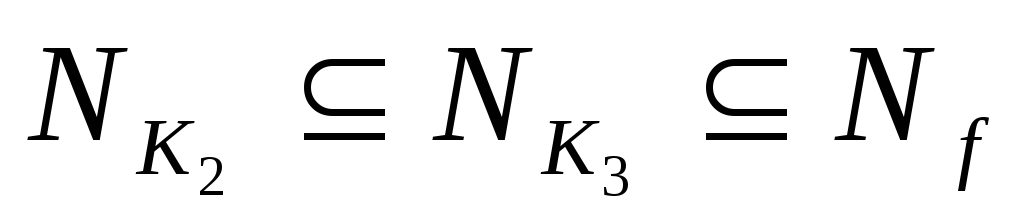Следовательно, покрытию подмножества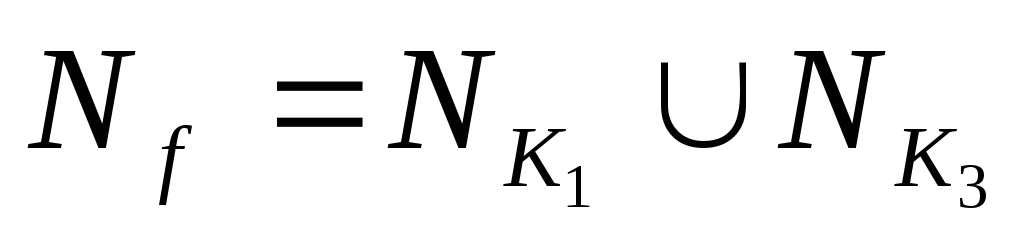
соответствует сокращенная ДНФ функции
,
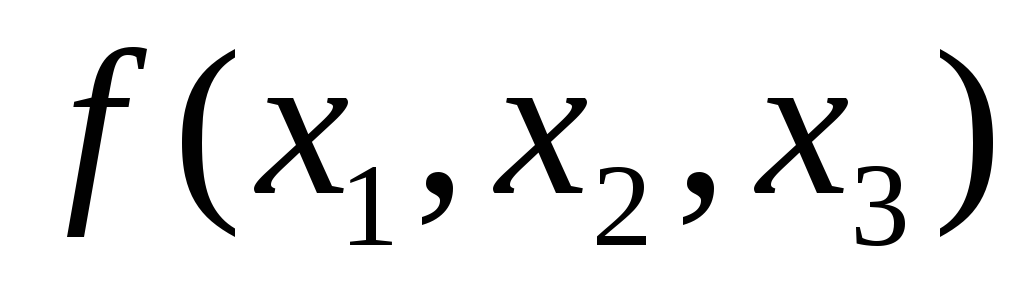равная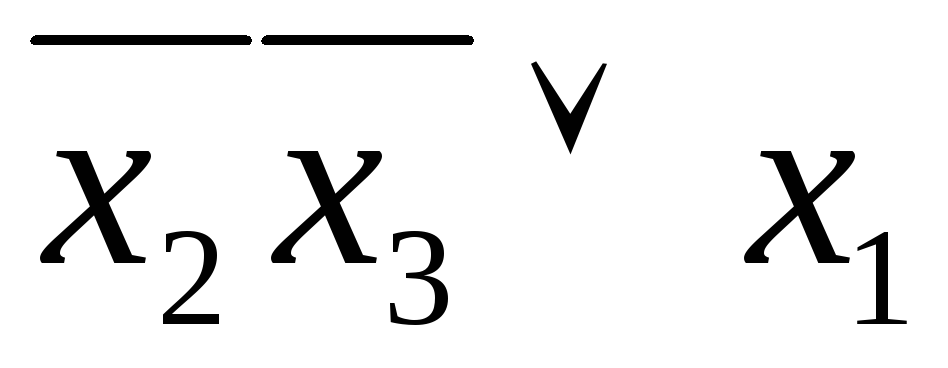
.
Данный геометрический подход дает и метод построения сокращенной
ДНФ.
Теперь рассмотрим аналитический метод построения сокращенной ДНФ – метод Блейка. Этот метод основан на следующей теореме.
Теорема 1 Если в произвольной ДНФ булевой функции f произвести все возможные обобщения склеивания и устранить затем все элементарные поглощения, то в результате получится сокращенная ДНФ функции f.
Следовательно,
чтобы найти сокращенную ДНФ, надо к
произвольной ДНФ данной функции применить
правило обобщенного склеивания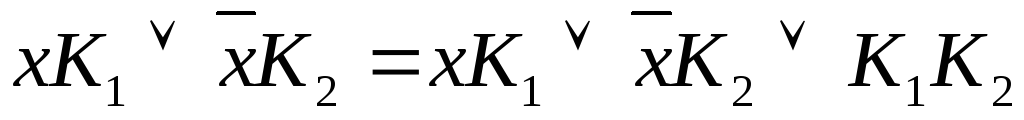 
до тех пор, пока это возможно, а затем
правило поглощения.
Пример 2Найти
сокращенную ДНФ для функции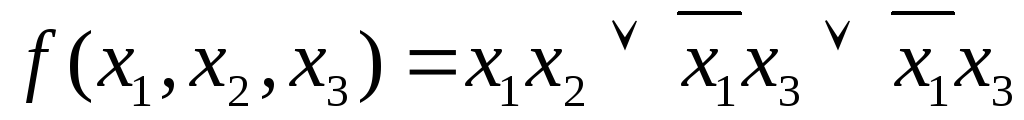
.
Применяя правило
обобщенного склеивания, получаем: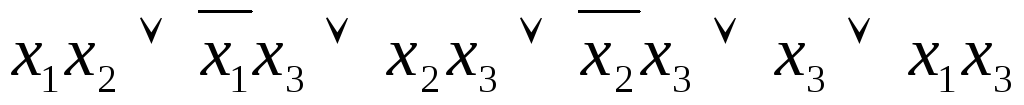 
,
а затем правило поглощения и находим
сокращенную ДНФ: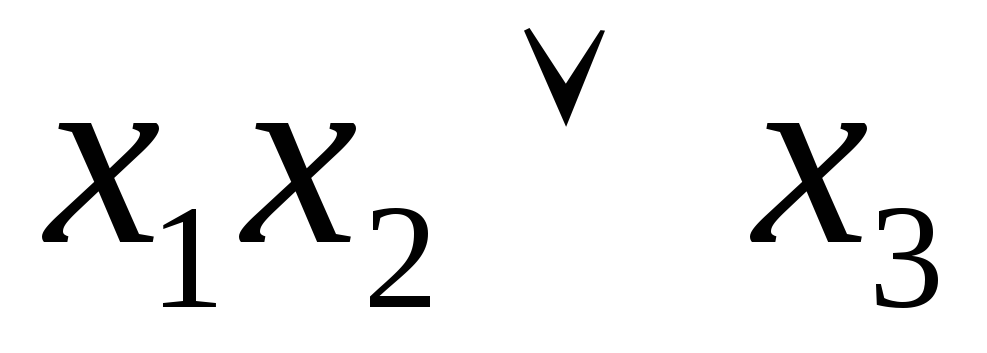
.
Рассмотрим еще один метод построения сокращенной ДНФ – метод Нельсона. Этот метод основан на следующей теореме.
Теорема 2 Если в произвольной КНФ булевой функции раскрыть все скобки в соответствии с дистрибутивным законом и устранить все элементарные поглощения, то в результате получится сокращенная ДНФ этой функции.
Пример 3Найти сокращенную ДНФ для функции
.
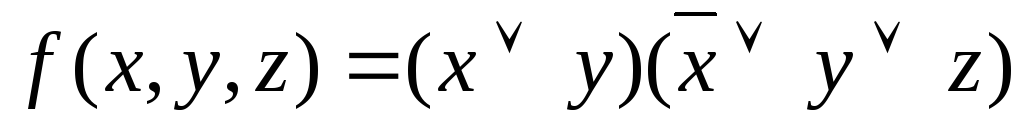После раскрытия скобок с помощью дистрибутивного закона, получаем:
.
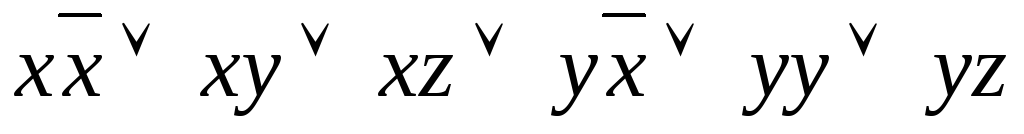Так как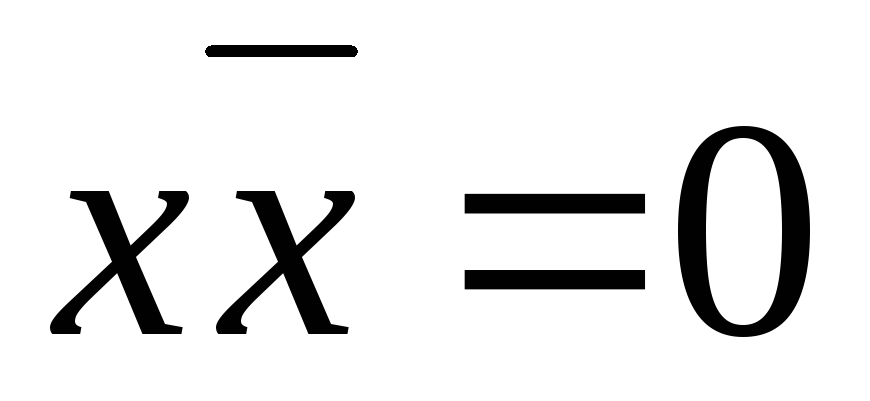 
,
,
то имеем:
.
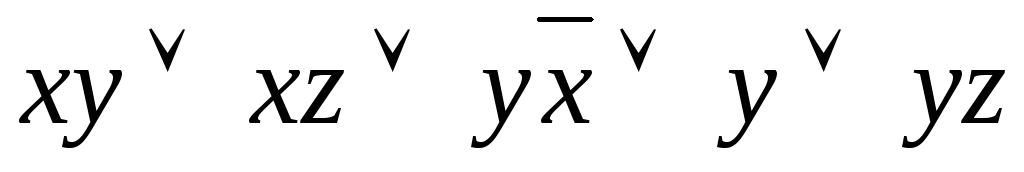Далее, применяя правило поглощения, получаем сокращенную ДНФ:
.
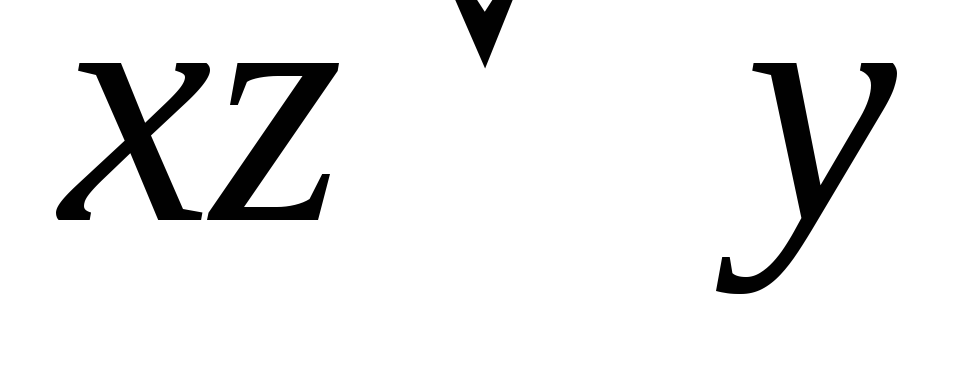Рассмотрим табличный метод построения сокращенной ДНФ. Этот метод основан на составлении прямоугольной таблицы (минимизирующей карты).
Минимизирующие карты для булевых функций от трех и от четырех переменных изображены в следующих таблицах:
x4 x3 x1 x2 | 0 0 | 0 1 | 1 1 | 1 0 |
0 0 | ||||
0 1 | ||||
1 1 | ||||
1 0 |
Объединяя соседние клетки, соответствующие единичным значениям булевой функции fв максимальные интервалы, и сопоставляя им элементарные конъюнкции, получим сокращенную ДНФ. Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.
Пример 4Найти сокращенную ДНФ для функции, заданной следующей таблицей.
x4 x3 x1 x2 | 0 0 | 0 1 | 1 1 | 1 0 |
0 0 | 1 | 1 | 0 | 1 |
0 1 | 0 | 1 | 1 | 0 |
1 1 | 1 | 1 | 1 | 0 |
1 0 | 0 | 1 | 0 | 0 |
В данной таблице объединены клетки в максимальные интервалы
.
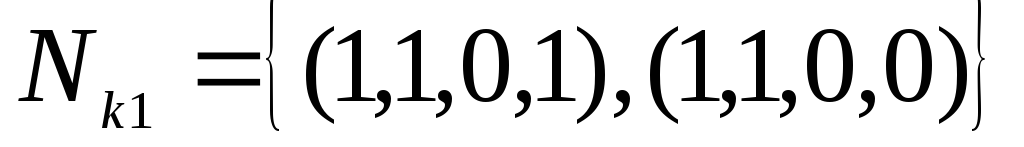
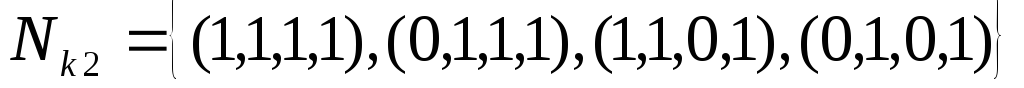
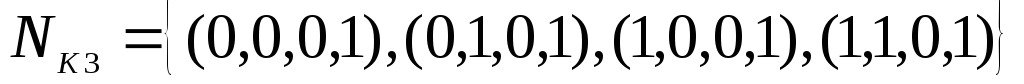
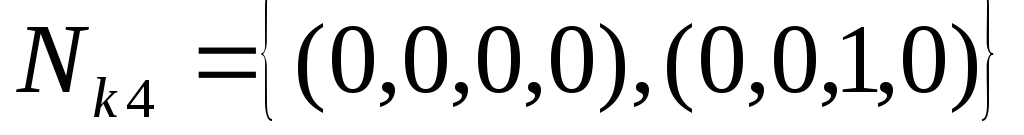
Этим интервалам соответствуют элементарные конъюнкции
, 
,
,
,
.
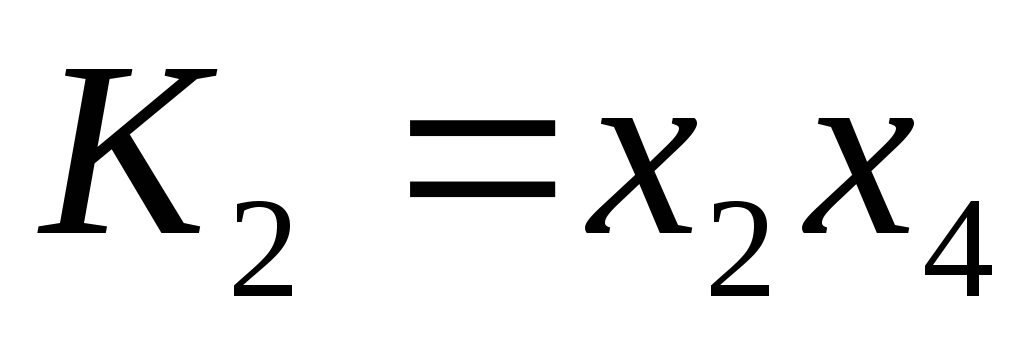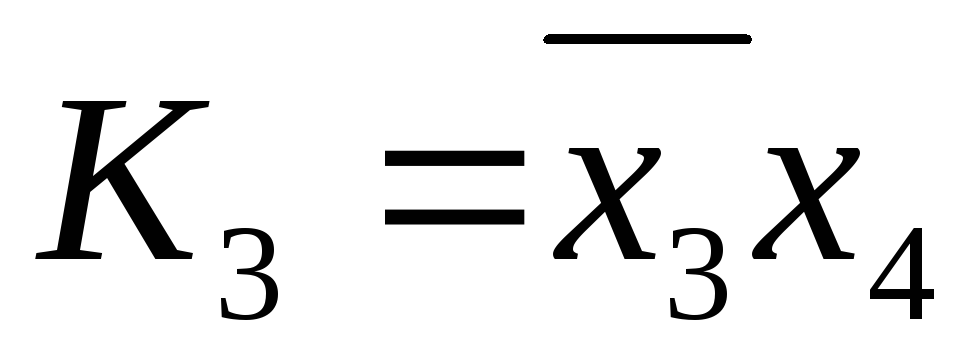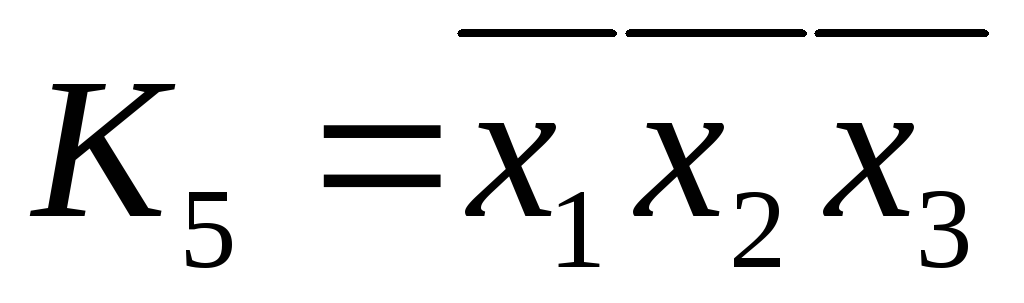Следовательно, сокращенная ДНФ для данной функции имеет вид:
.
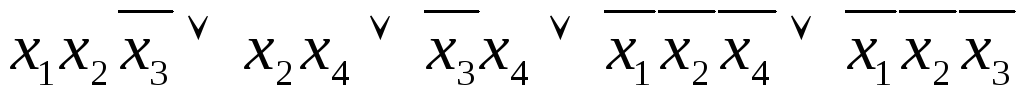Построение сокращенной ДНФ есть только первый этап решения задачи минимизации булевой функции. В общем случае сокращенная ДНФ не является минимальной. Следующая теорема устанавливает связь между минимальной и сокращенной ДНФ.
Теорема 3 Минимальная ДНФ булевой функции получается из сокращенной ДНФ данной функции путем удаления некоторых элементарных конъюнкций.
Доказательство
этого утверждения следует из того факта,
что покрытие подмножества 
,
отвечающее минимальной ДНФ, состоит
только из максимальных интервалов.
Действительно, если бы покрытие содержало
не максимальный интервал, то его можно
было бы заменить объемлющим максимальным
интервалом. В результате этого сумма
рангов интервалов данного покрытия
уменьшилась бы, что противоречит
предположению о минимальности ДНФ.
Покажем, что в классе монотонных функций понятия минимальной и сокращенной ДНФ совпадают.
Теорема 4 Сокращенная ДНФ монотонной булевой функции не содержит отрицаний переменных и является минимальной ДНФ этой функции.
Пусть К–
элементарная конъюнкция, входящая в
сокращенную ДНФ. Предположим, чтоКсодержит отрицание переменных. Обозначим
через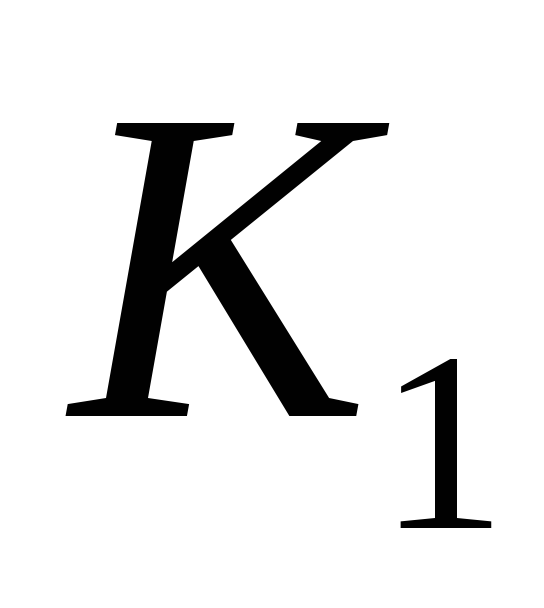
произведение всех переменных, входящих
вКбез отрицания. Пусть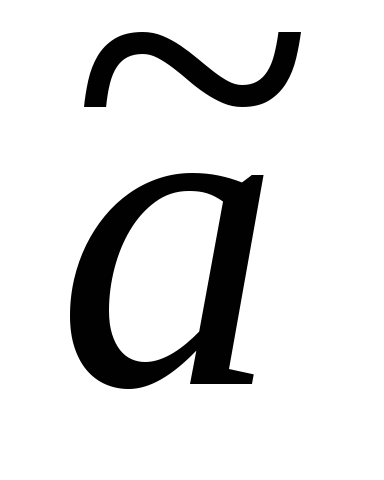
– набор переменных, в которых всем
переменным, входящим в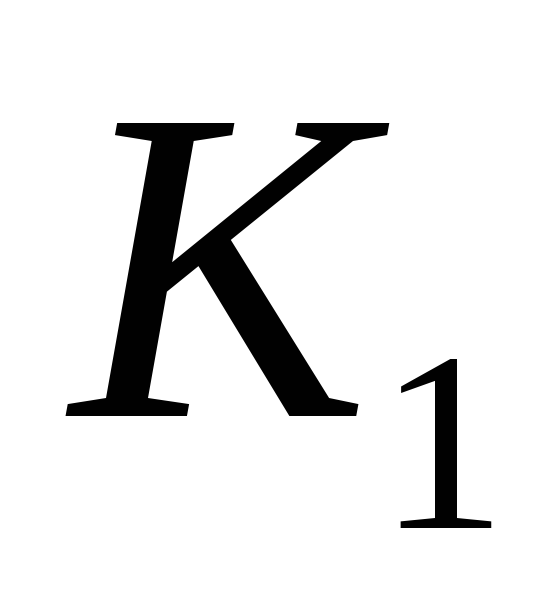
,
приписано значение 1, а всем остальным
– значение 0. Ясно, что при этом наборе
значение функции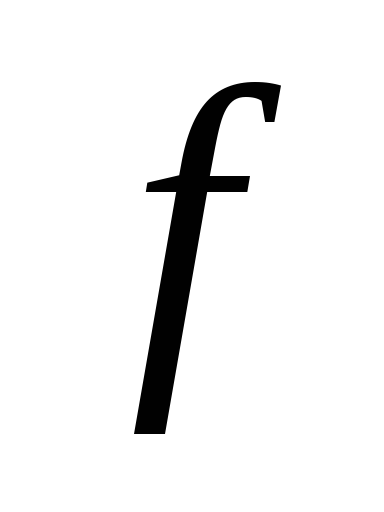
равно
1. Элементарная конъюнкция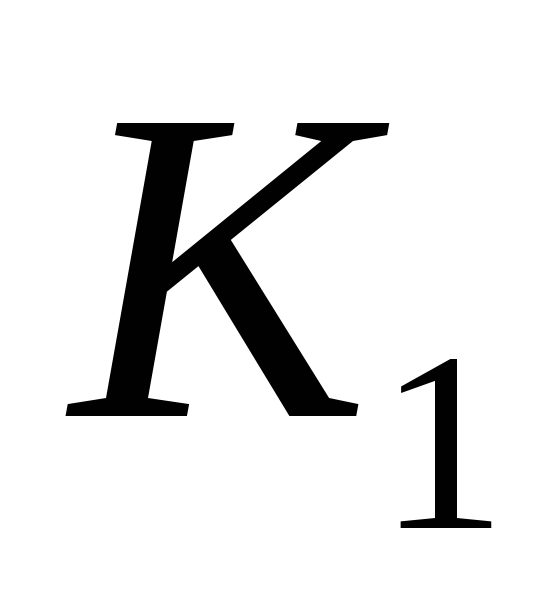
обращается в 1 при всех наборах
.
Очевидно, что при этих наборах значение
функции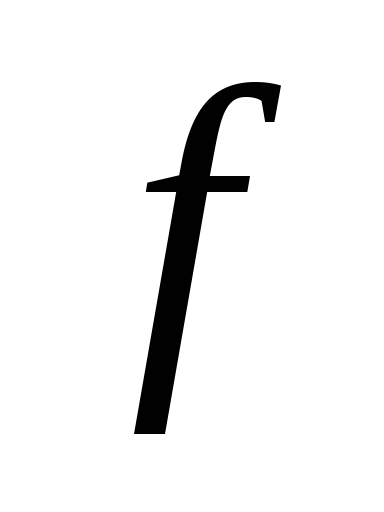
также равно 1. Следовательно,
.
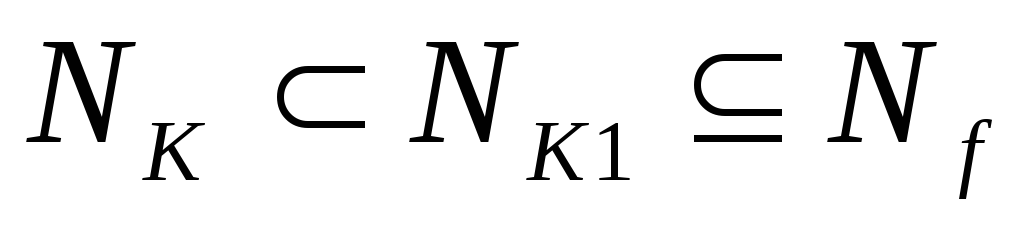Получили противоречие
с максимальностью интервала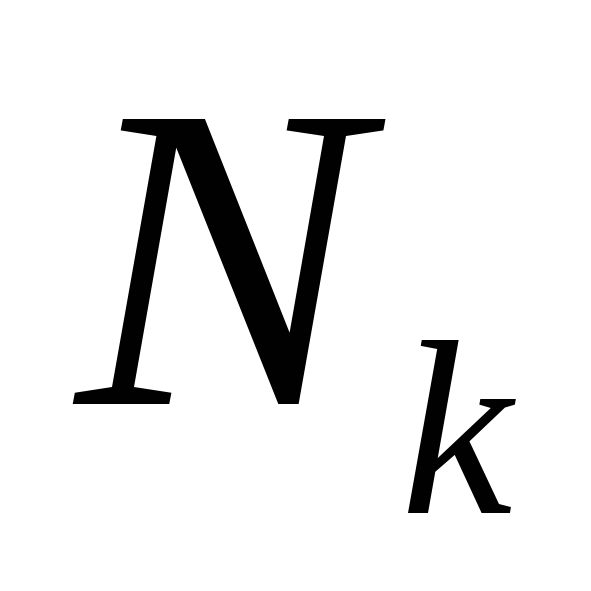 
.
Итак, сокращенная ДНФ булевой функции
не
содержит отрицаний переменных.
Пусть 
– любая элементарная конъюнкция из
сокращенной ДНФ. КонъюнкцияКявляется единственной конъюнкцией
сокращенной ДНФ, которая обращается в
единицу в вершине с координатами
.
Действительно, если бы в сокращенной
ДНФ какая-нибудь другая элементарная
конъюнкцияобращалась в этой вершине в 1, то не
содержала бы, во-первых, букв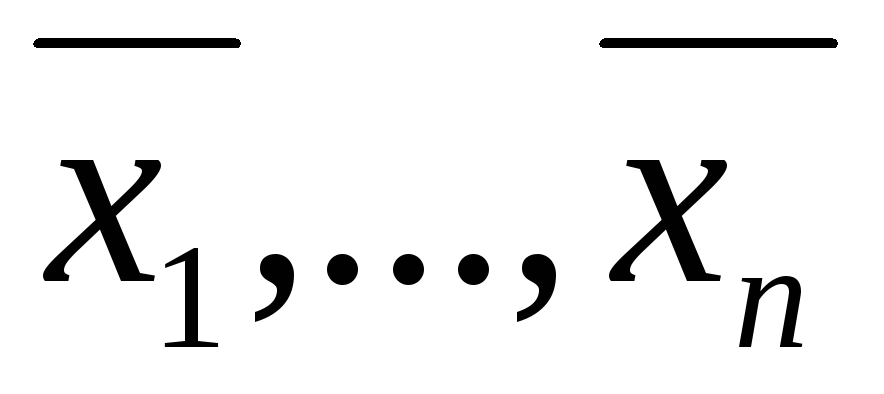
,
и, во-вторых, букв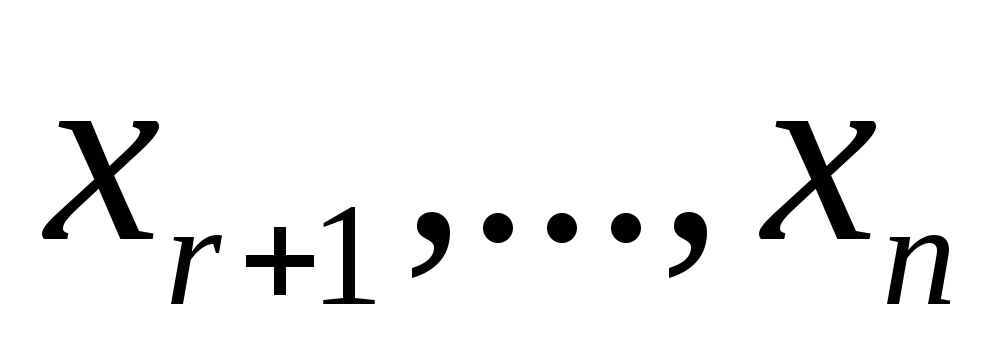
.
Поэтому в конъюнкцию
могли бы входить лишь буквы
,
причем не все. Но тогда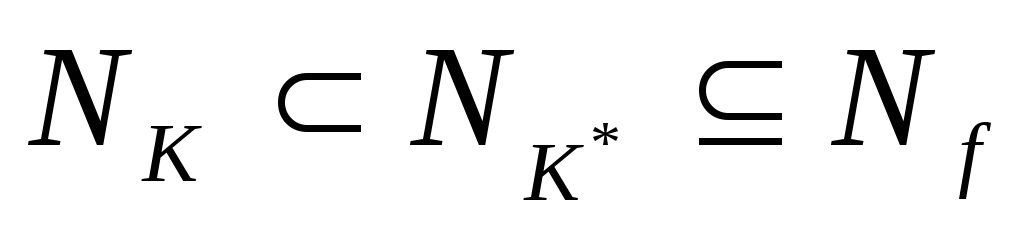
.
Получили противоречие с максимальностью
интервала
.
Следовательно, для любого максимального
интерваласуществует вершина куба
,
которая покрывается только этим
интервалом. Поэтому из покрытия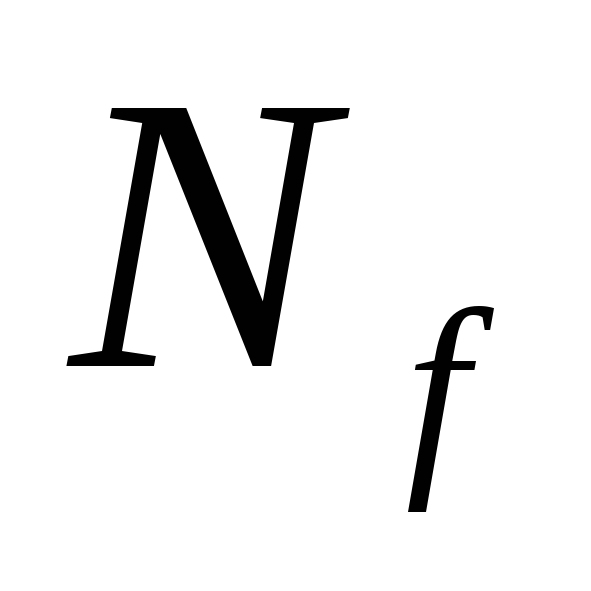
соответствующего сокращенной ДНФ,
нельзя удалить ни один из интервалов.
Теперь, применяя предыдущую теорему,
получаем требуемый результат.
Следует отметить, что сокращенная ДНФ в большинстве случаев допускает дальнейшие упрощения за счет того, что некоторые элементарные конъюнкции могут поглощаться дизъюнкциями других элементарных конъюнкций. Действительно, в сокращенной ДНФ
элементарная
конъюнкция 
поглощается дизъюнкцией остальных
элементарных конъюнкций, т.е.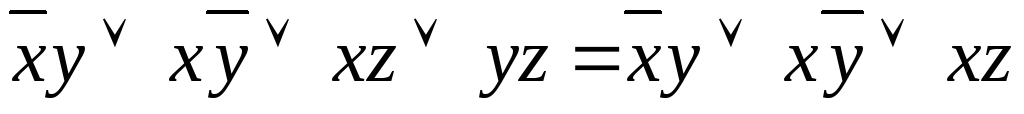
.
Ввиду этого введем следующее определение.
Покрытие области
истинности булевой функции максимальными
интервалами называется неприводимым,
если после удаления из него любого
интервала оно перестает быть покрытием.
ДНФ булевой функци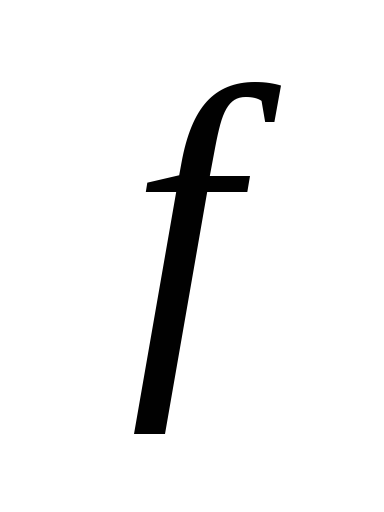и
,
соответствующая неприводимому покрытию,
называетсятупиковой.
Теорема 5 Всякая минимальная ДНФ является тупиковой.
Доказательство этого утверждения следует из того, что покрытие, соответствующее минимальной ДНФ, является неприводимым.
Заметим, что булева функция может обладать несколькими различными минимальными ДНФ. Существуют также тупиковые ДНФ, не являющиеся минимальными ДНФ. Соответствующие примеры будут разобраны ниже.
Из того, что минимальная ДНФ является тупиковой, следует общая схема решения задачи минимизации булевых функций.
1 Выделяются все максимальные интервалы, и строится сокращенная ДНФ.
2 Строятся все тупиковые ДНФ.
3 Среди всех тупиковых ДНФ выделяются все минимальные ДНФ.
Рассмотрим алгоритм построения всех тупиковых ДНФ. Суть данного алгоритма состоит в следующем:
1) для булевой
функции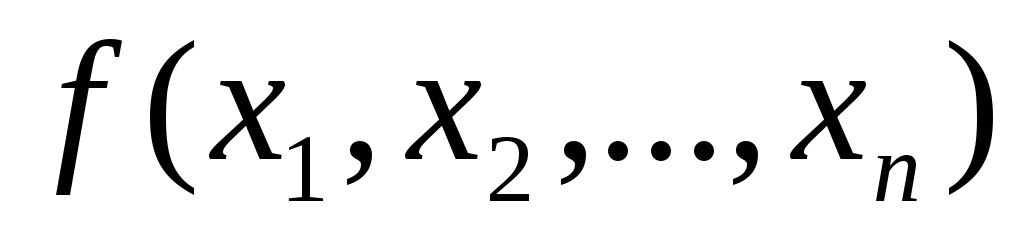 
строим сокращенную ДНФ;
2) для каждой вершины 
из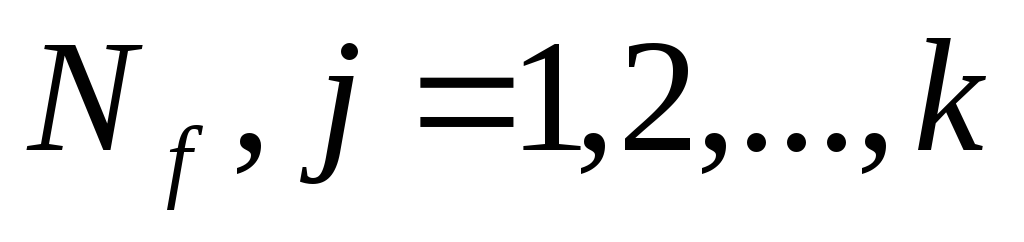
выделяем в сокращенной ДНФ функцииfвсе такие элементарные конъюнкции
,
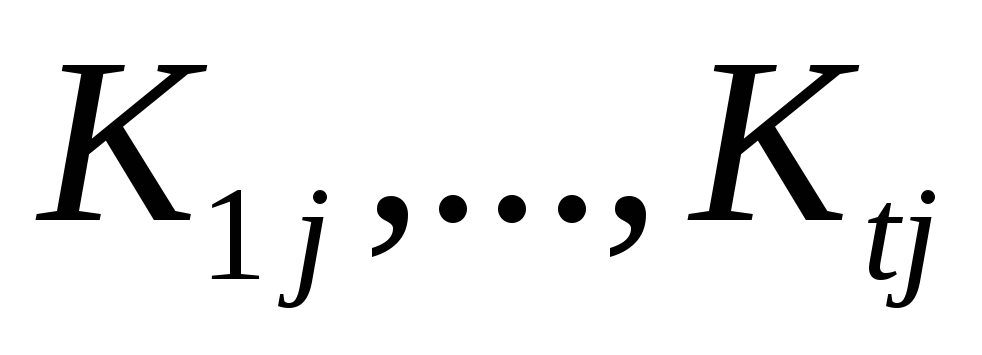что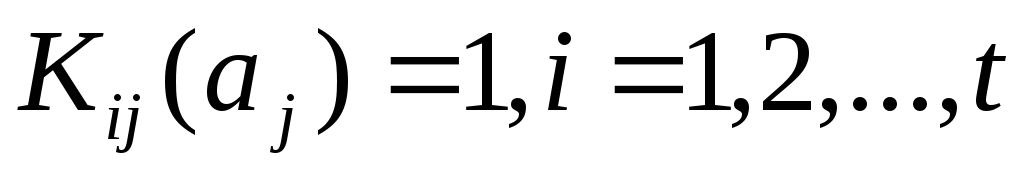
;
3) составляем выражение вида
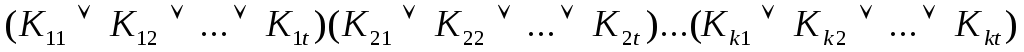(6.1)
4) применяем к
выражению вида (6.1) законы дистрибутивности
и поглощения. В результате получаем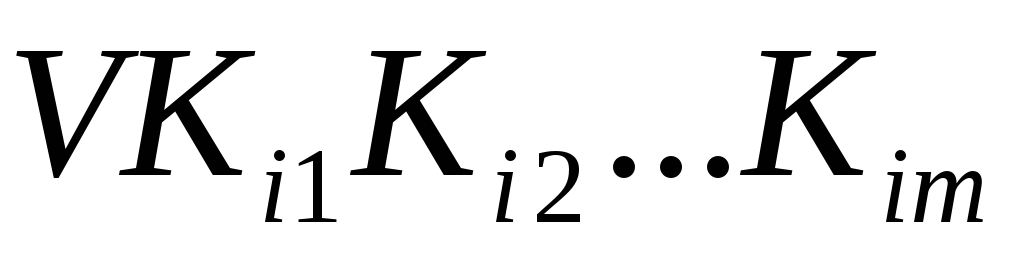 
.
Теперь каждая ДНФ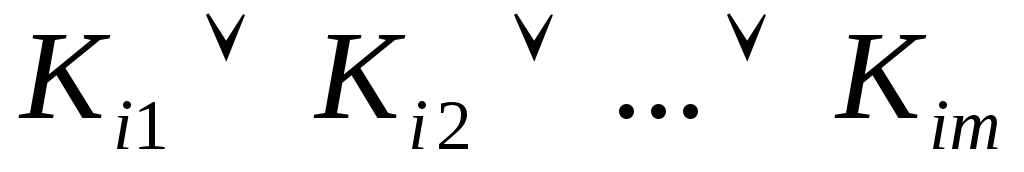 
является тупиковой ДНФ функции
.
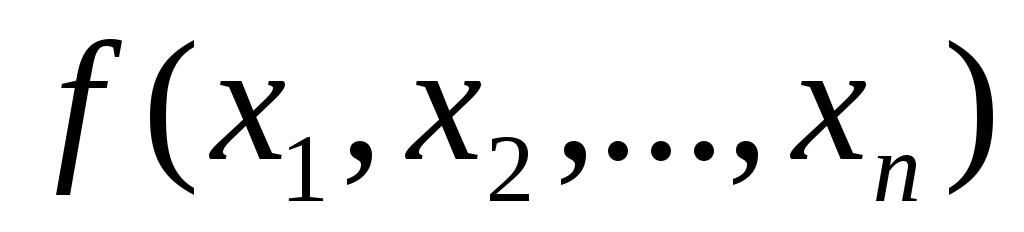Рассмотрим работу данного алгоритма на следующем примере.
Пример 5Рассмотрим булеву функцию, заданную следующей таблицей:
x | y | z |
|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
Найдем сокращенную
ДНФ данной функции по методу Нельсона.
Для этого составим КНФ данной функции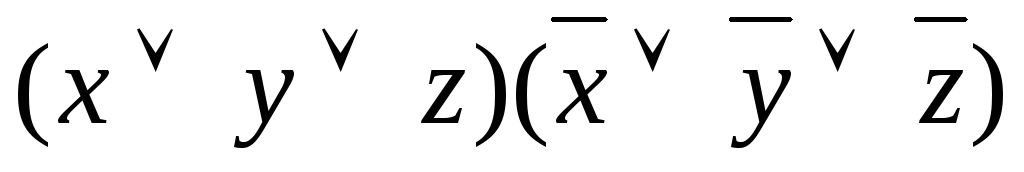 
.
Применяя законы дистрибутивности, получаем:
.
Обозначим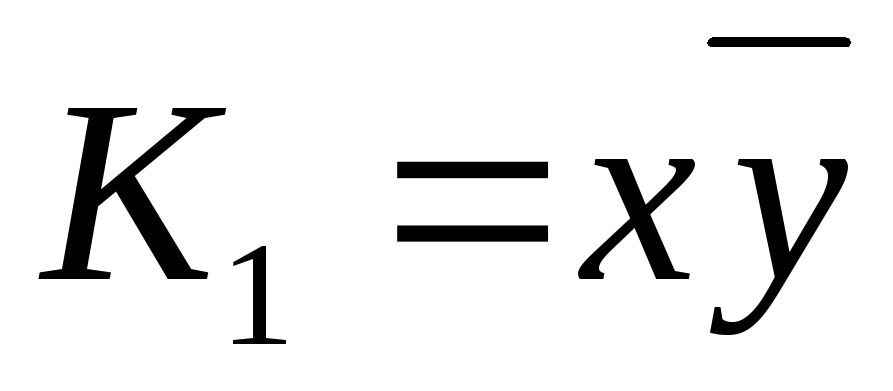 
,
,
,
,
,
.
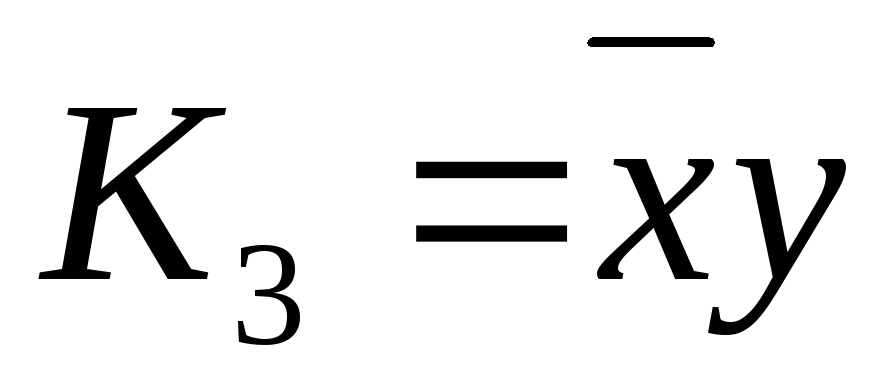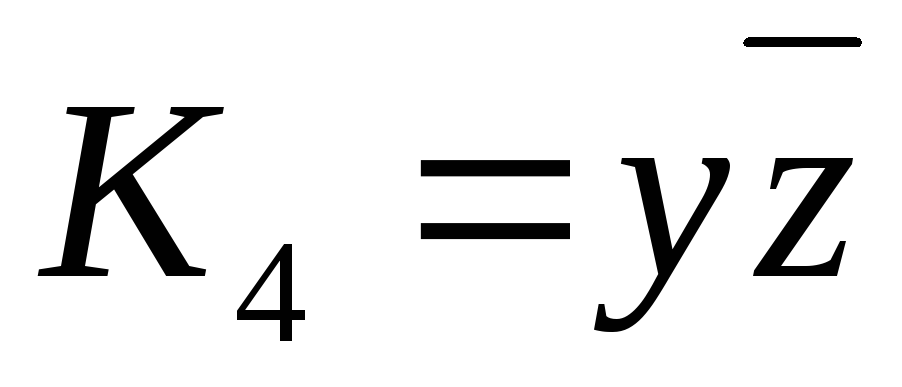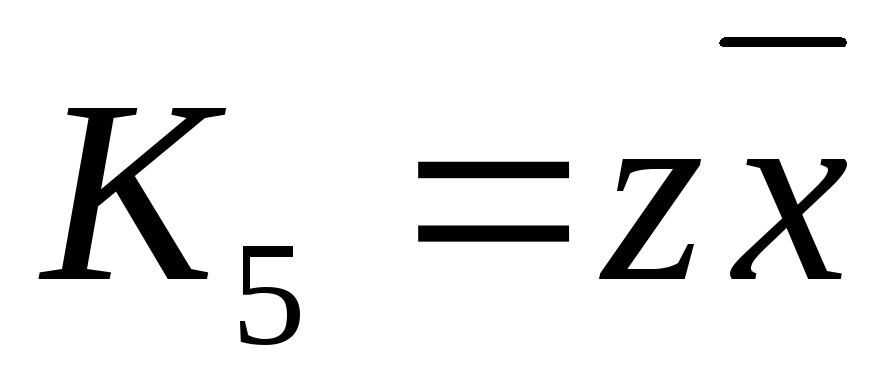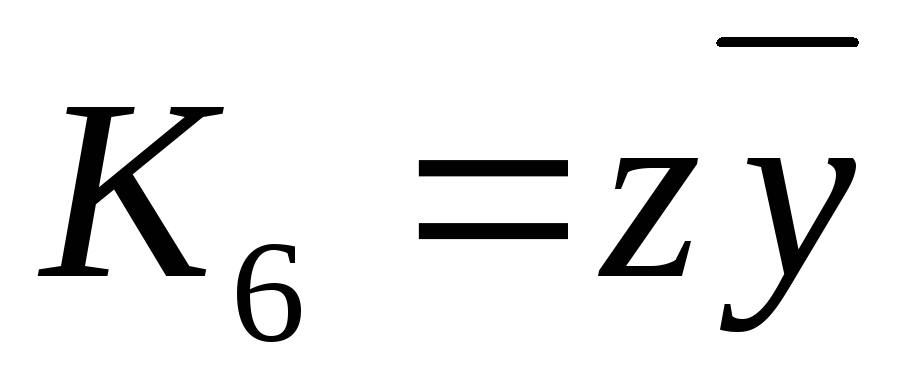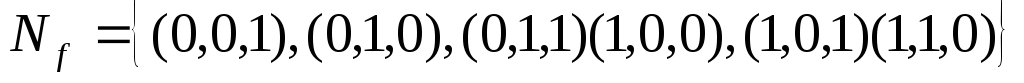
Составляем выражение (6.1)
.
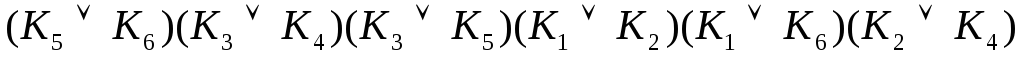Преобразуем данное выражение к виду
= 
=
.
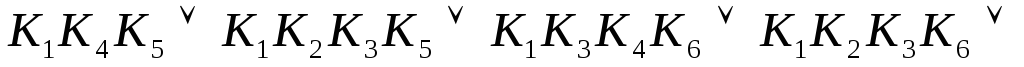
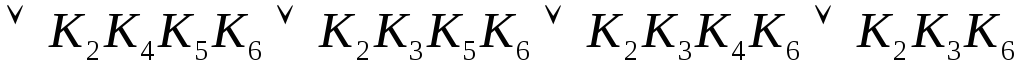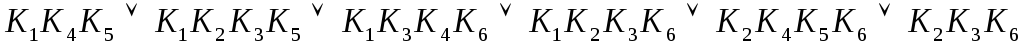Таким образом,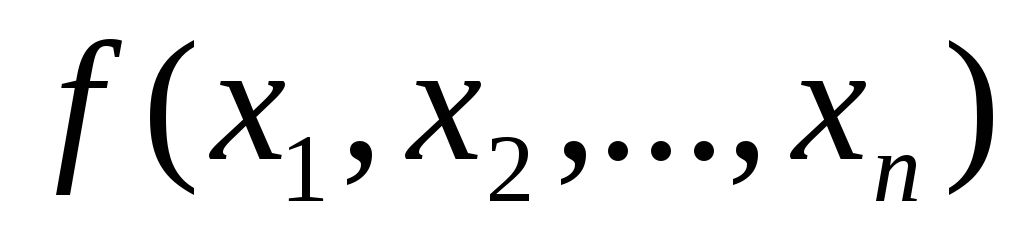 
имеет шесть тупиковых ДНФ:
- ;
- ;
- ;
- ;
- ;
- .
;
;
;
;
;
. Две из них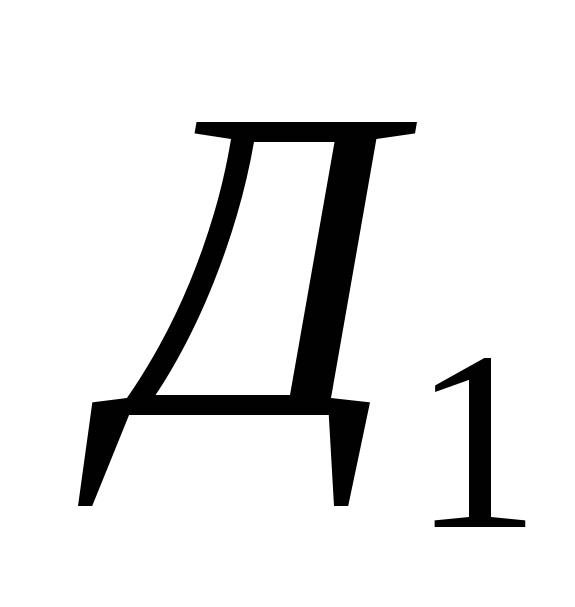 
и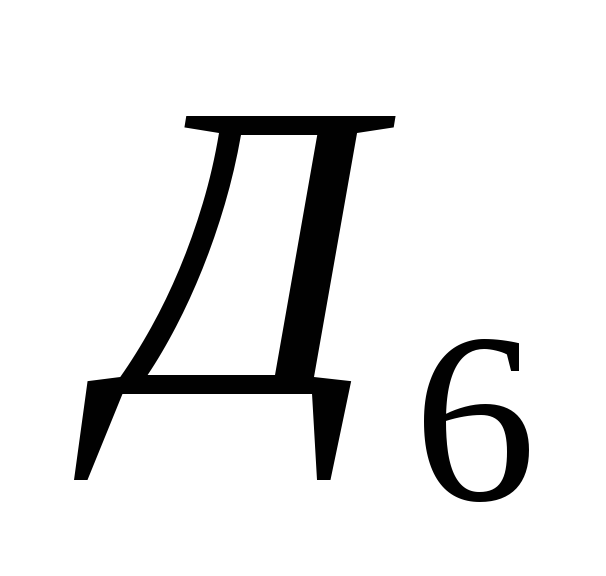
являются минимальными.
25 полезных примеров команд DNF для управления пакетами в Linux
Написал Джаррод 9 января 2017 г.Dandified Yum (DNF) — менеджер пакетов на основе RPM, который используется для установки и обновления пакетов в различных дистрибутивах Linux, включая CentOS, RHEL и Fedora.
DNF является следующей основной версией Yum, и поэтому он нацелен на поддержание совместимости CLI с Yum, поэтому большая часть информации здесь будет похожа на наши команды yum.
Как и Yum, DNF достаточно мощный, поскольку он способен автоматически решать проблемы с зависимостями, и похож на другие менеджеры пакетов, такие как «apt-get» в дистрибутивах на основе Debian.
Эти примеры должны послужить полезным введением, руководством или источником стилей, чтобы узнать, как использовать команду dnf в Linux.
Если DNF еще не используется по умолчанию в вашем дистрибутиве, но вы заинтересованы в его установке, ознакомьтесь с нашим руководством по установке DNF.
Как использовать dnf — Примеры команд
1.Установить новый пакет из репозитория
Команда dnf может использоваться для установки пакетов из репозитория с аргументом «install», за которым следует имя пакета. В приведенном ниже примере мы устанавливаем Apache, который предоставляется в пакете «httpd».
[[электронная почта защищена] ~] # dnf install httpd Использование метаданных чт 29 декабря 21:31:01 2016 Зависимости устранены. ================================================== ========= Размер архива версии архива пакета ================================================== ========= Установка: httpd x86_64 2.4.6-45.el7.centos база 2,7 М Сводка транзакций ================================================== ========= Установить 1 пакет Общий объем скачиваемых файлов: 2,7 М Установленный размер: 9,4 м Это нормально [да / нет]: и Загрузка пакетов: httpd-2.4.6-45.el7.centos.x86_64.rpm 4,3 МБ / с | 2,7 МБ 00:00 -------------------------------------------------- ---------------------- Всего 1,6 МБ / с | 2,7 МБ 00:01 Проверка выполнения транзакции Проверка транзакции прошла успешно.Проверка выполнения транзакции Проверка транзакции прошла успешно. Выполнение транзакции Установка: httpd-2.4.6-45.el7.centos.x86_64 1/1 Проверка: httpd-2.4.6-45.el7.centos.x86_64 1/1 Установлены: httpd.x86_64 2.4.6-45.el7.centos Complete!
Обратите внимание, что после подтверждения пакетов, которые будут установлены, вам будет предложено ввести данные. В этом случае мы ввели «y» для да, чтобы продолжить установку, которая затем успешно завершилась.
2.Предположим, да
В первом примере нам было предложено нажать клавишу «y», чтобы продолжить установку. Вместо того, чтобы каждый раз запрашивать ввод данных пользователем, мы можем просто указать опцию «-y» в нашей команде для предположения «да». Таким образом, мы не будем запрашивать какой-либо ввод, и dnf будет считать, что на все ответят yes.
[[электронная почта защищена] ~] # dnf install httpd-manual -y Использование метаданных чт 29 декабря 21:31:01 2016 Зависимости устранены.================================================== ==================== Размер архива версии архива пакета ================================================== ==================== Установка: httpd-manual noarch 2.4.6-45.el7.centos base 1.3 M Сводка транзакций ================================================== ==================== Установить 1 пакет Общий объем скачиваемых файлов: 1,3 М Установленный размер: 5,5 м Загрузка пакетов: HTTPD-ручной 2.4.6-45.el7.centos.noarch.rpm
Краткое руководство по DNF для пользователей yum
Dandified yum, более известный как DNF, — это менеджер пакетов программного обеспечения для дистрибутивов Linux на основе RPM, который устанавливает, обновляет и удаляет пакеты. Впервые он был представлен в Fedora 18 в тестируемом состоянии (т. Е. В техническом обзоре), но он был стандартным менеджером пакетов Fedora начиная с Fedora 22.
Поскольку это версия следующего поколения традиционного менеджера пакетов yum, он обладает более продвинутыми и надежными функциями, чем в yum. Некоторые особенности, которые отличают DNF от yum:- Расчет зависимости на основе современной технологии решения зависимостей
- Оптимизированные операции с интенсивным использованием памяти
- Возможность запуска в Python 2 и Python 3
- Доступна полная документация по API Python
DNF использует библиотеки hawkey, которые разрешают зависимости RPM для выполнения запросов на клиентских компьютерах.Они построены поверх libsolv, решателя зависимостей пакетов, который использует алгоритм выполнимости. Вы можете найти более подробную информацию об алгоритме в GitHub репозитории libsolv.
команд CLI, которые отличаются по DNF и yum
Ниже приведены некоторые изменения интерфейса командной строки (CLI) yum, которые вы найдете в DNF.
обновление dnf или обновление dnf: Выполнение обновления dnf или обновления dnf имеет одинаковый эффект в системе: оба обновления устанавливают установленные пакеты.Однако обновление dnf является предпочтительным, поскольку оно работает точно так же, как yum —obsoletes update .
resoldep: Эта команда не существует в DNF. Вместо этого выполните , dnf предоставляет , чтобы узнать, какой пакет предоставляет определенный файл.
deplist: Команда депиляции Yum, в которой перечислены зависимости RPM, была удалена в DNF, поскольку она использует алгоритм решателя зависимостей пакетов для решения запроса зависимостей.
dnf remove <пакет>: Необходимо указать конкретные версии всего, что вы хотите удалить.Например, dnf remove kernel удалит все пакеты, называемые «kernel», поэтому обязательно используйте что-то вроде dnf remove kernel-4.16.x .
откат истории dnf: Эта проверка, которая отменяет транзакции после указанной вами, была отброшена, поскольку не все возможные изменения в инструменте базы данных RPM хранятся в истории транзакций.
—skip-broken: Эта команда установки, которая проверяет пакеты на наличие проблем с зависимостями, запускается в yum с параметром —skip-broken.Тем не менее, теперь он является частью обновления dnf по умолчанию, поэтому в этом больше нет необходимости.
-b, —best: Эти переключатели выбирают лучшие из доступных версий пакетов в транзакциях. Во время обновления dnf, которое по умолчанию пропускает обновления, которые не могут быть установлены по причинам зависимости, этот переключатель заставляет DNF рассматривать только самые последние пакеты. Используйте dnf upgrade —best .
—allowerasing: Позволяет стирать установленные пакеты для устранения зависимостей.Эта опция может использоваться в качестве альтернативы команде yum swap X Y , в которой пакеты для удаления не определены явно.
Например: dnf — разрешить установку Y .
—enableplugin: Этот переключатель не распознан и был сброшен.
DNF Автомат
Инструмент DNF Automatic является альтернативой CLI для обновления dnf. Он может запускаться автоматически и регулярно из системных таймеров, заданий cron и т. Д.для автоматического уведомления, загрузки или обновления.
Для запуска установите dnf-automatic rpm и включите системный таймер (dnf-automatic.timer). Он ведет себя так, как указано в файле конфигурации по умолчанию (это /etc/dnf/automatic.conf).
# yum install dnf-automatic
# systemctl enable dnf-automatic.timer
# systemctl start dnf-automatic.timer
# systemctl status dnf-automatic.timer
Другие блоки таймера, которые переопределяют конфигурацию по умолчанию, перечислены ниже.Выберите тот, который соответствует вашим системным требованиям.
- dnf -automatic- notifyonly .timer: Уведомляет о доступных обновлениях
- dnf-automatic-download.timer: Загружает пакеты, но не устанавливает их
- dnf -automatic-install.timer: Загружает и устанавливает обновления
Основные команды DNF полезны для управления пакетами
# yum install dnf: Это устанавливает RPM DNF из менеджера пакетов yum.
# dnf –version: Указывает версию DNF.
# dnf перечислить все или # dnf list <имя-пакета>: Здесь перечислены все или конкретные пакеты; В этом примере перечислены RPM ядра, доступные в системе.
# dnf check-update или # dnf check-update kernel: При этом отображаются обновления в системе.
# dnf search <имя-пакета>: При поиске определенного пакета через DNF он будет искать точное совпадение, а также все подстановочные знаки поиска, доступные в хранилище.
# dnf repolist all: Это загружает и перечисляет все включенные репозитории в системе.
# dnf list —recent или # dnf list —recent <имя-пакета>: Опция —recent сбрасывает все недавно добавленные пакеты в системе. Другие варианты списка: — дополнительные , — обновления и — поддержка .
# dnf updateinfo доступен список или # dnf updateinfo доступен список sec: Здесь перечислены все рекомендации, доступные в системе; в том числе опция sec перечислит все рекомендации, помеченные как «исправление безопасности».»
# dnf updateinfo list available sec —sec-severity Critical: В этом списке перечислены все рекомендации по безопасности в системе, помеченные как «критические».
# dnf updateinfo FEDORA-2018-a86100a264 –info: Это проверяет информацию о любых рекомендациях через коммутатор —info .
# dnf upgrade —security или # dnf upgrade —sec-severity Критическое значение: Это относится ко всем рекомендациям по безопасности, доступным в системе.С опцией —sec-severity можно включить пакеты с серьезностью, помеченной как Критическая, Важная, Умеренная или Низкая.
Резюме
Это лишь небольшое количество функций, изменений и команд DNF. Для получения полной информации о CLI DNF, новых плагинах и подключаемых API обратитесь к руководству DNF.
,Как установить менеджер пакетов DNF в CentOS / RHEL
Как установить менеджер пакетов DNF в CentOS / RHEL
Написал Джаррод 2 января 2017 г.DNF, или Dandified Yum, который является следующей основной версией менеджера пакетов Yum, был представлен в Fedora 18. Начиная с Fedora 22, он стал менеджером пакетов по умолчанию.
Как вы, возможно, знаете, операционная система Fedora Linux по сути является передовым полигоном для тестирования пакетов, которые могут быть включены в дистрибутивы на основе RHEL / CentOS в будущем.
Поэтому вполне вероятно, что в некоторых будущих выпусках RHEL / CentOS также будет использовать DNF, а не Yum, чтобы воспользоваться новыми функциями, поэтому давайте посмотрим, что происходит при установке и использовании DNF в CentOS Linux, чтобы мы можем быть готовы к этому, когда он сделан по умолчанию.
DNF направлен на решение проблемы низкой производительности и высокого использования памяти, связанных с Yum.
Установка DNF
В настоящее время пакет DNF поступает из репозитория EPEL, поэтому, если ваша система Linux еще не настроена на использование этого репозитория, просто запустите приведенную ниже команду, чтобы настроить его.
[[электронная почта защищена] ~] # yum install epel-release -y
Теперь, когда EPEL готов к использованию, просто установите пакет dnf, как показано ниже.
[[электронная почта защищена] ~] # yum install dnf -y
Итак, мы используем менеджер пакетов для установки менеджера пакетов, вроде мета. Мне было интересно, попытается ли DNF удалить Yum во время установки, но этого не произошло, и кажется, что они способны работать бок о бок друг с другом.
Использование DNF
Теперь, когда DNF установлен, мы можем использовать его вместо Yum.Кажется, что большинство команд имеют один и тот же синтаксис, что значительно упрощает задачу, например:
Установка пакета
dnf install httpd
Обновление пакета
Обновление dnf httpd
Просмотр истории
История ДНФ
Удалить пакет
dnf удалить httpd
Посетите справочную страницу для получения дополнительной информации.
Резюме
Мы увидели, как легко можно установить DNF в дистрибутивах CentOS / RHEL Linux, что позволяет нам привыкнуть работать с ним, прежде чем он неизбежно заменит Yum в некоторых будущих обновлениях, как это уже было сделано в Fedora 22.
Основы Linux: 15 примеров команд DNF
Я надеюсь, вы знаете, что менеджер пакетов DNF заменен менеджером пакетов yum в Fedora 22. Вот несколько примеров использования менеджера пакетов DNF.
Поддерживает совместимость CLI с yum, вы не найдете никакой разницы в использовании DNF.
Вы все еще можете использовать команду YUM, но все команды будут перенаправлены на соответствующую команду DNF. Вы получите похожий вывод при вводе команды yum.
Команда Yum устарела, она перенаправлена на '/ usr / bin / dnf install httpd'
Пакеты можно установить с помощью следующей команды.
# dnf install vsftpd Последняя проверка срока действия метаданных выполнена 0:09:43 назад в среду, 27 мая 08:47:24 2015. Зависимости устранены. ================================================== ================================================== ================================================== ================== Размер архива версии архива пакета ================================================== ================================================== ================================================== ================== Установка: vsftpd x86_64 3.0.2-13.fc22 fedora 172 k Сводка транзакций ================================================== ================================================== ================================================== ================== Установить 1 пакет Общий размер загружаемого файла: 172 КБ Установленный размер: 348 К Это нормально [y / N]: y Загрузка пакетов: vsftpd-3.0.2-13.fc22.x86_64.rpm 107 кБ / с | 172 КБ 00:01 -------------------------------------------------- -------------------------------------------------- -------------------------------------------------- ------------------ Всего 48 кБ / с | 172 КБ 00:03 Проверка выполнения транзакции Проверка транзакции прошла успешно.Проверка выполнения транзакции Проверка транзакции прошла успешно. Выполнение транзакции Установка: vsftpd-3.0.2-13.fc22.x86_64 1/1 Проверка: vsftpd-3.0.2-13.fc22.x86_64 1/1 Установлены: vsftpd.x86_64 3.0.2-13.fc22 Complete!
Список доступных пакетов.Например, мы перечислим пакет apache.
# dnf связывание списка Последняя проверка срока действия метаданных выполнена 0:11:38 назад в среду, 27 мая 08:47:24 2015. Доступные пакеты bind.x86_64 32: 9.10.2-1.fc22 fedora
Чтобы переустановить пакет rpm.
# dnf переустановить httpd Последняя проверка срока действия метаданных выполнена 0:14:17 назад в среду, 27 мая 08:47:24 2015.Нет соответствия аргументу: httpd Ошибка: ничего не делать. [root @ localhost ~] # dnf переустановить vsftpd Последняя проверка срока действия метаданных выполнена 0:14:32 назад в среду, 27 мая 08:47:24 2015. Зависимости устранены. ================================================== ================================================== ================================================== ================== Размер архива версии архива пакета ================================================== ================================================== ================================================== ================== Переустановка: vsftpd x86_64 3.0.2-13.fc22 fedora 172 k Сводка транзакций ================================================== ================================================== ================================================== ================== Общий размер загружаемого файла: 172 КБ Это нормально [y / N]: y Загрузка пакетов: vsftpd-3.0.2-13.fc22.x86_64.rpm 118 кБ / с | 172 КБ 00:01 -------------------------------------------------- -------------------------------------------------- -------------------------------------------------- ------------------ Всего 53 кБ / с | 172 КБ 00:03 Проверка выполнения транзакции Проверка транзакции прошла успешно.Проверка выполнения транзакции Проверка транзакции прошла успешно. Выполнение транзакции Переустановка: vsftpd-3.0.2-13.fc22.x86_64 1/2 Стирание: vsftpd-3.0.2-13.fc22.x86_64 2/2 Проверка: vsftpd-3.0.2-13.fc22.x86_64 1/2 Проверка: vsftpd-3.0.2-13.fc22.x86_64 2/2 Заново: vsftpd.x86_64 3.0.2-13.fc22 Complete!
Чтобы удалить любые пакеты, которые вы хотите, выполните следующую команду.
# dnf удалить vsftpd Зависимости устранены. ================================================== ================================================== ================================================== ================== Размер архива версии архива пакета ================================================== ================================================== ================================================== ================== Удаление: vsftpd x86_64 3.0.2-13.fc22 @ System 348 k Сводка транзакций ================================================== ================================================== ================================================== ================== Удалить 1 пакет Установленный размер: 348 К Это нормально [y / N]: y Проверка выполнения транзакции Проверка транзакции прошла успешно. Проверка выполнения транзакции Проверка транзакции прошла успешно.Выполнение транзакции Стирание: vsftpd-3.0.2-13.fc22.x86_64 1/1 Проверка: vsftpd-3.0.2-13.fc22.x86_64 1/1 Удалены: vsftpd.x86_64 3.0.2-13.fc22 Complete!
Проверить историю установки пакета.
# dnf history Последняя проверка истечения срока действия метаданных выполнена 0:15:57 назад в среду, 27 мая 08:47:24 2015. ID | Логин пользователя | Дата а | Действие | ältere -------------------------------------------------- ----------------------------- 10 | корень | 2015-05-27 09:02 | Переустановить | 1 9 | корень | 2015-05-27 09:01 | Установить | 1 8 | корень | 2015-05-27 08:59 | Стереть | 1 7 | корень | 2015-05-27 08:59 | Стереть | 6 6 | корень | 2015-05-27 08:57 | Установить | 1 5 | корень | 2015-05-27 08:56 | Установить | 6 4 | корень | 2015-05-27 08:47 | Установить | 5 3 | Система | 2015-05-26 21:30 | Установить | 658 EE
Понизьте ваши пакеты.Эта команда не будет работать, если у вас не установлена более ранняя версия упомянутого пакета.
# dnf downgrade vsftpd
Для поиска конкретного пакета.
# dnf search telnet
Чтобы исключить пакет из установки. Например, пакет fedora-logos-httpd будет исключен при установке apache.
# dnf установить httpd - исключить fedora-logos-httpd
Включить / отключить репо при установке пакетов.
# dnf установить httpd --enablerepo fedora # dnf установить httpd --disablerepo fedora
Список доступных групп среды / пакетов.
# dnf grouplist
Установите любую группу пакетов.
# dnf groupinstall "MATE Desktop"
Загрузите выбранный пакет с его зависимостями в любой каталог.
# dnf загрузить httpd --resolve --destdir / tmp /
Для кэширования / очистки метаданных.
# dnf makecache # dnf очистить все
Вы можете получить больше информации из приведенных ниже команд.
# dnf --help # man dnf
Вот и все.
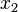
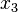
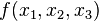
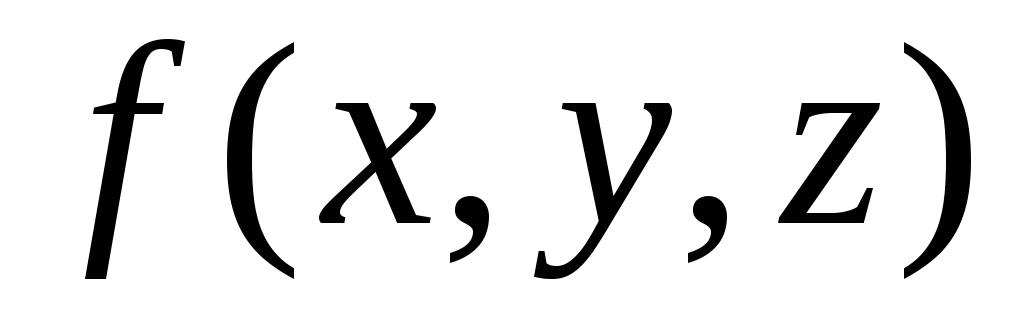
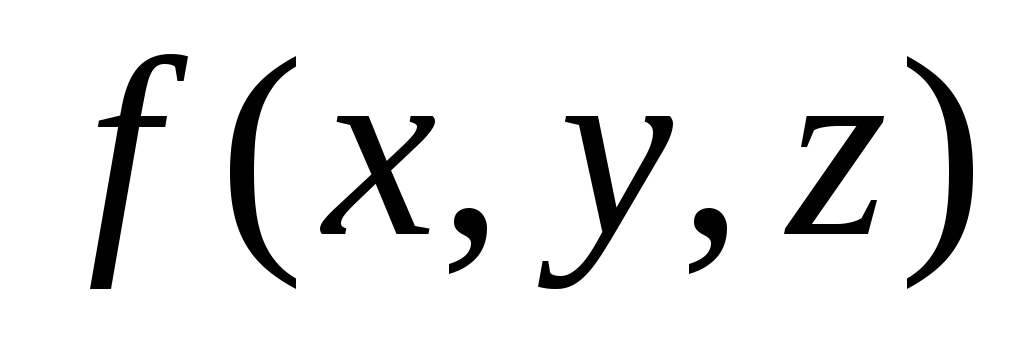
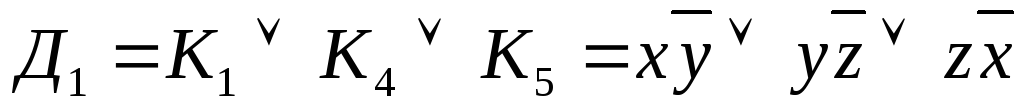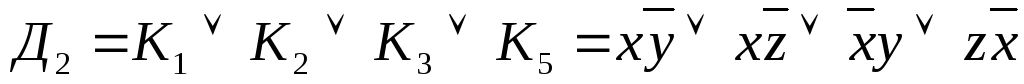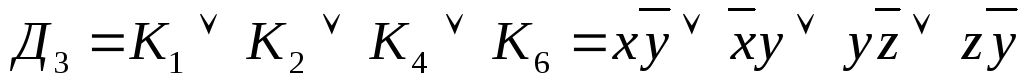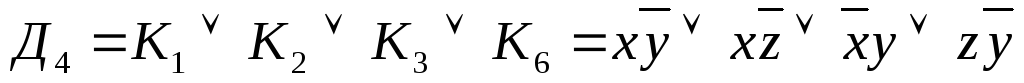