Как найти dy: Найти дифференциал dy. — примеры, решения

Дифференциал функции

• Понятие и геометрический смысл дифференциала
• О разных формах записи дифференциала
• Свойства дифференциала
• Применение дифференциала в приближенных вычислениях
• Абсолютная и относительная погрешности приближенных вычислений

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

Это записывается так:

или

или же

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(

x; y), при изменении x (аргумента) на величину (см. рисунок).

Почему дифференциал можно использовать в приближенных вычислениях?

Дифференциал, является главной, линейной относительно частью приращения функции; чем меньше , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

               

Дифференциал функции в точке x и обозначают

или

Следовательно,

                   (1)

или

,            (2)

поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.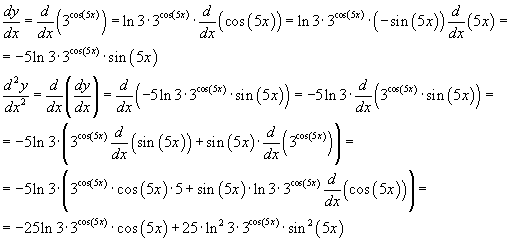

Замечание. Нужно помнить, что если x – исходное значение аргумента, а — наращенное значение, то производная в выражении дифференциала берётся в исходной точке x ; в формуле (1) этого не видно из записи.

Дифференциал функции можно записать в другой форме:

                      (3)

или

   (4)

---

Пример 1. Найти дифференциалы функций:

1) ;

2) ;

3) ;

4) .

Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:

1) ;

2) ;

3) ;

4) .

Найти дифференциалы самостоятельно, а затем посмотреть решения

Пример 2. Найти дифференциал функции

в точке x = 2,

1) выделив линейную часть;

2) по формуле.

Пример 3. Найти дифференциал функции

в точке x.

Пример 4. Найти дифференциал функции

в точках x = 0 и x = 1.

Посмотреть правильные решения примеров 2, 3, 4.

---

В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

 (С – постоянная величина)  (5)

                                (6)

                             (7)

                                      (8)

                            (9)

Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Одно из особеннейших свойств дифференциала — инвариантность формы дифференциала в случае сложных функций.

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Производная, дифференциал и их применение

---

Установленное во втором параграфе приближенное равенство

или

                           (10)

позволяет использовать дифференциал для приближенных вычислений значений функции.

Запишем приближенное равенство более подробно. Так как

а

то

или

                  (11)

---

Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.

Решение. Число ln 1,01 является одним из значений функции y = ln x .

Формула (11) в данном случае примет вид

Положим

тогда

Следовательно,

что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.

Пример 6. Пользуясь понятием дифференциала, вычислить приближенно

Решение. Число
является одним из значений функции

Так как производная этой функции

то формула (11) примет вид

Полагая

и

получаем

(табличное значение

).

Вычислить приближенно самостоятельно, а затем посмотреть решение

Пример 7. Вычислить приближенно:

1) ;

2) .

Посмотреть правильное решение и ответ.

---

Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.

Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:

                            (12)

Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:

                                 (13)

Если точное число неизвестно, то

                             (14)

Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.

---

Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.

Решение. Рассмотрим функцию

Её производная равна

а формула (11) примет вид

В данном случае было бы нерационально вычислять приближенно следующим образом:

так как значение

не является малым по сравнению со значением производной в точке

Здесь удобно предварительно вынести из под корня некоторое число, например 4/3.  Тогда

Теперь, полагая

получим

Умножая на 4/3, находим

Принимая табличное значение корня

за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Производная, дифференциал и их применение

Весь блок «Производная»

• Что такое производная
• Найти производную: алгоритм и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Правило Лопиталя
• Частные производные

Поделиться с друзьями

Дифференциалы высших порядков, формулы и примеры решения задач

Содержание:

• Случай независимой переменной
• Случай зависимой переменной

Пусть функция $y=f(x)$ зависит от переменной $x$ и дифференцируема в точке $x$.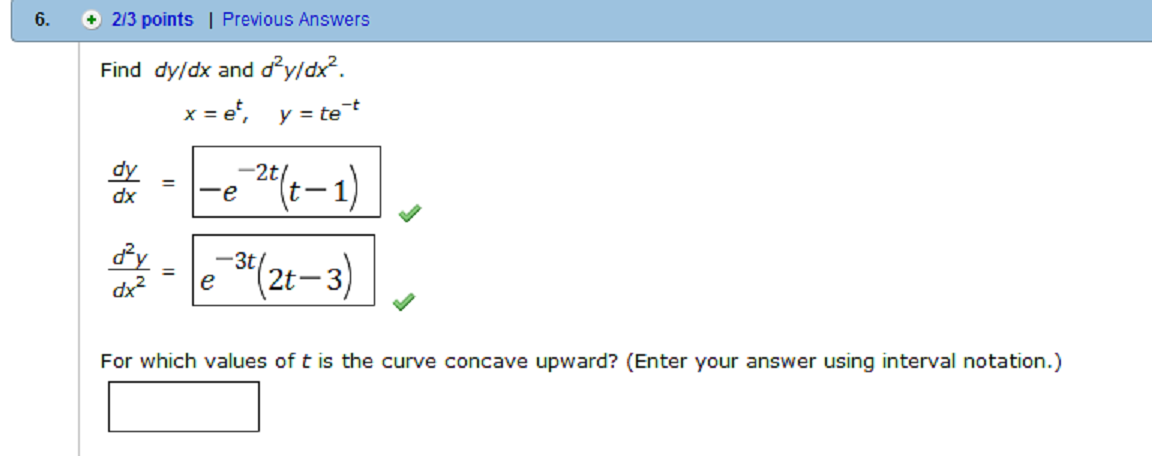 {2}$

Больше примеров решений Решение производных онлайн

Читать дальше: производная функции, заданной неявно.

1. Дифференциал

Ранее в главе о дифференцировании мы написали `dy/dx` и `f'(x)`, чтобы обозначить одно и то же. Мы использовали `d/dx` как оператор .

Теперь мы видим другой способ записи и осмысления производной.

Мы будем использовать эту новую форму производной на протяжении всей главы об интеграции.

Мини-лекция

См. мини-лекцию
по дифференциалам.

Определения

Дифференциалы — бесконечно малые величины. Обычно мы записываем дифференциалы как `dx,` `dy,` `dt` (и так далее), где:

`dx` — бесконечно малое изменение `x`;

`dy` — это бесконечно малое изменение `y`; и

`dt` — это бесконечно малое изменение `t`.

При сравнении небольших изменений величин, которые связаны друг с другом (например, в случае, когда ‘y’ является некоторой функцией f ‘x’, мы говорим дифференциал `dy`, `y = f(x)` записывается: 92−4x+2`, тогда f(x)=10x-4`.

Таким образом, дифференциал определяется как:

`dy = (10x-4)dx`

Примечание

Мы могли бы использовать дифференциал для оценки реальное изменение значения функции (`Δy`), вызванное небольшим изменение `x` (записывается как `Δx`). Много учебников сделать это, но это довольно глупо, так как мы можем легко найти точное изменение — зачем приближать это?

Мы вводим здесь дифференциалы как введение в обозначение, используемое в интеграция .

`Дельта y` означает «изменение `y`, а `Дельта x` означает «изменение `x`».

Ранее в главе «Дифференциация» мы узнали, что наклон кривой в точке P определяется как «dy/dx».

Связь dx, dy, delta x, delta yPΔydydx = ΔxОткрыть изображение на новой странице

Связь между `dx,` `dy,` `Delta x` и `Delta y`

Наклон пунктирной линии определяется отношением `(Delta y)/(Delta x).` По мере того, как `Delta x` становится меньше, этот наклон становится ближе к фактическому наклону в P , что является «мгновенным» отношением dy/dx.

То есть

`lim_(Дельта x->0) (Дельта y)/(Дельта x)=dy/dx`

См. «Наклон касательной» для получения дополнительной информации об этом.

Теперь мы переходим к изучению того, как дифференциал используется для осуществления противоположного процесса дифференцирования, который сначала мы назовем антидифференцировкой , а позже интеграцией .

Производные как dy/dx

 

Производные все о изменение …

… они показывают, как быстро что-то меняется (так называемая скорость изменения ) в любой момент.

 

В разделе «Введение в производные» (пожалуйста, прочтите сначала!) мы рассмотрели, как построить производную, используя различия и ограничения .

Здесь мы делаем то же самое, но с использованием нотации «dy/dx» (также называемой обозначение Лейбница ) вместо пределов.

 

Начнем с вызова функции «y»:

у = f(x)

1.

Добавьте Δx

Когда x увеличивается на Δx, тогда y увеличивается на Δy :

у + Δу = f(х + Δх)

2. Вычесть две формулы

От кого:		у + Δу = f(х + Δх)
Вычесть:		у = f(x)
Получить:		y + Δy − y = f(x + Δx) − f(x)
Упрощение:		Δy = f(x + Δx) − f(x)

3. Скорость изменения

Чтобы определить, насколько быстро (называется скорость изменения ) делим на Δx :

Δy Δx = f(x + Δx) − f(x) Δx

4. Уменьшить Δx близко к 0

Мы не можем допустить, чтобы Δx стало равным 0 (потому что это было бы делением на 0), но мы можем заставить его направиться к нулю и назвать его «dx»:

Δx dx

Вы также можете думать о «dx» как о бесконечно малом или бесконечно малом.

Точно так же Δy становится очень маленьким, и мы называем его «dy», чтобы получить:

д дх «=» е (х + дх) — е (х) дх

Попробуйте это на функции

Попробуем f(x) = x ²

д дх	= е (х + дх) — е (х) дх
	= (х + дх) 2 − х 2 дх		f(x) = x 2
	= x 2 + 2x(dx) + (dx) 2 − x 2 дх		Расширить (x+dx) 2
	= 2x(дх) + (дх) 2 дх		x 2 −x 2 =0
	= 2х + дх		Упростить дробь
	= 2х		dx идет к 0

Таким образом, производная от x ² равна 2x

.