Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции:
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
- Минимум и максимум функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
×
Где учитесь?
Для правильного составления решения, укажите:
(не выбрано)9 класс10 класс11 класс1-й курс2-й курс3-й курс4-й курсдругое
Вертикальные и горизонтальные асимптоты. Тема
Вертикальные и горизонтальные асимптоты. Тема
Как определяются асимптоты графиков функций, и как при помощи вычислений пределов найти вертикальные и горизонтальные асимптоты.
Асимптота — это прямая, которой график функции бесконечно приближается, никогда с ней не совпадая.
Асимптоты бывают горизонтальные, вертикальные и наклонные. В этом видео мы занимается вертикальными и горизонтальными асимптотами.
Чтобы найти горизонтальную асимптоту, нужно вычислить предел функции при бесконечно возрастающем аргументе. Если этот предел существует и конечен, то горизонтальная асимптота есть, и ее уравнение нетрудно записать.
Вертикальные асимптоты возможны только в точках разрыва исследуемой функции. Чтобы найти вертикальную асимптоту, нужно вычислить предел исследуемой функции при приближении переменной к точке разрыва. Если этот предел бесконечен, то вертикальная асимптота есть, и ее уравнение тоже несложно записать.
Вертикальные и горизонтальные асимптоты — это два частных случая более общей ситуации, наклонной асимптоты, но о наклонных асимптотах мы говорим в следующей теме.
Просмотрите видео по теме «Вертикальные и горизонтальные асимптоты». Затем перейдите к вопросам по теме «Вертикальные и горизонтальные асимптоты» и попробуйте самостоятельно найти вертикальные и горизонтальные асимптоты данных вам функций.
Тема «Вертикальные и горизонтальные асимптоты»
Вопросы по теме «Вертикальные и горизонтальные асимптоты»
Ответы на вопросы по теме «Вертикальные и горизонтальные асимптоты»
Для того чтобы лучше разобраться с темой «Вертикальные и горизонтальные асимптоты», обязательно решите все задания.
Все лекции здесь.
Популярные сообщения из этого блога
Двойной интеграл в полярных координатах. Вопросы
Даны два двойных интеграла. Требуется вычислить их путем перехода к полярным координатам.
Замена переменных в двойном интеграле.
 Вопросы
ВопросыДаны два двойных интеграла. Требуется подобрать замены так, чтобы области интегрирования перешли в прямоугольники со сторонами, параллельными осям, и вычислить интегралы в новых координатах.
Репетиторство и консультации по Skype
$ Общее время занятий включает в себя, помимо онлайн-занятия, несколько часов видео для предварительного изучения (которые не оплачиваются). Таким образом, занимаясь фактически 3, 4, 5 и более часов, вы оплачиваете только 2 академических часа. Это выгодно. Ознакомиться с условиями занятий
2.4.3: Горизонтальные асимптоты — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14203
Горизонтальные асимптоты
Вертикальные асимптоты описывают поведение функции, когда значения x приближаются к определенному числу. Горизонтальные асимптоты описывают поведение функции, когда значения x становятся бесконечно большими и бесконечно малыми. Поскольку функции не могут касаться вертикальных асимптот, не могут ли они касаться и горизонтальных асимптот?
Горизонтальные асимптоты описывают поведение функции, когда значения x становятся бесконечно большими и бесконечно малыми. Поскольку функции не могут касаться вертикальных асимптот, не могут ли они касаться и горизонтальных асимптот?
Нахождение горизонтальных асимптот
Горизонтальные асимптоты являются средством описания конечного поведения функции. Конечное поведение, по сути, представляет собой описание того, что происходит по обе стороны графика, когда функция продолжается бесконечно вправо и влево. Когда вы определяете горизонтальные асимптоты, важно учитывать как правую, так и левую стороны, потому что горизонтальные асимптоты не обязательно будут одинаковыми в обоих местах. Рассмотрим обратную функцию и обратите внимание, как при движении x вправо и влево она сглаживается до линии y=0.
[Рисунок 1] Иногда функции выравниваются, а иногда функции увеличиваются или уменьшаются без ограничений. Есть в основном три случая.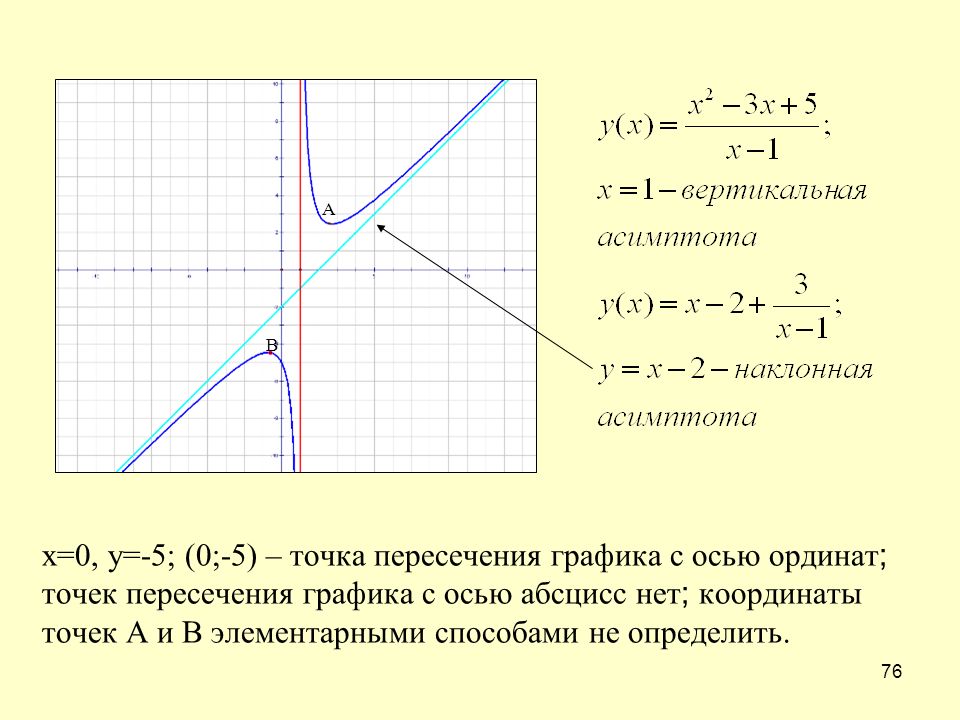
Случай 1: степень числителя меньше степени знаменателя
В первом случае функция сглаживается до 0, когда x становится бесконечно большим или бесконечно малым. Это происходит, когда степень числителя меньше степени знаменателя. Степень определяется наибольшим показателем x.
9{9}-12}\)Один из способов объяснить, почему это имеет смысл, заключается в том, что когда x является смехотворно большим числом, большинство частей функции практически не оказывают никакого влияния. Например, 100 ничто по сравнению с 3x 2 . Два важных термина для сравнения: x 8 и x 9 . Двойка сейчас даже не важна, потому что если х будет хотя бы миллионом, то х 9 будет в миллион раз больше, чем х 8 , а 2 снова вряд ли имеет значение. По сути, когда x становится достаточно большим, эта функция действует как \(\ 1 \over 2\), которая имеет 9{4}+144 x-0,001}\)
Обратите внимание, что степень числителя и знаменателя равна 4. Это означает, что горизонтальная асимптота равна \(\ y=\frac{6}{3}=2\ ). Один из способов объяснить, почему это имеет смысл, заключается в том, что когда x становится очень большим числом, все меньшие степени не будут иметь большого значения. Самые большие вкладчики — это только самые большие державы. Тогда значение числителя будет примерно в два раза больше значения знаменателя. По мере того, как x становится еще больше, функция становится еще ближе к 2.
Это означает, что горизонтальная асимптота равна \(\ y=\frac{6}{3}=2\ ). Один из способов объяснить, почему это имеет смысл, заключается в том, что когда x становится очень большим числом, все меньшие степени не будут иметь большого значения. Самые большие вкладчики — это только самые большие державы. Тогда значение числителя будет примерно в два раза больше значения знаменателя. По мере того, как x становится еще больше, функция становится еще ближе к 2.
Случай 3: степень числителя больше степени знаменателя
Если степень числителя больше степени знаменателя, горизонтальной асимптоты не существует. Вы должны определить, неограниченно ли возрастает или убывает функция как влево, так и вправо.
Посмотрите следующее видео, сосредоточив внимание на частях о горизонтальных асимптотах.
Примеры
Пример 1
Ранее вас спрашивали, могут ли функции касаться своих горизонтальных асимптот.
Решение
Функции могут неограниченно касаться горизонтальных асимптот и проходить через них. Это разница между вертикальной и горизонтальной асимптотами. В исчислении существуют строгие доказательства того, что функции, подобные той, что в примере C, становятся сколь угодно близкими к асимптоте.
Пример 2
Определите вертикальную и горизонтальную асимптоты следующей рациональной функции .
\(\ f(x)=\frac{(x-2)(4x+3)(x-4)}{(x-1)(4x+3)(x-6)}\)
Решение
Существует сокращающий коэффициент, который не является ни горизонтальной, ни вертикальной асимптотой . Вертикальные асимптоты встречаются при x=1 и x=6. Чтобы получить горизонтальную асимптоту, вы можете методично умножить каждый двучлен, однако, поскольку большинство этих членов не имеют значения, более эффективно сначала определить относительные степени числителя и знаменателя. В этом случае они оба равны 3.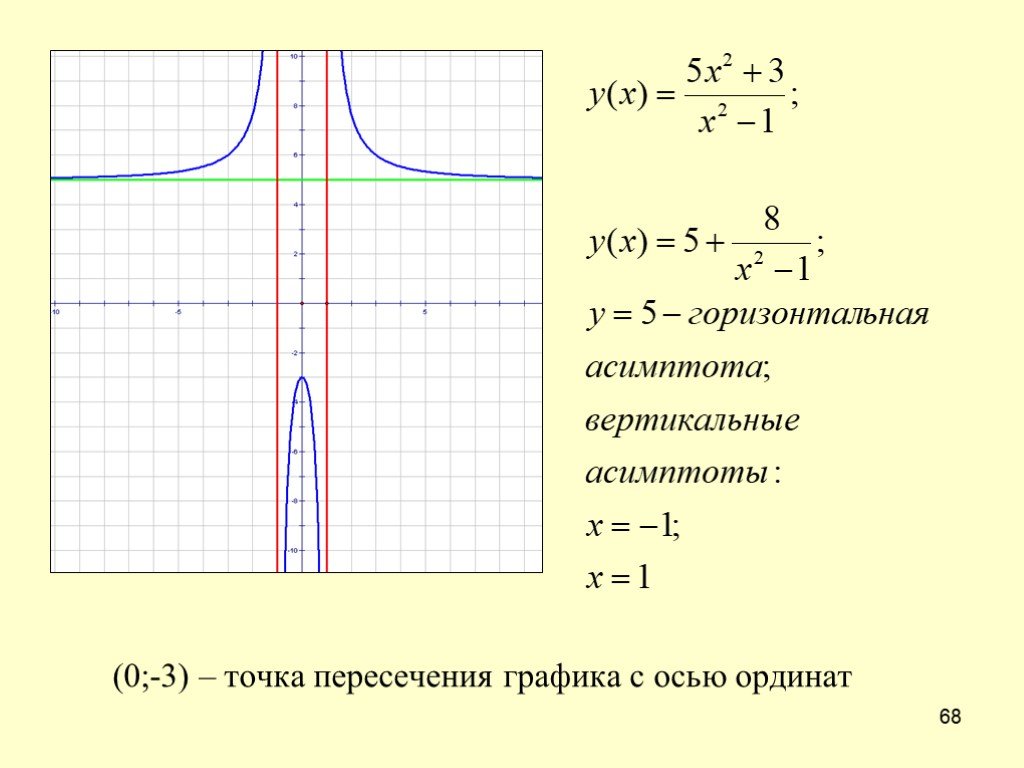 Затем определите коэффициент только кубических членов. В числителе будет 4x 3 , а в знаменателе будет 4x 3 , поэтому горизонтальная асимптота будет равна \(\ y=\frac{4}{4}=1\).
Затем определите коэффициент только кубических членов. В числителе будет 4x 3 , а в знаменателе будет 4x 3 , поэтому горизонтальная асимптота будет равна \(\ y=\frac{4}{4}=1\).
Пример 3
Опишите поведение правой части следующей функции.
[Рисунок 2]Решение
Обратите внимание, как быстро устанавливается эта затухающая волновая функция. По-видимому, справа имеется очевидная горизонтальная ось в точке y=1
Пример 4
Определите горизонтальные асимптоты следующей функции. 9{21}}\)
- Вертикальные асимптоты при x=1 и x=4
- Нули на 3 и 5
- Отверстие при x=6
- Горизонтальная асимптота в точке \(\ y=\frac{2}{3}\)
- Вертикальные асимптоты при x=−2 и x=2
- Нули в 1 и 5
- Отверстие при x=3
- Горизонтальная асимптота при y=1
- Вертикальные асимптоты при x=0 и x=3
- Нули в 1 и 2
- Отверстие при x=8
- Горизонтальная асимптота при y=2
- Вертикальные асимптоты на 2 и 6
- Ноль на 5
- Отверстие при x=4
- Горизонтальная асимптота при y=0
- Вертикальная асимптота на 4
- Нули на 0 и 3
- Отверстие при x=5
- Нет горизонтальных асимптот
Определите вертикальную и горизонтальную асимптоты следующих рациональных функций.
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 2.10.
Словарь
| Срок | Определение |
|---|---|
| Конечное поведение | Конечное поведение — это описание тренда функции по мере того, как входные значения становятся очень большими или очень маленькими, представленные как «концы» графически отображаемой функции. |
| Отверстие | На графике рациональной функции существует дыра при любом входном значении, при котором и числитель, и знаменатель функции равны нулю. |
| Горизонтальная асимптота | Горизонтальная асимптота — это горизонтальная линия, указывающая, где функция выравнивается, когда независимая переменная становится очень большой или очень маленькой.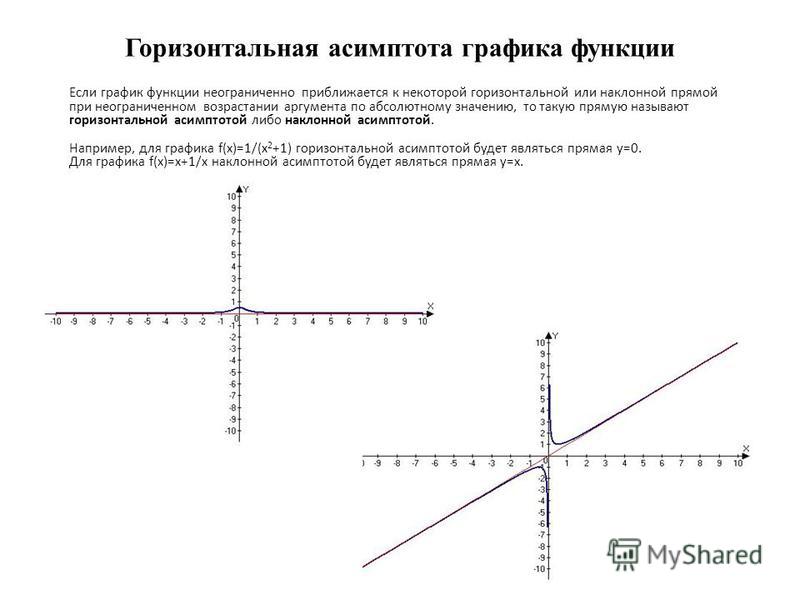 Функция может касаться горизонтальной асимптоты или проходить через нее. Функция может касаться горизонтальной асимптоты или проходить через нее. |
| Рациональная функция | Рациональная функция — это любая функция, которую можно записать как отношение двух полиномиальных функций. |
| Вертикальная асимптота | Вертикальная асимптота — это вертикальная линия, обозначающая определенное значение, к которому график функции может приближаться, но никогда не достигнет. |
| Ноль | Нули функции f(x) — это значения x, при которых f(x) становится равным нулю. |
| Нули | Нули функции f(x) — это значения x, при которых f(x) становится равным нулю. |
| Нули | Нули функции f(x) — это значения x, при которых f(x) становится равным нулю. |
Авторство изображений
- [Рис.
 1]
1]
Авторы и права: CK-12 Foundation
Лицензия: CC BY-SA - [Рис. 2]
Кредит: Фонд CK-12
Лицензия: CC BY-SA
Эта страница под названием 2.4.3: Горизонтальные асимптоты распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Теги
- источник@https://www.
 ck12.org/c/analysis
ck12.org/c/analysis
- источник@https://www.
Функции, графики и пределы Нахождение горизонтальных/наклонных/криволинейных асимптот
- Главная /
- Calculus /
- Функции, графики и ограничения /
- Темы /
- Горизонтальный, уклонный и криволинейный асимптоты /
- Обнаружение горизонтального / уклона / криволинейного асимптота
- Horizontal, Asymptotes 904
- Horizontal, Asymptotes 904
- , Horizontal, asmptotes
- . Горизонтальные/ наклонные/ криволинейные асимптоты
- Введение
- Темы
- Ограничения
- All About Asymptotes
- Ограничения при бесконечности
- Пределы функций при бесконечности
- Горизонтальные, уклонные и криволинейные асимптоты
- Asymptoles 10101103 -горизонтальный асимптат Asymptes11103 -горизонтальный асимптал1110 3 -х горизонтальные асимптары
- Slant Asymptes 3 -Memptes Asymptes1103 -Memptoles Asymptes1103.
- Как рисовать рациональные функции с нуля
- Сравнение функций
- Работа с пределами
- В реальном мире
- Примеры
- Упражнения
- викторины
- Условия
- Раздаточный материал
- Лучшее из Интернета
- Содержание
- НАЗАД
- СЛЕДУЮЩИЙ
- полином меньшей степени в числителе, чем в знаменателе, эта функция будет иметь горизонтальную асимптоту в 0. Готово!
- полином той же степени в числителе, что и в знаменателе, эта рациональная функция имеет горизонтальную асимптоту, которую мы можем найти, разделив только старшие члены.
- числитель на одну степень больше знаменателя, эта рациональная функция имеет наклонную асимптоту, которую мы можем найти делением в длину.
- ничего из вышеперечисленного, функция имеет криволинейную асимптоту, которую мы можем найти делением в длину.

Темы

Иногда, когда функция имеет горизонтальную асимптоту, мы можем видеть, какой она должна быть.
Пример задачи
Пусть f ( x ) = 4 — x .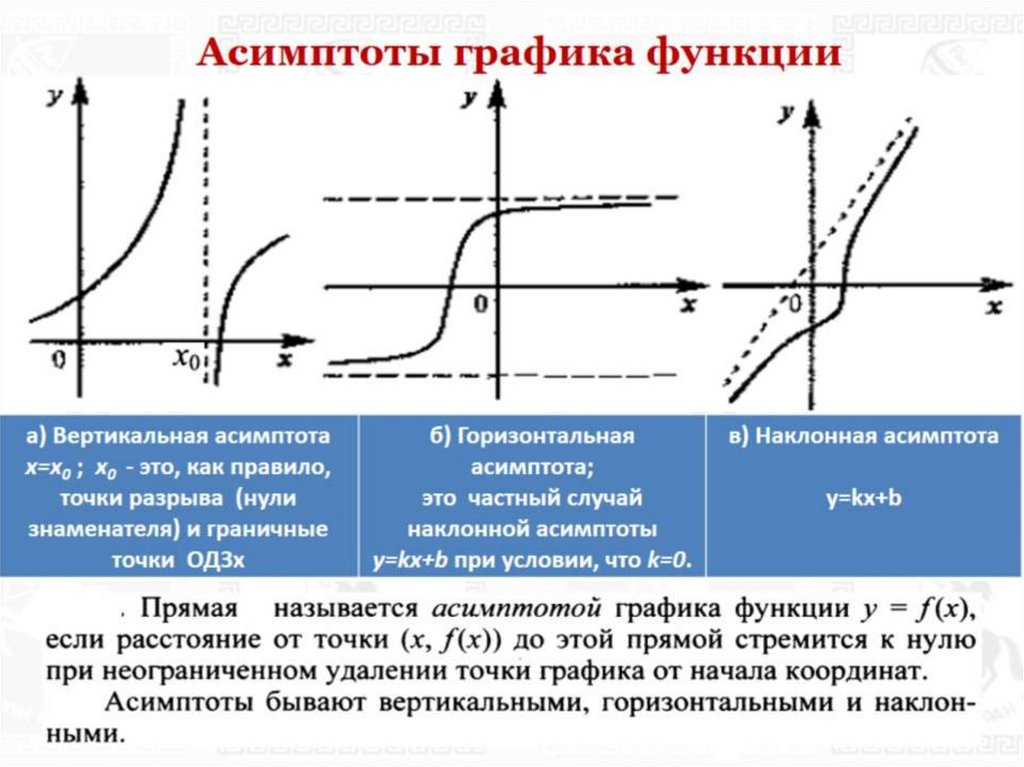 Затем, когда x приближается к ∞, функция f приближается к 0; есть горизонтальная асимптота при y = 0. Функция приближается к этой асимптоте, когда x приближается к ∞.
Затем, когда x приближается к ∞, функция f приближается к 0; есть горизонтальная асимптота при y = 0. Функция приближается к этой асимптоте, когда x приближается к ∞.
Когда x приближается к -∞, функция f неограниченно растет и, следовательно, не приближается к асимптоте, y = 0,
Иногда немного сложно понять, какой должна быть асимптота, но мы за это. Эти асимптоты часто появляются при рисовании рациональных функций. Сначала мы пройдемся по гарантированному методу, который расскажет нам, какой у нас тип асимптоты и что это такое, а затем мы покажем ярлык для нахождения горизонтальных асимптот.
Полиномиальный метод длинного деления
Гарантированный метод — полиномиальное длинное деление. Этот метод, вероятно, займет некоторое время, но он даст ответ.
При нахождении горизонтальной/наклонной/криволинейной асимптот рациональной функции мы делаем длинное деление, чтобы переписать функцию. Отбрасываем остаток, и остается наша асимптота. Если у нас осталось число, это горизонтальная асимптота (и помните, 0 — совершенно хорошее число). Если у нас останется строка вида y = m x + b (другими словами, полином степени 1), эта линия является нашей наклонной асимптотой.
Отбрасываем остаток, и остается наша асимптота. Если у нас осталось число, это горизонтальная асимптота (и помните, 0 — совершенно хорошее число). Если у нас останется строка вида y = m x + b (другими словами, полином степени 1), эта линия является нашей наклонной асимптотой.
Если у нас осталось что-то еще, это криволинейная асимптота.
Причина, по которой мы отбрасываем остаток, заключается в том, что это будет рациональная функция, числитель которой имеет меньшую степень, чем знаменатель, и мы знаем, что предел такой функции, когда x приближается к ∞, равен 0.
Рациональная функция приблизится к своей горизонтальной/наклонной/криволинейной асимптоте при x приближается к ∞, а когда x приближается к -∞.
Ярлык
Поздравляем! мы пережили долгое разделение. Наша награда — кратчайший путь к нахождению горизонтальных асимптот рациональных функций. Горизонтальная асимптота будет иметь место, когда числитель и знаменатель рациональной функции имеют одинаковую степень.
Найти горизонтальную асимптоту функции
.
Если мы делаем длинное деление, мы находим
, поэтому горизонтальная асимптота равна y = 3.
Пример задачи
Найти горизонтальную асимптоту функции = 2.
Заметили закономерность? Мы делим старший член числителя на старший член знаменателя, и это дает нам горизонтальную асимптоту. Вот и все.
Подытожим:
Если рациональная функция имеет…

 3
3 14159..
14159.. 1]
1]  ck12.org/c/analysis
ck12.org/c/analysis