Как ⚠️ найти наименьшее и наибольшее значение функции на отрезке: чему равно, примеры
Содержание:
- Наибольшее и наименьшее значение функции — ключевые понятия
- Как найти для отрезка, алгоритм вычисления
- Примеры решения задач
Содержание
- Наибольшее и наименьшее значение функции — ключевые понятия
- Как найти для отрезка, алгоритм вычисления
- Примеры решения задач
Наибольшее и наименьшее значение функции — ключевые понятия
Понятие самого большого и самого малого значения производной функции используется для определения оптимального показателя некоторого параметра.
Допустим, X — это некоторое множество, включенное в область определения функции y=f(x).
Определение
Наибольшее значение функции y=f(x) на заданном интервале x — это такое максимальное значение y=f(x0) при x∈X, когда неравенство f(x)≤f(x0) справедливо при всех значениях x, принадлежащих X и не равных нулю.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Наименьшее значение функции y=f(x) на заданном интервале x — это такое минимальное значение y=f(x 0) при x∈X, когда неравенство f(x)≥f(x0) верно при всех значениях x, принадлежащих X и не равных нулю.
Если упростить данные определения, то получим следующее: максимальное значение функции представляет собой наибольшее значение на известном промежутке при x0, а минимальное — это наименьшее значение, которое принимает функция на известном промежутке при x0.
Определение
При обращении производной функции в ноль значения аргумента именуются стационарными точками.
Согласно теореме Ферма, данное понятие представляет собой такую точку, где расположены локальный минимум и максимум дифференцируемой функции или ее экстремум. Отсюда следует, что наименьшее и наибольшее значения y=f(x) будут достигнуты в одной из стационарных точек.
Самое большое и самое маленькое значение функция может принимать в точках, где функция определена, а первой производной данной функции нет.
Наименьшее и наибольшее значения не всегда можно вычислить. К примеру, это невозможно при совпадении рубежей заданного интервала с рубежами области определения. Также максимальные и минимальные значения не получится определить, когда речь идет о бесконечном промежутке.
Кроме того, функция неизвестном отрезке или на бесконечном интервале будет принимать бесконечно малые либо бесконечно большие значения. Это значит, что наименьшее и наибольшее значения в этом случае невозможно рассчитать.
Это значит, что наименьшее и наибольшее значения в этом случае невозможно рассчитать.
Как найти для отрезка, алгоритм вычисления
Отрезок представляет собой часть прямой, которая ограничена двумя точками. Возьмем точки a и b за концы заданного отрезка. Тогда необходимо найти max y=f(x 0) и min y=f(x0) на промежутке [a,b].
Последовательность нахождения:
- Проверка заданной функции f(x) на нужном участке [a,b] на прерывность.
- При условии, что f(x) непрерывная, определить производную f’(x) и приравнять ее к 0.
- Найти точки максимума и минимума, которые вычисляются при решении уравнения f’(x)=0.
- Определить критические точки, которые находятся на отрезке [a,b].
- Произвести вычисления значений f(x) в этих критических точках и в точках a и b.
- Самое большое и самое маленькое число среди вычисленных будет наибольшим и наименьшим значением функции на отрезке [a,b].
 2}=\frac{32}{22}=1\frac{10}{22}=1\frac5{11}\)
2}=\frac{32}{22}=1\frac{10}{22}=1\frac5{11}\)Ответ: \(M=1\frac5{11}\), \(m=0\).
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Error
Sorry, the requested file could not be found
More information about this error
Jump to… Jump to…Согласие на обработку персональных данных Учебно-тематический планАвторы и разработчики курсаИнформация для студентов и преподавателейВводная лекцияIntroductory lectureЛекция о системе обозначений Lecture on the notation systemВидеолекция (часть 1)Lecture (Part 1)Видеолекция 2. Операции над функциями. Свойства функции.Lecture 2. Operations on functions. The properties of the functionТеоретический материал Практическое занятие. Исследование свойств функций по определениюPractical lesson.
 Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3.
Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3. Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1.
Предел функции в точкеВидеолекция. Непрерывность функции в точкеLecture 1. Сontinuity of a function at a pointПрактическое занятие. Исследование функций на непрерывность. Классификации точек разрываPractical lesson. The study of function continuity and classification of discontinuity pointsЗадачи для самостоятельной работыРешения задачТест 1.1.4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
 Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture.
Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture.
 Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2.
Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2.
Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2.
Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1.
Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2.
Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2.
Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.
Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2. 2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы.
2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2.
Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2.
Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.
Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3. 5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1.
5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)Поиск минимального и максимального элемента в массиве
Сложность: Средняя, Количество запросов: Facebook, Microsoft
Основные выводы подход.

- Цикл увеличивается на два (постоянная величина) для дальнейшей оптимизации кода. Мы можем использовать аналогичные идеи для оптимизации кода для решения других задач кодирования.
- Базовые условия, инициализация и условные операторы интуитивно понятны. Мы можем найти аналогичную закономерность и в других задачах кодирования.
- Временная сложность всех трех подходов равна O(n), но общее количество операций сравнения различно. Такой сценарий может возникнуть при решении других задач кодирования, где можно уменьшить количество критических операций для дальнейшей оптимизации решения.
- Кандидат: Являются ли входные значения уникальными? Интервьюер : Для удобства решения можно предположить, что.
- Кандидат: Нужно ли решать эту проблему на месте? Интервьюер : Да, мы ищем O(n) решение на месте с минимальным количеством сравнений.
- Подход грубой силы с использованием одного цикла: увеличение на 1
- Использование подхода «разделяй и властвуй», аналогичного сортировке слиянием
- Эффективный подход с использованием одного контура: увеличение на 2
- Мы объявляем и инициализируем переменные max и min для хранения максимума и минимума.

- Проходим по массиву от i = 1 до n — 1 и сравниваем каждый элемент с min и max.
- If (X[i] < min): Мы нашли значение меньше минимального до i-го индекса. Поэтому обновите min на X[i], т. е. min = X[i].
- else If(X[i] > max): Мы нашли значение больше максимального до i-го индекса. Поэтому обновите max на X[i], т. е. max = X[i].
- К концу цикла минимальное и максимальное значения массива будут сохранены в переменных мин и макс .
- Чтобы вернуть это, мы берем дополнительный массив maxMin[] размера два, где мы сохраняем максимум по первому индексу и минимум по второму индексу. На выходе мы возвращаем массив maxMin .
- Шаг деления: Мы делим массив на две равные части вокруг среднего индекса, т.е. мы делим задачу на две подзадачи одинакового размера.
- Шаг победы: Рекурсивно находим минимум и максимум левой и правой частей.

- Шаг объединения: Мы сравниваем максимум обеих половин, чтобы получить общий максимум, и минимум обеих половин, чтобы получить общий минимум.
- Пишем рекурсивную функцию, принимающую в качестве входных параметров массив и его начальный и конечный индекс, т.е. findMinMax (целое X[], целое число l, целое число r)
- Базовый вариант 1: Если размер массива равен 1, мы возвращаем этот единственный элемент как максимальный и минимальный.
Базовый вариант 2: Если размер массива равен 2, мы сравниваем оба элемента и возвращаем максимум и минимум.
если (л == г) { макс = Х[л] мин = Х[л] } иначе, если (l + 1 == r) { если (X[l] < X[r]) { макс = Х[г] мин = Х[л] } еще { макс = Х[л] мин = Х[г] } }- Разделить часть: Делим массив на две равные части, т.
 е. mid = l + (r - l)/2.
е. mid = l + (r - l)/2. - Завоевать часть:
- Мы рекурсивно вычисляем и сохраняем максимум и минимум для левой части, т.е. leftMinMax[2] = findMinMax(X, l, mid)
- Мы рекурсивно вычисляем и сохраняем максимум и минимум для правой части, т.е. rightMinMax[2] = findMinMax(X, mid + 1, r)
Объединить часть: Теперь найдем общий максимум и минимум, сравнив минимум и максимум обеих половин. Для этого нам нужно выполнить всего два сравнения.
, если (левый минмакс[0] > правый минмакс[0]) макс = левый минмакс [0] еще макс = справаМинМакс[0] если (слева МинМакс [1] < справа МинМакс [1]) мин. = левый мин. макс. [1] еще мин = правыйМинМакс[1]
- Мы сохраняем максимальное и минимальное значение в дополнительной памяти maxMin[2] и возвращаем его.
- Мы делим задачу на две подзадачи одинакового размера размером n/2.
- Мы выполняем 2 операции сравнения на этапе объединения.
- Ситуации базового случая возникают, когда n = 2 или n = 1. Когда n = 2, мы выполняем 1 операцию сравнения, а когда n = 0, мы выполняем 0 операцию сравнения. 9i - 2 = n + n/2 – 2 = 3n/2 – 2 .
- Если n не является степенью числа 2, будет выполнено более 3n/2 - 2 сравнений. Общая временная сложность = O(n)
- if (X[i] < X[i + 1]): Может быть вероятность того, что X[i] может быть меньше min, а X[i + 1] может быть больше max. Другими словами, X[i] будет кандидатом на минимум, а X[i + 1] будет кандидатом на максимум. Итак, мы сравниваем X[i] с минимумом и X[i + 1] с максимумом, чтобы обновить минимум и максимум до этой точки, т.е. если (X[i] < min), min = X[i] и if(X[ i + 1] > max), max = X[i + 1].
- if (X[i] > X[i + 1]): В этом сценарии можно применить тот же подход. Здесь X[i + 1] будет кандидатом на минимум, а X[i] будет кандидатом на максимум, т.
 е. если (X[i] > max), max = X[i] и если (X[i + 1 ] < min), min = X[i + 1].
е. если (X[i] > max), max = X[i] и если (X[i + 1 ] < min), min = X[i + 1]. - Объявить переменные max и min и проверить размер массива:
- Если нечетно, инициализировать min и max первым элементом.
Если четно, сравните элементы и установите для min меньшее значение, а для max большее значение.
если (n % 2 != 0) { макс = Х[0] мин = Х[0] я = 1 } еще { если (Х[0] < Х[1]) { макс = Х[1] мин = Х[0] } еще { макс = Х[0] мин = Х[1] } я = 2 }- Теперь пройдитесь по массиву и выберите элементы парами.
 Для каждой пары (i, i + 1) сравните оба элемента. На основе сравнения:
Для каждой пары (i, i + 1) сравните оба элемента. На основе сравнения: - Сравните больший элемент с максимальным значением и обновите максимальное значение.
Сравните меньший элемент с min и обновите min.
, пока (я < п) { если (X[i] < X[i + 1]) { если (X[i] < мин) мин = Х[я] если (X[i + 1] > макс) макс = Х[я + 1] } еще { если (X[i] > макс) макс = Х[я] если (X[i + 1] < мин) мин = Х[я + 1] } я = я + 2 }- Сохранить максимальное и минимальное значение в дополнительной памяти maxMin[2] и вернуть его.
- Почему увеличение цикла на два помогает уменьшить количество сравнений?
- Как изменить приведенные выше решения, если входные значения повторяются?
- Есть ли другой способ решить эту проблему?
- В каком сценарии количество сравнений по подходам 2 и 3 одинаково?
- Почему объемная сложность O(logn) в решении "разделяй и властвуй"? Почему существует два базовых случая? Какова будет временная сложность, если мы удалим базовый случай с размером массива 2?
- Что было бы лучшим и худшим случаем в подходе грубой силы?
- Подход грубой силы с использованием одного цикла: Временная сложность = O(n)
- Использование «разделяй и властвуй»: временная сложность = O(n)
- Эффективный подход с использованием одного цикла: временная сложность = O(n)
- Удалить дубликаты из отсортированного массива
- Допустимая гора в массиве
- Переместить нули в конец
- Количество зданий, обращенных к солнцу
- Найти строку с максимальным числом 1
- Сортировка массива нулей, единиц и двоек
Давайте разберемся с задачей
Учитывая массив X[] размера n, нам нужно найти максимальное и минимальное количество элементов, присутствующих в массиве. Наш алгоритм должен делать минимальное количество сравнений.
ПримерыВвод: X[] = [4, 2, 0, 8, 20, 9, 2], Вывод: макс. = 20, мин. = 0
Ввод: X[] = [-8, -3, -10, -32, -1], Вывод: max = -1, min = -32
Важное примечание: Прежде чем перейти к решениям, мы рекомендуем учащимся решить эту задачу. Если решилась, то молодец! Мы хотели бы услышать ваши идеи в сообщении ниже. В остальном нет проблем! Учтите, что это отличная возможность изучить новую модель решения проблем.
Если решилась, то молодец! Мы хотели бы услышать ваши идеи в сообщении ниже. В остальном нет проблем! Учтите, что это отличная возможность изучить новую модель решения проблем.
Теперь мы движемся вперед и шаг за шагом обсуждаем идеи решения. Практика этих шагов может помочь нам найти эффективное решение во время собеседования по программированию.
Обсуждаемые подходы к решению
Перебор с использованием одного цикла: Увеличение на 1
Идея решения и шаги int[] findMinMax(int X[], int n)
{
интервал макс = X[0]
интервал мин = Х[0]
для (int i = 1; i < n; i = i + 1)
{
если (X[i] > макс)
макс = Х[я]
иначе, если (X[i] < min)
мин = Х[я]
}
интервал maxMin[2] = {макс, мин}
вернуть максмин
} Реализация Python
def findMinMax(X, n):
макс = Х[0]
мин = Х[0]
для i в диапазоне (1, n):
если X[i] > max:
макс = Х[я]
Элиф X[i] < мин:
мин = Х[я]
maxMin = [макс, мин]
return maxMin Анализ решения В худшем случае мы делаем два сравнения на каждом шаге итерации. Этот случай возникнет, если массив отсортирован по убыванию. В этой ситуации первый оператор if будет каждый раз ложным, а второй оператор if будет каждый раз истинным. Таким образом, общее количество сравнений в худшем случае = 2*(n - 1) = 2n - 2
Этот случай возникнет, если массив отсортирован по убыванию. В этой ситуации первый оператор if будет каждый раз ложным, а второй оператор if будет каждый раз истинным. Таким образом, общее количество сравнений в худшем случае = 2*(n - 1) = 2n - 2
В лучшем случае элементы сортируются в порядке возрастания. В этой ситуации всего было выполнено n - 1 сравнение. Считать.
Временная сложность = O(n), Пространственная сложность = O(1)
Использование подхода «разделяй и властвуй», аналогичного сортировке слиянием
Идея решенияТеперь критический вопрос: можем ли мы решить эту проблему, используя другой подход ? Можем ли мы мыслить рекурсивно, чтобы разработать эффективное решение? Вот идея!
int[] findMinMax(int X[], int l, int r)
{
инт макс, мин
если (л == г)
{
макс = Х[л]
мин = Х[л]
}
иначе, если (l + 1 == r)
{
если (X[l] < X[r])
{
макс = Х[г]
мин = Х[л]
}
еще
{
макс = Х[л]
мин = Х[г]
}
}
еще
{
инт середина = l + (r - l)/2
int leftMinMax[2] = findMinMax(X, l, середина)
int rightMinMax[2] = findMinMax(X, середина + 1, r)
если (слева мин. макс. [0] > справа мин. макс. [0])
макс = левый минмакс [0]
еще
макс = справаМинМакс[0]
если (слева МинМакс [1] < справа МинМакс [1])
мин. = левый мин. макс. [1]
еще
мин = справаМинМакс[1]
}
интервал maxMin[2] = {макс, мин}
вернуть максмин
}
макс. [0] > справа мин. макс. [0])
макс = левый минмакс [0]
еще
макс = справаМинМакс[0]
если (слева МинМакс [1] < справа МинМакс [1])
мин. = левый мин. макс. [1]
еще
мин = справаМинМакс[1]
}
интервал maxMin[2] = {макс, мин}
вернуть максмин
} Реализация Python
def findMinMax(X, l, r):
макс, мин = 0, 0
если л == г:
макс = Х[л]
мин = Х[л]
Элиф л + 1 == г:
если X[l] < X[r]:
макс = Х[г]
мин = Х[л]
еще:
макс = Х[л]
мин = Х[г]
еще:
середина = л + (г - л) // 2
leftMinMax = найтиMinMax(X, l, середина)
rightMinMax = найтиMinMax(X, середина + 1, r)
если левыйМинМакс[0] > правыйМинМакс[0]:
макс = левый минмакс [0]
еще:
макс = справаМинМакс[0]
если левыйМинМакс[1] < правыйМинМакс[1]:
мин. = левый мин. макс. [1]
еще:
мин = справаМинМакс[1]
maxMin = [макс, мин]
вернуть maxMin Анализ решений Определим рекуррентное соотношение для анализа временной сложности. Предположим, что T(n) — временная сложность задачи размера n.
Предположим, что T(n) — временная сложность задачи размера n.
Пространственная сложность = Высота дерева рекурсии = O(logn), для стека вызовов рекурсии.
Примечание: Здесь временная сложность также равна O(n), но общее количество операций сравнения меньше, чем в предыдущем подходе.
Эффективный подход с использованием одного цикла: цикл Увеличение на 2
Идея решения В первом подходе мы делаем две операции сравнения для каждого элемента в худшем случае. Теперь критический вопрос: можем ли мы оптимизировать его дальше и уменьшить общее количество операций сравнения?
Теперь критический вопрос: можем ли мы оптимизировать его дальше и уменьшить общее количество операций сравнения?
Одна из идей : Выберите элементы парами и попытайтесь обновить минимум и максимум. Предположим, что до (i - 1)-го индекса максимум и минимум были обновлены в переменных max и min . Теперь мы рассматриваем пару i-го и (i + 1)-го индекса на следующей итерации.
В обоих сценариях мы делаем 3 сравнения (в худшем случае), чтобы обновить максимум и минимум 2 элементов. Другими словами, мы сохраняем одно сравнение по отношению к первому подходу, где нам нужно 4 сравнения для 2 элементов (в худшем случае).
Инициализация : Если размер массива нечетный, мы инициализируем первый элемент как min, так и max, а если размер массива четный, мы сравниваем первые два элемента и соответственно инициализируем min и max.
Шаги решения int[] findMinMax(int X[], int n)
{
интервал макс, мин, я
если (n % 2 != 0)
{
макс = Х[0]
мин = Х[0]
я = 1
}
еще
{
если (Х[0] < Х[1])
{
макс = Х[1]
мин = Х[0]
}
еще
{
макс = Х[0]
мин = Х[1]
}
я = 2
}
в то время как (я < п)
{
если (X[i] < X[i + 1])
{
если (X[i] < мин)
мин = Х[я]
если (X[i + 1] > макс)
макс = Х[я + 1]
}
еще
{
если (X[i] > макс)
макс = Х[я]
если (X[i + 1] < мин)
мин = Х[я + 1]
}
я = я + 2
}
интервал maxMin[2] = {макс, мин}
вернуть максмин
} Реализация Python
def findMinMax(X, n):
макс, мин, я = 0, 0, 0
если n % 2 != 0:
макс = Х[0]
мин = Х[0]
я = 1
еще:
если Х[0] < Х[1]:
макс = Х[1]
мин = Х[0]
еще:
макс = Х[0]
мин = Х[1]
я = 2
пока я < п:
если X[i] < X[i+1]:
если X[i] < мин:
мин = Х[я]
если X[i+1] > макс. :
макс = Х[я+1]
еще:
если X[i] > max:
макс = Х[я]
если X[i+1] < мин:
мин = Х[я+1]
я = я + 2
maxMin = [макс, мин]
вернуть maxMin
:
макс = Х[я+1]
еще:
если X[i] > max:
макс = Х[я]
если X[i+1] < мин:
мин = Х[я+1]
я = я + 2
maxMin = [макс, мин]
вернуть maxMin Анализ решения Для каждой пары есть три сравнения: первое среди элементов пары и два других с мин. и макс. Общее количество сравнений = 3 * (n-1)/2 (если n нечетное) или 3n/2 – 2 (если n четное).
Временная сложность = O(n). Здесь мы видим, что общее количество сравнений меньше, чем в первом подходе. Другими словами, сравнение попарно помогает нам еще больше оптимизировать первый подход. (Думай)
Критические мысли!
Сравнение временной и пространственной сложности
Пространственная сложность = O(1), общее количество сравнений в худшем случае = 2(n-1)
Сложность пространства = O(logn), общее количество сравнений = 3n/2 - 2 (если n является степенью 2)
Пространственная сложность = O(1), общее число сравнений в наихудшем случае = 3n/2 - 2
Пожалуйста, напишите в сообщении ниже, если вы обнаружите что-то неправильное или если вы хотите поделиться более подробной информацией.

 2}=\frac{32}{22}=1\frac{10}{22}=1\frac5{11}\)
2}=\frac{32}{22}=1\frac{10}{22}=1\frac5{11}\)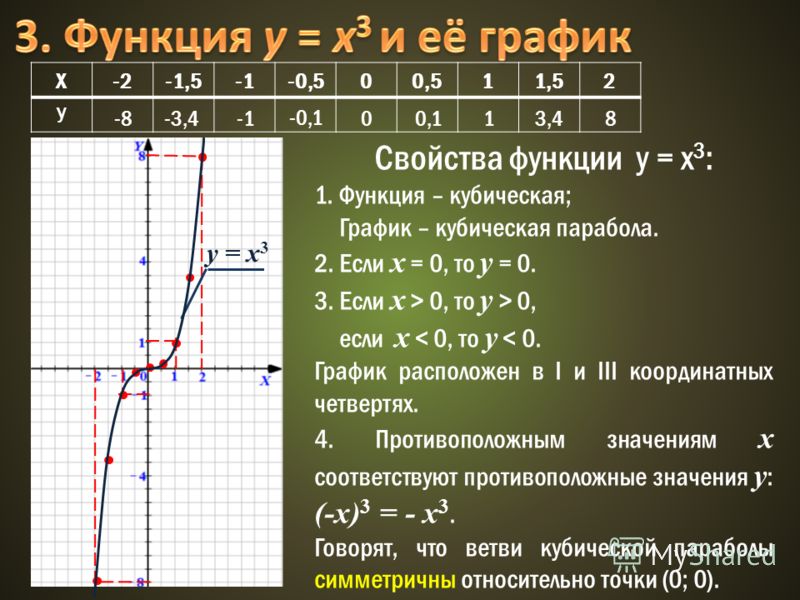 Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3.
Investigation of the properties of functions by definitionЗадачи для самостоятельной работыРешения задачТест 1.1.1(Часть 1). Числовые функцииQuiz 1.1.1 (part 1)Тест 1.1.1(Часть 2). Числовые функцииQuiz 1.1.1 (part 2)Видеолекция 1. Числовая последовательность Lecture 1. Numeric sequenceВидеолекция 2. Предел числовой последовательностиLecture 2. The limit of a numeric sequence.Practical lesson 1. Study of properties of a numerical sequence by conventionПрактическое занятие 1 (часть 2)Теоретический материалЗадачи для самостоятельной работыРешения задачТест 1.1.2. Числовые последовательностиВидеолекция 1. Предел функции в точкеLecture 1. The limit of a function at a pointВидеолекция (часть 2)Практическое занятие 1. Вычисление пределов, неопределенности.Practical lesson 1. Calculation of limits. UncertaintiesПрактическое занятие 2. Вычисление пределов. Замечательные пределы.Practical lesson 2. Calculation of limits. Remarkable limits.Задачи для самостоятельной работыРешения задачТест 1.1.3.
 Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
 Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture.
Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture.
 Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2.
Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2.
Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2.
Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1.
Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2.
Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2.
Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.
Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2. 2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы.
2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2.
Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТеоретический материалТест 3.1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2.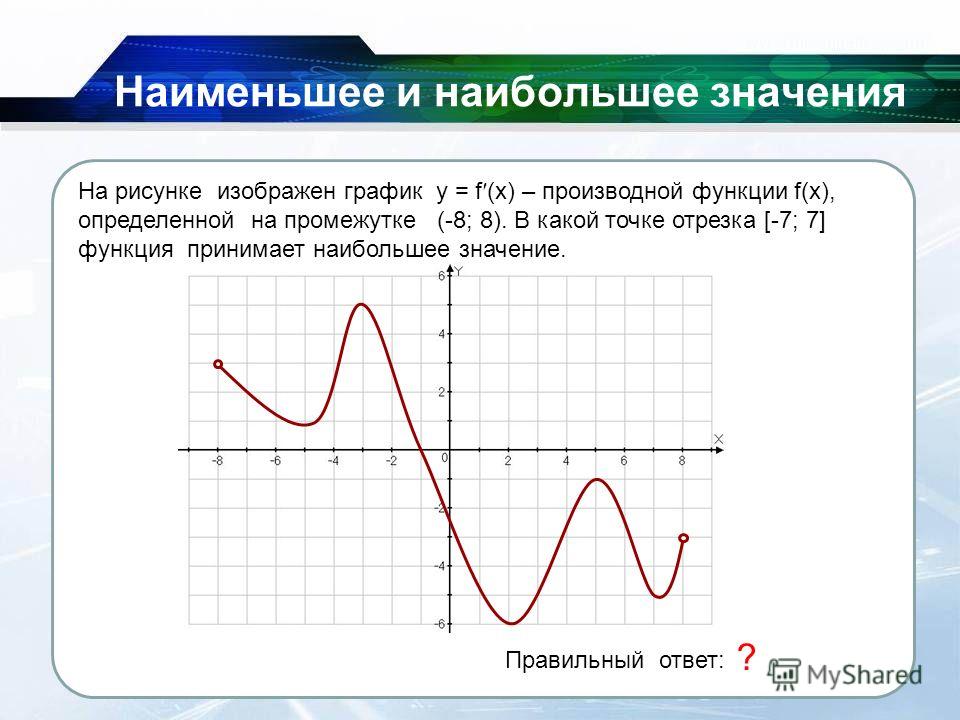 Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2.
Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.
Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3. 5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1.
5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1.
Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)


 е. mid = l + (r - l)/2.
е. mid = l + (r - l)/2.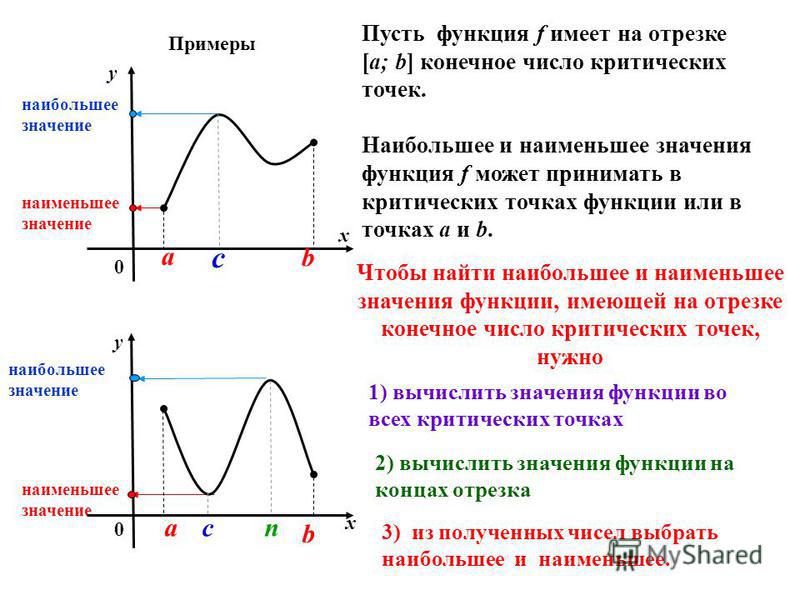 макс. [0] > справа мин. макс. [0])
макс = левый минмакс [0]
еще
макс = справаМинМакс[0]
если (слева МинМакс [1] < справа МинМакс [1])
мин. = левый мин. макс. [1]
еще
мин = справаМинМакс[1]
}
интервал maxMin[2] = {макс, мин}
вернуть максмин
}
макс. [0] > справа мин. макс. [0])
макс = левый минмакс [0]
еще
макс = справаМинМакс[0]
если (слева МинМакс [1] < справа МинМакс [1])
мин. = левый мин. макс. [1]
еще
мин = справаМинМакс[1]
}
интервал maxMin[2] = {макс, мин}
вернуть максмин
} 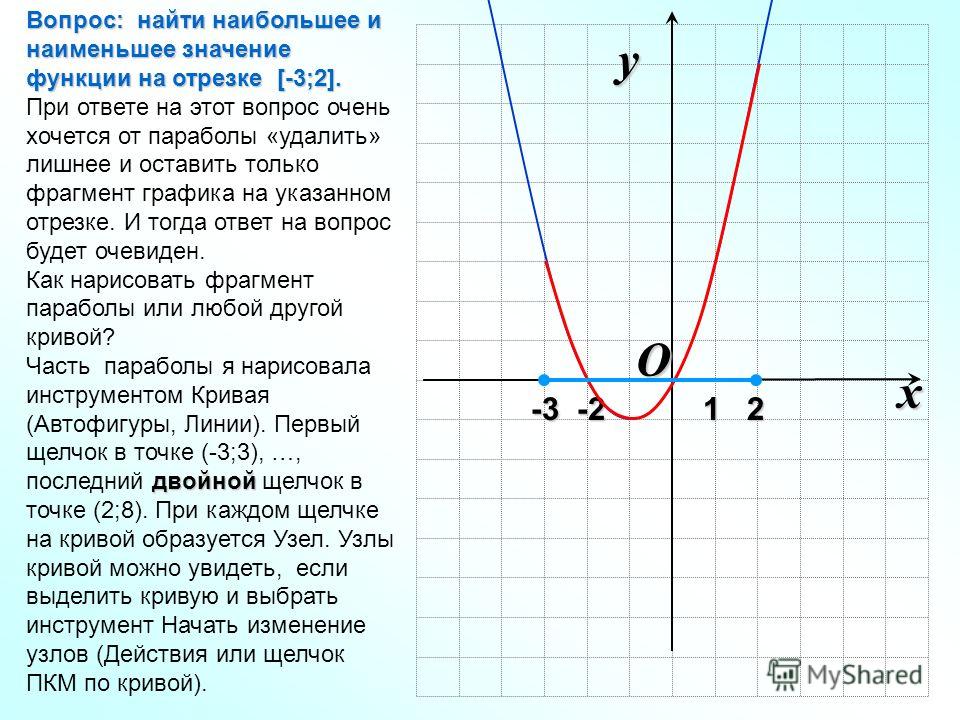 е. если (X[i] > max), max = X[i] и если (X[i + 1 ] < min), min = X[i + 1].
е. если (X[i] > max), max = X[i] и если (X[i + 1 ] < min), min = X[i + 1].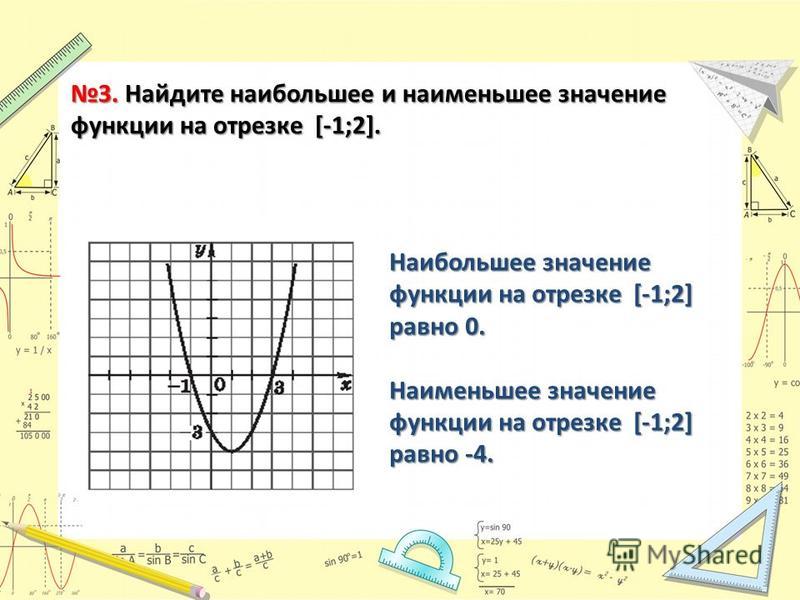 Для каждой пары (i, i + 1) сравните оба элемента. На основе сравнения:
Для каждой пары (i, i + 1) сравните оба элемента. На основе сравнения: :
макс = Х[я+1]
еще:
если X[i] > max:
макс = Х[я]
если X[i+1] < мин:
мин = Х[я+1]
я = я + 2
maxMin = [макс, мин]
вернуть maxMin
:
макс = Х[я+1]
еще:
если X[i] > max:
макс = Х[я]
если X[i+1] < мин:
мин = Х[я+1]
я = я + 2
maxMin = [макс, мин]
вернуть maxMin