Онлайн вычислитель матриц: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

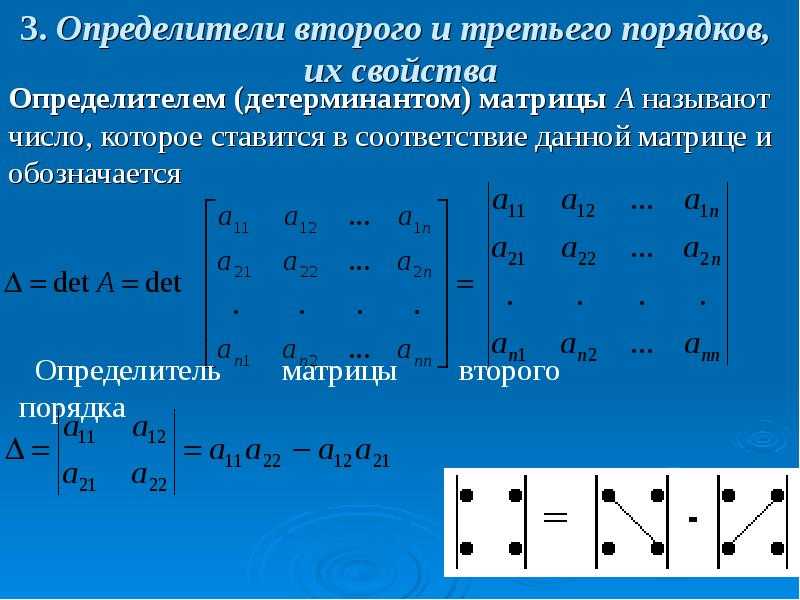
Калькулятор матриц, решение матрицу онлайн

Матрица А
(3×3)

Размер Матрицы А: кол-во строк:       23456
кол-во столбцов:123456

+-×

Матрица B
(3×3)

Размер Матрицы B: кол-во строк:       23456
кол-во столбцов:123456

Вы изучаете высшую математику в вузе или техникуме? Вам нужна помощь в вычислениях по теме математических матриц, теории вероятностей? Воспользуйтесь таким удобным гаджетом, как онлайн калькулятор матриц. Он всегда доступен на нашем сайте бесплатно, поэтому вы не ошибетесь в расчетах и правильно выполните все задания, оптимально и эффективно рассчитаете нужные уравнения.

Что такое матрица в математике

Это один из ключевых объектов изучения в рамках высшей математики, обладающий прямым прикладным смыслом, на фоне абстрактной математики. Возможно, по этой причине тема матричных вычислений интересна многим студентам больше остальных. Это красивая теория и очень практические результаты расчетов, которые всегда могут пригодиться в жизни и в работе.

Нередко их характеризуют как «таблицы прямоугольной формы с данными», но этим характеристика не исчерпывается. Простой пример – телефонная книга с номерами абонентов и фамилиями, адресами. Это большая матрица, вид которой очень легко представить. Данные в ней взаимосвязаны по строчкам и столбцам.

Очевидно, что эти табличные данные используются повсеместно: в учебе и работе, в бухгалтерии, для составления отчетов и списков, в школьном журнале успеваемости. Число строчек и столбцов может быть разным, насчитывать они могут миллионы, например, тот же справочник «Желтые страницы», служебная таблица контактов и внутренних номеров. Личная записная книжка – тоже аналог этого явления.

В рамках таблицы можно делать умножение, проводить самые разные операции, чтобы решить любые задачи. Например, если в столбце указаны единицы продукции, в строчках – годы, то можно рассчитать суммарное количество выпущенного товара. Если посчитать аналогично данные с разных предприятий, будет готова статистика по конкретной отрасли. Можно таким же образом высчитать себестоимость продукта по разным годам. Удобный калькулятор матриц помогает упростить и ускорить все математические выкладки.

Как пользоваться калькулятором матриц

Принцип использования этого онлайн-сервиса очень удобен и прост. Освоить эту технологию сможет любой желающий, разобраться можно в пару кликов. Это действительно комфортный метод расчетов, потому что обычные цифровые и даже логарифмические калькуляторы инженерного типа не могут предложить опции по вычислению матричных данных.

Пошаговый принцип использования калькулятора матриц онлайн следующий:

1. Просмотрите варианты переключателей (галочка в квадрате) и выберите нужную таблицу – одну или несколько.
2. Введите размеры, используя выскакивающие окошки со списками (пустые окна со стрелками прокрутки).
3. Введите рабочие элементы. Если они равны 0, то заполнять графы не нужно.
4. Далее выберите в следующем выпадающем перечне нужную функцию, если нужно – дополнительные показатели.
5. Нажмите клавишу «Посчитать».
6. Появится результат исчислений по данной матрице. Если он не совпадает с прогнозом или чем-то не устраивает, можно поменять результат, версию его визуализации. Это могут быть правильные/неправильные дроби, десятичные). Можно уточнить желаемое число знаков за запятой.

Как видим, это простой, практичный и эффективный инструмент, экономящий массу времени и терпения студента. Важно иметь доступ к сети Интернет, тогда все операции будут происходить моментально.

Что умеет матричный калькулятор

Рабочий элемент в действиях с матрицами – дроби, правильные и десятичные, а также экспоненту. Причем длина числового значения вообще не имеет ограничений, можно ставить хоть десять тысяч знаков за запятой (хотя это может притормозить процесс расчета).

Доступны все варианты действий, как при бумажном вычислении:

1. Транспонирование;
2. Расчет определяющего элемента;
3. Вычисление ранга и следа;
4. Возведение в степень;
5. Расчет обратных матриц;
6. Умножение;
7. Приход к виду треугольника или ступеней;
8. Поиск корректного расклада LU;
9. Выполнение элементарных видоизменений, а также действий с выражениями, которые содержат матрицы.

В работе используются традиционно одна либо две матрицы, если нужно работать с двумя, то нужно переставить выключатель, активируя вторую. Данные таблиц А и В нужно вставлять с помощью клавиш, также можно перемещать данные из одной ячейки в другую методом перетаскивания. Удобно пользоваться стрелками для перемещения на таблице.

Некоторые теоретические сведения

В математических вычислениях неотъемлемый элемент работы – теоретические термины и определения. В отношении матричных вычислений важно понимать и применять ряд терминов, раскрывающие непрактические аспекты матричной математики.

Ниже приведены основные рабочие понятия, ими оперируют студенты, в том числе при использовании онлайн-калькулятора.

Траспонирование – математический расчет, в ходе него происходит рокировка строчек и столбиков в составе матричной таблицы (например: a^T_ij=a_ji).

Главная диагональ – в составе квадрата элемент, пересекающий углы с верху вниз и слева направо (a_ii).

Единичная матрица (E_n×n) – матричный квадрат, включающий n столбиков и n строчек, где на основной диагонали стоят 1, а вне пределов – 0.

Ранг – ограничение по максимуму на число линейных столбцов и строчек в конкретной матрице. Рабочая маркировка: rank(A).

След – совокупность знаков, расположенных на основной диагонали. Отмечается так: tr(A) либо track(A).

Умножение на число – аналогичная по размеру таблица, похожая на оригинальную, но каждый ее элемент будет результатом перемножения первичного аналога в первой версии на конкретную цифру.

Возведение в степень – приумножение таблицы на себя n раз, причем n – это степень, наращивающая первую матрицу: Aⁿ.

Обратная матрица (A⁻¹) – ее умножение на исходную версию А будет равняться схеме: A^-1×A=A×A^-1=E

Треугольновидная матрица – квадратичный вариант таблицы, где по разные стороны основной диагонали (в верхнетреугольной или нижнетреугольной) стоят 0.

Разложение типа LU – форма визуализации в качестве перемножения двух разных таблиц (L – нижнетреугольная с одной диагональю, U – верхнетреугольная). Тип обозначений: A=L·U.

Сложение матриц (A_n×m+B_n×m) – итоговая табличка C_n×m, полученная в результате суммирования соответствующих значений А и В. Каждый член в третьей матрице С будет равняться комбинации: с_ij=a_ij+b_ij.

Разность (A_n×m и B_n×m) – итоговая C_n×m достигается за счет парной разницы элементов А и В по соответствию, каждый член С будет равен: с_ij=a_ij-b_ij.

Произведение матриц (A_n×k и B_k×m) – полученная таблица C_n×m, где элемент (c_ij) тождественен сложению умноженных данных i-строчки А на аналогичные элементы j-столбца В. Вид: c_ij=a_i1·b_1j+a_i2·b_2j+ …+a_ik·b_kj.

Использование этих терминов отражает грамотность и подготовку студента в области высшей математики, облегчает операции по вычислению, понимание темы.

Умножение матриц

Выполнить решение матриц онлайн можно с любым математическим действием. Умножение выполняется в разных версиях:

1. С умножением на число;
2. С произведением вектора на матрицу и наоборот;
3. Взаимное умножение матриц.

Сложение матриц

Если требуется сложить матрицы А и В и получить в итоге вариант С, где все элементы – это сложенные парно коррелирующие элементы исходных версий – выручит матричный калькулятор. Допустимо делать сложение только равноразмерных матриц, где есть одинаковое число строк и столбцов.

В математическом выражении сумма выглядит таким образом: А_m×n+B_m×n=C_m×n

Любая единица данных в составе итоговой матрицы тождественен сумме изначальных данных первых двух таблиц: c_ij = a_ij + b_ij.

Вычитание матриц

Вычитание – еще одна опция, доступная для пользователей онлайн-калькулятора. С ней удобно провести вычитание равномерных элементов матриц А и В, но только для таблиц зеркального размера. Например: А(2×2)-В(2×2), А(3×5)-В(3×5) и т.д. Итог вычитания – третья матрица С, ее масштаб будет аналогичным начальному варианту.

Деление матриц

Аналогичная опция выполняется методом подстановки данных из исходных таблиц А и В для получения результата деления в матрице С, равновеликой по всем параметрам своим исходникам.

Теперь в вашем распоряжении удобный и современный инструмент, с которым вы сможете решить матрицу онлайн быстро и точно. Успехов в изучении математики!

Матрица Судьбы онлайн калькулятор по дате рождения с расшифровкой.

Матрица Судьбы онлайн калькулятор по дате рождения с расшифровкой.

Зачем нужна Матрица судьбы?

Матрица дает ответы на вопросы, Матрица нужна тебе если тебя интересует:

Деньги

А почему у меня нет денег в достаточном количестве?

Любимые

Почему у меня не складываются отношения с партнёром и нет любимого человека?

Предназначения

В чём моё истинное предназначение души?

Болезни

Почему я болею и в чём первопричина болезни?

Агрессия

Почему я никак не могу справиться с неконтролируемой агрессией?

Свобода

И как мне стать свободным и уйти с нелюбимой работой, которая отнимает у меня силы и не является моим истинным предназначением.

Отношения

Почему у меня плохие отношения с родителями и детьми?

По кругу

Почему я всё время хожу по одному и тому же кругу ситуаций в жизни меняя только лица людей и время?

Род

Какова моя родовая карма и что мне передали предки?

Вина

Почему мне всё время кажется, что виноваты другие?

Творчество

И как мне понять и раскрыть своё творчество?

Одиночество

И как мне исцелить карму одиночества и выйти из программы «Демон и жертва»?

Услуги

• Для чего встретились
• Как проявляется пара
• Финанс. благополучие
• Проблемы/трудности
• Негативная карма

WhatsApp

• Личные качества
• Таланты
• Предназначения
• Деньги
• Отношения
• Прошлая жизнь
• Руководство
• Программы
• Сексуальность
• Родители
• Дети
• Здоровье
• Прогноз на год*

WhatsApp

* — расчет прогноза на год, начинается с 20го года рождения.

• «Вся матрица» х2
• «Совместимость» х1

WhatsApp

** — расчет двух персональных Матриц + расчет на совместимость по Матрице Судьбы (предложение действует для мужчины и женщины).

Для расчета Матрицы Судьбы в рамках пакета: «Совместимость», «Вся Матрица» или «Вся Матрица Плюс», напишите нам в Telegram, Viber или отправьте заявку через WhatsApp.

Telegram Viber

В связи с геополитической обстановкой, РКН России блокирует сервисы Facebook, в следствии чего не работает прямой переход в WhatsApp.

Для отправки заявки/сообщения через WhatsApp, напишите на номер:

+79299801380

В сообщении напишите свое имя, дату рождения, какой расчет и расшифровку вы хотели бы заказать или напишите в Telegram, Viber.

Как только изменится ситуация, прямой переход будет возобновлен. Приношу свои извинения за временные неудобства.

Калькулятор квадратного корня

— Калькулятор квадратного корня онлайн

Калькулятор квадратного корня вычисляет квадратный корень из заданного числа. Квадратный корень определяется как значение, которое можно умножить само на себя, чтобы получить исходное число. Квадратом числа x будет число y, удовлетворяющее уравнению y ² = x.

Что такое калькулятор квадратного корня?

Калькулятор квадратного корня — это онлайн-инструмент, используемый для вычисления квадратного корня из заданного положительного целого числа. Квадратный корень числа также может быть выражен как число, возведенное в степень 1/2. Чтобы использовать это Калькулятор квадратного корня , введите значения в поле ввода.

Калькулятор квадратного корня

ПРИМЕЧАНИЕ: Введите число, состоящее только из 3 цифр.

Как пользоваться калькулятором квадратного корня?

Выполните следующие простые действия, чтобы вычислить квадратный корень с помощью онлайн-калькулятора квадратного корня:

• Шаг 1 : Перейдите к онлайн-калькулятору квадратного корня.
• Шаг 2 : Введите положительное число в поле ввода калькулятора квадратного корня.
• Шаг 3 : Нажмите кнопку «Вычислить» , чтобы найти квадратный корень из числа.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор квадратного корня?

Квадратный корень числа — это число, которое при умножении само на себя дает произведение исходного числа.

‘√’ — это символ, который используется для представления квадратного корня числа. Существует четыре метода нахождения квадратного корня числа. Они перечислены следующим образом:

1. Метод повторного вычитания.
2. Метод простой факторизации.
3. Метод оценки.
4. Метод длинного деления.

Первые три метода очень полезны для определения квадратного корня из полного квадрата. Положительное число, которое можно записать как произведение числа само на себя, можно определить как полный квадрат. Однако метод деления в длину более трудоемкий, с его помощью можно найти квадратный корень из любого числа. Такое число не обязательно должно быть полным квадратом. Если на месте единицы числа стоит 2, 3, 7 или 8, то идеальный квадратный корень не существует. Однако, если на месте единицы числа стоит 1, 4, 5, 6 или 9то такое число может иметь совершенный квадратный корень. Формула квадратного корня выглядит так:

y = √x

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Решенные примеры на калькуляторе квадратного корня

Пример 1:

Найдите квадратный корень из 64 и проверьте его с помощью калькулятора квадратного корня.

Решение:

Использование метода основной факторизации

64 = 2 × 2 × 2 × 2 × 2 × 2

64 = 2 ² × 2 ² × 2 ²

64 =. (2 × 2 × 2) ²

64 = 8 ²

√64 = 8

Следовательно, 8 — это квадратный корень из 64.

9 Найдите 5 квадратный корень из 2:

и проверьте это с помощью калькулятора квадратного корня.

Решение:

Используя метод простой факторизации

25 = 5 × 5

25 = 5 ²

√25 = 5

Таким образом, 5 — это квадратный корень из 25,

. число, вы можете попробовать калькулятор квадратного корня для следующего:

• 800
• 216

☛ Связанные статьи:

• Квадратный корень
• Простая факторизация

☛ Математические калькуляторы:

Калькулятор научных обозначений — примеры, факты

Калькулятор научных обозначений помогает выразить заданное число с использованием научных обозначений. Научные обозначения дают нам способ легко выражать очень большие или очень маленькие числа. Он использует десятичную форму, а также степени 10 для представления числа.

Что такое научный калькулятор?

Калькулятор научных обозначений — это онлайн-инструмент, который помогает рассчитать научное представление заданного числа, используя десятичные дроби и степени 10. Если число очень велико, показатель степени (или степень 10) положителен. Однако, если у нас есть небольшое число, степень 10 отрицательна. Чтобы использовать это экспоненциальное представление калькулятор введите значение в поле ввода.

Калькулятор экспоненциального представления

Как использовать калькулятор экспоненциального представления?

Пожалуйста, следуйте инструкциям для расчета экспоненциального представления с помощью онлайн-калькулятора экспоненциального представления:

• Шаг 1: Перейдите к онлайн-калькулятору научного представления.
• Шаг 2: Введите число в поле ввода Калькулятора научной записи.
• Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти экспоненциальное представление.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор научной записи?

Очень большое или маленькое число может быть выражено с помощью научных обозначений. Тем не менее, для использования экспоненциальной записи необходимо соблюдать некоторые правила. Они даны следующим образом:

• Правило 1: Предположим, у нас есть большое число, которое больше 1. Затем мы перемещаем десятичную точку влево, и степень 10 становится положительной.
• Правило 2: Предположим, у нас есть небольшое число, меньшее 1. Десятичная точка сдвинута вправо и степень 10 отрицательна.

Ниже приведены шаги для представления числа с использованием экспоненциального представления.

1. Десятичную точку необходимо перемещать до тех пор, пока слева от точки не останется только одна ненулевая цифра. Это число обозначается c.
2. Теперь подсчитайте, на сколько знаков была перемещена десятичная точка. Это представлено н.
3. Если десятичная запятая была смещена влево, n будет положительным. Это указывает на то, что число большое.
4. Если десятичная запятая была смещена вправо, n будет отрицательным. Это показывает, что число небольшое.
5. Теперь подставьте эти значения в формулу c × 10 ⁿ , чтобы получить экспоненциальное представление.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запишитесь на бесплатный пробный урок

Решенные примеры на калькуляторе экспоненциального представления

Пример 1:

Найдите экспоненциальное представление для 0,00748 и проверьте его с помощью калькулятора экспоненциального представления.