Высшая математика как решать пределы: Как решать пределы для чайников, примеры решений

Содержание

определения, история развития, применение пределов на практике

Содержание:

Основные определения
История развития
Применение пределов на практике

Понятие предела последовательности или функции является одним из фундаментальных понятий математического анализа.

Основные определения

Определение

Предел числовой последовательности, подробнее →

Число $a$ называется пределом последовательности $\left\{x_{n}\right\}$ , если для любого $\epsilon>0$ существует номер $n_{0}=n_{0}(\epsilon)$ такой, что для любого $n>n_{0}$ выполняется неравенство $\left|x_{n}-a\right| \lt \epsilon$ :

$\lim _{n \rightarrow \infty} x_{n}=a \Leftrightarrow \forall \epsilon>0, \exists n_{0}=n_{0}(\epsilon) : \forall n>n_{0},\left|x_{n}-a\right| \lt \epsilon$

Предел функции в точке, подробнее →

Число $b$ называется пределом функции $f(x)$ в точке $a$, если для $\forall \epsilon>0 \exists \delta>0$ такое, что для $\forall x \in(a-\delta ; a+\delta) \cap D[f]$ из того, что $0 \lt |x-a| \lt \delta$ следует, что $|f(x)-b| \lt \epsilon$ : $\lim _{x \rightarrow a} f(x)=b$ или $f(x) \rightarrow b$ при $x \rightarrow a$ .

Предел функции на бесконечности, подробнее →

Число $b$ называется пределом функции $y=f(x)$ на бесконечности или при $x \rightarrow \infty$, если для любого $\forall \epsilon>0$ существует такое число $\delta=\delta(\epsilon)>0$ такое, что для всех $x \in D(f)$ из того, что $|x|>M$, выполняется неравенство $|f(x)-b| \lt \epsilon$.

История развития

Это понятие на интуитивном уровне использовалось ещё во второй половине 17 века английским физиком, математиком и астрономом Исааком Ньютоном (1642 — 1727), а также математиками 18 века — швейцарским, немецким и русским математиком Леонардом Эйлером (1707 — 1783) и французским математиком, астрономом и механиком Жозефом Луи Лагранжем (1736 — 1813). Это было связано с тем, что ученые того времени не ставили перед собой задачу построения теории пределов. Первые строгие определения предела последовательности дали в 1816 году чешский математик, философ, теолог Бернард Больцано (1781 — 1848) и французский математик Огустен Луи Коши (1789 — 1857) в 1821 году.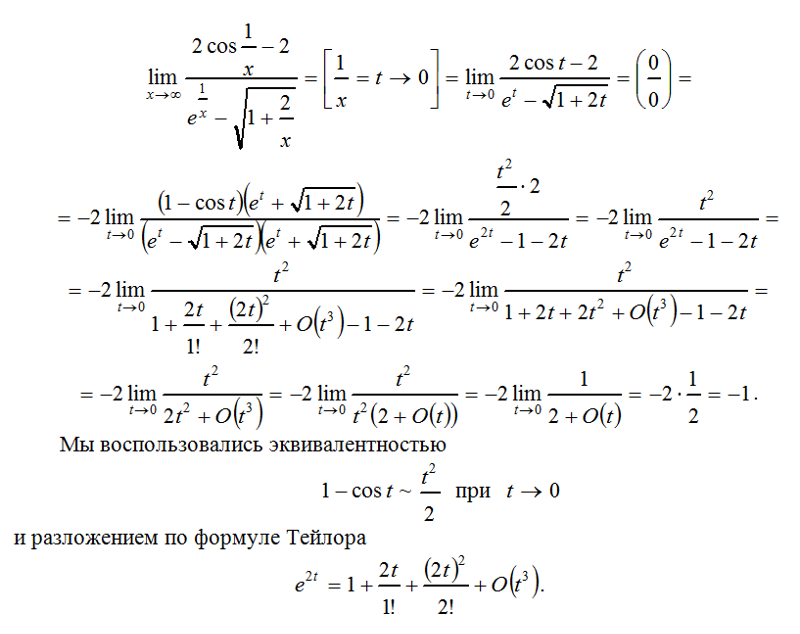

Применение пределов на практике

Теория пределов очень активно применяется в экономических расчетах, например, в доказательствах и расчетах, которые связаны с непрерывными процессами; в финансовых рентах. Пределы функции применяются для нахождения асимптот графика функции при ее исследовании.

Читать дальше: понятие числовой последовательности.

Понятие числовой последовательности

Односторонние пределы
Предел функции на бесконечности. Бесконечно большая функция
Свойства пределов функции
Бесконечно малые функции
Сравнение бесконечно малых функций
Эквивалентные бесконечно малые функции. Таблица эквивалентных б.м. функций
Признаки существования пределов
Первый замечательный предел
Второй замечательный предел
Правило Лопиталя
Ограниченные последовательности
Основные неопределенности и способы их раскрытия
Понятие непрерывности функции в точке
Непрерывность функции на промежутке
Точки разрыва функции и их классификация
Основные теоремы о непрерывности функций. Непрерывность элементарных функций
Бесконечно малые и бесконечно большие последовательности
Монотонные последовательности
Предел числовой последовательности

Предельный переход в неравенствах
Предел монотонной ограниченной последовательности. Число е
Фундаментальные последовательности. Критерий Коши
Предел функции в точке

08.3. Предел на бесконечности

Предел на бесконечности

Можно ли говорить о пределе функции, когда ? Имеет ли смысл выражение ? Ответы на эти вопросы позволят нам расширить понятие предела функции и глубже проникнуть в смысл абстракции бесконечности.

Рассмотрим пример. Пусть дана однородная пластина, размеры a, b, c, d которой известны (рис. 9.12). Найти координаты ее центра тяжести. При достаточно больших значениях d наличие выступа ALEF Не окажет существенного влияния на результаты расчета. Начиная с какого значения d, координаты центра тяжести пластины будут отличаться по абсолютной величине от координат центра тяжести прямоугольника менее, чем на величину E?

Рис.

9.12. Определение центра тяжести пластины.

Центр тяжести пластины может быть определен достаточно просто геометрически. Разбивая ее на прямоугольники AFEL и BCDL, Получим, что центр тяжести лежит на прямой M1N1, связывающей точки пересечения диагоналей этих прямоугольников. С другой стороны, разбивая эту же пластину на прямоугольники ABKF и EKCD, строим прямую M2N2, связывающую их центры тяжести. На пересечении прямых M1N1 и M2N2 получим точку P – центр тяжести пластины.

Естественно предположить, что с увеличением d центр тяжести будет смещаться по вертикали к середине отрезка BL, а по горизонтали будет неограниченно удаляться вправо. Покажем это аналитически. Введем систему координат Xoy, как показано на рис. 9.12. Считая пластину двухмассовой системой, состоящей из прямоугольников AFEL и BCDL, получим координаты xц и уц центра тяжести пластины

Где М1 (х1,у1) И N1 (x2,y2) – центры тяжести соответствующих прямоугольников. Так как пластина однородна, то

Где S1 и S2 – площади прямоугольников, а – их плотность. Но

Отсюда

Задав численные значения a, B и c, можно показать, проведя вычислительный эксперимент на ЭВМ, что с увеличением d координата xц будет стремиться к , а координата yц будет неограниченно возрастать. Но где гарантия того, что этим предельным значением будет , а не , к примеру? Как понимать “неограниченное возрастание yц” при “неограниченном возрастании d”? Геометрические cоображения, позволяющие интуитивно предвидеть ответ, еще не являются доказательством выдвигаемой гипотезы.

Чтобы ответить на поставленные вопросы, необходимо ввести новые строгие определения.

Будем называть число A ПРЕДЕЛОМ ФУНКЦИИ при , если для любого положительного числа E Существует такое положительное число , что для окажется справедливым неравенство :

Рис. 9.13. Предел функции на бесконечности.

График функции, имеющей предел A на бесконечности, может выглядеть, например, так, как на рис. 9.13.

Cтрелками на оси x обозначены направления, по которым значения аргумента обеспечат выполнение неравенства . В отличие от функции, изображенной на этом рисунке, существуют и функции, которые ведут себя не одинаково, когда и когда

, то есть когда x неограниченно удаляется вправо (влево) по оси абсцисс. Они могут иметь различные пределы, или только один из них и даже совсем не иметь предела. Дадим определение таких пределов (оно вытекает из уже сформулированного определения предела при ):

Примеры таких функций даны на рис. 9.14.

Теперь становится понятной задача отыскания предела координаты – центра тяжести пластины при : требуется найти cтоль большие значения размера d, что . Число E на практике характеризует обычно абсолютную погрешность, которая допустима при получении результата. Определение предела дает возможность в данном случае сделать важный для практики вывод: если найдено значение d=M, начиная с которого , то уже для значений d > M можно считать

, что упрощает вычисления. Возможность отыскания этого “порога” – числа M – позволяет обосновать теория пределов. Результат, полученный геометрически, означает возможность упрощения формы пластины до прямоугольника LBCD, если это позволяет заданная погрешность E при вычислении координат центра тяжести пластины.

Рис. 9.14. Возможные случаи предельного перехода

При , стремящемся к бесконечности:

А) предел функции при ;

Б) предел функции при .

Дадим теперь определение бесконечного предела функции.

Будем говорить, что функция при стремится к , если для любого положительного числа L найдется такое положительное число , что для и удовлетворяющих неравенству , в области определения функции будет справедливо неравенство :

На рис. 9.15 по заданному L указан промежуток значений x, для которых выполняется неравенство

Рис. 9.15. Бесконечный предел функции.

Искомая проколотая D-Окрестность – Это симметричный интервал с центром в точке a, принадлежащий этому промежутку.

< Предыдущая		Следующая >

13.2: Пределы и непрерывность в высших измерениях

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 8257

Цели обучения

Вычислить предел функции двух переменных.
Узнайте, как функция двух переменных может приближаться к разным значениям в граничной точке в зависимости от пути приближения.
Укажите условия непрерывности функции двух переменных.
Проверить непрерывность функции двух переменных в точке.
Вычислить предел функции трех и более переменных и проверить непрерывность функции в точке.

Мы рассмотрели функции более чем одной переменной и увидели, как их изобразить. В этом разделе мы увидим, как взять предел функции более чем одной переменной и что означает непрерывность функции более чем одной переменной в точке ее области определения. Оказывается, у этих концепций есть аспекты, которые просто не встречаются с функциями одной переменной.

Предел функции двух переменных

Напомним из раздела 2.5, что определение предела функции одной переменной:

Пусть $f(x)$ определено для всех $x≠a$ в открытом интервале, содержащем $a$. Пусть $L$ — действительное число. Тогда

\[\lim_{x→a}f(x)=L \nonumber \]

, если для каждого $ε>0,$ существует такое $δ>0$, что если \ (0<|x−a|<δ\) для всех $x$ в области определения $f$, тогда

\[|f(x)−L|<ε. \номер\] 92\} \nonumber \]

, как показано на рисунке $\PageIndex{1}$.

Рисунок $\PageIndex{1}$: диск $δ$ с центром вокруг точки $(2,1)$.

Идея круга $δ$ появляется в определении предела функции двух переменных. Если $δ$ мало, то все точки $(x,y)$ в круге $δ$ близки к $(a,b)$. Это совершенно аналогично тому, как х близко к а в определении предела функции одной переменной. В одном измерении мы выражаем это ограничение как

\[a−δ

В более чем одном измерении мы используем диск $δ$.

Определение: предел функции двух переменных

Пусть $f$ — функция двух переменных, $x$ и $y$. Предел $f(x,y)$ при приближении $(x,y)$ к $(a,b)$ равен $L$, записанному

\[\lim_{(x ,y)→(a,b)}f(x,y)=L \nonumber \]

, если для каждого $ε>0$ существует достаточно малое $δ>0$ такое, что для всех точек $(x,y)$ в диске $δ$ вокруг $(a,b)$, за исключением, возможно, самого $(a,b)$, значение $f( x,y)$ не более чем на $ε$ от $L$ (рисунок $\PageIndex{2}$). 92}<δ. \nonumber \]

Рисунок $\PageIndex{2}$: Предел функции с двумя переменными требует, чтобы $f(x,y)$ находилось в пределах $ε$ от $L$ всякий раз, когда $(x,y)$ находится в пределах $δ$ от $(a,b)$. Чем меньше значение $ε$, тем меньше значение $δ$.

Доказательство существования предела с использованием определения предела функции двух переменных может быть сложной задачей. Вместо этого мы воспользуемся следующей теоремой, которая поможет нам найти пределы. Формулы этой теоремы являются расширением формул теоремы о предельных законах из книги «Предельные законы».

Предельные законы для функций двух переменных

Пусть $f(x,y)$ и $g(x,y)$ определены для всех $(x,y)≠(a,b) $ в окрестности $(a,b)$, и предположим, что эта окрестность полностью содержится внутри области определения $f$. Предположим, что $L$ и $M$ — действительные числа такие, что

\[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \]

\[\lim_{(x,y)→(a,b)}g(x,y)=M, \nonumber \]

и пусть $c$ будет константой. Тогда верно каждое из следующих утверждений:

Постоянный закон:

\[\lim_{(x,y)→(a,b)}c=c \nonumber \]

Законы тождества:

\[\lim_{(x, y)→(a,b)}x=a \nonumber \]

\[\lim_{(x,y)→(a,b)}y=b \nonumber \]

Закон суммы:

\[\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M \nonumber \]

Разностный закон:

\[\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M \nonumber \]

Постоянный кратный закон:

9n \nonumber \]

для любого положительного целого числа $n$.

Корневой закон:

\[\lim_{(x,y)→(a,b)}\sqrt[n]{f(x,y)}=\sqrt[n]{L} \nonumber \]

для всех $L$, если $n$ нечетно и положительно, и для $L≥0$, если n четно и положительно.

Доказательства этих свойств аналогичны доказательствам для пределов функций одной переменной. Мы можем применить эти законы для нахождения пределов различных функций.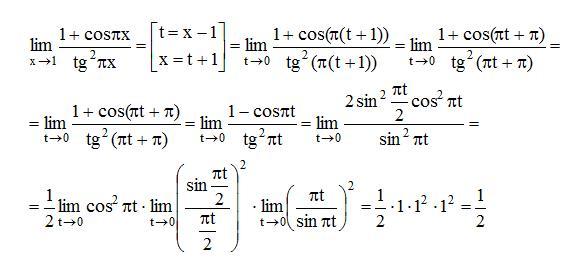

Пример $\PageIndex{1}$: нахождение предела функции двух переменных 92−4(2)+3(−1)−6 \\[4pt] =−6. \end{align*}\]

б. Перед применением частного закона нам нужно убедиться, что предел знаменателя отличен от нуля. Используя разностный закон, постоянный множественный закон и закон тождества,

\[\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x ,y)→(2,−1)}4x−\lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2, −1)}x)−3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \end{align*}\]

Поскольку предел знаменателя не равен нулю, применяется закон частного. Теперь вычислим предел числителя, используя разностный закон, закон констант-множителей и закон тождества:

\[\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\ lim_{(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x ,y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \end{align*}\]

Следовательно, в соответствии с частным законом имеем

\[\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+ 3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y)→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2, −1)}(4x−3y)} \\[4pt] =\dfrac{1}{11}. 2}=0 \номер\] 92}=\tfrac{1}{2}. \nonumber \]

Это верно для любой точки на прямой $y=x$. Если мы позволим $x$ приблизиться к нулю, оставаясь на этой линии, значение функции останется фиксированным на $\tfrac{1}{2}$, независимо от того, насколько мал $x$.

Выберите значение ε меньше $1/2$, например, $1/4$. Тогда, независимо от того, насколько маленький диск $δ$ мы нарисуем вокруг $(0,0)$, значения $f(x,y)$ для точек внутри этого диска $δ$ будут включают как $0$, так и $\tfrac{1}{2}$. Следовательно, определение предела в точке никогда не выполняется, и предел не существует. 92}.\) Вдоль прямой $y=0$ функция равна нулю; вдоль линии $y=x$ функция равна $\tfrac{1}{2}$.

б. Подобно а., мы можем приблизиться к началу координат по любой прямой, проходящей через начало координат. Если мы попытаемся использовать ось $x$ (т. е. $y=0$), то функция останется фиксированной на нуле. То же верно и для оси $y$. Предположим, мы приближаемся к началу координат по прямой линии наклона $k$. Уравнение этой линии $y=kx$. Тогда предел становится

92\) (Рисунок $\PageIndex{4}$).

Точка $P_0$ называется внутренней точкой $S$, если существует диск $δ$ с центром вокруг $P_0$, полностью содержащийся в $S$.
Точка $P_0$ называется граничной точкой $S$, если каждый круг $δ$ с центром вокруг $P_0$ содержит точки как внутри, так и снаружи $S$.

Рисунок $\PageIndex{4}$: В показанном наборе $S$ $(−1,1)$ является внутренней точкой, а $(2,3)$ является граничной точкой . 92\) (Рисунок $\PageIndex{4}$).

$S$ называется открытым множеством , если каждая точка $S$ является внутренней точкой.
$S$ называется замкнутым множеством , если оно содержит все свои граничные точки.

Примером открытого множества является диск $δ$. Если мы включим границу диска, то он станет замкнутым множеством. Множество, которое содержит некоторые, но не все, его граничные точки, не является ни открытым, ни закрытым. Например, если мы включаем половину границы круга $δ$, но не другую половину, то множество не является ни открытым, ни закрытым. 92\) (Рисунок $\PageIndex{4}$).

Открытое множество $S$ является связным множеством , если оно не может быть представлено в виде объединения двух или более непересекающихся непустых открытых подмножеств.
Множество $S$ является областью , если оно открыто, связно и непусто.

Определение предела функции двух переменных требует, чтобы круг $δ$ содержался внутри области определения функции. Однако если мы хотим найти предел функции в граничной точке области, $δ$ диск не содержится внутри домена. По определению некоторые точки диска $δ$ находятся внутри области, а некоторые — снаружи. Поэтому нам нужно рассматривать только точки, которые находятся как внутри круга $δ$, так и внутри области определения функции. Это приводит к определению предела функции в граничной точке. 2}<δ. \номер\] 92} \номер\]

Непрерывность функций двух переменных

В разделе Непрерывность мы определили непрерывность функции одной переменной и увидели, как она зависит от предела функции одной переменной. В частности, необходимы три условия для непрерывности $f(x)$ в точке $x=a$

$f(a)$.
$\displaystyle \lim_{x→a}f(x)$ существует.
$\displaystyle \lim_{x→a}f(x)=f(a).$

Эти три условия необходимы и для непрерывности функции двух переменных.

Определение: непрерывные функции

Функция $f(x,y)$ непрерывна в точке $(a,b)$ своей области определения, если выполняются следующие условия:

$f (а,б)$ существует.
$\displaystyle \lim_{(x,y)→(a,b)}f(x,y)$ существует.
$\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).$

Пример $\PageIndex{4}$: демонстрация непрерывности функции двух переменных

Покажите, что функция

\[f(x,y)=\dfrac{3x+2y}{x+y+1} \nonumber \]

непрерывна в точке $(5,−3). $

Решение

Согласно определению непрерывности должны быть выполнены три условия. В этом примере $a=5$ и $b=−3.$

1. $f(a,b)$ существует. Это верно, потому что область определения функции f состоит из тех упорядоченных пар, для которых знаменатель не равен нулю (т. Е. \ (x + y + 1 ≠ 0 \)). Точка $(5,−3)$ удовлетворяет этому условию. Кроме того,

\[f(a,b)=f(5,−3)=\dfrac{3(5)+2(−3)}{5+(−3)+1}=\dfrac{15−6 {2+1}=3. \nonumber \]

2. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)$ существует. Это также верно:

\[\begin{align*} \lim_{(x,y)→(a,b)}f(x,y) =\lim_{(x,y)→(5,− 3)} \ dfrac {3x + 2y} {x + y + 1} \\ = \ dfrac {\ displaystyle \ lim_ {(x, y) → (5, −3)} (3x + 2y)} {\ displaystyle \lim_{(x,y)→(5,−3)}(x+y+1)} \\ = \dfrac{15−6}{5−3+1} \\ = 3. \end{align *}\]

3. $\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).$ Это верно, потому что мы только что показано, что обе части этого уравнения равны трем. 92}<δ\) верно, $|f(x,y)−f(a,b)|<ε. $ Это определение можно комбинировать с формальным определением (то есть эпсилон–дельта определение ) непрерывности функции одной переменной для доказательства следующих теорем:

Сумма непрерывных функций непрерывна

Если $f(x,y)$ непрерывно в $(x_0,y_0)\ ), и \(g(x,y)$ непрерывна в $(x_0,y_0)$, то $f(x,y)+g(x,y)$ непрерывна в $( х_0,у_0)$.

Произведение непрерывных функций непрерывно 92\) в диапазон $R⊆R.$ Предположим, что $g$ непрерывна в некоторой точке $(x_0,y_0)∈D$ и определим $z_0=g(x_0,y_0)$ . Пусть f будет функцией, которая отображает $R$ в $R$, так что $z_0$ находится в области определения $f$. Наконец, предположим, что $f$ непрерывно в $z_0$. Тогда $f∘g$ непрерывен в $(x_0,y_0)$, как показано на рисунке $\PageIndex{7}$.

Рисунок $\PageIndex{7}$: Композиция двух непрерывных функций непрерывна.

Теперь воспользуемся предыдущими теоремами, чтобы показать непрерывность функций в следующих примерах. 3\)? Что значит быть непрерывным в точке в четырех измерениях? 92}<δ\большой\}. \nonumber \]

Чтобы показать, что предел функции трех переменных существует в точке $(x_0,y_0,z_0)$, достаточно показать, что для любой точки шара $δ$ с центром в $(x_0,y_0,z_0)$ значение функции в этой точке сколь угодно близко к фиксированному значению (предельное значение). Все предельные законы для функций двух переменных справедливы и для функций более чем двух переменных.

Пример $\PageIndex{6}$: нахождение предела функции трех переменных 92y−3z}{2x+5y−z}. \nonumber \]

Решение

Прежде чем мы сможем применить закон о частных, нам нужно проверить, что предел знаменателя не равен нулю. Используя разностный закон, закон тождества и постоянный закон,

\[\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z ) =2(\lim_{(x,y,z)→(4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y )−(\lim_{(x,y,z)→(4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{ align*}\]

Поскольку это не ноль, мы затем находим предел числителя. Используя закон произведения, степенной закон, разностный закон, постоянный множественный закон и закон тождества, 92}=2 \номер \]

Основные понятия

Для изучения пределов и непрерывности функций двух переменных мы используем диск $δ$ с центром вокруг заданной точки.
Функция многих переменных имеет предел, если для любой точки шара $δ$ с центром в точке $P$ значение функции в этой точке сколь угодно близко к фиксированному значению (предельное значение ).
Предельные законы, установленные для функции одной переменной, имеют естественное распространение на функции более чем одной переменной.
Функция двух переменных непрерывна в точке, если в этой точке существует предел, функция существует в этой точке и предел и функция в этой точке равны.

Глоссарий

граничная точка: точка $P_0$ в $R$ является граничной точкой, если каждый $δ$ круг с центром в $P_0$ содержит точки как внутри, так и вне $R$

закрытый набор: множество $S$, содержащее все его граничные точки 93\), лежащие на расстоянии менее $δ$ от $(x_0,y_0,z_0)$

внутренняя точка: точка $P_0$ в $\mathbb{R}$ является граничной точкой, если существует диск $δ$ с центром в $P_0$, полностью содержащийся в \(\mathbb{R}\ )

открытый набор: множество $S$, не содержащее ни одной из своих граничных точек

регион: открытое связное непустое подмножество $\mathbb{R}^2$

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Лицензия
CC BY-NC-SA
Показать страницу TOC
да
Включено
да
Теги
1. расчет: да

Математика | Пределы, непрерывность и дифференцируемость

Читать

Обсуждать

Практика

Видео

Курсы

Улучшить статью

Сохранить статью

1.

Пределы –

Для функции пределом функции в точке является значение, которого функция достигает в точке, очень близкой к .

Формально
Позвольте быть функцией, определенной на некотором интервале, содержащем , за исключением того, что она не может быть определена в этой точке.
Мы говорим, что если для каждого числа существует такое число, что
всякий раз, когда

Концепция предела поясняется графически на следующем изображении –

Как видно из приведенного выше рисунка, к пределу можно подойти с любой стороны числовой прямой, т. е. предел можно определить в терминах числа меньше или в терминах числа больше . Используя этот критерий, существует два типа пределов –
Левосторонний предел – Если предел определяется с помощью числа, которое меньше, то считается, что предел является левым пределом. Обозначается как, что эквивалентно где и .
Правый предел – Если предел определяется в виде числа, которое больше, чем предел, то говорят, что он является правым пределом. Обозначается как, что эквивалентно где и .

Существование предела — Предел функции at существует только тогда, когда ее левый и правый пределы существуют, равны и имеют конечное значение, т.е. ‘Правило больницы —
Если данный предел имеет вид или, т.е. оба и равны 0 или оба и равны , то предел может быть решен с помощью Правила больницы .
Если предел имеет вид, описанный выше, то Правило Больницы гласит, что –

где и получено дифференцированием и .
Если после дифференцирования форма все еще существует, то правило можно применять непрерывно, пока форма не будет изменена.

Example 1 – Evaluate
Solution – The limit is of the form , Using L’Hospital Rule and differentiating numerator and denominator
Example 2 – Evaluate
Решение – При умножении и делении на и переписывании предела получаем –

изгиб.

Пример 1 – При каком значении функция, определяемая числом

, непрерывна при ?
Решение – Чтобы функция была непрерывной, левый предел, правый предел и значение функции в этой точке должны быть равны.
Значение функции в точке

Правый предел-

RHL равно значению функции в точке 0-
Пример 2 – Найти все точки разрыва функции, определяемой –
.
Решение – Возможные точки разрыва, так как в этих точках меняется знак модуля.
для непрерывности AT,
LHL-

RHL

Стоимость

, LHANT = RONVER IS-FERNOUAL.

ПХЛ

Значение при ,

Поскольку LHL = RHL = , функция непрерывна при
Таким образом, точки разрыва нет.

3. Дифференцируемость –

Производная действительнозначной функции по функции и определяется как –

Функция называется дифференцируемой , если производная функции существует во всех точках ее домен. Для проверки дифференцируемости функции в точке должно существовать
.

Если функция дифференцируема в точке, то она и непрерывна в этой точке.
Примечание – Если функция непрерывна в какой-либо точке, это не означает, что эта функция также дифференцируема в этой точке. Например, непрерывно в, но не дифференцируемо в этой точке.

Угловые вопросы GATE CS

Ответы на следующие вопросы помогут вам проверить свои знания. Все вопросы были заданы в GATE в предыдущие годы или в пробных тестах GATE.