Как найти корни квадратного уравнения по теореме виета: § Как решать уравнения по теореме Виета

Содержание

§ Как решать уравнения по теореме Виета

После того, как вы внимательно изучите, как решать квадратные уравнения обычным образом с помощью формулы для корней можно рассмотреть другой способ решения квадратных уравнений — с помощью теоремы Виета.

Перед тем, как изучить теорему Виета, хорошо потренируйтесь в определении коэффициентов «a», «b» и «с» в квадратных уравнениях. Без этого вам будет трудно применить теорему Виета.

Когда можно применить теорему Виета

Не ко всем квадратным уравнениям имеет смысл использовать эту теорему. Применять теорему Виета имеет смысл только к приведённым квадратным уравнениям.

Запомните!

Приведенное квадратное уравнение — это уравнение, в котором старший коэффициент «a = 1». В общем виде приведенное квадратное уравнение выглядит следующим образом:

x² + px + q = 0

Обратите внимание, что разница с обычным общим видом квадратного уравнения «ax

2 + bx + c = 0» в том, что в приведённом уравнении «x² + px + q = 0» коэффициент «а = 1».

Если сравнить приведенное квадратное уравнение «x² + px + q = 0» с обычным общим видом квадратного уравнения «ax² + bx + c = 0», то становится видно,
что «p = b», а «q = c».

Теперь давайте на примерах разберем, к каким уравнениям можно применять теорему Виета, а где это не целесообразно.

Уравнение	Коэффициенты	Вывод
x² − 7x + 1 = 0	a = 1 p = −7 q = 1	Так как «a = 1» можно использовать теорему Виета.
3x² − 1 + x = 0 Приведем уравнение к общему виду: 3x² + x − 1 = 0	a = 3 p = 1 q = −1	Так как «a = 3» не следует использовать теорему Виета.
−x² = −3 + 2x Приведем уравнение к общему виду: −x² + 3 − 2x = 0 −x² − 2x + 3 = 0	a = −1 p = −2 q = 3	Так как «a = −1» не следует использовать теорему Виета.

Теперь мы готовы перейти к самому методу Виета для решения квадратных уравнений.

Запомните!

Теорема Виета для приведённых квадратных уравнений «x² + px + q = 0» гласит что справедливо следующее:

	x₁ + x₂ = −p
	x₁ · x₂ = q

, где «x₁» и «x₂» — корни этого уравнения.

Чтобы было проще запомнить формулу Виета, следует запомнить:
«Коэффициент «p» — значит плохой, поэтому он берется со знаком минус».

Рассмотрим пример.

x² + 4x − 5 = 0

Так как в этом уравнении «a = 1», квадратное уравнение считается приведённым, значит, можно использовать метод Виета. Выпишем коэффициенты «p» и «q».

p = 4
q = −5

Запишем теорему Виета для квадратного уравнения.

	x₁ + x₂ = −4
	x₁ · x₂ = −5

Методом подбора мы приходим к тому, что корни уравнения «x₁ = −5» и «x₂ = 1». Запишем ответ.

Ответ: x₁ = −5; x₂ = 1

Рассмотрим другой пример.

x² + x − 6 = 0

Старший коэффициент «a = 1» поэтому можно применять теорему Виета.

	x₁ + x₂ = −1
	x₁ · x₂ = −6

Методом подбора получим, что корни уравнения «x₁ = −3» и «x₂ = 2». Запишем ответ.

Ответ: x₁ = −3; x₂ = 2

Важно!

Если у вас не получается решить уравнение с помощью теоремы Виета, не отчаивайтесь. Вы всегда можете решить любое квадратное уравнение, используя формулу для нахождения корней.

Деление уравнение на первый коэффициент

Рассмотрим уравнение, которое по заданию требуется решить, используя теорему Виета.

2x² − 16x − 18 = 0

Сейчас в уравнении «a = 2», поэтому перед тем, как использовать теорему Виета нужно сделать так, чтобы «a = 1».

Для этого достаточно разделить все уравнение на «2». Таким образом, мы сделаем квадратное уравнение приведённым.

2x² − 16x − 18 = 0 | (:2)
2x²(:2) − 16x(:2) − 18(:2) = 0
x² − 8x − 9 = 0

Теперь «a = 1» и можно смело записывать формулу Виета и находить корни методом подбора.

	x₁ + x₂ = −(−8)
	x₁ · x₂ = −9

	x₁ + x₂ = 8
	x₁ · x₂ = −9

Методом подбора получим, что корни уравнения «x₁ = 9» и «x₂ = −1». Запишем ответ.

Ответ: x₁ = 9; x₂ = −1

Бывают задачи, где требуется найти не только корни уравнения, но и коэффициенты самого уравнения. Например, как в такой задаче.

Корни «x₁» и «x₂» квадратного уравнения «x² + px + 3 = 0» удовлетворяют условию «x₂ = 3x₁». Найти «p», «x₁», «x₂».

Запишем теорему Виета для этого уравнения.

x² + px + 3 = 0

	x₁ + x₂ = −p
	x₁ · x₂ = 3

По условию дано, что «x₂ = 3x₁». Подставим это выражение в систему вместо «x₂».

	x₁ + 3x₁ = −p
	x₁ · 3x₁ = 3

	4x₁ = −p
	3x₁² = 3 \|(:3)

	4x₁ + p = 0
	x₁² = 1

	p = −4x₁
	x₁² = 1

Решим полученное квадратное уравнение «x₁² = 1» методом подбора и найдем «x₁».

x₁² = 1

(Первый корень) x₁ = 1
(Второй корень) x₁ = −1

Мы получили два значения «x₁». Для каждого из полученных значений найдем «p» и запишем все полученные результаты в ответ.

(Первый корень) x₁ = 1
Найдем «x₂»
x₁ · x₂ = 3
1 · x₂ = 3
x₂ = 3
Найдем «p»
x₁ + x₂ = −p
1 + 3 = −p
4 = −p
p = −4;

(Второй корень) x₁ = −1
Найдем «x₂»
x₁ · x₂ = 3
−1 · x

2 = 3
−x₂ = 3 | ·(−1)
x₂ = −3
Найдем «p»
x₁ + x₂ = −p
−1 + −3 = −p
−4 = −p
p = 4

Ответ: (x₁ = 1; x₂ = 3; p = −4) и (x₁ = −1; x₂ = −3; p = 4)

Теорема Виета в общем виде

В школьном курсе математики теорему Виета используют только для приведённых уравнений, где старший коэффициент «a = 1», но, на самом деле, теорему Виета можно применить к любому квадратному уравнению.

В общем виде теорема Виета для квадратного уравнения выглядит так:

	x₁ + x₂ =
	x₁ · x₂ =

Убедимся в правильности этой теоремы на примере. Рассмотрим неприведённое квадратное уравнение.

3x² + 3x − 18 = 0

Используем для него теорему Виета в общем виде.

	x₁ + x₂ =
	x₁ · x₂ =

	x₁ + x₂ = −1
	x₁ · x₂ = −6

Методом подбора получим, что корни уравнения «x₁ = −3» и «x₂ = 2». Запишем ответ.

Ответ: x₁ = −3; x₂ = 2

В заданиях школьной математики мы не рекомендуем использовать теорему Виета в общем виде.

Другими словами, реальную пользу теорема Виета приносит только для приведённых квадратных уравнений, в которых «a = 1». Именно в таких случаях она не усложняет жизнь, а позволят без дополнительных расчетов быстро найти корни.

8.2.3. Теорема Виета.

Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 9.6k. Опубликовано 25 февраля 2013

I. Теорема Виета для приведенного квадратного уравнения.

Сумма корней приведенного квадратного уравнения x²+px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

x₁+x₂=-p; x₁∙x₂=q.

Найти корни приведенного квадратного уравнения, используя теорему Виета.

Пример 1) x²-x-30=0. Это приведенное квадратное уравнение ( x²+px+q=0), второй коэффициент p=-1, а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.

Находим дискриминант D=b²— 4ac=(-1)²-4∙1∙(-30)=1+120=121=11².

Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). Тогда:

x₁+x₂=1; x₁∙x₂=-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30, а сумма – единице. Это числа -5 и 6. Ответ: -5; 6.

Пример 2) x²+6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8. Убедимся, что есть целочисленные корни. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=3²-1∙8=9-8=1=1². Дискриминант D₁является полным квадратом числа 1, значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6, а произведение корней равно q=8. Это числа -4 и -2.

На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.

Пример 3) x²+2x-4=0. В этом приведенном квадратном уравнении второй коэффициент р=2, а свободный член q=-4. Найдем дискриминант D₁, так как второй коэффициент – четное число. D₁=1²-1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод: корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам для частного случая с четным вторым коэффициентом). Получаем:

Пример 4). Составьте квадратное уравнение по его корням, если x₁=-7, x₂=4.

Решение. Искомое уравнение запишется в виде: x²+px+q=0, причем, на основании теоремы Виета –p=x₁+x₂=-7+4=-3 → p=3; q=x₁∙x₂=-7∙4=-28. Тогда уравнение примет вид: x²+3x-28=0.

Пример 5). Составьте квадратное уравнение по его корням, если:

II. Теорема Виета для полного квадратного уравнения ax²+bx+c=0.

Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:

x₁+x₂=-b/a; x₁∙x₂=c/a.

Пример 6). Найти сумму корней квадратного уравнения 2x²-7x-11=0.

Решение.

Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D=7²-4∙2∙(-11)>0. А теперь воспользуемся теоремой Виета для полных квадратных уравнений.

x₁+x₂=-b:a=- (-7):2=3,5.

Пример 7). Найдите произведение корней квадратного уравнения 3x²+8x-21=0.

Решение.

Найдем дискриминант D₁, так как второй коэффициент (8) является четным числом. D₁=4²-3∙(-21)=16+63=79>0. Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x₁∙x₂=c:a=-21:3=-7.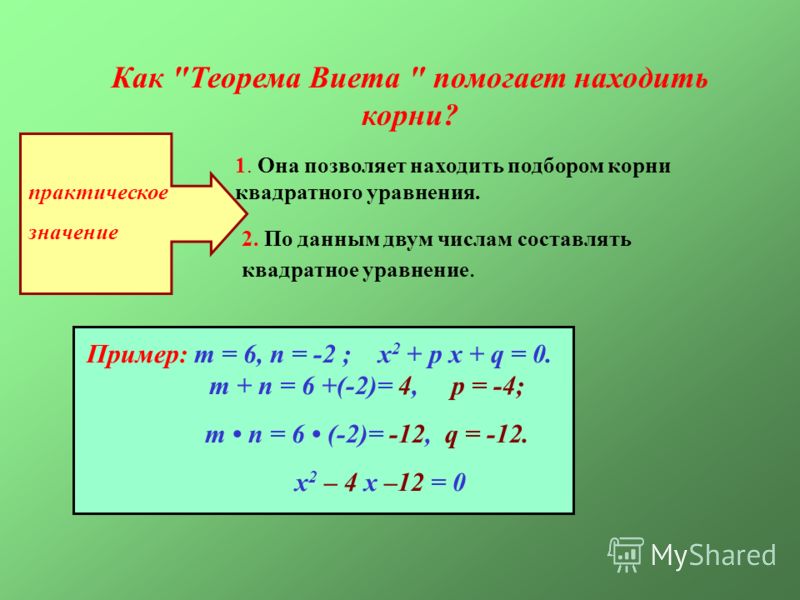

Формула Виета — GeeksforGeeks

Алгебра является одним из основных разделов математики. Многочлены являются неотъемлемой частью алгебры. Формула Виета используется в многочленах. Эта статья о формуле Виета, которая связывает сумму и произведение корней с коэффициентом многочлена. Эта формула специально используется в алгебре.

Формула Виета

Формулы Виета – это те формулы, которые обеспечивают соотношение между суммой и произведением корней многочлена на коэффициенты многочленов. Формула Виета описывает коэффициенты многочлена в виде суммы и произведения его корня.

Формула Виета имеет дело с суммой и произведением корней и коэффициентом многочлена. Он используется, когда нам нужно найти многочлен, когда даны корни, или мы должны найти сумму или произведение корней.

Формула Виета для квадратного уравнения

Если f(x) = ax ² + bx + c является квадратным уравнением с корнями α и β Сумма корней
αum = 9 корней
α β = -б/а
Произведение корней = αβ = c/a
Если сумма и произведение корней заданы, то квадратное уравнение будет иметь вид:
x ² – (сумма корней)x + ( product of roots) = 0
Vieta’s Formula for the Cubic Equation
If f(x) = ax ³ + bx ² + cx +d is a quadratic equation with roots α, β и γ затем,
Сумма корней = α + β + γ = -b/a
Сумма произведения двух корней = αβ + αγ + βγ = c/a
Произведение корней = αβγ = -d/ a
Если сумма и произведение корней даны, кубическое уравнение будет иметь вид: x – (произведение корней) = 0

Формула Виета для обобщенного уравнения
Если f(x) = a _n x ⁿ + a _n-1 x ^n-1 + a _n-2 x ^{n-2 … + a 900. .. ₂ x ² + A ₁ x + A ₀}-это квадратное уравнение с корнями R ₁, R ₂, R ₃, …… R _{N-198, R ₃, …… R _{N-1988, R ₃, …… r _n}} затем,
r ₁ + r ₂ + r ₃ +………. + r _n-1 + r _n = -a _N-1 /A _N
(R ₁ R ₂ + R ₁ R ₃ +…. + R ₁ R _N) + (R ₁ R _N) + (R ₁ R _N) + (R ₁ R _N) + (R ₁ R _N) + (R ₁ R _{N _{) + (R ₁ R _N) + (R ₁ R _N + (R ₁ R _. R ₃ + R ₂ R ₄ + ……. + R ₂ R _N) + ……… + R _N-1 R _N = _N-2 N-} R _N = _N-2 N-} R _{= _N-2 R} R /A _N
:
:
R ₁ R ₂… R _N = (-1) ^N (A ₀ /a _n )

Примеры задач
Задача 1. Если α , β корни уравнения : x ² – 10x + 5 = 0 (α , то найти значение ² + β ² )/(α ² β + αβ ² ).
Решение:
Уравнение Уравнение: x ² -10x + 5 = 0
Формула Vieta
α + β = -B/A = -(10)/1 = 10
αβ = с/а = 5/1 = 5
AS (α ² + β ²) = (α + β) ² — 2αβ
= (10) ² — 2 × 5
= 100 — 10 0003
(α 2
= 100 — 100003
(α ^{2 2}
= 100 — 100003
(α 2
= 100 — 100003
(α 2
= 100 — 100003
(α 2
= 100 — 10 0003
+ β ²) = 90
Теперь значение (α ² + β ²)/(α ² β + αβ ²)
= (α ² + β ²⁹⁰⁰³
= (α ² + β ^{2 ^{2 9003}}
= (α ² + β ^{2 ⁾}
= (α ² + β ^{2 ^). )/(αβ(α + β))
= 90/(5×10)
= 90/50
= 1,8}
Задача 2. Если α , β являются корнями уравнения : х ² + 7x + 2 = 0 , затем найдите значение 14÷(1/α + 1/β).
Решение:
Данное уравнение: x ² + 7x + 2 = 0
По формуле Виета c/a = 2/1 = 2
Теперь (1/α + 1/β) = (α + β)/αβ
(1/α + 1/β) = -7/2
Сейчас значение из 14÷(1/α + 1/β)
= 14 ÷ (-7/2)
= 14 × (-2/7)
= -4
Задача 3. Если α , β являются корнями уравнения: x ² + 10x + 2 = 0 , то найдите значение (α/β + β/α).
Решение:
Уравнение: x ² + 10x + 2 = 0
Формула Ветя
α + β = -B/A = 10/1 = 10
αβ = c/α + -b/a = 10/1 = 100003
αβ = c/c/β = 10/1 = 100003
αβ = c/c = -b/a = 10/1 = 100003
αβ = c/β = -b/a = 10/1 = 100003
а = 2/1 = 2
As (α ² +β ² ) = (α + β ) ² – 2αβ
= 10 ² – 0 9 – 2 9 0 2 9 0 0 0 2 1 0 0 0 2 9 0 0
= 96
Теперь значение (α/β + β/α) = (α ² +β ² )/αβ
= 96/2
= 48 9 01
3 Задача Если α и β являются корнями уравнения и учитывая, что α + β = -100 и αβ = -20, найдите квадратное уравнение.

Решение:
Дано
Сумма корней = α + β = -1000002 х ² – (сумма корней)х + (произведение корней) = 0
х ² – (-100)х + (-20) = 0
х ² + 100х – 20 = 0
Задача 5. Если α , β и γ являются корнями уравнения и учитывая, что α + β + γ = 10, αβ + αγ + βγ = -1 и αβ γ = -6, то найдите кубическое уравнение.
Решение:
Дано,
Сумма корней = α + β + γ= 10,
Сумма произведения двух корней = αβ + αγ + βγ = -1
Произведение корней = αβγ = -6
Кубическое уравнение: = 0
x ³-10x ² + (-1) x-(-6) = 0
x ³-10x ²-x + 6 = 0
. 6: Если α , β и γ являются корнями уравнения x ³ + 1569x ² – 3 = 0, то найдите значение [(1/α) + (1/β )] ³ + [(1/γ) + (1/β )] ³ + [(1/γ) + (1/α )] ³
Решение:
2 Дано3,
2
Сумма корней = α + β + γ= -b/a = -1569/1 = -1569
Сумма произведения двух корней = αβ + αγ + βγ = c/a = 0/1 = 0
Произведение корней = αβγ = -d/a = -(-3)/1 = 3
Так как, (p ³ + q ³ + r ³ – 3pqr) = (p + q + r)( p ² +q ² + r ² – pq – qr – pr) ……(1)
Пусть, p = (1/α) + (1/β ) , q = (1/γ) + (1/β ) , r = (1/γ) + (1/α )
p + q + r = 2[(1/α) + (1/β ) + (1/γ) ] = 2(αβ + αγ + βγ)/αβγ
= 2(0/3) = 0
Из уравнения ( 1):
(стр ³ + Q ³ + R ³ — 3PQR) = 0
P ³ + Q ³ + R ³ = 3PQR
[1/α α ³ = 3PQR
[1/α α (1/α ³ = 3PQR
[1/α ³ = 3PQR
[1/α. ) + (1/β )] ³ + [(1/γ) + (1/β )] ³ + [(1/γ) + (1/α )] ³ = 3[(1 /α) + (1/β)][(1/γ) + (1/β)][(1/γ) + (1/α)]
= 3(-1/γ)(-1/α) (-1/β )
= -3/αβγ = -3/3
= -1
Задача 7. Если α и β являются корнями уравнения x ² – 3x +2 =0, тогда найдите значение α ² – β ² .
Решение:
Дано,
Сумма корней = α + β = -b/a = -(-3)/1 = 3
Произведение корней = αβγ = c/a = 2/ 1 = 2
As (α – β) ² = (α + β) ² -4αβ
(α – β) ² = (3) ² – 4(2) = 9 – 8 = 1
(α – β) = 1
Так как,
8 α – β ² = (α – β)(α + β) = (1)(3) = 3
α ² – β ² = 3
Решение квадратного уравнения с помощью теоремы Виета продолжайте ходить по кругу.

No related posts.