Как найти косинус по теореме косинусов: Калькулятор расчета стороны треугольника по теореме косинусов

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Треугольники

Теорема Пифагорав

Теорема косинусов

Теорема Пифагора

      Теорема Пифагора. В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы.

      Доказательство. Докажем, что длины сторон произвольного прямоугольного треугольника ABC (рис.1)

Рис.1

удовлетворяют равенству

c² = a² + b²

      С этой целью рассмотрим квадратквадрат со стороной, равной c, изображённый на рисунке 2.

Рис.2

      Площадь этого квадрата равна сумме площадей четырёх одинаковых прямоугольных треугольников, равных треугольнику ABC (рис.3, рис.4), и площади квадрата со стороной, равной a – b (рис.5).

Рис.3

Рис.4

Рис.5

      Поэтому справедливо равенство

что и требовалось доказать.

Теорема косинусов

      Теорема косинусов. Квадрат длины стороны треугольника равен сумме квадратов длин других сторон минус удвоенное произведение длин этих сторон на косинус угла между ними.

      Доказательство. Рассмотрим сначала треугольник ABC, у которого углы A и С – острые (рис.6).

Рис. 6

      Докажем, что длины сторон этого треугольника удовлетворяют равенству

a2 = b 2 + c 2 – – 2bc cos A

(1)

      С этой целью проведём высоту BD из вершины B (рис.7).

Рис.7

      В соответствии с определениями синуса и косинуса угла прямоугольного треугольника справедливы равенства

BD = c sin A,   AD = c cos A,   DC = b – AD = b – c cos A.

      Из теоремы Пифагора, применённой к прямоугольному треугольнику BDC, получим

a ² = BD ² + DC ² =
= c ² sin² A + (b – c cos A)² =
= c ² sin² A + b² –
– 2 bc cos A + c ² cos² A =
= b² + c ² – 2 bc cos A.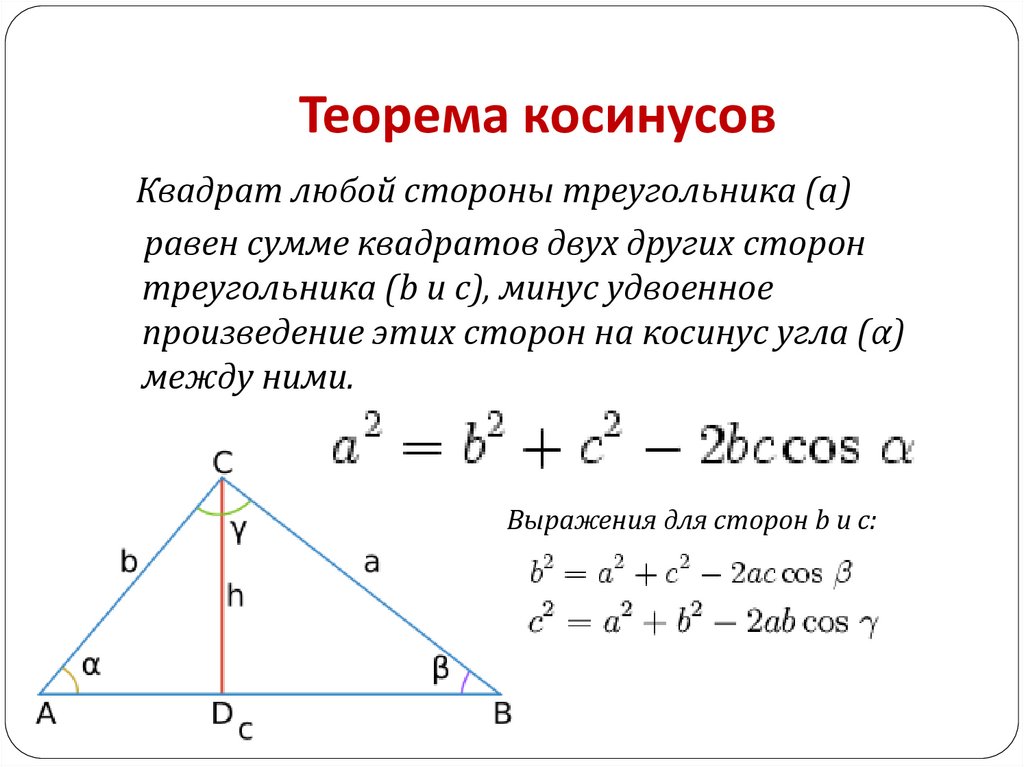

      Таким образом, в случае треугольника ABC с острыми углами A и С теорема косинусов доказана.

      Замечание 1. Для того, чтобы получить полное доказательство теоремы косинусов, необходимо рассмотреть также и следующие случаи:

1. Угол A – острый, угол C – тупой (рис.8)

   Рис.8

2. Угол A – прямой (рис. 9).

   Рис.6

3. Угол A – тупой (рис.10).

   Рис.10

      Во всех перечисленных случаях доказательства теоремы косинусов проводятся совершенно аналогично тому, как это было сделано для случая острых углов A  и C, и мы рекомендуем читателю провести эти доказательства в качестве полезного и несложного упражнения.

      Замечание 2. В случае, когда угол A является прямым углом, формула (1) принимает вид

a² = b² + c²,

откуда вытекает, что теорема Пифагора является частным случаем теоремы косинусов.

      Замечание 3. Если у треугольника известны длины всех сторон, то с помощью теоремы косинусов можно найти косинус любого угла треугольника, например,

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Теорема косинусов

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2012-12-24

Теорема косинусов и теорема Пифагора. В этой статье мы рассмотрим теорему косинусов и как она используется для нахождения элементов треугольника. А так же разберём её взаимосвязь с теоремой Пифагора.

Знать эту теорему НЕОБХОДИМО. Что мы можем найти, используя её?

Если нам будут известны две стороны и угол между ними, мы без труда найдём третью сторону. Для этого нужно просто подставить в формулу известные величины. Для других сторон всё то же самое:

Можно ли использовать теорему косинусов для нахождения третьей стороны, если известны любые две стороны и  угол, не лежащий между этими сторонами? Например, нам известны стороны a и b и угол альфа. Тогда из формулы

мы можем найти сторону «с».  Приводим к виду:

То есть, мы получаем квадратное уравнение с переменной «с» (все остальные величины нам известны). Решив его, получим искомую сторону.

Мы можем найти любой угол, если нам известны все три стороны треугольника:

Разумеется, что учить все эти формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А косинус любого угла не трудно выразить используя простые алгебраические преобразования.

*Если вы вычисляете косинус тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах получите положительное значение, то ищите ошибку.

Следующий вопрос: а если нам дана сторона и любые два угла, что делать? В этом случае теорема косинусов не используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из следующих статей, не пропустите!

Если вы будете  в совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением  треугольников (в большинстве задач).

Следующий факт знают все, но всё же о взаимосвязи  теоремы косинусов с теоремой Пифагора  сказать стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то получим:

То есть, по сути, теорема Пифагора это как бы частный случай теоремы косинусов.

Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями:

По теореме косинусов:

Так как угол С равен 90, то

Напомню, что зная любые две стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без труда можем  найти значение любой тригонометрической функции острого угла в нём. Можете изучить статью об этом.

Получить материал статьи в формате PDF

На этом всё. Успехов вам!!!

С уважением, Александр Крутицких. 

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Формулы Теория | ТреугольникФормулы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Объяснение урока: закон косинусов

В этом объяснении мы научимся находить стороны и углы в непрямоугольных треугольниках, используя закон косинусов.

Закон косинусов, также известный как правило косинусов, позволяет нам связать все три стороны треугольник с одним из его углов.

Определение: Закон косинусов

Рассмотрим треугольник 𝐴𝐵𝐶 с соответствующими длинами сторон 𝑎, 𝑏 и 𝑐. Для этого треугольника каждый сторона была помечена строчной буквой противоположного угла.

Закон косинусов говорит нам, что Теорема Пифагора. Чтобы убедиться в этом, рассмотрим произвольный треугольник с углом 𝐴=90∘.

Вводя это значение в закон косинусов, мы видим, что наш окончательный член принимает вид 2𝑏𝑐⋅90cos∘: 𝑎=𝑏+𝑐−2𝑏𝑐⋅90.∘cos

Поскольку мы знаем, что cos90=0∘, мы можем см., что последний член исчезнет из нашего уравнения: 𝑎=𝑏+𝑐−2𝑏𝑐⋅0𝑎=𝑏+𝑐.

Здесь мы видим, что для частного случая прямоугольного треугольника закон косинусов сводит по теореме Пифагора, где длина стороны 𝑎 определяется как гипотенуза.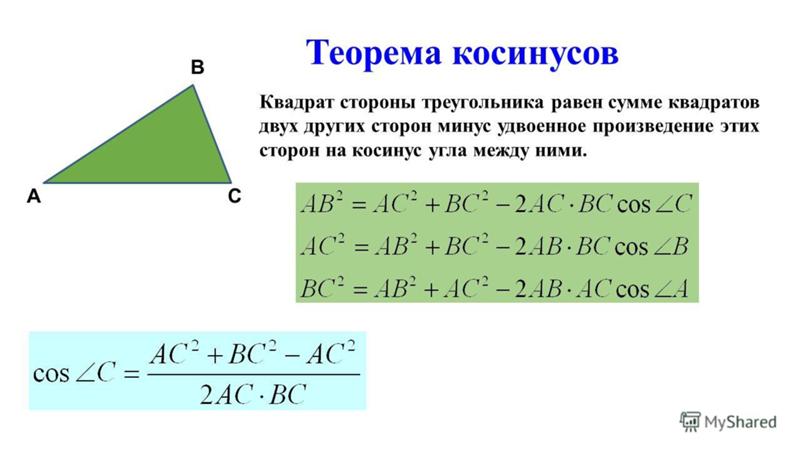

Закон косинусов можно использовать в нескольких разных случаях. Первый случай – при нахождении неизвестная длина стороны, если заданы противоположный угол и длины двух соседних сторон. Ты может увидеть угол, называемый в этой ситуации «закрытым углом».

Понимание каждого из условий поможет нам правильно использовать правило косинусов: 𝐴⟹, 𝑎⟹, 𝑏⟹, 𝑐⟹.угол, замкнутый двумя известными сторонами сторона, противоположная0003

В этом случае мы решили наблюдать соотношение между длинами сторон с относительно вложенного угла 𝐴. Стоит отметить, что закон косинусов можно применить к треугольнику относительно любых его углов.

Вместо этого мы могли бы наблюдать соотношение между длинами сторон по отношению к любому из оставшиеся два угла (нижний левый и нижний правый на диаграмме), просто переобозначив наш треугольник, чтобы соответствовать известной информации.

Давайте теперь посмотрим на несколько примеров, где закон косинусов используется для нахождения неизвестной длины в треугольнике.

Пример 1: Использование закона косинусов для вычисления неизвестной длины в треугольнике

𝐴𝐵𝐶 — это треугольник, где 𝐵𝐶=25см, 𝐴𝐶=13см, и 𝑚∠𝐶=142∘. Найдите длину 𝐴𝐵, дающую ответ с точностью до трех знаков после запятой.

Ответ

Часто набросок треугольника может быть полезен для визуализации такого типа задач. (схема не в масштабе).

Глядя на наш треугольник, мы видим, что у нас есть две длины сторон, 𝐵𝐶 и 𝐴𝐶, и вложенный угол, 𝐶. Эта ситуация говорит нам, что мы можем использовать закон косинусов: 𝑎=𝑏+𝑐−2𝑏𝑐⋅𝐴.cos

Мы можем определить значения нашего треугольника по закону косинусов, начиная с закрытым углом. Таким образом, последний член нашего уравнения будет содержать следующий элемент: coscos𝐴⟹142.∘

При необходимости неизвестная длина стороны, 𝐴𝐵, находится напротив заключенного угол. Поэтому мы определяем длины сторон следующим образом: 𝑎⟹𝐴𝐵,𝑏⟹25,𝑐⟹13.0003

Подставляя эти значения в закон косинуса, находим следующее уравнение: 𝐴𝐵=25+13−2(25)(13)⋅142.∘cos

Наконец, мы можем упростить и извлечь квадратный корень из обеих частей нашего уравнения. Мы можем также игнорировать отрицательное решение нашего квадратного корня, так как мы решаем найти длина: 𝐴𝐵=√1306,2069…=36,14148…≈36,141.см

Наш ответ округлен до трех знаков после запятой, как того требует вопрос.

Пример 2. Использование закона косинусов для вычисления неизвестной длины в треугольнике

𝐴𝐵𝐶 — треугольник, где 𝑎=13см, 𝑏=10см, и cos𝐶=0,2. Найдите значение 𝑐, дающее ответ до трех знаков после запятой.

Ответ

При решении задач такого типа может быть полезно начертить треугольник, как показано ниже (не в масштабе).

Глядя на наш треугольник, мы видим, что у нас две длины сторон, 𝑎 и 𝑏, а также тригонометрическая оценка для вложенного угла, 𝐶.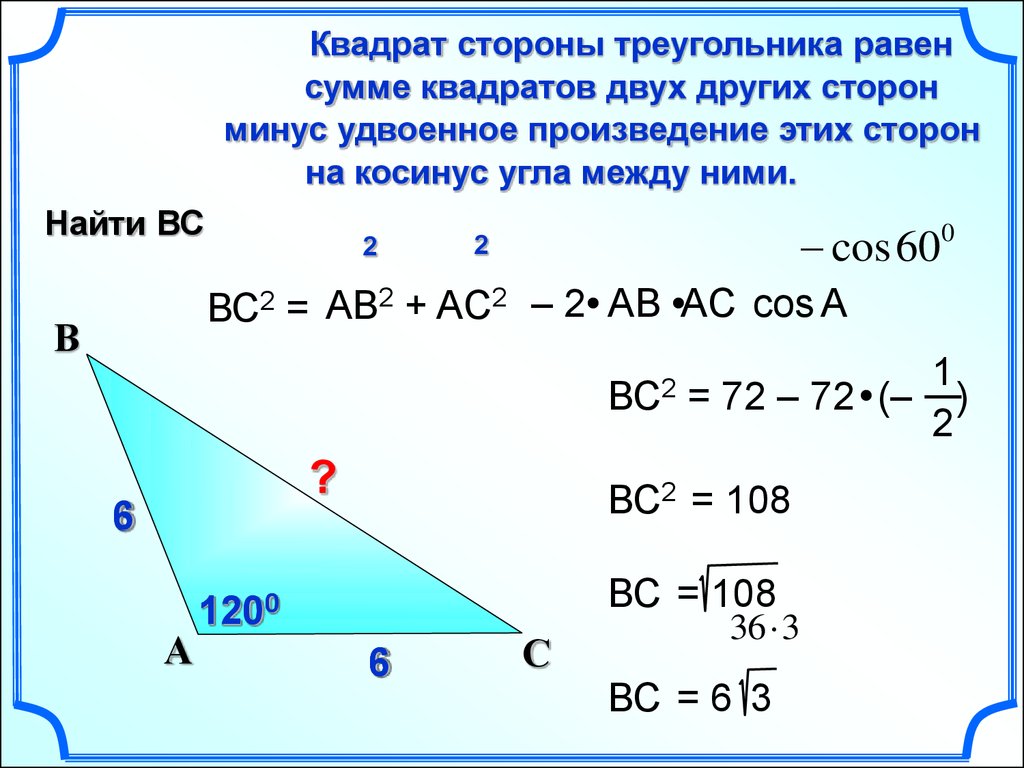 Эта ситуация говорит нам, что мы можем использовать закон косинусов: 𝑐=𝑎+𝑏−2𝑎𝑏⋅𝐶.cos

Подставляя эти значения в закон косинусов, находим следующее уравнение: 𝑐=13+10−2(13)(10)⋅0,2.

Упрощая наше уравнение и решая 𝑐, получаем следующую сторону длину, которую мы округлим до трех знаков после запятой: 𝑐=√217=14,73091…≈14,731,см

Теперь рассмотрим второй случай, когда закон косинусов можно использовать для решения проблемы. Вопросы, которые мы рассматривали до сих пор, включали в себя нахождение неизвестной длины стороны, когда учитывая его противоположный угол и длины двух смежных сторон.

Теперь рассмотрим новый случай, когда у нас есть треугольник с длинами сторон 𝑎, 𝑏 и 𝑐, и мы хотим найти неизвестный угол 𝐴.

Как изменить закон косинусов

Чтобы помочь нам решить эту задачу, мы можем преобразовать наше текущее уравнение в более удобное форма. Для начала мы можем добавить 2𝑏𝑐⋅𝐴cos к обеим частям закона косинусы: 𝑎=𝑏+𝑐−2𝑏𝑐⋅𝐴𝑎+2𝑏𝑐⋅𝐴=𝑏+𝑐. coscos

Теперь мы можем вычесть 𝑎 из обеих частей: 2𝑏𝑐⋅𝐴=𝑏+𝑐−𝑎.cos

Наконец, мы можем разделить обе стороны на 2𝑏𝑐, что даст нам косинус угла 𝐴 через длины сторон нашего треугольника: cos𝐴=𝑏+𝑐−𝑎2𝑏𝑐.

В этом примере мы выбрали угол 𝐴; однако эта форма по закону косинусов можно найти любой из углов треугольника, наблюдая следующие отношения между переменными:0003

Пример 3. Использование закона косинусов для вычисления угла в треугольнике

𝐴𝐵𝐶 — треугольник, где 𝑎=12см, 𝑏=20см, и 𝑐=26см. Найдите наименьший угол в 𝐴𝐵𝐶, дающий ответ на ближайший второй.

Ответ

Как и в большинстве задач этого типа, может быть полезно начертить треугольник (не масштаб), чтобы помочь визуализировать проблему.

Мы знаем, что для любого треугольника наименьшая сторона будет противоположна наименьшей угол.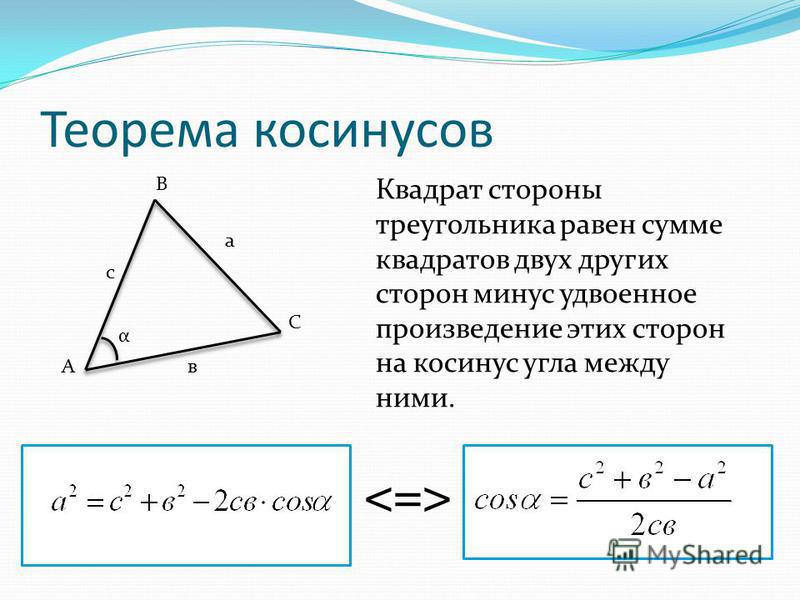

Проверяя длины наших сторон, мы видим, что 𝑎𝑏𝑐. Мы можем поэтому делаем вывод, что угол 𝐴 наименьший, так как он является противоположной стороной 𝑎.

Чтобы найти 𝐴, мы можем использовать следующую форму закона косинусы: cos𝐴=𝑏+𝑐−𝑎2𝑏𝑐. Тогда наши длины сторон принимают следующие значения: 𝑎⟹12,𝑏⟹20,𝑐⟹26.cmcmcm

Подставляя эти значения в закон косинусов, находим следующее уравнение: cos𝐴=20+26−12(2)(20)(26). Затем мы можем умножить каждый из членов и упростить правая часть уравнения: cos𝐴=400+676−1441040=233260.

Наконец, найдем угол 𝐴: 𝐴=233260=26,342975….cos∘

Теперь мы нашли 𝐴 в градусах; однако вопрос требует, чтобы мы дали решение ближайшая секунда. Для этого можно вспомнить следующее соотношение между градусы (∘), минуты (′) и секунды (′′). 1=60′,1′=60′′.∘

Глядя на наше решение, мы видим, что 𝐴=26∘ с остатком 0,342975…∘.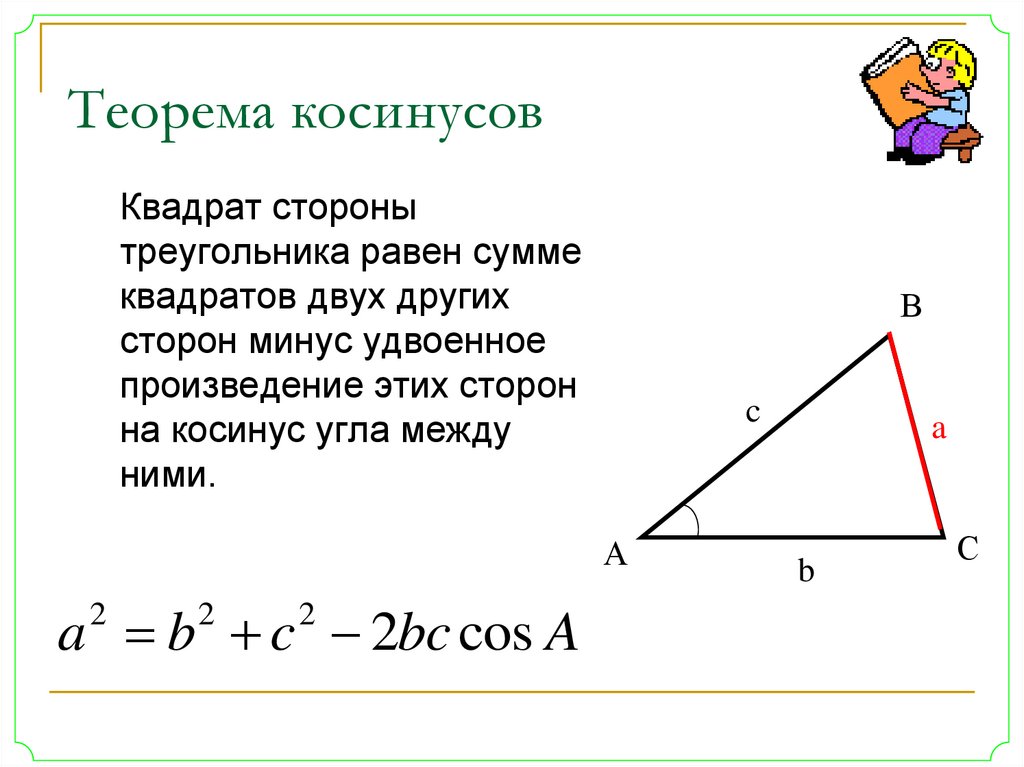 Мы можем умножить этот остаток на 60, чтобы найдем количество минут в нашем решении: 60×0,342975…=20,578532′.∘

Используя тот же метод, мы видим, что этот остаток содержит 20′ с остатком 0,578532…′. Снова умножив это на 60, мы можем вычислить количество секунд: 60×0,578532…′=34,711959…≈35.

Теперь мы можем записать наше решение с точностью до секунды: 𝐴=2620′35′′.∘

Некоторые вопросы могут потребовать использования комбинации обеих форм закона косинусов в чтобы решить треугольник. Теперь мы рассмотрим примеры, где уравнение используется как в формируется последовательно.

Пример 4. Использование закона косинусов для нахождения неизвестных углов и длин треугольника

𝐴𝐵𝐶 — это треугольник, где 𝑎=28см, 𝑏=17см, и 𝑚∠𝐶=60∘. Найдите недостающую длину, округленную до трех знаков после запятой, и округленные недостающие углы.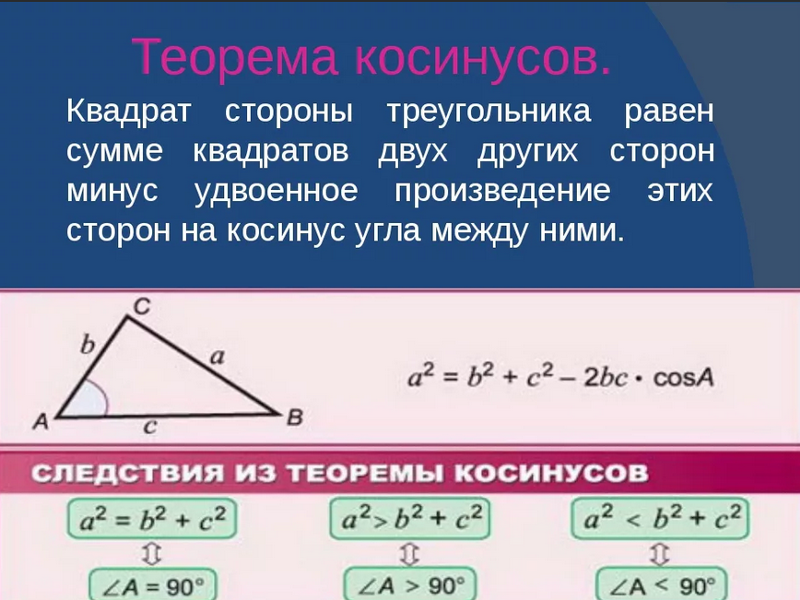

до ближайшей степени.

Ответ

Сначала мы набросаем наш треугольник, чтобы визуализировать проблему.

При осмотре мы видим, что наш треугольник содержит один известный угол, заключенный между две известные длины сторон: 𝐶⟹, 𝑐⟹, 𝑎⟹, 𝑏⟹. угол, заключенный двумя известными сторонами, является стороной, противоположной замкнутому углу0003

Эта ситуация говорит нам, что мы можем использовать первую форму закона косинусов. Используя это виде уравнения, мы можем сформулировать связь между углом 𝐶 и три стороны нашего треугольника: 𝑐=𝑎+𝑏−2𝑎𝑏⋅𝐶.cos

Теперь мы можем подставить известную информацию из нашего треугольника: 𝑐=28+17−2(28)(17)⋅60.∘cos

Затем мы оцениваем каждый отдельный член в правой части нашего уравнения и упростить его. При этом мы можем признать, что cos60∘ одно из точных тригонометрических соотношений: 𝑐=784+289−952⋅12=597.



Теперь мы можем извлечь квадратный корень из обеих частей нашего уравнения, игнорируя отрицательное решение, так как мы решаем найти длину, 𝑐. Округляем ответ до трех знаков после запятой, как указано в вопросе: 𝑐=√597=24,433583…≈24,434.

Давайте теперь перерисуем наш треугольник с вновь найденной информацией.

Теперь у нас есть треугольник с тремя известными сторонами и одним известным углом. Чтобы найти любой из двух оставшихся углов, мы можем использовать вторую форму закона косинусов. Позволять найдем угол 𝐴, используя следующее уравнение: cos𝐴=𝑏+𝑐−𝑎2𝑏𝑐.

Теперь подставим длины наших сторон в уравнение. Здесь мы решили использовать точная длина стороны 𝑐=√597 вместо округленного ответа, чтобы поддерживать точность: cos𝐴=17+√597−28(2)(17)√597.

Затем мы можем перемножить каждое из слагаемых и упростить правую часть уравнение: cos𝐴=289+597−784830,741…=102830,741….

Теперь находим 𝐴 и округляем до ближайшего градуса, как указано в вопросе: 𝐴==82,947…≈83.cos…∘∘

Наконец, мы знаем, что сумма углов в треугольнике равна 180∘. Так как два угла в треугольник теперь известен, мы можем найти третий, подставив в следующее уравнение: 𝐴+𝐵+𝐶=18082,947…+𝐵+60=180.

Находя 𝐵, мы завершаем информацию для треугольника, давая нашу окончательный ответ в ближайшей степени: 𝐵=180−82,947…−60=37,053…≈37,∘

В некоторых ситуациях мы не можем сразу использовать закон косинусов. В таких случаях, может быть необходимо сначала использовать другие геометрические методы, чтобы найти угол или длину стороны. Это позволит нам продолжить, используя один из методов, описанных выше в этом объяснитель.

Здесь мы показываем пример, используя площадь треугольника и стандартные тригонометрические методы.

Пример 5. Решение треугольника с помощью тригонометрии в сочетании с законом косинусов

𝐴𝐵𝐶 — это треугольник, где 𝐵𝐶=38см, 𝑚∠𝐴𝐶𝐵=60∘, и площадь 399√3 см ² . Найдите другие длины и углы, приведя длины к ближайшим сантиметр и углы с точностью до ближайшего минута.

Ответ

Здесь мы рисуем треугольник, используя известную информацию.

Глядя на наш треугольник, у нас есть один известный угол и длина одной из его смежных сторон. К сожалению, этой информации недостаточно, чтобы использовать закон косинусов ни в том, ни в другом случае. форма! Чтобы продолжить, нам нужно будет использовать комбинацию методов:

1. Используйте заданную площадь, чтобы найти высоту треугольника.
2. Используйте тригонометрию в сочетании с высотой треугольника, чтобы найти длину стороны (𝑏).
3. Используйте закон косинусов, чтобы найти оставшиеся неизвестные.

1. Используйте заданную площадь, чтобы найти высоту треугольника

Помимо заданного угла и длины стороны, вопрос также дает нам площадь треугольника. Вспомним формулу площади треугольника: высота базы=×2.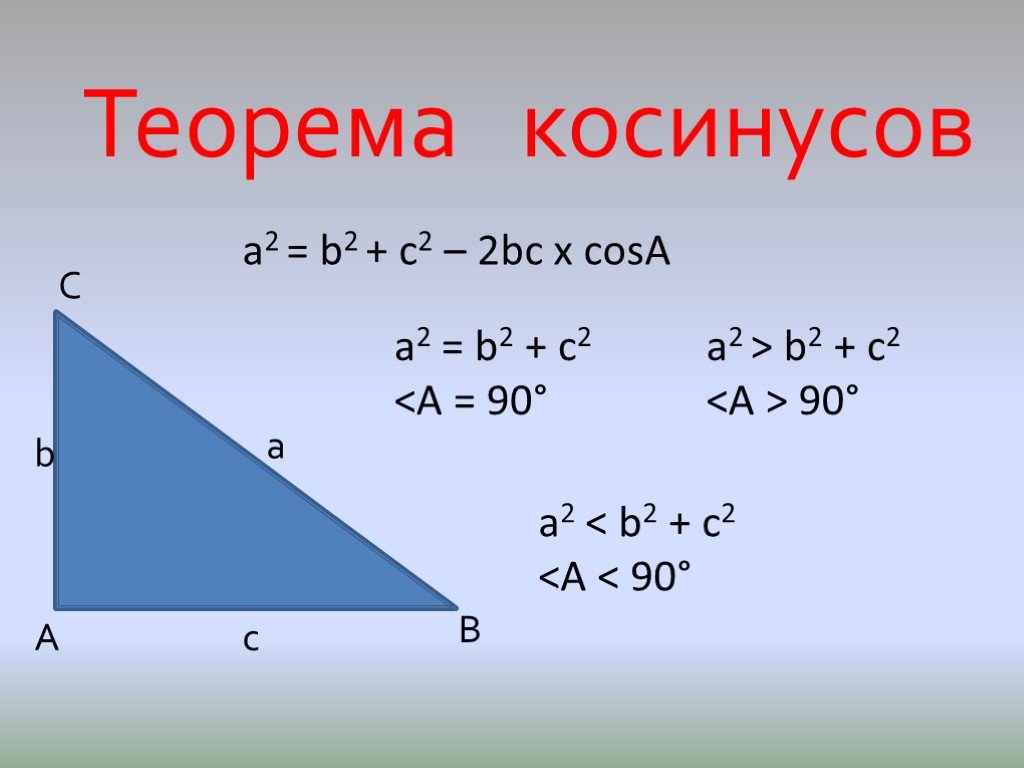 Приняв 𝐵𝐶 за основание нашего треугольника, давайте Теперь перерисуйте нашу диаграмму. Новая точка, 𝐷, была отмечена на основе треугольник прямо под точкой 𝐴. Сегмент линии 𝐴𝐷, следовательно, является перпендикулярной высотой (ℎ) треугольник.

Используя формулу площади треугольника, мы можем подставить известные данные: 399√3=38×ℎ2. Теперь мы можем решите найти ℎ, умножив обе части уравнения на 2 и деление на 38: ℎ=(2)399√338=21√3.cm

2. Используйте тригонометрию в сочетании с высотой треугольника, чтобы найти длину стороны 𝑏

Теперь, когда мы нашли высоту треугольника треугольник, давайте рассмотрим треугольник 𝐴𝐶𝐷. При осмотре мы видим, что это прямоугольный треугольник с одним неизвестным сторона (𝑏) и один известный угол (𝐶).

Таким образом, мы можем использовать правила тригонометрии, чтобы найти длину стороны 𝑏: синусопротивоположная гипотенуза𝜃=. Глядя на угол 𝐶, мы находим, что ℎ — противоположная сторона, а 𝑏 — гипотенуза. (внутри треугольника 𝐴𝐶𝐷): sin𝐶=ℎ𝑏. Мы можем подставить известную информацию и переставить наши уравнение для нахождения признавая, что sin60∘ это тогда одно из точных тригонометрических соотношений позволяет решить:𝑏=21√3=(2)21√3√3=(2)(21)=42.√см0003

Здесь мы видим наш треугольник с новой информацией.

3. Используйте закон косинусов для решения оставшихся неизвестных

Теперь, когда мы нашли 𝑏, у нас есть знакомая ситуация внутри треугольника 𝐴𝐵𝐶, где известный угол заключен между двумя известными длинами сторон: 𝐶⟹, 𝑐⟹, 𝑎⟹, 𝑏⟹. угол, заключенный двумя известными сторонами, стороной, противоположной замкнутому углу, одной из головных сторон, прилегающих к замкнутому углу. Используя первую форму закона косинусов, сформулируем отношение между углом 𝐶 и тремя сторонами нашего треугольника: 𝑐=𝑎+𝑏−2𝑎𝑏⋅𝐶.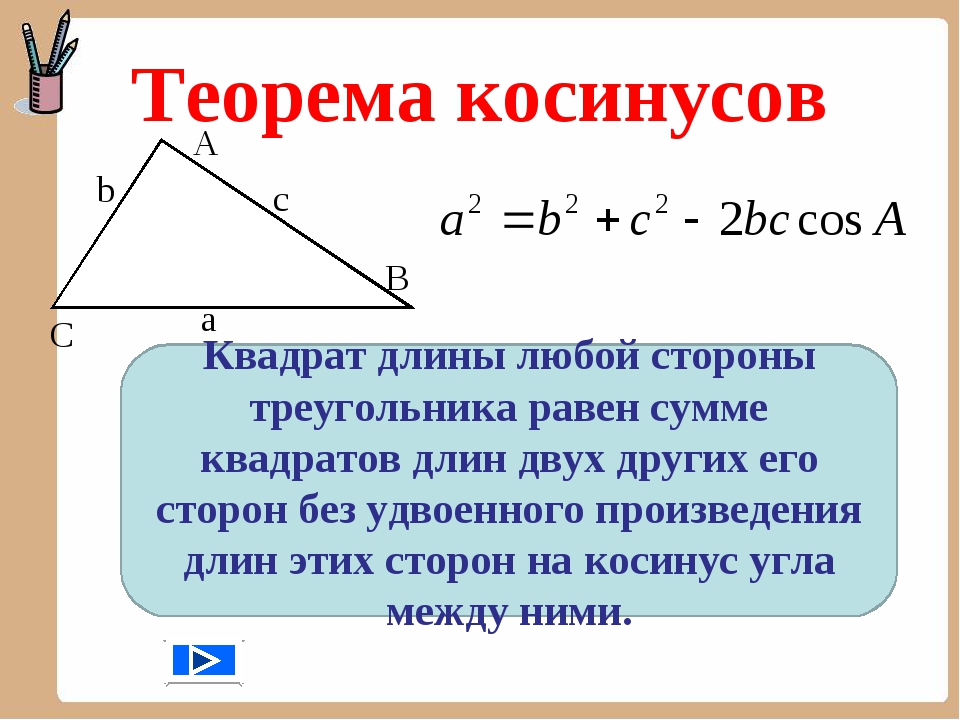 потому что мы сейчас подставляем в известную информацию из нашего треугольника: 𝑐=38+42−2(38)(42)⋅60.∘cos Далее упростим правую часть нашего уравнения, учитывая что cos60∘ одно из точных тригонометрических соотношений: 𝑐=1444+1764−3192⋅12=1612.

Теперь мы можем извлечь квадратный корень из обеих частей нашего уравнения, игнорируя отрицательное решение, так как мы решаем найти длину, 𝑐. Наш ответ округляется до одного десятичного знака, как указано в вопросе: 𝑐=√1612=40,149….

Так как нас попросили дать ответ ближайшему сантиметр, пишем 𝑏=40см.

Вторая форма закона косинусов может быть использована для нахождения любого из оставшихся углов, но давайте выберем угол 𝐵 и построим отношение, используя следующее уравнение: cos𝐵=𝑎+𝑐−𝑏2𝑎𝑐. Сначала подставим длины сторон в уравнение: cos𝐵=38+√1612−42(2)(38)√1612. Теперь мы можем найти 𝐵, упростив наши условия и возьмем арккосинус обеих сторон. Наш ответ округляется до ближайшего градуса как указано в вопросе: 𝐵=12923051,378…=64,949….cos∘

Поскольку нас попросили дать ответ ближайшему минуту, мы пишем 𝐵=553′∘.

Теперь, когда мы нашли два угла, мы можем использовать тот факт, что сумма углов в треугольнике равна 180∘ решить для 𝐴, давая наш ответ с точностью до степени: 𝐴=180−64,949…−60=55,051….

Так как нас попросили дать ответ ближайшему минуту, мы пишем 𝐴=6457′∘.

Ключевые моменты

• Закон косинусов позволяет нам связать все три стороны треугольника с одной из его сторон. углы.
• Закон косинусов можно рассматривать как обобщенную форму теоремы Пифагора и будет работать для всех треугольников.
• Чтобы найти неизвестную длину стороны треугольника по заданному противоположному углу и длины двух смежных сторон, мы можем использовать следующую форму закона косинусов: 𝑎=𝑏+𝑐−2𝑏𝑐⋅𝐴. cos
• Чтобы найти неизвестный угол в треугольнике по всем трем длинам сторон, мы можно использовать следующую переставленную форму закона косинусов: cos𝐴=𝑏+𝑐−𝑎2𝑏𝑐.

Как использовать и практические примеры – Блог Educator.com

Мы уже видели, как решать треугольники, используя закон синусов. Такие задачи включают две стороны и два угла. Закон косинусов (или правило косинусов) используется, когда задействованы все три стороны и только один угол. Формула: 9{2} – 2ab\text{cos}y[/latex]

 

• c неизвестная сторона
• a и b заданные стороны
• ? не любой угол в треугольнике, а угол между данными сторонами.

Мы используем закон косинусов для решения треугольников, которые не являются прямоугольными.

Как запомнить

Это правило очень похоже на теорему Пифагора. Если угол ? если бы угол был прямым, мы бы получили

 [latex latex size=”3″]c^2 = a^2 + b^2 – 2ab\text{cos}9\circ[/latex]

[латекс латекс размер=”3″]а = 9 + 4 – 12 * (-0,17)[/латекс]

[латекс латекс размер=”3″]а = 15,04[/латекс ]

Пример II

Найдите наибольший угол треугольника, стороны которого равны 12, 16 и 9.