Как найти максимальное значение функции: Наименьшее и наибольшее значения функции на отрезке

Наименьшее и наибольшее значения функции на отрезке

• Как найти наименьшее и наибольшее значения функции на отрезке
• Ищем наименьшее и наибольшее значения функции вместе
• Найти наименьшее и наибольшее значения функции самостоятельно, а затем посмотреть решение
• Продолжаем искать наименьшее и наибольшее значения функции вместе

На рисунках ниже показано, где функция может достигать наименьшего и наибольшего значения. На левом рисунке наименьшее и наибольшее значения зафиксированы в точках локального минимума и максимума функции. На правом рисунке — на концах отрезка.

Если функция y = f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего и наибольшего значений. Это, как уже говорилось, может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции

, непрерывной на отрезке [a, b], нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций.

Пусть, например, требуется определить наибольшее значение функции f(x) на отрезке [a, b]. Для этого следует найти все её критические точки, лежащие на [a, b].

Критической точкой называется точка, в которой функция определена, а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f(a) и f(b)). Наибольшее из этих чисел и будет

наибольшим значением функции на отрезке [a, b].

Аналогично решаются и задачи на нахождение наименьших значений функции.

Для нахождения критических точек нужно неплохо разбираться в производных и решении несложных алгебраических уравнений. В любом случае будет нужна таблица производных (откроется в новом окне), так как в примерах указано, какая именно табличная производная найдена.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2].

Решение. Находим производную (первое и второе слагаемые — табличная производная 3, третье — табличная производная 1) данной функции . Приравняем производную нулю () и, решив уравнение, получим две критические точки: и . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на концах отрезка и в точке , так как точка не принадлежит отрезку [-1, 2]. Эти значения функции — следующие: , , . Из этого следует, что

наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке , а наибольшее (тоже красное на графике), равно 9, — в критической точке .

Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.

Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо следующее свойство непрерывных функций.

Если функция непрерывна в промежутке и имеет единственный экстремум, то он является наименьшим значением в случае минимума и наибольшим — в случае максимума.

Как наименьшее значение функции, так и её наибольшее значение, могут быть найдены не только в одной точке, принадлежащей заданного интервала, а, как, например, далее — в двух.

Пример 2. Найти наименьшее и наибольшее значения функции на отрезке [-3, 3].

Решение. Находим производную (первое и второе слагаемые — табличная производная 3, третье — табличная производная 1) данной функции . Привыкаем к однообразным действиям: приравниваем производную нулю () и решение этого уравнения даёт нам три критические точки: , и . Все критические точки принадлежат отрезку [-3, 3]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и во всех критических точках. Эти значения следующие:

Видим, что функция достигает наименьшего значения, равного -13, в двух точках и и наибольшего значения, равного 12, также в двух точках и (то есть на концах отрезка).

Нередки случаи, когда уравнение, полученное от приравнивания производной функции нулю, не имеет действительных решений. Тогда наименьшее и наибольшее значения функции можно найти только на концах отрезка. Таков следующий пример.

Пример 3. Найти наименьшее и наибольшее значения функции на отрезке [0, 4].

Решение. Находим производную (первое слагаемое — табличная производная 2, второе — табличная производная 5) данной функции . Приравниваем производную нулю: . Видим, что это уравнение не имеет действительных корней. Поэтому наименьшее и наибольшее значения функции можем найти только на концах данного отрезка. Находим значения функции на концах отрезка:

Обе точки, следуя условию, годятся, так что функция достигает наименьшего значения, равного 0, в точке и наибольшего значения, равного 6, в точке .

Нет времени вникать в решение? Можно заказать работу!

Неплохо было бы взять и случаи, когда производная функции вычисляется не одним махом, как в предыдущих примерах.

Это мы сейчас и сделаем, решив пример, где требуется найти производную частного.

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3].

Решение. Находим производную данной функции как производную частного по соответствующему правилу:

.

Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Сравниваем эти значения. Вывод: функция достигает наименьшего значения

, равного -5/13, в точке и наибольшего значения, равного 1, в точке .

Пример 5. Найти наименьшее и наибольшее значения функции на отрезке .

Правильное решение и ответ.

Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .

Правильное решение и ответ.

Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .

Правильное решение и ответ.

• Страница 2 (Тренинг по нахождению критических точек функции)

Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция — многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами, поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных).

Поэтому в ход пойдут логарифм и тригонометрическая функция.

Пример 8. Найти наименьшее и наибольшее значения функции на отрезке [1, e].

Решение. Находим производную данной функции как производную произведения:

Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку [1, e]. Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Результат всех действий: функция достигает наименьшего значения, равного 0, в точке и в точке и наибольшего значения, равного e², в точке .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 9. Найти наименьшее и наибольшее значения функции на отрезке .

Решение. Находим производную (первое слагаемое — табличная производная 2, второе — табличная производная 7) данной функции:

Приравниваем производную нулю:

Единственная критическая точка принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:

Вывод: функция достигает наименьшего значения, равного , в точке и наибольшего значения, равного , в точке .

В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.

Пример 10. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?

Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S:

или

.

Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в ]0, +∞[, причём

.

Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением. Итак, сторона основания резервуара должна быть равна 2 м, а его высота .

Для самопроверки при расчётах можно воспользоваться онлайн калькулятором производных.

Пример 11. Из пункта A, находящегося на линии железной дороги, в пункт С, отстоящий от неё на расстоянии l, должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?

Пусть , , (см. рисунок ниже).

Тогда , , . Стоимость провоза p единиц груза по шоссе СМ составит , а по железной дороге МА она составит . Общая стоимость провоза груза по пути СМА выражается функцией

,

где .

Нужно найти наименьшее значение этой функции. Она дифференцируема при всех значениях x, причём

.

Приравняв производную нулю, получим иррациональное уравнение , решение которого даёт единственную критическую точку (так как точка не входит в область определения функции).

Взяв контрольные точки и слева и справа от критической точки, убедимся, что производная меняет знак с минуса на плюс. Следовательно, при стоимость провоза груза из А и С является наименьшей, если . Если же , т. е. , то шоссе должно пройти по прямой АС (см. рисунок ниже).

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Производная, дифференциал и их применение

Весь блок «Производная»

• Что такое производная
• Найти производную: алгоритм и примеры решений
• Производные произведения и частного функций
• Производная суммы дробей со степенями и корнями
• Производные простых тригонометрических функций
• Производная сложной функции
• Производная логарифмической функции
• Дифференциал функции
• Дифференциал сложной функции, инвариантность формы дифференциала
• Уравнение касательной и уравнение нормали к графику функции
• Правило Лопиталя
• Частные производные
• Применение производной к исследованию функций
• Экстремумы функции
• Асимптоты
• Возрастание, убывание и монотонность функции
• Выпуклость и вогнутость графика функции, точки перегиба
• Полное исследование функций и построение графиков
• Функции двух и трёх переменных
• Экстремумы функции двух переменных
• Условные экстремумы и функция Лагранжа

Наибольшее и наименьшее значение функции

На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно осуществить поиск и определить оптимальное значение какого-либо параметра или количество. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.

Обычно нами строится выражение этих значений в рамках некоторого интервала x, который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [a; b], так и открытый интервал (a; b), (a; b], [a; b), бесконечный интервал (a; b), (a; b], [a; b) либо бесконечный промежуток -∞; a, (-∞; a], [a; +∞), (-∞; +∞).

В этом материале мы расскажем, как найти наибольшее и наименьшее значение явно заданной функции с одной  переменной y=f(x)y=f(x), чтобы вам не нужно было искать это самостоятельно онлайн.

Основные определения

Начнем, как всегда, с формулировки основных определений: какое значение называют максимальным и минимальным?.

Определение 1

Наибольшее значение функции y=f(x) на некотором промежутке x – это значение max y=f(x0)x∈X, которое при любом значении xx∈X, x≠x0 делает справедливым неравенство f(x)≤f(x0).

Определение 2

Минимальное значение функции y=f(x) на некотором промежутке x– это значение minx∈Xy=f(x0), которое при любом значении x∈X, x≠x0 делает справедливым неравенство f(Xf(x)≥f(x0).

Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее наибольшее число, которое она может принимать на известном интервале при абсциссе x0, а наименьшее – это самое маленькое принимаемое значение на том же интервале при x0.

Определение 3

Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0.

Зачем нам нужно знать, что такое стационарные точки?  Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.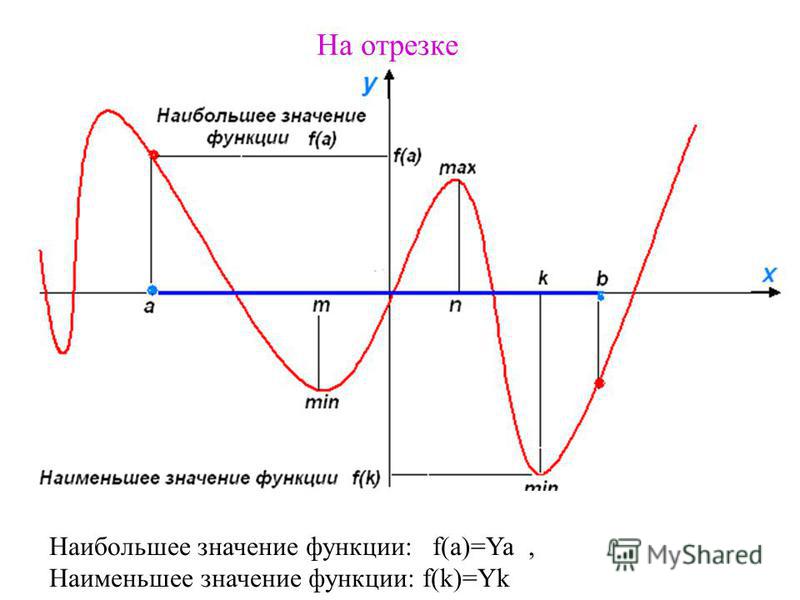 е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или то, что больше всего, значение на некотором промежутке именно в одной из стационарных точек.

Еще  функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.

Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы можем определить наибольшее или найти наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с  границами области определения, или если мы имеем дело с интервалом, не имеющим конца. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения (мало и много). В этих случаях определить или найти наибольшее и/или наименьшее значение не представляется возможным.

Более понятными эти моменты станут после изображения на графиках:

Наибольшее и наименьшее значение функции на отрезке

Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (max y и min y) в стационарных точках, расположенных на отрезке [-6;6].

Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [1;6] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.

На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [-3;2]. Они соответствуют наибольшему и наименьшему значению заданной функции.

Наибольшее и наименьшее значение функции на открытом интервале

Теперь посмотрим на четвертый рисунок. В нем функция принимает max y (наибольшее значение) и min y (наименьшее значение) в стационарных точках на открытом интервале (-6;6).

Если мы возьмем интервал [1;6), то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x, равном 6, если бы x=6 принадлежала интервалу. Именно этот случай нарисован на графике 5.

На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (-3;2], а о наибольшем значении мы не можем сделать определенных выводов.

Наибольшее и наименьшее значение функции на бесконечности

На рисунке 7 мы видим, что функция будет иметь max y в стационарной точке, имеющей абсциссу, равную 1. Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y=3.

Если мы возьмем интервал x∈2; +∞, то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2, то значения функции будут стремиться к минус бесконечности, поскольку прямая x=2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y=3. Именно этот случай изображен на рисунке 8.

Как найти наибольшее и наименьшее значение непрерывной функции на заданном отрезке

Как найти наибольшее и наименьшее значение функции на отрезке?

В этом пункте мы приведем последовательность действий, которую нужно выполнить, чтобы найти наибольшее значение функции на некотором отрезке или как найти наименьшее значение функции.

1. Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
2. Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
3. Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
4. Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x=a и x=b.
5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.

Посмотрим, как правильно применить этот алгоритм при решении задач.

Пример 1

Условие: задана функция y=x3+4×2. Определите ее наибольшее и наименьшее значение на отрезках [1;4] и [-4;-1].

Решение:

Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0. Иными словами, D(y): x∈(-∞; 0)∪0; +∞. оба отрезка, заданных в условии, будут находиться внутри области определения.

Теперь вычисляем производную функции согласно правилу дифференцирования дроби:

y’=x3+4×2’=x3+4’·x2-x3+4·x2’x4==3×2·x2-(x3-4)·2xx4=x3-8×3

Мы узнали, что производная функции будет существовать во всех точках отрезков [1;4] и [-4;-1].

Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x3-8×3=0. У него есть только один действительный корень, равный 2. Он будет стационарной точкой функции и попадет в первый отрезок [1;4].

Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x=1, x=2 и x=4:

y(1)=13+412=5y(2)=23+422=3y(4)=43+442=414

Мы получили, что наибольшее значение функции max yx∈[1; 4]=y(2)=3 будет достигнуто при x=1, а наименьшее min yx∈[1; 4]=y(2)=3 – при x=2.

Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:

y(-1)=(-1)3+4(-1)2=3

Значит,  max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.

Ответ: Для отрезка [1;4] — max yx∈[1; 4]=y(2)=3, min yx∈[1; 4]=y(2)=3, для отрезка [-4;-1] — max yx∈[-4; -1]=y(-1)=3, min yx∈[-4; -1]=y(-4)=-334.

См. на рисунке:

Как найти наибольшее и наименьшее значение непрерывной функции на открытом или бесконечном интервале

Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнавать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.

1. Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
2. Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
3. Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0, решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям.  Их определяет вид интервала.

• Если интервал имеет вид [a;b), то нам надо вычислить значение функции в точке x=a и односторонний предел limx→b-0f(x).
• Если интервал имеет вид (a;b], то нам надо вычислить значение функции в точке x=b и односторонний предел limx→a+0f(x).
• Если интервал имеет вид  (a;b), то нам надо вычислить односторонние пределы limx→b-0f(x),limx→a+0f(x).
• Если интервал имеет вид [a; +∞), то надо вычислить значение в точке x=a и предел на плюс бесконечности limx→+∞f(x).
• Если интервал выглядит как (-∞; b], вычисляем значение в точке x=b и предел на минус бесконечности limx→-∞f(x).
• Если -∞; b, то считаем односторонний предел limx→b-0f(x) и предел на минус бесконечности limx→-∞f(x)
• Если же -∞; +∞, то считаем пределы на минус и плюс бесконечности limx→+∞f(x),  limx→-∞f(x).

4. В конце нужно сделать вывод на основе полученных значений функции и пределов. Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4-8 в первой части материала.

Пример 2

Условие: дана функция y=3e1x2+x-6-4. Вычислите ее наибольшее  и наименьшее значение в интервалах  -∞; -4, -∞; -3, (-3;1], (-3;2), [1;2), 2; +∞, [4; +∞).

Решение

Первым делом находим область определения функции. В знаменателе дроби стоит квадратный (квадратичный) трехчлен, который не должен обращаться в 0:

x2+x-6=0D=12-4·1·(-6)=25×1=-1-52=-3×2=-1+52=2⇒D(y): x∈(-∞; -3)∪(-3; 2)∪(2; +∞)

Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.

Теперь выполним дифференцирование функции и получим:

y’=3e1x2+x-6-4’=3·e1x2+x-6’=3·e1x2+x-6·1×2+x-6’==3·e1x2+x-6·1’·x2+x-6-1·x2+x-6′(x2+x-6)2=-3·(2x+1)·e1x2+x-6×2+x-62

Следовательно, производные функции существуют на всей области ее определения.

Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x=-12. Это стационарная точка, которая находится в интервалах (-3;1] и (-3;2).

Вычислим значение функции при x=-4 для промежутка (-∞; -4], а также предел на минус бесконечности:

y(-4)=3e1(-4)2+(-4)-6-4=3e16-4≈-0.456limx→-∞3e1x2+x-6=3e0-4=-1

Поскольку 3e16-4>-1, значит, max yx∈(-∞; -4]=y(-4)=3e16-4. Это не дает нам возможности однозначно определяться с наименьшим значением функции. Мы можем только сделать вывод, что внизу есть ограничение -1, поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.

Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к -3 с левой стороны, мы получим только интервал значений:

limx→-3-03e1x2+x-6-4=limx→-3-03e1(x+3)(x-3)-4=3e1(-3-0+3)(-3-0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→-∞3e1x2+x-6-4=3e0-4=-1

Значит, значения функции будут расположены в интервале -1; +∞

Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке  x=-12, если x=1. Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к -3 с правой стороны:

y-12=3e1-122+-12-6-4=3e425-4≈-1.444y(1)=3e112+1-6-4≈-1.644limx→-3+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1-3+0+3(-3+0-2)-4==3e1(-0)-4=3e-∞-4=3·0-4=-4

У нас получилось, что наибольшее значение функция примет в стационарной точке max yx∈(3; 1]=y-12=3e-425-4. Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до -4.

Для интервала (-3;2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:

y-12=3e1-122+-12-6-4=3e-425-4≈-1.444limx→-3+03e1x2+x-6-4=-4limx→2-03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2-0+3)(2-0-2)-4==3e1-0-4=3e-∞-4=3·0-4=-4

Значит, max yx∈(-3; 2)=y-12=3e-425-4, а наименьшее значение определить невозможно, и значения функции ограничены снизу числом -4.

Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [1;2) наибольшее значение функция примет при x=1, а найти наименьшее невозможно.

На промежутке (2; +∞) функция не достигнет ни наибольшего, ни наименьшего значения, т.е. она будет принимать значения из промежутка -1; +∞.

limx→2+03e1x2+x-6-4=limx→-3+03e1(x+3)(x-2)-4=3e1(2+0+3)(2+0-2)-4==3e1(+0)-4=3e+∞-4=+∞limx→+∞3e1x2+x-6-4=3e0-4=-1

Вычислив, чему будет равно значение функции при x=4, выясним, что max yx∈[4; +∞)=y(4)=3e114-4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y=-1.

Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.

Это все, что мы  хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.

Как найти максимальные значения

Все ресурсы AP Расчет AB

3 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

AP Calculus AB Справка » Как найти максимальные значения

Каков локальный максимум  когда ?

Возможные ответы:

Локального максимума нет.

Правильный ответ:

Пояснение:

Чтобы найти максимум, нам нужно посмотреть на первую производную.

Чтобы найти первую производную, мы можем использовать правило степени. Для этого мы уменьшаем показатель степени переменных на единицу и умножаем на исходный показатель степени.

Мы будем считать, что все в нулевой степени равно единице.

Обратите внимание, что, поскольку любое произведение, умноженное на ноль, равно нулю.

Глядя на первую производную, помните, что если результат этого уравнения положительный, исходная функция возрастает. Если производная отрицательна, то функция убывает.

Обратите внимание, что меняется с положительного на отрицательное, когда .

Мы можем найти этот корень, используя квадратное уравнение: 

Поскольку мы ищем отрицательное значение, мы вычтем.

Таким образом, максимальное значение равно .

Сообщить об ошибке

Каков локальный максимум между и ?

Возможные ответы:

Между этими двумя точками нет максимума.

Правильный ответ:

Объяснение:

Чтобы найти максимум, мы должны найти, где график смещается от возрастания к убыванию. Чтобы узнать скорость, с которой график смещается с увеличения на уменьшение, мы смотрим на вторую производную и видим, когда значение меняется с положительного на отрицательное.

Другими словами, мы посмотрим на вторую производную и увидим, где (если вообще) график пересекает ось x и движется от положительного значения y к отрицательному значению y.

Теперь надо найти вторую производную. К сожалению, производные триггерных функций нужно запоминать. Первая производная:

.

Чтобы найти вторую производную, мы берем производную нашего результата.

.

Следовательно, вторая производная будет .

Пересекает ли наше новое уравнение ось x и движется ли оно от положительного к отрицательному между и ? Да. Это происходит один раз, когда . Поэтому наш локальный максимум будет при . Подставьте это значение обратно в наше первое уравнение, чтобы найти, что максимум будет в точке .

Сообщить об ошибке

Найдите координату x максимума  за интервал .

Возможные ответы:

6

0

5

-2

2

Правильный ответ:

2

Объяснение:

Сначала найдите производную, а именно:

 

Приравняйте ее к нулю, чтобы получить критические точки:

Вы также должны принять во внимание -1 и 2 как критические точки, поскольку они являются вашими конечными точками. . Оцените каждую из этих критических точек в исходной функции:

Максимум — ваш максимум. Координата x равна 2,9.0005

Сообщить об ошибке

Найдите значение, при котором функция достигает своего локального максимума.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти максимум, нам нужно найти критические точки. Для этого нужно найти производную функции.

И мы видим, что и являются критическими точками для этой функции.

Простой способ узнать, что является максимальным, а какое — минимальным, состоит в том, чтобы подставить значения критических точек в исходное уравнение.

и

Следовательно, максимальное значение равно 3, а значение, при котором функция достигает максимума, равно 0.

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы AP Calculus AB

3 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

Калькулятор максимума функции

Поиск инструмента

Поиск инструмента на dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Максимум функции

Инструмент для определения максимального значения функции: максимальное значение, которое может принимать функция. Это глобальный максимум, а не локальный максимум.

Результаты

Максимум функции — dCode

Теги: Функции

Поделиться

dCode и многое другое

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах решать каждый день! 92 $, определенной над $ \mathbb{R} $, функция достигает своего максимума в $ x=0 $, $ f(x=0) = 0 $ и $ f(x)

максимум функции всегда определяется с интервалом, может быть локальным (между 2-мя значениями) или глобальным: над областью определения функции.

Как вычислить максимум функции?

максимума функции обнаруживаются, когда производная становится равной нулю и меняет знак (переходит через 0 с положительной стороны на отрицательную). 9- $. Тогда глобальный экстремум функции равен $1$ при $x=0$.

Как рассчитать локальный максимум на интервале?

Добавьте одно или несколько ограничений, указывающих условия для каждой переменной.

Пример: Найти максимум $ \cos{x} $ для $ -\pi

Указать, чтобы dCode несколько уравнений с оператором && (логическое И) для разделения уравнений

Что такое экстремум?

Экстремум — это название, данное экстремальному значению функции, значению, которое может быть максимальным ( максимум функции ) или минимум (минимум функции).

Что такое мажоранта функции?

Мажоранта — это любое значение, большее или равное максимальному значению, достигнутому функцией.

Каков максимум постоянной функции?

Постоянная функция $f(x)=c$ является прямой и всегда равна $c$, поэтому ее максимум $c$ ​​достигается при любом значении $x$

Каков максимум аффинной функции ?

Аффинная функция $ f (x) = ax + b $ — это прямая, которая всегда имеет максимум $ +\infty $ 92 + bx + c $ then

— Если $ a

— Если $ a > 0 $, максимум $ f $ равен $ +\infty $, когда $ x $ стремится к $ +\infty $ исходный код. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Максимальная функция», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Максимальная функций» (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанных на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и все данные загрузка, сценарий или доступ к API для «Максимальной функции» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Максимум функции» или любых ее результатов разрешено, если вы цитируете dCode!
Экспорт результатов в виде файла .csv или .txt осуществляется бесплатно, если щелкнуть значок export
Ссылка на источник (библиография):
Максимум функции на dCode. fr [онлайн-сайт], получено 2023-04 -17, https://www.dcode.fr/maximum-function

Резюме

• Калькулятор максимума
• Калькулятор минимума
• Каково определение максимума функции?
• Как вычислить максимум функции?
• Как рассчитать локальный максимум на интервале?
• Что такое экстремум?
• Что такое мажоранта функции?
• Каков максимум постоянной функции?
• Каков максимум аффинной функции?
• Каков максимум полиномиальной функции 2-й степени?

Similar pages

• Minimum of a Function
• Derivative
• Extremum of a Function
• Stationary Point of a Function
• Polynomial Degree
• Error Function
• Domain of Derivative of a Function
• DCODE’S TOOLS LIST

Поддержка

• PayPal
• Patreon
• Подробнее

Форум/Помощь

Ключевые слова

Максимум, максимум, функция, дериватив, дериватив, дериватив, дериватив, дериватор, дериватор, дериватор, калькулятор, минимум, экстремума

.