Как найти объем параллелепипеда формула: Найдите объем прямоугольного параллелепипеда , измерения которого равны 24 м 30м и 450дм

Математика Объемы. Объем прямоугольного параллелепипеда

Материалы к уроку

• Ob_Ob_pr_par.ppt

  1.23 MBСкачать

Конспект урока

Объёмы. Объём прямоугольного параллелепипеда

 

Объём

Если наполнять формочку влажным песком, а потом переворачивать и снимать ее, получатся фигуры, имеющие одинаковый объём. Если формочку наполнять водой, то объем воды будет равен объёму каждой фигуры из песка.

Для измерения объемов применяют следующие единицы:

Кубический миллиметр     мм³
Кубический сантиметр      см³
Кубический дециметр       дм³
Кубический метр               м³
Кубический километр       км³

Например, кубический сантиметр – это объем куба с ребром 1 см

Кубический дециметр – литр
1 дм³ = 1 л

Фигура на рисунке состоит из 4 кубиков с ребром 1 см, значит её объем равен 4 см³.

Выведем правило для вычисления объема прямоугольного параллелепипеда. Пусть прямоугольный параллелепипед имеет длину 4 см, ширину 3 см и высоту 2 см. Разобъем его на два слоя толщиной 1 см. Каждый из этих слоёв состоит из 3 столбиков длиной 4 см, а каждый столбик из 4 кубиков с ребром 1 см. Значит, объем каждого столбика равен 4 см³, каждого слоя – 4 · 3 см³, а всего прямоугольного параллелепипеда – 4 · 3 · 2 = 24 см³. 

Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.

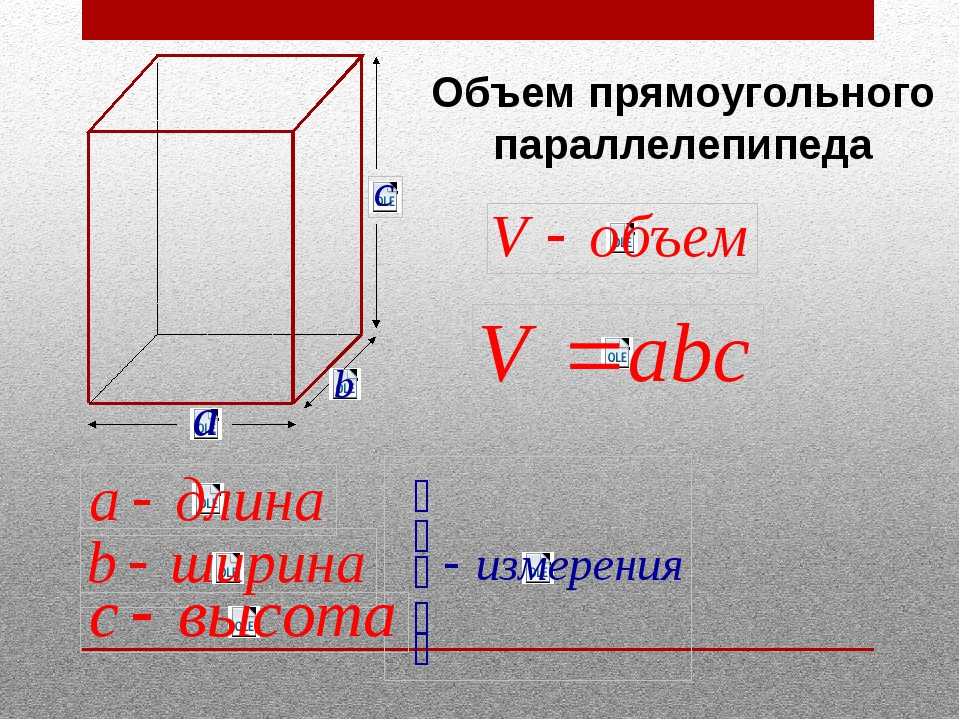
Формула объема прямоугольного параллелепипеда:
                       V = abc
V — объем
a, b, c — измерения, т. е. длина, ширина и высота.

Если ребро куба равно 4 см, то объем куба равен 4 · 4 · 4 = 64 см³

Если ребро куба равно а, то объем куба равен: V = а · a · a = a³

Формула объема куба:

V = a³

Именно поэтому запись а³ называют кубом числа а.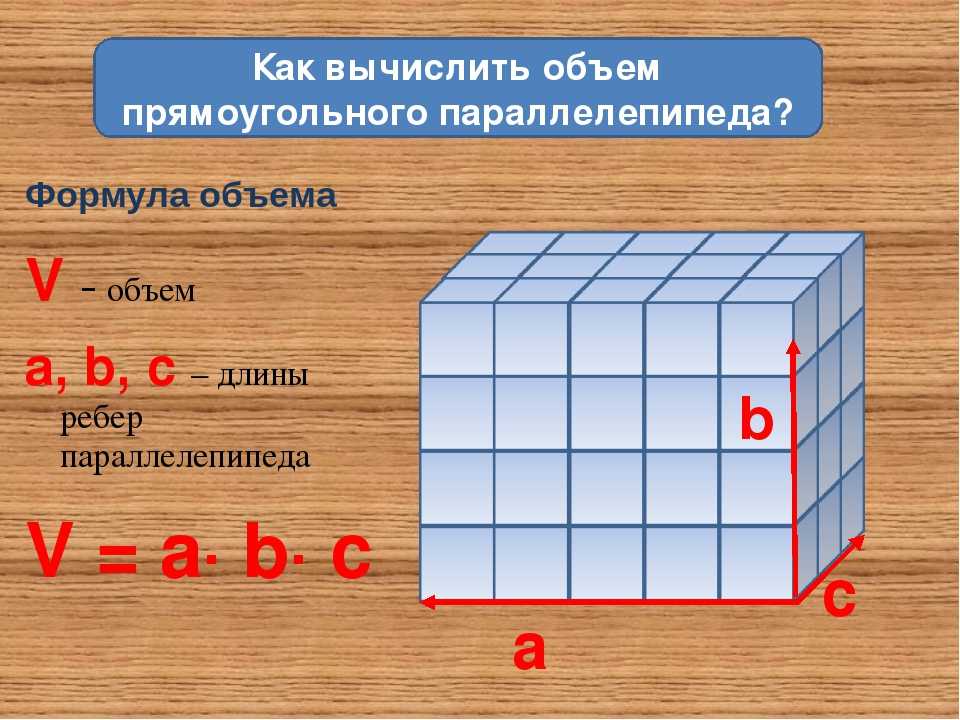

Объем куба с ребром 1 м равен 1 м³
А т. к. 1 м = 10 дм, то 1м³ = 1000 дм³ = 1000 л
Таким же образом находим, что 1 л = 1 дм³ = 1000 см³
1 см³ = 1000 мм³
1 км³ = 1000000000 м³

 

Вопросы:

1. Фигура состоит из 19 кубиков со стороной 1 см каждый; чему равен объем этой фигуры?
2. Что такое кубический сантиметр; кубический метр?
3. Скольким кубическим сантиметрам равен 1 литр?
4. Скольким литрам равен кубический метр?
5. Сколько кубических метров в кубическом километре?

6. Напишите формулу объема прямоугольного параллелепипеда.
7. Что означает в этой формуле буква V; буквы a, b, c?
8. Напишите формулу объема куба.

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитора

Объем параллелепипеда равен

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-02-11

Для вас очередная статья, сегодня мы мы рассмотрим задания с параллелепипедом.  Освежим в памяти само понятие…

Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными.

Если сказать просто, то у прямого параллелепипеда его боковые рёбра перпендикулярны основанию, боковые грани прямоугольники, основания параллелограммы; у наклонного параллелепипеда верхнее и нижнее основания как бы смещены параллельным сдвигом, посмотрите рисунок в первой задаче. 

В предыдущих статьях мы рассматривали задачи с прямоугольным параллелепипедом (все грани прямоугольники). Представленные ниже задания я выделил в отдельную группу, так как в ходе решения рассматривается пирамида — стоят вопросы о нахождении её объёма. Решаются они практически устно, но мы их разберём подробно. Что нужно помнить?

С площадью основания всё ясно. А что такое высота? Если параллелепипед прямой, то понятно – его высота равна боковому ребру. Если же  параллелепипед наклонный? Его высота равна расстоянию между основаниями, то есть простыми словами можно сказать, что это длина отрезка, который перпендикулярен основаниям и соединяет их:

Но в данных задачах находить саму площадь основания и высоту будет не нужно.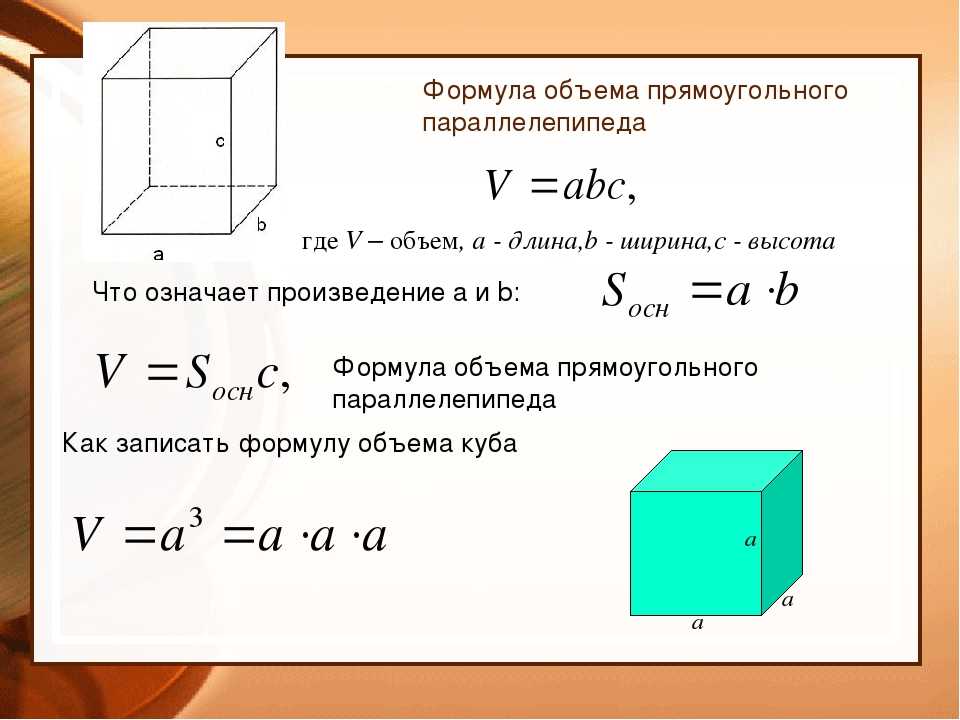

Формула объёма пирамиды:

*Запомните навсегда, что объём пирамиды равен одной трети объёма параллелепипеда с тем основанием и высотой.

Рассмотрим задачи:

Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды ABDA₁.

Известно, что объём параллелепипеда равен произведению площади его основания и высоты, то есть:

Объём  пирамиды равен:

Рассмотрим пирамиду ABDA₁, её высота равна  высоте параллелепипеда, так она у них общая. Площадь её основания в два раза меньше площади основания параллелепипеда, так как диагональ BD делит параллелограмм ABCD на два равных по площади треугольника, значит:

Следовательно:

Получили, что объём пирамиды в шесть раз меньше объёма параллелепипеда и будет равен  9:6 = 1,5.

Ответ: 1,5

*В подобных заданиях, где дан объём параллелепипеда и требуется найти объём какой-либо составляющей его части, не нужно пытаться найти саму площадь основания или высоту.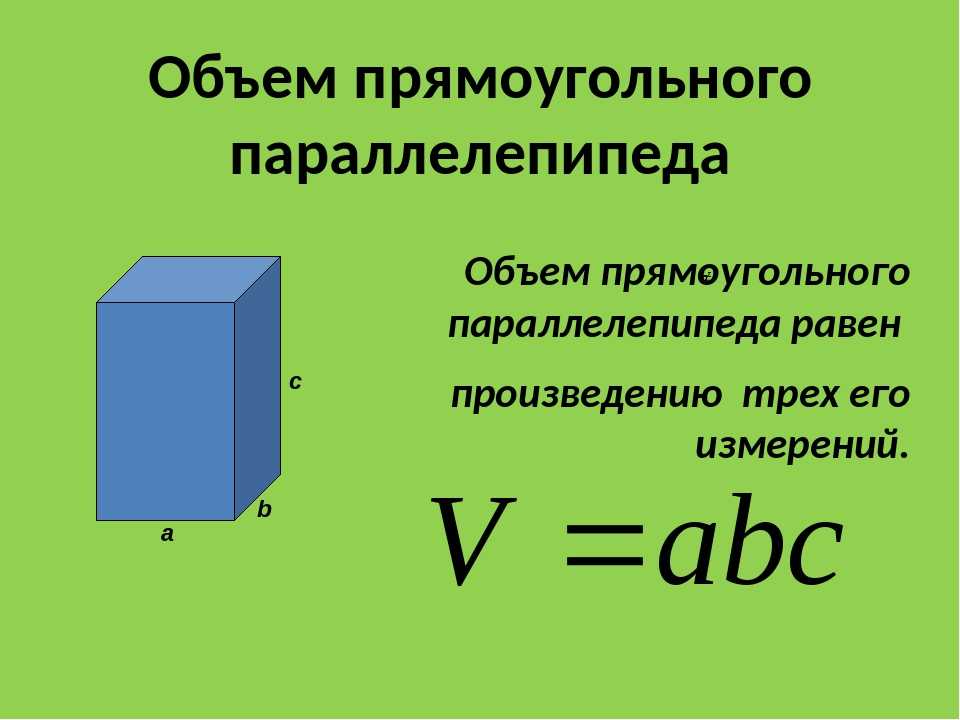 Необходимо просто установить соотношение объёмов используя известные свойства.

Объем куба равен 94. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Объем призмы равен произведению площади основания на высоту:

Поскольку высота призмы равна высоте куба, то их объемы пропорциональны площадям их оснований. Определим, как соотносятся площади оснований призмы и куба.

Пусть ребро куба равно а. Тогда площадь основания куба равна а².

Определим площадь основания призмы:

Видно, что площадь основания построенной призмы в 8 раз меньше площади основания куба, поэтому искомый объем призмы также будет в 8 раз меньше объёма куба, то есть:

Ответ: 12

Объем куба равен 123. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Объем пирамиды равен:

Площади оснований куба и пирамиды равны, высота пирамиды в два раза меньше ребра куба. Обозначим ребро куба как  a, тогда объём пирамиды:

Ответ: 20,5

Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 3,6. Найдите объем треугольной пирамиды B₁AD₁C.

Данную задачу можно решить разными способами. Можно найти площадь основания AD₁C и высоту пирамиды (отрезок соединяющий центр куба и вершину B₁), но это долгий путь. Проще поступить следующим образом.

Искомый объем равен разности объемов параллелепипеда и четырех пирамид:

То есть мы как бы вычленяем (вырезаем) пирамиду из куба «отсекая» лишнее. Обозначим для простоты восприятия рёбра следующим образом, пусть:

AB = a     BC = b     BB₁ = c

Тогда

Ответ: 1,2

Найдите объем параллелепипеда ABCDA₁B₁C₁D₁, если объем треугольной пирамиды ABDA₁ равен 10.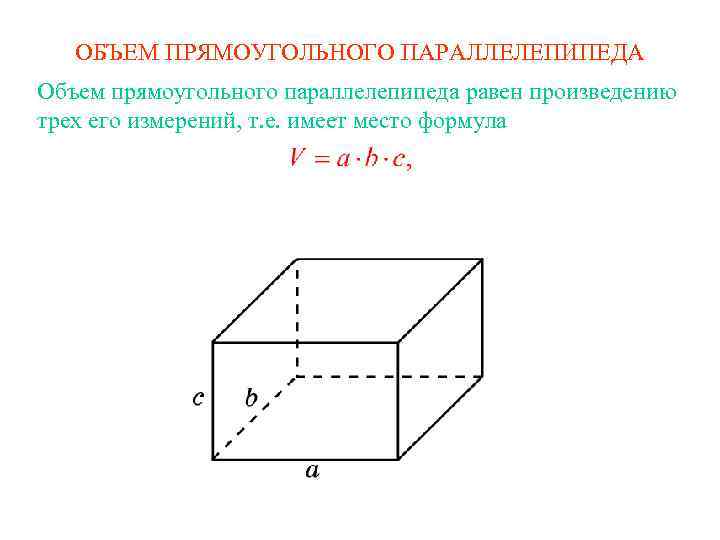

Эта задача обратная той, которую мы рассмотрели в самом начале. Мы установили, что объём такой пирамиды в шесть раз меньше объёма параллелепипеда, значит  объём параллелепипеда будет равен 60.

Запишем подробнее. Объем параллелепипеда равен:

Объём данной пирамиды равен:

Площадь основания пирамиды равна половине площади основания параллелепипеда, то есть:

Следовательно

Можем записать:

Ответ: 60

27182. Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 12. Найдите объем треугольной пирамиды B₁ABC.  Ответ: 2

27183. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Посмотреть решение

27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.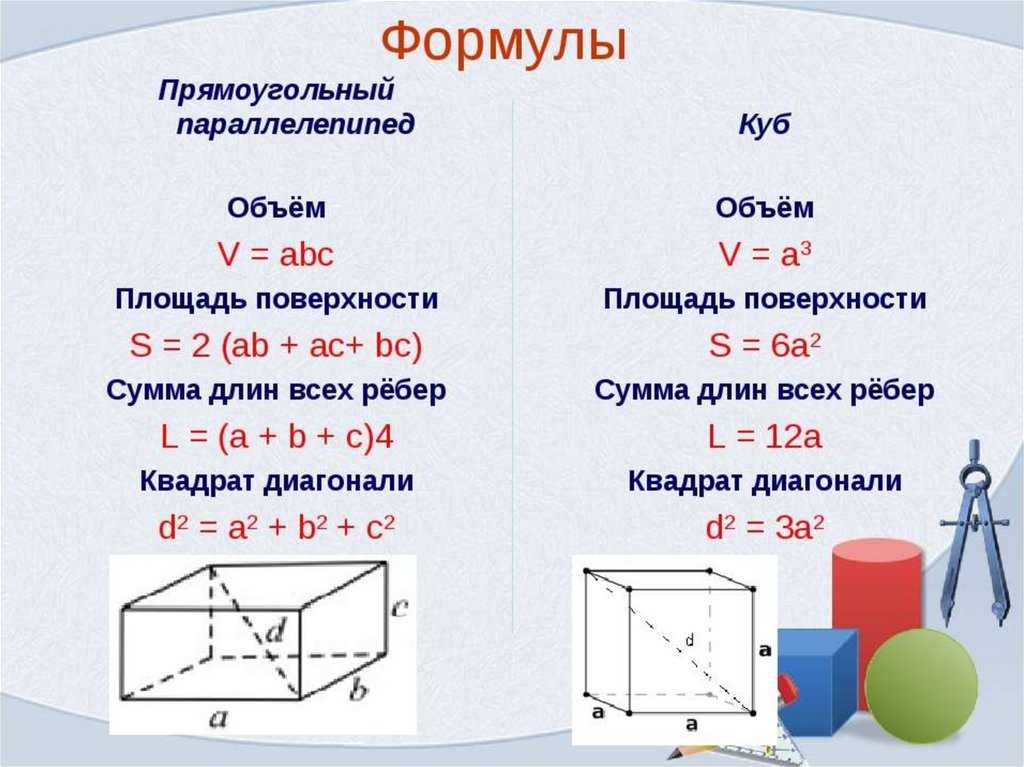

Посмотреть решение

27209. Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 4,5. Найдите объем треугольной пирамиды AD₁CB₁.

Посмотреть решение

77154. Найдите объем параллелепипеда ABCDA₁B₁C₁D₁, если объем треугольной пирамиды ABDA₁ равен 3.

Посмотреть решение

Как вы поняли, главное в подобных заданиях знать свойства. Например, что диагональ параллелограмма делит  его на два равных по площади треугольника; две диагонали параллелограмма разбивают его на четыре равных по площади треугольника; то, что центр куба делит его высоту пополам, равноотстоит от его граней и вершин и прочее.

Понимая это и другие простые свойства фигур вы без труда вычислите (устно) во сколько раз объём пирамиды будет меньше объёма куба или параллелепипеда, а также сможете быстро решать другие подобные задания.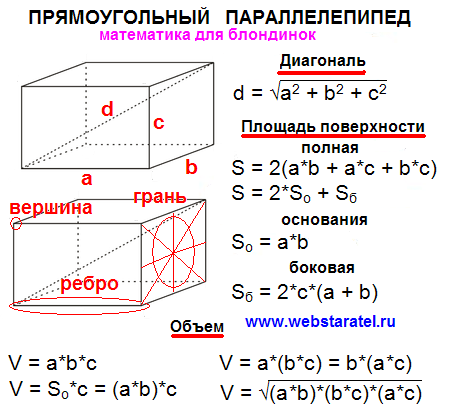

Например, решим такую задачу: дан наклонный параллелепипед, его основание и основание пирамиды находятся в одной плоскости. Площадь основания пирамиды в 4 раза меньше, её высота в 3 раза меньше высоты параллелепипеда. Найдите объём пирамиды, если объём параллелепипеда равен 360.

Сразу отметим, что у пирамиды с тем же основанием и высотой объём в три раза меньше. Сказанной, что площадь её основания в 4 раза меньше, то есть объём уменьшается ещё в 4 раза, и высота в 3 раза, получаем:

Успеха вам!

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Вопрос Видео: Использование множителей Лагранжа для нахождения максимального объема, который может иметь прямоугольный параллелепипед, вписанный в эллипсоид больше 𝑏 в квадрате плюс 𝑧 в квадрате больше 𝑐 в квадрате равно единице.

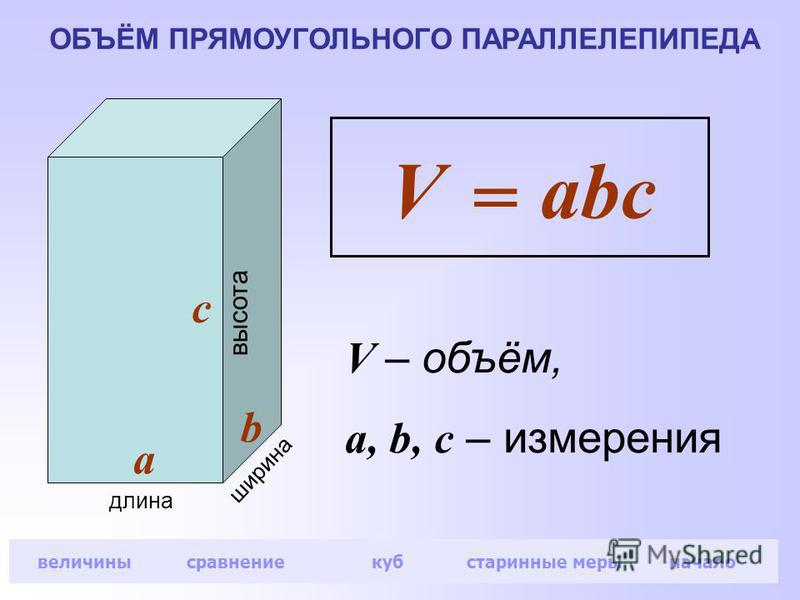Это (а) восемь 𝑎𝑏𝑐 на три корня три, (б) 𝑎𝑏𝑐 на три корня три, (в) восемь 𝑎𝑏𝑐 на корень три, (г) шесть 𝑎𝑏𝑐 на корень три или (д) восемь 𝑎𝑏𝑐?

Чтобы найти объем прямоугольного параллелепипеда, самый простой способ — взять одну вершину, затем взять произведение длин трех ее смежных ребер. Так вот, например, если эти три ребра имеют длину 𝛼, 𝛽 и 𝛾, то объем этой формы 𝑉 всего 𝛼 раз 𝛽 раз 𝛾. Это кажется достаточно простым. Но для максимизации этого значения для параллелепипеда, вписанного внутрь эллипсоида, не очевидно, как эта фигура будет ориентирована внутри эллипсоида. Таким образом, нам, по сути, нужно найти по крайней мере 12 переменных, 𝑥-, 𝑦- и 𝑧-координаты первой вершины и всех трех соседних вершин.

Однако вместо этого мы можем использовать то, что мы знаем об отношениях эллипсоида с более простой трехмерной формой, сферой. Эллипсоид — это просто сфера, масштабированная по трем перпендикулярным осям. В частности, эллипсоид с данным уравнением 𝑥 в квадрате на 𝑎 в квадрате плюс 𝑦 в квадрате на 𝑏 в квадрате плюс 𝑧 в квадрате на 𝑐 в квадрате равен единице, это просто единичная сфера, масштабированная по оси 𝑥 с коэффициентом 𝑎, вдоль 𝑦 по оси в 𝑏 раз, а по оси 𝑧 в 𝑐 раз. Таким образом, эллипсоид является результатом трех масштабирований вдоль трех перпендикулярных осей.

Важным свойством преобразования масштабирования является то, что одно и то же масштабирование, примененное к любой трехмерной фигуре, будет масштабировать ее объем с тем же коэффициентом масштабирования, что и любая другая трехмерная фигура. Это немного легче продемонстрировать в двух измерениях, поэтому давайте расчистим немного места. Рассмотрим, например, единичный квадрат. У него длина стороны равна единице, а площадь всего одна единица. Теперь представьте, что квадрат растягивается вдоль некоторой оси в 𝑆 раз. Легко видеть, что если мы растянем ось, параллельную одной из его сторон, его площадь увеличится в 𝑆 раз. Итак, новая область 𝑆. Но на самом деле это применимо независимо от того, в каком направлении мы тянемся.

Например, рассмотрим растяжение в 𝑆 раз вдоль оси, параллельной диагонали квадрата. Результатом является ромб с одной неизменной длиной диагонали корня два, а другой из 𝑆 корня два.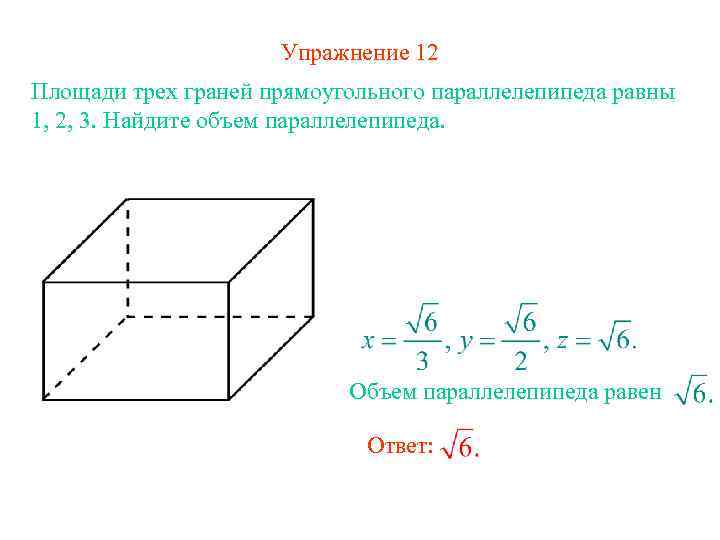 Площадь ромба равна половине произведения двух диагоналей. Таким образом, у нас есть половинный корень, умноженный на два, умноженный на 𝑆, корень два, что как раз равно 𝑆, той же новой площади, что и у нас, когда мы растягивали вдоль оси, параллельной одной из сторон квадрата. С помощью матричных преобразований довольно просто доказать, что это увеличение площади одинаково вдоль любой оси и что это также обобщается на объем в трех измерениях.

В результате мы можем найти максимальный объем прямоугольного параллелепипеда, который можно вписать внутрь сферы, а затем просто масштабировать параллелепипед, используя то же преобразование, что и для преобразования сферы в эллипсоид. И это даст нам новый максимальный объем параллелепипеда, который можно вписать в эллипсоид. Мы можем быть уверены, что этот параллелепипед будет иметь максимальный объем, так как он был преобразован из параллелепипеда с максимальным объемом в сферу. И любой другой параллелепипед, вписанный в эллипсоид, должен был изменить объем во столько же раз, что и этот. Таким образом, параллелепипед максимального объема в сфере соответствует параллелепипеду максимального объема в эллипсоиде.

Это, как мы увидим, значительно упростит задачу. Итак, нам нужно найти максимальный объем параллелепипеда, который можно вписать внутрь единичной сферы. Интуиция может подсказать вам, что это куб, и это действительно так. Но мы собираемся доказать это с помощью множителей Лагранжа. Итак, рассмотрим единичную сферу с центром в начале координат. Его поверхность имеет уравнение 𝑥 в квадрате плюс 𝑦 в квадрате плюс 𝑧 в квадрате равно единице. Чтобы параллелепипед имел максимальный объем, хотя бы одна его вершина должна касаться поверхности сферы. В противном случае мы могли бы легко расширить параллелепипед по одной стороне и увеличить объем. Рассмотрим тогда без ограничения общности одну вершину параллелепипеда, касающуюся сферы в положительном октанте; т. е. имеет координаты 𝑥, 𝑦, 𝑧, где 𝑥, 𝑦 и 𝑧 все положительны.

Теперь рассмотрим ребра, к которым примыкает эта вершина. Мы только что нарисовали первую часть краев. Поскольку в вопросе указан прямоугольный параллелепипед, и мы будем масштабировать эту форму со сферой по трем перпендикулярным осям, эти ребра также должны быть под прямым углом друг к другу. Таким образом, они останутся под прямым углом друг к другу после преобразования масштабирования. Поскольку эта сфера симметрична по всем трем осям, мы снова можем считать без ограничения общности, что ребра параллельны каждой из координатных осей. Если мы теперь расширим эти ребра дальше, мы можем сделать вывод, что все три ребра будут иметь максимальную длину. И, следовательно, прямоугольный параллелепипед будет иметь максимальный объем, когда все три ребра касаются сферы в другой своей концевой вершине.

Поскольку сфера симметрична относительно всех трех осей, а эти линии параллельны трем осям, вершины параллелепипеда на другом конце этих ребер должны находиться на одинаковом расстоянии вдоль соответствующих им параллельных осей, но в отрицательном направлении от исходная точка. Значит, эта точка должна иметь отрицательные координаты 𝑥, 𝑦, 𝑧. Эта точка должна иметь координаты 𝑥, минус 𝑦, 𝑧. И эта точка должна иметь координаты 𝑥, 𝑦, минус 𝑧. Это, в свою очередь, означает, что эта сторона имеет длину два 𝑥, эта сторона имеет длину два 𝑦, а эта сторона имеет длину два 𝑧, а значит, объем полного прямоугольного параллелепипеда должен быть 𝑉 равен двум 𝑥, умноженным на два 𝑦, умноженным на два. два 𝑧 равно восьми 𝑥𝑦𝑧.

Это функция, которую нужно максимизировать. И наше ограничение состоит в том, что наша исходная выбранная точка в 𝑥, 𝑦, 𝑧 должна лежать на сфере, что означает, что значения 𝑥, 𝑦 и 𝑧 удовлетворяют уравнению сферы 𝑥 в квадрате плюс 𝑦 в квадрате плюс 𝑧 в квадрате равно единице. Если представить это в обычной форме функции ограничений, то 𝑔 равно 𝑥 в квадрате плюс 𝑦 в квадрате плюс 𝑧 в квадрате минус единица равно нулю. Напомним, что функция Лагранжа задается как 𝐿 из 𝐱, 𝜆 равно 𝑓 из 𝐱 плюс 𝜆𝑔 из 𝐱, где 𝑓 — максимизируемая функция, 𝑔 — функция ограничений, а 𝜆 — скаляр, известный как множитель Лагранжа.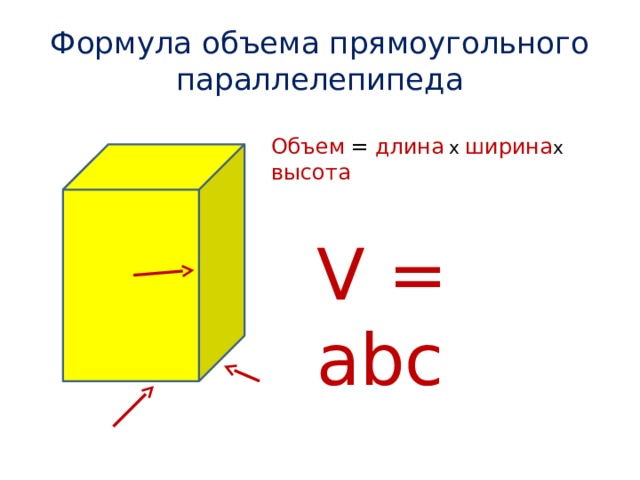 Вектор 𝐱 представляет собой набор переменных 𝑓, в данном случае 𝑥, 𝑦, 𝑧.

Итак, в нашем случае 𝐿 из 𝑥, 𝑦, 𝑧, 𝜆 равно восьми 𝑥𝑦𝑧 плюс 𝜆 умножить на 𝑥 в квадрате плюс 𝑦 в квадрате плюс 𝑧 в квадрате минус один. Чтобы найти максимум или минимум 𝑓 с учетом ограничения 𝑔, мы берем частные производные лагранжиана 𝐿 по 𝑥, 𝑦, 𝑧 и 𝜆; установите их равными нулю; затем решите полученную систему уравнений для 𝑥, 𝑦 и 𝑧. Нам не нужно явно решать для 𝜆. Давайте сначала освободим немного места и переместим нашу функцию сюда.

Теперь нам нужно взять частные производные от 𝐿 по 𝑥, 𝑦, 𝑧 и 𝜆. 𝜕𝐿 𝜕𝑥 𝜕𝑥 равно восемь 𝑦𝑧 плюс два 𝜆𝑥, 𝜕𝐿 на 𝜕𝑦 𝜕𝑦 равно восемь 𝑥𝑧 плюс два 𝜆𝑦, 𝜕𝐿 𝜕𝑧 𝜕𝑧 равно восемь 𝑥𝑦 плюс два 𝜆𝑧 и 𝜕𝐿 𝜕𝜆 равны 𝑥 квадрат плюс 𝑦 квадрат плюс 𝑧 𝑧 квадрат минус один, который, как мы заметим, точно такой же, как функция ограничения 𝑔. Теперь мы приравняем их все к нулю и решим эту систему уравнений для 𝑥, 𝑦 и 𝑧.

Судя по симметрии этой системы уравнений, вы можете увидеть, к чему все идет, но давайте продолжим. Мы можем решать эти уравнения в любом порядке. Давайте начнем с уравнения один, и нам понадобится немного больше места. Из уравнения один мы можем переставить, чтобы получить 𝑧 равно отрицательному 𝜆𝑥 по четырем 𝑦. Подставляя это выражение для 𝑧 во второе уравнение, мы получаем, что восемь 𝑥 умножить на отрицательное 𝜆𝑥 на четыре 𝑦 плюс два 𝜆𝑦 равно нулю. Разделив на два и приняв 𝜆 в качестве общего множителя перед упрощением, мы получим 𝜆, умноженное на 𝑦 минус 𝑥 в квадрате над 𝑦, равно нулю, что означает, что либо 𝜆 равно нулю, либо 𝑦 минус 𝑥 в квадрате над 𝑦 равно нулю. Если вместо этого мы подставим это выражение для 𝑧 в третье уравнение, мы получим восемь 𝑥𝑦 плюс два 𝜆, умноженных на отрицательное 𝜆𝑥 на четыре 𝑦, равно нулю.

Перестановка и деление на 𝑥, что мы можем сделать, поскольку 𝑥, равное нулю, было бы тривиальным результатом с параллелепипедом нулевого объема, мы получаем 16𝑦 в квадрате равно 𝜆 в квадрате. 𝑦 также не равно нулю, поэтому 𝜆 не равно нулю. Следовательно, из нашего предыдущего уравнения мы должны иметь 𝑦 минус 𝑥 в квадрате над 𝑦 равно нулю.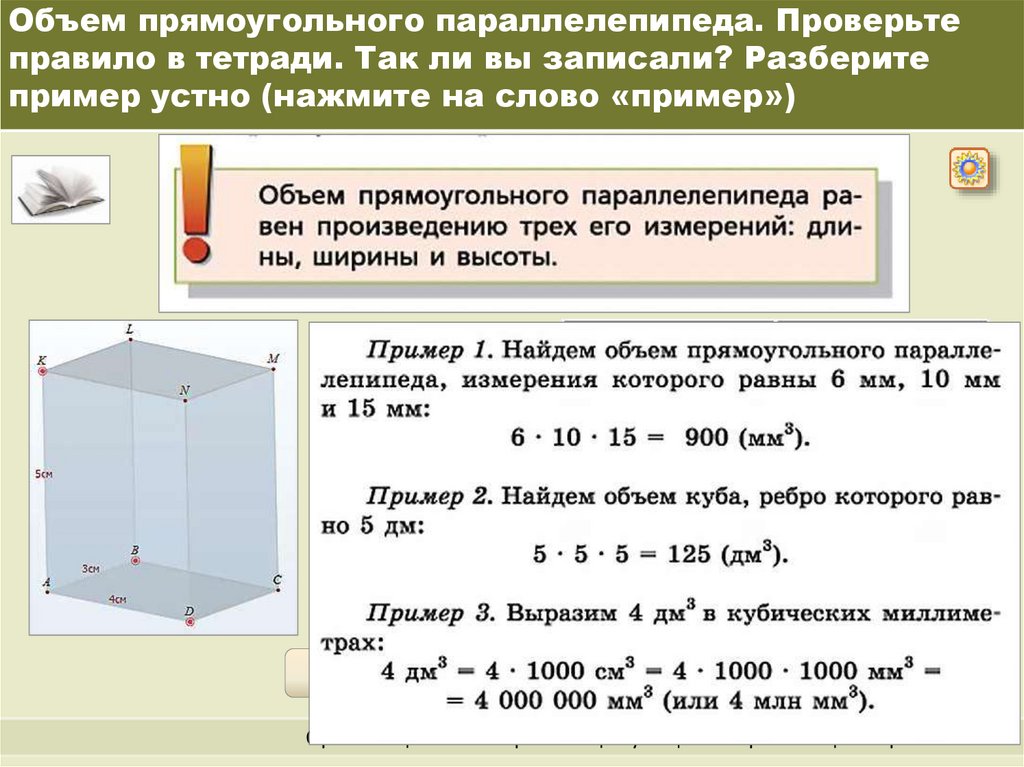 Переставляя это уравнение, мы получаем 𝑥 в квадрате равно 𝑦 в квадрате, что также равно 𝜆 в квадрате на 16. Если теперь мы воспользуемся уравнением четыре и подставим 𝑦 в квадрате на 𝑥 в квадрате и 𝑧 в квадрате отрицательного 𝜆𝑥 на четыре 𝑦, мы получим 𝑥 в квадрате плюс 𝑥 в квадрате плюс минус 𝜆𝑥 из корней четырех 𝜆 в квадрате из 16 все в квадрате равно единице.

Все это упрощается до трех 𝑥 в квадрате равно единице, что означает, что 𝑥 в квадрате равно 𝑦 в квадрате равно одной трети. Из нашего уравнения для 𝑧 мы можем получить 𝑧 в квадрате равно 𝜆 в квадрате 𝑥 в квадрате на 16𝑦 в квадрате, что упрощается до 𝑥 в квадрате, поэтому 𝑧 в квадрате также равно одной трети. Итак, мы решили эту систему уравнений для 𝑥, 𝑦 и 𝑧, и 𝑥 равно 𝑦 равно 𝑧 равно единице над корнем три. И это положительный корень три, потому что мы изначально заявили, что 𝑥, 𝑦 и 𝑧 все положительны. Помните, что каждая сторона параллелепипеда имеет длину два 𝑥, два 𝑦 и два 𝑧 соответственно. Итак, каждая сторона этого параллелепипеда имеет одинаковую длину, две над корнем три.

Значит, это действительно куб. А его объем равен восьми 𝑥𝑦𝑧, что как раз восемь раз один над корнем трижды один над корнем трижды один над корнем три, что дает нам восемь над тремя корнями три, максимальный объем прямоугольного параллелепипеда, который можно вписать внутрь единичная сфера. Теперь нам нужно растянуть эту единичную сферу и куб внутри нее по оси 𝑥 в 𝑎 раз, по оси 𝑦 в 𝑏 раз и по оси 𝑧 в 𝑐 раз. Это масштабирование умножит объем куба на 𝑎, 𝑏 и 𝑐. Таким образом, это дает объем наибольшего прямоугольного параллелепипеда, который можно вписать в этот эллипсоид, как восемь 𝑎𝑏𝑐 над тремя корнями из трех. Возвращаясь к нашим возможным ответам, мы видим, что это соответствует (a) восьми 𝑎𝑏𝑐 из трех корней три.

Вычисление площадей и объемов

В этой статье мы обсудим, как вычислять площади и объемы геометрических фигур с помощью векторов. Вектор является одним из важных понятий в исчислении. Прежде чем перейти к конкретным примерам и пошагово описать, как это сделать, сначала разберемся, что такое векторы.

Рассмотрим движение самолета во время полета. Какие две части информации наиболее важны для того, чтобы убедиться, что все идет гладко? Что ж, ответ прост. Направление, в котором движется самолет, и его скорость являются двумя наиболее важными факторами. При вычислении силы, например, тяги двигателя самолета, важно объяснить не только величину/силу этой силы, но и направление, в котором эта сила приложена. Таким образом, мы можем сказать, что некоторые величины не полны без описания как величины, так и направления. Вектор определяется как:

Величина, которая имеет величину, а также направление, известна как вектор

Математическая запись вектора

Вектор обозначается буквой v с отрезком линии (стрелкой) над ним, как показано ниже :

Вектор обозначается .

Конечные точки этого отрезка называются начальной и конечной точками вектора, потому что стрелка, начинающаяся от начальной к конечной точке, указывает нам направление вектора. Величина определяется длина сегмента линии. У нас может быть вектор с одинаковыми начальной и конечной точками . Этот вектор известен как нулевой вектор и обозначается 0. Единственный вектор, который не имеет направления, — это нулевой вектор. эквивалентных векторов являются векторами с той же величиной и направлением. Эквивалентные векторы могут иметь разные начальные точки и представлены как:

v = w

Теперь мы увидим, как вычислить площади и объемы геометрических фигур, зная векторы.

Лучшие репетиторы по математике

Поехали

Площадь параллелограмма

Протяженность векторного произведения двух векторов соответствует площади параллелограмма, сторонами которой являются эти векторы.

Геометрически величина перекрестного произведения двух векторов совпадает с площадью параллелограмма, сторонами которого являются эти векторы. Например, рассмотрим следующий рисунок.

Площадь параллелограмма указана ниже:

Теперь давайте решим следующие примеры.

Пример 1

Учитывая векторы и , вычислите площадь параллелограмма, стороны которого являются векторами и .

Решение

Перемножим два вектора, чтобы вычислить площадь параллелограмма.

Площадь параллелограмма =

Указанный определитель имеет вид 3×3, т. е. имеет 3 строки и 3 столбца. Мы будем использовать следующую формулу для вычисления определителя этой матрицы.

Рассмотрим следующую матрицу 3×3:

Определитель матрицы А будет рассчитана как:

Пример 2

. параллелограмм, стороны которого являются векторами и .

Решение

Перемножим два вектора, чтобы вычислить площадь параллелограмма.

Площадь параллелограмма =

Приведенный выше определитель имеет вид 3×3, т. е. имеет 3 строки и 3 столбца. Мы будем использовать следующую формулу для вычисления определителя этой матрицы.

Рассмотрим следующую матрицу 3×3:

Определитель матрицы А будет рассчитана как:

. его высоты, то формула площади треугольника:

Площадь треугольника =

Пример

Определить площадь треугольника, вершинами которого являются точки A = (1, 1, 3), B = (2, −1, 5) и C = (− 3, 3, 1).

Решение

Найдем, взяв разность координат вершин B и A.

Тот же процесс повторим для: матрица 3×3, посчитаем площадь треугольника:

Определяющая среда матрицы B будет рассчитывать как:

Том параллелевой пастой

Абсолютный значение. . Ребра параллелепипеда — это три вектора, соединяющие одну вершину.

Пример

Найдите объем параллелепипеда, образованного следующими векторами:

               

Найдите определитель по следующей формуле:

=

Найдите различных репетиторов по математике на Superprof.