Как найти область значений функции 10 класс: Нахождение области определения и области значений числовой функции

100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА

В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.

— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?

— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.

Зарегистрироваться можно будет электронно на сайте Национального центра тестирования.

Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.

— Расскажите поподробнее?

— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.

— Система оценивания останется прежней?

Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.

— А апелляция?

— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.

— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?

— Мы решили оставить прежнее время — 240 минут.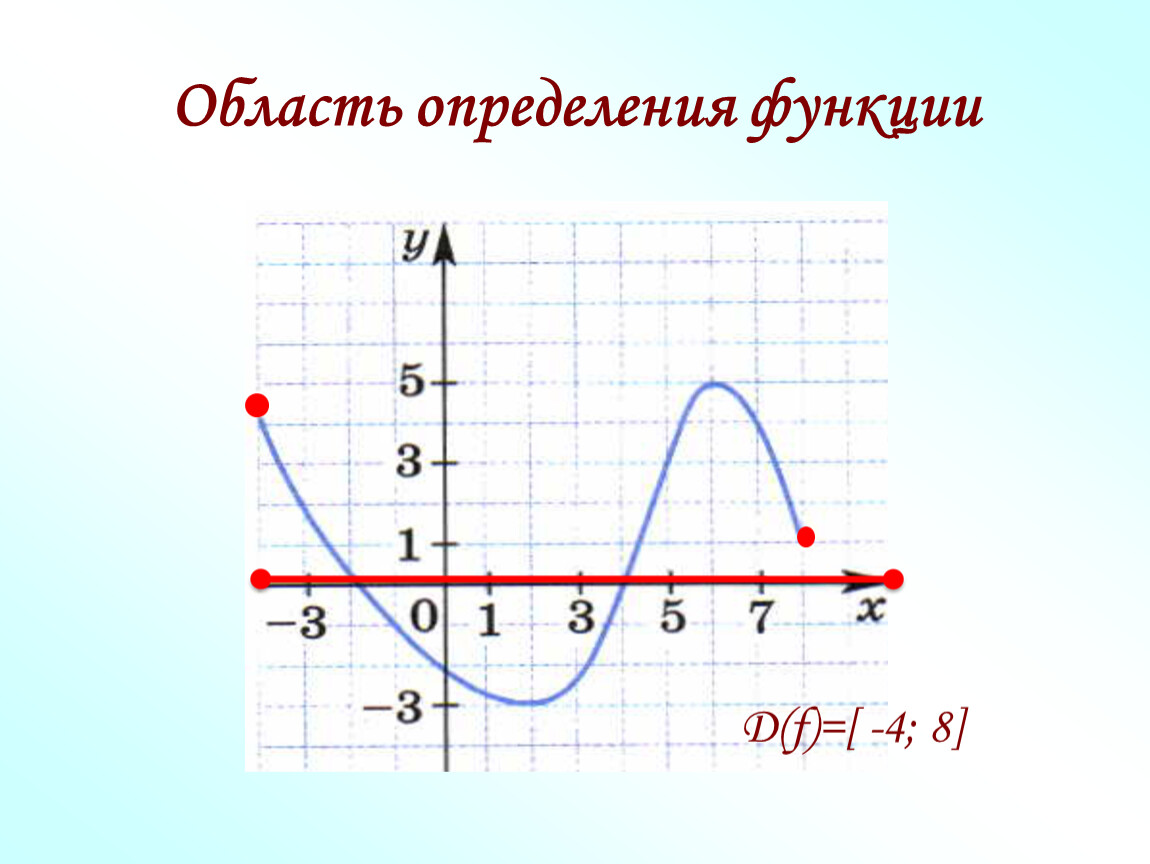 Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.

— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?

— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.

— На сколько процентов будет обновлена база вопросов?

— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.

— По вашему мнению система справится с возможными хакерскими атаками, взломами?

— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.

Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.

— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?

— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.

— Сколько человек будет сидеть в одной аудитории?

— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.

— Будут ли ужесточены требования по дисциплине, запрещенным предметам?

— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.

Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.

— А наблюдатели будут присутствовать во время сдачи тестирования?

— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.

— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?

— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.

Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.

— Сколько средств выделено на проведение ЕНТ в этом году?

Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.

— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?

— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.

Урок алгебры в 10 классе для детей с нарушением слуха по теме: «Функция. Область определения и область значений функций». | План-конспект урока по алгебре (10 класс) по теме:

План-конспект урока алгебры в 10 классе                                                    

Тема:«Функция. Область определения и область значений функции».

Тип урока:комбинированный.

Вид урока:урок закрепления изученного материала.

Цели:

• Образовательные:повторить и обобщить изучаемый материал;закрепить знания учащихся о различных видах функций и их графиках; проверить усвоение изученного материала при выполнении теста и самостоятельной работы;
• Развивающие: создать условия для развития памяти, слуха, речи, познавательного интереса к предмету; формирования представлений о математическом языке, его компонентах; способствовать развитию произносительных навыков и пополнению словаря учащихся;
• Воспитательные: создать условия для воспитания аккуратности, дисциплины, настойчивости, умения внимательно выслушивать мнение других, уважительно относиться к ответам одноклассников.

Оборудование:

1) таблички с названием функций, их формулами и графиками;

2) заготовки для тестов на каждого учащегося;

3) карточки с текстом самостоятельной работы для каждого учащегося.

План урока.

1. Организационный момент.

2. Устная работа.

3. Выполнение теста.

4. Решение упражнений у доски.

5. Самостоятельная работа.

6. Подведение итогов урока.

Ход урока.

I. Организационный момент.

-Кто дежурный в классе?

-Кого сегодня нет в классе?

-Какую тему мы изучаем?

-Что мы будем делать на уроке? (читаем план урока)

-Как мы будем говорить?

II. Устная работа(словарная работа, ответы на вопросы).

     1) Объяснить значение слов:

независимая переменная; зависимая переменная; аргумент; функция; область определения функции; область значений функции.

     2) Дать определение функции, записать на доске общий вид, найти соответствующий график из предложенных учителем:

          а) линейная функция;

          б) прямая пропорциональность;

          в) обратная пропорциональность;

          г) квадратичная функция;

          д) кубическая функция.

(после устного опроса вывешиваются таблички с названием функций, их формулами и графиками)

III. Выполнение теста.

Задание. Для функций у = х-1; у = ; у =  ; у = х²; у = -х; у = х³; у = 2-х; у = — указать соответствующий график (приложение 1).

Ответы (приложение 2).

  Функции       Графики

1) у = х-1              в

2) у =                е

3) у =                   г

4) у = х²                ж

5) у = -х                б

6) у = х³                з

7) у = 2-х              д

8) у = —                а

(после выполнения теста учащиеся обмениваются заготовками и проверяют друг у друга, выставляя оценки. Табличка с правильными ответами вывешивается на доске.

Критерии оценок: нет ошибок – 5;

                                1-2 ошибки – 4;

                                3-4 ошибки – 3;

                          более 4 ошибок – 2)

IV. Решение упражнений у доски.

Задание. Найти область определения функции, заданной формулой

а) у =                           б) у =

(к доске одновременно вызываются 2 человека, остальные учащиеся выполняют в тетради)

     Ответы:

а) область определения – все числа, кроме х = 2; х = -3;

б) D(у) = [8; + ∞)

V. Самостоятельная работа(приложение 3).

                          I вариант                                                                        II вариант

   Задайте формулой

         прямую пропорциональность                                   обратную пропорциональность

                                                       график которой расположен

    во II и IV координатных четвертях                              в I и III координатных четвертях

                                                   Постройте график этой функции.

                         Укажите область определения и область значений функции

VI. Итоги урока.

-Наш урок подошёл к концу. Давайте вспомним, что мы делали на уроке?

-Какие знания помогали вам на уроке?

-Как оцениваете свою работу на уроке?

-Как работали сегодня ваши товарищи? Какую оценку вы им поставили бы?

(Объявляются оценки за урок и даётся домашнее задание)

Приложение 1.

Ф.И.________________________________________________________________                                                    

Приложение2.

Приложение 3.

Как найти область определения функции заданной формулой, примеры и способы решения 10 класс, ручной и автоматизированный методы, онлайн-калькулятор

При решении различных задач и в научных исследованиях математики сталкиваются с необходимостью найти область определения функции.

В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров).

Общие сведения

Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному».

Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком.

Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Исследование функции — естественный процесс, который встречается в различных дисциплинах.

Программирование на разных языках пользуется огромной популярностью. В нем нужны математические знания для написания некоторых программ и игр. В последних следует производить точные расчеты и описывать некоторые функции героя. Например, удар мечом подчиняется определенному математическому закону или функции. Для корректной ее работы и тестирования следует находить грамотно ее область определения.

Основные понятия

Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения.

Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений.

Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д.

Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений.

Например, D (y) = [0, 157). Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[«) до 157 не включительно.

Типы функций

Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические.

Рациональные целые — выражения полиномиального типа (линейные). Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа.

Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом.

К иррациональным функциям относят выражения, которые содержат переменную величину под корнем. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0.

Правильное обозначение

Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере.

Следует руководствоваться такими правилами:

Использовать скобку «[» и/или «]», когда нужно указать принадлежность к множеству.

Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству.

Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50].

Алгоритмы определения

Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z.

Если функция является дробной, то следует использовать следующий алгоритм:

Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность).

Однако если корень нечетный, то D (f) — множество действительных чисел. Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.

Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел.

Другие методы

Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции.

Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.

В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f).

После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат.

Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы.

Примеры решения

Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.

С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.

Для линейного вида

Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:

Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = — x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика.

В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.

Дробные и иррациональные

Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f).

Решается задача таким способом:

Нужно решить уравнение (x — 4) * (x + 4) = 0. Из него видно, что x1 = 4 и x2 = -4, поскольку эти значения «превращают» знаменатель в неопределенность. Следовательно, D (y) = (-бесконечность, -4) U (4, +бесконечность).

В случае с иррациональным выражением: y = sqrt[4 * sqr (x) — 12 * x + 9], нужно решить уравнение подкоренного выражения. 2] — (4 * 4 * 9) = 144 — 144 = 0.

Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность).

Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.

АлгебраТеория вероятности формула и примеры для чайников, задачи с решениями, как найти классическую вероятность в математике, как обозначается и в чем выражается вероятность

АлгебраТригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки

Тема 7.

Тема 7. Функции

1. Понятие функции

    Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.

    x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).

    График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).

    График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.

    Нули функции – значения x такие, что f(x)=0. Интервалы знакопостоянства – множества значений аргумента, при которых значения функции только положительны или только отрицательны.

3. Некоторые алгебраические функции

    Функция возрастает при a>0, убывает при a<0.

    Частные случаи: y=b – прямая, параллельная оси OX;

    y=ax – прямая, проходящая через начало координат.

    Точки пересечения с осями координат:

    с осью OX  – (x₁, 0) и (x₂, 0),

    с осью OY – (0, c).

Пример 1. График какой функции является возрастающим:

    Решение:

        Рассмотрим каждую из функций в отдельности:

        Возьмём два значения х₁ = 1 и х₂ = 4. Им соответствует у₁ = – 1, у₂ = – 2. Видим, что если х₁ < x₂ , то у₁ > у₂.         Функция убывающая.

        б) у = х³ – 27 – алгебраическая функция. Область определения – множество всех действительных чисел. На всей области определения функция монотонна. Возьмём два значения х₁ = 3, х₂ = 4. Им соответствует у₁ = 0, у₂ = 37.

        Видим, что если х₁ < x₂ , то и у₁ < у₂. Функция возрастающая.

        в) y=2^-x – показательная функция. Областью определения является множество всех действительных чисел. На всей области определения функция монотонна. Пусть х₁ = 0, х₂ = 1. Им соответствуют у₁ = 1, у₂ = 0,5.

        Видим, что если х₁ < x₂ , то у₁ > у₂. Функция убывающая.

    Ответ: б) у = х³ – 27.

Пример 2. Парабола у = 2х² – (а – 3)х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.

    Решение:

        Найдём значение параметра а. Т.к. парабола проходит через начало системы координат, то координаты точки (0; 0) являются корнями уравнения параболы:  0 = 2 ∙ 0² – (а – 3) ∙ 0 + а + 3;  а = – 3. 

        Уравнение параболы примет вид: у = 2х² + 6х.

    Ответ: – 1, 5.

Пример 3. В каких точках график функции f(x) = x² – 3 пересекает прямую у(х) = х – 1?

    Решение:

        х² – 3 = х – 1;  х² – х – 2 = 0;  х₁= – 1, или х₂ = 2. 

        Соответственно, у₁ = – 2, у₂ = 1.

    Ответ: (– 1; – 2), (2; 1).

Пример 4. При каких значениях k прямые – kх + 7у = – 13 и 14у – 3х + 5 = 0 параллельны?

    Решение:

        Две различные прямые у = k₁х + b₁ и у = k₂х + b₂ параллельны, если k₁ = k₂, но при этом b₁ ≠ b₂.

        В обоих уравнениях выразим у через х.

    Ответ: при k = – 1,5.

Пример 5. Найти точки пересечения прямой у = 5 + х с осями координат.

    Решение:

        Когда график функции пресекает ось ОХ, значение у = 0.

        Получаем уравнение 5 + х = 0, х = – 5. 

        Когда график функции пересекает ось OY, значение х = 0, т.е. у = 5.

    Ответ: (– 5; 0), (0; 5).

Пример 6. Найти нули функции у = (х + 1)∙(х – 2).

    Решение:

        Решаем уравнение (х + 1)∙(х – 2) = 0.

        х + 1 = 0 или х – 2 = 0; х₁ = – 1, х₂ = 2.

    Ответ: (– 1; 0), (2; 0).

    Решение:

        Оцениваем последовательно:

Пример 8. Найдите сумму целых значений функции у = 3 – 2 sin x.

    Решение:

        Оценим значение 3 – 2 sin x.

        Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.

    Ответ: 15.

Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А(0; 2), проходящая через точку В(2; – 6). Задайте эту функцию формулой.

    Решение:

        Уравнение квадратичной функции у = ах² + bх + с.

            Уравнение примет вид: у = ах² + с.

        2) точка А принадлежит графику, следовательно её координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2. 

            Уравнение примет вид: у = ах² + 2.

        3) график проходит через точку В. Её координаты также удовлетворяют уравнению: – 6 = а ∙ 2² + 2, – 8 = 4 ∙ а,          а = – 2.

        Получили уравнение у = – 2х² + 2.

    Ответ: у = – 2х² + 2.

Пример 13. Найдите g (x) , если f (x) = 2x – 3, g (f (x)) = x. Вычислите g (1).

    Решение:

        Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.

        2x – 3 = 1, х = 2.

        Следовательно, g (f (x)) = 2, т.е. g (1) = 2.

    Ответ: g (1) = 2.

Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y=5^2x, y=5^3x-1 и через точку параболы y=(2x-1)², в которой производная функции, задающей параболу, равна 8.

    Решение:

        1) найдём точку пересечения кривых:

        2) найдём точку параболы, в которой производная равна 8:  

        – 21х + 21 = 0,5у – 12,5;  – 42х + 42 = у – 25;  у = – 42х + 47.

    Ответ: у = – 42х + 47.

Задания для самостоятельного решения

Базовый уровень

Укажите длину интервала области определения для функций: 

    25) y=log₄(5x+6-x²)  

    26) y=log₆(x²+3).

Укажите области значения функций:

    27) y=-3sinx.

    28) y=0,7cos3x.

Решите задачи:

    30) Сколько натуральных значений может принять функция y=log₂(4-x²) на всей области определения?

    31) Найдите сумму целых значений функции y=3cosx-5.

    33) Укажите график функции, возрастающей на отрезке [-3; 2]. 

    34) Укажите функцию, которая возрастает на всей области определения.

    1) y=-x^0,5; 2) y=1-e^-x; 3) y=ctg2x; 4) y=|-x|.

    37) Найдите наименьшее значение функции f(x)=3^2x-1 на промежутке [-3; 1].

    38) Вычислите координаты точек пересечения графика функции у = – 2х² + 4х + 6 с осью OY.

    39) Вычислите ординату точки пересечения прямой у = 5 – 2х с осью ОY.

    40) Укажите точки пересечения графиков функций у = 2х + 4 и у = – 2х.

    41) В каких точках график функции f (x) = 3x² + 6x пересекает прямую у = 6 – х?

Ответы

область определения, нули функции, четность функции и все остальные.

Функция — это одно из важнейших математических понятий. Функция — зависимость переменной у от переменной

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!

Для построения графика функции советуем использовать нашу программу — Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!

Основные свойства функций.

1) Область определения функции и область значений функции.

Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции — это множество всех действительных значений y, которые принимает функция.

В элементарной математике изучаются функции только на множестве действительных чисел.

2) Нули функции.

Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

3) Промежутки знакопостоянства функции.

4) Монотонность функции.

Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

5) Четность (нечетность) функции.

Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.

6) Ограниченная и неограниченная функции.

Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

7) Периодическость функции.

Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

Изучив данные свойства функции Вы без проблем сможете исследовать функцию и по свойствам функции сможете построить график функции. Также посмотрите материал про таблицу истинности, таблицу умножения, таблицу Менделеева, таблицу производных и таблицу интегралов.

Слишком сложно?

Свойства функции не по зубам? Тебе ответит эксперт через 10 минут!

Найдите множество значений функции у = 7 — sin 2x — Математика 10 класс — Школьная математика — Каталог статей

Презентация для урока «Определение числовой функции. Область определения, область значений функции»

  Балакирева Галина Викторовна  МБОУ СОШ №2 им.А.И.Исаевой

Класс: 9

Тема урока: «Определение числовой функции. Область определения, область значений функции»     

Тип урока:   Урок закрепления изучаемого материала.

Цели урока:

— закрепить навыки работы с графиком числовой функции, находить её область определения и область значений;

— развивать логическое мышление, умение обобщать изучаемый материал, делать выводы;

 — воспитывать уверенность, внимание, самостоятельность при работе на уроке.

Историческая справка:  Общее определение функции, которое мы называем теперь «классическим» сформировалось не очень давно – лишь в начале прошлого века. И хотя математики имели дело с различными конкретными функциями почти на каждом шагу развития науки, все же должен был пройден долгий путь отбора элементарных понятий и их обобщений, пока ученые пришли к необходимости общего определения функции и нашли его.

Экспериментальное задание.   На столах лежат листы, на которых написаны определения функции, данные учеными в CVIII- CIC веках.

Определение функции

Функция переменной величины есть аналитическое выражение, составленное из этой величины и постоянных.                                                                  

  И. Бернулли, 1718г.

 Функция есть кривая, начертанная свободным влечением руки.                                                    

 Л. Эйлер, 1748г.

Когда некоторые количества зависят от других таким образом, что при изменении последних изменяются и первые, то первые называются функциями вторых.                                                    

   Л. Эйлер, 1755г.

Всякое количество, значение которого зависит от одного или многих других количеств, называется функцией этих последних, независимо от того, известно или нет, какие операции нужно произвести, чтобы перейти от них к первому.

                                                                  С. Лукруа,1797г.

Функция от х есть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа. Зависимость может существовать и оставаться неизвестной.                                                                      

 Н. Лобачевский, 1834г.

1. есть функция от х, если всякому значению х соответствует вполне определенное значение у, причем совершенно неважно, каким именно способом установлено указанное соответствие.

   П. Дирихле, 1837г.

Сравните эти определения с определением, которое дано в учебнике. Какое из этих определений более соответствует определению функции на ваш взгляд? (выслушать ответы)

•    Мы увидели, как совершенствовалось определение функции. И последняя его форма не означает конца истории. Можно не сомневаться, что и в дальнейшем под воздействием новых требований как самой математики, так и других наук определение функции будет изменяться. А эти изменения будут приводить к новым важным открытиям.

Устная работа:

Вопросы:

1)Какую зависимость называют функцией?

2)Как читают запись y = f(x)?

3)Что называют аргументом функции?

4)Что такое область определения функции?

5)Что называют значением функции?

6)Как читают запись f(2) = 6 и что она означает?

7)Что называют областью значений функции?

Найдите область определения функции, значений функции

2) Индивидуальная работа по карточкам.

Карточка №1.

Карточка №2.

3) Самостоятельная работа с самопроверкой. Функция задана формулой. Найдите:

а) f(2) =?                                             а) f(16) =?

б) D(f) = ?                                          б) D(f) = ?

4) Работа по учебнику : №8.13(а), 3 8.14(а)

6) Повторение. Подготовка к ГИА. Задания из открытого банка, прототипы заданий №5.

6) Рефлексия   Заполните карточки и сдайте учителю.

Ф. И.

Усвоил(а) хорошо

Иногда ошибаюсь

Пока усвоил(а) плохо

Понятие «Функция»

Область определения функции

Область значений функции

 Что такое график функции

7.Домашняя работа: №№№8.13(б,в,г), 3 8.14(б,в,г),8.15.

Функциональные зависимости вокруг нас

Вопросы

• Какую зависимость называют функцией?
• Как читают запись y = f(x) ?
• Что называют аргументом функции?
• Что такое область определения функции?
• Что называют значением функции?
• Как читают запись f(2) = 6 и что она означает?
• Что называют областью значений функции?

Условные обозначения

• Область определения функции D(f)
• Область значения функции E(f)

Примеры записи:

• E(f) = (-15; 2,6)  [10; +  ) – промежуток (или объединение промежутков) D(f) = {-5; -2; -0,3; 11} – перечисление элементов D(f) = R – указание числового множества
• E(f) = (-15; 2,6)  [10; +  ) – промежуток (или объединение промежутков)
• D(f) = {-5; -2; -0,3; 11} – перечисление элементов
• D(f) = R – указание числового множества

1 . Укажите область определения и область значений функции, которая задана таблицей:

x

— 4

y

-8

— 3

— 2

— 6

— 1

— 4

0

— 2

1

0

2

2

3

4

6

Область значений

Область определения

D(f)={ -4; -3; -2; -1; 0;1; 2; 3}

E(f)={-8; -6; -4;-2; 0;2; 4; 6}

2. Укажите область определения и область значений функции.

D(f)= [- 3; 3]

Область определения

E(f)= [- 2; 3]

Область значений

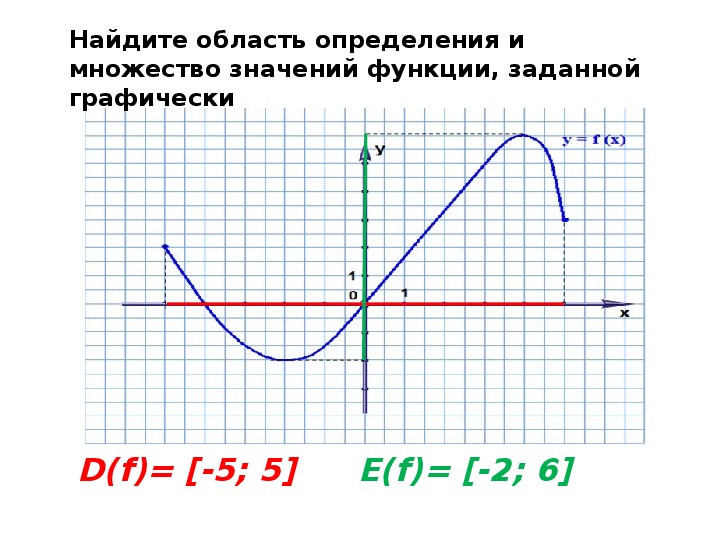
4. Функция задана графиком. Заполните пропуски.

• f(-3) =
• f(- 1) =
• f(x) = — 1,5 при x =
• f(x) = 2 при х = х = , x =
• D(f) =
• E(f) =

— 2

?

3

?

-2,5

?

— 1 ,5

?

?

4

-0,5

?

[- 3; 4]

?

[- 2; 3]

?

5 . Функция задана формулой. Найдите:

а) f(2) = ?

б) D(f) = ?

а) f( 16 ) = ?

б) D(f) = ?

Решение:

Решение:

Готовимся к ГИА

• Вычислите значение функции

в точке x=2

1) 2)

3) 4)

2. Функция y=f(x) задана графиком на отрезке ( — 4 ; 5)

Найдите f(2) :

б)

1) 1;

2) 2;

3) -1 ;

4) — 2 .

3.Найдите область определения функции

4. Найдите область значений функции

5.Установите соответствие между функциями и их графиками:

1)

2)

3)

4)

6.Используя график функции у = f( x ) , определите, какое утверждение верно.

Найдите домен и диапазон по графикам

Другой способ определить область и диапазон функций — использовать графики. Поскольку домен относится к набору возможных входных значений, домен графа состоит из всех входных значений, показанных на оси x . Диапазон — это набор возможных выходных значений, которые отображаются на оси y . Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения.См. Рисунок 6.

Рисунок 6

Мы можем заметить, что граф простирается по горизонтали от [latex] -5 [/ latex] вправо без границ, поэтому доменом является [latex] \ left [-5, \ infty \ right) [/ latex]. График по вертикали — это все значения диапазона [latex] 5 [/ latex] и ниже, поэтому диапазон равен [latex] \ left (\ mathrm {- \ infty}, 5 \ right] [/ latex]. Обратите внимание, что домен и диапазон всегда записываются от меньших к большим значениям или слева направо для домена и от нижней части графика до верхней части графика для диапазона.

Пример 6: Поиск домена и диапазона из графика

Найдите область и диапазон функции [latex] f [/ latex], график которой показан на рисунке 7.

Рисунок 7

Решение

Мы можем заметить, что горизонтальная протяженность графа составляет от –3 к 1, поэтому домен [latex] f [/ latex] равен [latex] \ left (-3,1 \ right] [/ latex].

Рисунок 8

График по вертикали составляет от 0 до –4, поэтому диапазон равен [latex] \ left [-4,0 \ right] [/ latex].

Пример 7: Поиск области и диапазона по графику добычи нефти

Найдите область и диапазон функции [latex] f [/ latex], график которой показан на рисунке 9.

Решение

Введенное количество по горизонтальной оси — «годы», которые мы представляем переменной [latex] t [/ latex] для времени. Выходное количество составляет «тысячи баррелей нефти в день», что мы представляем переменной [латекс] b [/ латекс] для баррелей.График может продолжаться влево и вправо за пределы того, что просматривается, но на основе видимой части графика мы можем определить домен как [латекс] 1973 \ le t \ le 2008 [/ latex], а диапазон — как примерно [латекс] 180 \ ле б \ ле 2010 [/ латекс].

В обозначении интервалов это [1973, 2008], а диапазон — примерно [180, 2010]. Для области и диапазона мы аппроксимируем наименьшие и наибольшие значения, поскольку они не попадают точно на линии сетки.

Попробуй 6

По графику на рисунке 10 определите домен и диапазон, используя обозначение интервалов.

Рисунок 10

Решение

Вопросы и ответы

Могут ли домен и диапазон функции совпадать?

Да. Например, домен и диапазон функции корня куба являются набором всех действительных чисел.

Как найти диапазон — Алгебра 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Что такое диапазон по математике?

Обновлено 19 декабря 2020 г.

Лиза Мэлони

У вас есть два разных способа определить диапазон в математике.Если вы ведете статистику, «диапазон» обычно означает разницу между самым высоким и самым низким значениями в наборе данных. Если вы занимаетесь алгеброй или математическим расчетом, под «диапазоном» понимается набор возможных результатов или выходных значений функции.

Диапазон в статистике

Если вас попросят найти диапазон в статистике, вас просто попросят найти самое высокое и самое низкое значения в вашем наборе данных, а затем найти разницу между ними. Каждый раз, когда вы слышите слово «разница», это признак того, что вы собираетесь вычесть его, поэтому формула, которую вы будете использовать, следующая:

\ text {максимальное значение} — \ text {минимальное значение} = \ text {диапазон}

Пример 1: Представьте, что вы заглянули в записную книжку учителя и увидели, что до сих пор процент оценок учащихся в классе составляет {95, 87, 62, 72, 98, 91, 66, 75 }.Фигурные скобки часто используются для заключения набора данных, поэтому вы знаете, что все внутри фигурных скобок принадлежит друг другу.

Каков диапазон этого набора данных или, другими словами, диапазон оценок учащихся? Сначала определите наивысшую точку данных (98) и самую низкую точку данных (62). Затем вычтите наименьшее значение из наибольшего:

98 — 62 = 36

Таким образом, диапазон этого конкретного набора данных составляет 36 процентных пунктов.

Диапазон функции

Когда вы начнете изучать функции в математике, вы столкнетесь со вторым определением диапазона.Чтобы понять диапазон, полезно думать о функциях как о маленьких математических машинах. Набор значений, которые вы можете ввести в математическую машину, называется доменом (еще одно очень важное понятие). Набор возможных результатов, когда вы проверяете эти значения с помощью математической машины, называется доменом . И набор фактических результатов, которые вы получаете, называется диапазоном .

Есть несколько важных взаимосвязей между диапазоном и доменом, которые вам необходимо понять.Во-первых, каждое значение в домене соответствует только одному значению в диапазоне вашей функции. Если какое-либо значение в домене соответствует более чем одному значению в диапазоне, у вас может быть связь между двумя наборами данных, но это технически не классифицируется как функция. Однако возможно, что несколько значений домена будут соответствовать одному и тому же значению в диапазоне этой функции.

Один из лучших способов понять это — представить свой собственный математический класс. Студенты в классе представляют предметную область (или информацию, которая входит в функцию), в то время как сам класс является функцией или «математической машиной».»Ваши итоговые оценки представляют собой диапазон, или то, что вы получите после проверки элементов предметной области (студентов) с помощью функции (математический класс).

Когда вы посмотрите на этот пример, вы интуитивно увидите, что каждый ученик получит только одна итоговая оценка по окончании урока. Каждое значение в домене соответствует только одному значению в диапазоне. Однако одну и ту же оценку могут получить несколько учащихся. Например, в группе может быть два или три учащихся. ваш класс, который очень усердно учился и сумел получить окончательную оценку 96 процентов.Несколько значений в домене могут соответствовать одному значению в диапазоне.

Пример 2: Представьте, что вы имеете дело с функцией x ² , с доменом, ограниченным до {−3, −2, −1, 1, 2, 3, 4} . Каков диапазон этой функции?

Хотя вы узнаете о более продвинутых способах поиска диапазона позже, на данный момент самый простой способ найти диапазон этой функции — это применить функцию к каждому элементу домена и отслеживать свои результаты.Другими словами, вставляйте каждый элемент домена по одному как x в функцию x ² . Это дает вам набор результатов:

\ {9, 4, 1, 1, 4, 9, 16 \}

Но, как вы можете видеть, некоторые элементы там повторяются. Вспоминая пример оценок по математике как функции, это нормально; более одного ученика могут получить одну и ту же оценку, или более одного элемента домена могут «указывать» на один и тот же элемент в диапазоне. Но вы не хотите записывать повторяющиеся элементы, когда указываете диапазон.Итак, ваш ответ прост:

\ {1, 4, 9, 16 \}

Исчисление I — Функции

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон).Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 1-1: Функции

В этом разделе мы хотим убедиться, что вы знакомы с функциями и их обозначениями.Оба они появятся почти в каждом разделе класса Calculus, поэтому вам нужно будет иметь с ними дело.

Во-первых, что такое функция? Самым простым определением является то, что уравнение будет функцией, если для любого \ (x \) в области определения уравнения (область — это все \ (x \), которые могут быть включены в уравнение), уравнение будет дают ровно одно значение \ (y \), когда мы оцениваем уравнение при конкретном \ (x \).

Обычно это легче понять на примере.2} = 3 + 1 = 4 \]

Теперь есть два возможных значения \ (y \), которые мы могли бы использовать здесь. Мы могли бы использовать \ (y = 2 \) или \ (y = — 2 \). Поскольку есть два возможных значения \ (y \), которые мы получаем из одного \ (x \), это уравнение не является функцией.

Обратите внимание, что это должно быть только для одного значения \ (x \), чтобы уравнение не было функцией. Например, мы могли бы использовать \ (x = — 1 \), и в этом случае мы получили бы одиночный \ (y \) (\ (y = 0 \)). Однако из-за того, что происходит при \ (x = 3 \), это уравнение не будет функцией.2} — 5x + 3 \\ \ end {выровнено} \\ & \ vdots & \ end {array} \]

Напомним, что это НЕ буква, умноженная на \ (x \), это просто причудливый способ записи \ (y \).

Итак, чем это полезно? Итак, возьмем приведенную выше функцию и получим значение функции в \ (x = -3 \). Используя обозначение функции, мы представляем значение функции в точке \ (x = -3 \) как \ (f \ left (-3 \ right) \). Обозначение функций дает нам удобный компактный способ представления значений функций.

Теперь, как мы на самом деле оцениваем функцию? Это действительно просто.2} + 6x — 11 \) найдите каждое из следующих.

1. \ (f \ влево (2 \ вправо) \)
2. \ (f \ left ({- 10} \ right) \)
3. \ (е \ влево (т \ вправо) \)
4. \ (f \ left ({t — 3} \ right) \)
5. \ (е \ влево ({x — 3} \ вправо) \)
6. \ (е \ влево ({4x — 1} \ вправо) \)

\ [f \ left (2 \ right) = — {\ left (2 \ right) ^ 2} + 6 (2) — 11 = — 3 \]

Будьте осторожны при возведении в квадрат отрицательных чисел!

Помните, что мы заменяем \ (x \) на ВСЕ В скобках слева. 2} + 6t = 0 \]

Во-первых, мы должны максимально разложить уравнение на множители.2} — 4 \ left (3 \ right) \ left (2 \ right)}}} {{2 \ left (3 \ right)}} \\ & = \ frac {{6 \ pm \ sqrt {12}} } {6} \\ & = \ frac {{6 \ pm \ sqrt {\ left (4 \ right) \ left (3 \ right)}}} {6} \\ & = \ frac {{6 \ pm 2 \ sqrt 3}} {6} \\ & = \ frac {{3 \ pm \ sqrt 3}} {3} \\ & = 1 \ pm \ frac {1} {3} \ sqrt 3 \\ & = 1 \ pm \ frac {1} {{\ sqrt 3}} \ end {align *} \]

Чтобы напомнить вам, как упрощать радикалы, мы дали несколько форм ответа.

Чтобы решить проблему, вот полный список всех корней этой функции.

Обратите внимание, что мы не использовали окончательную форму для корней из квадратичного. Обычно на этом мы останавливаемся на упрощении для такого рода корней. Также обратите внимание, что для практики мы разделили компактную форму на два корня квадратичной. Вам нужно будет уметь это сделать, поэтому убедитесь, что у вас есть такая возможность.

В этом примере было еще несколько моментов, помимо поиска корней функций.

Первый напомнил вам о квадратной формуле. Это будет не последний раз, когда он вам понадобится на этом занятии.

Второй — чтобы вы привыкли видеть «беспорядочные» ответы. На самом деле, ответы в приведенном выше примере на самом деле не такие уж и беспорядочные. Однако большинство студентов, окончивших уроки алгебры, привыкли видеть в ответах только целые числа и случайную «красивую» дробь.

Итак, вот справедливое предупреждение. В этом классе я часто намеренно делаю ответы «беспорядочными», чтобы вы избавились от привычки всегда ожидать «хороших» ответов.В «реальной жизни» (что бы это ни было) ответом редко бывает простое целое число, например два. В большинстве задач ответом будет десятичная дробь, полученная из беспорядочной дроби и / или ответа с участием радикалов. 2} + 12x + 5 \)

Мы знаем, что это линия, а не горизонтальная линия (потому что наклон равен 5, а не нулю…).Это означает, что эта функция может принимать любое значение, поэтому диапазон состоит из действительных чисел. Используя «математические» обозначения, это

В более общем смысле это многочлен, и мы знаем, что можем подставить любое значение в многочлен, и поэтому домен в этом случае также состоит из всех действительных чисел или,

Это квадратный корень, и мы знаем, что квадратные корни всегда положительны или равны нулю.Тогда мы знаем, что диапазон будет

Для домена нам нужно немного поработать, но не так много. Нам нужно убедиться, что мы не извлекаем квадратные корни из отрицательных чисел, поэтому нам нужно это потребовать,

Тогда домен:

Итак, как уже говорилось, мы знаем, что это будет наивысшая точка на графике или наибольшее значение функции, а парабола будет принимать все значения меньше этого, поэтому диапазон равен

Эта функция содержит абсолютное значение, и мы знаем, что абсолютное значение будет либо положительным, либо нулевым.В этом случае абсолютное значение будет равно нулю, если \ (z = 6 \), и поэтому часть абсолютного значения этой функции всегда будет больше или равна нулю. Мы вычитаем 3 из части абсолютного значения, и тогда мы знаем, что диапазон будет

Мы можем подставить любое значение в абсолютное значение, и поэтому доменом снова будут все действительные числа или,

Эта функция поначалу может показаться немного сложной, но на самом деле она самая простая в этом наборе примеров.Это постоянная функция, поэтому любое значение \ (x \), которое мы вставляем в функцию, даст значение 8. Это означает, что диапазон представляет собой одно значение или

В домене все реальные числа,

В общем, определение диапазона функции может быть несколько затруднительным. 2} — 2x — 15 = \ left ({x — 5} \ right) \ left ({x + 3} \ right) = 0 \ hspace {0.2} — t — 6 = \ left ({t — 3} \ right) \ left ({t + 2} \ right) = 0 \]

Итак, функция будет равна нулю при \ (t = — 2 \) и \ (t = 3 \). Напомним, что эти точки будут единственным местом, где функция может менять знак . Менять знак в этих точках не требуется, но это будут единственные точки, где функция может изменить знак. Это означает, что все, что нам нужно сделать, это разбить числовую линию на три области, избегая этих двух точек, и проверить знак функции в одной точке в каждой из областей.Если функция положительна в одной точке региона, она будет положительной во всех точках в этой области, потому что не содержит ни одной из точек, где функция может менять знак. У нас будет аналогичная ситуация, если функция будет отрицательной для контрольной точки.

Итак, вот числовая строка, показывающая эти вычисления.

Из этого мы видим, что единственная область, в которой квадратичная (в ее модифицированной форме) будет отрицательной, находится в средней области.2} — 9> 0 \]

Обратите внимание, что нам нужно, чтобы неравенство здесь было строго больше нуля, чтобы избежать проблем с делением на ноль. Мы можем либо решить эту проблему методом из предыдущего примера, либо, в этом случае, ее достаточно легко решить путем проверки. Домен в данном случае

Следующая тема, которую нам нужно обсудить, — это композиция функций .2} — x + 10 \) и \ (g \ left (x \ right) = 1 — 20x \) найдите каждое из следующих значений.

1. \ (\ left ({f \ circ g} \ right) \ left (5 \ right) \)
2. \ (\ left ({f \ circ g} \ right) \ left (x \ right) \)
3. \ (\ left ({g \ circ f} \ right) \ left (x \ right) \)
4. \ (\ left ({g \ circ g} \ right) \ left (x \ right) \)

В этом случае у нас есть число вместо \ (x \), но оно работает точно так же.2} + 20x — 199 \ end {align *} \]

И еще раз подчеркнем суть дела. Этот ответ отличается от предыдущей части. Порядок важен в композиции.

В этом случае не радуйтесь тому факту, что это та же функция. Композиция по-прежнему работает.

Давайте поработаем еще один пример, который приведет нас к следующему разделу.

1. \ (\ left ({f \ circ g} \ right) \ left (x \ right) \)
2. \ (\ left ({g \ circ f} \ right) \ left (x \ right) \)

\ [\ begin {align *} \ left ({f \ circ g} \ right) \ left (x \ right) & = f \ left ({g \ left (x \ right)} \ right ») \\ & = f \ left ({\ frac {1} {3} x + \ frac {2} {3}} \ right) \\ & = 3 \ left ({\ frac {1} {3} x + \ frac {2 } {3}} \ right) — 2 \\ & = x + 2 — 2 \\ & = x \ end {align *} \]

\ [\ begin {align *} \ left ({g \ circ f} \ right) \ left (x \ right) & = g \ left ({f \ left (x \ right)} \ right ») \\ & = g \ left ({3x — 2} \ right) \\ & = \ frac {1} {3} \ left ({3x — 2} \ right) + \ frac {2} {3} \\ & = x — \ frac {2} {3} + \ frac {2} {3} \\ & = x \ end {align *} \]

В данном случае две композиции были одинаковыми, и на самом деле ответ был очень простым.

Обычно этого не происходит. Однако, когда обе композиции являются \ (x \), между двумя функциями существует очень хорошая связь. Мы рассмотрим эти отношения в следующем разделе.

Python range () — GeeksforGeeks

range () — это встроенная функция Python. Он используется, когда пользователю необходимо выполнить действие определенное количество раз. range () в Python (3.x) — это просто переименованная версия функции под названием xrange в Python (2.x). Функция range () используется для генерации последовательности чисел.

range () обычно используется для циклов, поэтому знание этого является ключевым аспектом при работе с любым типом кода Python. Наиболее распространенное использование функции range () в Python — перебирать тип последовательности (список, строка и т. Д.) С помощью цикла for и while.

Python range () Основы:
Проще говоря, range () позволяет пользователю генерировать серию чисел в пределах заданного диапазона.В зависимости от того, сколько аргументов пользователь передает функции, пользователь может решить, где эта последовательность чисел будет начинаться и заканчиваться, а также насколько большой будет разница между одним числом и другим. range () в основном принимает три аргумента.

• начало : целое число, начиная с которого должна возвращаться последовательность целых чисел
• стоп: целое число, перед которым должна возвращаться последовательность целых чисел.
  Диапазон целых чисел заканчивается на остановке — 1.
• шаг: целочисленное значение, которое определяет приращение между каждым целым числом в последовательности

0 1 2 3 4 5 6 7 8 9
10 20 30 40
Сумма первых 10 натуральных чисел: 55
 

Есть три способа вызвать range ():

• range (stop) принимает один аргумент.
• диапазон (старт, стоп) принимает два аргумента.
• диапазон (начало, остановка, шаг) принимает три аргумента.

диапазон (стоп)

Когда пользователь вызывает range () с одним аргументом, пользователь получит серию чисел, которая начинается с 0 и включает в себя все целые числа вплоть до номера, предоставленного пользователем, но не включая его. как остановка. Например -

Выход:

0 1 2 3 4 5 6 7 8 9
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
 

range (start, stop)

Когда пользователь вызывает range () с двумя аргументами, пользователь может решить не только, где заканчивается серия чисел, но и где она начинается, поэтому пользователю не нужно начинать с 0 все время.Пользователь может использовать range () для генерации серии чисел от X до Y с использованием диапазона (X, Y). Для примера - аргументы

Выход:

0 3 6 9 12 15 18 21 24 27
0 5 10 15 20 25 30 35 40 45
 

25 23 21 19 17 15 13 11 9 7 5 3
30 26 22 18 14 10 6 2
25 22 19 16 13 10 7 4 1-2-5
 

для i в диапазоне (3.3):
TypeError: объект float нельзя интерпретировать как целое число
 

Объединение результата
0 1 2 3 4 10 12 14 16 18
 

Первый элемент: 0

Последний элемент: 9

Пятый элемент: 4