Как найти обратную матрицу методом присоединенной матрицы: Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.

Обратная матрица.

Обратная матрица.

Навигация по странице:

• Определение обратной матрицы
• Свойства обратной матрицы
• Методы вычисления обратной матрицы
  • Вычисления обратной матрицы с помощью присоединённой матрицы
  • Вычисления обратной матрицы с помощью союзной матрицы

Онлайн калькулятор. Обратная матрица с помощью присоединённой матрицы.

Онлайн калькулятор. Обратная матрица с помощью союзной матрицы.

Определение.

Обратная матрица A⁻¹ — матрица, произведение которой на исходную матрицу A равно единичной матрице E:

A·A^-1 = A^-1·A = E

Замечание.

Обратная матрица существует только для квадратных матриц определитель которых не равен нулю.

Свойства обратной матрицы

●	det(A-1) =  1 det(A)
●	(A·B)-1 = A-1·B-1
●	(A-1)T = (AT)-1
●	(kA)-1 =  A-1 k
●	(A-1)-1 = A

Методы вычисления обратной матрицы

Вычисление обратной матрицы с помощью присоединённой матрицы

Теорема.

Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.

Замечание.

Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.

Пример 1.

Найти обратную матрицу матрицы A

A =		2	4	1
		0	2	1
		2	1	1

Решение: Приписываем к матрице A справа единичную матрицу третьего порядка:

A|E =		2	4	1	1	0	0		~
		0	2	1	0	1	0
		2	1	1	0	0	1

Преобразуем левую часть полученной матрицы в единичную.

Для этого от 3-тей строки отнимем 1-ую строку:

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		2 — 2	1 — 4	1 — 1	0 — 1	0 — 0	1 — 0

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		0	-3	0	-1	0	1

Третью строку поделим на (-3) и поменяем местами со второй строкой:

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		0	1	0	1/3	0	-1/3

~		2	4	1	1	0	0		~
		0	1	0	1/3	0	-1/3
		0	2	1	0	1	0

Отнимем он 1-ой строки 2-ую умноженную на 4; от 3-тей строки 2-ую умноженную на 2:

~		2 — 4·0	4 — 4·1	1 — 4·0	1 — 4·(1/3)	0 — 4·0	0 — 4·(-1/3)		~
		0	1	0	1/3	0	-1/3
		0 — 2·0	2 — 2·1	1 — 2·0	0 — 2·1/3	1 — 2·0	0 — 2·(-1/3)

~		2	0	1	-1/3	0	4/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Отнимем он 1-ой строки 3-ую строку:

~		2 — 0	0 — 0	1 — 1	-1/3 — (-2/3)	0 — 1	4/3 — 2/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

~		2	0	0	1/3	-1	2/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Разделим 1-ую строку на 2:

~		1	0	0	1/6	-1/2	1/3
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Ответ: A-1 =		1/6	-1/2	1/3
		1/3	0	-1/3
		-2/3	1	2/3

Вычисление обратной матрицы с помощью союзной матрицы

Определение.

Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.

A-1 =	1	ÃT
	det(A)

Пример 1.

Найти обратную матрицу матрицы A

A =		2	4	1
		0	2	1
		2	1	1

Решение: Найдем определитель матрицы A:

det(A) =	2	4	1	=
	0	2	1
	2	1	1

= 2·2·1 + 4·1·2 + 1·0·1 — 1·2·2 — 2·1·1 — 4·0·1 = 4 + 8 + 0 — 4 — 2 — 0 = 6

Найдем алгебраические дополнения матрицы A:

A11 = (-1)1 + 1 ·	2	1	= 2·1 — 1·1 = 1
	1	1

A12 = (-1)1 + 2·	0	1	= -(0·1 — 1·2) = 2
	2	1

A13 = (-1)1 + 3·	0	2	= 0·1 — 2·2 = -4
	2	1

A21 = (-1)2 + 1·	4	1	= -(4·1 — 1·1) = -3
	1	1

A22 = (-1)2 + 2·	2	1	= 2·1 — 1·2 = 0
	2	1

A23 = (-1)2 + 3·	2	4	= -(2·1 — 4·2) = 6
	2	1

A31 = (-1)3 + 1·	4	1	= 4·1 — 1·2 = 2
	2	1

A32 = (-1)3 + 2·	2	1	= -(2·1 — 1·0) = -2
	0	1

A33 = (-1)3 + 3·	2	4	= 2·2 — 4·0 = 4
	0	2

Запишем союзную матрицу:

à =		1	2	-4
		-3	0	6
		2	-2	4

Найдем обратную матрицу:

A-1 =  1 ÃT  =  1 det(A) 6

1 -3 2 2 0 -2 -4 6 4

=

1/6 -1/2 1/3 1/3 0 -1/3 -2/3 1 2/3

Ответ: A-1 =		1/6	-1/2	1/3
		1/3	0	-1/3
		-2/3	1	2/3

Онлайн калькуляторы с матрицами.

Упражнения с матрицами.

Алгоритм вычисления обратной матрицы второго и третьего порядков (метод присоединённой матрицы)

1. Найдите определитель матрицы . Если определитель отличен от нуля, то матрица имеет обратную матрицу.

2. Транспонируйте матрицу . (Поменяйте местами столбцы и строки матрицы с сохранением порядка, т.е. первый столбец поставьте на месть первой строки, второй столбец на место второй строки и т.д.).

3. Найдите алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы его алгебраическим дополнением: , – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i-ой строки и j-го столбца. Составьте союзную (присоединённую) матрицу из алгебраических дополнений транспонированной матрицы.

4. Вычисляем обратную матрицу .

5. Проверить правильность вычисления обратной матрицы по формуле: .

Пример. Найти матрицу, обратную к матрице , если дана матрица .

Решение: Применим алгоритм нахождения обратной матрицы.

1. Найти определитель матрицы . Если определитель отличен от нуля, то матрица имеет обратную матрицу.

Матрица имеет обратную матрицу, так как .

2.Найдем матрицу , транспонированную к матрице поменяем строки и столбцы местами с сохранением порядка: .

3. Найдем алгебраические дополнения элементов матрицы . Заменим каждый элемент матрицы его алгебраическим дополнением: , – дополнительный минор, он равен определителю матрицы, которая получается вычёркиванием i-ой строки и j-го столбца.

.

Составим союзную матрицу:

4. Вычисляем обратную матрицу .

5. Проверим правильность вычисления обратной матрицы по формуле:

Ответ.

Выберите свой вариант и решите задачу.

Задание 3. Найдите матрицу, обратную к данной

Задание 4. Решить систему: а) методом Крамера; б) методом обратной матрицы.

а)Решить систему линейных уравнений по формулам Крамера.

Рассмотрим систему трёх линейных уравнений с тремя неизвестными

Система имеет единственное решение при условии, что определитель системы отличен от нуля, т.е. , которое определяется по формулам (*), где

Формулы (*) называются формулами Крамера.

Теорема Крамера.Система уравнений с неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.

Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта

1. и каждый определитель . Это имеет место только тогда, когда коэффициенты при неизвестных пропорциональны, то есть каждое уравнение системы получается из первого уравнения умножением обеих его частей на число . Очевидно, что при этом система имеет бесчисленное множество решений.

2. и хотя бы один из определителей . Это имеет место только тогда, когда коэффициенты при всех неизвестных, кроме пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.

Например, для системы из трёх уравнений:

Ответ. .

Алгоритм:

1. Вычислите определитель матрицы .

2. Заменяя первый второй и третий (поочередно) столбцы матрицы на столбец свободных членов, вычислите дополнительные определители

3. Подставить найденные определители в формулу (*): .

4.Запишите ответ.

Пример. Решить систему линейных уравнений по формулам Крамера

Решение.

1. Найдем определитель матрицы системы . Выпишем столбец свободных членов

2. Заменим первый столбец матрицы на столбец из свободных членов и вычислим полученный определитель . Тогда .

Заменим второй столбец матрицы на столбец из свободных членов и вычислим полученный определитель

. Находим неизвестную .

Для нахождения неизвестной в матрице заменяем третий столбец на столбец из свободных членов.

3. Находим неизвестную .

4. Ответ. .

б) Решить систему линейных уравнений методом обратной матрицы (матричным методом)

Рассмотрим систему уравнений

Данная система может быть записана в матричном виде , где

Тогда решение системы (3.1.) имеет вид ( обратная матрица).

Алгоритм:

1. Составить матрицу системы из коэффициентов при переменных , матрицу- столбец свободных членов .

2. Найти матрицу , обратную к матрице .

3. Умножить обратную матрицу на матрицу столбец свободных членов

Пример.Решить систему методом обратной матрицы (матричным методом)

Решение.

Составить матрицу системы из коэффициентов при переменных , матрицу- столбец свободных членов . Найдем матрицу обратную матрице системы: .

Алгебраические дополнения

, ,

, , ,

, , .

Матрица из алгебраических дополнений .

Обратная матрица

Находим решение системы

, ,

Ответ. , , .

Выберите свой вариант и решите задачу.

Задание 4. Решите систему: а) методом Крамера; б) методом обратной матрицы

Задание 5. Решить систему методом Гаусса.

При решении систем линейных уравнений используют также метод Гаусса (метод последовательного исключения неизвестных). Он состоит в следующем: систему уравнений приводят к эквивалентной ей системе со ступенчатой матрицей (системы называются эквивалентными, если множества их решений совпадают). Эти действия называют прямым ходом. Из полученной ступенчатой системы переменные находят с помощью последовательных подстановок (обратный ход).

При выполнении прямого хода используют следующие преобразования:

1) умножение и деление коэффициентов и свободных членов на одно и то же число;

2) сложение и вычитание уравнений;

3) перестановку уравнений в системе;

4) исключение из системы уравнений, в которых все коэффициенты при неизвестных и свободные члены равны нулю.

Алгоритм:

1.Выпишите расширенную матрицу системы

2. Методом элементарных преобразований свести расширенную матрицу к ступенчатому виду

3. Запишите систему, эквивалентную матрице, полученной в пункте 2.

4. Выполняя «обратный ход» решите полученную систему. «Поднимитесь» от последнего уравнения к первому.

5. Запишите ответ.

Примервыполнения задания.

а)

Решение. Запишем расширенную матрицу системы

.

Обведем первый ненулевой элемент первой строки и укажем знаком элементы, которые нужно занулить

 

 

Умножаем первую строку на 3 и складываем со второй

Результат запишем вместо второй строки. Умножаем первую строку на 2 и вычитаем из результата третью строку

Результат запишем вместо третьей строки. Умножаем первую строку на 2 и вычитаем из результата четвертую строку

Результат записываем вместо четвертой строки

 

 

 

Первый ненулевой элемент во второй строке указан и обведены элементы подлежащие занулению. Какие элементарные преобразования нужно сделать для зануления требуемых элементов? После преобразований получаем эквивалентную матрицу

 

 

Запишем эквивалентную систему

В эквивалентной системе получили противоречивое равенство (последняя строка 0=1). Поэтому система несовместна.

Ответ. Система несовместна.

б) Решить систему методом Гаусса

Решение. 1.Запишем расширенную матрицу системы

 

 

Здесь уже указан первый ненулевой первой строки и обведены элементы под ним, которые нужно занулить. Для зануления требуемых элементов выполнить действия:

Из первой строки вычесть две вторые строки. Результат записать вместо второй строки.

Первую строку умножить на 3 и из результата вычесть две третьи строки. Результат записать вместо третьей строки.

Из первой строки вычесть две четвертые строки. Результат записать вместо четвертой строки. Результат всех действий

 

 

Здесь указан первый ненулевой элемент второй строки и обведены элементы под ним, которые нужно занулить. Схематически указаны требуемые действия:

Вторую строку умножаем на 13 и из результата вычитаем девять третьих строк.

Вторую строку складываем с тремя четвертыми строками. Результат действий

 

 

 

Нулевую строку вычеркиваем. Вторую строку можно разделить на 3. Результат действий

 

Первые ненулевые находятся в первом, третьем и пятом столбце. Поэтому , , –зависимые переменные, остальные , – независимые переменные. Запишем эквивалентную систему

Независимые переменные переносим в правые части уравнений

4. Поднимаемся от последнего уравнения к первому

1)

2) .

3)

Ответ: , , .

Выберите свой вариант и решите задачу.

Задание 5. Решите систему методом Гаусса

Задание 6. Вычислить площадь параллелограмма, построенного на векторах и

Площадь параллелограмма, построенного на векторах равна длине вектора, равного векторному произведению заданных векторов.

Алгоритм:

1. Найдите векторное произведение векторов по формуле ,

коэффициенты при единичных векторах полученного произведения есть координаты вектора .

2. Вычислите модуль найденного векторного произведения по формуле

.

3. Запишите ответ.

Пример решения задания: Вычислить площадь параллелограмма, построенного на векторах и .

Коэффициенты при единичных векторах есть координаты вектора .

Найдем его длину . Длина вектора и есть искомая площадь.

.

Выберите свой вариант и решите задачу.

Обратная матрица. Вычисление обратной матрицы методом присоединённой матрицы. Решение систем линейных уравнений методом обратной матрицы.

Определение. Матрица А^-1называется обратной к матрице А, если выполняется условие: АА^-1= А^-1А=Е, где Е — единичная матрица того же порядка, что и матрица А. Обратная А^-1матрица имеет ту же размерность, что и матрица А.

Определение. Квадратная матрица А=называется невырожденной, если её определитель неравен нулю, в противном случае матрица называется вырожденной.

Теорема.Всякая невырожденная матрица имеет обратную.

Определение. Присоединенной матрицейк матрице А называется матрица вида:

=, где А_ij-алгебраическое дополнение элемента а_ij.

Находят обратную матрицу поформуле: А^-1_=.

Пример 3.1

Найти обратную матрицу методом присоединенной матрицы.

А=

Решение.

1. Выясним, является ли данная матрица невырожденной. Для этого найдем определитель матрицы:

=3(-1)¹⁺¹+0(-1)²⁺¹+1(-1)³⁺¹=3(12-4)+0+(2-6)=24-4=20.

Т.к. 0, следовательно, данная матрица имеет обратную.

2. Найдем транспонированную матрицу.

А^Т=

3. Вычислим присоединенную матрицу. Для этого найдем алгебраическое дополнение каждого элемента матрицы.

= (-1)¹⁺¹=12-4=8

= (-1)¹⁺²= -(4-4)= 0

= (-1)¹⁺³= 2-6= -4

= (-1)²⁺¹= -(0-2)=2

= (-1)²⁺²= 12-2=10

= (-1)²⁺³= -(6-0)= -6

= (-1)³⁺¹= 0-3= -3

= (-1)³⁺²= -(6-1)= -5

= (-1)³⁺³= 9-0=9.

=

4. Воспользуемся формулой: А^-1_=.

А^-1==.

Решение систем линейных уравнений методом обратной матрицы

Пусть дана система линейных уравнений. Обозначим её через (1). Выпишим основную матрицу данной системы: А=, вектор-столбец неизвестных:X=и вектор-столбец свободных членов:B=. Теперь перепишем систему (1) в матричной форме:AX=BX=A^-1B- решение системы (1).

Пример 3.2

Решить систему линейных уравнений: методом обратной матрицы.

Решение.

Формула, по которой будем находить решение системы: X=A^-1B.

Основная матрица системы А=, вектор-столбец неизвестных:X=и вектор-столбец свободных членов:B=.

Найдем определитель =3(-1)¹⁺¹+0(-1)²⁺¹+1(-1)³⁺¹=3(12-4)+0+(2-6)=24-4=20.

Т.к. 0, следовательно, данная матрица имеет обратную.

Найдем обратную матрицу с помощью присоединенной матрицы (см. пример 3.1):

А^-1=.

Подставим в формулу X=A^-1B, получим:X===

Ответ: =, ,.

Правильность решения легко проверить, подставив полученные результаты, , в данную систему уравнения.

Пусть дана система линейных уравнений.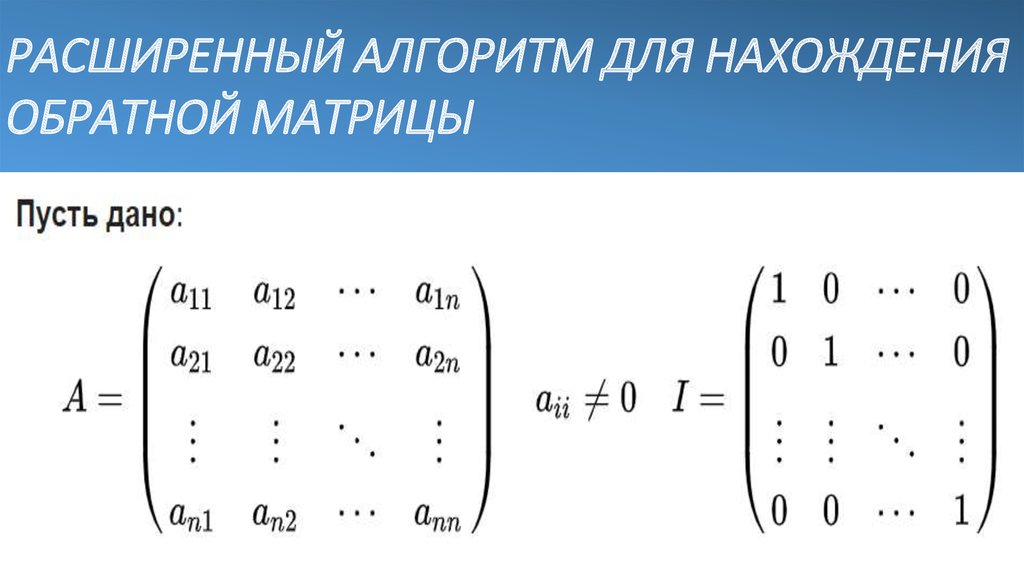 Обозначим её через (1). Основная матрица данной системы: А=, вектор-столбец неизвестных:X=и вектор-столбец свободных членов:B=. Теперь запишем систему (1) в матричной форме:AX=B.

Теорема Крамера. Пусть —определитель матрицы А, _j—определитель матрицы, получаемой из А заменойj-го столбца столбцом свободных членов. Тогда, если0, то система имеет единственное решение:, (1jn).

Пример 4.1

Решить систему линейных уравнений: методом Крамера.

Решение.

Основная матрица системы А=и вектор-столбец свободных членов:B=.

Найдем определитель ==3(-1)¹⁺¹+0(-1)²⁺¹+1(-1)³⁺¹=3(12-4)+0+(2-6)=24-4=20. Т.к.0, следовательно, можно применить формулы Крамера.

Найдем определители ,,, полученные заменой соответствующих столбцов столбцом свободных членов:

==1(12-4)-1(8-6)+2(4-9)=8-2-10= -4;

==3(8-6)-0+1(2-4)=6-2=4;

==3(9-4)-0+1(2-3)=15-1=14.

Тогда, по формуле Крамера:

== -=;

=;

=.

Ответ: =, ,.

Решение систем линейных уравнений методом Гаусса

Пусть дана система линейных уравнений. Рассмотрим расширенную матрицу (АВ) данной системы и с помощью элементарных преобразований приведем её к ступенчатому виду, в результате получим расширенную матрицу (АВ).

Если ранг основной матрицы системы меньше ранга расширенной матрицы r(A)<r(АВ), то система несовместна. Еслиr(A)=r(АВ)=n, гдеn-число неизвестных, то система совместна и определена. Еслиr(A)=r(АВ)<n, гдеn-число неизвестных, то система совместна и неопределенна.

Записываем систему линейных уравнений из полученной ступенчатой матрицы. Определяем базисные и свободные переменные, и выражая базисные переменные через свободные получаем решение системы.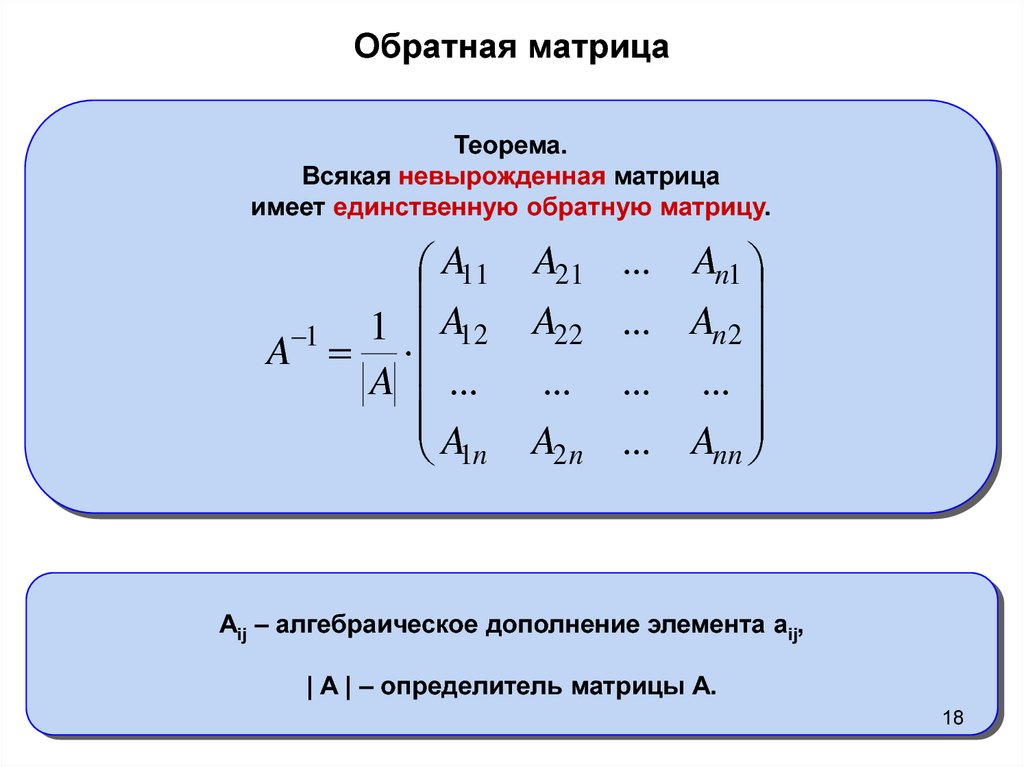

Пример 4.2

Решить систему линейных уравнений: методом Гаусса.

Решение.

r(A)=r(АВ)=nсистема совместна и определена.

Отсюда, запишем эквивалентную систему уравнений, имеем:

Решая её, получаем:

Ответ: =, ,.

Пример 4.3

Найти общее решение системы: .

Решение.

Составим матрицу системы: А=

Приведем её к треугольному виду:

r(A)=2. Запишем эквивалентную систему уравнений:

Примем за базисные переменные и, а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (3-2)=1, т. е. у нас одна свободная переменная это.

Выразим базисные переменные через свободные: . Обозначая свободную переменную:=, получаем общее решение в виде:

Пример 4. 4

Найти общее решение системы:

Решение.

Приведем расширенную матрицу системы к ступенчатому виду:

АВ=

r(A)=r(AВ)=2<n, гдеn-число неизвестных, то система совместная и неопределенная. Запишем эквивалентную систему уравнений:

Примем за базисные переменные и, а свободные находим из условия (n-r), гдеn-число неизвестных, получаем (5-2)=3, значит,-свободные переменные.

Выразим базисные переменные через свободные: Обозначая свободную переменную:=,,получаем общее решение в виде:.

Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы

Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы

• Обратная матрица
• Ранг матрицы

Обратная матрица

Обратной матрицей A^-1 матрицы A называют матрицу, удовлетворяющую следующему равенству:

где – E это единичная матрица.

Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.

Исходная матрица:

Союзная ей матрица A*:

Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A*^T:

Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A^-1, обратную матрице A:

➣ Численный пример

Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:

Для начала найдем определитель матрицы A:

Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:

Союзная матрица будет иметь следующий вид:

Присоединенная матрица получается из союзной путем транспонирования:

Находим обратную матрицу:

➤ Пример на Python

Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():

>>> A = np.matrix('1 -3; 2 5')
>>> A_inv = np.linalg.inv(A)
>>> print(A_inv)
[[ 0.45454545 0.27272727]
 [-0.18181818 0.09090909]]

Рассмотрим свойства обратной матрицы.

Свойство 1. Обратная матрица обратной матрицы есть исходная матрица:

➤Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> A_inv = np.linalg.inv(A)
>>> A_inv_inv = np. linalg.inv(A_inv)
>>> print(A)
[[1. -3.]
 [2. 5.]]
>>> print(A_inv_inv)
[[1. -3.]
 [2. 5.]]

Свойство 2. Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:

➤ Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
 [ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
 [ 0.27272727 0.09090909]]

Свойство 3. Обратная матрица произведения матриц равна произведению обратных матриц:

➤ Пример на Python

>>> A = np.matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')
>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))
>>> print(L)
[[ 0. 09454545 0.03272727]
 [-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
 [-0.03454545 0.00727273]]

Ранг матрицы

Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.

Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:

>>> m_eye = np.eye(4)
>>> print(m_eye)
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 1.]]

Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():

>>> rank = np. linalg.matrix_rank(m_eye)
>>> print(rank)
4

Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:

>>> m_eye[3][3] = 0
>>> print(m_eye)
[[1. 0. 0. 0.]
 [0. 1. 0. 0.]
 [0. 0. 1. 0.]
 [0. 0. 0. 0.]]
>>> rank = np.linalg.matrix_rank(m_eye)
>>> print(rank)
3

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas.  Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Объяснение урока: обратная матрица: метод сопряжения

В этом объяснении мы узнаем, как найти обратную матрицу 3×3, используя метод сопряжения.

Начнем с того, что вспомним, как определить обратную матрицу 2×2.

Определение: обратная матрица 2 × 2

Пусть 𝐴 — матрица 2 × 2. Обратное к 𝐴 (обозначается 𝐴) — матрица 2×2, удовлетворяющая условию 𝐴𝐴=𝐼,𝐴𝐴=𝐼, где 𝐼 — единичная матрица 2 × 2. Если такая матрица существует, то говорят, что матрица 𝐴 обратим.

Более того, на самом деле можно вывести точную формулу для обратного выражения, которая выглядит следующим образом.

Формула: обратная матрица 2 × 2

Пусть 𝐴=𝑎𝑏𝑐𝑑 такое, что det(𝐴)≠0, где det(𝐴)=𝑎𝑑−𝑏𝑐 — определитель 𝐴. Тогда инверсия 𝐴 определяется выражением 𝐴=1(𝐴)𝑑−𝑏−𝑐𝑎.det

Если det(𝐴)=0, матрица 𝐴 необратима.

Само собой разумеется, что если есть обратная матрица 2×2, она должна быть справедливо для матриц более высокого порядка. Как и ожидалось, определение обратной матрицы 2×2 действительно может можно расширить для включения матриц любого порядка следующим образом.

Определение: обратная матрица

Пусть 𝐴 будет матрицей 𝑛×𝑛. Обратное к 𝐴 (обозначается 𝐴) — это матрица 𝑛×𝑛, которая удовлетворяет 𝐴𝐴=𝐼,𝐴𝐴=𝐼, где 𝐼 — единичная матрица 𝑛×𝑛. Если такая матрица существует, то говорят, что матрица 𝐴 обратима.

Сказав, что такое расширение возможно, легче сказать, чем сделать, чтобы вывести формулы для таких матриц или узнать если они вообще существуют. В случае 2×2 заметим, что обратное получается по формуле манипуляции с элементами матрицы и деление на определитель, если он не равен нулю. Мы могли бы задаться вопросом существует ли аналогичный подход для многомерных случаев.

Как мы узнаем из этого объяснения, существует формула для обратной матрицы, которая обобщает случай 2×2. В частности, нахождение определителя и необходимых для этого шагов является ключевым компонентом процесс. Поскольку основное внимание в этом объяснении уделяется матрицам 3×3, мы рассмотрим метод вычисления определителя матрицы 3 × 3 с использованием кофакторного разложения. Однако, поскольку полный метод понадобится только позже, давайте начнем с первого шага в этом процессе, который является расчетом миноры и кофакторы.

Определение: миноры и кофакторы

Пусть 𝐴=(𝑎) — матрица порядка 3×3. Затем минор элемента 𝑎 (обозначается 𝐴) является определителем матрицы 2×2, полученной после удаления строки 𝑖 и столбца 𝑗 из 𝐴.

Тогда кофактор элемента 𝑎 (обозначается 𝐶) равен 𝐶=(−1)𝐴, где 𝐴 — минор элемента 𝑎.

До сих пор мы видели только кофакторы, используемые для вычисления определителя матрицы. Однако, как оказалось, они тоже существенное значение при нахождении обратной матрицы с помощью сопряженного метода.

Прежде чем мы должным образом объясним сопряженный метод для нахождения обратного, нам нужно определить матрицы кофакторов .

Определение: Матрица кофакторов

Матрица кофакторов квадратной матрицы 𝐴=(𝑎) определяется как 𝐶=𝐶, где каждый 𝐶 является кофактором входа 𝑎 𝐴.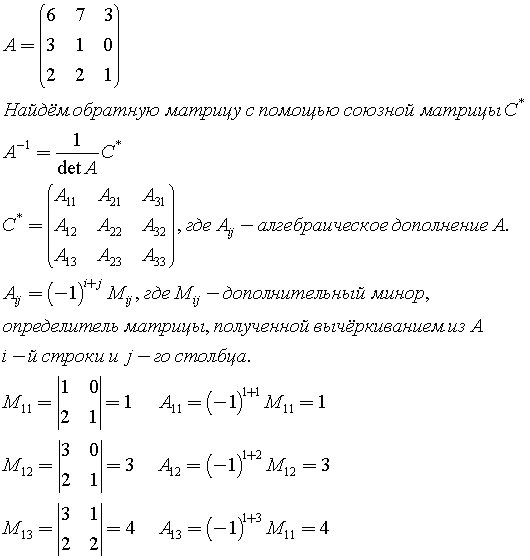

Приведенное выше определение применимо к любой квадратной матрице, но в случае 3×3 это 𝐶=𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶.

Другими словами, каждый соответствующий элемент матрицы является сомножителем в исходном элементе матрицы.

Хотя это простая формула, ее может быть сложно рассчитать на практике, так как мы должны найти минор и его кофактор для каждого элемента матрицы кофакторов. Давайте попрактикуемся в этом на примере.

Пример 1. Нахождение матрицы кофакторов матрицы 3 × 3

Найдите матрицу кофакторов 𝐴=7−5−8−3−7−20−4−8.

Ответ

Напомним, что матрица кофакторов — это матрица, полученная путем нахождения кофактора каждого соответствующего элемента матрицы. Позволять данная матрица будет 𝐴.

Чтобы найти кофакторы, сначала нужно найти миноры. Для этого для каждого элемента матрицы удаляем строку и столбец, которому он принадлежит, и взять определитель полученной матрицы 2×2.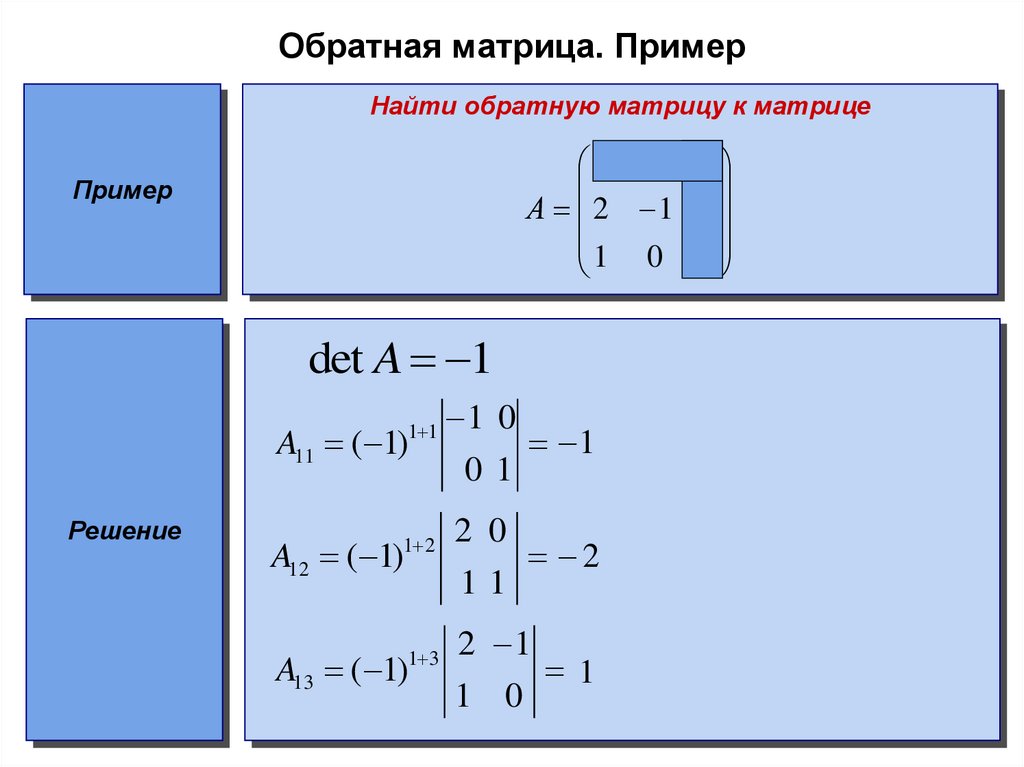 Например, минор записи 𝑎 можно найти следующим образом:

Повторяя этот процесс, мы получаем девять различных определителей, где каждый раз мы удаляем строку и столбец, которые соответствующая запись принадлежит. Для первой строки имеем 𝐴=||−7−2−4−8||𝐴=||−3−20−8||𝐴=||−3−70−4||=(−7)⋅(−8)−( −2)⋅(−4)=(−3)⋅(−8)−0⋅(−2)=(−3)⋅(−4)−0⋅(−7)=56−8=24−0 =12−0=48,=24,=12.

Для второй строки имеем 𝐴=||−5−8−4−8||𝐴=||7−80−8||𝐴=||7−50−4||=(−5)⋅(−8)−(−4 )⋅(−8)=7⋅(−8)−0⋅(−8)=7⋅(−4)−0⋅(−5)=40−32=−56−0=−28−0=8 ,=−56,=−28.

Для последней строки имеем 𝐴=||−5−8−7−2||𝐴=||7−8−3−2||𝐴=||7−5−3−7||=(−5)⋅(−2) −(−7)⋅(−8)=7⋅(−2)−(−3)⋅(−8)=7⋅(−7)−(−3)⋅(−5)=10−56=− 14−24=−49−15=−46,=−38,=−64.

Теперь нам нужно найти кофакторы. Напомним, что кофакторы могут быть получены из соответствующих миноров путем умножения их на 1 или -1 в соответствии с их положением в следующей матрице: +-+-+-+-+.

Например, 𝐶 стоит в позиции (1,2), которая имеет отрицательный знак, что показывает нам, что 𝐶=−𝐴. Таким образом, мы имеем 𝐶=𝐴𝐶=−𝐴𝐶=𝐴=48,=−24,=12,𝐶=−𝐴𝐶=𝐴𝐶=−𝐴=−8,=−56,=28,𝐶=𝐴𝐶=−𝐴𝐶=𝐴=−46, =38,=−64.

900 их в матрицу, чтобы сформировать матрицу кофактора. Это дает нам 48-2412-8-5628-4638-64.

Прежде чем мы введем формулу, обратную матрице 3×3, мы должны ввести одно последнее понятие: присоединенная матрица . Мы определяем его следующим образом.

Определение: сопряженные матрицы

Сопряженная матрица 𝐴 (также известная как сопряженная) является транспонированной матрицей кофакторов 𝐶; то есть, adj(𝐴)=𝐶.

Как мы видим, после того, как мы вычислили матрицу кофакторов, получить сопряженную матрицу несложно, поскольку мы просто нужно взять транспонирование. Теперь рассмотрим пример, в котором нам нужно вычислить сопряженную матрицу.

Пример 2. Нахождение сопряженной матрицы матрицы 3 × 3

Найти сопряженную матрицу матрицы 𝐴=2−72−9−7−9−85−4.

Ответ

Напомним, что сопряженная матрица представляет собой транспонированную матрицу кофакторов, которая представляет собой матрицу, в которой каждая запись является кофактором соответствующей записи. Пусть задана матрица 𝐴.

Чтобы найти кофакторы 𝐴, мы сначала должны найти миноры, что мы можем сделать, взяв каждую запись матрицу одну за другой, удаляя строки и столбцы, которым они принадлежат, и взяв определители результирующего Матрицы 2×2. Продемонстрируем это для минора 𝑎:

Давайте продолжим этот подход, чтобы найти каждый из девяти миноров, где каждый раз, когда мы удаляем строку и столбец, которые соответствующая запись принадлежит. Для первой строки имеем 𝐴=||−7−9−5−4||𝐴=||−9−9−8−4||𝐴=||−9−7−85||=(−7)⋅(−4) −(−5)⋅(−9)=(−9)⋅(−4)−(−8)⋅(−9)=(−9)⋅5−(−8)⋅(−7)=28+ 45=36−72=−45−56=73,=−36,=−101.

Для второй строки имеем 𝐴=||−725−4||𝐴=||22−8−4||𝐴=||2−7−85||=(−7)⋅(−4)−5⋅2=2⋅( −4)−(−8)⋅2=2⋅5−(−8)⋅(−7)=28−10=−8+16=10−56=18,=8,=−46.  

Для последней строки имеем 𝐴=||−72−7−9||𝐴=||22−9−9||𝐴=||2−7−9−7||=(−7)⋅(−9)−(−7 )⋅2=2⋅(−9)−(−9)⋅2=2⋅(−7)−(−9)⋅(−7)=63+14=−18+18=−14−63=77 ,=0,=-77.

Теперь мы можем использовать миноры, чтобы найти кофакторы. Напомним, что кофакторы могут быть получены из соответствующих миноры, умножив их на 1 или -1 в соответствии с их положением в следующей матрице: +-+-+-+-+.

Таким образом, мы имеем 𝐶=𝐴𝐶=-𝐴𝐶=𝐴=73,=36,=-101,𝐶=-𝐴𝐶=𝐴𝐶=-𝐴=-18,=8,=46,𝐶=𝐴𝐶=-𝐴𝐶=𝐴=77,=0 ,=−77.

Теперь мы можем сформировать матрицу кофакторов, поместив элементы в следующую матрицу: 𝐶=7336−101−18846770−77.

Наконец, чтобы найти сопряженную матрицу, мы транспонируем 𝐶. Это означает, что мы должны переписать каждую из строк как столбец новой матрицы. Это дает нам adj(𝐴)=𝐶=73−18773680−10146−77.

Прежде чем перейти к определению формулы обратной матрицы, напомним сначала способ нахождения определителя матрицы 3 × 3 с использованием расширения кофактора.

Определение: определители матриц 3 × 3 (расширение кофакторов)

Для любого фиксированного 𝑖=1, 2 или 3 определитель 𝐴 равен det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶, где каждый 𝐶 является кофактором элемента 𝑎. Это известно как Расширение кофактора (или расширение Лапласа) по строке 𝑖. Альтернативно, для любого фиксированного 𝑗=1, 2 или 3, мы имеем det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶.

Это расширение кофактора по столбцу 𝑗.

С этим определением и предыдущими определениями кофактора и присоединенных матриц мы теперь в состоянии написать формула обратной матрицы.

Формула: обратная матрица

Если 𝐴 — обратимая матрица, то ее обратная матрица 𝐴=1(𝐴)(𝐴),detadj где adj(𝐴) является сопряженным к 𝐴 и det(𝐴) является определителем 𝐴.

Заметим, что эта формула применима к квадратным матрицам любого порядка, хотя мы будем использовать ее только для нахождения 3×3 инверсии здесь. Однако можно показать, что эта формула работает и для случая 2×2. Чтобы увидеть это, давайте рассмотрим общую матрицу 2 × 2: 𝐴=𝑎𝑏𝑐𝑑.

Чтобы найти adj(𝐴), мы сначала вычисляем матрицу кофакторов, находя каждый из миноров. Мы отмечаем, что в этом случае поиск минора для каждой записи довольно тривиален, так как удаление строки и столбца из 2×2 матрица приводит к матрице 1 × 1, которая является просто числом. Итак, четыре минора — это просто записи в противоположные углы, как показано: 𝐴=𝑑,𝐴=𝑐,𝐴=𝑏,𝐴=𝑎.

чтобы получить следующую матрицу: 𝐶=𝑑−𝑐−𝑏𝑎.

Наконец, мы получаем adj(𝐴), транспонируя 𝐶, чтобы получить прил(𝐴)=𝑑−𝑏−𝑐𝑎.

Подставляя это в приведенную выше формулу, мы имеем 𝐴=1(𝐴)𝑑−𝑏−𝑐𝑎.det

Поскольку это то же самое, что и формула для обратной 2 × 2, которую мы уже имели, мы можем видеть, что две формулы согласованы.

Важно отметить, что 𝐴 обратимо тогда и только тогда, когда определитель отличен от нуля. Это означает, что всякий раз, когда нам нужно найти обратную матрицу, мы всегда должны начинать с вычисления определителя. Если оно отлично от нуля, то мы можем продолжить; в противном случае мы должны заключить, что матрица вырождена (т. е. не имеет обратной).

Давайте проверим нашу способность находить обратную матрицу 3×3.

Пример 3. Проверка того, является ли матрица 3 × 3 вырожденной, и нахождение ее обратной, если возможно

Определить, является ли матрица 123021267 имеет обратный, определяя, отличен ли определитель от нуля. Если определитель отличен от нуля, найдите обратный, используя обратная формула, включающая матрицу кофакторов.

Ответ

Первая часть вопроса требует от нас проверки, отличен ли определитель от нуля. Естественно, это можно сделать путем непосредственное вычисление определителя. Однако мы также можем использовать свойства определителей, чтобы помочь нам вычислить определить определитель проще и в некоторых случаях показать, что он должен быть равен нулю.

Напомним, что если мы прибавим скаляр, кратный одной строке, к другой строке, значение определителя не изменится. Таким образом, давайте добавим -2 строки 1 к строке 3. Мы решили сделать это, потому что это приведет к нижнему левому запись становится нулевой. Это дает нам ||||123021267||||=||||123021021||||.

Теперь, обычно, мы продолжаем вычислять определитель, используя разложение на кофакторы в первом столбце. Однако на На этом этапе важно понимать, что и вторая, и третья строки равны (0,2,1). Позволь нам Вспомним еще одно свойство определителей: если две строки матрицы равны, то определитель равен нулю. С тех пор в этом случае нам больше не нужно выполнять остальные вычисления, потому что свойство говорит нам, что оно равно нулю.

Таким образом, обратного нет, так как определитель равен нулю.

В предыдущем примере матрица была вырожденной, поэтому нам не пришлось проходить все этапы вычисления обратной. Это показывает, что всегда очень полезно найти определитель, прежде чем утруждать себя поиском сопряженной матрицы. Давайте рассмотрим другой пример, где мы должны попытаться найти обратную матрицу 3×3.

Пример 4. Проверка того, является ли матрица 3 × 3 вырожденной, и нахождение ее обратной, если возможно

Рассмотрим матрицу 103101310.

1. Определите, есть ли обратная матрица, найдя, равен ли определитель ненулевой.
2. Если определитель отличен от нуля, найдите обратный по формуле для обратная, которая включает матрицу кофакторов.

Ответ

Часть 1

В первой части вопроса нам нужно найти, отличен ли определитель от нуля, поэтому давайте вычислим определитель. Заметим, что во втором столбце два нуля, а значит, он уже в оптимальном виде для применения метода расширение кофактора. Напомним, что расширение кофактора по столбцу 𝑗 есть det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶. 

Пусть задана матрица 𝐴=(𝑎). Теперь, если мы возьмем 𝑗=2, расчет упрощается до Таким образом, нам нужно найти только . Чтобы вычислить его, мы сначала найдем минор 𝑎 удалив строку и столбец, в которых находится 𝑎, и взяв определитель. Это дает нам

Далее мы можем найти кофактор, применяя определение 𝐶=(−1)𝐴.

Поскольку 𝑖=3, 𝑗=2 и 𝑖+𝑗=5, имеем 𝐶=(−1)𝐴=(−1)⋅(−2)=2.

Таким образом, det(𝐴)=2. Поскольку определитель отличен от нуля, матрица имеет обратную.

Часть 2

Напомним, что обратное дается формулой 𝐴=1(𝐴)(𝐴).detadj

Мы уже вычислили det(𝐴), поэтому давайте теперь вычислим сопряженную матрицу, которая является транспонировать матрицу кофакторов.

Чтобы найти матрицу кофакторов, мы должны сначала найти минор в каждой позиции матрицы. Для первой строки эти миноры равны 𝐴=||0110||𝐴=||1130||𝐴=||1031||=0⋅0−1⋅1=1⋅0−3⋅1=1⋅1−3⋅0=0−1= 0−3=1−0=−1,=−3,=1. 

Продолжая вторую и третью строки, где мы для краткости опустили промежуточные шаги, мы имеем 𝐴=||0310||𝐴=||1330||𝐴=||1031||=−3,=−9,=1,𝐴=||0301||𝐴=||1311||𝐴=|| 1010||=0,=−2,=0.

Теперь мы можем использовать миноры для нахождения кофакторов. Напомним, что кофакторы могут быть получены из соответствующих миноров умножив их на 1 или -1 в соответствии с их положением в следующей матрице: +-+-+-+-+.

Делая это для каждого кофактора и помещая их в матрицу, мы имеем 𝐶=−1313−9−1020.

Теперь мы можем найти сопряженное, транспонируя эту матрицу. Мы делаем это, переписывая каждую из строк 𝐶 как столбец adj(𝐴). Это дает нам прил(𝐴)=−1303−921−10.

Наконец, мы используем формулу для обратной, 𝐴=1(𝐴)(𝐴)detadj: 𝐴=12−1303−921−10=⎛⎜⎜⎜⎜⎝−1232032−92112−120⎞⎟⎟⎟⎟⎠.

К этому моменту мы должны быть немного знакомы с методом нахождения обратная матрица 3 × 3, но нам еще предстоит сделать что-нибудь интересное с полученной обратной матрицей. Одним из ключевых применений обратной матрицы является решение матрицы уравнения. Рассмотрим уравнение вида 𝐴𝑋=𝐵, где 𝐴 и 𝐵 заданы матрицы 3 × 3, а 𝑋 — неизвестная матрица 3×3. Если 𝐴 не единственное число, то обратное 𝐴 существует, и мы можем умножить обе части уравнения слева на 𝐴, чтобы получить 𝐴𝐴𝑋=𝐴𝐵𝑋=𝐴𝐵.

Таким образом, если мы найдем обратную 𝐴, мы можем использовать ее для нахождения неизвестной матрицы 𝑋, как показано. Позволять мы видим полный пример этого.

Пример 5. Решение матричного уравнения с помощью обратной матрицы

Предположим, что 𝐴𝑋=𝐵, где 𝐴=4−135043−32,𝐵=2103−4527−6, а 𝑋 — матрица 3×3.

1. Вычислите значение, обратное 𝐴.
2. И используйте его, чтобы найти 𝑋.

Ответ

Часть 1

Начнем с вычисления обратной величины 𝐴 с помощью сопряженного метода. Напомним, что у нас 𝐴=1(𝐴)(𝐴).detadj

Таким образом, давайте сначала вычислим det(𝐴), а затем adj(𝐴) и использовать их, чтобы найти обратное. Теперь мы можем найти обратную 𝐴, используя расширение кофактора по столбцу 2 (поскольку одна запись уже равна нулю). Другими словами, мы используем формулу det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶=(−1)(−1)𝐴+0𝐶+(−3)(−1)𝐴=𝐴+3𝐴,  где 𝐴 и 𝐴 — миноры 𝑎 и 𝑎 соответственно. Мы можем найти миноры, удалив соответствующие строки и столбцы из таблицы. матрица и взятие определителя результата. Делая это для обоих миноров, мы получаем

Таким образом, det(𝐴)=−2+3⋅1=1. Это действительно подтверждает, что существует обратное (хотя это предполагается, поскольку в противном случае вопрос не имел бы однозначного решения). Теперь нам нужно найти сопряжение 𝐴. Мы делаем это, сначала вычисляя миноры, а затем матрицу кофакторов. Миноры 𝐴 следующие: 𝐴=||04−32||𝐴=−2,𝐴=||503−3||=12,=−15,𝐴=||−13−32||𝐴=||4332||𝐴=| |4−13−3||=7,=−1,=−9,𝐴=||−1304||𝐴=1,𝐴=||4−150||=−4,=5. 

Теперь мы можем построить матрицу кофакторов, умножив каждый минор на 1 или −1 в соответствии с их положение в следующей матрице: +-+-+-+-+.

В результате мы получим следующую матрицу кофакторов: 𝐶=122−15−7−19−4−15.

Наконец, мы можем получить сопряженную матрицу, транспонировав приведенную выше матрицу. Это дает нам прил(𝐴)=12−7−42−1−1−1595.

Так как определитель равен 1, мы имеем 𝐴=11(𝐴)adj, что означает, что обратный равно приведенной выше матрице: 𝐴=12−7−42−1−1−1595.

Часть 2

Теперь мы нашли 𝐴, можем найти 𝑋 в уравнении 𝐴𝑋=𝐵. Если мы умножаем слева от обеих частей уравнения на 𝐴, тогда находим, что 𝐴𝐴𝑋=𝐴𝐵𝑋=𝐴𝐵.

Таким образом, нам просто нужно выполнить матричное умножение 𝐴 и 𝐵. Давайте продемонстрируем это для первой записи:

, где мы сделали расчет 12⋅2+(−7)⋅3+(−4)⋅2=−5. Повторяя это для оставшихся записей, мы получаем 𝑋=12−7−42−1−1−15952103−4527−6=−512−11−1−117−1615.

В качестве последнего примера мы рассмотрим ситуацию, когда нам нужно найти обратную матрицу 3×3. где записи являются переменными величинами.

Пример 6. Нахождение обратной матрицы с переменными элементами с помощью сопряженного метода

Найти обратную матрицу 𝑒𝑡𝑡𝑒−𝑡𝑡𝑒−𝑡−𝑡.cossinsincossin

Ответ

В этом вопросе предполагается, что данная матрица обратима, поэтому нам не нужно строго проверять, является ли определитель отличен от нуля. Тем не менее, необходимо вычислить определитель, чтобы найти обратный, так как он дается выражением 𝐴=1(𝐴)(𝐴),detadj где det(𝐴) — определитель, а adj(𝐴) — сопряженная матрица (т. е. транспонирование матрицы кофакторов). Пусть задана матрица 𝐴. Напомним, что определитель может быть рассчитано с использованием расширения кофактора по строке 𝑖: det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶.

Обычно полезно манипулировать матрицей так, чтобы два из трех элементов в одной строке или столбце были равны 0. Это означает, что нам нужно найти только один кофактор. Однако, поскольку нам все равно придется вычислять все кофакторы для матрица кофакторов, давайте просто продолжим использовать расширение кофактора в первой строке.

Чтобы найти кофакторы строки 1, мы сначала должны найти миноры. Мы можем сделать это для каждой записи, удалив строку и столбец, которому принадлежит эта запись, и получение определителя результирующей матрицы 2 × 2. За например, минор для 𝑎 равен

, где мы использовали тригонометрическое тождество Пифагора, sincos𝑡+𝑡=1. Продолжая две другие записи, мы получаем 𝐴=|||𝑒𝑡𝑒−𝑡|||𝐴=|||𝑒−𝑡𝑒−𝑡|||=−𝑒(𝑡+𝑡),=𝑒(𝑡−𝑡). cossinsincossincossincos

Отсюда напомним, что 𝐶=(−1)𝐴. Таким образом, у нас есть 𝐶=1,𝐶=𝑒(𝑡+𝑡),𝐶=𝑒(𝑡−𝑡).sincossincos

Теперь формула для разложения кофакторов вдоль строки 1 имеет вид det(𝐴)=𝑎𝐶+𝑎𝐶+𝑎𝐶.

Используя тот факт, что 𝑎=𝑒, 𝑎=𝑡cos, и 𝑎=𝑡грех, это означает, что DetCossOssInsIncossossOssInsincoss (𝐴) = 𝑒om1+𝑡om𝑒 (𝑡+𝑡)+𝑡om𝑒 (𝑡−𝑡) = 𝑒1+𝑡𝑡+𝑡+𝑡 — = 2𝑒. 

Как и ожидалось, определитель не равен нулю. Теперь нам нужно найти остальные сомножители, вычислив соответствующие несовершеннолетние. Для второй и третьей строк миноры равны 𝐴=|||𝑡𝑡−𝑡−𝑡|||𝐴=|||𝑒𝑡𝑒−𝑡|||𝐴=|||𝑒𝑡𝑒−𝑡|||=0,=−2𝑒𝑡,=−2𝑒𝑡,𝐴=|| |𝑡𝑡−𝑡𝑡|||𝐴=|||𝑒𝑡𝑒𝑡|||𝐴=|||𝑒𝑡𝑒−𝑡|||=1,=𝑒(𝑡−𝑡),=−𝑒(𝑡+𝑡). cossincossinsinsinsincossossincossinsincossincossincossinsincos

Давайте теперь вычислим −1 соответствующие или минорные, в соответствии с их положением в следующей матрице: +-+-+-+-+.

Вычисляя эти кофакторы и помещая их в матрицу, мы имеем 𝐶 = 1𝑒 (𝑡+𝑡) 𝑒 (𝑡 ​​- 𝑡) 0–2𝑒𝑡2𝑒𝑡1𝑒 (𝑡 — 𝑡) −𝑒 (𝑡+𝑡) .sincossossossossossossoss

Далее, соответствующая матрица может быть получена при транспонировании этой матрицы, что означает переписывание строк как столбцов. Это дает нам Adjsincossinsincossossossincoss (𝐴) = 101𝑒 (𝑡+𝑡) −2𝑒𝑡𝑒 (𝑡 — 𝑡) 𝑒 (𝑡 ​​- 𝑡) 2𝑒𝑡 — 𝑒 (𝑡+𝑡) .

Наконец, мы используем формулу 𝐴 =1(𝐴)(𝐴)detadj, чтобы получить 𝐴 = 12𝑒101𝑒 (𝑡+𝑡) −2𝑒𝑡𝑒 (𝑡 — 𝑡) 𝑒 (𝑡 ​​- 𝑡) 2𝑒𝑡 — 𝑒 (𝑡+𝑡)  = ⎛⎜⎜⎜⎜⎝12𝑒012𝑒12 (𝑡+𝑡) −𝑡12 (𝑡- 𝑡)12(𝑡−𝑡)𝑡−12(𝑡+𝑡)⎞⎟⎟⎟⎟⎠. sincossinsincossincossincossincossincossincossincossincossin

Давайте суммируем ключевые моменты, которые мы узнали во время этого объяснения.

Ключевые моменты

• Пусть 𝐴=(𝑎) — матрица порядка 3×3. Тогда минор элемента 𝑎 (обозначается 𝐴) является определителем матрицы 2×2, полученной после удаления строки 𝑖 и столбца 𝑗 из 𝐴.
  Тогда кофактор элемента 𝑎 (обозначается 𝐶) равен 𝐶=(−1)𝐴, где 𝐴 — минор элемента 𝑎.
• Если 𝐴 — квадратная матрица, то ее кофакторная матрица определяется формулой 𝐶=𝐶, где каждый 𝐶 является кофактором входа 𝑎 𝐴.
• Сопряженный к 𝐴 (также известный как адъюгат) является транспонированием кофакторной матрицы 𝐶; то есть, adj(𝐴)=𝐶.
• Если 𝐴 — обратимая матрица (т. е. det(𝐴)≠0), то ее обратной является 𝐴=1(𝐴)(𝐴),detadj где det(𝐴) — определитель 𝐴.
• Поскольку матрица обратима только в том случае, если определитель отличен от нуля, важно проверить, верно ли это, прежде чем пытаемся найти обратное сопряженным методом. Мы можем упростить этот процесс, используя свойства определителей.
• Имея матричное уравнение вида 𝐴𝑋=𝐵, мы можем найти 𝑋, умножив слева на 𝐴 следующим образом: 𝐴𝐴𝑋=𝐴𝐵𝑋=𝐴𝐵.

Классическое сопряжение квадратной матрицы

Пусть A = [ a _ij ] — квадратная матрица. Транспонирование матрицы, элементом которой ( i , j ) является кофактор a _ij , называется классическим присоединенным к A :

 

Пример 1 : Найдите сопряженную матрицу

 

Первым шагом является оценка кофактора каждой записи: 

Следовательно,

Зачем формировать присоединенную матрицу? Во-первых, проверьте следующий расчет, в котором матрица A выше умножается на ее сопряженную:

 

Теперь, после разложения Лапласа по первому столбцу A дает

   

Уравнение

(*) становится

Этот результат дает следующее уравнение для обратного уравнения A :

 

Обобщая эти вычисления на произвольную n на n матрицу, можно доказать следующую теорему:

Теорема H . Квадратная матрица A обратима тогда и только тогда, когда ее определитель отличен от нуля, а ее обратная матрица получается путем умножения сопряженного числа A по (det A ) ⁻¹ . [Примечание: матрица, определитель которой равен 0, называется сингулярной ; следовательно, матрица обратима тогда и только тогда, когда она неособая.]

Пример 2 : Определите обратную следующую матрицу, сначала вычислив ее сопряженную:

 

Сначала оцените кофактор каждой записи в A : 

Из этих вычислений следует, что

Теперь, поскольку разложение Лапласа по первой строке дает

обратное число А равно

, что можно проверить, проверив, что AA ^-1 = A ^-1 A = I .

Пример 3 : Если A является обратимой матрицей n на n , вычислите определитель Adj A через det A .

Поскольку A обратимо, уравнение A ⁻¹ = Adj A /det A подразумевает

Напомним, что если B равно n x n и k является скаляром, то det( kB ) = k ⁿ det 90.3 B 90.3 Применение этой формулы с k = det A и B = A ⁻¹ дает

Таким образом,

 

Пример 4 : Покажите, что сопряженное сопряженное A гарантированно равно A , если A является обратимой матрицей 2 на 2, но не тогда, когда A является обратимой квадратной матрицей более высокого порядка.

Во-первых, уравнение A · Adj A = (det A ) I можно переписать как

   

что подразумевает

Далее уравнение A · Adj A = (det A ) I также подразумевает

 

Это выражение вместе с результатом Примера 3 преобразует (*) в

где n размер квадратной матрицы A . Если n = 2, то (det A ) ^{n −2} = (det A ) ⁰ = 1, поскольку det A ≠ 0 ) = А , по желанию. Однако, если n > 2, то (det A ) ^{n −2} не будет равно 1 для каждого ненулевого значения det A , поэтому Adj (Adj A ) не обязательно будет10 равным 903 А . Однако это доказательство показывает, что независимо от размера матрицы Adj (Adj A ) будет равно A , если det A = 1,

.

Пример 5 : Рассмотрим векторное пространство C ² ( a, b ) функций, имеющих непрерывную вторую производную на интервале ( a, b ) ⊂ R . Если f, g и h функции в этом пространстве, то следующий определитель,

   

называется Вронскиан из f, g и h . Что говорит значение вронскиана о линейной независимости функций f, g и h ?

Функции ф, г , и H являются линейно независимыми, если единственные скаляры C ₁ , C ₂ и C ₃ , которые удовлетворяют уравнению C , которые удовлетворяют уравнению C , которые удовлетворяют уравнению. 2 = c ₃ = 0. Один из способов получить три уравнения для решения трех неизвестных c ₁ , c ₂ и c _{4 ), а затем снова дифференцировать его. В результате получается система}

, что можно записать в матричной форме как

.

где c = ( c ₁ , c ₂ , c ₃ ) ^T . Однородная квадратная система, такая как эта, имеет тривиальное решение только тогда и только тогда, когда определитель матрицы коэффициентов отличен от нуля. Но если c = 0 является единственным решением (**), то c ₁ = c ₂ = c ₃ = 0 является единственным решением (*), а функции f, g и h линейно независимы. Следовательно,

Чтобы проиллюстрировать этот результат, рассмотрим функции f, g и h , определенные уравнениями

Поскольку вронскиан этих функций равен

эти функции линейно зависимы.

Вот еще одна иллюстрация. Рассмотрим функции f, g и h в пространстве C ² (1/2, ∞), определяемом уравнениями

Согласно разложению Лапласа по второму столбцу, вронскиан этих функций равен

Поскольку эта функция не тождественно равна нулю на интервале (1/2, ∞) — например, когда x = 1, Вт ( x ) = Вт (1) = e ≠ 0 – функции f, g и h линейно независимы. 9{-1} = \dfrac{adj(A)}{|A|}; |А| \neq 0$

Что такое матрица кофакторов?

Рассмотрим A = [a] _n как квадратную матрицу порядка n. Пусть A _pq представляет собой кофактор элементов, индексы которых равны (p, q).

Матрица кофакторов A представляет собой квадратную матрицу для порядка N.

\[C = \begin{bmatrix} A_{11}& A_{12} & . & . & . & A_{1n}\\  A_{21}& A_{22 }& . & . & . & A_{2n} \\  . & . & . & . & . & .\\  . & . & . & . & . & .\\  . & . & . & . & . & .\\  A_{n1} & A_{n2} & . & . & . & A_{nn} \end{bmatrix}\]

Матрица кофакторов также известна как матрица кофакторов или коматрица.

Формула матрицы кофакторов

В математике кофактор — это число, используемое для нахождения обратной матрицы, присоединенной. Кофактор определяется как число, которое получается при удалении строк или столбцов выбранных элементов в данной матрице, которая представляет собой просто числовую сетку в виде квадрата или прямоугольника.

Кофакторы всегда обозначаются положительным (+) или отрицательным (-) символом. Рассмотрим X как матрицу размера n x n, и пусть M _ij как (n — 1) x (n — 1) матрица, полученная удалением строки i ^th и столбца j ^th . Тогда det (M _ij известен как минор _ij . Кофактор A _ij  из _ij  определяется в терминах минора: A _ij = (-1) ^{i + j} det (M _ij })

Матрица сомножителей Пример

Пусть $A  = \begin{bmatrix} 2 & 6 & -1 \\  0 & 1 & 4 \\ 3 & -2 & -6 \end{bmatrix}$ 9{3+2} (8) = -8$

Сопряженная матрица

Пусть X = [a _ij ] — квадратная матрица порядка n. Сопряженная матрица X (также известная как сопряженная к матрице X) определяется как транспонированная кофакторная матрица X. Она представлена ​​adj X. Сопряженная матрица также известна как сопряженная матрица.

Чтобы определить сопряжение матрицы, сначала найдите кофактор данной матрицы. Затем найдите транспонирование кофакторов матрицы.

Adjugate Matrix Пример

Найдите сопряженную матрицу,

$A  = \begin{bmatrix}3 & 1 & -1 \\ 2 & -2 & 0 \\ 1 & 2 & -1\end{bmatrix}$

Кофактор 3 $= A_{11} = \begin{vmatrix}-2 & 0\\ 2 & -1\end{vmatrix} = 2$

Сомножитель 1 $= A_{12} = — \begin{vmatrix}2 & 0\\ 1 & -1\end{vmatrix} = 2$

Сомножитель -1 $= A_{13} = \begin{vmatrix}2 & -2\\ 1 & 2\end{vmatrix} = 6 $

Сомножитель 2 $= A_{21} = — \begin{vmatrix}1 & -1\\ 2 & -1\end{vmatrix} = -1$

Кофактор -2 $= A_{22} = \begin{vmatrix}3 & -1\\ 1 & -1\end{vmatrix} = -2$

Кофактор 0 $= A_{23} = — \begin{vmatrix}3 & 1\\ 1 & 2\end{vmatrix} = -5$

Сомножитель 1 $= A_{31} = \begin{vmatrix}1 & -1\\ -2 & 0\ end{vmatrix} = -2$

Кофактор 2 $= A_{32} = — \begin{vmatrix}3 & -1\\ 2 & 0\end{vmatrix} = -2$

Кофактор -1 $= A_{33} = \begin{vmatrix}3 & 1\\ 2 & -2\end{vmatrix} = -8$

$\therefore$ Сомножитель матрицы $A$ равен $A_{ij} = \begin{vmatrix}2 & 2 & 6\\ -1 & -2 & -5\\-2 & -2 & -8\end{vmatrix}$ 9T$

$ \begin{vmatrix}2 & -1 & -2\\ 2 & -2 & -2\\6 & -5 & -8\end{vmatrix}$

Следовательно, сопряженная матрица $ A = \begin{vmatrix}2 & -1 & -2\\ 2 & -2 & -2\\6 & -5 & -8\end{vmatrix}$

Минор матриц

В квадратной матрице каждый элемент имеет свой минор. Минор определяется как значение, полученное из определителей квадратной матрицы путем удаления столбца и строки, соответствующих элементу матрицы.

Для квадратной матрицы X под минором элемента понимается значение определителя, полученное удалением i ^-й -й строки и j ^-го -го столбца матрицы. Он представлен M ^ij .

Чтобы найти минор квадратной матрицы, мы должны удалить строку и столбец один за другим и вычислить их определитель, пока не будут вычислены все миноры. Ниже приведены шаги для вычисления минора из матрицы.

1. Скрыть ^{-я строка} и j ^{-й столбец} по отдельности из заданной матрицы, где i относится к m, а j относится к n, то есть к общему количеству строк и столбцов в матрицах.

2. Вычислите значение определителя матрицы после скрытия строк и столбцов из шага 1. миноры матрицы $A = \begin{bmatrix}a & b & c\\ d & e & f\\ g & h & i\end{bmatrix}$

   $M_{11} = \begin{bmatrix}e & f\\ h & i \end{bmatrix} = (ei — hf)$

   $M_{12} = \begin{bmatrix}d & f\ \ g & i \end{bmatrix} = (di — ff)$

   $M_{13} = \begin{bmatrix}d & e\\ g & h \end{bmatrix} = (dh — eg)$

   $M_{21} = \begin{bmatrix}b & c\\ h & i \end{bmatrix} = (bi — ch)$

   $M_{22} = \begin{bmatrix}a & c\\ g & i \end{bmatrix} = (ai — cg)$

   $M_{23} = \begin{bmatrix}a & b\\ g & h \end{bmatrix} = (ah — bg)$

   $M_{31} = \begin{bmatrix}b & c\\ e & f \end{bmatrix} = (bf — ce)$

   $M_{32} = \begin{bmatrix}a & c\ \ d & f \end{bmatrix} = (af — cd)$

   $M_{33} = \begin{bmatrix}a & b\\ d & e \end{bmatrix} = (ae — bd)$

   Нахождение обратной матрицы с использованием миноров, кофакторов и сопряжения?

   Ниже приведены шаги по нахождению обратной матрицы с использованием миноров, кофакторов и сопряженных элементов.

   1. Первым шагом к нахождению обратной матрицы является определение матрицы миноров.

   2. Второй шаг — преобразовать данную матрицу в матрицу кофакторов.

   3. Третий шаг — найти сопряжение матрицы.

   4. В конце умножьте на 1/Определитель.

   Обратная матрица с использованием миноров, кофакторов и сопряженной Пример

   Давайте научимся находить обратную матрицу с использованием миноров, кофакторов и сопряженной на примере:

   1. Найдите обратную матрицу

   $X = \ begin{bmatrix}3 & 1 & 2\\ 2 & 1 & -2\\0 & 1 & 1 \end{bmatrix}$

   Решение:

   Шаг 1: Чтобы найти обратную матрицу X, мы сначала найдем матрицу миноров.

   Матрица миноров $=\begin{bmatrix}3 & 2 & 2\\ -1 & 3 & 3\\-4 & -10 & 1 \end{bmatrix}$

   Шаг 2. На этом шаге мы найдем кофакторы указанной выше минорной матрицы

   Кофакторы минорной матрицы $ — \begin{bmatrix}3 & 2 & 2\\ -1 & 3 & 3\\-4 & -10 & 1 \end{bmatrix } \times \begin{bmatrix}+ & — & +\\ — & + & -\\+ & — & + \end{bmatrix} = \begin{bmatrix}3 & -2 & 2\\ 1 & 3 & -3\\-4 & 10 & 1 \end{bmatrix}$

   Шаг 3: Теперь мы найдем сопряженную или сопряженную вышеуказанную матрицу, поменяв местами элементы по диагонали таким образом, что: 3 & 10\\2 & -3 & 1 \end{bmatrix}$

   Шаг 4: Теперь найдем определители исходной матрицы X, используя следующую формулу определителей:

   $\text{det} \begin{ bmatrix}a & b & c\\ d & e & f\\g & h & i \end{bmatrix} = a \cdot \text{det} \begin{bmatrix}e & f\\ h & i\end {bmatrix} — b \cdot \text{det} \begin{bmatrix}d & f\\ g & i\end{bmatrix} + c \cdot \text{det} \begin{bmatrix}d & e\\ g & ч \end{bmatrix}$

   $\text{det} \begin{bmatrix}3 & 1 & 2\\ 2 & 1 & -2\\0 & 1 & 1 \end{bmatrix} = 3 \cdot \text{det} \begin{ bmatrix}1 & -2\\ 1 & 1\end{bmatrix} — (1) \cdot \text{det} \begin{bmatrix}2 & -2\\ 0 & 1\end{bmatrix} + 2 \cdot \text{det} \begin{bmatrix}2 & 1\\ 0 & 1 \end{bmatrix}$

   $\Rightarrow 3 [1 — (- 2)] -1[2 — (-0)] + 2 [2 -0]$

   $\Стрелка вправо 3(1 + 2) -1(2+ 0) + 2 (1)$

   $\Стрелка вправо 3(3) -1(2) + 2$

   $ \Стрелка вправо 9{-1} = \begin{bmatrix}\dfrac{3}{11} &\dfrac{1}{11} & \dfrac{-4}{11}\\ \dfrac{-2}{11} & \ dfrac{3}{11} & \dfrac{10}{11}\\\dfrac{2}{11} & \dfrac{-3}{11} & \dfrac{1}{11} \end{bmatrix} $

   Знаете ли вы?

   • Английский математик XIX века Джеймс Сильвестр ввел термин «матрица». {-1} = \dfrac{adj(A)}{|A|}; |А| \neq 0$.

   Сопряженная матрица

   Горячая математика

   Позволять А знак равно [ а я Дж ] быть квадратная матрица порядка н . Сопряжение матрицы А представляет собой транспонирование кофакторной матрицы А . Обозначается прил. А . Сопряженная матрица также называется сопряженной матрицей.

   Пример:

   Найдите сопряженную матрицу.

   А знак равно [ 3 1 − 1 2 − 2 0 1 2 − 1 ]

   Чтобы найти сопряженную матрицу, сначала найдите матрицу кофакторов данной матрицы. Затем найдите транспонированную матрицу кофакторов.

   Кофактор 3 знак равно А 11 знак равно | − 2 0 2 − 1 | знак равно 2

   Кофактор 1 знак равно А 12 знак равно − | 2 0 1 − 1 | знак равно 2

   Кофактор − 1 знак равно А 13 знак равно | 2 − 2 1 2 | знак равно 6

   Кофактор 2 знак равно А 21 знак равно − | 1 − 1 2 − 1 | знак равно − 1

   Кофактор − 2 знак равно А 22 знак равно | 3 − 1 1 − 1 | знак равно − 2

   Кофактор 0 знак равно А 23 знак равно − | 3 1 1 2 | знак равно − 5

   Кофактор 1 знак равно А 31 знак равно | 1 − 1 − 2 0 | знак равно − 2

   Кофактор 2 знак равно А 32 знак равно − | 3 − 1 2 0 | знак равно − 2

   Кофактор − 1 знак равно А 33 знак равно | 3 1 2 − 2 | знак равно − 8

   Матрица кофакторов А является [ А я Дж ] знак равно [ 2 2 6 − 1 − 2 − 5 − 2 − 2 − 8 ]

   Теперь найдите транспонирование А я Дж .

   а д Дж А знак равно ( А я Дж ) Т знак равно [ 2 − 1 − 2 2 − 2 − 2 6 − 5 − 8 ]

   Обратная матрица с использованием миноров, кофакторов и вспомогательных элементов

   10 декабря 2020 г. by Prasanna

   Миноры и кофакторы

   Если взять минор элемента:
   3 удалить) строку и столбец, содержащие этот элемент, определитель слева называется минором этого элемента. Обозначается M _ij .
   
   Аналогично можно найти миноры других элементов. Используя эту концепцию, значение определителя может быть
   ∆ = a ₁₁ M ₁₁ – a ₁₂ M ₁₂ + a ₁₃ M ₁₃
   or, ∆ = – a ₂₁ M ₂₁ + a ₂₂ M ₂₂ – a ₂₃ M ₂₃
   or, ∆ = a ₃₁ M ₃₁ – a ₃₂ M ₃₂ + a ₃₃ M ₃₃

   Cofactor of an element:
   Кофактор элемента a _ij  (т. е. элемент в i ^th строка и j ^й столбец) определяется как (–1) ^i+j , умноженное на меньшую часть этого элемента. Он обозначается C _ij или A _{ij или} F _ij .
   C _ij = (–1) ^i+j M _ij .
   
   , где C ₁₁ = (–1) ¹⁺¹ M ₁₁ =+M ₁₁ , C ₁₂ = (–1) ¹⁺² M ₁₂ = (–1) — ¹⁺² M ₁₂ = (–1) — ¹⁺² M ₁₂ . 12 и С ₁₃ = (–1) ¹⁺³  М ₁₃ = +М ₁₃
   Точно так же мы можем найти кофакторы других элементов.

   Сопряженная (также называемая сопряженной) квадратной матрицы

   Пусть A = [a _ij ] – квадратная матрица порядка n, а C _ij   – кофактор a _ij  из A. Тогда транспонирование матрица кофакторов элементов А называется сопряженной к А и обозначается прил А
   Таким образом, прил А = [С _ij ] ^Т ⇒ (прил А) _ij = С _ji = кофактор из 92

3. прил(А ^Т ) = (прил А) ^Т
4. прил(АВ) = (прил В)(прил А)
5. прил(А ^m ) = (прил А) , m ∈ N
6. adj(kA) = k ^n-1 (adj A), k ∈ R
7. adj(I _n ) = I _n
8. adj(0) = 6 0 9016 A симметрично ⇒ adj A также симметрично.
9. A диагональное ⇒ прил. A также диагональное.
10. A треугольный ⇒ прил. A также треугольный.
11. A в единственном числе ⇒ |adj A|= 0

Adjoint of a Square Matrix Problems with Solutions

1.

Solution:

2.

Solution:

Inverse of a Matrix

A non-singular square matrix порядка n обратима, если существует квадратная матрица B того же порядка такая, что AB = I _n =BA .
В таком случае мы говорим, что обратным к А является В, и пишем А ^-1 = В. Обратное к А определяется как

Необходимое и достаточное условие существования обратной квадратной матрицы A состоит в том, что |A| ≠ 0.

Свойства обратной матрицы:
Если A и B обратимые матрицы одного порядка, то

1. (A ^-1 ) ^-1 = A

(A T

2. ) ^-1 =(А ^-1 ) ^Т
3. (АВ) ^-1 = В ^-1 А ^-1
8 к0381 = (A ^-1 ) ^k , k ∈ N [В частности, (A ² ) ^-1 = (A ^-1 ) ² ]
4. прил. ) = (прил. A) ^-1
6. A = DIAG (A ₁ A ₂ … A _N ) ⇒ A ^-1 = DIAG (A _{13 1} 1414141414. 14. 1414. 14. 14. 14. 14. 14) ⇒ ^-1 = диаг. ). ₂ ^-1 …a _n ^-1 )
7. A симметричен ⇒ A ^-1 также симметричен.
8. А диагональ, |А| ≠ 0 ⇒ А ^-1 тоже диагональ.
9. A является скалярной матрицей ⇒ A ^-1 также является скалярной матрицей.
10. A треугольный, |A| ≠ 0 ⇒ A ^-1 тоже треугольный.
11. Каждая обратимая матрица имеет единственную обратную.
12. Закон об отмене в отношении умножения.
    Если A невырожденная матрица, т. е. |A|≠ 0 , то A ^-1 существует и AB = AC ⇒ A ^-1 (AB) = A ^-1 (AC)
    ⇒ ( А ^-1 А)В =(А ^-1 A)C
    ⇒ IB = IC ⇒ B=C
    ∴ AB=AC ⇒ B = C ⇔|A|≠ 0.

Обратные матричные задачи с решениями

1.

92 9 Решение

2.

Решение:

3.

. , Обратная матрица с использованием второстепенных кофакторов и вспомогательных, Минор элемента, Миноры и кофакторы, Свойства сопряженной матрицы, Свойства обратной матрицы

5. Нахождение обратной матрицы

М. Борна

Что мы делаем?

Если мы умножим матрицу A на , обратную матрицы A , мы получим матрицу тождества , I .

Концепция решения систем с использованием матриц аналогична концепции решения простых уравнений.

Например, чтобы решить 7 x = 14, мы умножаем обе части на одно и то же число. Мы находим «инверсию» `7`, то есть `1/7`. Умножение обеих сторон слева на «1/7» дает:

`(1/7) × 7x = (1/7) × 14`

На слева имеем (частично):

`(1/7) × 7 = 1`

Число ` 1` — это «тождество» для умножения обычных чисел. На справа получаем:

`1/7 х х 14 = 2`.

Решение нашего уравнения:

х = 2

Мы расширяем эту концепцию поиска обратной для решения одного уравнения до решения систем одновременных уравнений.

Нам нужно найти обратные матрицы, чтобы мы могли решать системы одновременных уравнений.

(Мы увидим, как решать системы, в следующем разделе «Матрицы и линейные уравнения»).

Мы найдем обратную матрицу двумя разными способами. Вы можете решить, какой из них использовать в зависимости от ситуации.

Первый метод ограничивается нахождением обратной матрицы 2 × 2. Он включает в себя использование определителя матрицы, которую мы видели ранее.

Напоминание: Мы можем найти определитель только квадратной матрицы . Например, если A является квадратной матрицей

`((2,3),(-1,5))`

, то мы можем найти определитель числа A :

`|(2,3),(-1,5)|=10+3=13`

Для удобства мы могли бы записать определитель матрицы `A` как `|A|`, и тогда наш окончательный ответ будет таким:

`|А| = 13`9-1`, из

`А=((2,-3),(4,-7))`

с использованием метода 1.

Ответить

Способ 1 заключается в следующем.

[1] Поменять местами ведущие диагональные элементы:

`-7 → 2`; `2 → -7`

`((-7,-3),(4,2))`

[2] Изменить знаки двух других элементов:

`-3 → 3`; `4 → -4`

`((-7,3),(-4,2))`

[3] Найдите определитель `|A|`

`|(2,-3),(4,-7)|=-14+12=-2` 9-1A=((3.5,-1.5),(2,-1))((2,-3),(4,-7))`

`=((7-6,-10.5+10.5), (4-4,-6+7))`

`=((1,0),(0,1))`

`=I`

Мы можем лечь спать счастливыми, зная, что наш ответ правильный.

Метод 2 — Дополнительная матрица (может быть расширена до любого размера)

ПРИМЕЧАНИЕ. Я оставил метод 2 здесь по историческим причинам. Мы будут использовать компьютеры для поиска обратного (или, что более важно, решение системы уравнений) матриц больше 2×2.

9-1=(«прил»A)/(detA)`

«adj A » является сокращением от «примыкание к A «. Мы используем кофакторы (с которыми мы познакомились ранее) для определить сопряженное матрицы.

Кофакторы

Отзыв: Кофактор элемент в матрице — это значение, полученное путем оценки определитель, образованный элементами, не входящими в эту конкретную строку или столбец.

Пример 2a

Рассмотрим матрицу:

`((5,6,1),(0,3,-3),(4,-7,2))`

Кофактор 6 равен

`|(0,-3),(4,2)|=0+12=12`

Кофактор -3 равен

`|(5,6),(4,-7)|=-35-24=-59`

Находим сопряженную матрицу заменой каждый элемент в матрице с его кофактором и применение + или — распишитесь следующим образом:

`((+,-,+),(-,+,-),(+,-,+))`

, а затем найти , транспонировать из результирующая матрица. Транспонирование означает 1 9Колонка 0380 st становится 1 ^st строка; 2 ^nd столбец становится 2 ^nd ряд и т. -1=(«прил»A)/detA` 9-1=((0,094,0,119,0,132),(0,075,-0,038,-0,094),(0,075,-0,371,-0,094))`

Пример 2c

Найдите обратное число

`((-2,6,1),(0,3,-3),(4,-7,3))`

с использованием метода 2.

Solution

`text(C of) A` `=((+(-12),-(12),+(-12)),(-(25),+ (-10),-(-10)),(+(-21),-(6),+(-6)))`

`=((-12,-12,-12),(- 25,-10,10),(-21,-6,-6))`

Поменять местами строки и столбцы:

`»adj»A=((-12,-25,-21),(-12 ,-10,-6),(-12,10,-6))` 9-1=(«adj»A)/(detA)`

`=1/-60((-12,-25,-21),(-12,-10,-6),(-12,10 ,-6))`

`=( (1/5,5/12,7/20),(1/5,1/6,1/10),(1/5,-1/6,1 /10))`

`=((0.2,0.417,0.35),(0.2,0.167,0.1),(0.2,-0.167,0.1))`

Использование компьютера для поиска обратной матрицы

Теперь посмотрим как делать все это удобнее с помощью компьютера…

Обратные матрицы больших матриц (метод 3)

Большинство реальных систем уравнений очень большие (обычно до 100 на 100).

No related posts.