29. Обратная функция. Функция, заданная неявно и параметрически
Функция где называется Обратимой на множестве если каждому значению У из множества значений функции соответствует единственное значение
Если – обратимая функция, то на множестве определена функция G, которая каждому значению ставит в соответствие такое, что т. е. определена Поэтому
Функция G называется Обратной функцией к F.
Функции F И G Называются Взаимно-обратными функциями. Графики взаимно-обратных функций F И G Симметричны относительно прямой
Если функции F И G Взаимно-обратны, то и
Для нахождения обратной функции из равенства выражают Х через У (если это возможно), а затем переобозначают переменные (через Х – независимую переменную, через У – зависимую).
Пусть У является функцией переменной U, а переменная U, в свою очередь, является функцией от переменной
 е. и Тогда функция называется Сложной функцией (или Функцией от функции), если область определения функции F содержит множество значений функции J. Переменная U в этом случае называется Промежуточной переменной.
е. и Тогда функция называется Сложной функцией (или Функцией от функции), если область определения функции F содержит множество значений функции J. Переменная U в этом случае называется Промежуточной переменной.Всякую линию на координатной плоскости, которая не имеет разрывов, называют Кривой линией.
График функции который не имеет разрывов, является кривой линией. Однако не всякая кривая линия является графиком функции (график функции задается при условии, что каждому значению Х соответствует Единственное значение Y).
Говорят, что функция задана неявно уравнением
(4.2)
Где F – некоторое выражение от переменных X, Y при условии
Функцию, заданную явно уравнением можно привести к виду (4.2):
(4.3)
(в равенстве (4.3) ). Однако не всякую функцию, заданную неявно, можно задать в виде Уравнение (4.2) не всегда однозначно разрешимо относительно переменной У или вообще не разрешимо. Оно задает часто кривую линию, но не график функции.
Оно задает часто кривую линию, но не график функции.
Для нахождения точки, лежащей на линии, которая задается уравнением (4.2), необходимо придать переменной X некоторое числовое значение, а затем из уравнения (4.2) найти соответствующее значение Y (возможно, несколько значений Y). Для построения соответствующей кривой придают переменной X некоторое количество числовых значений, получают множество точек, принадлежащих искомой линии (4.2). Эти точки следует соединить непрерывной линией.
Уравнения вида
(4.4)
Называют Параметрическими уравнениями линии, где T – параметр или вспомогательная переменная, а и – функции параметра T.
Каждому значению параметра T из заданного промежутка соответствуют определенные значения
Для построения линии, заданной параметрическими уравнениями, выбирают достаточное количество значений параметра где вычисляют соответствующие значения Затем на координатной плоскости отмечают точки которые потом соединяют непрерывной линией.
Чтобы от уравнений (4.4) перейти к уравнению типа необходимо исключить параметр T из уравнений системы (4.4).
Пример 1. Найти функцию, обратную данной (если она существует), и построить графики данной функции и ей обратной в одной системе координат:
1) 2)
Решение. 1) Функция монотонна, поэтому для нее существует обратная функция. Выразим Х через У:
Т. е.
Обозначим независимую переменную через Х, а зависимую – через У:
Обратная к заданной функции F есть функция и она имеет вид:
Где
А
Строим графики функции F и (рис. 4.5).
2) Так как функция не является монотонной на промежутке то обратной функции для нее не существует.
Рис. 4.5
Пример 2. Из уравнения окружности выразить явно У через Х.
Решение. Из уравнения выразим откуда получаем совокупность двух функций
Графиком первой функции в совокупности является полуокружность, расположенная в верхней полуплоскости системы Оху, при условии, что Графиком второй функции – полуокружность в нижней полуплоскости при условии, что
Пример 3. Построить кривую, заданную параметрически уравнениями
Построить кривую, заданную параметрически уравнениями
Решение. Для построения кривой выберем достаточное количество значений параметра и вычислим соответствующие значения Данные занесем в таблицу:
T | |||||
X | 4 | 0 | –4 | –8 | –12 |
Y | 0 | 2 | 4 |
Построим точки в системе координат Оху и соединим их плавной линией (рис. 4.6).
Рис. 4.6
| < Предыдущая | Следующая > |
|---|
Понятие функции. Способы задания функции
- Каждому элементу — один и только один элемент
- Способы задания функций
- Сложная функция
- Обратная функция
Понятие функции является одним из важнейших понятий математики и её
приложений. С помощью различных функций могут быть описаны многие процессы и явления
реального мира.
С помощью различных функций могут быть описаны многие процессы и явления
реального мира.
Пусть X и Y — какие-то множества. Имеет место функция, определённая на множестве X со значениями на множестве Y, если в силу некоторого закона f каждому элементу x∈X ставится в соответствие один и только один элемент y∈Y.
Это записывается в виде
y = f(x).
Другими словами, с помощью функции y = f(x) множество X отображается в множество Y. Поэтому функцию называют также отображением. Кстати, будет полезным открыть в новом окне материал Свойства и графики элементарных функций
Например, авиапассажиры сидят в креслах салона пассажирского самолёта.
Пусть X — множество пассажиров, а Y —
множество кресел салона. Тогда возникает соответствие f :
каждому пассажиру x∈X сопоставляется
то кресло y = f(x),
в котором он сидит.
Тогда возникает соответствие f :
каждому пассажиру x∈X сопоставляется
то кресло y = f(x),
в котором он сидит.
Наблюдается, таким образом, простой пример функции, областью определения которой является множество X пассажиров, а областью значений — множество f(X) занимаемых ими кресел. Если заполнены не все кресла Y, то множество значений функции будет подмножеством Y, не совпадающим со всем множеством Y.
Если в кресле
находятся два пассажира и
(например, мать и ребёнок), то это никак не противоречит определению функции f, которая и , и
однозначно ставит в соответствие кресло .
При этом такая функция принимает одно и то же значение
при разных значениях и
аргумента,
подобно тому как числовая функция y = f(x) = x²
принимает одно и то же значение 9 при x = — 3 и
при x = 3.
Если, однако, какому-то пассажиру удастся сесть сразу в два кресла и , то нарушится принцип однозначной определённости значений функции, поэтому такая ситуация не является функциональной в смысле данного выше определения функций, поскольку требуется, чтобы каждому значению x аргумента соответствовало бы одно определённое значение y = f(x) функции.
В математическом анализе часто X обозначают как D (область определения функции
Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от
икса или f(x). И это неслучайно. Функции составляют бОльшую
часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также
широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления
в функции.
Пример 1. Даны множества A = {a, b, c, d, e} и L = {l, m, n}. Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому соответствует.
Решение. Итак, множество A содержит
5 элементов, а множество L — 3 элемента. Если мы
поставим стрелки, ведущие от каждого элемента множества L к
элементам множества A, то некоторым элементам L будут соответствовать более одного элемента A. Такое
соответствие не является функцией по определению. Но если мы проведём стрелки от элементов A к элементам L,
то некоторым элементам A будут соответствовать одни и те
же элементы L, но при этом каждому элементу A будет соответствовать не более одного элемента L. Такое
соответствие не противоречит определение функции, следовательно, ответ на вопрос задания —
положительный.
Такое
соответствие не противоречит определение функции, следовательно, ответ на вопрос задания —
положительный.
Можно задать, например, такое соответствите между элементами данных множеств, которое будет функцией:
Пример 2. Даны множества A = {70, 140, 30, 48} и В = {35, 15, 12}. Установить между элементами множеств соответствие, заданное правилом «элемент A можно нацело поделить на элемент В«. Будет ли такое соответствие функцией?
Решение. Между элементами множеств A и В устанавливается следующее соответствие:
Это соответствие является функцией, так как каждому элементу из множества A соответствует не более одного элемента из множества В.
Аналитическое задание функции.
Функция задана аналитически, если функциональная зависимость выражена
в виде формулы, которая указывает совокупность тех математических операций, которые
должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение
функции.
При аналитическом задании функции указывают область определения, либо не указывают. В первом случае функция задаётся в виде y = f(x), x∈D, где D — область определения функции, во втором случае — в виде y = f(x). Во втором случае областью определения функции считается наибольшее множество, на котором имеет смысл формула, которой задана функция, то есть наибольшее множество аргумента, которое приводит к действительным значениям функции.
Важно, что функцию не следует отождествлять с формулой, с помощью которой она задана. Например, функции y = x², x∈]-∞,+∞[ и y = x², x∈[2, 4], выраженные одной и той же формулой y = x², так как они имеют разные области определения.
Наоборот, одна и та же функция может быть задана разными формулами на
различных участках области определения. Пусть, например,
Пусть, например,
Здесь две формулы задают одну функцию, определённую на всей числовой прямой. При x≤0 значения этой функции определяются по первой формуле, а при x>0 — по второй.
Пример 3. Площадь круга вычисляется как функция радиуса . Каковы должны быть требования к аналитическому заданию этой функции, то есть, можно ли записывать без указания области определения функции или же нужно указывать область определения и записывать ?
Решение. Нельзя опускать запись области определения функции , так как хотя выражение имеет смысл при всех действительных значениях r, но для площади круга допустимы лишь значения r≥0.
Аналитический способ задания функции удобен тем, что значения функции можно вычислить при любых значениях аргумента. Недостатком этого способа задания функции является его малая наглядность.
Графический способ задания функции
График функции даёт наглядное представление о её свойствах. Например,
график линейной функции y = kx + b — прямая линия, график квадратичной функции y = ax² + bx + c —
парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде
формул или уравнений. Таким образом, под графиком функции понимается множество точек
плоскости, декартовы координаты которых удовлетворяют заданному уравнению.
Например,
график линейной функции y = kx + b — прямая линия, график квадратичной функции y = ax² + bx + c —
парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде
формул или уравнений. Таким образом, под графиком функции понимается множество точек
плоскости, декартовы координаты которых удовлетворяют заданному уравнению.
Графический способ задания функции помимо геометрического изображения функции, заданной уравнением, удобен тогда, когда функцию трудно задать аналитически. Задать функцию графически — это значит построить её график. Это часто делают самопишущие приборы. Например, в медицине электрокардиограф строит электрокардиограмму — кривую изменения электрических импульсов сердечной мышцы.
Графиком числовой функции y = f(x)
называется множество точек плоскости с координатами (x; f(x)),
абсциссы которых — числа из области определения функции, а ординаты — соответствующие значения
функции.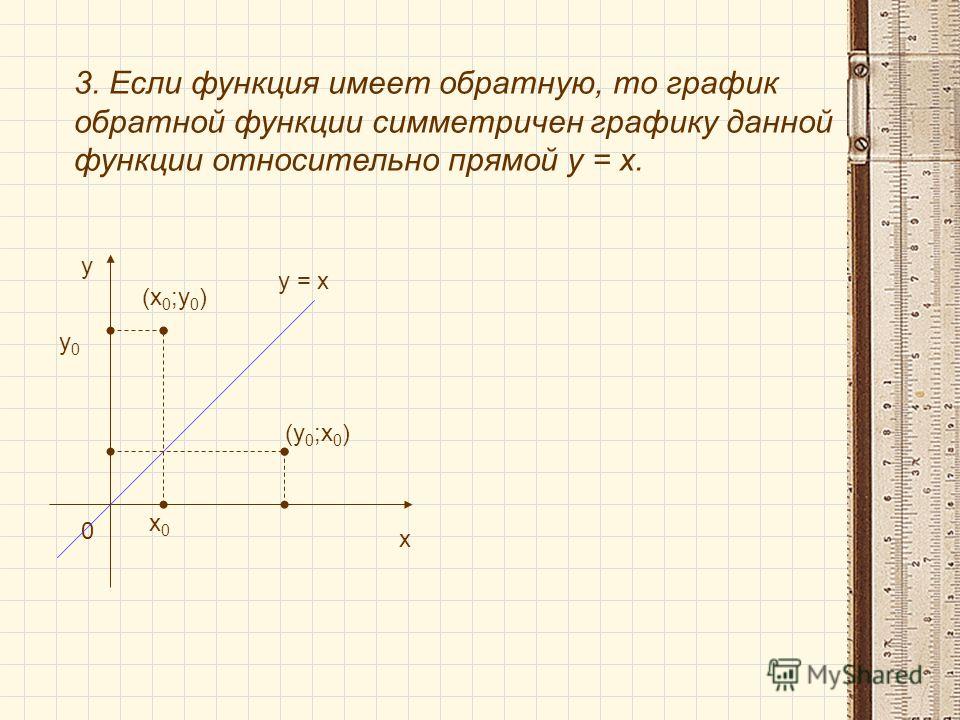
Не всякое множество точек координатной плоскости, даже не всякая линия может служить графиком функции. Линия только в том случае задаёт функцию, если любая прямая, параллельная оси 0y, пересекает её не более чем в одной точке.
Пример 4. На рисунке ниже — график параболы, заданной уравнением y² = 2x. Является ли этот график графиком функции?
Решение. График параболы, заданной уравнением y² = 2x, не является графиком функции, поскольку прямая, параллельная оси 0y, пересекает его в двух точках при всех значениях x, кроме x = 0. Заданное уравнение эквивалентно двум уравнениям , каждое из которых определяет функцию. Графиком функции служит верхняя половина параболы, а графиком функции — её нижняя половина.
Нет времени вникать в решение? Можно заказать работу!
Табличный способ задания функции
При табличном способе задания функции рядом с числовым значением аргумента
записывается соответствующее значение функции. Широко известных таблицы квадратов и кубов
чисел, квадратных корней, то есть таблицы функций ,
,
.
Широко известных таблицы квадратов и кубов
чисел, квадратных корней, то есть таблицы функций ,
,
.
Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены или утрачены.
Если функция y зависит от переменной u, то есть y = f(u), а u, в свою очередь, является какой-либо функцией от независимой переменной x, то есть u = g(x), то переменная y называется функцией от функции или сложной функцией от x.
Это записывается в виде
y = f(u), u = g(x)
или
y = f[g(x)].
Таким образом, сложной называется функция, аргументом которой является
не независимая переменная, а некоторая функция от неё.
Область определения сложной функции — это множество тех значений x из X, для которых соответствующие значения u принадлежат области определения U функции y = f(u). Ни для каких других значений x сложная функция не имеет смысла.
Из определения следует, что сложная функция y = f[g(x)] может быть представлена в виде цепочки простых функций y = f(u), u = g(x). Переменную u принято называть промежуточным аргументом в отличие от независимой переменной x. Цепочка, составляющая сложную функцию, может состоять не только из двух, но и из большего числа звеньев.
Например, функция состоит из трёх звеньев: , , .
Пример 5. Представить сложную функцию в виде звеньев — простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих
звеньев:
Цепочка, составляющая данную функцию, состоит из следующих
звеньев:
Пример 6. Представить сложную функцию в виде звеньев — простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:
Если функция y задана уравнением вида f(x, y) =0, не разрешённым относительно y, то она называется неявной функцией аргумента x (Что такое разрешить уравнение относительно одной из переменных — в примере 8).
Пусть задана некоторая функция y = f(x),
т. е. некоторое соответствие между множествами D(f)
(область определения) и E(f)
(множество значений). Если обратное соответствие есть функция,
т. е. каждому значению y∈E(f)
соответствует одно единственное значение x∈E(f),
то её называют обратной функцией по отношению к функции f(x).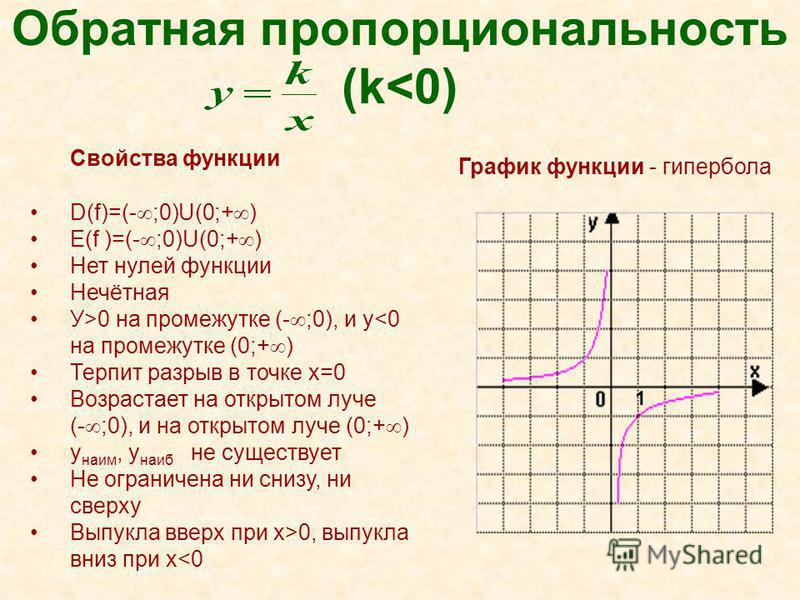
В этом случае уравнение y = f(x) определяет x как неявную функцию от y. Если это уравнение разрешимо относительно x, то получим явное выражение обратной функции: x = g(y).
Пример 7. Будет ли функцией соответствие, обратное функции ? А соответствие, обратное функции ?
Решение. Соответствие, обратное функции, заданной в первом условии, также является функцией:
.
Соответствие, обратное функции, заданной во втором условии, не является функцией, так как , то есть значениям икса, кроме нуля, соответствуют два значения игрека.
Пример 8. Найти функцию, обратную функции .
Решение. Множество значений данной функции . Разрешив уравнение, которым задана функция, относительно x, получаем . Заменив в этом уравнении x на y, получим функцию, обратную данной:
,
где ,
.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Предел
Весь раздел «Исследование функций»
- Непрерывность функции
- Точки разрыва функции и их виды
- Экстремумы функции
- Наименьшее и наибольшее значения функции
- Асимптоты
- Возрастание, убывание и монотонность функции
- Выпуклость и вогнутость графика функции, точки перегиба
- Полное исследование функций и построение графиков
- Функции двух и трёх переменных
- Экстремумы функции двух переменных
- Условные экстремумы и функция Лагранжа
Как найти обратную функцию? – Обзоры Вики
Нахождение обратной функции
- Сначала замените f (x) на y. …
- Замените каждый x на ay и замените каждый y на x.

- Решите уравнение для y из шага 2. …
- Заменим y на f − 1 (x) f — 1 (x). …
- Проверьте свою работу, проверив, что (f∘f − 1) (x) = x (f ∘ f — 1) (x) = x и (f − 1∘f) (x) = x (f — 1 ∘ f) (x) = x истинны.
Отсюда, что такое формула обратной вариации? Обратная вариация может быть представлена уравнением xy = k или y = kx . То есть y изменяется обратно пропорционально x, если существует некоторая ненулевая константа k такая, что xy = k или y = kx, где x ≠ 0, y ≠ 0.
Как найти обратную викторину? Обратные функции — это отражения друг друга на прямой y = x. Вы находите обратное путем переключения x и y в уравнении. Область определения функции всегда становится областью определения ее обратной функции.
Как написать уравнение обратной зависимости? Математически это записывается как y ∝ 1/x.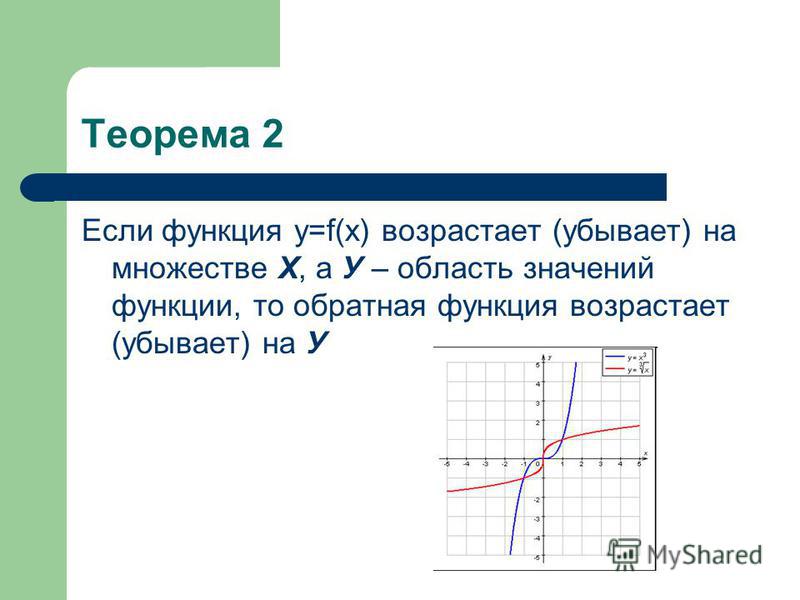 Общее уравнение обратной вариации: у = к / х, где k — константа пропорциональности. Мы также можем записать это как y × x = k или y × x = константа.
Общее уравнение обратной вариации: у = к / х, где k — константа пропорциональности. Мы также можем записать это как y × x = k или y × x = константа.
Как найти обратную зависимость?
Чтобы найти обратное алгебраическое отношение с точки зрения x и y, просто поменяйте местами переменные x и y и решите уравнение для y. Например, чтобы найти обратную зависимость y = x3, поменяйте местами x и y, а затем решите это для y. Тогда мы получаем х = у3 ⇒ у = х1/3.
Как узнать, правильно ли обратное? Для этого нужно показать, что оба f(g(x)) и g(f(x)) = x. Когда вас попросят найти обратную функцию, вы должны самостоятельно убедиться, что полученная вами обратная функция верна, если позволяет время. Покажите, что f(g(x)) = x. Покажите, что g(f(x)) = x.
Что значит найти обратную функцию Quizizz? Что значит найти обратную функцию? х и у поменялись местами. х и у делятся на 2. x и y сделаны отрицательными.
Как определить, является ли график обратной функцией?
Пусть f — функция. Если какая-либо горизонтальная линия пересекает график f более одного раза, то f не имеет обратной. Если ни одна горизонтальная линия не пересекает график f более одного раза, тогда f действительно имеет обратный. Свойство иметь обратное очень важно в математике, и у него есть название.
Также Как вы решаете обратные вариационные задачи? Решение обратной вариационной задачи
- Напишите уравнение вариации: y = k/x или k = xy.
- Подставьте указанные значения и найдите значение k.
- Перепишите вариационное уравнение: y = k/x с известным значением k.
- Подставьте оставшиеся значения и найдите неизвестное.
Как найти прямую и обратную вариацию?
Для прямой вариации используйте уравнение y = kx, где k — константа пропорциональности. Для обратной вариации используйте уравнение у = к/х, опять же, с k в качестве константы пропорциональности.
Что является примером обратной вариации? Например, если y изменяется обратно пропорционально x, и x = 5, когда y = 2, то постоянная вариации k = xy = 5(2) = 10. … Таким образом, уравнение, описывающее это обратное изменение, имеет вид xy = 10 или y = .
Какой пример обратной связи?
Примеры обратных отношений:
Скорость и время, необходимое для путешествия, обратно связаны.. По мере увеличения скорости время в пути уменьшается. … Закон спроса и предложения – это обратная зависимость. По мере увеличения спроса на товар его предложение будет уменьшаться.
Как найти обратную функцию один к одному?
Если горизонтальная линия пересекает график функции более чем в одном месте, функция НЕ является взаимно однозначной. ТЕСТ ГОРИЗОНТАЛЬНОЙ ЛИНИИ: функция f взаимно однозначна и имеет обратную функцию тогда и только тогда, когда ни одна горизонтальная линия не пересекает график f более чем в одной точке.
Что значит найти обратную функцию *? Обратная функция – это функция отменяет действие другой функции. Функция g является обратной функцией f, если всякий раз, когда y=f(x), тогда x=g(y). Другими словами, применить f, а затем g — это то же самое, что ничего не делать.
Функция g является обратной функцией f, если всякий раз, когда y=f(x), тогда x=g(y). Другими словами, применить f, а затем g — это то же самое, что ничего не делать.
Через какое уравнение будут отражаться две обратные функции? Это будет верно в целом; график функции и обратная к ней есть отражение над линия у = ху=ху=х .
Являются ли синий и красный графики обратными функциями?
Обратные функции: графическое представление: График функции (Красный) и график его обратной функции (синий) являются отражениями друг друга относительно линии y=x (черная пунктирная линия). … Например, (0,1) на красной кривой (функция) отражается на линии y=x и становится (1,0) на синей кривой (обратная функция).
Как вы решаете вариации в математике? Поскольку k постоянно (одинаково для каждой точки), мы можем найти k, когда для любой точки путем деления координаты y на координату x. Например, если y изменяется прямо как x, а y = 6, когда x = 2, постоянная вариации равна k = = 3. Таким образом, уравнение, описывающее это прямое изменение, будет y = 3x.
Таким образом, уравнение, описывающее это прямое изменение, будет y = 3x.
Как построить график обратных вариаций?
Что такое обратная вариация и прямая вариация? Прямая вариация — это линейная функция, определяемая уравнением вида у = кх, когда х не равно нулю. Обратная вариация — это нелинейная функция, определяемая уравнением вида xy = k, когда x не равно нулю, а k — ненулевая вещественная числовая константа.
Как обратная вариация используется в повседневной жизни?
Применение обратной вариации в повседневной жизни
Игровой автомат количество членов семьи (которые не работают) обратно пропорционально сбережениям. Количество рабочих дней, необходимых для выполнения работы, обратно пропорционально числу рабочих. … Мощность батареи обратно пропорциональна времени, в течение которого она используется. y
y
x?y:zx then y else zx==yx!=yx<yx<=yx>yx>=yМатематические функции
Векторы и матрицы: создание
eye(n) | Создает единичную матрицу n x n |
length(y) | Возвращает длину вектора y |
linspace(from,to,n) | Вещественный вектор с n линейно расставленными компонентами между from и to |
logspace(from,to,n) | Вещественный вектор с n логарифмически расставленными компонентами между from и to |
Векторы и матрицы: основные матричные функции
adjoint(x) | Сопряженная с x матрица (транспонированная и комплексно-сопряженная) |
det(x) | Детерминант матрицы x |
inverse(x) | Инверсия матрицы x |
transpose(x) | Транспонированная матрица для x (столбцы и строки меняются местами) |
Элементарные математические функции: основные вещественные и комплексные функции
abs(x) | Абсолютное значение, модуль комплексного числа |
angle(x) | Фазовый угол (в радианах) комплексного числа. Синоним arg() Синоним arg() |
arg(x) | Фазовый угол (в радианах) комплексного числа |
conj(x) | Сопряжение комплексного числа |
deg2rad(x) | Преобразует фазу из градусов в радианы |
hypot(x,y) | Функция евклидового расстояния |
imag(x) | Мнимая часть комплексного числа |
mag(x) | Модуль комплексного числа |
norm(x) | Квадрат абсолютного значения вектора |
phase(x) | Фазовый угол (в градусах) комплексного числа |
polar(m,p) | Преобразование полярных координат m и p в комплексное число |
rad2deg(x) | Преобразует фазу из радианов в градусы |
real(x) | Вещественная часть комплексного числа |
sign(x) | Знаковая функция |
sqr(x) | Квадрат (вторая степень) числа |
sqrt(x) | Квадратный корень |
unwrap(p[,tol[,step]]) | Разворачивает угол p (радианы) – по умолчанию step = 2pi, tol = pi |
Элементарные математические функции: экспоненциальные и логарифмические функции
exp(x) | Экспоненциальная функция с основанием e |
limexp(x) | Ограниченная экспоненциальная функция |
log10(x) | Десятичный логарифм |
log2(x) | Двоичный логарифм |
ln(x) | Натуральный логарифм (основание e ) |
Элементарные математические функции: тригонометрия
cos(x) | Косинус |
cosec(x) | Косеканс |
cot(x) | Котангенс |
sec(x) | Секанс |
sin(x) | Синус |
tan(x) | Тангенс |
Элементарные математические функции: обратные тригонометрические функции
arccos(x) | Арккосинус (известный также как “обратный косинус”) |
arccosec(x) | Арккосеканс |
arccot(x) | Арккотангенс |
arcsec(x) | Арксеканс |
arcsin(x) | Арксинус (известный также как “обратный синус”) |
arctan(x[,y]) | Арктангенс (известный также как “обратный тангенс”) |
Элементарные математические функции: гиперболические функции
cosh(x) | Гиперболический косинус |
cosech(x) | Гиперболический косеканс |
coth(x) | Гиберболический котангенс |
sech(x) | Гиперболический секанс |
sinh(x) | Гиперболический синус |
tanh(x) | Гиперболический тангенс |
Элементарные математические функции: обратные гиперболические функции
arcosh(x) | Гиперболический ареакосинус |
arcosech(x) | Гиперболический ареакосеканс |
arcoth(x) | Гиперболический ареакотангенс |
arsech(x) | Гиперболический ареасеканс |
arsinh(x) | Гиперболический ареасинус |
artanh(x) | Гиперболический ареатангенс |
Элементарные математические функции: округление
ceil(x) | Округление до ближайшего большего целого |
fix(x) | Отбрасывание десятичных разрядов вещественного числа |
floor(x) | Округление до ближайшего меньшего целого |
round(x) | Округление до ближайшего целого |
Элементарные математические функции: специальные математические функции
besseli0(x) | Модифицированная функция Бесселя нулевого порядка |
besselj(n,x) | Функция Бесселя первого рода и n-го порядка |
bessely(n,x) | Функция Бесселя второго рода и n-го порядка |
erf(x) | Функция ошибки |
erfc(x) | Комплиментарная функция ошибки |
erfinv(x) | Обратная функция ошибки |
erfcinv(x) | Обратная комплиментарная функции ошибки |
sinc(x) | Sinc-функция (sin(x)/x или 1 при x = 0) |
step(x) | Шаговая функция |
Анализ данных: основные операции
cumprod(x) | Накопительное произведение элементов вектора |
cumsum(x) | Накопительная сумма элементов вектора |
interpolate(f,x[,n]) | Spline interpolation of vector f using n equidistant points of x |
prod(x) | Произведение элементов вектора |
sum(x) | Сумма элементов вектора |
xvalue(f,yval) | Returns x-value nearest to yval in single dependency vector f |
yvalue(f,xval) | Returns y-value nearest to xval in single dependency vector f |
Анализ данных: дифференцирование и интегрирование
ddx(expr,var) | Дифференцирует математическое выражение expr по переменной var |
diff(y,x[,n]) | Дифференцировать вектор y по вектору x n раз.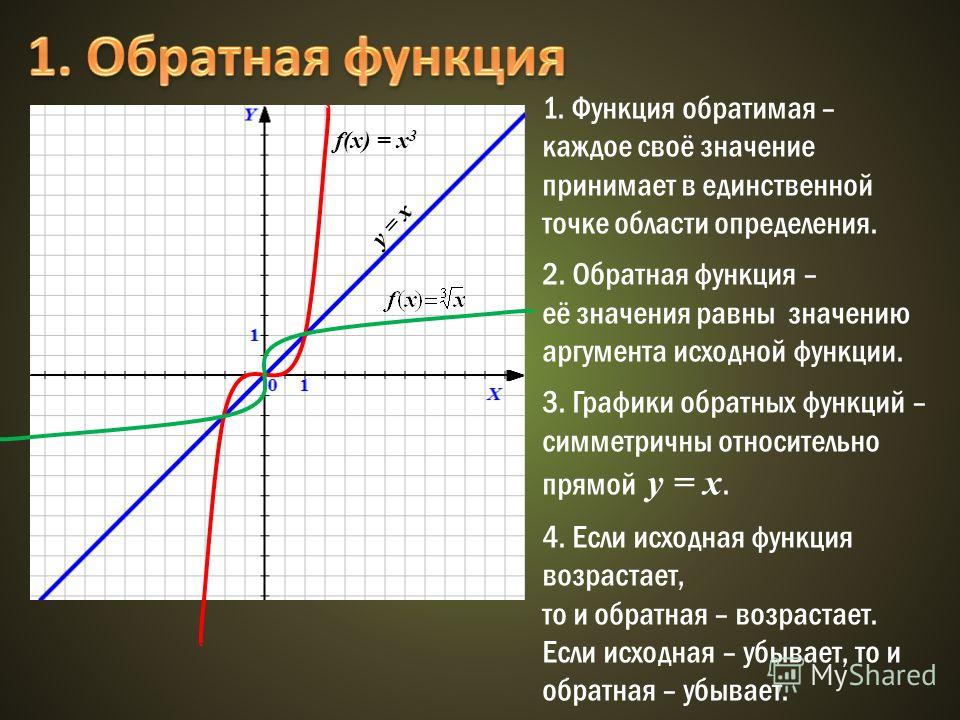 По умолчанию По умолчанию n = 1 |
integrate(x,h) | Численно интегрировать вектор x, считая, что размер шага h постоянный |
Функции из электроники
Преобразование единиц измерения
dB(x) | Значение в дБ |
dbm(x) | Преобразовать напряжение в мощность в дБм |
dbm2w(x) | Преобразовать мощность в дБм в мощность в ваттах |
w2dbm(x) | Преобразовать мощность в ваттах в мощность в дБм |
vt(t) | Температурный потенциал для данной температуры t в градусах Кельвина |
Коэффициенты отражения и КСВН
rtoswr(x) | Преобразует коэффициент отражения в коэффициент стоячей волны по напряжению (КСВН) |
rtoy(x[,zref]) | Преобразует коэффициент отражения в полную проводимость; по умолчанию zref равно 50 Ом |
rtoz(x[,zref]) | Преобразует коэффициент отражения в полное сопротивление; по умолчанию zref равно 50 Ом |
ytor(x[,zref]) | Преобразует полную проводимость в коэффициент отражения; по умолчанию zref равно 50 Ом |
ztor(x[,zref]) | Преобразует полное сопротивление в коэффициент отражения; по умолчанию zref равно 50 Ом |
N-портовые матричные преобразования
stos(s,zref[,z0]) | Преобразует матрицу S-параметров в матрицу S-параметров с другим Z0 |
stoy(s[,zref]) | Преобразует матрицу S-параметров в матрицу Y-параметров |
stoz(s[,zref]) | Преобразует матрицу S-параметров в матрицу Z-параметров |
twoport(m,from,to) | Преобразует двух-портовую матрицу: from и to — это ‘Y’, ‘Z’, ‘H’, ‘G’, ‘A’, ‘S’ и ‘T’.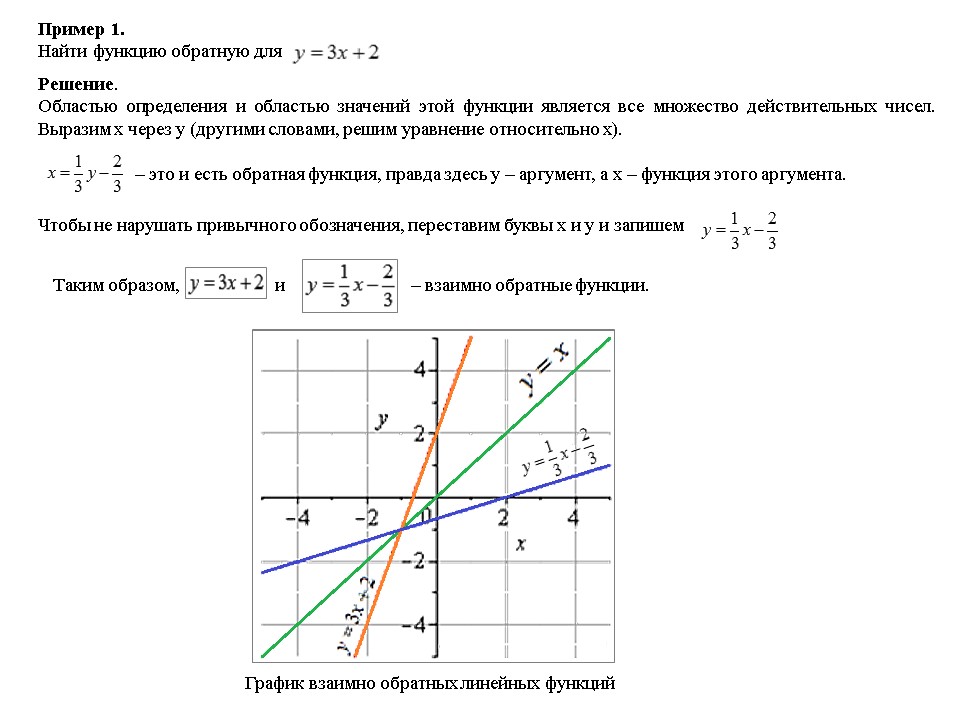 |
ytos(y[,z0]) | Преобразует матрицу Y-параметров в матрицу S-параметров |
ytoz(y) | Преобразует матрицу Y-параметров в матрицу Z-параметров |
ztos(z[,z0]) | Преобразует матрицу Z-параметров в матрицу S-параметров |
ztoy(z) | Преобразует матрицу Z-параметров в матрицу Y-параметров |
Усилители
GaCircle(s,Ga[,arcs]) | Доступный коэффициент усиления мощности Ga окружностей (плоскость источника) |
GpCircle(s,Gp[,arcs]) | Операционный коэффициент усиления мощности Gp окружностей (плоскость нагрузки) |
Mu(s) | Mu — фактор устойчивости двухпортовой матрицы S-параметров |
Mu2(s) | Mu’ — фактор устойчивости двухпортовой матрицы S-параметров |
NoiseCircle(Sopt,Fmin,Rn,F[,Arcs]) | Окружности диаграммы шума(ов) F |
PlotVs(data,dep) | Возвращает данные, выбранные из data: зависимость dep |
Rollet(s) | Фактор устойчивости Роллета для двухпортовой матрицы S-параметров |
StabCircleL(s[,arcs]) | Окружность устойчивости в плоскости нагрузки |
StabCircleS(s[,arcs]) | Окружность устойчивости в плоскости источника |
StabFactor(s) | Фактор устойчивости двухпортовой матрицы S-параметров |
StabMeasure(s) | Мера устойчивости B1 двухпортовой матрицы S-параметров |
Номенклатура
Интервалы
LO:HI | Интервал от LO до HI |
:HI | Вплоть до HI |
LO: | От LO |
: | Нет ограничений интервала |
Матрицы и элементы матриц
M | Вся матрица M |
M[2,3] | Элемент, находящийся во 2-м ряду и 3-м столбце матрицы M |
M[:,3] | Вектор, состоящий из 3-го столбца матрицы M |
Непосредственно
2. | Вещественное число |
1.4+j5.1 | Комплексное число |
[1,3,5,7] | Вектор |
[11,12;21,22] | Матрица |
Приставки к единицам
E | экса, 1e+18 |
P | пета, 1e+15 |
T | тера, 1e+12 |
G | гига, 1e+9 |
M | мега, 1e+6 |
k | кило, 1e+3 |
m | милли, 1e-3 |
u | микро, 1e-6 |
n | нано, 1e-9 |
p | пико, 1e-12 |
f | фемто, 1e-15 |
a | атто, 1e-18 |
Названия величин
S[1,1] | Значение S-параметра |
nodename. V | Напряжение постоянного тока в узле nodename |
name.I | Постоянный ток через компонент name |
nodename.v | Переменное напряжение в узле nodename |
name.i | Переменный ток через компонент name |
nodename.vn | Шумовое напряжение переменного тока в узле nodename |
name.in | Шумовой переменный ток через компонент name |
nodename.Vt | Переходное напряжение в узле nodename |
name.It | Переходной ток через компонент name |
Примечание: Все напряжения и токи — пиковые значения.Примечание: Шумовые напряжения — СКЗ значения в полосе частот 1 Hz.
Константы
i, j | Мнимая единица (“квадратный корень из -1”) |
pi | 4*arctan(1) = 3.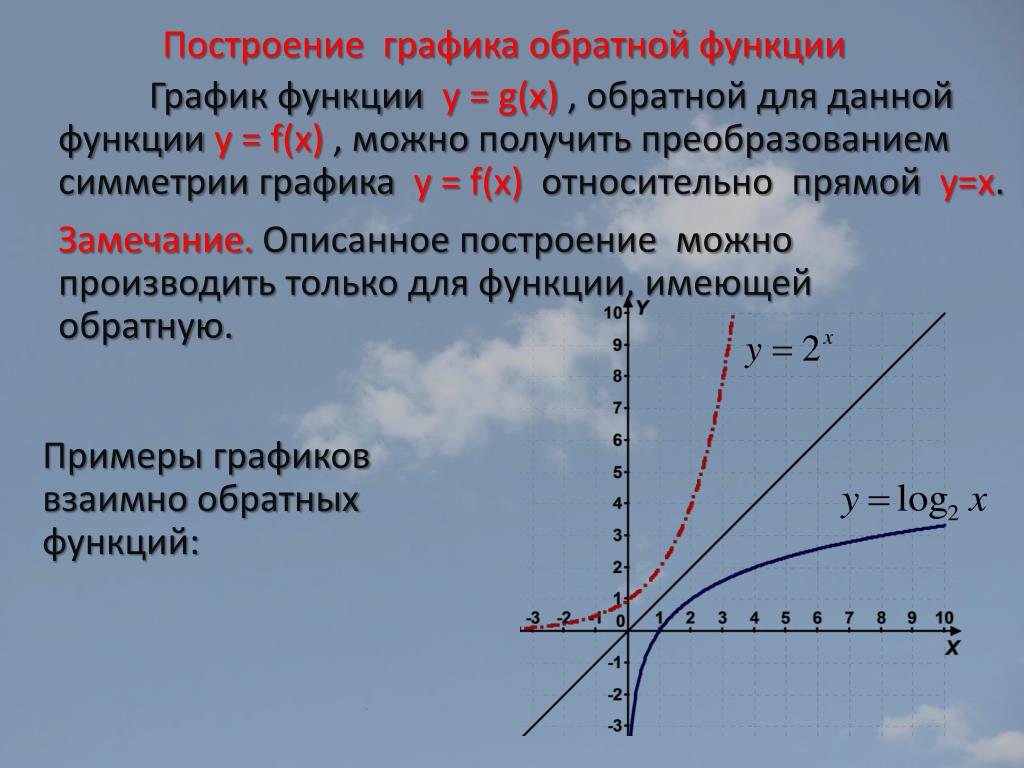 14159… 14159… |
e | e = 2.71828… |
kB | Постоянная Больцмана = 1.38065e-23 Дж/K |
q | Элементарный заряд = 1.6021765e-19 Кл |
back to the top
3-8Как найти обратную функцию — объяснение!
Определения / инвертирование графикаЯвляется ли обратная функция? Ограниченные доменыРаботающие примерыДоказательство обратной функции
Purplemath
Как найти обратную функцию?
Шаги для нахождения обратной функции, где они дали вам формулу для функции, следующие:
- Замените « f ( x )» на лет .

- Попробуйте решить уравнение для x =.
- Поменяйте местами x и на .
- Заменить и на « f −1 ( x )»
Содержание продолжается ниже
MathHelp.com
Обратные функции
Примечание. Некоторые учебники и преподаватели заставляют вас менять местами переменные (шаг 3 выше) перед решением (шаг 2 выше). Если вы должны найти инверсию таким образом, то шаги таковы:
- Замените « f ( x )» на y .
- Поменяйте местами x и на .
- Попробуйте решить уравнение для y =.
- Заменить и на « f −1 ( x )»
Я буду использовать порядок из первого набора шагов выше. Какой бы метод вы ни использовали, убедитесь, что вы практикуете его достаточно, чтобы запомнить шаги следующего теста.
- Найдите обратное число y = 3 x − 2.
Вот как работает процесс: Я начинаю с моей исходной функции:
y = 3 x − 2
Теперь я попытаюсь решить для « x =»:
x =», я поменяю местами x и y ; новый » y =» является обратным.
Тогда обратное число:
y = ( x + 2) / 3
Если вам нужно найти домен и диапазон, посмотрите на исходную функцию и ее график. Область определения исходной функции — это набор всех допустимых значений x ; в данном случае функция была простым полиномом, поэтому областью определения были «все действительные числа».
Диапазон исходной функции — все значения y , которые вы передадите по вертикальной оси; в этом случае прямая линия бесконечно продолжается в любом направлении, поэтому диапазон также представляет собой «все действительные числа». Чтобы найти домен и диапазон обратной функции, просто поменяйте местами домен и диапазон исходной функции.
Чтобы найти домен и диапазон обратной функции, просто поменяйте местами домен и диапазон исходной функции.
- Найдите обратную величину y = −2 / ( x — 5) , укажите домен и диапазон и определите, является ли обратная функция также функцией.
Поскольку переменная стоит в знаменателе, это рациональная функция. Кроме того, поскольку я не могу делить на ноль, область определения этой функции составляет x ≠ 5. Дробь равна нулю, когда ее числитель равен нулю, а этот числитель никогда не будет таким, поэтому диапазон равен 9.0916 y ≠ 0. Я буду использовать это, чтобы найти домен и диапазон обратного значения.
Вот алгебра для нахождения этой обратной функции, начиная с исходной функции:
Я умножаю знаменатель до левой части уравнения:
y ( x − 5) = −2
Я беру y через круглые скобки:
xy − 5 y = −2
. 0907
0907
xy = 5 y − 2
Затем я решаю x =:
. , и это еще одна рациональная функция; в частности, обратная действительно является функцией.
Область определения и диапазон этой обратной функции являются обратными значениями области определения и диапазона исходной функции. Итак, мой ответ:
обратно:
y = (5 x − 2) / x домен: x ≠ 0
диапазон: г ≠ 5
обратная функция
- Найдите обратную y = x 2 + 1 и укажите, является ли обратная функция функцией.
Будут времена, когда вам дадут функции, у которых нет инверсий, и по графику данной функции легко увидеть, что эта функция не может иметь инверсию, так как она нарушает тест горизонтальной линии :
Обычно считается приемлемым нарисовать приведенный выше график, провести через него горизонтальную линию, которая дважды пересекает график, а затем сказать что-то вроде «Обратное значение этой функции само по себе не является функцией из-за теста горизонтальной линии».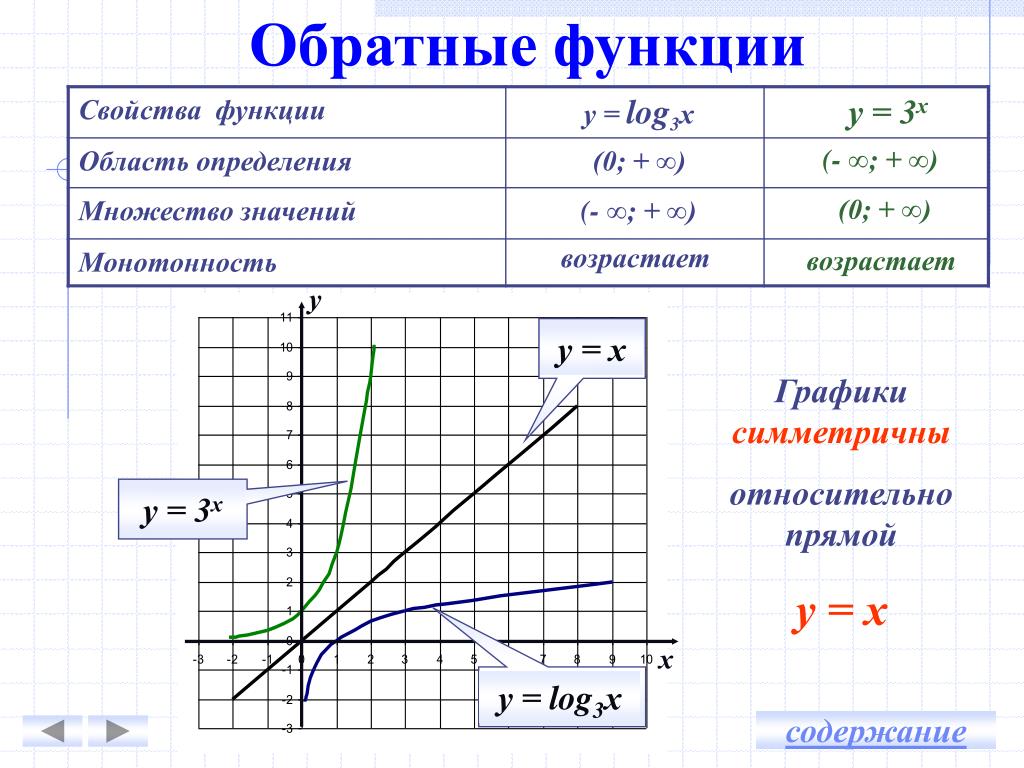 Но некоторые учителя все равно хотят видеть алгебру. Обязательно посоветуйтесь со своим учителем и уточните, какой ответ будет приемлемым, и сделайте это перед тестом!
Но некоторые учителя все равно хотят видеть алгебру. Обязательно посоветуйтесь со своим учителем и уточните, какой ответ будет приемлемым, и сделайте это перед тестом!
Как это будет выглядеть, когда я попытаюсь найти обратное алгебраически? Тест вертикальной линии говорит, что у меня не может быть двух девяток.0916 y , которые имеют общее значение x . То есть каждое x должно иметь УНИКАЛЬНОЕ соответствующее значение y . Но посмотрите, что происходит, когда я пытаюсь решить для « x »:
Моя исходная функция:
y = x 2 + 1
Теперь я пытаюсь найти «x ». =»:
y — 1 = x 2
± √( x — 1) = y
Ну, а я нашел обратную функцию? Нет; потому что для любого входа x в обратном порядке, но я не получу УНИКАЛЬНЫЙ вывод y . Вместо этого я показал, что любое заданное значение x на самом деле будет соответствовать двум различным значениям y , одно из «плюс» квадратного корня, а другое — из «минус». Поэтому мой ответ таков:
Поэтому мой ответ таков:
обратное:
y = ± √( x − 1)Обратное не является функцией.
Каждый раз, когда вы встречаете знак «±», вы можете быть уверены, что обратная функция не является функцией.
URL: https://www.purplemath.com/modules/invrsfcn3.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске обратной функции. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Найти инверсию», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок).
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.) 9{-1}(x).$ Обратите внимание, что не так просто определить обратную функцию этой формы. Итак, рассмотрим следующий пошаговый подход к поиску инверсии:  Обратную линейную функцию найти намного проще, чем другие виды функций, такие как квадратичные и рациональные. Причина в том, что область определения и диапазон линейной функции естественным образом охватывают все действительные числа, если область определения не ограничена. Прежде чем перейти к пяти (5) примерам, иллюстрирующим процедуру, я хочу показать вам, как связаны домен и диапазон заданной функции и ее обратной функции. Домен и диапазон только что поменялись местами! Примечания к диаграмме : Общий подход к тому, как алгебраически найти обратное, следующий: 9{ — 1}}\left( x \right), чтобы получить обратную функцию. Пример 1: Поиск обратной линейной функции Эта функция работает хорошо, потому что область определения и диапазон являются действительными числами. Это гарантирует, что его обратная функция тоже должна быть функцией. Возможно, вы знакомы с тестом горизонтальной линии, который гарантирует, что он будет обратным всякий раз, когда ни одна горизонтальная линия не пересекается или не пересекает график более одного раза. Используйте приведенные выше ключевые шаги в качестве руководства для решения обратной функции: Это было легко! Пример 2: Найдите обратную линейную функцию В конце решения я хочу сделать знаменатель положительным, чтобы оно выглядело «хорошо». Пример 3: Найти обратную линейную функцию Некоторые учащиеся могут считать это рациональной функцией, поскольку уравнение содержит некоторые рациональные выражения. Не путайте дроби здесь. Да, дроби есть, но в знаменателе нет переменных. Это делает его просто обычной линейной функцией. Чтобы понять это, я должен избавиться от знаменателя. Я добьюсь этого, умножив обе части уравнения на их наименьший общий знаменатель (LCD). Как показано выше, вы можете записать окончательные ответы двумя способами. Одна с одним знаменателем, а другая разложена на неполные дроби. Пример 4: Найдите обратную линейную функцию ниже и укажите ее область определения и диапазон. Это «нормальная» линейная функция, но с ограниченной областью определения. Допустимые значения x начинаются с x=2 и доходят до положительной бесконечности. Диапазон можно определить по его графику. Обратите особое внимание на то, как домен и диапазон определяются с помощью его графа. Найти обратную эту функцию очень просто. Но помните, как правильно описать область определения и область значений обратной функции. Мы рассмотрели эту концепцию в начале этого раздела о замене домена и диапазона. Всегда проверяйте домен и диапазон обратной функции, используя домен и диапазон оригинала. Они просто взаимозаменяемы. Пример 5: Найдите обратную линейную функцию ниже и укажите ее область определения и диапазон. Первым шагом является построение графика функции по оси xy. Четко обозначьте домен и диапазон. Незакрашенный кружок (незаштрихованная точка) означает, что номер в этой точке исключен. Если вам нужно освежить в памяти эту тему, посмотрите мой отдельный урок о решении линейных неравенств. Во-вторых, найдите обратное алгебраически, используя предложенные шаги. Переменная x в исходном уравнении имеет коэффициент -1. Следите за этим, когда будете решать обратное. Я надеюсь, что вы получили некоторые базовые идеи о том, как найти обратную линейную функцию . Я рекомендую вам просмотреть соответствующие уроки о том, как найти инверсию других типов функций. Вас также может заинтересовать: Обратная матрица 2×2 Обратная функция абсолютного значения Обратная функция постоянной Обратная функция экспоненциальной Обратная логарифмическая функция Обратная квадратичная функция Обратная рациональная функция Обратная функция квадратного корня Фрэнк Уилсон, Общественный колледж Чендлера-Гилберта; Скотт Адамсон, Общественный колледж Чендлера-Гилберта; Трей Кокс, Общественный колледж Чендлера-Гилберта; и Алан О’Брайан, Университет штата Аризона Что бы вы сделали, если бы обнаружили, что популярный подход к обучению обратным функциям отрицательно влияет на понимание учащимися основных идей? Вы бы продолжали преподавать проблемную процедуру или искали бы лучший способ помочь студентам разобраться в математике? Популярный подход к нахождению обратной функции состоит в том, чтобы поменять местами переменные \(x\) и \(y\) и найти переменную \(y\). Основополагающие идеи о функциях и их обратных функциях Эти две концепции формируют основополагающие идеи концепции обратной функции и справедливы для функций, представленных в уравнениях, графиках, таблицах или словах. Проблемные концепции, возникающие из Перестановки x и y Подход к нахождению обратных функций Некоторым преподавателям может показаться ересью называть это утверждение проблемной концепцией . Однако легко увидеть концептуальную проблему, когда переменным присваиваются реальные значения. Учебный пример представляет собой традиционное упражнение, в котором учащиеся сосредотачиваются только на заученной процедуре. Карлсон и Ортман предупреждают, что «этот процедурный подход к определению «ответа» не имеет большого значения или не имеет никакого реального значения для студента, если он или она также не понимает, почему процедура работает (2005)». Концептуальная слабость проблематичного подхода к нахождению обратного становится ясно очевидной с функциями, представляющими контексты реального мира. Шаг 1: Замените $f(x)$ на $y. 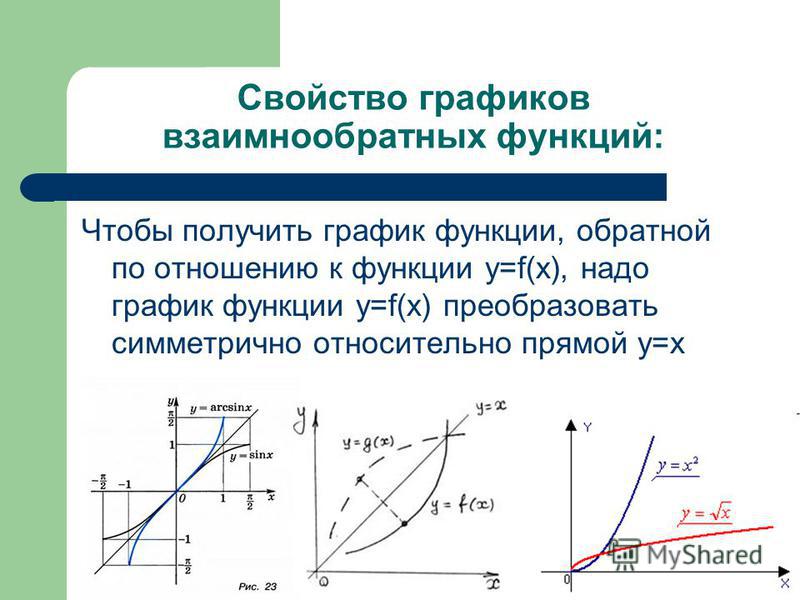 {-1}\circ f)(x) = x$.
9{-1}(х) = \sqrt{х}
\конец{выравнивание*}
{-1}\circ f)(x) = x$.
9{-1}(х) = \sqrt{х}
\конец{выравнивание*} Обратная линейная функция — ChiliMath
Поиск
Примеры поиска обратной линейной функции
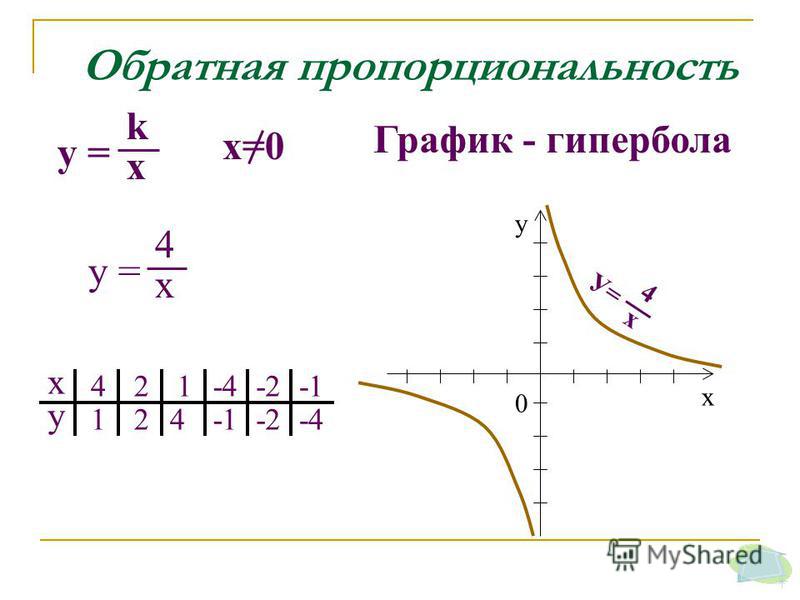 Я сделал это, умножив и числитель, и знаменатель на -1.
Я сделал это, умножив и числитель, и знаменатель на -1.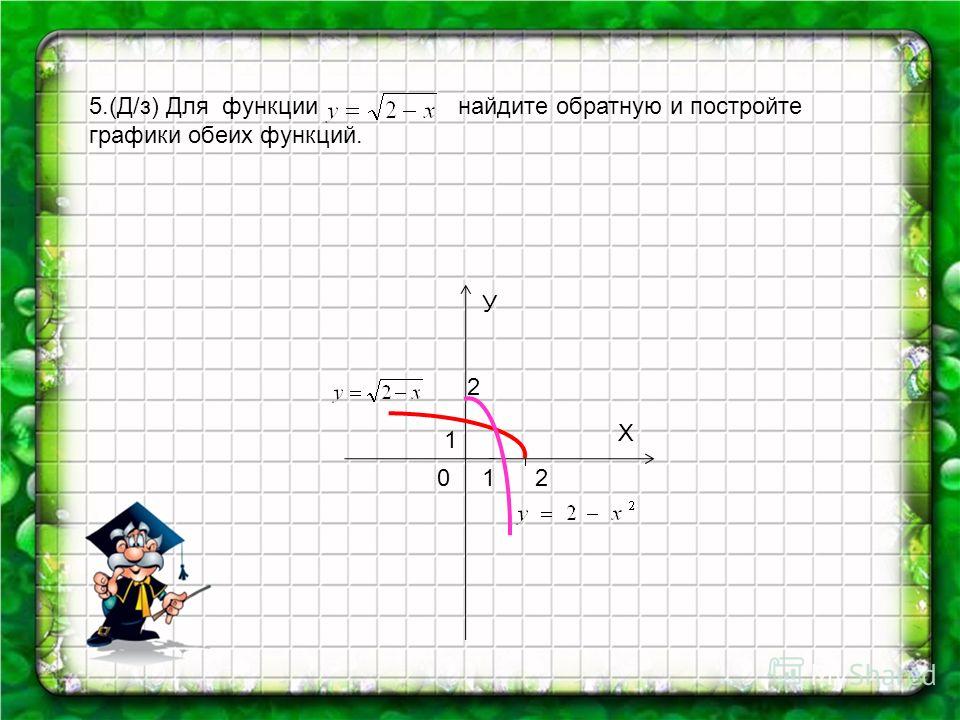 Помните, что диапазон — это набор всех значений y, когда допустимые значения x (домен) подставляются в функцию.
Помните, что диапазон — это набор всех значений y, когда допустимые значения x (домен) подставляются в функцию.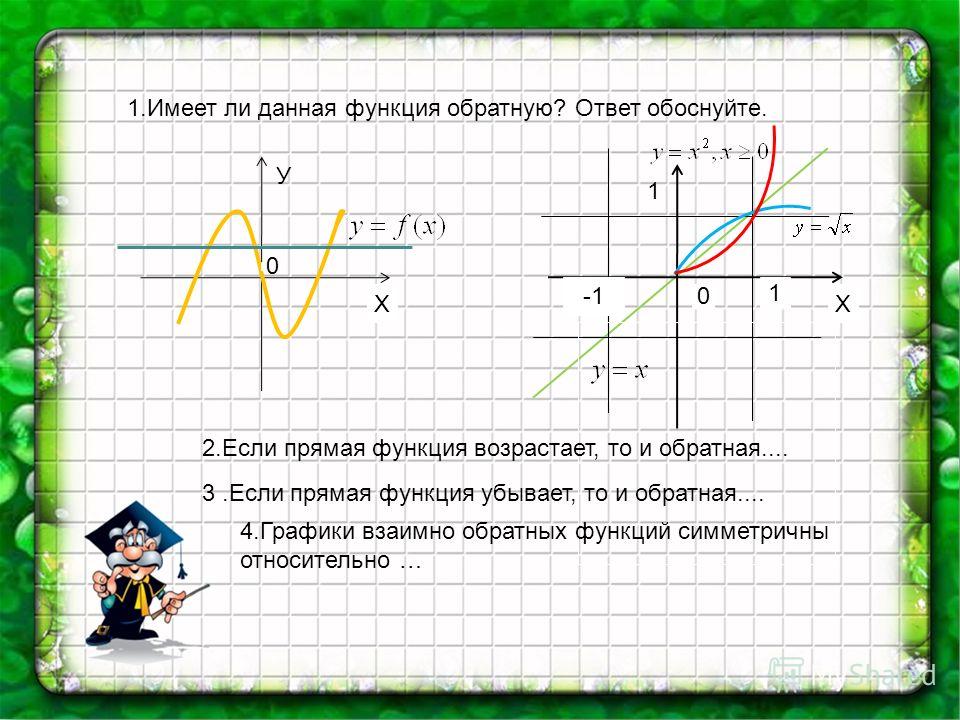 Убедитесь, что вы указали правильный домен и диапазон обратной функции.
Убедитесь, что вы указали правильный домен и диапазон обратной функции. Мы учим всему неправильно! |
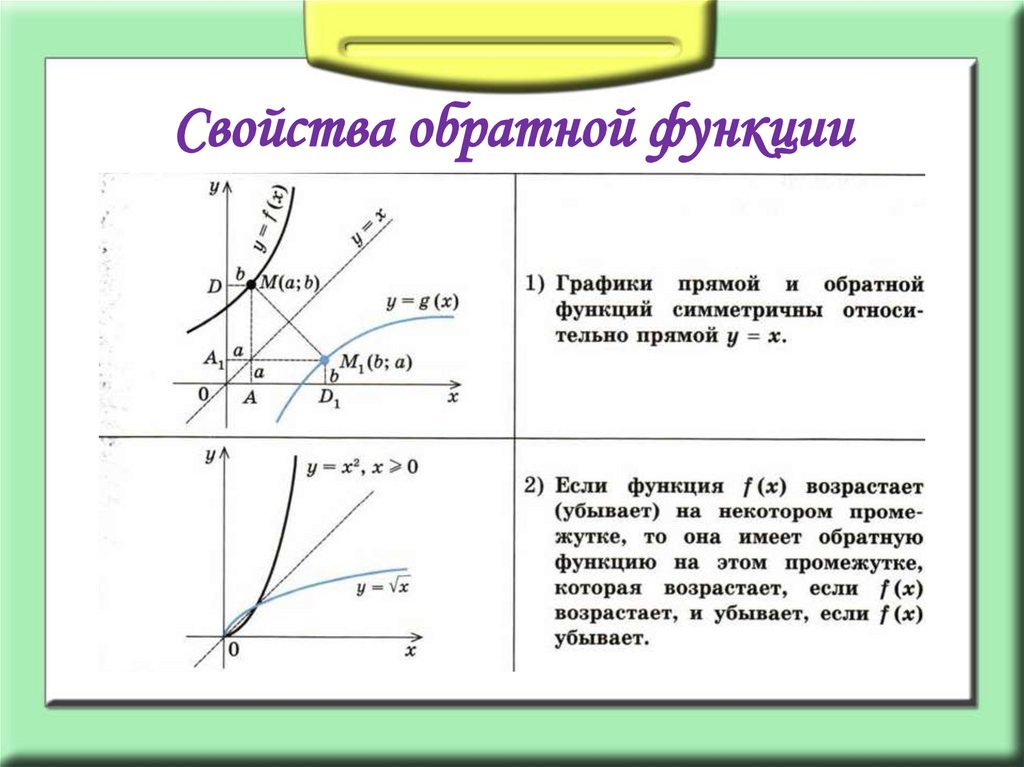 Стратегия замены переменных не основана на математических операциях и, как мы покажем, бессмысленна. Тем не менее, процедура настолько укоренилась в учебниках и других учебных планах, что многие учителя принимают ее за математическую истину, не подвергая сомнению концептуальную достоверность. В результате учащиеся пытаются запомнить стратегию, но с трудом «точно выполняют математические процедуры, понимают, почему эти процедуры работают, знают, как их можно использовать и интерпретировать их результаты» (NCTM, 2009).; Карлсон и Эртман, 2005). Как мы проиллюстрируем, этот общий процесс нахождения обратной функции усложняет учащимся понимание фундаментальных концепций обратной функции.
Стратегия замены переменных не основана на математических операциях и, как мы покажем, бессмысленна. Тем не менее, процедура настолько укоренилась в учебниках и других учебных планах, что многие учителя принимают ее за математическую истину, не подвергая сомнению концептуальную достоверность. В результате учащиеся пытаются запомнить стратегию, но с трудом «точно выполняют математические процедуры, понимают, почему эти процедуры работают, знают, как их можно использовать и интерпретировать их результаты» (NCTM, 2009).; Карлсон и Эртман, 2005). Как мы проиллюстрируем, этот общий процесс нахождения обратной функции усложняет учащимся понимание фундаментальных концепций обратной функции.
Функция \(f\) описывает отношение между двумя ковариантными величинами, представленными переменными \(x\) и \(y\). Без ограничения общности пусть \(x\) будет независимой переменной для функции \(f\), а \(y\) будет зависимой переменной для функции \(f\). {-1}\). 9{-1}(f(x))=x\). С точки зрения непрофессионала, обратная функция отменяет независимо от того, что делает функция (Bayazit & Gray, 2004).
{-1}\). 9{-1}(f(x))=x\). С точки зрения непрофессионала, обратная функция отменяет независимо от того, что делает функция (Bayazit & Gray, 2004).
Мы определяем концепцию как «проблемную», если она описывает понимание, которое затемняет связи со связанными идеями, вводит математические несоответствия и/или вероятно чтобы помешать учащимся развивать мощные значения будущих тем. Есть две проблематичные концепции, которые возникают из 9{-1}(x) &= \frac{x-15}{86} \end{align*}\]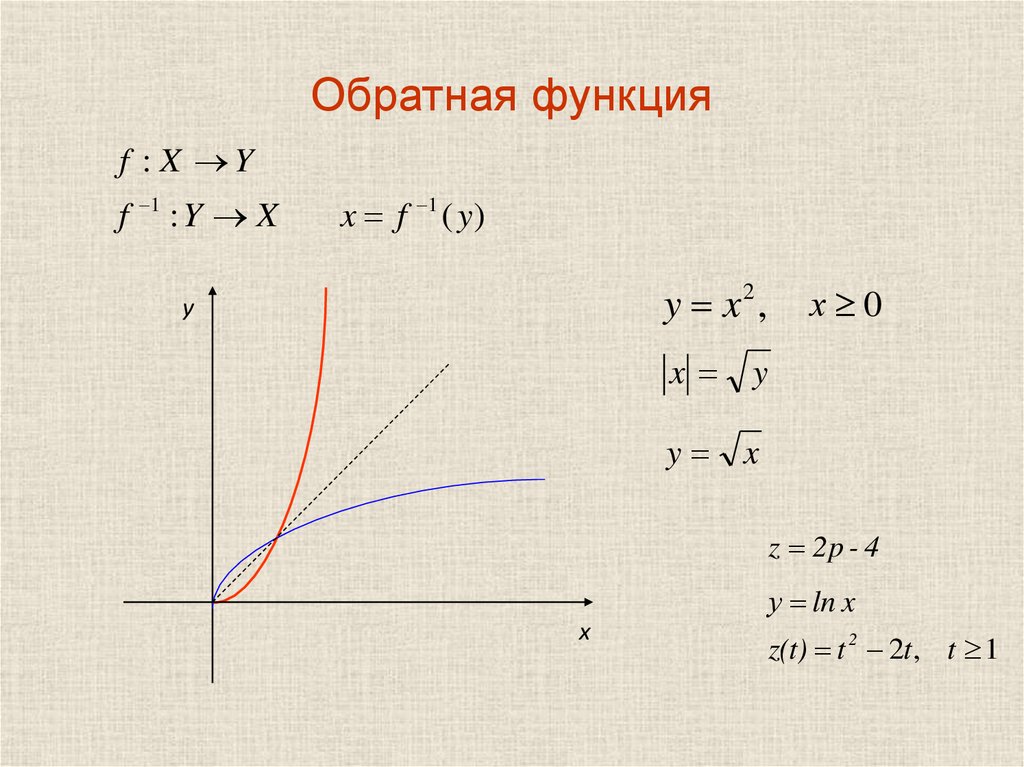 {-1} (445)\). Использование 9{-1}(х)\).
{-1} (445)\). Использование 9{-1}(х)\).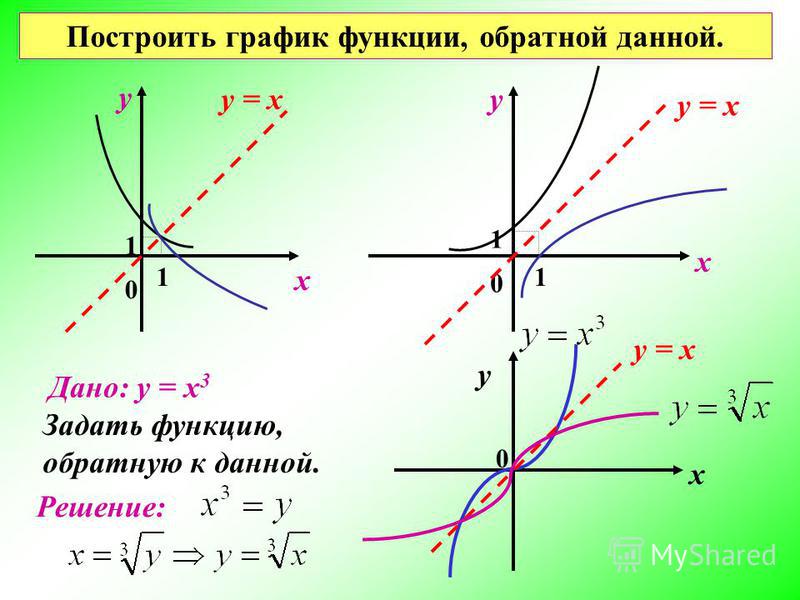 {-1} (20)=2\). 9{-1} (30)=3\).
{-1} (20)=2\). 9{-1} (30)=3\).
Баязит и Грей (2004) утверждают, что учащиеся с концептуальным пониманием обратных функций были в состоянии иметь дело с концепцией обратной функции в ситуациях, не связанных с формулами, в то время как учащиеся ограничены процедурным пониманием обратных функций (например, switch \(x\ ) и \(y\) ) с меньшей вероятностью будут успешными в контексте без формулы.
Дополнительным преимуществом отказа от подхода с переключением \(x\) и \(y\) является то, что он освобождает учащихся от \(x\)-зависимости — представления о том, что только \(x\) может быть независимая переменная. На графике ось \(x\) становится горизонтальная ось и ось \(y\) становится вертикальной осью . Реальность такова, что дисциплины за пределами математики редко используют \(x\) для представления горизонтальной оси и \(y\) для представления вертикальной оси. Скорее, они используют имена переменных (возможно, даже полные слова), которые имеют смысл в контексте ситуации.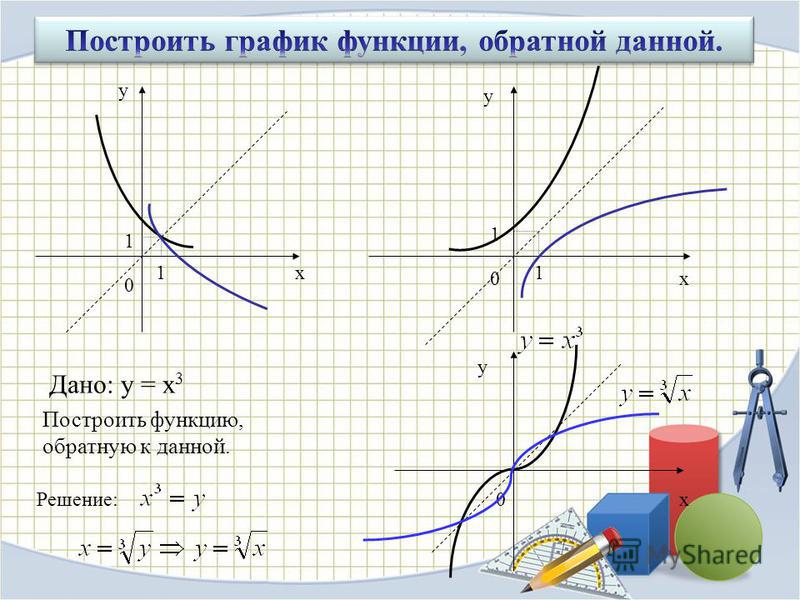 Поскольку, как мы предлагаем, оси больше не привязаны к \(x\) и \(y\), учащиеся более глубоко задумываются о концепциях независимых и зависимых переменных при построении графиков моделей данных реального мира, таких как \(p=f (t)\), где \(f(t)=29t\) и \(\textit{высота}\ = f(\textit{время})\), где \(f(\textit{время})=-8,99\cos(\frac{\pi}{6} \cdot \textit{time})+12.74.\)
Поскольку, как мы предлагаем, оси больше не привязаны к \(x\) и \(y\), учащиеся более глубоко задумываются о концепциях независимых и зависимых переменных при построении графиков моделей данных реального мира, таких как \(p=f (t)\), где \(f(t)=29t\) и \(\textit{высота}\ = f(\textit{время})\), где \(f(\textit{время})=-8,99\cos(\frac{\pi}{6} \cdot \textit{time})+12.74.\)
Когда учащиеся понимают концепцию обратной функции в контексте реальной ситуации, они начинают рассуждать (процесс делать выводы на основе фактов или сделанных предположений (NCTM, 2009)) и осмысление (развитие понимания ситуации, контекста или концепции путем соединения их с существующими знаниями (NCTM, 2009)). Это напрямую связано со стандартами математических методов, в частности с математическим упражнением № 1 (осмысление задач и упорство в их решении) и математическим упражнением № 2 (рассуждения абстрактно и количественно) (Национальная ассоциация губернаторов, 2010 г.). Математическая ассоциация Америки поощряет подобные мысли в своем Руководстве по программе бакалавриата по математике (MAA, 2015). Когнитивная рекомендация № 1 гласит, что Учащиеся должны развивать эффективное мышление и навыки общения . Все такие связи помогают учащимся понимать и запоминать новую информацию, что становится более сложной задачей, если учащиеся не занимаются рассуждениями и осмыслением (Hiebert et al., 1997).
Когнитивная рекомендация № 1 гласит, что Учащиеся должны развивать эффективное мышление и навыки общения . Все такие связи помогают учащимся понимать и запоминать новую информацию, что становится более сложной задачей, если учащиеся не занимаются рассуждениями и осмыслением (Hiebert et al., 1997).
Резюме
Правильное понимание обратных функций расширяет математические возможности учащихся. Путем устранения переключателя \(x\) и \(y\) подхода и реализации решения для зависимой переменной 9{-1}(y)\), учащиеся могут понимать обратные функции в различных математических контекстах, включая анализ и моделирование реальных данных.
Адаптировано из статьи тех же авторов, перечисленных в ссылках ниже.
Ссылки
Баязит, И. и Грей, Э. (2004, июль). Понимание обратных функций: взаимосвязь между педагогической практикой и обучением студентов. Материалы 28-й конференции Международной группы психологии математического образования: Vol.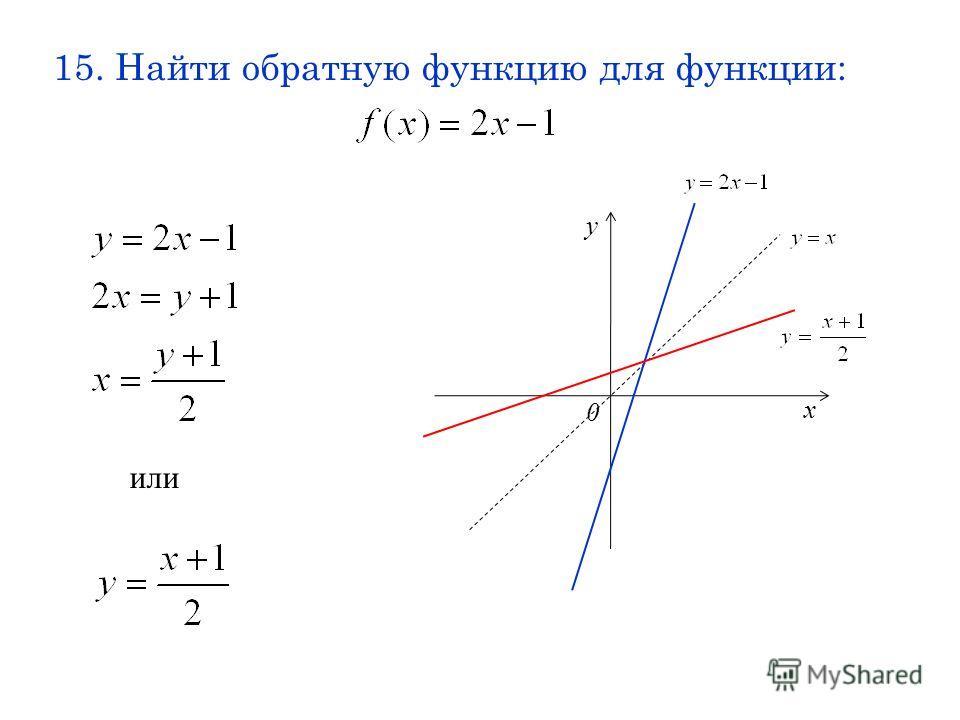 2 . (стр. 103–110).
2 . (стр. 103–110).
Карлсон, М. и Ортман, М. (2005). Ключевые аспекты знания и изучения концепции функции. Mathematical Association of America Research Sampler, No. 9, March 2005.
Hiebert, J., Carpenter, T., Fennema, E., Fuson, K., Wearne, D., Murray, H., et al. (1997). Осмысление: Преподавание и изучение математики с пониманием . Портсмут, Нью-Хэмпшир: Хайнеманн.
Математическая ассоциация Америки (2015). 2015 Учебный план CUPM для специальностей математических наук . Кэрол С. Шумахер и Марта Дж. Сигель, сопредседатели, редактор Пол Цорн. Вашингтон, округ Колумбия: MAA
Мур, К.С., Лисс II, Д.Р., Сильверман, Дж., Паолетти, Т., Лафорест, К.Р., и Масгрейв, С. (2013). Значения учителей до службы и неканонические графики. В Martinez, M. & Castro Superfine, A. (Eds.), Труды 35-го ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр. 441-448). Чикаго, Иллинойс: Иллинойсский университет в Чикаго.
Национальный совет учителей математики (2009). Основное внимание в математике средней школы: рассуждения и осмысление . Рестон, Вирджиния: NCTM
Центр передового опыта Национальной ассоциации губернаторов, Совет руководителей государственных школ (2010 г.). Общие базовые государственные стандарты – Математика . Центр передового опыта Национальной ассоциации губернаторов, Совет руководителей школ штата, Вашингтон, округ Колумбия,
Бюро переписи населения США. (2006). Таблица 96. Ожидаемая продолжительность жизни при рождении, 1970–2003 годы, и прогнозы, 2005 и 2010 годы . (NTIS № PB2006500023)
Ван Дайк, Ф. (февраль 1996 г.). Обратная функция. Учитель математики . 89, стр. 121–126.
Уилсон, Ф. (2007). Конечная математика и прикладное исчисление. Бостон: Компания Houghton Mifflin.
Уилсон Ф.К., Адамсон С., Кокс Т. и О’Брайан А. (март 2011 г.). Обратные функции: о чем нам не сказали наши учителя. Учитель математики . 104, стр. 500-507.
104, стр. 500-507.
Всемирная организация здравоохранения. (2006). Всемирная статистика здравоохранения, 2006 г. . ВОЗ Пресс. Женева, Швейцария.
Эта запись была размещена в Классная практика и помечена как Концептуальное понимание, обратная функция. Добавьте постоянную ссылку в закладки.
Глава 13. Обратные функции
Глава 13. Обратные функцииГлава 13. Обратные функции
Во второй части этой книги, посвященной Исчисление, мы посвятим наше исследование другому типу функций, экспоненциальная функция и ее близкая родственница функция синуса. Прежде чем мы погрузиться в это сложное и аналитическое исследование, нам сначала нужно понять кое-что об обратных функциях.
Обратная функция определение функции, выход которой становится входом или зависимым переменная становится независимой переменной. Например, учитывая функцию:
Что такое
Второй закон Ньютона, или сила, действующая на тело массой m, представляет собой
функция
придаваемое ему ускорение. Мы вольны вводить любое значение a и то, что мы получаем
вне
сила. Обратная этой силовой функции, согласно
определение,
даст нам ускорение как функцию Силы. Это делается
просто
решение для независимой переменной, a:
Мы вольны вводить любое значение a и то, что мы получаем
вне
сила. Обратная этой силовой функции, согласно
определение,
даст нам ускорение как функцию Силы. Это делается
просто
решение для независимой переменной, a:
Теперь я могу позволить F быть чем угодно, а затем найти ускорение как функцию от него.
Обратной функцией f(x) является обычно пишется как, . Теперь рассмотрим более общий случай построения графика. функция и обратная ей функция в одних и тех же координатных плоскостях. Учитывая функция , чтобы вычислить его обратную, нам нужно решить это только для x получить . Обратите внимание, что мы вообще не изменили функцию, мы решили только для независимой переменной. График этих двух функции будут точно такими же. Наше определение обратного функция поэтому придется немного изменить. После нахождения обратного функция мы просто меняем местами x и y, чтобы получить:
Что это делает с обратной функцией?
Это существенно переворачивает график f (x) вокруг линии y = x так, что для
каждый
точки (x,y) есть соответствующая точка (y,x) на графике
обратный
функция. Теперь обе функции можно изобразить в одной плоскости x-y.
Теперь обе функции можно изобразить в одной плоскости x-y.
Помните, что если мы просто решим для зависимого, мы не меняем уравнение, а просто переписываем его. За по этой причине его график такой же. Поменяв местами x и y, мы получим еще один функция x, отношение которой к f(x) состоит в том, что она была представлена на графике как хотя ось x была осью y и наоборот. Лучше всего мы посмотрим на два графики:
Обратите внимание, как каждый точка (x, y) имеет соответствующую точку (y, x) на обратной функции. график обратная функция точно такая же, как исходная функция за исключением того, что оси x и y поменялись местами:
Так как каждая точка (x, y) имеет соответствующую точку (y,x), то любую точку y из обратной функции, когда введенный в исходную функцию должен дать x:
Запомни а
функция и ее обратная функция являются функциями x. Как они
связанный
что обратная функция представляет исходную функцию, просто имея
это
зависимая и независимая переменная поменялись местами. Как вы можете видеть из
в
первый график, когда две функции изображены вместе, обратная
функция
содержит все точки (x, y) первой функции, представленные как (y, x)
с
за исключением того, что y задается как функция x. По этой причине
Как вы можете видеть из
в
первый график, когда две функции изображены вместе, обратная
функция
содержит все точки (x, y) первой функции, представленные как (y, x)
с
за исключением того, что y задается как функция x. По этой причине
Что такое Важно понимать об обратной функции то, что она получается по найти независимую переменную, а затем заменить ее на y, чтобы создать а функция, которая также является функцией x и может быть изображена на графике вместе с оригинальная функция.
Теперь, когда мы знаем, как функция и его обратная функция тесно связана, это приводит нас к вопросу, как производные связаны? Логика подскажет нам, что вместо мы должны просто найти взяв обратная производная. Например, если бы у нас было:
Производная обратной функции может быть:
Или производная от составляет 1/2x. Но это не так, производная:
Давайте рассмотрим
график f(x) и его обратной функции, чтобы увидеть, что именно происходит
на.
Обратите внимание, что в x=2, наклоны не обратны, а обратны только при значениях y на обратную функцию или через (x, f(x)) и (f -1 (f(x)), x). Или точка (3,9) будет иметь обратный наклон в точке (9,3), так как в этой точке x и ты меняются местами, поэтому наклон становится обратным или Это важный момент, чтобы понять о функции и ее обратной, они Только ведут себя как противоположности в точках (a,b) и (b,a). Это означает, что в точке а происходит что-то другое. Тогда возникает вопрос, как мы можем найти производная обратной функции по оси x? Ищу опять таки по адресу:
Путем замены x с y и y с x в этом последнем выражении мы получаем:
Что у нас есть только что сделано вычисление производной обратной функции только по Ищу на исходную функцию и ее производную. Причина, по которой производная была нет просто обратное значение y=2x было потому, что мы забыли сделать следующие два шагов:
1) Замените x его эквивалентом
выражение через y.
Склон в следующий график при x=2 наклон равно (2)(2)=4
Путем замены x с мы можем найти производная по то же ось x , но вместо этого со значением y .
При y=4 наклон является какой ответ вместо этого мы использовали x=2.
Поскольку обратная функция нарисован в той же плоскости xy, что и , мы можем найти производную обратной функции с относительно оси, взяв обратное выражение а затем замена каждый y с x и наоборот.
Этот последний выражение является производной функции, обратной по отношению к в ось х.
Подводя итог, можно констатировать следующая теорема:
Чтобы найти производная обратной функции,
1) Помните, обратная функция связана с основной функцией в том смысле, что если вы отразите ее над линией y=x, вы приземлитесь на основную функцию.
2) Первая находка производная f(x)
3) Заменить любой x
в производной с ее y-эквивалентом, чтобы иметь возможность найти
производная с любым заданным значением y.


 5
5