Найти фундаментальную систему решений — пример с решением
Содержание:
- Решения системы линейных однородных уравнений обладают следующими свойствами:
- Пример с решением
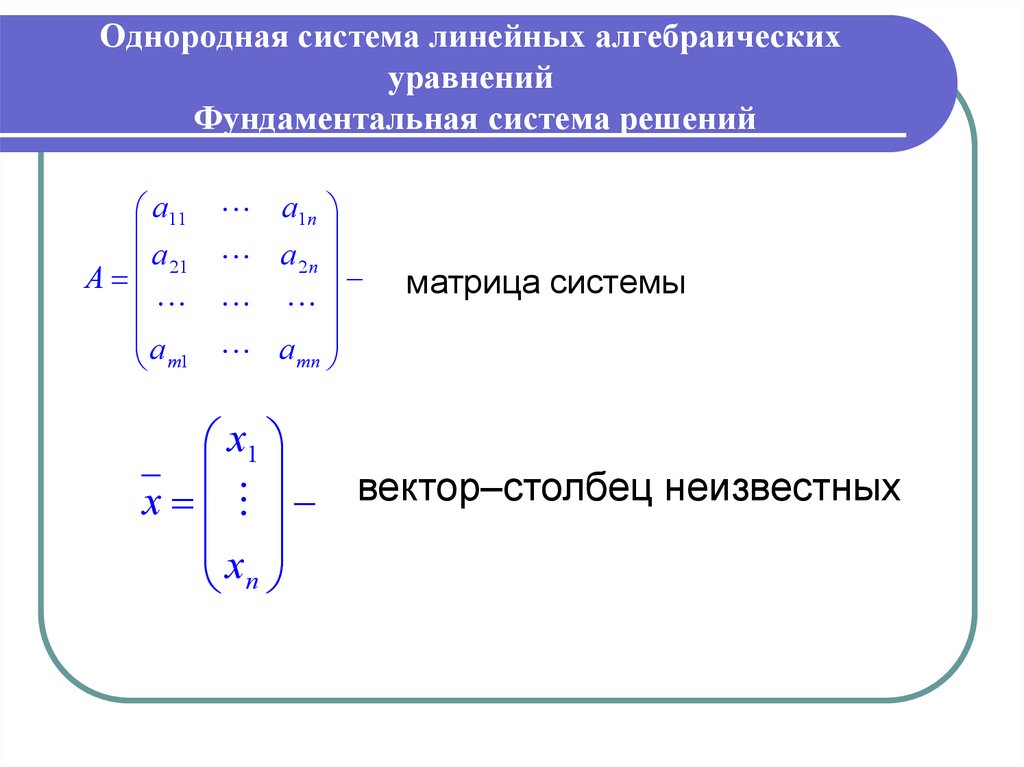
Фундаментальная система решений
ОПРЕДЕЛЕНИЕ. Система т линейных уравнений с п переменными называется однородной, если во всех ее уравнениях свободные члены равны нулю.
В общем случае однородная система (или система однородных уравнений) имеет вид:
Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0; 0; …; 0). Действительно, набор значений неизвестных удовлетворяет всем уравнениям системы.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
ОПРЕДЕЛЕНИЕ
По отношению к системе (1.25) система (1.34) называется приведенной.Если в системе (1.34) , то она имеет только одно нулевое решение (см. теорему 1.7).
ТЕОРЕМА 1.11. Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг этой системы меньше числа ее неизвестных, т.е. при .
Следствие 1. Если число уравнений однородной системы меньше числа ее неизвестных, то эта система имеет ненулевое решение.
Следствие 2. Если в однородной системе число уравнений равно числу неизвестных, то она имеет ненулевое решение тогда и только тогда, когда определитель матрицы системы равен нулю.
Обозначим решение системы (1.34) в виде строки
Возможно вам будут полезны данные страницы:
Найти общее решение уравнения |
| Общее решение уравнения |
Решение систем уравнений |
Исследовать ряд на абсолютную сходимость |
Решения системы линейных однородных уравнений обладают следующими свойствами:
- Если строка — решение системы (1.
34), то и строка — также решение этой системы. - Если строки — решения системы (1.34), то при любых с} и с2 их линейная комбинация — также решение данной системы.
34), то и строка — также решение этой системы.Убедиться в справедливости указанных свойств решений системы линейных однородных уравнений можно непосредственной подстановкой их в уравнения системы.
Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому целесообразно найти такие линейно независимые решения системы (1.34), через которые линейно выражались бы все остальные ее решения.
ОПРЕДЕЛЕНИЕ.
Система линейно независимых решений называется фундаментальной, если каждое решение системы (1.34) является линейной комбинацией решений
ТЕОРЕМА 1.12.
Если ранг г матрицы однородной системы линейных уравнений (1.34) меньше числа неизвестных то всякая ее фундаментальная система решений состоит из решений (или матрица фундаментальной системы имеет столбцов).
■
Поэтому общее решение системы (1.34) линейных однородных уравнений имеет вид:
где —любая фундаментальная система решений; — произвольные числа и Замечание. Общее решение системы линейных уравнений с неизвестными (1.25) равно сумме общего решения соответствующей ей приведенной системы линейных уравнений (1.34) и произвольного частного решения этой системы (1.25).
Для нахождения фундаментальной системы решений предположим, что ранг Тогда базисные неизвестные этой системы линейно выражаются через свободные переменные Положим значения свободных переменных Затем находим второе решение, принимая Иными словами, мы последовательно присваиваем каждой свободной переменной единичное значение, положив остальные нулями.
Пример с решением
Найти решение и фундаментальную систему решения системы линейных однородных уравнений:
Решение:
Составим матрицу системы, и прямым ходом метода Гаусса приведем ее к ступенчатому виду:
Выпишем систему уравнений:
Обратный ход метода Гаусса дает значения базисных неизвестных , выраженные через свободную переменную х5.
Обозначим ее . Из последнего уравнения находим Затем, поднимаясь вверх по системе, определяем все неизвестные
Эти последние выражения представляют запись общего решения нашей однородной системы. Если теперь давать переменной с числовые значения, можно получить фундаментальное решение системы.
Поскольку ранг однородной системы равен четырем, то фундаментальная система решений для нее состоит из решения.
Положив значение свободной переменной (других свободных переменных у нас нет), получим фундаментальное решение системы:
Заметим, что если и решением будет нулевой вектор о; его называют тривиальным решением; этот вектор всегда есть среди решений однородной системы.
Фундаментальная система решений однородной системы уравнений — КиберПедия
Фундаментальная система решений – это множество линейно независимых векторов , каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов , где – произвольные действительные числа.
Количество векторов фундаментальной системы рассчитывается по формуле:
Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов фундаментальной системы равно количеству свободных неизвестных.
Представим общее решение Примера №3 в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора . Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать и получить: .
Координаты вектора должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.
Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор (подстрочный индекс расшифровывается «Общее Однородной»).
Ответ: общее решение: , где (любое вещественное число)
Придавая параметру различные действительные значения, можно получить бесконечно много частных решений, например, если , то вектор частного решения однородного уравнения («Частное Однородной») равен:
Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять и из общего решения системы получить вектор с целыми координатами:
И тогда ответ запишется в эквивалентной форме:
, где (любое вещественное число)
Оба варианта ответа правильны, однако чайникам я всё-таки рекомендую классику жанра.
Поблагодарим задачник Рябушко за предоставленные примеры и перейдём к более основательным системам:
Пример 4
Решить однородную систему линейных уравнений
Ответ записать с помощью фундаментальной системы решений
Самостоятельно, plz.
Примерный образец оформления в конце урока.
Закинем в копилку знаний ещё один полезный факт:
Взаимосвязь решений неоднородной
и соответствующей однородной системы уравнений
Представьте двух близких родственниц: неоднородную систему (у которой хотя бы одно число правой части отлично от нуля) и такую же систему– только справа одни нули (то бишь, однородную систему). Нетрудно предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. И это действительно так! Материал целесообразнее рассмотреть на конкретной задаче, которая, как и все другие, взята из реальной контрольной работы:
Пример 5
Дана система линейных алгебраических уравнений
Требуется:
1) найти общее решение;
2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.
Решение: по условию дана обычная неоднородная система уравнений, и первая часть не отличается новизной:
1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –1.
К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.
(2) Последние три строки одинаковы, две из них удалили.
Обратным ходом метода Гаусса получим общее решение:
– базисные переменные;
– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
– подставим в 1-е уравнение:
Общее решение неоднородной системы обозначим через («Общее Неоднородной»).
Ответ:
2) Во второй части задания требуется найти общее решение такой же, только однородной системы , причём по условию необходимо использовать ответ предыдущего пункта.
Выполнять элементарные преобразования заново, разумеется, не нужно.
Правило: общее решение неоднородной системы равно сумме общего решения соответствующей однородной системы и какого-либо частного решения неоднородной системы :
Откуда легко выражается общее решение нашей однородной системы:
Найдём какое-нибудь частное решение неоднородной системы.
Проще всего взять нулевые значения свободных переменных :
Таким образом, общее решение соответствующей однородной системы:
Представим в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений будет состоять из двух векторов.
Пойдём классическим путём:
Рассмотрим пару значений свободных переменных и получим первый вектор:
– координаты данного вектора удовлетворяют каждому уравнению однородной системы (всегда желательна проверка!).
Теперь рассматриваем пару и получаем второй вектор:
– координаты данного вектора также удовлетворяют каждому уравнению однородной системы (тоже проверяем!).
И вообще – любая линейная комбинация векторов фундаментальной системы , где – произвольные действительные числа, является решением данной системы:
Ответ: , где
Иными словами, если взять два любых вещественных числа, например, , то получится вектор частного решения однородной системы:
Если хотите избежать дробей, то при нахождении вектора следует выбрать значения и получить второй вектор в виде:
В этом случае ответ запишется в эквивалентной форме:
, где
Порядком многих я, наверное, подзапутал, но коль скоро задание не придумано, то его нельзя было обойти стороной.
Более распространённая тема для самостоятельного решения:
Пример 6
Дана однородная система
Найти общее решение и записать ответ с помощью векторов фундаментальной системы. В образце решения завершающим элементарным преобразованием я уже потихоньку начинаю приобщать вас к методу Гаусса-Жордана.
Чтобы окончательно закрепить алгоритм, разберём финальное задание:
Пример 7
Решить однородную систему, ответ записать в векторной форме.
Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:
(1) У первой строки сменили знак.
Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.
(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.
(3) Последние три строки пропорциональны, две из них удалили.
В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:
– базисные переменные;
– свободные переменные.
Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
– подставим в 1-е уравнение:
Таким образом, общее решение:
Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.
Подставим тройку значений в общее решение и получим вектор , координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.
Для тройки значений находим вектор
И, наконец, для тройки получаем третий вектор:
Ответ: , где
Желающие избежать дробных значений могут рассмотреть тройки и получить ответ в эквивалентном виде:
К слову о дробях. Посмотрим на полученную в задаче матрицу и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную , потом через дроби базисную переменную , и, надо сказать, процесс это был не самый простой и не самый приятный.
Второй вариант решения:
Идея состоит в том, чтобы попытаться выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:
(4) К первой строке прибавили вторую строку, умноженную на –1.
Здесь базисные переменные легко и практически мгновенно выражаются через свободные переменные :
По существу, мы применили метод Гаусса-Жордана, который как раз и направлен на скорейшее получение базисного решения посредством дополнительных элементарных преобразований.
В результате общее решение:
Последовательно выбираем в качестве значений свободных неизвестных тройки
и подстановкой их в получаем соответствующие векторы фундаментальной системы:
Не забываем проверить координаты каждого вектора!
Ответ: общее решение:
2 Приведение квадратичной формы к нормальному виду. Метод Лагранжа.
http://sci.alnam.ru/book_alin.php?id=36
http://spargalki.ru/mathematiks/210-lineinaya-algebra.html?start=9
Постановка задачи. Привести квадратичную форму
к каноническому виду методом Лагранжа.
План решения.
Метод Лагранжа заключается в последовательном выделении полных квадратов. Не ограничивая общности рассуждений, полагаем, что .
где – квадратичная форма, в которую входят лишь переменные .
Делаем замену
,
после которой
,
где .
Предложенный алгоритм применяем к и после конечного числа шагов приходим к каноническому виду квадратичной формы:
.
Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа
.
Применяя метод Лагранжа, получаем:
где .
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8
1. Общее решение неоднородной системы линейных уравнений.
http://matworld.ru/calculator/non-homogeneous-system-online.php
http://www.cleverstudents.ru/systems/solving_systems_of_linear_equations.html#fundamental_system_of_solutions
2. Критерий Сильвестра положительной определенности квадратичной формы.
http://www.studfiles.ru/preview/3072512/page:4/
Критерий Сильвестра
Тип квадратичной формы можно определить, не приводя ее к каноническому виду. Следующий ниже критерий Сильвестра позволяет определить тип квадратичной формы по знакам угловых миноров ее матрицы.
Рассмотрим угловые миноры ( ), являющиеся определителями подматриц матрицы квадратичной формы:
Теорема 6(критерий Сильвестра знакоопределенности квадратичной формы).
Квадратичная форма является:
1) положительно определенной тогда и только тогда, когда все угловые миноры матрицы положительны:
( )
2) отрицательно определенной тогда и только тогда, когда все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус:
В заключение приведем таблицу оценки знакоопределенности квадратичных форм по двум основным критериям.
| Квадратичная форма | Обозна- чение | Оценка знакоопределенности формы | |
| по главным минорам матрицы квадратичной формы | по собственным значениям матрицы квадратичной формы | ||
| положительно определенная | если все угловые миноры матрицы положительны: ( ) | если все собственные значения положительны | |
| отрицательно определенная | если все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус: | если все собственные значения отрицательны | |
| неотрицательно определенная | если все угловые миноры матрицы неотрицательны: ( ) | если все собственные значения неотрицательны | |
| неположительно определенная | если в угловых минорах матрицы чередуются знаки, причем: | если все собственные значения неположительны | |
| знакопеременная | среди собственных значений имеются как положительные, так и отрицательные |
Пример 6.
Исследовать на знакоопределенность следующие квадратичные формыот двух переменных
, ,
, .
Решение.
1) Матрица формы имеет вид
.
Ее угловые миноры равны
, .
Согласно критерию Сильвестра, так как все угловые миноры положительны, квадратичная форма являетсяположительно определенной.
2) Матрица формы имеет вид
.
Ее угловые миноры равны
, .
Согласно критерию Сильвестра, так как все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус, то квадратичная форма являетсяотрицательно определенной.
3) Матрица формы имеет вид
.
Ее угловые миноры равны
, .
Так как в этом случае второй угловой минор отрицателен, то согласно таблице квадратичная форма являетсязнакопеременной.
4) Матрица формы имеет вид
.
Ее угловые миноры равны
, .
Так первый угловой минор положителен, а второй угловой минор равен нулю, то согласно таблице квадратичная форма являетсянеотрицательно определенной.
Заметим, что в данном случае
.
Пример 7.Исследовать на знакоопределенность квадратичную формуот трех переменных
.
Решение.Матрица формы имеет вид
.
Ее угловые миноры положительны:
, , .
Согласно критерию Сильвестра, так как все угловые миноры положительны, то квадратичная форма является положительно определенной.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9
1. Линейные пространства. Базис. Размерность.
http://mathhelpplanet.com/static.php?p=razmernost-i-bazis-linyeinogo-prostranstva
Линейное пространство
VV
называется n-мерным, если в нем существует система из
nn
линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число
nn
называется размерностью (числом измерений) линейного пространства
VV
и обозначается
dimVdimV
.
Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве
VV
найдется система, состоящая из
nn
линейно независимых векторов, то такое пространство называют бесконечномерным (записывают:
dimV=∞dimV=∞
). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность
nn
линейно независимых векторов (базисных векторов).
2 Преобразование матрицы билинейной формы при смене базиса.
http://www.studfiles.ru/preview/5826382/page:8/
Решение уравнений методом вариации произвольных постоянных онлайн. Примеры на метод вариации произвольной постоянной
Метод вариации произвольных постоянных
Метод вариации произвольных постоянных для построения решения линейного неоднородного дифференциального уравнения
a n (t )z (n ) (t ) + a n − 1 (t )z (n − 1) (t ) + .
.. + a 1 (t )z «(t ) + a 0 (t )z (t ) = f (t )
состоит в замене произвольных постоянных c k в общем решении
z (t ) = c 1 z 1 (t ) + c 2 z 2 (t ) + … + c n z n (t )
соответствующего однородного уравнения
a n (t )z (n ) (t ) + a n − 1 (t )z (n − 1) (t ) + … + a 1 (t )z «(t ) + a 0 (t )z (t ) = 0
на вспомогательные функции c k (t ) , производные которых удовлетворяют линейной алгебраической системе
Определителем системы (1) служит вронскиан функций z 1 ,z 2 ,…,z n , что обеспечивает её однозначную разрешимость относительно .
Если — первообразные для , взятые при фиксированных значениях постоянных интегрирования, то функция
является решением исходного линейного неоднородного дифференциального уравнения.
Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам .
Метод вариации произвольных постоянных для построения решений системы линейных дифференциальных уравнений в векторной нормальной форме
состоит в построении частного решения (1) в виде
где Z (t ) — базис решений соответствующего однородного уравнения, записанный в виде матрицы, а векторная функция , заменившая вектор произвольных постоянных, определена соотношением . Искомое частное решение (с нулевыми начальными значениями при t = t 0 имеет вид
Для системы с постоянными коэффициентами последнее выражение упрощается:
Матрица Z (t )Z − 1 (τ) называется матрицей Коши оператора L = A (t ) .
Метод вариации произвольной постоянной, или метод Лагранжа — еще один способ решения линейных дифференциальных уравнений первого порядка и уравнения Бернулли.
Линейные дифференциальные уравнения первого порядка — это уравнения вида y’+p(x)y=q(x). Если в правой части стоит нуль: y’+p(x)y=0, то это — линейное однородное уравнение 1го порядка. Соответственно, уравнение с ненулевой правой частью, y’+p(x)y=q(x), — неоднородное линейное уравнение 1го порядка.
Метод вариации произвольной постоянной (метод Лагранжа) состоит в следующем:
1) Ищем общее решение однородного уравнения y’+p(x)y=0: y=y*.
2) В общем решении С считаем не константой, а функцией от икса: С=С(x). Находим производную общего решения (y*)’ и в первоначальное условие подставляем полученное выражение для y* и (y*)’. Из полученного уравнения находим функцию С(x).
3) В общее решение однородного уравнения вместо С подставляем найденное выражение С(x).
Рассмотрим примеры на метод вариации произвольной постоянной. Возьмем те же задания, что и в , сравним ход решения и убедимся, что полученные ответы совпадают.
1) y’=3x-y/x
Перепишем уравнение в стандартном виде (в отличие от метода Бернулли, где форма записи нам нужна была только для того, чтобы увидеть, что уравнение — линейное).
y’+y/x=3x (I). Теперь действуем по плану.
1) Решаем однородное уравнение y’+y/x=0. Это уравнение с разделяющимися переменными. Представляем y’=dy/dx, подставляем: dy/dx+y/x=0, dy/dx=-y/x. Обе части уравнения умножаем на dx и делим на xy≠0: dy/y=-dx/x. Интегрируем:
2) В полученном общем решении однородного уравнения будем считать С не константой, а функцией от x: С=С(x). Отсюда
Полученные выражения подставляем в условие (I):
Интегрируем обе части уравнения:
здесь С — уже некоторая новая константа.
3) В общее решение однородного уравнения y=C/x, где мы считали С=С(x), то есть y=C(x)/x, вместо С(x) подставляем найденное выражение x³+C: y=(x³+C)/x или y=x²+C/x. Получили такой же ответ, как и при решении методом Бернулли.
Ответ: y=x²+C/x.
2) y’+y=cosx.
Здесь уравнение уже записано в стандартном виде, преобразовывать не надо.
1) Решаем однородное линейное уравнение y’+y=0: dy/dx=-y; dy/y=-dx. Интегрируем:
Чтобы получить более удобную форму записи, экспоненту в степени С примем за новую С:
Это преобразование выполнили, чтобы удобнее было находить производную.
2) В полученном общем решении линейного однородного уравнения считаем С не константой, а функцией от x: С=С(x). При этом условии
Полученные выражения y и y’ подставляем в условие:
Умножим обе части уравнения на
Интегрируем обе части уравнения по формуле интегрирования по частям, получаем:
Здесь С уже не функция, а обычная константа.
3) В общее решение однородного уравнения
подставляем найденную функцию С(x):
Получили такой же ответ, как и при решении методом Бернулли.
Метод вариации произвольной постоянной применим и для решения .
y’x+y=-xy².
Приводим уравнение к стандартному виду: y’+y/x=-y² (II).
1) Решаем однородное уравнение y’+y/x=0. dy/dx=-y/x. Умножаем обе части уравнения на dx и делим на y: dy/y=-dx/x. Теперь интегрируем:
Подставляем полученные выражения в условие (II):
Упрощаем:
Получили уравнение с разделяющимися переменными относительно С и x:
Здесь С — уже обычная константа.
В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.
3) В общее решение однородного уравнения y=C(x)/x подставляем найденную функцию С(x):
Получили такой же ответ, что и при решении способом Бернулли.
Примеры для самопроверки:
1. Перепишем уравнение в стандартном виде:y’-2y=x.
1) Решаем однородное уравнение y’-2y=0. y’=dy/dx, отсюда dy/dx=2y, умножаем обе части уравнения на dx, делим на y и интегрируем:
Отсюда находим y:
Выражения для y и y’ подставляем в условие (для краткости будем питать С вместо С(x) и С’ вместо C»(x)):
Для нахождения интеграла в правой части применяем формулу интегрирования по частям:
Теперь подставляем u, du и v в формулу:
Здесь С =const.
3) Теперь подставляем в решение однородного
Рассмотрим теперь линейное неоднородное уравнение
. (2)
Пусть y 1 ,y 2 ,.., y n — фундаментальная система решений, а — общее решение соответствующего однородного уравнения L(y)=0 .
Аналогично случаю уравнений первого порядка, будем искать решение уравнения (2) в виде
. (3)
Убедимся в том, что решение в таком виде существует. Для этого подставим функцию в уравнение. Для подстановки этой функции в уравнение найдём её производные. Первая производная равна
. (4)
При вычислении второй производной в правой части (4) появится четыре слагаемых, при вычислении третьей производной — восемь слагаемых и так далее. Поэтому, для удобства дальнейшего счёта, первое слагаемое в (4) полагают равным нулю. С учётом этого, вторая производная равна
. (5)
По тем же, что и раньше, соображениям, в (5) также полагаем первое слагаемое равным нулю. Наконец, n-я производная равна
. (6)
Подставляя полученные значения производных в исходное уравнение, имеем
. (7)
Второе слагаемое в (7) равно нулю, так как функции y j , j=1,2,..,n, являются решениями соответствующего однородного уравнения L(y)=0. Объединяя с предыдущим, получаем систему алгебраических уравнений для нахождения функций C» j (x)
(8)
Определитель этой системы есть определитель Вронского фундаментальной системы решений y 1 ,y 2 ,.
.,y n соответствующего однородного уравнения L(y)=0 и поэтому не равен нулю. Следовательно, существует единственное решение системы (8). Найдя его, получим функции C» j (x), j=1,2,…,n, а, следовательно, и C j (x), j=1,2,…,n Подставляя эти значения в (3), получаем решение линейного неоднородного уравнения.
Изложенный метод называется методом вариации произвольной постоянной или методом Лагранжа.
Пример №1
. Найдём общее решение уравнения y»» + 4y» + 3y = 9e -3 x . Рассмотрим соответствующее однородное уравнение y»» + 4y» + 3y = 0. Корни его характеристического уравнения r 2 + 4r + 3 = 0 равны -1 и -3. Поэтому фундаментальная система решений однородного уравнения состоит из функций y 1 = e — x и y 2 = e -3 x . Решение неоднородного уравнения ищем в виде y = C 1 (x)e — x + C 2 (x)e -3 x . Для нахождения производных C» 1 , C» 2 составляем систему уравнений (8)
C′ 1 ·e -x +C′ 2 ·e -3x =0
-C′ 1 ·e -x -3C′ 2 ·e -3x =9e -3x
решая которую, находим , Интегрируя полученные функции, имеем
Окончательно получим
Пример №2
.
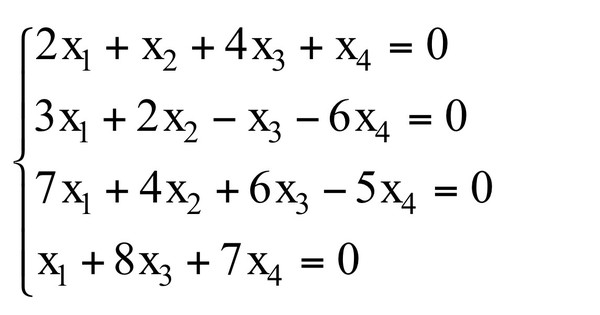Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
y(0) =1 + 3ln3
y’(0) = 10ln3
Решение:
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 -6 r + 8 = 0
D = (-6) 2 — 4·1·8 = 4
Корни характеристического уравнения: r 1 = 4, r 2 = 2
Следовательно, фундаментальную систему решений составляют функции: y 1 =e 4x , y 2 =e 2x
Общее решение однородного уравнения имеет вид: y
=C 1 ·e 4x +C 2 ·e 2x
Поиск частного решения методом вариации произвольной постоянной.
Для нахождения производных C» i составляем систему уравнений:
C′ 1 ·e 4x +C′ 2 ·e 2x =0
C′ 1 (4e 4x) + C′ 2 (2e 2x) = 4/(2+e -2x)
Выразим C» 1 из первого уравнения:
C» 1 = -c 2 e -2x
и подставим во второе.
В итоге получаем:
C» 1 = 2/(e 2x +2e 4x)
C» 2 = -2e 2x /(e 2x +2e 4x)
Интегрируем полученные функции C» i:
C 1 = 2ln(e -2x +2) — e -2x + C * 1
C 2 = ln(2e 2x +1) – 2x+ C * 2
Поскольку y
=C 1 ·e 4x +C 2 ·e 2x , то записываем полученные выражения в виде:
C 1 = (2ln(e -2x +2) — e -2x + C * 1) e 4x = 2 e 4x ln(e -2x +2) — e 2x + C * 1 e 4x
C 2 = (ln(2e 2x +1) – 2x+ C * 2)e 2x = e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
Таким образом, общее решение дифференциального уравнения имеет вид:
y = 2 e 4x ln(e -2x +2) — e 2x + C * 1 e 4x + e 2x ln(2e 2x +1) – 2x e 2x + C * 2 e 2x
или
y = 2 e 4x ln(e -2x +2) — e 2x + e 2x ln(2e 2x +1) – 2x e 2x + C * 1 e 4x + C * 2 e 2x
Найдем частное решение при условии:
y(0) =1 + 3ln3
y’(0) = 10ln3
Подставляя x = 0, в найденное уравнение, получим:
y(0) = 2 ln(3) — 1 + ln(3) + C * 1 + C * 2 = 3 ln(3) — 1 + C * 1 + C * 2 = 1 + 3ln3
Находим первую производную от полученного общего решения:
y’ = 2e 2x (2C 1 e 2x + C 2 -2x +4 e 2x ln(e -2x +2)+ ln(2e 2x +1)-2)
Подставляя x = 0, получим:
y’(0) = 2(2C 1 + C 2 +4 ln(3)+ ln(3)-2) = 4C 1 + 2C 2 +10 ln(3) -4 = 10ln3
Получаем систему из двух уравнений:
3 ln(3) — 1 + C * 1 + C * 2 = 1 + 3ln3
4C 1 + 2C 2 +10 ln(3) -4 = 10ln3
или
C * 1 + C * 2 = 2
4C 1 + 2C 2 = 4
или
C * 1 + C * 2 = 2
2C 1 + C 2 = 2
Откуда: C 1 = 0, C * 2 = 2
Частное решение запишется как:
y = 2e 4x ·ln(e -2x +2) — e 2x + e 2x ·ln(2e 2x +1) – 2x·e 2x + 2·e 2x
Метод вариации произвольных постоянных применяется для решения неоднородных дифференциальных уравнений.
Данный урок предназначен для тех студентов, кто уже более или менее хорошо ориентируется в теме. Если вы только-только начинаете знакомиться с ДУ, т.е. являетесь чайником, то рекомендую начать с первого урока: Дифференциальные уравнения первого порядка. Примеры решений . А если уже-уже заканчиваете, пожалуйста, отбросьте возможное предвзятое мнение, что метод сложный. Потому что он простой.
В каких случаях применяется метод вариации произвольных постоянных?
1) Метод вариации произвольной постояннОЙ можно использовать при решении линейного неоднородного ДУ 1-го порядка . Коль скоро уравнение первого порядка, то и постоянная (константа) тоже одна.
2) Метод вариации произвольнЫХ постоянных используют для решения некоторых линейных неоднородных уравнений второго порядка . Здесь варьируются две постоянные (константы).
Логично предположить, что урок будет состоять из двух параграфов…. Вот написал это предложение, и минут 10 мучительно думал, какую бы еще умную хрень добавить для плавного перехода к практическим примерам.
Но почему-то мыслей после праздников нет никаких, хотя вроде и не злоупотреблял ничем. Поэтому сразу примемся за первый параграф.
Метод вариации произвольной постоянной
для линейного неоднородного уравнения первого порядка
Перед рассмотрением метода вариации произвольной постоянной желательно быть знакомым со статьей Линейные дифференциальные уравнения первого порядка . На том уроке мы отрабатывали первый способ решения неоднородного ДУ 1-го порядка. Этот первый способ решения, напоминаю, называется метод замены или метод Бернулли (не путать с уравнением Бернулли !!!)
Сейчас мы рассмотрим второй способ решения – метод вариации произвольной постоянной. Я приведу всего три примера, причем возьму их из вышеупомянутого урока . Почему так мало? Потому что на самом деле решение вторым способом будет очень похоже на решение первым способом. Кроме того, по моим наблюдениям, метод вариации произвольных постоянных применяется реже метода замены.
Пример 1
(Диффур из Примера №2 урока Линейные неоднородные ДУ 1-го порядка )
Решение: Данное уравнение является линейным неоднородным и имеет знакомый вид:
На первом этапе необходимо решить более простое уравнение:
То есть, тупо обнуляем правую часть – вместо пишем ноль.
Уравнение я буду называть вспомогательным уравнением .
В данном примере нужно решить следующее вспомогательное уравнение:
Перед нами уравнение с разделяющимися переменными , решение которого (надеюсь) уже не представляет для вас сложностей:
Таким образом:
– общее решение вспомогательного уравнения .
На втором шаге заменим константу некоторой пока ещё неизвестной функцией , которая зависит от «икс»:
Отсюда и название метода – варьируем константу . Как вариант, константа может быть некоторой функцией , которую нам предстоит сейчас найти.
В исходном неоднородном уравнении проведём замену:
Подставим и в уравнение :
Контрольный момент – два слагаемых в левой части сокращаются .
Если этого не происходит, следует искать ошибку выше.
В результате замены получено уравнение с разделяющимися переменными. Разделяем переменные и интегрируем.
Какая благодать, экспоненты тоже сокращаются:
К найденной функции приплюсовываем «нормальную» константу :
На заключительном этапе вспоминаем про нашу замену:
Функция только что найдена!
Таким образом, общее решение:
Ответ: общее решение:
Если вы распечатаете два способа решения, то легко заметите, что в обоих случаях мы находили одни и те же интегралы. Отличие лишь в алгоритме решения.
Теперь что-нибудь посложнее, второй пример я тоже прокомментирую:
Пример 2
Найти общее решение дифференциального уравнения
(Диффур из Примера №8 урока Линейные неоднородные ДУ 1-го порядка )
Решение: Приведем уравнение к виду :
Обнулим правую часть и решим вспомогательное уравнение:
Общее решение вспомогательного уравнения:
В неоднородном уравнении проведём замену:
По правилу дифференцирования произведения:
Подставим и в исходное неоднородное уравнение :
Два слагаемых в левой части сокращаются, значит, мы на верном пути:
Интегрируем по частям.
Вкусная буква из формулы интегрирования по частям у нас уже задействована в решении, поэтому используем, например, буквы «а» и «бэ»:
Теперь вспоминаем проведённую замену:
Ответ: общее решение:
И один пример для самостоятельного решения:
Пример 3
Найти частное решение дифференциального уравнения, соответствующее заданному начальному условию.
,
(Диффур из Примера №4 урока Линейные неоднородные ДУ 1-го порядка )
Решение:
Данное ДУ является линейным неоднородным. Используем метод вариации произвольных постоянных. Решим вспомогательное уравнение:
Разделяем переменные и интегрируем:
Общее решение:
В неоднородном уравнении проведем замену:
Выполним подстановку:
Таким образом, общее решение:
Найдем частное решение, соответствующее заданному начальному условию:
Ответ: частное решение:
Решение в конце урока может служить примерным образцом для чистового оформления задания.
Метод вариации произвольных постоянных
для линейного неоднородного уравнения второго порядка
с постоянными коэффициентами
Часто приходилось слышать мнение, что метод вариации произвольных постоянных для уравнения второго порядка – штука не из легких. Но я предполагаю следующее: скорее всего, метод многим кажется трудным, поскольку встречается не так часто. А в действительности особых сложностей нет – ход решения чёткий, прозрачный, понятный. И красивый.
Для освоения метода желательно уметь решать неоднородные уравнения второго порядка способом подбора частного решения по виду правой части. Данный способ подробно рассмотрен в статье Неоднородные ДУ 2-го порядка . Вспоминаем, что линейное неоднородное уравнение второго порядка с постоянными коэффициентами имеет вид:
Метод подбора, который рассматривался на вышеупомянутом уроке, проходит лишь в ограниченном ряде случаев, когда в правой части находятся многочлены, экспоненты, синусы, косинусы.
Но что делать, когда справа, например, дробь, логарифм, тангенс? В такой ситуации на помощь как раз и приходит метод вариации постоянных.
Пример 4
Найти общее решение дифференциального уравнения второго порядка
Решение: В правой части данного уравнения находится дробь, поэтому сразу можно сказать, что метод подбора частного решения не прокатывает. Используем метод вариации произвольных постоянных.
Ничто не предвещает грозы, начало решения совершенно обычное:
Найдем общее решение соответствующего однородного уравнения:
Составим и решим характеристическое уравнение:
– получены сопряженные комплексные корни, поэтому общее решение:
Обратите внимание на запись общего решения – если есть скобки, то их раскрываем.
Теперь проделываем практически тот же трюк, что и для уравнения первого порядка: варьируем константы , заменяя их неизвестными функциями . То есть, общее решение неоднородного уравнения будем искать в виде:
Где – пока ещё неизвестные функции.
Похоже на свалку бытовых отходов, но сейчас всё рассортируем.
В качестве неизвестных выступают производные функций . Наша цель – найти производные , причем найденные производные должны удовлетворять и первому и второму уравнению системы.
Откуда берутся «игреки»? Их приносит аист. Смотрим на полученное ранее общее решение и записываем:
Найдем производные:
С левыми частями разобрались. Что справа?
– это правая часть исходного уравнения, в данном случае:
Коэффициент – это коэффициент при второй производной:
На практике почти всегда , и наш пример не исключение.
Всё прояснилось, теперь можно составить систему:
Систему обычно решают по формулам Крамера , используя стандартный алгоритм. Единственное отличие состоит в том, что вместо чисел у нас функции.
Найдем главный определитель системы:
Если позабылось, как раскрывается определитель «два на два», обратитесь к уроку Как вычислить определитель? Ссылка ведёт на доску позора =)
Итак: , значит, система имеет единственное решение.
Находим производную:
Но это еще не всё, пока мы нашли только производную.
Сама функция восстанавливается интегрированием:
Разбираемся со второй функцией:
Здесь добавляем «нормальную» константу
На заключительном этапе решения вспоминаем, в каком виде мы искали общее решение неоднородного уравнения? В таком:
Нужные функции только что найдены!
Осталось выполнить подстановку и записать ответ:
Ответ: общее решение:
В принципе, в ответе можно было раскрыть скобки.
Полная проверка ответа выполняется по стандартной схеме, которая рассматривалась на уроке Неоднородные ДУ 2-го порядка . Но проверка будет непростой, поскольку предстоит находить достаточно тяжелые производные и проводить громоздкую подстановку. Это неприятная особенность, когда вы решаете подобные диффуры.
Пример 5
Решить дифференциальное уравнение методом вариации произвольных постоянных
Это пример для самостоятельного решения.
На самом деле в правой части тоже дробь. Вспоминаем тригонометрическую формулу , её, к слову, нужно будет применить по ходу решения.
Метод вариации произвольных постоянных – наиболее универсальный метод. Им можно решить любое уравнение, которое решается методом подбора частного решения по виду правой части . Возникает вопрос, а почему бы и там не использовать метод вариации произвольных постоянных? Ответ очевиден: подбор частного решения, который рассматривался на уроке Неоднородные уравнения второго порядка , значительно ускоряет решение и сокращает запись – никакого трахча с определителями и интегралами.
Рассмотрим два примера с задачей Коши .
Пример 6
Найти частное решение дифференциального уравнения, соответствующее заданным начальным условиям
,
Решение: Опять дробь и экспонента в интересном месте.
Используем метод вариации произвольных постоянных.
Найдем общее решение соответствующего однородного уравнения:
– получены различные действительные корни, поэтому общее решение:
Общее решение неоднородного уравнения ищем в виде: , где – пока ещё неизвестные функции.
Составим систему:
В данном случае:
,
Находим производные:
,
Таким образом:
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.
Восстанавливаем функцию интегрированием:
Здесь использован метод подведения функции под знак дифференциала .
Восстанавливаем вторую функцию интегрированием:
Такой интеграл решается методом замены переменной :
Из самой замены выражаем:
Таким образом:
Данный интеграл можно найти методом выделения полного квадрата , но в примерах с диффурами я предпочитаю раскладывать дробь методом неопределенных коэффициентов :
Обе функции найдены:
В результате, общее решение неоднородного уравнения:
Найдем частное решение, удовлетворяющее начальным условиям .
Технически поиск решения осуществляется стандартным способом, который рассматривался в статье Неоднородные дифференциальные уравнения второго порядка .
Держитесь, сейчас будем находить производную от найденного общего решения:
Вот такое вот безобразие. Упрощать его не обязательно, легче сразу составить систему уравнений. В соответствии с начальными условиями :
Подставим найденные значения констант в общее решение:
В ответе логарифмы можно немного запаковать.
Ответ: частное решение:
Как видите, трудности могут возникнуть в интегралах и производных, но никак не в самом алгоритме метода вариации произвольных постоянных. Это не я вас запугал, это всё сборник Кузнецова!
Для расслабления заключительный, более простой пример для самостоятельного решения:
Пример 7
Решить задачу Коши
,
Пример несложный, но творческий, когда составите систему, внимательно на неё посмотрите, прежде чем решать;-),
В результате общее решение:
Найдем частное решение, соответствующее начальным условиям .
Подставим найденные значения констант в общее решение:
Ответ: частное решение:
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 8 из 10Следующая ⇒ Система m линейных уравнений с n переменными называется системой линейных однородныхуравнений, если все их свободные члены равны нулю.
Система линейных однородных уравнений всегда совместна, т.к. она всегда имеет, по крайней мере, нулевое (тривиальное) решение (0;0;…;0).
Если в системе (2) m=n, а её определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера.
Ненулевые решения, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или, когда m=n, но определитель системы равен нулю. Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т. Обозначим решение системы , в виде строки . Свойства решений системы линейных однородных уравнений. 1. Если строка -решение системы, то и строка -также решение этой системы. 2. Если строки и -решения системы (2), то при и их линейная комбинация -так же решение этой системы. Из свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Определение. Система линейно независимых решений называется фундаментальной, если каждое решение системы является линейной комбинацией решений .
Теорема: Если ранг матрицы коэффициентов при переменных системы линейных однородных уравнений (2) меньше числа переменных n, то всякая фундаментальная система решений системы (2) состоит из n-r решений.
Поэтому общее решение системы (2) линейных однородных уравнений имеет вид: , где — любая фундаментальная система решений, -произвольные числа, .
Пример решения задач. Пример. Найти фундаментальную систему решений системы линейных однородных алгебраических уравнений.
Такая система совместна всегда, так как имеет тривиальное решение (0; 0; 0; 0; 0).
Решение.
система имеет множество решений. система имеет три свободные переменные — базисные переменные, , , — свободные переменные Условия для нахождения фундаментальных решений:
1)
2)
3) Данные строки — , , (векторы) – образуют фундаментальную систему решений данной системы линейных однородных алгебраических уравнений. РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ Расчетная работа № 1. Обработка экспериментальных данных Методом наименьших квадратов Основные положения При обработке данных экспериментов возникает необходимость определения закономерности их изменения: — представление в виде какой-либо функциональной зависимости с целью исследования и прогнозирования характера и протекания процесса; Из методов построения эмпирической прямой наиболее обоснован и распространён метод наименьших квадратов, заключающийся в следующем: — из множества функциональных зависимостей определённого вида выбирается та, для которой сумма квадратов отклонений экспериментальных значений от теоретических (вычислительных) является наименьшей.
⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Все правила по сольфеджио
е. .
Обратная связь — 161.97.168.212 (0.008 с.)Однородные системы линейных уравнений
Однородной называется система линейных уравнений, свободные члены которой равны нулю:
| (4.5.1) |
Очевидно, что система однородных уравнений (4.5.1) всегда совместна, так как имеет нулевое решение .
Это следует также из теоремы Кронекера-Капелли: в случае однородной системы .
При решении системы однородных уравнений можно поставить вопрос: при каком условии однородная система (4.5.1) является неопределенной, т.е. имеет ненулевые решения. Ответ на этот вопрос дает следующая теорема.
Теорема. Для того чтобы система (4.5.1) имеет ненулевые решения, необходимо и достаточно, чтобы выполнялось условие .
Действительно, если , то система имеет единственное и, значит, только нулевое решение: . Если , то система (4.
5.1) является неопределенной (несовместной она быть не может) и, значит, имеет бесчисленное множество решений.
Пусть — какое-нибудь ненулевое решение однородной системы (4.5.1). Представим это решение как вектор-строку . Тогда тоже, очевидно, будет решением системы (4.5.1). Далее, если какое-то другое решение системы (4.5.1), отличное от , то при любых линейная комбинация данных решений тоже будет решением системы, так как если
Итак, любая линейная комбинация решений однородной системы (4.5.1) тоже будет ее решением.
Определение. Линейно независимая система решений системы (4.5.1) называется фундаментальной, если каждое решение системы (4.5.1) является линейной комбинацией решений .
Теорема. Если , то система (4.5.1) обладает фундаментальными системами решений.
Доказательство. Пусть , r<n и пусть для определенности базисный минор порядка r стоит в верхнем левом углу матрицы А.
Отсюда следует, что первые r уравнений системы (4.5.1) линейно независимы. Перенеся свободные неизвестные первых r уравнений системы (4.6.1) в правые части, получим систему
| (4.5.2) |
Придавая свободным неизвестным значения , получим соответствующие значения первых r неизвестных. Аналогично, придавая свободным неизвестным значения , получим: и т.д. В результате будет найдено k=n-r решений системы (4.5.1):
Решения линейно независимы, т.к. ранг образованной ими матрицы равен К.
Покажем теперь, что каждое решение системы (4.5.1) линейно выражаются через . Пусть — произвольное решение системы (4.5.1). Составим новое решение как следующую линейную комбинацию решений :
Очевидно, что все элементы, начиная с k-ого элемента, в решении равны нулю, то из однородной системы (4.5.2), определитель которого отличен от нуля, получаем, что и значения всех остальных неизвестных в должны быть равны нулю, т.
е. и тогда , т.е. произвольное решение является линейной комбинацией линейно независимых решений . Теорема доказана.
Рассмотрим систему уравнений
| (4.5.3) |
и соответствующую ей систему однородных уравнений
| (4.5.4) |
Пусть — какое-то решение системы (4.5.3) и любое другое ее решение, отличное от . Очевидно, что разность
будет решением системы (4.5.4), и если — произвольное решение однородной системы (4.5.4), то очевидно, что
является решением системы (4.5.3). Отсюда следует, что все решения системы (4.5.3) можно получить, прибавляя к одному какому-нибудь ее решению всевозможные решения однородной системы (4.5.4).
Таким образом, общее решение системы (4.5.3) равно линейной комбинации общего решения однородной системы (4.5.4) и произвольного, но фиксированного решения системы (4.
5.3). Если фундаментальная система решений однородной системы (4.5.4) и — произвольное фиксированное решение системы (4.5.3), то общее решение системы (4.5.3) имеет вид , где — произвольные числа.
Пример. Найти фундаментальную систему однородной системы уравнений
Решение. Решаем систему методом Жордана-Гаусса:
Общее решение имеет вид: .
Решение получим, придавая свободным неизвестным значения :
,
и решение получим, полагая :
.
Таким образом, одна из фундаментальных систем решений имеет вид:
, .
Общее решение системы можно представить в следующем виде:
,
где — произвольные числа. Например, полагая , получим одно из частных решений: .
4.6. Задания для самостоятельной работы по главе 4
4.
1. Решить систему линейных уравнений по правилу Крамера.
4.2. Решить систему линейных уравнений по правилу Крамера.
4.3. Решить систему линейных уравнений по правилу Крамера.
4.4. Решить систему линейных уравнений по правилу Крамера.
4.5. Решить систему линейных уравнений по правилу Крамера.
4.6. Решить систему линейных уравнений методом Жордана-Гаусса.
4.7. Решить систему линейных уравнений методом Жордана-Гаусса.
4.8. Решить систему линейных уравнений методом Жордана-Гаусса.
4.9. Решить систему линейных уравнений методом Жордана-Гаусса.
4.10. Решить систему линейных уравнений методом Жордана-Гаусса.
4.11. Исследовать совместимость и найти общее и одно базисное решение системы линейных уравнений.
4.
12. Исследовать совместимость и найти общее и одно базисное решение системы линейных уравнений.
4.13. Исследовать систему и найти общее решение в зависимости от значения параметра .
4.14. Найти общее решение и фундаментальную систему решений для однородной системы уравнений
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот…
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор…
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Построение фундаментальной системы решений — МегаЛекции
Положим .
Пусть общее решение системы (2) записано в виде
,
где ,…, – главные (базисные) переменные, ,…, – значения свободных переменных ,…, . Выберем решений системы (2), полученных из общего решения следующим образом: одно из значений свободных переменных полагается равным 1, а остальные – равными 0:
, , …, .
Эти решения образуют нормальную фундаментальную систему решений однородной системы (2). Они обладают следующим свойством:
Любое решение системы (2) может быть единственным образом представлено в виде:
,
где ,…, – некоторые числа.
Любой набор из решений системы (2), обладающий указанным свойством, называется фундаментальной системой решений системы (2).
Задания
Задание 1.Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.
1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
1.
7.
1.8.
1.9.
1.10.
Задание 2. Найти фундаментальныйнабор решений однородной системы линейных уравнений.
2.1.
2.2.
2.3.
2.4.
2.5.
2.6.
2.7.
2.8.
2.9.
2.10.
Задание 3.Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
3.10.
Методика и порядок выполнения работы
Пример 1
Решить однородную систему линейных алгебраических уравнений. Указать общее решение системы и фундаментальный набор решений.
Решение
|
С помощью элементарных преобразований приведем матрицу системы к ступенчатому виду:
~ ~ ~ .
Из последней ступенчатой системы видно, что ранг матрицы системы равен , а количество переменных равно , так как , то система неопределенна.
Количество базисных переменных равно . В качестве главных переменных можно выбрать и , соответствующие столбцам ненулевого минора второго порядка: , в качестве свободной переменной – .
Запишем систему, соответствующую полученной матрице:
Из второго уравнения выражаем через , получим: . Подставляя это выражение в первое уравнение, получим: . Обозначив , получим общее решение системы . это решение можно записать в виде: . Фундаментальную систему решений образует решение .
Пример 2
Найти фундаментальныйнабор решений однородной системы линейных уравнений.
Решение
|
С помощью элементарных преобразований приведем матрицу системы к ступенчатому виду:
|
~ ~
|
~ ~ .
Из последней ступенчатой системы видно, что ранг матрицы системы равен , а количество переменных равно , так как , то система неопределенна.
Количество базисных переменных равно . В качестве главных переменных можно выбрать , и , соответствующие столбцам ненулевого минора третьего порядка: , в качестве свободной переменной – .
Запишем систему, соответствующую полученной матрице:
Из третьего уравнения получим: . Подставляя это выражение в первое и второе уравнения, получим: , . Обозначив , получим общее решение системы . это решение можно записать в виде: . Фундаментальную систему решений образует решение .
Пример 3
Найти общее решение системы линейных уравнений методом Гаусса, выделив базисные неизвестные, и одно частное решение.
Решение
Проведем элементарные преобразование расширенной матрицы системы по методу Гаусса:
|
|
~ ~ ~
~ .
Из последней ступенчатой системы видно, что ранг матрицы системы равен , ранг расширенной матрицы равен , а количество переменных равно , так как , то система совместна и неопределенна.
Количество базисных переменных равно . В качестве главных переменных можно выбрать , и , соответствующие столбцам ненулевого минора третьего порядка: , в качестве свободных переменных – и .
Запишем систему, соответствующую полученной матрице:
Из третьего уравнения выражаем через , получим: . Подставляя это выражение во второе уравнение, получим: . Подставляя выражения для и в первое уравнение, получим: . Обозначив , а получим общее решение системы
Придавая свободным переменным любые значения, будем получать частные решения системы. Частным решением системы будет являться решение .
Вопросы для защиты работы
1. Однородные и неоднородные системы.
2. Совместные и несовместные системы.
3. Что называется решением системы?
4.
Сформулировать теорему Кронекера-Капелли.
5. Что означает «исследовать систему уравнений»?
6. Что можно сказать о множестве решений системы линейных уравнений, если ранг матрицы этой системы и ранг расширенной матрицы равны нулю?
7. Фундаментальная система решений?
Воспользуйтесь поиском по сайту:
тем же методом мы решаем системы линейной оды, но ясно, что это матричное умножение не определено.
Как мне подойти к этому? Большое спасибо!
- обыкновенные дифференциальные уравнения
$\endgroup$
1
$\begingroup$
Матрица системы $$A=\pmatrix{0&2&2\\-1&3&1\\-1&1&3}$$ имеет характеристический полином
$$
\det(A-\лямбда I)
%=\det\pmatrix{-λ&2&2\\-1&3-λ&1\\-1&1&3-λ}
=-λ(3-λ)^2-4+λ+4(3-λ)
\\
=-λ^3+6λ^2-12λ+8=(-λ+2)^3
$$
так что подстановка $u_k=x_k/t^2$, $u_k’=(tx_k’-2x_k)/t^3$ приводит к системе
$$
\ влево \ {\ начать {выровнено}
tu_1’&=-2u_1+2u_2+2u_3+te^t\\
tu_2’&=-u_1+u_2+u_3+t^2\\
tu_3’&=-u_1+u_2+u_3+te^t
\end{выровнено}\right.
t+d_3
\end{выравнивание}
с $c=-d_1+d_2+d_3$. При установке $d_2=a+c$, $d_3=b+c$, $d_1=d_2+d_3-c=a+b+c$ получаются выражения, близкие к приведенным вами, но с дополнительными членами. 9t\exp(-A\tau)b(\tau)\,d\tau$, следовательно
$$
х(0) = \ехр(-А(т)) х(т) — с(т)
$$
Если у вас есть два решения $u_1,u_2$, то вы получите два решения $x_1(0),x_2(0)$. Предположим, что $x_1(0),x_2(0)$ линейно независимы, тогда можно взять $x_3(0) = x_1(0)\times x_2(0)$ и записать общее решение в виде
$$
a_1 x_1(0)+a_2 x_2(0) + a_3 x_3(0) = \exp(-A(t)) x_{a}(t) — c(t)
$$
L.H.S такой же, как
$$
a_1 (\exp(-A(t))x_1(t)-c(t)) + a_2 (\exp(-A(t))x_2(t)-c(t)) +a_3(\exp(- A(t))x_1(t)-c(t))\times (\exp(-A(t))x_2(t)-c(t))=L_a(t)
$$
И получаем,
$$ х_а (т) = \ ехр (А (т)) (L_а (т) + с (т)) $$ И вы можете выразить все решения с помощью решений $x_1(t)$ и $x_2(t)$
$\endgroup$
4
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
обыкновенных дифференциальных уравнений — Доказательство общего решения однородного линейного ОДУ второго порядка?
Спросил
Изменено 1 год, 2 месяца назад
Просмотрено 13 тысяч раз
$\begingroup$
На уроке дифференциальных уравнений профессор заявил, что общее решение однородного линейного ОДУ второго порядка будет иметь вид: $$y = c_1y_1 + c_2y_2$$ 92} + A\frac{dy}{dx} + By = 0$$
Где $A$ и $B$ — постоянные коэффициенты.
Я понимаю, как получить отдельные решения, но чего я не понимаю, так это того, почему общее решение находится в той форме, в которой оно есть, и каково его доказательство?
- обыкновенные дифференциальные уравнения
$\endgroup$
2
$\begingroup$
Возьмем решение $y$ и пока предположим, что $y=c_1y_1+c_2y_2$. Рассмотрим $y(t_0)=y_0$ и $y'(t_0)=y_0’$. Таким образом, у нас есть
$$y(t_0)=c_1y_1(t_0)+c_2y_2(t_0)=y_0$$
$$\текст{и}$$
$$y'(t_0)=c_1y_1′(t_0)+c_2y_2′(t_o)=y_0’$$
Теперь мы должны найти $c_1$ и $c_2$. У нас есть линейная система
$$\left(\begin{массив}{cc}
y_1(t_0) и y_2(t_0) \\
у_1′(т_0) и у_2′(т_0)
\конец{массив}\справа)
\left(\begin{массив}{с}
с_1 \\
с_2
\конец{массив}\справа)=
\left(\begin{массив}{с}
у_0 \\
у_0′
\end{массив}\right)\qquad (1)$$
Теперь, поскольку $y_1$ и $y_2$ являются фундаментальными решениями, то есть их вронскианскими
$$W[y_1,y_2]=\влево|
\begin{массив}{cc}
y_1 (т) и y_2 (т) \\
у_1′(т) и у_2′(т)
\конец{массив}
\право|\neq 0$$
$\для всех t$ в интервале, на котором $y_1$ и $y_2$ берутся в качестве решений, мы имеем явное решение $(1)$, которое
$$\влево(\начать{массив}{с}
с_1 \\
с_2
\end{массив}\right)=\frac{1}{W[y_1,y_2](t_0)}\left(\begin{массив}{cc}
y_2′(t_0) и -y_2(t_0) \\
-y_1′(t_0) и y_1(t_0)
\end{массив}\right)\left(\begin{массив}{c}
у_0 \\
у_0′
\end{массив}\right)$$
Следовательно, существуют $c_1$ и $c_2$ такие, что $y=c_1y_1+c_2y_2$, и по теореме существования-единственности это единственный возможный $y$ такой, что $y(t_0)=y_0$ и $y'( t_0)=y_0’$, заставляя $y$ иметь эту форму.
КЭД
Выше я привел доказательство того, почему все решения однородного линейного ОДУ должны иметь вид $y=c_1y_1+c_2y_2$. Но если вы только хотите убедиться, почему $y=c_1y_1+c_2y_2$ является решением, то поймите, что, поскольку оператор $L[y]$, $$L[y]=y»+Ay’+By$$ линейно у нас есть $$L[c_1y_1+c_2y_2]=L[c_1y_1]+L[c_2y_2]=c_1L[y_1]+c_2L[y_2]=0$$ потому что, поскольку $y_1$ и $y_2$ являются решениями ДУ, $L[y_1]=L[y_2]=0$, а поскольку $L[c_1y_1+c_2y_2]=0$, это также решение ДУ. 9{r_2x}$.
Теперь мы исчерпали все возможности, и в каждом случае общее решение имеет вид $y=c_1y_1+c_2y_2$, что и требовалось.
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Общее Решение данной системы уравнений
Заданный вопрос
Изменено 8 лет, 1 месяц назад
Просмотрено 2к раз
$\begingroup$
Найдите общее решение этой системы уравнений:
$$x’ = \pmatrix{-1&0&0\\1&0&-1\\1&1&0}x$$
Я получил следующие собственные значения: $\lambda = -1,\pm i$
Собственные векторы, соответствующие каждому собственному значению:
$v_1 = \pmatrix{1\\-1\\0}$, $v_2 = \pmatrix{0\\i\\1}$, $v_3 = \pmatrix{0\\-i\\1}$
Но как тогда написать общее решение?
- обыкновенные дифференциальные уравнения
$\endgroup$
4
$\begingroup$
Запишите общее решение как
9{-t}},z \left( t \right) ={\it C_1}\, \sin \left( t \right) +{\it C_2}\,\cos \left( t \right) \right\} $$$\endgroup$
2
$\begingroup$
Вчера я оставил комментарий, в котором были опечатки, и он все еще содержит ошибки, поэтому я опубликую полный ответ на исходный вопрос.
{-t}+c_2 \begin{bmatrix}
0\\
-\sin т\\
\Стоимость
\end{bmatrix}+c_3\begin{bmatrix}
0\\
\Стоимость\\
\sin т
\end{bmatrix},
$$
это именно тот ответ, который у вас есть в ваших комментариях. 9{-(t-t_0)} & \cos(t-t_0) & -\sin(t-t_0) \\ \sin(t-t_0) & \sin(t-t_0) & \cos(t-t_0) \end{bmatrix} х(t_0)$$
$\endgroup$
5
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Однородные линейные системы — дифференциальные уравнения
Все ресурсы по дифференциальным уравнениям
1 Диагностический тест 29 практических тестов Вопрос дня Карточки Learn by Concept
Дифференциальные уравнения Помощь » Система линейных дифференциальных уравнений первого порядка » Однородные линейные системы
Найдите общее решение данной системы.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти общее решение данной системы
, сначала найдите собственные значения и собственные векторы.
Следовательно, собственные значения равны
Теперь вычислим собственные векторы0005
для
Таким образом,
Следовательно,
Теперь общее решение —
Отчет о ошибке
Решение исходной проблемы. Где
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы решить однородную систему, нам понадобится фундаментальная матрица.
В частности, это поможет получить экспоненциальную матрицу. Для этого проведем диагонализацию матрицы. Во-первых, мы найдем собственные значения, которые мы можем сделать, вычислив определитель .
Найдя собственные пространства для лямбда = 1, мы имеем
Прибавив -1/2 строки 1 к строке 2 и разделив на -1/2, мы получим, что означает
Таким образом, у нас есть собственный вектор .
Для лямбда = 4
Добавляя строку 1 к строке 2, мы получаем
То же самое и с собственным вектором.
Таким образом, имеем и . Используя обратную формулу для матриц 2×2, мы получаем это. Поскольку мы это знаем, у нас есть
Решение однородной системы линейных уравнений состоит в простом умножении матричной экспоненты на начальное условие. Для других фундаментальных матриц также необходима обратная матрица.
Thus, our final answer is
Report an Error
Solve the homogenous equation:
With the initial conditions:
Possible Answers:
ни один из этих ответов
Правильный ответ:
Пояснение:
Итак, это однородное дифференциальное уравнение второго порядка.
Чтобы решить это, нам нужно найти корни уравнения. Это уравнение можно записать так:
Что с помощью квадратичной формулы или разложения на множители дает нам корни и
Решение однородных уравнений записывается в виде:
поэтому мы не знаем констант, но можем подставить найденные нами значения в качестве корней:
У нас есть два начальных значения, одно для y(t) и одно для y'(t), оба с t=0\ в другое уравнение для решения
SO, решаем, мы получаем: затем
Это дает окончательный ответ:
Отчет о ошибке
Решите уравнение второго порядка:
подлежат первоначальным значениям:
Возможные ответы:
ни один из этих ответов
Правильный ответ: 1 55
5
Объяснение:
Итак, это однородное дифференциальное уравнение второго порядка.
Чтобы решить это, нам нужно найти корни уравнения. Это уравнение может быть записано как:
Что, используя квадратную формулу или разложение на множители, дает нам корни и
Решение однородных уравнений записывается в виде:
поэтому мы не знаем констант, но можем подставить значения, которые мы нашли для корней:
У нас есть два начальных значения, одно для y(t) и одно для y'(t), оба с t=0
SO:
SO:
Мы можем решить, затем подключиться к другому уравнению, чтобы решить
Итак, решаем, мы получаем: тогда
Это дает окончательный ответ:
Отчет. an Ошибка
Решите дифференциальное уравнение для y:
При начальном условии:
Возможные ответы:
Правильный ответ: 5
200010 Пояснение:
Итак, это однородное дифференциальное уравнение первого порядка.
Чтобы решить это, нам нужно найти корни уравнения. Это уравнение можно записать так:
дает нам корень из
Решение однородных уравнений записывается в виде:
поэтому мы не знаем константу, но можем подставить найденные значения в качестве корня:
У нас есть одно начальное значение для y(t) при t=0
SO:
Это дает окончательный ответ:
Отчет о ошибке
Решение дифференциального уравнения третьего порядка:
. ни один из этих ответов Правильный ответ: Пояснение: Итак, это однородное дифференциальное уравнение третьего порядка. Чтобы решить это, нам нужно найти корни уравнения. Это уравнение можно записать так: Который, используя кубическую формулу или разложение на множители, дает нам корни , и Решение однородных уравнений записывается в виде: поэтому мы не знаем констант, но можем подставить значения, которые мы решили вместо корней : У нас есть три начальных значения: одно для y(t), одно для y'(t) и для y»(t) все с t=0 Так что это можно решить либо подстановкой, либо созданием матрицы 3X3 и уменьшением. Это дает окончательный ответ: Отчет о ошибке Решение дифференциального уравнения: При условии начальных условий: ответ: 
После выполнения любого из этих методов значения констант будут следующими: Then и
Пояснение:
Итак, это однородное дифференциальное уравнение третьего порядка. Чтобы решить это, нам нужно найти корни уравнения. Это уравнение можно записать так:
Который, используя кубическую формулу или разложение на множители, дает нам корни , и
Решение однородных уравнений записывается в виде:
поэтому мы не знаем констант, но можем подставить значения, которые мы решили вместо корней :
У нас есть три начальных значения, одно для y(t), одно для y'(t) и для y»(t) все с t=0
Итак:
Так что это можно решить либо подстановкой, либо составлением матрицы 3X3 и уменьшением.
После выполнения любого из этих методов значения констант будут следующими: Then и
Это дает окончательный ответ:
Сообщить об ошибке
Найдите общее решение для данной системы.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти общее решение данной системы
, сначала найдите собственные значения и собственные векторы.
Следовательно, собственные значения равны
Теперь рассчитайте собственные векторы
для
Таким образом,
для
.
Сообщить об ошибке
При подстановке в однородную линейную систему для , какая из следующих матриц будет иметь равновесие в седловой точке на своей фазовой плоскости?
Возможные ответы:
Правильный ответ:
Объяснение:
Фазовая плоскость седловой точки получается из двух действительных собственных значений разных знаков.
Три из этих матриц треугольные, что означает, что их собственные значения лежат на диагонали. Для этих трех собственные значения действительны, но оба имеют один и тот же знак, что означает, что у них нет седел. Для оставшихся двух нам нужно найти собственные значения, используя характеристические уравнения.
Для у нас есть
Дискриминант для этого равен , поэтому решения нереальны. Таким образом, эта матрица не дает седловой точки.
Для у нас есть,
Мы видим, что эта матрица дает два действительных собственных значения с разными знаками. Таким образом, это правильный выбор.
Сообщить об ошибке
Найти общее решение системы обыкновенных дифференциальных уравнений
где
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Нахождение собственных значений и собственных векторов с помощью характеристического уравнения матрицы0002
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по дифференциальным уравнениям
1 Диагностический тест 29 практических тестов Вопрос дня Карточки Обучение по понятиям
7.
2 Неоднородные линейные уравнения. Расчет, том 3Цели обучения
- 7.2.1 Напишите общее решение неоднородного дифференциального уравнения.
- 7.2.2 Решить неоднородное дифференциальное уравнение методом неопределенных коэффициентов.
- 7.2.3 Решить неоднородное дифференциальное уравнение методом вариации параметров.
В этом разделе мы рассмотрим, как решать неоднородные дифференциальные уравнения. Терминология и методы отличаются от тех, которые мы использовали для однородных уравнений, поэтому давайте начнем с определения некоторых новых терминов.
Общее решение неоднородного линейного уравнения
Рассмотрим неоднородное линейное дифференциальное уравнение
a2(x)y″+a1(x)y′+a0(x)y=r(x).a2(x)y″+a1(x)y′+a0(x)y=r(x) .
Ассоциированное однородное уравнение
a2(x)y″+a1(x)y′+a0(x)y=0a2(x)y″+a1(x)y′+a0(x)y=0
(7.3)
называется дополнительным уравнением. Мы увидим, что решение дополнительного уравнения является важным шагом в решении неоднородного дифференциального уравнения.
Определение
Решение yp(x)yp(x) дифференциального уравнения, не содержащее произвольных констант, называется частным решением уравнения.
Теорема 7.4
Общее решение неоднородного уравнения
Пусть yp(x)yp(x) — любое частное решение неоднородного линейного дифференциального уравнения
a2(x)y″+a1(x)y′+a0(x)y=r(x).a2( х)y″+a1(x)y′+a0(x)y=r(x).
Также пусть c1y1(x)+c2y2(x)c1y1(x)+c2y2(x) обозначает общее решение дополнительного уравнения. Тогда общее решение неоднородного уравнения имеет вид (Икс).
(7,4)
Доказательство
Чтобы доказать, что y(x)y(x) является общим решением, мы должны сначала показать, что оно является решением дифференциального уравнения, и, во-вторых, что любое решение дифференциального уравнения может быть записано в этой форме. Подставив y(x)y(x) в дифференциальное уравнение, получим
a2(x)y″+a1(x)y′+a0(x)y=a2(x)(c1y1+c2y2+yp)″+a1(x)(c1y1+c2y2+yp)′+a0(x )(c1y1+c2y2+yp)=[a2(x)(c1y1+c2y2)″+a1(x)(c1y1+c2y2)′+a0(x)(c1y1+c2y2)]+a2(x)yp″+ a1(x)yp′+a0(x)yp=0+r(x)=r(x).a2(x)y″+a1(x)y′+a0(x)y=a2(x)( c1y1+c2y2+yp)″+a1(x)(c1y1+c2y2+yp)′+a0(x)(c1y1+c2y2+yp)=[a2(x)(c1y1+c2y2)″+a1(x)( c1y1+c2y2)′+a0(x)(c1y1+c2y2)]+a2(x)yp″+a1(x)yp′+a0(x)yp=0+r(x)=r(x).
Итак, y(x)y(x) является решением.
Теперь пусть z(x)z(x) — любое решение a2(x)y″+a1(x)y′+a0(x)y=r(x).a2(x)y″+a1( х)у’+а0(х)у=г(х). Затем
a2(x)(z−yp)″+a1(x)(z−yp)′+a0(x)(z−yp)=(a2(x)z″+a1(x)z′+a0( х)z)−(a2(x)yp″+a1(x)yp′+a0(x)yp)=r(x)−r(x)=0,a2(x)(z−yp)″+ a1(x)(z−yp)′+a0(x)(z−yp)=(a2(x)z″+a1(x)z′+a0(x)z)−(a2(x)yp″ +a1(x)yp′+a0(x)yp)=r(x)−r(x)=0,
, поэтому z(x)−yp(x)z(x)−yp(x) является решением дополнительного уравнения. Но c1y1(x)+c2y2(x)c1y1(x)+c2y2(x) является общим решением дополнительного уравнения, поэтому существуют константы c1c1 и c2c2 такие, что
z(x)−yp(x)=c1y1(x)+c2y2(x). z(x)−yp(x)=c1y1(x)+c2y2(x).
Отсюда мы видим, что z(x)=c1y1(x)+c2y2(x)+yp(x).z(x)=c1y1(x)+c2y2(x)+yp(x).
□
Пример 7.11
Проверка общего решения
Учитывая, что yp(x)=xyp(x)=x является частным решением дифференциального уравнения y″+y=x,y″+y=x, запишите общее решение и проверьте по проверка того, что решение удовлетворяет уравнению.
Решение
Дополнительное уравнение y″+y=0,y″+y=0 имеет общее решение c1cosx+c2sinx.c1cosx+c2sinx. Итак, общее решение неоднородного уравнения равно
y(x)=c1cosx+c2sinx+x.y(x)=c1cosx+c2sinx+x.
Чтобы убедиться, что это решение, подставьте его в дифференциальное уравнение. У нас есть
y′(x)=−c1sinx+c2cosx+1andy″(x)=−c1cosx−c2sinx.y′(x)=−c1sinx+c2cosx+1andy″(x)=−c1cosx−c2sinx.
Тогда
y″(x)+y(x)=−c1cosx−c2sinx+c1cosx+c2sinx+x=x.y″(x)+y(x)=−c1cosx−c2sinx+c1cosx+c2sinx+x=x .
Итак, y(x)y(x) является решением y″+y=x. y″+y=x.
Контрольно-пропускной пункт 7.10
Учитывая, что yp(x)=−2yp(x)=−2 является частным решением y″−3y′−4y=8,y″−3y′−4y=8, запиши общее решение и убедись, что общее решение удовлетворяет уравнению.
В предыдущем разделе мы научились решать однородные уравнения с постоянными коэффициентами. Поэтому для неоднородных уравнений вида ay″+by′+cy=r(x),ay″+by′+cy=r(x) мы уже знаем, как решать дополнительное уравнение, и задача сводится к нахождение частного решения неоднородного уравнения. Рассмотрим теперь для этого два приема: метод неопределенных коэффициентов и метод вариации параметров.
Неопределенные коэффициенты
Метод неопределенных коэффициентов включает обоснованные предположения о форме конкретного решения на основе формы r(x).r(x). Когда мы берем производные полиномов, показательных функций, синусов и косинусов, мы получаем многочлены, показательные функции, синусы и косинусы. Поэтому, когда r(x)r(x) имеет одну из этих форм, возможно, что решение неоднородного дифференциального уравнения может принять ту же форму. Давайте посмотрим на несколько примеров, чтобы увидеть, как это работает.
Пример 7.12
Неопределенные коэффициенты, когда r(x)r(x) является многочленом
Найдите общее решение уравнения y″+4y′+3y=3x.y″+4y′+3y=3x.
Решение
Дополнительное уравнение y″+4y′+3y=0,y″+4y′+3y=0 с общим решением c1e−x+c2e−3x.c1e−x+c2e−3x. Поскольку r(x)=3x,r(x)=3x, конкретное решение может иметь вид yp(x)=Ax+B.yp(x)=Ax+B. Если это так, то мы имеем yp′(x)=Ayp′(x)=A и yp″(x)=0.yp″(x)=0. Чтобы ypyp было решением дифференциального уравнения, мы должны найти такие значения AA и BB, что
y″+4y′+3y=3×0+4(A)+3(Ax+B)=3x3Ax+(4A+3B)=3x.y″+4y′+3y=3×0+4(A)+3( Ах+В)=3х3Ах+(4А+3В)=3х.
Приравняв коэффициенты подобных членов, получим
3A=34A+3B=0,3A=34A+3B=0.
Тогда A=1A=1 и B=-43,B=-43, поэтому yp(x)=x-43yp(x)=x-43 и общее решение
y(x)=c1e- х+с2е-3х+х-43.у(х)=с1е-х+с2е-3х+х-43.
Обратите внимание, что в примере 7.12, хотя r(x)r(x) не включает постоянный член, нам необходимо было включить постоянный член в наше предположение. Если бы мы приняли решение в виде yp=Axyp=Ax (без постоянного члена), мы не смогли бы найти решение. (Проверьте это!) Если функция r(x)r(x) является полиномом, наша догадка для конкретного решения должна быть полиномом той же степени, и он должен включать все члены более низкого порядка, независимо от того, являются ли они присутствует в r(x).r(x).
Пример 7.13
Неопределенные коэффициенты, когда r(x)r(x) является экспонентой
Найдите общее решение для y″−y′−2y=2e3x.y″−y′−2y=2e3x.
Решение
Дополнительное уравнение y″−y′−2y=0,y″−y′−2y=0 с общим решением c1e−x+c2e2x.c1e−x+c2e2x. Поскольку r(x)=2e3x,r(x)=2e3x, конкретное решение может иметь вид yp(x)=Ae3x.yp(x)=Ae3x. Тогда имеем yp′(x)=3Ae3xyp′(x)=3Ae3x и yp″(x)=9Ae3x.yp″(x)=9Ae3x. Чтобы ypyp было решением дифференциального уравнения, мы должны найти такое значение AA, что
y″−y′−2y=2e3x9Ae3x−3Ae3x−2Ae3x=2e3x4Ae3x=2e3x.y″−y′−2y=2e3x9Ae3x−3Ae3x−2Ae3x=2e3x4Ae3x=2e3x.
Итак, 4А=24А=2 и А=1/2.А=1/2. Тогда yp(x)=(12)e3x,yp(x)=(12)e3x, и общее решение
y(x)=c1e−x+c2e2x+12e3x.y(x)=c1e−x +c2e2x+12e3x.
Контрольно-пропускной пункт 7.11
Найдите общее решение для y″−4y′+4y=7sint-cost.y″−4y′+4y=7sint-cost.
В предыдущей контрольной точке r(x)r(x) включала как синус, так и косинус. Однако, даже если r(x)r(x) включает только синусоидальный или только косинусоидальный член, в предположении должны присутствовать оба члена. Метод неопределенных коэффициентов также работает с произведениями многочленов, экспонент, синусов и косинусов. Некоторые ключевые формы r(x)r(x) и связанные с ними предположения для yp(x)yp(x) приведены в таблице 7.2.
| р(х)р(х) | Начальное предположение для yp(x)yp(x) |
|---|---|
| кк (константа) | АА (постоянный) |
| топор+бакс+б | Ax+BAx+B ( Примечание : Предположение должно включать оба термина, даже если b=0. b=0.) |
| ax2+bx+cax2+bx+c | Ax2+Bx+CAx2+Bx+C ( Примечание : Предположение должно включать все три члена, даже если bb или cc равны нулю.) |
| Полиномы высшего порядка | Многочлен того же порядка, что и r(x)r(x) |
| aeλxaeλx | АеХхАеХх |
| acosβx+bsinβxacosβx+bsinβx | Acosβx+BsinβxAcosβx+Bsinβx ( Примечание : Предположение должно включать оба условия, даже если a=0a=0 или b=0.b=0.) |
| aeαxcosβx+beαxsinβxaαxcosβx+beαxsinβx | Aeαxcosβx+BeαxsinβxAeαxcosβx+Beαxsinβx |
| (ax2+bx+c)eλx(ax2+bx+c)eλx | (Ax2+Bx+C)eλx(Ax2+Bx+C)eλx |
| (a2x2+a1x+a0)cosβx+(b2x2+b1x+b0)sinβx(a2x2+a1x+a0)cosβx+(b2x2+b1x+b0)sinβx | (A2x2+A1x+A0)cosβx+(B2x2+B1x+B0)sinβx(A2x2+A1x+A0)cosβx+(B2x2+B1x+B0)sinβx |
| (a2x2+a1x+a0)eαxcosβx+(b2x2+b1x+b0)eαxsinβx(a2x2+a1x+a0)eαxcosβx+(b2x2+b1x+b0)eαxsinβx | (A2x2+A1x+A0)eαxcosβx+(B2x2+B1x+B0)eαxsinβx(A2x2+A1x+A0)eαxcosβx+(B2x2+B1x+B0)eαxsinβx |
Стол
7. 2
Основные формы метода неопределенных коэффициентов
Имейте в виду, что у этого метода есть ключевая ловушка. Рассмотрим дифференциальное уравнение y″+5y′+6y=3e−2x.y″+5y′+6y=3e−2x. Основываясь на виде r(x),r(x), мы угадываем частное решение вида yp(x)=Ae−2x.yp(x)=Ae−2x. Но когда мы подставляем это выражение в дифференциальное уравнение, чтобы найти значение для A, A, мы сталкиваемся с проблемой. У нас есть
yp'(x)=-2Ae-2xyp'(x)=-2Ae-2x
и
yp″=4Ae−2x,yp″=4Ae−2x,
поэтому нам нужно
y″+5y′+6y=3e-2x4Ae-2x+5(-2Ae-2x)+6Ae-2x=3e-2x4Ae-2x-10Ae-2x+6Ae-2x=3e-2×0=3e-2x,y ″+5y′+6y=3e-2x4Ae-2x+5(-2Ae-2x)+6Ae-2x=3e-2x4Ae-2x-10Ae-2x+6Ae-2x=3e-2×0=3e-2x,
, что невозможно.
Присмотревшись, мы видим, что в этом случае общее решение дополнительного уравнения есть c1e−2x+c2e−3x.c1e−2x+c2e−3x. Экспоненциальная функция в r(x)r(x) на самом деле является решением дополнительного уравнения, поэтому, как мы только что видели, все члены в левой части уравнения сокращаются. Мы все еще можем использовать метод неопределенных коэффициентов в этом случае, но мы должны изменить наше предположение, умножив его на x.x. Используя новое предположение, yp(x)=Axe−2x,yp(x)=Axe−2x, мы имеем
yp'(x)=A(e-2x-2xe-2x)yp'(x)=A(e-2x-2xe-2x)
и
yp″(x)=−4Ae−2x+4Axe−2x.yp″(x)=−4Ae−2x+4Axe−2x.
Замена дает
y″+5y′+6y=3e−2x(−4Ae−2x+4Axe−2x)+5(Ae−2x−2Axe−2x)+6Axe−2x=3e−2x−4Ae−2x+4Axe−2x+ 5Ae−2x−10Axe−2x+6Axe−2x=3e−2xAe−2x=3e−2x.y″+5y′+6y=3e−2x(−4Ae−2x+4Axe−2x)+5(Ae−2x− 2Axe-2x)+6Axe-2x=3e-2x-4Ae-2x+4Axe-2x+5Ae-2x-10Axe-2x+6Axe-2x=3e-2xAe-2x=3e-2x.
Итак, A=3A=3 и yp(x)=3xe−2x.yp(x)=3xe−2x. Это дает нам следующее общее решение
y(x)=c1e-2x+c2e-3x+3xe-2x.y(x)=c1e-2x+c2e-3x+3xe-2x.
Обратите внимание: если бы xe−2xxe−2x также было решением дополнительного уравнения, нам пришлось бы снова умножать на xx, и мы попытались бы yp(x)=Ax2e−2x.yp(x)=Ax2e−2x.
Стратегия решения проблем
Стратегия решения задач: метод неопределенных коэффициентов
- Решите дополнительное уравнение и запишите общее решение.
- Основываясь на форме r(x),r(x), сделайте начальное предположение для yp(x).yp(x).
- Проверить, является ли какой-либо член предположения для yp(x)yp(x) решением дополнительного уравнения. Если да, умножьте предположение на x.x. Повторяйте этот шаг до тех пор, пока в yp(x)yp(x) не останется членов, решающих дополнительное уравнение.
- Подставьте yp(x)yp(x) в дифференциальное уравнение и приравняйте одинаковые члены, чтобы найти значения неизвестных коэффициентов в yp(x).yp(x).
- Сложите общее решение дополнительного уравнения и только что найденное частное решение, чтобы получить общее решение неоднородного уравнения.
Пример 7.14
Решение неоднородных уравнений
Найдите общие решения следующих дифференциальных уравнений.
- y″−9y=−6cos3xy″−9y=−6cos3x
- х″+2x′+x=4e−tx″+2x′+x=4e−t
- y″−2y′+5y=10×2−3x−3y″−2y′+5y=10×2−3x−3
- y″−3y′=−12ty″−3y′=−12t
Решение
- Дополнительное уравнение y″−9y=0,y″−9y=0 имеет общее решение c1e3x+c2e−3xc1e3x+c2e−3x (шаг 1). Основываясь на форме r(x)=-6cos3x,r(x)=-6cos3x, наше начальное предположение для конкретного решения: yp(x)=Acos3x+Bsin3xyp(x)=Acos3x+Bsin3x (шаг 2). Ни одно из условий в yp(x)yp(x) не решает дополнительное уравнение, так что это правильное предположение (шаг 3).
Теперь мы хотим найти значения для AA и B,B, поэтому подставим ypyp в дифференциальное уравнение. У нас естьyp′(x)=−3Asin3x+3Bcos3xandyp″(x)=−9Acos3x−9Bsin3x,yp′(x)=−3Asin3x+3Bcos3xandyp″(x)=−9Acos3x−9Bsin3x,
, поэтому мы хотим найти значения AA и BB такие, что (Acos3x+Bsin3x)=-6cos3x-18Acos3x-18Bsin3x=-6cos3x.
Следовательно,−18A=−6−18B=0,−18A=−6−18B=0.
Это дает A=13A=13 и B=0,B=0, поэтому yp(x)=(13)cos3xyp(x)=(13)cos3x (шаг 4).
Соединяя все вместе, мы получаем общее решениеy(x)=c1e3x+c2e−3x+13cos3x.y(x)=c1e3x+c2e−3x+13cos3x.
- Дополнительное уравнение x″+2x′+x=0,x″+2x′+x=0 имеет общее решение c1e−t+c2te−tc1e−t+c2te−t (шаг 1). Основываясь на форме r(t)=4e−t,r(t)=4e−t, наше начальное предположение для конкретного решения: xp(t)=Ae−txp(t)=Ae−t (шаг 2). Однако мы видим, что это предположение решает дополнительное уравнение, поэтому мы должны умножить на t,t, что дает новое предположение: xp(t)=Ate-txp(t)=Ate-t (шаг 3). Проверяя это новое предположение, мы видим, что оно тоже решает дополнительное уравнение, поэтому мы должны умножить на t снова, что дает xp(t)=At2e-txp(t)=At2e-t (снова шаг 3). Теперь, проверяя это предположение, мы видим, что xp(t)xp(t) не решает дополнительное уравнение, так что это верное предположение (снова шаг 3).
Теперь мы хотим найти значение для A,A, поэтому подставим xpxp в дифференциальное уравнение. Имеемxp(t)=At2e-t,soxp'(t)=2Ate-t-At2e-txp(t)=At2e-t,soxp'(t)=2Ate-t-At2e-t
и xp ″(t)=2Ae-t-2Ate-t-(2Ate-t-At2e-t)=2Ae-t-4Ate-t+At2e-t.xp″(t)=2Ae-t-2Ate-t-( 2Ate-t-At2e-t)=2Ae-t-4Ate-t+At2e-t.
Подставляя в дифференциальное уравнение, мы хотим найти такое значение AA, что +At2e-t=4e-t2Ae-t=4e-t.x″+2x’+x=4e-t2Ae-t-4Ate-t+At2e-t+2(2Ate-t-At2e-t)+At2e-t= 4e-t2Ae-t=4e-t.
Это дает A=2,A=2, поэтому xp(t)=2t2e-txp(t)=2t2e-t (шаг 4). Собрав все вместе, мы получим общее решениеx(t)=c1e-t+c2te-t+2t2e-t.x(t)=c1e-t+c2te-t+2t2e-t.
- Дополнительное уравнение y″−2y′+5y=0,y″−2y′+5y=0 имеет общее решение c1excos2x+c2exsin2xc1excos2x+c2exsin2x (шаг 1). Основываясь на форме r(x)=10×2−3x−3,r(x)=10×2−3x−3, наше начальное предположение для конкретного решения: yp(x)=Ax2+Bx+Cyp(x)=Ax2+ Bx+C (шаг 2). Ни одно из условий в yp(x)yp(x) не решает дополнительное уравнение, так что это правильное предположение (шаг 3). Теперь нам нужно найти значения для A, A, B, B и C, C, поэтому мы подставляем ypyp в дифференциальное уравнение. У нас есть yp′(x)=2Ax+Byp′(x)=2Ax+B и yp″(x)=2A,yp″(x)=2A, поэтому мы хотим найти значения A,A,B,B , и CC такие, что
y″−2y′+5y=10×2−3x−32A−2(2Ax+B)+5(Ax2+Bx+C)=10×2−3x−35Ax2+(5B−4A)x+(5C−2B+2A)= 10×2−3x−3.y″−2y′+5y=10×2−3x−32A−2(2Ax+B)+5(Ax2+Bx+C)=10×2−3x−35Ax2+(5B−4A)x+(5C− 2В+2А)=10х2-3х-3.
Следовательно,5A=105B−4A=−35C−2B+2A=−3,5A=105B−4A=−35C−2B+2A=−3.
Это дает A=2,A=2,B=1,B=1 и C=−1,C=−1, поэтому yp(x)=2×2+x−1yp(x)=2×2+x− 1 (этап 4). Собрав все вместе, мы получим общее решениеy(x)=c1excos2x+c2exsin2x+2×2+x−1.y(x)=c1excos2x+c2exsin2x+2×2+x−1.
- Дополнительное уравнение y″−3y′=0,y″−3y′=0 имеет общее решение c1e3t+c2c1e3t+c2 (шаг 1). Основываясь на форме r(t)=−12t,r(t)=−12t, наше начальное предположение для конкретного решения: yp(t)=At+Byp(t)=At+B (шаг 2). Однако мы видим, что постоянный член в этом предположении решает дополнительное уравнение, поэтому мы должны умножить на t,t, что дает новое предположение: yp(t)=At2+Btyp(t)=At2+Bt (шаг 3) . Проверяя это новое предположение, мы видим, что ни одно из условий в yp(t)yp(t) не решает дополнительное уравнение, поэтому это верное предположение (снова шаг 3). Теперь нам нужно найти значения для AA и B,B, поэтому мы подставляем ypyp в дифференциальное уравнение. У нас есть yp′(t)=2At+Byp′(t)=2At+B и yp″(t)=2A,yp″(t)=2A, поэтому мы хотим найти такие значения AA и BB, что
y″−3y′=−12t2A−3(2At+B)=−12t−6At+(2A−3B)=−12t.
y″−3y′=−12t2A−3(2At+B)=−12t−6At+ (2А-3В)=-12t.
Следовательно,−6A=−122A−3B=0,−6A=−122A−3B=0.
Это дает A=2A=2 и B=4/3,B=4/3, поэтому yp(t)=2t2+(4/3)typ(t)=2t2+(4/3)t (шаг 4) . Собрав все вместе, мы получим общее решениеy(t)=c1e3t+c2+2t2+43t.y(t)=c1e3t+c2+2t2+43t.
Контрольно-пропускной пункт 7.12
Найдите общее решение следующих дифференциальных уравнений.
- у″−5y′+4y=3exy″−5y′+4y=3ex
- y″+y′−6y=52cos2ty″+y′−6y=52cos2t
Изменение параметров
Иногда r(x)r(x) не является комбинацией полиномов, экспонент или синусов и косинусов. В этом случае метод неопределенных коэффициентов не работает, и приходится использовать другой подход для нахождения частного решения дифференциального уравнения. Мы используем подход, называемый методом вариации параметров.
Чтобы немного упростить наши расчеты, мы собираемся разделить дифференциальное уравнение на a,a, так что у нас есть старший коэффициент 1. Тогда дифференциальное уравнение имеет вид
y″+py′+qy=r(x),y″+py′+qy=r(x),
, где pp и qq — константы.
Если общее решение дополнительного уравнения задается выражением c1y1(x)+c2y2(x),c1y1(x)+c2y2(x), то мы будем искать частное решение вида yp(x)=u (x)y1(x)+v(x)y2(x).yp(x)=u(x)y1(x)+v(x)y2(x). В этом случае мы используем два линейно независимых решения дополнительного уравнения для формирования нашего частного решения. Однако мы предполагаем, что коэффициенты являются функциями x , а не константы. Мы хотим найти функции u(x)u(x) и v(x)v(x) такие, что yp(x)yp(x) удовлетворяет дифференциальному уравнению. У нас есть
yp=uy1+vy2yp′=u′y1+uy1′+v′y2+vy2′yp″=(u′y1+v′y2)′+u′y1′+uy1″+v′y2′+vy2″ .yp=uy1+vy2yp′=u′y1+uy1′+v′y2+vy2′yp″=(u′y1+v′y2)′+u′y1′+uy1″+v′y2′+vy2″ .
Подставляя в дифференциальное уравнение, получаем
yp″+pyp′+qyp=[(u′y1+v′y2)′+u′y1′+uy1″+v′y2′+vy2″]+p[u′y1+uy1′+v′y2 +vy2′]+q[uy1+vy2]=u[y1″+py1′+qy1]+v[y2″+py2′+qy2]+(u′y1+v′y2)′+p(u′y1 +v′y2)+(u′y1′+v′y2′). yp″+pyp′+qyp=[(u′y1+v′y2)′+u′y1′+uy1″+v′y2′ +vy2″]+p[u′y1+uy1′+v′y2+vy2′]+q[uy1+vy2]=u[y1″+py1′+qy1]+v[y2″+py2′+qy2] +(u′y1+v′y2)′+p(u′y1+v′y2)+(u′y1′+v′y2′).
Обратите внимание, что y1y1 и y2y2 являются решениями дополнительного уравнения, поэтому первые два члена равны нулю. Таким образом, у нас есть
(u′y1+v′y2)′+p(u′y1+v′y2)+(u′y1′+v′y2′)=r(x).(u′y1+v′y2)′ +p(u′y1+v′y2)+(u′y1′+v′y2′)=r(x).
Если мы упростим это уравнение, наложив дополнительное условие u′y1+v′y2=0,u′y1+v′y2=0, первые два члена равны нулю, и это сводится к u′y1′+v′y2 ′=r(x).u′y1′+v′y2′=r(x). Итак, при этом дополнительном условии имеем систему двух уравнений с двумя неизвестными:
u’y1+v’y2=0u’y1’+v’y2’=r(x).u’y1+v’y2=0u’y1’+v’y2’=r(x).
Решение этой системы дает нам u′u′ и v′,v′, которые мы можем интегрировать, чтобы найти u и v .
Тогда yp(x)=u(x)y1(x)+v(x)y2(x)yp(x)=u(x)y1(x)+v(x)y2(x) является частным решение дифференциального уравнения. Решение этой системы уравнений иногда бывает сложной задачей, поэтому давайте воспользуемся этой возможностью, чтобы рассмотреть правило Крамера, которое позволяет нам решать систему уравнений с помощью определителей.
Правило: правило Крамера
Система уравнений
a1z1+b1z2=r1a2z1+b2z2=r2a1z1+b1z2=r1a2z1+b2z2=r2
имеет единственное решение тогда и только тогда, когда определитель коэффициентов отличен от нуля. В этом случае решение имеет вид
z1=|r1b1r2b2||a1b1a2b2|andz2=|a1r1a2r2||a1b1a2b2|.z1=|r1b1r2b2||a1b1a2b2|andz2=|a1r1a2r2||a1b1a2b2|.
Пример 7.15
Использование правила Крамера
Используйте правило Крамера для решения следующей системы уравнений.
x2z1+2xz2=0z1-3x2z2=2xx2z1+2xz2=0z1-3x2z2=2x
Решение
Имеем
a1(x)=x2a2(x)=1b1(x)=2xb2(x)=−3x2r1(x)=0r2(x)=2x.a1(x)=x2a2(x)=1b1( х)=2xb2(x)=-3x2r1(x)=0r2(x)=2x.
Тогда
|a1b1a2b2|=|x22x1−3×2|=−3×4−2x|a1b1a2b2|=|x22x1−3×2|=−3×4−2x
и
|r1b1r2b2|=|32x2x −4×2=−4×2.|r1b1r2b2|=|02x2x−3×2|=0−4×2=−4×2.
Таким образом,
z1=|r1b1r2b2||a1b1a2b2|=−4×2−3×4−2x=4x3x3+2.z1=|r1b1r2b2||a1b1a2b2|=−4×2−3×4−2x=4x3x3+2.
Кроме того,
|a1r1a2r2|=|x2012x|=2×3−0=2×3.|a1r1a2r2|=|x2012x|=2×3−0=2×3.
Таким образом,
z2=|a1r1a2r2||a1b1a2b2|=2×3−3×4−2x=−2x23x3+2.z2=|a1r1a2r2||a1b1a2b2|=2×3−3×4−2x=−2x23x3+2.
Контрольно-пропускной пункт 7.13
Используйте правило Крамера, чтобы решить следующую систему уравнений.
2xz1−3z2=0x2z1+4xz2=x+12xz1−3z2=0x2z1+4xz2=x+1
Стратегия решения проблем
Стратегия решения проблем: метод варьирования параметров
- Решите дополнительное уравнение и запишите общее решение
c1y1(x)+c2y2(x).c1y1(x)+c2y2(x).
- Используйте правило Крамера или другой подходящий метод, чтобы найти функции u′(x)u′(x) и v′(x)v′(x), удовлетворяющие
u′y1+v′y2=0u′y1′+v′y2 ′=r(x).
u′y1+v′y2=0u′y1′+v′y2′=r(x). - Интегрируйте u′u′ и v′v′, чтобы найти u(x)u(x) и v(x).v(x). Тогда yp(x)=u(x)y1(x)+v(x)y2(x)yp(x)=u(x)y1(x)+v(x)y2(x) является частным решением к уравнению.
- Сложите общее решение дополнительного уравнения и частное решение, найденное на шаге 3, чтобы получить общее решение неоднородного уравнения.
Пример 7.16
Методом вариации параметров
Найдите общее решение следующих дифференциальных уравнений.
- y″−2y′+y=ett2y″−2y′+y=ett2
- у″+у=3sin2xy″+у=3sin2x
Решение
- Дополнительное уравнение y″−2y′+y=0y″−2y′+y=0 с соответствующим общим решением c1et+c2tet.c1et+c2tet. Следовательно, y1(t)=ety1(t)=et и y2(t)=tet.y2(t)=tet. Вычисляя производные, получаем y1′(t)=ety1′(t)=et и y2′(t)=et+tety2′(t)=et+tet (шаг 1). Затем мы хотим найти функции u′(t)u′(t) и v′(t)v′(t) так, чтобы
u’et+v’tet=0u’et+v'(et+tet)=ett2.
u’et+v’tet=0u’et+v'(et+tet)=ett2.
Применяя правило Крамера, мы имеемu′=|0tetett2et+tet||ettetett+tet|=0−tet(ett2)et(et+tet)−ettet=−e2tte2t=−1tu′=|0tetett2et+tet| |ettetetet+tet|=0−tet(ett2)et(et+tet)−ettet=−e2tte2t=−1t
иv′=|et0etett2||ettetetet+tet|=et(ett2)e2t=1t2( шаг 2).v′=|et0etett2||ettetetet+tet|=et(ett2)e2t=1t2(шаг 2).
Интегрируя, получаемu=−∫1tdt=−ln|t|v=∫1t2dt=−1t(шаг 3).u=−∫1tdt=−ln|t|v=∫1t2dt=−1t(шаг 3).
Тогда у нас естьyp=-etln|t|-1ttet=-etln|t|-et(шаг 4).yp=-etln|t|-1ttet=-etln|t|-et(шаг 4).
Член etet является решением дополнительного уравнения, поэтому нам не нужно явно переносить этот член в наше общее решение. Общее решение:y(t)=c1et+c2tet-etln|t|(шаг 5).y(t)=c1et+c2tet-etln|t|(шаг 5).
- Дополнительное уравнение y″+y=0y″+y=0 с соответствующим общим решением c1cosx+c2sinx.c1cosx+c2sinx. Итак, y1(x)=cosxy1(x)=cosx и y2(x)=sinxy2(x)=sinx (шаг 1). Затем мы хотим найти функции u′(x)u′(x) и v′(x)v′(x) такие, что
u’cosx+v’sinx=0-u’sinx+v’cosx=3sin2x.
u’cosx+v’sinx=0-u’sinx+v’cosx=3sin2x.
Применение правила Cramer, мы имеемU ′ = | 0sinx3sin2xcosx || cosxsinx — sinxcosx | = 0–3sin3xcos2x+sin2x = −3sin3xu ′ = | 0sinx3sin2xcosx || +sinx — ssinxcos ′ = | 0sinx3sin2xcosx || и
v′=|cosx0−sinx3sin2x||cosxsinx−sinxcosx|=3sin2xcosx1=3sin2xcosx(шаг 2).v′=|cosx0−sinx3sin2x||cosxsinx−sinxcosx|=3sin2xcosx1=3sin2xcosx(шаг 2).
Интегрируя сначала, чтобы найти u , мы получаемu=∫−3sin3xdx=−3[−13sin2xcosx+23∫sinxdx]=sin2xcosx+2cosx.u=∫−3sin3xdx=−3[−13x∫xcosx]s+23sin2xcosx] =sin2xcosx+2cosx.
Теперь мы интегрируем, чтобы найти и . Используя подстановку (с w=sinxw=sinx), мы получаемv=∫3sin2xcosxdx=∫3w2dw=w3=sin3x.v=∫3sin2xcosxdx=∫3w2dw=w3=sin3x.
Затемyp=(sin2xcosx+2cosx)cosx+(sin3x)sinx=sin2xcos2x+2cos2x+sin4x=2cos2x+sin2x(cos2x+sin2x)(шаг 4).=2cos2x+sin2x=cos2x+1yp=x+sin2xcosxp=x+sin2xcosx )cosx+(sin3x)sinx=sin2xcos2x+2cos2x+sin4x=2cos2x+sin2x(cos2x+sin2x)(шаг 4).
=2cos2x+sin2x=cos2x+1
Общее решение:y(x)=c1cosx+c2sinx+ 1+cos2x(шаг 5).y(x)=c1cosx+c2sinx+1+cos2x(шаг 5).
Контрольно-пропускной пункт 7.14
Найдите общее решение следующих дифференциальных уравнений.
- y″+y=secxy″+y=secx
- х″−2x′+x=ettx″−2x′+x=ett
Раздел 7.2 Упражнения
Решите следующие уравнения методом неопределенных коэффициентов.
54.
2y″−5y′−12y=62y″−5y′−12y=6
55.
3y″+y′−4y=83y″+y′−4y=8
56.
y″−6y′+5y=e−xy″−6y′+5y=e−x
57.
y″+16y=e−2xy″+16y=e−2x
58.
у″−4y=x2+1y″−4y=x2+1
59.
у″−4y′+4y=8×2+4xy″−4y′+4y=8×2+4x
60.
y″−2y′−3y=sin2xy″−2y′−3y=sin2x
61.
y″+2y′+y=sinx+cosxy″+2y′+y=sinx+cosx
62.
y″+9y=excosxy″+9y=excosx
63.
у″+y=3sin2x+xcos2xy″+y=3sin2x+xcos2x
64.
у″+3y′−28y=10e4xy″+3y′−28y=10e4x
65.
у″+10y′+25y=xe−5x+4y″+10y′+25y=xe−5x+4
В каждой из следующих задач
- Напишите форму частного решения yp(x)yp(x) для метода неопределенных коэффициентов.
- [T] Используйте систему компьютерной алгебры, чтобы найти конкретное решение данного уравнения.
66.
y″−y′−y=x+e−xy″−y′−y=x+e−x
67.
у″−3y=x2−4x+11y″−3y=x2−4x+11
68.
y″−y′−4y=excos3xy″−y′−4y=excos3x
69.
2y″−y′+y=(x2−5x)e−x2y″−y′+y=(x2−5x)e−x
70.
4y″+5y′−2y=e2x+xsinx4y″+5y′−2y=e2x+xsinx
71.
y″−y′−2y=x2exsinxy″−y′−2y=x2exsinx
Решите дифференциальное уравнение, используя либо метод неопределенных коэффициентов, либо вариацию параметров.
72.
y″+3y′−4y=2exy″+3y′−4y=2ex
73.
у″+2y′=e3xy″+2y′=e3x
74.
y″+6y′+9y=e−xy″+6y′+9y=e−x
75.
у″+2y′−8y=6e2xy″+2y′−8y=6e2x
Решить дифференциальное уравнение методом вариации параметров.
76.
4y″+y=2sinx4y″+y=2sinx
77.
у″−9y=8xy″−9y=8x
78.
y″+y=secx,0 79. y″+4y=3csc2x,0 Найдите единственное решение, удовлетворяющее дифференциальному уравнению и заданным начальным условиям, где yp(x)yp(x) — частное решение. 80. y″−2y′+y=12ex,y″−2y′+y=12ex,yp(x)=6x2ex,yp(x)=6x2ex,y(0)=6,y′(0)=0y (0)=6,у'(0)=0 81. y″−7y′=4xe7x,y″−7y′=4xe7x,yp(x)=27x2e7x−449xe7x,yp(x)=27x2e7x−449xe7x,y(0)=−1,y′(0)= 0y(0)=−1,y′(0)=0 82. y″+y=cosx−4sinx,y″+y=cosx−4sinx,yp(x)=2xcosx+12xsinx,yp(x)=2xcosx+12xsinx,y(0)=8,y′(0) =−4y(0)=8,y′(0)=−4 83. y″−5y′=e5x+8e−5x,y″−5y′=e5x+8e−5x,yp(x)=15xe5x+425e−5x,yp(x)=15xe5x+425e−5x,y( 0)=−2,y′(0)=0y(0)=−2,y′(0)=0 В каждой из следующих задач заданы два линейно независимых решения — y1y1 и y2y2, удовлетворяющие соответствующему однородному уравнению. 84. x2y″+2xy′−2y=3x,x2y″+2xy′−2y=3x,y1(x)=x,y2(x)=x−2y1(x)=x,y2(x)=x− 2 85. x2y″−2y=10×2−1,x2y″−2y=10×2−1,y1(x)=x2,y2(x)=x−1y1(x)=x2,y2(x)=x−1 Общее однородное линейное дифференциальное уравнение второго порядка имеет вид Если a ( x ), b ( x ) и c ( x ) фактически являются константами, A ( x ) ≡ A гать 0, B ( x ) ≡ B , C ( x B , C ( x B , C ( x Это общее однородное линейное уравнение второго порядка с постоянными коэффициентами . Теорема А выше утверждает, что общее решение этого уравнения является общей линейной комбинацией любых двух линейно независимых решений. Так как же находятся эти два линейно независимых решения? Следующий пример иллюстрирует основную идею. Пример 1 : решить дифференциальное уравнение Хитрость заключается в подстановке y = e m x ( m константа) в уравнение; Вскоре вы увидите, почему этот подход работает. If y = e mx , then y ′ = me mx and y ″ = m 2 e m x , поэтому дифференциальное уравнение принимает вид Термин e m x может быть вынесен за скобки и немедленно сокращен (поскольку e m x никогда не равняется нулю): Это квадратное полиномиальное уравнение можно решить, разложив на множители: Теперь вспомним, что решение начиналось с записи y = e м x . — это общее решение дифференциального уравнения. Обратите внимание, что решение однородного дифференциального уравнения depends entirely on the roots of the auxiliary polynomial equation that results from substituting y = e mx and then canceling out the e mx term. Как только корни этого вспомогательного полиномиального уравнения найдены, вы можете сразу же записать общее решение данного дифференциального уравнения. Также обратите внимание, что линейное однородное дифференциальное уравнение -го порядка с постоянными коэффициентами всегда приводит к второе вспомогательное полиномиальное уравнение степени, то есть квадратное полиномиальное уравнение. Корни любого квадратного уравнения задаются известной квадратичной формулой Величина под знаком квадратного корня, b 2 – 4 ac , называется дискриминантом уравнения, и ее знак определяет характер корней. Нужно рассмотреть ровно три случая. Случай 1: дискриминант положительный. В этом случае корни действительны и различны. Если два корня обозначены как m 1 и m 2 , то общее решение дифференциального уравнения равно Случай 2: Дискриминант равен нулю. В этом случае корни действительны и идентичны; то есть полиномиальное уравнение имеет двойной (повторный) корень. Если этот двойной корень обозначить просто м , то общее решение дифференциального уравнения равно Случай 3: Дискриминант отрицательный. В этом случае корнями являются различные сопряженные комплексные числа: r ± si . Методом вариации параметров найти частное решение данного неоднородного уравнения. Предположим x > 0 в каждом упражнении. Постоянные коэффициенты
Поскольку значения м теперь найдены м = −1, м = 2), оба являются решениями. Поскольку эти функции линейно независимы (ни одна из них не является постоянным кратным другой), теорема А утверждает, что общая линейная комбинация