Калькулятор определения рационального и иррационального числа онлайн
Найти {$ main.types[data.type] $}
Числитель
Знаменатель
Степень
Число
Результаты расчёта
- Значение: {$ result.value|number $}
- Число рациональное
- Число иррациональное
Используемые нами числа подразделяются на различные множества: натуральные, целые, рациональные, комплексные или действительные. Существует также особый пласт бесконечных непериодических чисел, которые составляют иррациональное множество. Определить категорию выбранного числа можно при помощи онлайн-калькулятора.
Рациональные числа
К множеству рациональных относятся числа, которые можно представить в замкнутом виде, то есть в виде обыкновенной дроби. Такие дроби в числителе содержат целые числа, а в знаменателе — натуральные. К множеству натуральных относятся числа, которые мы используем при счете, к примеру, 1, 5 или 120. Целые числа — это расширенное множество натуральных, к которым добавляется нуль, а также отрицательные элементы, например, -5 или -120. Следовательно, рациональное множество содержит нуль, отрицательные и положительные числа.
К множеству натуральных относятся числа, которые мы используем при счете, к примеру, 1, 5 или 120. Целые числа — это расширенное множество натуральных, к которым добавляется нуль, а также отрицательные элементы, например, -5 или -120. Следовательно, рациональное множество содержит нуль, отрицательные и положительные числа.
Также любое рациональное число можно представить в виде бесконечной периодической десятичной дроби. К примеру, 0,6666… является рациональным, так как представляется в замкнутом виде в форме дроби 2/3, а также является бесконечным и периодичным. Число 0,25 легко записать в виде 1/4, а бесконечность и периодичность легко выразить при помощи нулей — 0,2500000…
Таким образом, любая обыкновенная дробь — рациональное число. Любое число, представленное в замкнутом виде, также рациональное. Однако существует целый спектр чисел, которые невозможно представить в виде дробного соотношения или периодической десятичной дроби.
Иррациональные числа
Иррациональное число — это элемент иррационального множества, которое невозможно представить в виде дроби m/n, где m – целое число, а n – натуральное. Об иррациональности некоторых чисел знали с давних времен: античные геометры определили проблему несоизмеримости стороны квадрата и его диагонали, что соответствует иррациональности корня из 2. Кроме того, древние ученые впервые встретились с проблемой подсчета иррационального числа Пи, которое определяется как соотношение длины окружности к ее диаметру.
Об иррациональности некоторых чисел знали с давних времен: античные геометры определили проблему несоизмеримости стороны квадрата и его диагонали, что соответствует иррациональности корня из 2. Кроме того, древние ученые впервые встретились с проблемой подсчета иррационального числа Пи, которое определяется как соотношение длины окружности к ее диаметру.
На протяжении веков предпринимались попытки представить Пи в замкнутом виде, например как 22/7 или 355/113, однако с течением времени математики определяли Пи все точнее и точнее. Сегодня при помощи мощных компьютеров найдено число Пи с точностью 10 триллионов цифр после запятой. Представить Пи в виде соотношения целых чисел или периодичной десятичной дроби невозможно.
К данному множеству относятся следующие элементы:
- корни неквадратных чисел, например, корни из 2, 3, 5 или 7;
- число Пи и выражение типа pix;
- экспоненциальные выражения типа ex;
- натуральные логарифмы для любых положительных чисел больше 1.

Также к иррациональному множеству относятся различные математические константы, такие как золотое и серебряное сечение, экспонента, постоянная Эйлера — Маскерони или постоянная Апери.
Свойства чисел
Арифметические операции с иррациональными числами могут приводить к разным результатам. Так, действия с рациональными и иррациональными числами всегда приводит к образованию новой иррациональности. Однако арифметические операции с двумя иррациональными элементами могут заканчиваться образованием рациональной дроби.
Например, числа 0,3003000300003 и 0,033033303333 иррациональны. Первое образуется по принципу, что после каждой тройки количество нулей постоянно увеличивается. Второе формируется по принципу увеличения количества троек после каждого нуля. Эти числа невозможно представить в виде обыкновенных дробей по отдельности, однако, если сложить их мы получим следующий результат:
0,3003000300003 + 0,033033303333 = 0,3333333333 = 1/3.
В сухом остатке бесконечная периодичная дробь, которую легко выразить в замкнутом виде.
Наш калькулятор позволяет определить тип числа, которое вы можете выразить в виде обыкновенной дроби или корня любой степени из произвольного числа. Программа мгновенно определит множество, к которому относится выбранный элемент. Давайте попробуем на практике.
Примеры использования калькулятора
Определим рациональность нескольких чисел. Калькулятор предлагает нам задать число в виде правильной дроби, которое по определению является рациональным числом. Поэтому определять иррациональность при помощи калькулятора целесообразно только для чисел, выраженных в виде корняn-ной степени. Определим рациональность для следующих выражений:
- квадратный корень из 2 — 1,414, иррациональное;
- кубический корень 27 — 3, рациональное;
- корень пятой степени из 147 — 2,713, иррациональное.
Очевидно, что в некоторых случаях корни могут быть рациональными, что верно для квадратных и кубических чисел.
Заключение
Математические объекты разделяются на разные классы. В повседневной жизни мы оперируем натуральными числами, то есть целыми и положительными числами, которые используем при счете. Рациональные числа используются при измерениях, а иррациональные практически не находят распространения в быту — область их применения лежит в высокой науке. При помощи нашего онлайн-калькулятора вы можете проверить принадлежность любого числа к определенному множеству.
В повседневной жизни мы оперируем натуральными числами, то есть целыми и положительными числами, которые используем при счете. Рациональные числа используются при измерениях, а иррациональные практически не находят распространения в быту — область их применения лежит в высокой науке. При помощи нашего онлайн-калькулятора вы можете проверить принадлежность любого числа к определенному множеству.
Рациональное число — frwiki.wiki
Представление иррациональных чисел согласно распределению вещественных чисел на рациональные , конструктивные , алгебраические и трансцендентные числа . Щелкните по одному из чисел на диаграмме, чтобы получить дополнительную информацию о выбранном элементе. ( Исходное изображение )
В математике рациональное число — это число, которое можно выразить как частное двух относительных целых чисел . Мы можем написать нецелые рациональные числа в качестве фракции , часто отмечал , где , то числитель , является относительным числом и б , то знаменатель является относительным числом от нуля. вб{\ displaystyle \ textstyle {\ frac {a} {b}}}
Целое число — это рациональное число: его можно выразить дробью формы . вб{\ displaystyle \ textstyle {\ frac {a} {b}}}
Каждое рациональное число может быть записано бесконечным числом различных способов в виде дроби, например 1/2 = 2/4 = 3/6 = . .. но есть привилегированная форма записи: любое ненулевое рациональное число является однозначно выражается в виде дроби, числитель и знаменатель которой взаимно просты с положительным знаменателем . Это выражение называется несократимой дробью .
.. но есть привилегированная форма записи: любое ненулевое рациональное число является однозначно выражается в виде дроби, числитель и знаменатель которой взаимно просты с положительным знаменателем . Это выражение называется несократимой дробью .
Расширение десятичного рационального числа всегда периодическое после определенной знака после запятой (например , в случае конечной десятичной записи, добавление нулей обеспечивает периодичность). Это верно в любой базе . И наоборот, если число имеет периодическое десятичное разложение хотя бы по одному основанию, то это рациональное число.
Действительное число , которое не является рациональным, называется иррациональным . Множество рациональных чисел является коммутативной поле , обозначаемое Q или ℚ (так крещен Пеано в 1895 году после того, как первоначальный итальянского слова quoziente , фактор). По определению:
- Qзнак равно{мнет|(м,нет)∈Z×(Z∖{0})}{\ displaystyle \ mathbb {Q} = \ left \ {\ left. {\ frac {m} {n}} \ right | (m, n) \ in \ mathbb {Z} \ times (\ mathbb {Z} \ setminus \ {0 \}) \ right \}}
где ℤ — кольцо целых относительных чисел.
Резюме
- 1 десятичное разложение
- 2 Рациональная арифметика
- 3 египетская фракция
- 4 Формальная конструкция
- 5 Недвижимость
- 6 Топология
- 6.1 Ограничения
- 7 Число p -адическое
- 8 Ссылка
- 9 См. Также
Десятичное разложение
Как и все действительные числа , рациональные числа допускают представление в неограниченном десятичном расширении . Десятичное развитие рациональных чисел имеет особенность быть периодическим . То есть существует суффикс, состоящий из конечной последовательности непрерывно повторяющихся цифр . Эта последовательность называется «период неограниченного десятичного разложения».
Неограниченное десятичное расширение действительного числа, а тем более рационального числа, является уникальным, если нам не разрешено заканчивать периодической последовательностью, состоящей из «9».
Но также :
- 1знак равно1,0_…знак равно0,9_…знак равно0,99999 …{\ displaystyle 1 = 1 {,} {\ underline {0}} … = 0 {,} {\ underline {9}} … = 0 {,} 99999 …}
Неограниченное десятичное разложение рационального числа является периодическим, и, наоборот, число с периодическим десятичным разложением всегда рационально. Тем не менее этот критерий неудобен для оценки рациональности числа. Второй критерий — непрерывная дробь . Число рационально тогда и только тогда, когда его разложение в цепную дробь конечно. Этот метод в начале первых демонстраций иррациональности базовых е из натурального логарифма и из П .
Таким образом, число (где у нас есть последовательности из «2» все более длинной) иррационально, потому что нет точки. 0,12122122212222 …{\ Displaystyle 0 {,} 12 \, 122 \, 1222 \, 12222 … \,}
Рациональная арифметика
Пусть a, b, c, d — четыре целых числа, причем b и d не равны нулю. {- 1} = {\ frac {b} {a}} {\ mbox {si}} a \ neq 0.}
{- 1} = {\ frac {b} {a}} {\ mbox {si}} a \ neq 0.}
Мы делаем вывод, что коэффициент определяется по формуле:
- (вб)/(противd)знак равновdбпротив.{\ displaystyle \ left ({\ frac {a} {b}} \ right) / \ left ({\ frac {c} {d}} \ right) = {\ frac {ad} {bc}}.}
Египетская фракция
Любое положительное рациональное число может быть выражено как сумма обратных различных натуральных чисел. Например, у нас есть:
- 57знак равно12+16+121 год.{\ displaystyle {\ frac {5} {7}} = {\ frac {1} {2}} + {\ frac {1} {6}} + {\ frac {1} {21}}.}
Формальное строительство
Построение рациональных чисел на столе
Мы можем видеть рациональное число как класс эквивалентности в качестве упорядоченной пары целых чисел следующего соотношения эквивалентности:
- ∀(в,б)∈Z×(Z∖{0})∀(против,d)∈Z×(Z∖{0})(в,б)р(против,d)⟺вdзнак равнобпротив.{\ displaystyle \ forall \ left (a, b \ right) \ in \ mathbb {Z} \ times (\ mathbb {Z} \ setminus \ left \ {0 \ right \}) \ quad \ forall \ left ( c, d \ right) \ in \ mathbb {Z} \ times (\ mathbb {Z} \ setminus \ left \ {0 \ right \}) \ quad (a, b) \, {\ mathcal {R} } \, (c, d) \ Longleftrightarrow ad = bc.
 }
}
Затем отметил , что есть множество рациональных чисел является частным от отношения эквивалентности. Qзнак равно(Z×(Z∖{0}))/р{\ Displaystyle \ mathbb {Q} = {\ big (} \ mathbb {Z} \ times (\ mathbb {Z} \ setminus \ left \ {0 \ right \}) {\ big)} / {\ mathcal {R}}}Z×(Z∖{0}){\ Displaystyle \ mathbb {Z} \ раз (\ mathbb {Z} \ setminus \ left \ {0 \ right \})}
Затем мы можем ввести целые числа в рациональные числа и определить законы внутреннего состава, чтобы получить структуру тела.
Эта конструкция верна для любого целого кольца , тогда мы говорим о поле частных .
Характеристики
Счетность строго положительных рациональных чисел
- Множество ℚ, снабженное приведенными выше законами сложения и умножения, образует коммутативное поле — поле дробей целых чисел.
- Рациональные числа — это наименьшее поле с нулевой характеристикой . Любое другое поле с нулевой характеристикой содержит копию.
- Алгебраическое замыкание на ℚ, то есть поле корней многочленов с рациональными коэффициентами есть множество алгебраических чисел .
 {- n}.}
{- n}.} - С точки зрения диофантова приближения рациональные числа являются наименее аппроксимируемыми действительными числами: подробнее см. « Мера иррациональности ».
- Множество рациональных чисел счетно . Однако с помощью диагонального аргумента Кантора мы знаем, что поле действительных чисел — нет. Затем мы говорим, что действительные числа почти все иррациональны в смысле меры Лебега . Мы говорим, что — незначительное множество . Следующая функция
 {\ displaystyle {\ begin {cases} g (0) = 0 \\ g \ left ({\ dfrac {p} {q}} \ right) = {\ begin {cases} 2g ({\ frac {qp} { p}}), & {\ text {si}} q> p \\ 2g ({\ frac {pq} {q}}) + 1, & {\ text {si}} q \ leq p. \ end { case}} \ end {case}}}
{\ displaystyle {\ begin {cases} g (0) = 0 \\ g \ left ({\ dfrac {p} {q}} \ right) = {\ begin {cases} 2g ({\ frac {qp} { p}}), & {\ text {si}} q> p \\ 2g ({\ frac {pq} {q}}) + 1, & {\ text {si}} q \ leq p. \ end { case}} \ end {case}}}
Топология
Оснащенная топологией обычного порядка , ℚ является топологическим полем . Это означает, что арифметические операции непрерывны. Сложение также совместимо с порядком (мы говорим о упорядоченной группе ).
Ограничения
С другой стороны, ℚ не обладает свойством верхней границы : множество рациональных чисел x таких, что x 2 <2 , увеличивается, но не имеет меньшей верхней границы.
С другой стороны, ℚ не является полным пространством : существуют последовательности Коши рациональных чисел, которые не сходятся к рациональному числу, как последовательность ( x n ), определенная индукцией по методу Герона :
- х 0 = 1
- для всех n натуральных чисел, отличных от нуля: x n +1 =х п/2 + 1/х п.

- |0|пзнак равно0{\ displaystyle | 0 | _ {p} = 0}.
Определенная таким образом функция является полностью мультипликативной , что позволяет без двусмысленности постулировать любое рациональное число : в/б{\ displaystyle a / b}
- |вб|пзнак равно|в|п|б|п{\ displaystyle \ left | {\ frac {a} {b}} \ right | _ {p} = {\ frac {| a | _ {p}} {| b | _ {p}}}}.
Итак, определите метрическое пространство. dп(Икс,у)знак равно|Икс-у|п{\ displaystyle d_ {p} \ left (x, y \ right) = | xy | _ {p}}
Метрическое пространство не является полным, а его завершение этого поля ℚ р из р -адических чисел . Теорема Ostrowski показывает , что любой нетривиальный абсолютное значение ℚ является топологический эквивалентна либо к обычному абсолютному значению или абсолютное значение р -адическому. (Q,dп){\ displaystyle \ left (\ mathbb {Q}, d_ {p} \ right)}
Справка
- ↑ То есть у них число 1 как единственный положительный общий делитель
- ↑ Жан К.
 Боде (2005), Математика и истина. Философия чисел , Париж, изд. L’Harmattan, сб. «Философская увертюра», ( ISBN 978-2-296-39195-6 ) , часть «Но что такое число?» «, Гл. «Наборы цифр», примечание 11, с. 124 : «Набор рациональных чисел обычно обозначается буквой Q. […] Обозначение, предложенное Джузеппе Пеано в 1895 году, из итальянского quoziente (частное). »
Боде (2005), Математика и истина. Философия чисел , Париж, изд. L’Harmattan, сб. «Философская увертюра», ( ISBN 978-2-296-39195-6 ) , часть «Но что такое число?» «, Гл. «Наборы цифр», примечание 11, с. 124 : «Набор рациональных чисел обычно обозначается буквой Q. […] Обозначение, предложенное Джузеппе Пеано в 1895 году, из итальянского quoziente (частное). »
Смотрите также
Штерн-Броко дерево
Числовое понятие | ||
|---|---|---|
| Обычные наборы | Целое число ( ) НЕТ{\ Displaystyle \ scriptstyle \ mathbb {N}} · относительно Целого числа ( ) Z{\ Displaystyle \ scriptstyle \ mathbb {Z}} · Десятичного числа ( ) D{\ Displaystyle \ scriptstyle \ mathbb {D}} · рационального числа ( ) Q{\ Displaystyle \ scriptstyle \ mathbb {Q}} · Фактического ( ) р{\ Displaystyle \ scriptstyle \ mathbb {R}} · Комплексного числа ( )ПРОТИВ{\ Displaystyle \ scriptstyle \ mathbb {C}} | |
| Расширения | Кватерниона ( ) ЧАС{\ Displaystyle \ scriptstyle \ mathbb {H}} · октонионы ( ) О{\ Displaystyle \ scriptstyle \ mathbb {O}} · седенионы ( ) S{\ Displaystyle \ scriptstyle \ mathbb {S}} · Комплексного число развернет · Tessarine · Количество бикомплекс ( ) ПРОТИВ2{\ Displaystyle \ scriptstyle \ mathbb {C} _ {2}} · Числа мультикомплекс ( ПРОТИВнет{\ displaystyle \ scriptstyle \ mathbb {C} _ {n}} · ) · бикватернионных · расщепленные кватернионы · гиперболических кватернионы · октонионы развернуты · Число hypercomplexe · Число р-адический ( ) · Число гиперреальное · Число superréel · Число двойственное · законченное действительное Справа · Число Кардинал · Порядковое число · Число сюрреалистическое · Число псевдореальноеMПРОТИВнет{\ Displaystyle \ scriptstyle {\ mathcal {M}} \ mathbb {C} _ {n}} Qп{\ Displaystyle \ scriptstyle \ mathbb {Q} _ {p}} | |
| Особые свойства | Четность · Номер первое · Номер состоит · Количества фигурного · Номер идеально · Количество положительного · Количество отрицательна · доли диадического · Число иррациональное · Алгебраического Количество · Количество трансцендентный · Количество чисто мнимое · Количество Лиувилля · Период · Количество Нормального · Номер вселенная · Номер здание · Актуально вычислимое · число трансфини · бесконечно малое | |
| Примеры | Пи ( π ) · квадратный корень из двух ( ) · Число золота (φ) · Ноль (0) · Мнимая единица ( i ) · Константа Непер ( e ) · Алеф-ноль (ℵ 0 ) · Табличные математические константы2{\ displaystyle \ scriptstyle {\ sqrt {2}}} | |
| Статьи по Теме | Продажи · Количество · Дробь · Операция · Вычисление · Алгебра · Арифметика · Следующее целое число · бесконечность ( ∞ ) · Значащая цифра | |
<img src=»//fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Рациональные числа — Энциклопедия по экономике
Исходя из указанных соображений, перед построением технологической модели составляется перечень работ (операций), необходимых для достижения поставленной цели. На основе анализа всего перечня операций устанавливается рациональное число работ для составления сетевого графика. В перечень работ необходимо включать и так называемые внешние работы (поставка материалов и оборудования, работы обслуживающих и подсобно-вспомогательных производств и т. д.). [c.40]После установления рационального числа работ в перечне оценивается их трудоемкость, т. е. устанавливается их продолжительность и количество людских и материальных ресурсов, необходимых для выполнения работ. [c.40]
При изменении временных характеристик работ и числа рабочих вахт при помощи таких комплексных графиков можно определить рациональное число рабочих звеньев (вахт) и целесообразность их специализации. [c.67]
[c.67]
Унификация — это процесс установления рационального числа разновидностей строительных конструкций и деталей одинакового функционального назначения. Целью унификации проектных решений является создание такой объемно-планировочной и конструктивной системы зданий и сооружений, которая бы обеспечивала достижение наибольшей эффективности при проектировании, изготовлении изделий, в строительном производстве и эксплуатации. Объектами унификации в строительстве могут быть [c.205]
Особенности организации производственных процессов в газодобыче заключаются в необходимости извлечения газа из недр Земли. При этом газ является безвозмездным даром природы, а следовательно, в газодобывающей промышленности, как и в любой добывающей отрасли, отсутствуют затраты на сырье, что оказывает влияние на структуру, уровень и планирование технико-экономических показателей газодобычи. Например, здесь сырье не является частью себестоимости добычи газа. Влияние природного фактора проявляется и в процессе воздействия на предмет труда (газ в пластовых условиях) необходимость рационального использования и поддержания пластового давления, выбор рационального числа и расстановки скважин для увеличения отдачи пластов и сокращения эксплуатационных расходов, капитальных вложений и приведенных затрат. [c.107]
[c.107]
Более того, при этом можно считать, что компоненты всех векторов и являются рациональными числами. [c.137]
Нормы управляемости Рациональное число работников, закрепленных за одним руководителем на разных уровнях управления [c.23]
Нормы обслуживания Определяет рациональное число рабочих и служащих, закрепленных за одним работником сферы управления [c.23]
Числа целые и дробные составляют множество рациональных чисел Q. Всякое рациональное число выражается отношением двух целых чисел или бесконечной периодической дробью. [c.18]
Рациональное число промежуточных станций, обслуживаемых локомотивом опорной станции, определяется по максимальной величине экономии приведенных затрат Еэк при сопоставлении вари- [c.146]
Самой продолжительной операцией, выполняемой на промышленном железнодорожном транспорте, является операция по погрузке и выгрузке грузов у фронтов предприятия. Оптимальная техническая оснащенность грузовых фронтов, рациональное число подач и вагонов в них оказывает благоприятное влияние на систему организации грузовой работы на подъездных путях предприятия. Многовариантность задачи определения технической оснащенности и числа подач вызвала необходимость в систематизации народнохозяйственных расходов по перемещению вагонов и выполнению с ними грузовых операций. Получение оптимального варианта организации грузовых работ осуществляется в настоящее время путем определения минимальных народнохозяйственных затрат. Использование ЭВМ в решении этой задачи позволяет значительно сократить время вычислительного процесса и его трудоемкость.
[c.241]
Многовариантность задачи определения технической оснащенности и числа подач вызвала необходимость в систематизации народнохозяйственных расходов по перемещению вагонов и выполнению с ними грузовых операций. Получение оптимального варианта организации грузовых работ осуществляется в настоящее время путем определения минимальных народнохозяйственных затрат. Использование ЭВМ в решении этой задачи позволяет значительно сократить время вычислительного процесса и его трудоемкость.
[c.241]
Решением является квадратный корень из двух. Однако такого рационального числа, которое в квадрате было бы равно двум, не существует. Решение — иррациональное число с точностью до десяти знаков после запятой — 1,4142135624. В действительности же ответ имеет бесконечное количество десятичных цифр. [c.374]
Образцовые средства измерений образуют цепочку», во которой передаются размеры единиц измеряемых фактических величие от эталонов к рабочим средствам измерений. Каждый узел» (ступень) этой цепочки получает информацию о размере единицы от предыдущей ступени и передает последующей. Рациональное число ступеней (образцовых средств измерений различной точности), обеспечивающее охват всего парка средств измерений в данной области в зависимости от назначения и условий применений рабочих средств измерений, устанавливается поверочными схемами.
[c.112]
Рациональное число ступеней (образцовых средств измерений различной точности), обеспечивающее охват всего парка средств измерений в данной области в зависимости от назначения и условий применений рабочих средств измерений, устанавливается поверочными схемами.
[c.112]
Согласно действующей терминологии, унификация изделий — это приведение к единообразию на основе определения рационального числа их разновидностей. На стадии проектирования использование в конструкции унифицированных составных частей, а тем более применение деталей и узлов, стандартизованных и изготовленных на специализированном производстве, резко сокращает трудоемкость разработки изделий за счет того, что отпадает необходимость в проведении целого ряда работ в процессе конструкторской и технологической подготовки производства. Величина экономии и номенклатура источников ее получения в значительной степени зависит также и от формы унификации. Иными словами, унифицированное изделие с позиции его распространенности может быть очень разным.
 Во-первых, изделие может быть стандартизованным. В таком случае гарантировано, что оно оптимально по эффективности применения в народном хозяйстве, т. е. обоснованно выбрана или разработана конструкция, оно отработано на технологичность, все данные по изделию имеются в каталогах, на микрофильмах и т. д. Кроме того, стандартизованное изделие во многих случаях можно не изготавливать на данном предприятии, а покупать готовое, созданное в условиях специализированного производства. В конструкциях, как правило, исполь-
[c.131]
Во-первых, изделие может быть стандартизованным. В таком случае гарантировано, что оно оптимально по эффективности применения в народном хозяйстве, т. е. обоснованно выбрана или разработана конструкция, оно отработано на технологичность, все данные по изделию имеются в каталогах, на микрофильмах и т. д. Кроме того, стандартизованное изделие во многих случаях можно не изготавливать на данном предприятии, а покупать готовое, созданное в условиях специализированного производства. В конструкциях, как правило, исполь-
[c.131]До настоящего времени в условиях относительной стабильности функционирования предприятия как системы отчетность базировалась на обычных арифметических операциях над рациональными числами. В условиях убыстряющейся смены ситуаций для предприятий этих средств становится уже недостаточно для того, чтобы в установленной степени выразить неопределенность получаемых прогнозов. Для этого, на наш взгляд, наилучшим из существующих на сегодняшний день математических аппаратов является аппарат теории нечетких (или размытых) множеств или нечетких оценок типа доверительных интервалов. Иллюстрации этих возможностей и посвящаются последующие главы.
[c.37]
Иллюстрации этих возможностей и посвящаются последующие главы.
[c.37]
Натуральные, целые, рациональные числа и их применение в финансовой экономике и исчислении вероятностей [c.1]
Александрова О.В., Вуколова Т.М., Потапов М.К. Натуральные, целые, рациональные числа и их применение в финансовой экономике и исчислении вероятностей. [c.2]
Рациональные числа — это числа вида -, где р — целое, q - [c.10]
Ч натуральное число. Если р > 0, то такие рациональные числа [c.10]
Одно и то же рациональное число г может быть представ- [c.11]
Как уже отмечалось, рациональное число г может быть записано в виде дроби многими способами. Однако среди всех [c.11]
Однако, не всегда имеет решение следующая задача для данного натурального k > 2 и данного положительного г (Е Q найти положительное число р G Q такое, что pfe = г, т.е. не всегда из положительного рационального числа г извлекается рациональный корень степени k.
[c. 13]
13]
Теорема. Не существует рационального числа, квадрат которого равен 2. [c.13]
Для тех, кто знаком с теоремой Пифагора, сделаем следующее замечание. Из приведенного доказательства следует, что диагональ квадрата со стороной 1 не является рациональным числом. Считается, что открытие чисел, не являющихся рациональными, настолько поразило древних греков, что они стали называть их «иррациональными» для разума». [c.14]
Как известно, компьютер может оперировать только с рациональными числами, поскольку для задания иррационального числа в десятичной форме требуется бесконечное число разрядов. Поэтому информацию об относительной важности критериев будем называть машинно реализуемой, если все компоненты- абора векторов, задающих эту информацию, являются рациональными числами. Поскольку всякий вектор из множества Nm задает определенную количественную информацию об относительной важности критериев, то полученный результат в терминах теории относительной важности критериев может быть переформулирован следующим образом. [c.139]
[c.139]
Обоснование рационального числа уровней управления может быть в основном объективизировано, так как предопределено организационно-производственной структурой управляемого объекта. Для современных предприятий характерен уровень общеобъектного руководства производственными единицами и входящими в их состав цехами, участками, бригадами. Высший уровень руководства для предприятия может представлять орган межотраслевого, отраслевого и регионального управления, реже — среднее звено. В исключительных случаях предприятие может подчиняться непосредственно органам общегосударственного управления. В соответствии с этими факторами строится иерархия структуры управления— от первичного звена до высших органов отраслевого и территориального руководства. [c.62]
Научно-методические основы поверочной деятельности по сравнению с другими видами метрологических работ развиты на сегодняшний день наиболее полно. Так, имеются научно обоснованные рекомендации по выбору точностных характеристик средств поверки (см. разд. 3.7), числа и значений поверяемых точек, разработаны принципы автоматизации поверочного оборудования (см. разд. 3.3), выбора рационального числа ступеней поверочных схем, планирования поверочных работ и др. И вместе с тем, имеются еще неиспользованные возможности, внутренние резервы повышения эффективности поверочных работ (их оперативности, экономичности и точности). Общим методологическим приемом решения рассмотренных ниже вопросов, связанных с повышением эффективности поверки, является использование априорной информации о каких-либо свойствах поверяемых средств измерений. Эта информация получается в процессе государственных испытаний средств измерений, содержится в результатах их периодических поверок и, как правило, в настоящее время используется неоправданно мало.
[c.188]
разд. 3.7), числа и значений поверяемых точек, разработаны принципы автоматизации поверочного оборудования (см. разд. 3.3), выбора рационального числа ступеней поверочных схем, планирования поверочных работ и др. И вместе с тем, имеются еще неиспользованные возможности, внутренние резервы повышения эффективности поверочных работ (их оперативности, экономичности и точности). Общим методологическим приемом решения рассмотренных ниже вопросов, связанных с повышением эффективности поверки, является использование априорной информации о каких-либо свойствах поверяемых средств измерений. Эта информация получается в процессе государственных испытаний средств измерений, содержится в результатах их периодических поверок и, как правило, в настоящее время используется неоправданно мало.
[c.188]
Удалось также показать, что Я-экспертоны приобретают особый интерес, когда желательно превратить экспертоны в рациональные числа. [c.109]
Серия брошюр «Математика для нематематиков «составлена на основе известного учебного пособия М. К.Потапова, В.В.Александрова и П.И.Пасиченко «Алгебра, тригонометрия и элементарные функции» и предназначена для желающих поступить в ВУЗ на нематематические специальности. Начинается серия с брошюры «Натуральные, целые, рациональные числа и их применение в финансовой экономике и исчислении вероятностей».
[c.2]
К.Потапова, В.В.Александрова и П.И.Пасиченко «Алгебра, тригонометрия и элементарные функции» и предназначена для желающих поступить в ВУЗ на нематематические специальности. Начинается серия с брошюры «Натуральные, целые, рациональные числа и их применение в финансовой экономике и исчислении вероятностей».
[c.2]
Часто задают вопрос зачем изучать математику На этот вопрос нет универсального ответа кому-то математика нужна, чтобы лучше узнать окружающий мир, а кому-то для прагматической цели — например, чтобы делать успехи в бизнесе. На второй вопрос — какие разделы школьной математики наиболее интересны для приложений на практике — может дать ответ серия брошюр, которая выпускается на базе известного учебного пособия авторов М.К.Потапова, В.В.Александрова, П.И.Пасиченко. Первый выпуск — это брошюра «Натуральные, целые, рациональные числа и их применение в финансовой экономике и исчислении вероятностей». Второй выпуск будет посвящен числовым неравенствам и их применению для анализа элементарных функций. [c.4]
[c.4]
Основной причиной, по которой стали рассматриваться рациональные числа, послужило то, что одно рациональное число всегда можно поделить на другое рациональное число, отлич- [c.11]
Задачи на пропорции и проценты (от латинского pro ento, что означает «от ста» или «сотая доля») возникают естественным образом в кругу задач, связанных с рациональными числами. Равенство двух отношений [c.20]
Сопоставим каждому действительному числу xl некоторое рациональное число г(ж1) такое, что иь(х 2) > г(ж1) > иь(х 1). Заметим, что если хг> хг, то по определению лексикографического упорядочения имеем иь(ж151) > UL(X 2). Кроме того, иь(х 2) > г(ж1) > иь(х 1] и%(ж1, 2) >г(ж1 )>ыь(ж1, 1). [c.30]
Как определить рациональное число? – Обзоры Вики
Рациональное число — это число, которое можно записать в виде отношения. Это означает, что его можно записать в виде дроби, в которой числитель (число вверху) и знаменатель (число внизу) являются целыми числами. Число 8 — рациональное число, потому что его можно записать как дробь 8/1.
Число 8 — рациональное число, потому что его можно записать как дробь 8/1.
Таким образом, является ли 2 рациональным числом? 2 — рациональное число потому что оно удовлетворяет условию рационального числа и может быть записано в форме p/q, что математически представляется как 2/1, где 1≠0.
Как узнать, иррационально это или рационально? Ответ: Если число можно записать или преобразовать в форму p/q, где p и q — целые числа, а q — ненулевое число, то оно называется рациональным, а если его нельзя записать в такой форме, Затем это иррационально.
3 — рациональное число?
Здесь данное число 3 может быть выражено дробью как 3/1. Следовательно, это рациональное число.
IS/- 2 рационально или иррационально? Ранее мы говорили —2 — рациональное число потому что мы можем выразить это как отношение двух целых чисел. π иррационально, потому что нет двух чисел, которые можно разделить и получить ровно 3.141592654… .
Как доказать, что число 2 иррационально? Доказательство того, что корень 2 — иррациональное число.
- Ответ: Учитывая √2.
- Чтобы доказать: √2 — иррациональное число. Доказательство. Предположим, что √2 — рациональное число. Таким образом, это может быть выражено в форме p / q, где p, q — взаимно простые целые числа, а q 0. √2 = p / q. …
- Решение. √2 = p / q. Возводя обе стороны в квадрат, получаем => 2 = (p / q) 2
2.11 — рациональное число?
Ханна; 2.11 — рациональное число, потому что оно десятичное.. Ханна; 2.11 — это конечная десятичная дробь, которую можно записать как 2 11/100. Рациональные числа можно выразить дробями.
Также Что является примером иррационального числа? Иррациональное число – это любое число, которое нельзя записать в виде дроби от целых чисел. Чай число пи и квадратные корни несовершенных квадратов являются примерами иррациональных чисел.
Чай число пи и квадратные корни несовершенных квадратов являются примерами иррациональных чисел.
81 рационально или иррационально?
Интерактивные вопросы
| Правда | |
|---|---|
| Квадратный корень 81 — рациональное число . | TrueTrue — квадратный корень из 81 является рациональным числом. |
| Корень третьей степени из 81 равен 9. | TrueTrue — корень третьей степени из 81 равен 9. |
| 81 — это квадрат 9. | TrueTrue — 81 — это квадрат 9. |
| -9 не является корнем 81. | TrueTrue — -9 не является корнем 81. |
Является ли 5.676677666777 рациональным числом? Да, потому что все целые числа имеют десятичные дроби. Нет, потому что целые числа не имеют десятичных знаков. … Джереми говорит, что 5.676677666777… рациональное число потому что это десятичная дробь, которая продолжается вечно с шаблоном.
Каковы примеры рациональных чисел?
Любое число, которое можно записать в виде дроби с целыми числами, называется рациональным числом. Например, 17 и −34 — рациональные числа. (Обратите внимание, что существует несколько способов записать одно и то же рациональное число в виде отношения целых чисел. Например, 17 и 214 представляют одно и то же рациональное число.)
65.4349224 — рациональное число?
Следовательно, 65.4349224 равно рациональное число.
Сколько иррациональных чисел находится между 1 и 6? Между любыми двумя числами, как бы ни была велика или мала разница между ними, мы имеем бесконечное рациональное а также иррациональные числа. Таким образом, между 1 и 6 у нас также есть бесконечные иррациональные числа. Иррациональные числа в их десятичной форме — это неповторяющиеся и не завершающиеся числа.
Какое число не является иррациональным? Целые являются рациональными числами, но не иррациональными. Все целые числа, будь они положительными, отрицательными или нулевыми, могут быть записаны в виде p/q. Пример: 2, 3 и 5 — рациональные числа, потому что мы можем представить их как 2/1, 3/1 и 5/1.
Пример: 2, 3 и 5 — рациональные числа, потому что мы можем представить их как 2/1, 3/1 и 5/1.
3.14 — рациональное число?
3.14 можно записать в виде дроби двух целых чисел: 314100 и поэтому рационально. π нельзя записать в виде дроби от двух целых чисел.
Является ли 1.5 рациональным числом? 15 и 10 оба целые числа поэтому 1.5 — рациональное число.
0.6 — рациональное число?
0.6 =610 поскольку это может быть записано в виде дроби, это рациональное число.
Является ли 0.5 рациональным числом? Например, 0.5 — рациональное число. Это не целое, натуральное или целое число, но его можно выразить как 1/2, что является долей двух других целых чисел: 1 — числитель, а 2 — знаменатель. Итак, 0.5 или 1/2 — рациональное число.
2 в квадрате — рациональное число?
Поскольку √2 не является целым числом (2 не является полным квадратом), √2 поэтому должно быть иррациональным . Это доказательство можно обобщить, чтобы показать, что любой квадратный корень любого натурального числа, не являющийся полным квадратом, иррационален.
…
Доказательство диофантовыми уравнениями.
| x, y | z | |
|---|---|---|
| Оба странные | Даже | Возможное |
| Один четный, другой нечетный | Странный | Возможное |
Является ли 2 в квадрате иррациональным числом? В частности, греки обнаружили, что диагональ квадрата со стороной в 1 единицу имеет диагональ, длина которой не может быть рациональной. По теореме Пифагора длина диагонали равна квадратному корню из 2. Итак, квадратный корень из 2 иррационален!
Является ли корень 2 действительным числом?
√2 иррационально. Теперь мы знаем, что эти иррациональные числа действительно существуют, и у нас даже есть один пример: √2. Оказывается, что большинство других корней также иррациональны.
Является ли 2 корень 2 рациональным или иррациональным? Таким образом, 2 корень 2 является иррациональное число.
3Положительное рациональное число
№3Положительное
рациональное число. Теорема о существовании
несократимого представителя положительного
рационального числа.
Теорема о существовании
несократимого представителя положительного
рационального числа.
Определение. Рациональным положительным числом называется смежный класс по эквивалентности равносильных дробей, заданный на множестве рациональных чисел .
Любая дробь из класса равносильных дробей определить единственное положительное рациональное число. Например ,класс равносильных дробей -есть положительное рациональное число а. Любая дробь этого класса называется представлением положительного рационального числа. Множество положительных рациональных чисел обозначают через Q.
Несократимая запись рационального числа
Если
рассмотреть множество классов п.р.ч.,то
не трудно заметить,что среди множества
всех представителей какого-либо
положительного рационального числа,можно
выделить такую дробь числитель и
знаменатель которой взаимно-простые
числа. Например,это дробиКаждая
из них является несократимой записью
рационального числа.
Определение. Дробь называеться несократимой ,если числа m и n взаимно-простые.
Определение. Несократимая дробь называется простейшей формой записи рационального числа.
Определение. Рациональное число ,где d(m,n )=1 Л m n,записанное в простейшей форме называется стандартной формой рационального числа.
Теорема.Всякое рациональное положительное число имеет и притом единственного несократимого представителя.
Дано: доказательство проводим в 2 этапа .
1.докажем существование:
Пусть -представитель числа ,то
Возможны два случая:
1) НОД ( m,n)=1
2) НОД ( m,n)1 (
Докажем ,что
По основному свойству дроби :Таким образом ,существует несократимый представитель числа
Докажим единственность методом от противного.Пусть НОД( m,n)=1 и НОД(p.q)=1Проверим делится ли левая часть (*) на n?
Npно НОД( m,n)=1 подставляем в (*)mnk=np
Cокр.на
Аналогично
проверим,делится ли правая часть (*)на
q.
Mqподставим в(*)mq=q1np).
Подставим(***)в (**)1pk=p
m=1pЛ1=1 n=q1Л1=1 | |
p=mkЛ k=1 n=q1Л1 =1 |
Наше предложение, что сушествует два разных несократимых представителя числа неверно-единственный представитель числа a
№4 Положительное рациональное число. Равенство положительных рациональных чисел. Теорема о существовании представителей положительных рациональных чисел с разными значениями
Определение. Рациональным положительным числом называется смежный класс по эквивалентности равносильных дробей, заданный на множестве рациональных чисел .
Любая дробь
из класса равносильных дробей определить
единственное положительное рациональное
число. Например ,класс равносильных
дробей
-есть
положительное рациональное число а. Любая дробь этого класса называется
представлением положительного
рационального числа. Множество
положительных рациональных чисел
обозначают через Q.
Любая дробь этого класса называется
представлением положительного
рационального числа. Множество
положительных рациональных чисел
обозначают через Q.
Определение.(Пример. Докажем ,что ,представляем которого являеться дробь меньше числа b,представителем которого является .
Итак, ;по определению отношения «»во множестве Q,имеем:
Теорема. У любых двух положительных рациональных чисел a и b имеються представители с одинаковыми значениями .
Доказательство:
Имеем
Имеется два случая:
1.n=s теорема доказана
2.nнеобходимость доказать, что существует другие дроби ,у которых общий знаменатель и первая –представитель числа а,вторая –представитель числа b.
Рассмотрим дроби: и .
Докажем ,что Л .
По основному свойству дроби:
Л
№5Положительное
рациональное число. Теорема о существовании
представителей положительных рациональных
чисел с равными числителями
Теорема о существовании
представителей положительных рациональных
чисел с равными числителями
Определение. Рациональным положительным числом называется смежный класс по эквивалентности равносильных дробей, заданный на множестве рациональных чисел .
Любая дробь из класса равносильных дробей определить единственное положительное рациональное число. Например ,класс равносильных дробей -есть положительное рациональное число а. Любая дробь этого класса называется представлением положительного рационального числа. Множество положительных рациональных чисел обозначают через Q.
Теорема. У любых двух положительных рациональных чисел a и b имеются представители с одинаковыми числителями.
Доказательство:
Возможны два случая:
1)m=k
2),необходимость
доказать,что существуют другие дроби,у
которых общий числитель и первая дробь
есть представитель числа а, вторая –
представитель числа b.
Рассмотрим дроби: .
Докажем,что .
По основному свойству дроби, имеем
∧
Иррациональное число — Квадратный Корень
Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби , где — целые числа, . Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. Множество иррациональных чисел обычно обозначается заглавной латинской буквой в полужирном начертании без заливки. Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел. О существовании иррациональных чисел, точнее отрезков, несоизмеримых
с отрезком единичной длины, знали уже древние математики: им была
известна, например, несоизмеримость диагонали и стороны квадрата, что
равносильно иррациональности числа . Свойства
Примеры
Иррациональными являются:
Примеры доказательства иррациональностиКорень из 2Допустим противное: рационален, то есть представляется в виде несократимой дроби , где — целое число, а — натуральное число.
Отсюда следует, что чётно, значит, чётно и . Пускай , где целое. Тогда Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число. Двоичный логарифм числа 3Допустим противное: рационален, то есть представляется в виде дроби , где и — целые числа. Поскольку , и могут быть выбраны положительными. Тогда Но чётно, а нечётно. Получаем противоречие. eСм. раздел «Доказательство иррациональности» в статье «e». ИсторияКонцепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены. Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок.
Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы. Феодор Киренский
доказал иррациональность корней натуральных чисел до 17 (исключая,
естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом,
так как имевшаяся в его инструментарии алгебра не позволяла доказать
иррациональность квадратного корня из 17. Позже Евдокс Книдский
(410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию
пропорций, которая принимала во внимание как рациональные, так и
иррациональные отношения. Это послужило основанием для понимания
фундаментальной сути иррациональных чисел. Величина стала считаться не
числом, но обозначением сущностей, таких как отрезки прямых, углы,
площади, объёмы, промежутки времени — сущностей, которые могут меняться
непрерывно (в современном понимании этого слова). Величины были
противопоставлены числам, которые могут меняться лишь «прыжками» от
одного числа к соседнему, например, с 4 на 5. Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин. Средние векаСредние века ознаменовались принятием таких понятий как ноль,
отрицательные числа, целые и дробные числа, сперва индийскими, затем
китайскими математиками. Позже присоединились арабские математики,
которые первыми стали считать отрицательные числа алгебраическими
объектами (наряду и на равных правах с положительными числами), что
позволило развить дисциплину, ныне называемую алгеброй. Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:
В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:
Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.)
был первым, кто счел приемлемым признать иррациональные числа решением
квадратных уравнений или коэффициентами в уравнениях — в основном, в
виде квадратных или кубических корней, а также корней четвёртой степени.
Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза. Наше времяВ XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер
(1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и
чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные
(доказав при этом существование трансцендентных чисел), тем самым
переосмыслив работы Евклида по классификации иррациональных чисел. Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей. В 1761 году Ламберт показал, что π не может быть рационально, а также что eⁿ иррационально при любом ненулевом рациональном n. | |||||||||||
Как определить рациональные числа?
Метод представления чисел и работы с ними известен как система счисления. Система счисления — это система записи для представления чисел. Это математическая запись, используемая для представления чисел данного набора с помощью цифр или других символов. Он имеет арифметические операции для выполнения деления, умножения, сложения и вычитания между числами. Вот некоторые важные системы счисления:
Система счисления — это система записи для представления чисел. Это математическая запись, используемая для представления чисел данного набора с помощью цифр или других символов. Он имеет арифметические операции для выполнения деления, умножения, сложения и вычитания между числами. Вот некоторые важные системы счисления:
- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
В системе счисления натуральные числа — это числа, которые начинаются с 1 и считаются до бесконечности. Например – (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,12, 13, 14, 15, 16, 17, 18, 19, 20, 21. .……. .∞) — натуральные числа.
.……. .∞) — натуральные числа.
Рациональное число — это число, которое может быть представлено в форме p/q таким образом, что q не равно 0. Множество рациональных чисел включает положительные, отрицательные числа и ноль и обозначается Q. Рациональное число может также выражать в виде дроби.
Когда число выражается в форме p/q или в форме дроби, где и числитель, и знаменатель являются целыми числами, тогда это число называется рациональным числом.
Некоторые примеры рациональных чисел: 1/2, -2/7, 7/10, -7/10, 14/99
Число «0» также является рациональным числом, поскольку мы можем представить его во многих такие формы, как 0/1, 0/2, 0/3 и т. д. Но 1/0, 2/0, 3/0 и т. д. не являются рациональными числами, потому что они дают нам бесконечные значения.
Типы рациональных чиселПримечание: Рациональные числа также могут быть представлены в десятичной форме.
Существуют различные типы рациональных чисел, а именно:
- Натуральные числа: Все натуральные числа являются рациональными числами, потому что они могут быть записаны в форме p/q.
 Подобно 2 можно выразить в форме 2/1 (p/q).
Подобно 2 можно выразить в форме 2/1 (p/q).
Пример – 1, 2, 3, 4, 5 …. и т. д.
- Конечные десятичные дроби: Рациональные числа также могут быть представлены в десятичной форме, потому что десятичные числа могут быть представлены в форме p/q. Например, 1,1 можно записать как 1,1 = 11/10. Таким образом, все конечные десятичные дроби являются рациональными числами.
Пример- (0,45, 0,7120, 0,9778 и т. Д.)
- Непосредственные десятичные дскуималы: Непосредственные десятичные коэффициенты, имеющие неоднократные числа после десятичной точки, такой, как 0,2222 …, 0,121212121212121212121212121212121212121212 гг.… . также являются рациональными числами. Поскольку 0,222… можно записать как 1/2, следовательно, это рациональное число.
Пример – ( 0,22222….., 0,121212…..
и т. д. )
- Дроби: Когда число выражено в форме p/q или в форме дроби, где и числитель, и числитель часть являются целыми числами, то это рациональное число.
Пример – 3/4, 2/7, 7/10, -7/10, 14/99 (все они в форме p/q)
- Целые числа: Все целые числа являются рациональными числами, потому что целые числа могут быть выражены в форме дроби p/q.
Как определить рациональные числа?Пример – 0 является рациональным числом, потому что его можно записать как плавник 0/1, 0/-2,… и т. д.
Примеры вопросовСуществуют некоторые условия для проверки того, является ли число рациональным или нет. Это:
1. Всегда представляется в виде p/q, где q≠0. Например – 3/4 , 2/7, 7/10, -7/10, 0/1 и т. д.
2. Рациональное число можно упростить и представить в десятичной форме.
Например – 0,9, -0,875, 3,25, -2,0 и т. д.
Вопрос 1. Является ли 2,2 рациональным числом?
Ответ:
Да, 2,2 — рациональное число, потому что 2,2 также можно записать в виде p/q, то есть 22/10.
Вопрос 2. Определите, является ли смешанная дробь 1 5/4 рациональным числом или нет?
Ответ:
Простейшая форма смешанной дроби 1 5/4 равна 9/4. Это в форме p/q. Таким образом, 9/4 является рациональным числом.
Вопрос 3. Как определить рациональное число?
Ответ:
Когда число выражается в форме p/q, где p, q — целые числа, а q не равно нулю, тогда оно называется рациональным числом.
Вопрос 4. Является ли 12 рациональным числом?
Ответ:
Да, 13 — рациональное число, потому что оно может быть выражено в виде 12/1, то есть в форме p/q.
Вопрос 5. Является ли 0 рациональным числом?
Ответ:
Да, 0 — рациональное число, потому что это целое число, и его можно записать в форме p/q, например 0/1, 0/2, где b — ненулевое целое число. . Следовательно, 0 — рациональное число.
Вопрос 6. Является ли 1 рациональным числом?
Ответ:
Да, 1 — это рациональное число, потому что оно может быть выражено в виде 1/1, то есть в форме p/q.
Вопрос 7. Какие из следующих рациональных чисел являются положительными?
(i) (-4)/3 (ii) 9/8 (iii) (-14)/(-9) (iv) (-21)/13
Ответ: 93 9/8 — единственное положительное рациональное число.
Примеры и определение рациональных чисел
Рациональные числа — это числа, которые могут быть выражены как частное (результат в обычном уравнении деления) или как простая дробь. Даже если вы представите полученное число не в виде дроби и оно будет повторяться бесконечно, оно все равно может быть рациональным числом. Ноль — рациональное число.
Даже если вы представите полученное число не в виде дроби и оно будет повторяться бесконечно, оно все равно может быть рациональным числом. Ноль — рациональное число.
Примеры рациональных чисел
Реклама
Определение рационального числа
Рациональное число — это любое число, которое удовлетворяет следующим трем критериям:
- Оно может быть представлено в виде простой дроби с числителем (p), деленным на (/) a знаменатель (q).
- И числитель, и знаменатель должны быть правильными целыми числами. Целое число — это то, что мы обычно называем «целым числом», например 3 или 15. Оно может быть положительным или отрицательным.
- Знаменатель (q) не может быть равен нулю.
Любое число, деленное на ноль (т. е. знаменатель которого равен нулю), приближается к бесконечности (или отрицательной бесконечности), но не определено.
Ноль — рациональное число
Имея в виду это объяснение, вы можете понять, что ноль (0) — рациональное число. Это потому, что, хотя есть ограничение на знаменатель («нижнее» число в дроби), нет аналогичного ограничения на числитель («верхнее» число в дроби).
Это потому, что, хотя есть ограничение на знаменатель («нижнее» число в дроби), нет аналогичного ограничения на числитель («верхнее» число в дроби).
Таким образом, если числитель равен нулю (0), а знаменатель — любое ненулевое целое число, результирующее частное равно нулю.
- 0/5 = 0
- 0/200 = 0
- 0/(-25) = 0
Вычисление рациональных чисел
Числа должны удовлетворять только трем требованиям, перечисленным выше, чтобы считаться рациональными числами. Числитель или знаменатель могут быть положительными или отрицательными, если знаменатель не равен нулю.
В таблице ниже показано несколько примеров положительных и отрицательных рациональных чисел. Он показывает взаимосвязь между числителем (p) и знаменателем (q), дробью (p/q) и рациональным числом.
Numerator (p) | Denominator (q) | p / q | Rational Number |
6 | 1 | 6/1 | 6. |
1 | 1 | 666666666196166619000 | |
2 | 3 | 2/3 | 0.667 |
1 | 1000 | 1/1000 | 0.001 |
86 | 34 | 86/34 | 2.529 |
122 | 70 | 122/70 | 1.743 |
353 | 10 | 353/10 | 35.3 |
-2 | 1 | -2/1 | -2.0 |
-5 | 4 | -5/4 | -1. |
You’ll also notice two more вещи о рациональных числах:
- Они могут быть выражены с любым количеством знаков после запятой. Когда вы вычисляете 6/1, результирующее рациональное число 6 также может быть записано как 6,0, 6,00, 6,000 и так далее.
- Рациональные числа могут иметь бесконечное количество десятичных разрядов, если цифры повторяются по предсказуемой схеме. В случае 2/3 на приведенной выше диаграмме показано рациональное число 0,667. Однако истинное число на самом деле имеет «6», повторяющуюся до бесконечности. Вы помещаете горизонтальную полосу (называемую винкулумом) над повторяющимся числом (в данном случае «6»), чтобы обозначить это.
Во второй точке может быть более одной повторяющейся цифры, если она соответствует повторяющемуся шаблону. Например, 123/999 равно 0,123123123… где «123» повторяется до бесконечности. Это по-прежнему рациональное число, поскольку его можно выразить как 123/999, правильную дробь.
Реклама
Рациональные и иррациональные числа
Как и многие другие понятия, как в математике, так и за ее пределами, у рациональных чисел также есть аналог или противоположность. Неудивительно, что этот аналог называется иррациональным числом. Как вы могли догадаться, иррациональное число — это число, которое нельзя представить в виде дроби или частного целого числа.
Хорошо известным примером иррационального числа является пи (π), определяемое как отношение длины окружности к ее диаметру. Обычно он приблизительно равен 3,14, но его истинное значение распространяется на бесконечные десятичные точки без повторяющегося шаблона. Ознакомьтесь с некоторыми примерами иррациональных чисел, чтобы глубже изучить эту математическую концепцию.
- 7 класс
- 8 класс
- 9 класс
- средняя школа
- средняя школа
- колледж
Статьи по теме
Какие существуют типы чисел в математике?
Что такое число? Ответ на этот вопрос может показаться очевидным, но на самом деле существуют разные типы чисел.
 Расширьте свой математический кругозор, изучая различные виды чисел.
Расширьте свой математический кругозор, изучая различные виды чисел.Десятичные разряды: простые примеры для понимания и использования
Возможно, вы уже знаете, что десятичные знаки — это маленькие точки между числами, которые выглядят как точки. Но почему они важны и что они делают? Продолжайте читать, чтобы узнать все о десятичных дробях и десятичных разрядах в малых и больших числах.
Является ли 0 иррациональным или рациональным числом? – Стратегии для родителей
Математика стала проще, чем когда-либо, теперь, когда у нас есть калькуляторы под рукой и в наших телефонах. Но иметь дело с числами, которые что-то значат, легко. Число 0 из-за его множества свойств, безусловно, может поставить многих людей в тупик.
Ноль — рациональное число, потому что это целое число. Целое число — это полное число, не содержащее десятичной дроби или дроби. Рациональные числа также выражаются в числителях и знаменателях, где оба являются равными целыми числами. Поскольку 0 не имеет повторяющегося десятичного знака, это рациональное число.
Поскольку 0 не имеет повторяющегося десятичного знака, это рациональное число.
Многие люди до сих пор боятся таких слов, как целые числа, иррациональные и рациональные числа. Этот страх необоснован. Продолжайте читать, пока мы разбираем самые простые способы понимания рациональных и иррациональных чисел.
Что такое рациональные и иррациональные числа?Рациональное число — это число, которое мы можем записать как отношение двух целых чисел, иначе известное как дробь (источник). Рациональные числа могут быть как положительными, так и отрицательными.
Числа с неповторяющимся десятичным знаком также могут быть рациональными числами. Целые числа, целые числа и совершенные квадратные корни — все это примеры рациональных чисел.
Иррациональные числа — это числа, не являющиеся целыми. Любое число, содержащее непрерывную и неповторяющуюся десятичную точку, например (пи), равное 3,14159…, является иррациональным числом.
Существует несколько тестов и инструментов, с помощью которых можно определить, является ли число рациональным или иррациональным.
Главное в рациональных числах заключается в том, что внутри дроби числитель (верхнее число) и знаменатель (нижнее число) должны быть целыми числами. Рациональные числа сосредоточены не на рациональности, а на слове «отношение».
Типы рациональных чисел
Вы встретите несколько типов чисел, которые могут быть рациональными, включая целые и целые числа, десятичные дроби и дроби.
Целые числа и целые числа
Наиболее простыми типами рациональных чисел являются целые числа. Целые числа иногда называют целыми числами, но они немного отличаются. Целые числа относятся к положительным числам, которые не содержат дроби или десятичной точки. Примеры целых чисел: 1, 15, 3900, 6245 и т. д.
Целые числа, с другой стороны, включают целые числа, а также их отрицательные аналоги. Таким образом, число 3 является одновременно целым числом и целым числом. Число -3 не целое число, а целое (источник).
Дроби
Дроби — это рациональные числа, потому что сама природа рациональных чисел связана с отношениями. Поскольку у дробей есть и числитель, и знаменатель, они являются рациональными числами.
Десятичные числа
Поскольку дробь также может быть записана в виде десятичной дроби, десятичные дроби также являются примером рационального числа. Существенное отличие здесь состоит в том, что десятичная дробь может либо повторяться, либо заканчиваться. Например, дробь 1/3 также может быть представлена как десятичная дробь .3, повторяющаяся.
Другим примером является дробь 9/10, которая также может быть представлена как 0,9 и является конечной десятичной дробью — она не повторяется.
Повторяющееся десятичное число относится к числам после десятичного числа, которые повторяются с тем же числом или с тем же набором чисел до бесконечности (источник).
Это не всегда должно быть первое повторяющееся число после запятой. Например, в дроби 1/11 вы получите повторяющееся десятичное число 0,0
.
Завершающий десятичный знак относится к десятичному знаку, который не повторяется. Признаком этого является то, что число заканчивается на 0. Например, дробь 1/2 представлена как десятичное число 0,50 или 0,5.
Поскольку это ровно половина, его не нужно повторять, и он называется завершающим десятичным числом.
Есть также несколько методов, которые вы можете использовать, чтобы определить, является ли число рациональным или иррациональным — мы рассмотрим эти стратегии далее.
Image by Scott Graham via UnsplashСтратегия 1
Спросите себя: «Является ли число целым числом, целым числом, дробью или содержит повторяющуюся или заканчивающуюся десятичную дробь?»
Если ваш ответ положительный, у вас на руках рациональное число. Хотя этот метод является самым простым, он требует знания некоторых из этих концепций. Если вы не уверены или у вас нет практики, то использование метода тестирования может сработать для вас лучше.
Одна из уловок, которую используют некоторые математики для определения рациональных чисел, — это сила вашего воображения. Обычно вы не связываете воображение с математикой, но математик может сказать, что если число легко представить, то оно, скорее всего, является рациональным числом.
Хотя мы можем считать текстовые задачи школьными понятиями, визуальная концептуализация элементов жизненно важна и очень полезна в математике.
Если представить Джейн с 20 яблоками, а Джона с 15, количественное определение этих чисел как физических объектов облегчит понимание.
В случае с дробями представление 1/2 части пирога, четверти или 1/5 части пирога позволяет вам вычислять в уме простые дроби, а также пробуждает здоровый аппетит к десерту.
Таким образом, любое число или понятие, которое вы можете легко представить, обычно является рациональным числом, потому что никто не думает о 23,4658742 процентах пирога, но вы, конечно, можете представить себе 25 % пирога.
Также легко представить себе пустую тарелку для пирога, и поскольку вы можете представить число 0 как отсутствие числа, 0 является подтвержденным рациональным числом с использованием этого метода.
Стратегия 2
Быстрый способ определить, является ли число рациональным, — это выполнить тест отношения. Мы рассмотрим пример с числом 1.
1 = 1/1 = 23/23 = 4500/4500
Единица является универсальным числом и может быть представлена в бесконечном числе соотношений, так как все они равны единице. Однако этот тест можно повторить с любым целым числом. Если число содержит десятичную дробь, оно не может пройти тест отношения и, следовательно, не будет рациональным числом.
Даже невероятно большие числа могут быть рациональными числами, если они проходят тест на отношение. Пока число используется в качестве числителя над знаменателем «1» и дает точно такой же результат, это рациональное число.
Вот еще несколько примеров:
6/1 34/1 100/1 78600/1
Поскольку все эти числа делятся на 1 и дают тот же результат, что и исходный числитель, все они являются рациональными числами.
При просмотре числителей и знаменателей рационального числа числители могут быть любыми числами, а знаменатели могут быть любыми целыми числами, кроме 0. Поскольку 0/1 по-прежнему равно 0, это подтверждает, что 0 является рациональным числом с использованием этой стратегии (источник) .
Стратегия 3
Другой способ — проверить, является ли квадратный корень совершенным или несовершенным числом. Большинство результатов квадратных корней являются иррациональными числами, но результатом полного квадратного корня является целое число, и, следовательно, это также рациональные числа.
Квадратный корень — это число, которое дает определенный результат при умножении само на себя. Например, 2 — это квадратный корень из 4. Это означает, что если 2 умножить само на себя, вы получите 4, или 2 = √4.
Несколько других примеров идеальных квадратных корней: √1 равно 1, √9равно 3, √16 равно 4, а √25 равно 5.
Поскольку эти числа образуют совершенные целые числа, совершенные квадратные корни являются рациональными числами.
Для сравнения, у других чисел не будет идеальных квадратных корней. Например, √15 равно 3,87298334621 и содержит неповторяющуюся и непрерывную десятичную дробь, что делает его иррациональным числом.
Поскольку √0 равно 0, 0 снова подтверждается как рациональное число с использованием всех трех методов.
Положительные и отрицательные рациональные числа
При обсуждении рациональных чисел есть как положительные, так и отрицательные рациональные числа. Поскольку целые числа обозначают рациональные числа, любая точка на числовой прямой является допустимым рациональным числом (источник).
При обсуждении положительных и отрицательных чисел лучше всего представить эти числа на числовой прямой. Число 0 будет в середине строки, и все положительные числа появятся справа, а все отрицательные числа появятся слева.
Положительные числа возрастают от 1 до 2, затем до 3 и так далее. Конечно, между целыми числами есть место и для десятичных знаков. Отрицательные числа отсчитываются аналогичным образом, от -1 до -2, до -3 и так далее.
Положительные рациональные числа просто выражаются в их нормальной форме как целое, дробное или десятичное число. Отрицательные рациональные числа должны включать знак минус перед числом, чтобы указать его место в числовой строке по сравнению с положительным числом.
Свойства числа 0 Image by Antoine Dautry via UnsplashЭто подводит нас к числу 0. Поскольку 0 означает отсутствие чего-либо, это, вероятно, самая простая для понимания концепция.
Ведутся споры о том, является ли 0 рациональным числом. Поскольку 0 нельзя разделить на 0 или представить как 0/0, некоторые люди утверждают, что это делает его иррациональным числом, поскольку оно не отвечает всем требованиям, предъявляемым к рациональному числу (источник).
Однако Siri саркастически напомнит вам, если вы спросите, чему равно 0, деленное на 0 — представьте, что вы пытаетесь поделиться ноль куки с нолью друзей, нет ни куки, ни друзей. Ноль нельзя разделить на ноль, что делает его скорее неопределимым, чем иррациональным.
Ноль нельзя разделить на ноль, что делает его скорее неопределимым, чем иррациональным.
По теме 0/0 можно ожидать 1 из 3 результатов. Во-первых, если число делится само на себя, оно должно равняться единице, как показано в вычислениях ранее. Во-вторых, 0, деленный на что-либо, все равно должен быть 0. В-третьих, если вы введете 0, разделенный на 0, на калькуляторе, он напомнит вам, что это невозможно вычислить.
Поскольку 0 не является отрицательным числом, это одновременно целое и целое число. Оно может не удовлетворять всем требованиям рационального числа, но оно не отвечает ни одному требованию иррационального числа.
Интересно, что ноль — это число, наиболее интуитивно понятное людям. Это «нет» математического мира. В первые несколько лет нашей академической жизни мы имели дело только с 0 и положительными числами.
Многим учащимся сложно понять концепцию отрицательных чисел, поскольку мы не можем представить число меньше нуля. Ноль также обладает некоторыми другими интересными свойствами. Например, 0 — четное число.
Например, 0 — четное число.
Ноль — это также единственное число, которое не является ни положительным, ни отрицательным, а также это единственное число, кратное всем числам, хотя результатом всегда будет 0.
Ноль также известен как элемент идентичности, что означает, что как только любое число прибавляется к нулю, исходное число является общей суммой. Ноль также не является простым числом или составным числом, так как он не требуется при производстве самого себя.
Ноль также является прилагательным, как и все другие числа, когда они используются для модификации существительного. Но числа, используемые в качестве прилагательных, имеют гораздо большее значение, поэтому вам стоит прочитать «Являются ли числа прилагательными?» чтобы убедиться, что вы всегда правильно используете цифры при письме.
Наконец, если сложить два числа и получить 0, два сложенных числа называются аддитивными инверсиями и противоположностями. Примером этого является -5 + 5 = 0. Только ноль может придать числам такое качество.
Положительные числа и 0 неразрывно связаны с нашим мировоззрением чего-то осязаемого в случае положительных чисел и чего-то неосязаемого и отсутствующего в случае 0.
В то время как положительные числа имеют быть добавленным к чему-то физическому, чтобы сделать их осязаемыми, 0 — это число, которое существует само по себе.
Само это ничтожество делает 0 уникальным и мощным числом во многих областях, от математики до кодирования и электроники. В конечном счете, это может быть самое рациональное число из всех.
Разница между рациональными и иррациональными числами (с таблицей сравнения)
Последнее обновление by Surbhi S
Математика — не что иное, как игра с числами. Число — это арифметическое значение, которое может быть цифрой, словом или символом, указывающим количество, которое имеет множество значений, таких как подсчет, измерения, расчеты, маркировка и т. д. Числа могут быть натуральными числами, целыми числами, целыми числами, действительными числами, комплексными числами. числа. Действительные числа далее делятся на рациональные числа и иррациональные числа. Рациональные числа — это числа, которые являются целыми числами и дробями
д. Числа могут быть натуральными числами, целыми числами, целыми числами, действительными числами, комплексными числами. числа. Действительные числа далее делятся на рациональные числа и иррациональные числа. Рациональные числа — это числа, которые являются целыми числами и дробями
С другой стороны, Иррациональные числа — это числа, выражение которых в виде дроби невозможно. В этой статье мы собираемся обсудить различия между рациональными и иррациональными числами. Взглянуть.
Содержание: Рациональные и иррациональные числа
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Основа для сравнения | Рациональные числа | Иррациональные числа |
|---|---|---|
| Значение | Рациональные числа — это числа, которые могут быть выражены в виде отношения двух целых чисел. | Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. |
| Дробь | Выражается дробью, где знаменатель ≠ 0. | Не может быть выражен дробью. |
| Включает | Идеальные квадраты | Сыр |
| Десятичное расширение | Конечные или повторяющиеся десятичные дроби | Неконечные или неповторяющиеся десятичные дроби. |
Определение рациональных чисел
Термин «отношение» происходит от слова «отношение», которое означает сравнение двух величин, выраженное простой дробью. Число называется рациональным, если его можно записать в виде дроби, такой как p/q, где p (числитель) и q (знаменатель) являются целыми числами, а знаменатель — натуральным числом (ненулевым числом). Целые числа, дроби, включая смешанные дроби, повторяющиеся десятичные дроби, конечные десятичные дроби и т. д. — все это рациональные числа.
Примеры рационального числа
- 1/9 – И числитель, и знаменатель являются целыми числами.
- 7 — может быть выражено как 7/1, где 7 — это частное целых чисел 7 и 1.
- √16 — поскольку квадратный корень можно упростить до 4, что является частным дроби 4/1
- 0,5 — может быть записано как 5/10 или 1/2, и все конечные десятичные дроби рациональны.
- 0.3333333333 — Все повторяющиеся десятичные дроби рациональны.
Определение иррациональных чисел
Число называется иррациональным, если его нельзя упростить до какой-либо доли целого числа (x) и натурального числа (y). Его также можно понимать как иррациональное число. Десятичное расширение иррационального числа не является ни конечным, ни повторяющимся. Он включает в себя surds и специальные числа, такие как π («пи» — наиболее распространенное иррациональное число) и e. Сурд — это несовершенный квадрат или куб, который нельзя уменьшить, чтобы удалить квадратный или кубический корень.
Примеры иррационального числа
- √2 – √2 не может быть упрощено и поэтому иррационально.
- √7/5 – Данное число является дробью, но это не единственный критерий, который можно назвать рациональным числом. И числитель, и знаменатель должны быть целыми числами, а √7 не является целым числом. Следовательно, данное число иррационально.
- 3/0 — Дробь со знаменателем ноль, иррациональна.
- π — поскольку десятичное значение π бесконечно, никогда не повторяется и никогда не показывает какой-либо закономерности. Следовательно, значение числа пи не равно какой-либо дроби. Число 22/7 просто и приблизительно.
- 0,3131131113 — Десятичные дроби не являются ни конечными, ни повторяющимися. Поэтому его нельзя выразить как частное дроби.
Ключевые различия между рациональными и иррациональными числами
Разницу между рациональными и иррациональными числами можно ясно увидеть на следующих основаниях
- Рациональное число определяется как число, которое можно записать в виде отношения двух целых чисел.
 Иррациональное число – это число, которое не может быть выражено в отношении двух целых чисел.
Иррациональное число – это число, которое не может быть выражено в отношении двух целых чисел. - В рациональных числах и числитель, и знаменатель являются целыми числами, где знаменатель не равен нулю. В то время как иррациональное число нельзя записать дробью.
- Рациональное число включает в себя числа, являющиеся полными квадратами, такие как 9, 16, 25 и так далее. С другой стороны, иррациональное число включает такие сурды, как 2, 3, 5 и т. д.
- В рациональное число входят только те десятичные дроби, которые конечны и повторяются. И наоборот, к иррациональным числам относятся те числа, десятичная развертка которых бесконечна, неповторяема и не имеет закономерностей.
Заключение
После рассмотрения вышеизложенного становится совершенно ясно, что выражение рациональных чисел возможно как в дробной, так и в десятичной форме. И наоборот, иррациональное число может быть представлено только в десятичной форме, но не в виде дроби. Все целые числа являются рациональными числами, но все нецелые числа не являются иррациональными числами.
Подготовка к SAT: что такое рациональное число?
Хотя учащимся может и не понадобиться прямо называть рациональные или иррациональные числа на SAT, они будут много работать с обоими этими типами. Действительно, большинство студентов учатся решать сложные задачи, связанные как с рациональными, так и с иррациональными числами, на уроках алгебры, однако многие студенты вскоре забывают разницу между ними.
Что такое рациональное число? Что такое иррациональное число? Какое отношение это имеет к математическому разделу теста SAT? Читайте краткий, но всесторонний обзор.
Что такое рациональные числа?
\(1,2,3,4,5,\) и т. д. — все целые числа, как и \(-1, -2, -3, -4\) и т. д. \(1.23\) – это десятичная дробь, а \(\frac{3}{8}\) – дробь. Все они называются по-разному, но все считаются рациональными числами.
По своей сути рациональное число — это любое число, которое может быть представлено в виде дроби \(\frac{p}{q}\), где числитель \(p\) и знаменатель \(q\) равны ненулевые целые числа (например, \(\frac{p}{q}=\frac{15}{8}, \frac{1}{2}, \frac{200}{3}\)). Обратите внимание, что 1 является целым числом и, следовательно, может быть значением q, поэтому все целые числа являются рациональными числами (например, \(\frac{4}{1}=4\)).
Обратите внимание, что 1 является целым числом и, следовательно, может быть значением q, поэтому все целые числа являются рациональными числами (например, \(\frac{4}{1}=4\)).
Другими примерами рациональных чисел являются десятичные числа с конечными десятичными числами (например, \(3,125=\frac{25}{8}\)) и десятичные числа с повторяющимся шаблоном (например, \(1,33333333333…\)). Это связано с тем, что оба эти типа десятичных дробей могут быть преобразованы в дроби с целым числителем и знаменателем (чтобы узнать больше, прочитайте наш пост: Как преобразовать десятичную дробь в дробь).
Из этого логически следует, что любое число, не подпадающее хотя бы под одну из этих категорий, считается иррациональным числом. Какие числа относятся к иррациональным?
Например, \(\pi\) представляет \(3,1415926535897932384626433832795…\) и так далее. У \(\pi\) нет конечного конца, поэтому это число считается иррациональным.
Точно так же многие квадратные корни, кубические корни и т. д. считаются иррациональными числами, поскольку они также решаются как десятичные числа без конечного конца. \(\sqrt{3}\) является одним из таких примеров, поскольку он равен \(1,7320508075688772935274463415059…\) и так далее.
д. считаются иррациональными числами, поскольку они также решаются как десятичные числа без конечного конца. \(\sqrt{3}\) является одним из таких примеров, поскольку он равен \(1,7320508075688772935274463415059…\) и так далее.
Однако важно отметить, что не все корни являются иррациональными числами. Например, \(\sqrt{16}\) равно \(4\), что является рациональным числом. Следовательно, \(\sqrt{16}\) также считается рациональным числом.
Итак, давайте проведем небольшой тест, чтобы убедиться, что мы правильно поняли эти понятия:
\(3,181818181818\overline{18}\) является рациональным или иррациональным числом?
Ответ: Рациональное число! Десятичные дроби бесконечны, но в этом есть закономерность.
Является ли \(\sqrt{169}\) рациональным или иррациональным числом?
Ответ: рациональное число! \(13\:\cdot\:13 = 169\).
Последний вопрос: является ли число Эйлера \(e\) рациональным или иррациональным числом?
Ответ: иррациональное число! Число Эйлера представляется десятичной дробью без обнаруженного конца. Первые несколько десятичных знаков: \(2,71828182845
Первые несколько десятичных знаков: \(2,71828182845
- 353602874713527…\) Что нужно знать для SAT?
Целые числа, например, \(-3, 5,\) и \(4\).
Дроби вида \(p / q\), где \(p\) и \(q\) — целые числа, например, \(1/2\).

Числа без бесконечных десятичных знаков, например, \(1/4\) от \(0,25\). Их также называют с завершающими десятичными знаками .
Числа с бесконечными десятичными знаками, например, \(1/3\) от \(0,333….., 1,222…..\) и т. д. Они известны как некончающихся десятичных знаков. .
Целые числа.
Проверить тип дроби, если они похожи на дроби или нет.
Преобразовать данную дробь в подобную дробь, если они не равны. Перейдите к шагу 4, если они похожи на дроби.
Найдите наименьшее общее кратное для данных знаменателей. Затем умножьте на эквивалентное число все данные знаменатели, чтобы получить то же значение знаменателя.
Сложите/вычтите числитель, сохранив знаменатель без изменений.
Если возможно, сократите полученные дроби.
Преобразуем все знаменатели в положительные числа, если любой из них отрицательный.

Используйте LCM, чтобы сделать все знаменатели одинаковыми, если они разные.
Сложите/вычтите целые числа в числителе, следуя правилам целых чисел. И оставьте знаменатель как есть.
Упростите рациональное число.
Умножьте числители всех заданных чисел друг на друга.
Умножьте знаменатели всех чисел друг на друга.
Упростите полученную дробь/рациональное число.
Найдите обратную вторую дробь/рациональное число, поменяв местами числитель со знаменателем и наоборот.

Изменить знак деления на умножение после выполнения обратного действия.
Следуйте правилам умножения рациональных чисел и дробей, как указано выше.
Очень немногие вопросы на SAT будут напрямую спрашивать вас, что является рациональным числом, а что нет. Вместо этого вы увидите много рациональных и иррациональных чисел, используемых в разделе SAT Math, и вам нужно будет знать, как их решать, манипулировать и применять.
В частности, вам обычно разрешается оставлять иррациональные числа в том виде, в каком они есть на SAT, и вам не нужно их упрощать или решать. Например, если вам говорят упростить выражение, в котором есть \(\pi\) или \(e\), вы знаете, что не сможете упростить эти две переменные, и ваши ответы должны быть выражаться в виде \(\pi\) или \(e\).
Вот несколько примеров задач SAT, связанных как с рациональными, так и с иррациональными числами.
Источник: SAT Math Practice Problems
1. Какое из следующих чисел в комплексной системе счисления равно \((14-2i)(7+12i)\)? (\(я = \sqrt{-1}\))?
A. \(74\)
\(74\)
B. \(122\)
C. \(74 + 154i\)
D. \(122 + 154i\)
2
2 Ответ: D
3 В этом случае \(i\) является иррациональным числом, потому что \(\sqrt{-1}\) не упрощается до целого числа, конечного десятичного числа или дроби с ненулевыми целыми числами в числителе и знаменателе. Следовательно, вы можете обращаться с \(i\) как с переменной, поскольку вы не можете еще больше упростить ее. 92 = -1\).
Следовательно, приведенное выше выражение можно переписать как: \(98 + 168i − 14i − (−24)\).
Объединение одинаковых членов: \(122 + 154i\).
2. Упростить: \(\frac{\sqrt[3]{81}}{\sqrt[3]{9}}\)
A. \(9\)
B. \(\ sqrt[3]{9}\)
C. \(3\)
D. \(2.08908\)
Ответ: B.
\(\frac{\sqrt[3]{ 81}}{\sqrt[3]{9}}=\sqrt[3]{\frac{81}{9}}\)
\(=\sqrt[3]{9}\)
\(\sqrt[3]{9}\) — бесконечное неповторяющееся десятичное число, иррациональное число. Чтобы наш ответ был чище, мы оставим его как есть. SAT не должен заставлять вас записывать иррациональные числа в десятичной форме, поэтому вы можете оставить их в самой чистой/простой форме.
Чтобы наш ответ был чище, мы оставим его как есть. SAT не должен заставлять вас записывать иррациональные числа в десятичной форме, поэтому вы можете оставить их в самой чистой/простой форме.
Для получения дополнительной информации
Не терпится узнать больше об обзоре концепции CollegeVine и советах по тестированию, чтобы вы могли успешно сдать SAT? Ознакомьтесь с нашими полезными предыдущими сообщениями в блоге:
25 советов и рекомендаций для SAT
30 математических формул SAT, которые необходимо знать
15 самых сложных вопросов по математике SAT
Подготовка к SAT? Загрузите наше бесплатное руководство с нашими 8 советами по освоению SAT.
Хотите знать, как ваш результат SAT влияет на ваши шансы на поступление в школу вашей мечты? Наш бесплатный Chancing Engine не только поможет вам спрогнозировать ваши шансы, но и сообщит вам, как вы выглядите на фоне других претендентов и какие аспекты вашего профиля нужно улучшить. Зарегистрируйте бесплатную учетную запись CollegeVine сегодня по номеру , чтобы получить доступ к нашему Chancing Engine и получить толчок к реализации стратегии обучения в колледже!
Зарегистрируйте бесплатную учетную запись CollegeVine сегодня по номеру , чтобы получить доступ к нашему Chancing Engine и получить толчок к реализации стратегии обучения в колледже!
Рациональные числа и дроби: типы, методы и примеры
Вы готовитесь с вашим другом Максом к экзамену, и вы оба начали обсуждать, как долго вы учились. Макс сказал, что вы оба учились \(3,5\) часа, но вы считаете, что оба учились \(3\) и полчаса \((3\frac{1}{2})\). Но кто из вас прав насчет времени? Если вы оба учились на одинаковую сумму, то почему разница в количестве? Ну, и \(3.5\), и \(3\frac{1}{2}\) одинаковы. Это разные формы чисел. Один в форма рационального числа , а другая в форме дроби .
В этом разделе мы поймем понятие рациональных чисел и дробей и чем они отличаются.
Значение рациональных чисел и дробей
Рациональные числа и дробные числа — это два математических понятия, которые кажутся очень тесно связанными и чаще всего используются взаимозаменяемо. Однако в этом разделе мы познакомим вас со значением рациональных чисел и дробей, а также с различиями в их описании.
Однако в этом разделе мы познакомим вас со значением рациональных чисел и дробей, а также с различиями в их описании.
Рациональные числа — это тип вещественных чисел, которые можно записать как отношение двух целых чисел. Они выражаются в виде \(\frac{p}{q}\).
Обратите внимание, что \(p\) и \(q\) являются целыми числами, а \(q\) ненулевым. Примеры рациональных чисел: \(12, 10/12, 3/10,\) и \(0,5\). Множество рациональных чисел всегда обозначается \(\mathbb{Q}\).
Целые числа — это множество всех положительных, отрицательных чисел и нуля. Они не содержат десятичной или дробной формы.
Дроби — это числа, которые определяют часть или часть любого целого количества, записанного как отношение целых чисел. Они имеют вид \(a / b\), где \(a\) — числитель, а \(b\) — знаменатель.
Обратите внимание, что и числитель, и знаменатель являются целыми числами, а знаменатель не может быть равен нулю. Примеры дробей: \(10/32, 12/10, 4/23,\) и \(6/7\).
Целые числа представляют собой набор натуральных чисел и нуля. Это все положительные целые числа с нулем без какой-либо десятичной, дробной или отрицательной части.
Хотя дроби и рациональные числа выглядят одинаково, они не всегда одинаковы. Поскольку рациональные числа имеют целые числа и содержат отрицательные числа, их нельзя считать дробями. Поскольку дроби не включают отрицательные числа.
Рациональное число
Как определено выше, рациональное число — это тип действительного числа, который выражается в форме \(p/q\), где \(p\) и \(q\) — целые числа, а не равно \(0\). Проще говоря, можно сказать, что любая дробь с ненулевым знаменателем является рациональным числом.
Стандартная форма рациональных чисел выражается так: не имеет общих делителей , кроме одного делимого и делителя, и, следовательно, делитель положителен. Итак, стандартный вид дробей достигается за счет упрощения дробей. Например, \(3/9\) является примером рационального числа, но, кроме того, оно может делиться на \(1/3\). В форме \(1/3\) это считается стандартной формой, поскольку число больше не делится ни на какое число, кроме \(1\) и самого себя.
В форме \(1/3\) это считается стандартной формой, поскольку число больше не делится ни на какое число, кроме \(1\) и самого себя.
Помните, что число, которое вы делите, называется делимым , а число, на которое вы выполняете деление, называется делителем .
Дроби
Математическая концепция дробей используется для описания частей целого . Например, когда мы берем кусок пиццы от целого, мы говорим, что у нас есть его часть. Дроби — это числа, представленные в виде \(\frac{a}{b}\), где \(a\) и \(b\) — целые числа, а \(b\) не равно \(0\).
Дробь с числителем \(0\) равна \(0\), но дробь со знаменателем \(0\) не определена. Дробь обозначается простым «/» в форме \(a/b\), где \(a\), верхнее число называется числителем, а \(b\), нижнее число называется знаменателем. Примеры дробей: \(12/20, 5/6,\) и \(50/100\).
Доли частей круга
Различия между рациональными числами и дробями
Между рациональными числами и дробями существуют существенные различия, и они заключаются в следующем:
Рациональные числа Дробь 1. Рациональные числа имеют вид \(p/q\), где \(p\) и \(q\) — целых чисел .
Рациональные числа имеют вид \(p/q\), где \(p\) и \(q\) — целых чисел . 1. Рациональные числа имеют вид \(a/b\), где \(a\) и \(b\) — целых чисел . 2. Рациональное число имеет положительную и отрицательную форму чисел. 2. Дробь имеет только положительную форму чисел. 3. Рациональные числа нельзя считать дробями. 3. Дробь можно рассматривать как рациональное число. 4. Примеры — \(-3/7, 1/3, 12\) 4. Примеры — \(4/5, 1\frac{2}{5}, 23/6\)
Типы рациональных чисел
Существует несколько типов рациональных чисел, и они следующие:
Типы дробей
Существует довольно много типов дробей. Если мы хотим использовать числитель и знаменатель в качестве основы, их можно рассматривать как три; правильная дробь, смешанная дробь и неправильная дробь. Тем не менее, они подразделяются на различные типы.
Правильная дробь
Правильная дробь – это дробь, у которой числитель меньше знаменателя (числитель < знаменателя). Например, \(3/4\) — правильная дробь.
Смешанная фракция
Смешанные дроби представляют собой комбинации целых чисел и правильных дробей. Они записываются как \(a\frac{m}{n}\), где \(a\) — целое число. Примером смешанной дроби является \(1\frac{2}{5}\).
Они записываются как \(a\frac{m}{n}\), где \(a\) — целое число. Примером смешанной дроби является \(1\frac{2}{5}\).
Неправильная дробь
Неправильная дробь, в отличие от правильной дроби, это дробь, у которой знаменатель меньше числителя. (знаменатель < числитель). Примером является \(4/3\).
Подобные дроби
Подобные дроби — это дроби, имеющие одинаковые знаменатели. Например, \(1/7\) и \(4/7\). Обе дроби здесь имеют тот же знаменатель, что и \(7\), поэтому считаются дробями.
В отличие от дробей
Эти типы дробей отличаются от подобных дробей. Они имеют разные значения в знаменателе. Примером разной дроби являются \(11/13\) и \(4/9\).
Эквивалентная дробь
Две дроби могут считаться эквивалентными после упрощения путем выполнения умножения или деления. они оба дают то же самое. Например, \(2/3\) и \(4/6\) являются эквивалентными дробями, потому что \(4/6\) можно упростить до \(2/3\).
Дроби единиц
Когда числитель дроби равен \(1\), она называется единичной дробью. Примеры: \(1/2\) (половина целого) и \(1/4\) (четверть целого).
Примеры: \(1/2\) (половина целого) и \(1/4\) (четверть целого).
Сложение и вычитание рациональных чисел и дробей
Знаменатель играет важную роль при сложении и умножении рациональных чисел и дробей. Давайте посмотрим, как мы можем выполнять операции сложения и вычитания над рациональными числами и дробями.
Сложение и вычитание дробей
Для сложения и вычитания дробей необходимо выполнить следующие шаги:
Сложение и вычитание рациональных чисел
Мы используем тот же процесс для сложения и вычитания дробей рациональных чисел:
Умножение и деление рациональных чисел и дробей
Умножение и деление рациональных чисел и дробей подчиняются тому же правилу с добавлением правил целых чисел для рациональных чисел.
Умножение рациональных чисел и дробей
Умножение рациональных чисел и дробей осуществляется по заданным правилам:
Помните, что при работе с рациональными числами всегда соблюдайте правила умножения положительных и отрицательных знаков.
Деление рациональных чисел и дробей
Деление рациональных чисел выглядит следующим образом:
Пример с рациональными числами и дробями
Давайте рассмотрим примеры с рациональными числами и дробями.
Определите типы дробей.
1. \(\frac{6}{7}, \frac{4}{7}\)
2. \(2\frac{3}{8}\)
3. \(\frac {12}{9}\)
Решение:
1. Как дробь — так как оба знаменателя одинаковы.
2. Смешанная дробь — Имеет дробь с целым числом.
3. Неправильная дробь — Числитель больше знаменателя.
Разделите рациональное число \(\frac{-3}{10}\) на \(\frac{7}{5}\).
Решение:
Здесь нам нужно выполнить
\[\frac{-3}{10}\div\frac{7}{5}\]
Шаг 1 — Возьмем обратное значение \(\ frac{7}{5}\)
\[\Rightarrow \frac{5}{7}\]
Шаг 2 — Изменение знака деления на умножение после получения обратной величины, которую мы имеем,
\[\ frac{-3}{10}\times \frac{5}{7}\]
Шаг 3 — Теперь мы умножаем числитель обоих чисел друг на друга и то же самое со знаменателями.
\begin{align} \frac{-3}{10}\times \frac{5}{7} &= \frac{-3\times 5}{10\times 7} \\ &=\frac{ -15}{70} \\ \end{align}
Шаг 4 — Теперь сократим полученное рациональное число.
\[\Rightarrow \frac{-15}{70} = \frac{-3}{14}\]
Вычислите данную дробь.
\[\frac{1}{3}+\frac{4}{5}\]
Решение:
Шаг 1 — Здесь обе дроби не похожи на дроби. Итак, мы преобразуем его в подобные дроби.
Шаг 2 — Считаем НОК знаменателей \(3\) и \(5\), чтобы преобразовать данные дроби в одинаковые дроби.
Следовательно, НОК \(3\) и \(5\) равен \(15\).
Шаг 3 — Теперь мы умножаем \(5\) на \(\frac{1}{3}\), чтобы получить знаменатель \(15\). Точно так же мы умножаем \(3\) на \(\frac{4}{5}\) и складываем оба полученных числителя,
\begin{align} \Rightarrow \frac{1\times 5}{3\ раз 5} + \frac{4\times 3}{5\times 3} &= \frac{5}{15}+\frac{12}{15} \\ &=\frac{5+12}{15 } \\ &=\frac{17}{15} \\ \end{align}
Здесь \(\frac{17}{15}\) уже находится в сокращенной форме.
 Чтобы наш ответ был чище, мы оставим его как есть. SAT не должен заставлять вас записывать иррациональные числа в десятичной форме, поэтому вы можете оставить их в самой чистой/простой форме.
Чтобы наш ответ был чище, мы оставим его как есть. SAT не должен заставлять вас записывать иррациональные числа в десятичной форме, поэтому вы можете оставить их в самой чистой/простой форме. Зарегистрируйте бесплатную учетную запись CollegeVine сегодня по номеру , чтобы получить доступ к нашему Chancing Engine и получить толчок к реализации стратегии обучения в колледже!
Зарегистрируйте бесплатную учетную запись CollegeVine сегодня по номеру , чтобы получить доступ к нашему Chancing Engine и получить толчок к реализации стратегии обучения в колледже!  Однако в этом разделе мы познакомим вас со значением рациональных чисел и дробей, а также с различиями в их описании.
Однако в этом разделе мы познакомим вас со значением рациональных чисел и дробей, а также с различиями в их описании.
 В форме \(1/3\) это считается стандартной формой, поскольку число больше не делится ни на какое число, кроме \(1\) и самого себя.
В форме \(1/3\) это считается стандартной формой, поскольку число больше не делится ни на какое число, кроме \(1\) и самого себя. Рациональные числа имеют вид \(p/q\), где \(p\) и \(q\) — целых чисел .
Рациональные числа имеют вид \(p/q\), где \(p\) и \(q\) — целых чисел . Они записываются как \(a\frac{m}{n}\), где \(a\) — целое число. Примером смешанной дроби является \(1\frac{2}{5}\).
Они записываются как \(a\frac{m}{n}\), где \(a\) — целое число. Примером смешанной дроби является \(1\frac{2}{5}\). Примеры: \(1/2\) (половина целого) и \(1/4\) (четверть целого).
Примеры: \(1/2\) (половина целого) и \(1/4\) (четверть целого).



 }
} {- n}.}
{- n}.} {\ displaystyle {\ begin {cases} g (0) = 0 \\ g \ left ({\ dfrac {p} {q}} \ right) = {\ begin {cases} 2g ({\ frac {qp} { p}}), & {\ text {si}} q> p \\ 2g ({\ frac {pq} {q}}) + 1, & {\ text {si}} q \ leq p. \ end { case}} \ end {case}}}
{\ displaystyle {\ begin {cases} g (0) = 0 \\ g \ left ({\ dfrac {p} {q}} \ right) = {\ begin {cases} 2g ({\ frac {qp} { p}}), & {\ text {si}} q> p \\ 2g ({\ frac {pq} {q}}) + 1, & {\ text {si}} q \ leq p. \ end { case}} \ end {case}}}
 Боде (2005), Математика и истина. Философия чисел , Париж, изд. L’Harmattan, сб. «Философская увертюра», ( ISBN 978-2-296-39195-6 ) , часть «Но что такое число?» «, Гл. «Наборы цифр», примечание 11, с. 124 : «Набор рациональных чисел обычно обозначается буквой Q. […] Обозначение, предложенное Джузеппе Пеано в 1895 году, из итальянского quoziente (частное). »
Боде (2005), Математика и истина. Философия чисел , Париж, изд. L’Harmattan, сб. «Философская увертюра», ( ISBN 978-2-296-39195-6 ) , часть «Но что такое число?» «, Гл. «Наборы цифр», примечание 11, с. 124 : «Набор рациональных чисел обычно обозначается буквой Q. […] Обозначение, предложенное Джузеппе Пеано в 1895 году, из итальянского quoziente (частное). »
 Возведём предполагаемое равенство в квадрат:
Возведём предполагаемое равенство в квадрат: 500 гг. до н. э.), пифагорейцу,
который нашёл это доказательство, изучая длины сторон пентаграммы. Во
времена пифагорейцев считалось, что существует единая единица длины,
достаточно малая и неделимая, которая целое число раз входит в любой
отрезок. Однако Гиппас обосновал, что не существует единой единицы
длины, поскольку предположение о её существовании приводит к
противоречию. Он показал, что если гипотенуза равнобедренного
прямоугольного треугольника содержит целое число единичных отрезков, то
это число должно быть одновременно и четным, и нечетным. Доказательство
выглядело следующим образом:
500 гг. до н. э.), пифагорейцу,
который нашёл это доказательство, изучая длины сторон пентаграммы. Во
времена пифагорейцев считалось, что существует единая единица длины,
достаточно малая и неделимая, которая целое число раз входит в любой
отрезок. Однако Гиппас обосновал, что не существует единой единицы
длины, поскольку предположение о её существовании приводит к
противоречию. Он показал, что если гипотенуза равнобедренного
прямоугольного треугольника содержит целое число единичных отрезков, то
это число должно быть одновременно и четным, и нечетным. Доказательство
выглядело следующим образом: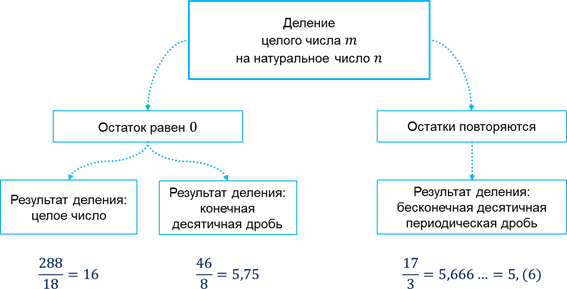
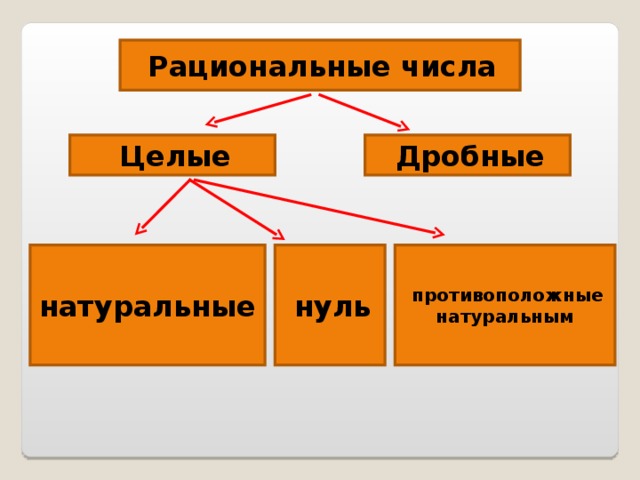 По поводу того, каким могло
быть это доказательство, историками математики было высказано несколько
различных предположений. Согласно наиболее правдоподобному предположению
Жана Итара (1961), оно было основано на пифагорейской теории чётных и
нечётных чисел, в том числе — на теореме о том, что нечётное квадратное
число за вычетом единицы делится на восемь треугольных чисел.
По поводу того, каким могло
быть это доказательство, историками математики было высказано несколько
различных предположений. Согласно наиболее правдоподобному предположению
Жана Итара (1961), оно было основано на пифагорейской теории чётных и
нечётных чисел, в том числе — на теореме о том, что нечётное квадратное
число за вычетом единицы делится на восемь треугольных чисел.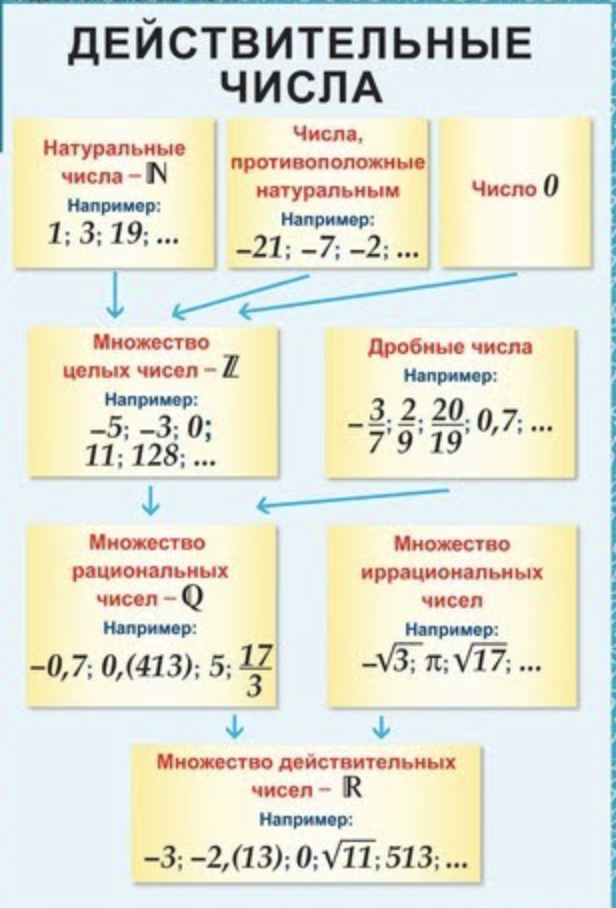 Числа составляются из
наименьшей неделимой величины, в то время как величины можно уменьшать
бесконечно.
Числа составляются из
наименьшей неделимой величины, в то время как величины можно уменьшать
бесконечно.
 Например, квадратные корни чисел таких так 10,
15, 20 — не являющихся квадратами.
Например, квадратные корни чисел таких так 10,
15, 20 — не являющихся квадратами. В X веке иракский математик Аль Хашими вывел общие доказательства (а не
наглядные геометрические демонстрации) иррациональности произведения,
частного и результатов иных математических преобразований над
иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г.
н. э.) приводит следующее определение рациональной и иррациональной
величины:
В X веке иракский математик Аль Хашими вывел общие доказательства (а не
наглядные геометрические демонстрации) иррациональности произведения,
частного и результатов иных математических преобразований над
иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г.
н. э.) приводит следующее определение рациональной и иррациональной
величины:
 По
этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ
начал рассмотрения, схожие с Гейне, именно 1872 год принято считать
годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои
теории при помощи бесконечных рядов, в то время как Дедекинд работал с
(ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
По
этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ
начал рассмотрения, схожие с Гейне, именно 1872 год принято считать
годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои
теории при помощи бесконечных рядов, в то время как Дедекинд работал с
(ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.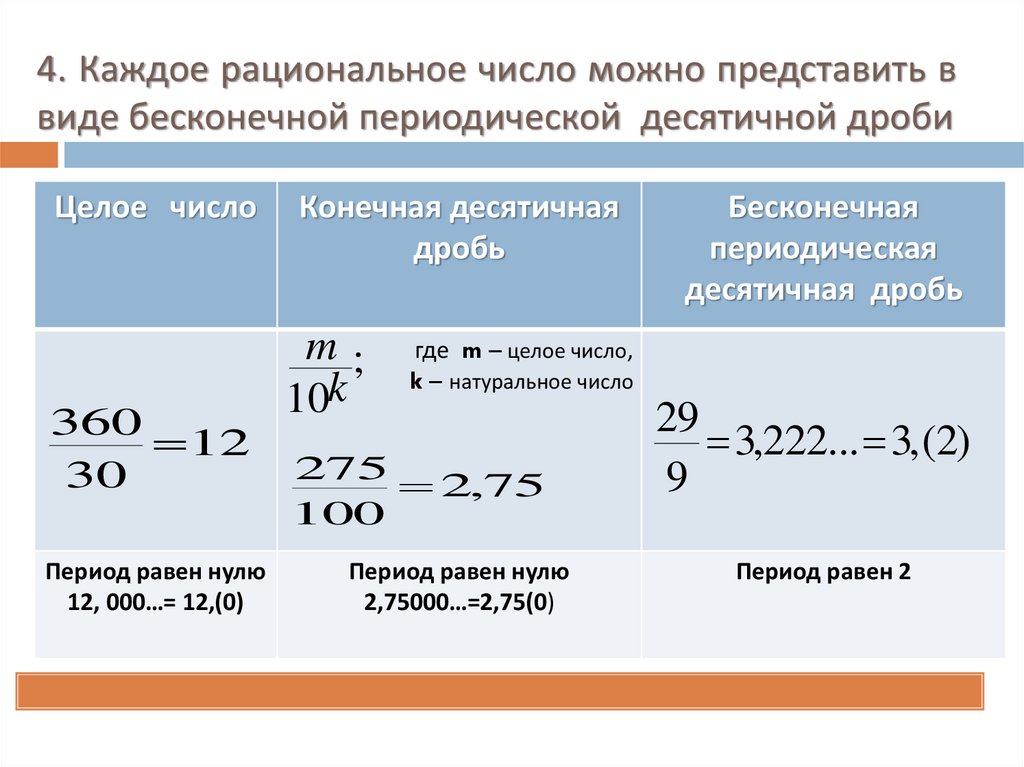 Хотя доказательство Ламберта можно назвать незавершённым, принято
считать его достаточно строгим, особенно учитывая время его написания.
Лежандр в 1794 году, после введения функции Бесселя-Клиффорда, показал,
что π² иррационально, откуда иррациональность π следует тривиально (рациональное число в квадрате дало бы рациональное). Существование трансцендентных чисел было доказано Лиувиллем
в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование,
используя другой метод, и обосновал, что любой интервал вещественного
ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.
Хотя доказательство Ламберта можно назвать незавершённым, принято
считать его достаточно строгим, особенно учитывая время его написания.
Лежандр в 1794 году, после введения функции Бесселя-Клиффорда, показал,
что π² иррационально, откуда иррациональность π следует тривиально (рациональное число в квадрате дало бы рациональное). Существование трансцендентных чисел было доказано Лиувиллем
в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование,
используя другой метод, и обосновал, что любой интервал вещественного
ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом. Подобно 2 можно выразить в форме 2/1 (p/q).
Подобно 2 можно выразить в форме 2/1 (p/q). и т. д. )
и т. д. ) Например – 0,9, -0,875, 3,25, -2,0 и т. д.
Например – 0,9, -0,875, 3,25, -2,0 и т. д.
 000
000 25
25 Расширьте свой математический кругозор, изучая различные виды чисел.
Расширьте свой математический кругозор, изучая различные виды чисел.