Как найти отношение сторон треугольника: Соотношения в треугольнике

Содержание

Как рассчитать соотношение сторон прямоугольника

Статьи › Находится › Известно что стороны прямоугольника находятся в отношении 2 к 22 площадь прямоугольника равна 396

Следовательно, чтобы узнать, чему равна вторая сторона, необходимо отнять от длины первой стороны прямоугольника 5 см: 12 см — 5 см = 7 см. Теперь можно найти отношение сторон прямоугольника. Большая сторона относится к меньшей как 12: 7, a меньшая к большей — как 7: 12.

Как определять соотношение сторон
Как найти сторону прямоугольника зная соотношение сторон
Как найти боковые стороны прямоугольника
Как рассчитать сумму сторон
Что значит соотношение сторон 3 на 4
Что значит соотношение сторон 16 на 9
Как найти стороны прямоугольника если известен периметр и соотношение сторон
Чему равна диагональ прямоугольника стороны которого 5 см и 12 см
Как узнать сторону прямоугольника если известна только площадь
Сколько сторон у прямоугольника
Чему равна диагональ прямоугольника если его стороны 8 см и 15 см
Какие стороны у прямоугольника
Как найти длину другой стороны прямоугольника
Как найти общую длину прямоугольника
Как найти стороны прямоугольника по периметру
Что такое соотношение сторон 20 9
Какие разрешения 21 на 9
Что лучше 16 на 9 или 4 на 3
Как найти одну из сторон треугольника если известен периметр
Что нужно сделать чтобы найти ширину прямоугольника
Как найти периметр прямоугольника если известна площадь и соотношение сторон
Что лучше 16 на 9 или 16 на 10
Как лучше снимать фото в 4:3 или 16:9

Как определять соотношение сторон

Чтобы определить соотношение сторон изображения:

Определите размеры изображения в пикселях. Подробнее.
Вычислите отношение ширины (первое число) к высоте (второе число). Например: Изображения размером 1 600 x 900 пикселей и 3 200 x 1 800 пикселей имеют соотношение сторон 16:9.

Как найти сторону прямоугольника зная соотношение сторон

Если известен периметр и вторая сторона: а = Р/2 — в, где Р — периметр прямоугольника, а — одна сторона прямоугольника, в — вторая сторона прямоугольника; 2.

Как найти боковые стороны прямоугольника

Ответы1:

Периметр нашего прямоугольника делим на 2.
Выражаем одну из сторон прямоугольника.
Составляем уравнение с двумя неизвестными по теореме Пифагора, где нашу диагональ возводим в квадрат.
Подставляем нашу сторону, которую мы выражали раннее во вторую формулу.
Через дискриминант находим ответ.

Как рассчитать сумму сторон

Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Зная любую сторону и площадь:

Поделите площадь на длину известной стороны.
Прибавьте результат к известной стороне.
Умножьте полученное число на два.

Что значит соотношение сторон 3 на 4

Соотношение 4: 3 обычно используется для телевизионных дисплеев, компьютерных мониторов и цифровых камер. На каждые 4 единицы ширины приходится 3 единицы высоты, образуя прямоугольную форму.

Что значит соотношение сторон 16 на 9

Например, соотношение 16:9 может иметь ширину 1600 пикселей на 900 пикселей в высоту. Это может быть 1920 x 1080, 1280 x 720 или любые другие комбинации ширины и высоты, которые можно вычислить, равные 16:9.

Как найти стороны прямоугольника если известен периметр и соотношение сторон

Если известен периметр и одна из сторон прямоугольника, допусти В, находим из формулы сторону А: 2А = Р — 2В; А = (Р — 2В) / 2. Ответ: А = (Р — 2В) / 2.

Чему равна диагональ прямоугольника стороны которого 5 см и 12 см

C = √(a^2 + b^2) = √(12^2 + 5^2) = √(144 + 25) = √169 = 13 см длина диагонали.

Как узнать сторону прямоугольника если известна только площадь

Чтобы найти сторону квадрата, если известна только его площадь, надо извлечь квадратный корень из числа равному площади квадрата или найти число при умножении которого на такое же число получим число равное площади квадрата.

Сколько сторон у прямоугольника

У прямоугольника тоже четыре стороны, но равны только противоположные, параллельные друг другу стороны. Вы знаете ответ на этот вопрос?

Чему равна диагональ прямоугольника если его стороны 8 см и 15 см

C = 17 см. диагональ прямоугольника.

Какие стороны у прямоугольника

Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны. Диагонали любого прямоугольника равны. Стороны прямоугольника являются его высотами. Середины сторон прямоугольника образуют ромб.

Как найти длину другой стороны прямоугольника

P = a + b + a + b = 2a + 2b. Отсюда можно выразить длину стороны а: 2а = P — 2b; а = (P — 2b): 2.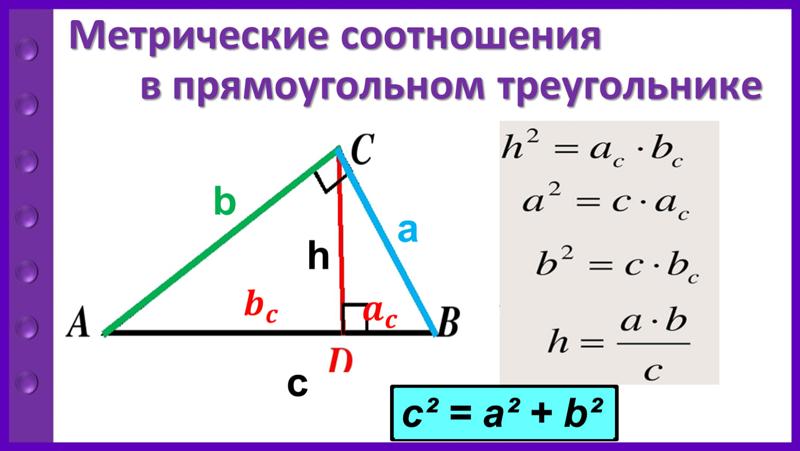

Как найти общую длину прямоугольника

Для того, чтобы найти длину этого прямоугольника нужно из данной величины периметра вычесть две ширины прямоугольника и полученный результат разделить на два.

Как найти стороны прямоугольника по периметру

S = 2(a + b), где а и b — это стороны прямоугольника.

Что такое соотношение сторон 20 9

Одно из наиболее вытянутых по длинной стороне соотношений сторон, встречающееся в современных смартфонах. По ряду причин пользуется значительно большей популярностью, чем схожее по пропорциям 21:9. Разрешение таких дисплеев обычно составляет 1600х720 для стандарта HD (см.

Какие разрешения 21 на 9

Разрешение экрана монитора

Название формата	Количество отображаемых на мониторе точек	Пропорции соотношениям сторон изображения
UWHD	2560 × 1080	64:27 (21:9)
WQXGA (WQHD) (QHD)	2560 × 1440	16:9
WQXGA	2560 × 1600	16:10
QSXGA	2560 × 2048	5:4

Что лучше 16 на 9 или 4 на 3

16: 9 в целом расширяет видимость, а на 4:3 обрезается карта по сторонам, но горизонтальные линии остаются такими же. Поэтому сверху и снизу вы будете наблюдать одинаковую картину на обоих соотношениях.

Как найти одну из сторон треугольника если известен периметр

Периметр равен сумме сторон геометрической фигуры. Таким образом, если известен периметр треугольника Р и две стороны треугольника а и в, то третью сторону с можно найти как разность периметра треугольника и суммы двух других его сторон: с = Р — (а + в).

Что нужно сделать чтобы найти ширину прямоугольника

Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P — 2b) / 2.

Как найти периметр прямоугольника если известна площадь и соотношение сторон

Из условия известно, что площадь прямоугольника равна 18, а отношение соседних сторон равна 1: 2. А найти нам нужно периметр прямоугольника. Для нахождения периметра применим формулу: P = 2(a + b).

Что лучше 16 на 9 или 16 на 10

Модель с соотношением сторон 16:9 меньше модели 16:10 (с аналогичной диагональю) по высоте, но больше по ширине. Для примера сравним два монитора с диагональю 24 дюйма и разным соотношением сторон: 16:9 имеет физические размеры 531 х 298 мм, а 16:10 — 516 х 323 мм.

Как лучше снимать фото в 4:3 или 16:9

Пришло время ответить на самый главный вопрос: какой именно формат стоит выбрать? Дело в том, что однозначный ответ дать нельзя. При соотношении 16:9 длина почти в 2 раза больше ширины. Этот формат полезен, когда «небо» и «земля»в кадре не нужны, а важно то что слева и справа от объекта.

Russian — Соотношение сторон в треугольнике с углами 30-60-90

0:04 — 0:06

Здравствуйте!

0:06 — 0:11

В этом видео я хочу рассмотреть специфический класс треугольников

0:11 — 0:15

(треугольников с углами 30-60-90°).

0:15 — 0:17

Думаю, вы понимаете, почему они так называются

0:17 — 0:24

(т. к. у них углы равны 30, 60 и 90°). Это видео, а именно знания

0:24 — 0:27

о соотношении сторон в треугольнике с углами 30-60-90,

0:27 — 0:31

будут очень полезными для всего, что вы в дальнейшем встретите

0:31 — 0:33

в геометрии и тригонометрии.

0:33 — 0:37

Допустим, что гипотенуза равна х (помните, что гипотенуза –

0:37 — 0:42

это сторона, противолежащая углу в 90°). И мы собираемся доказать,

0:42 — 0:45

что длина самой короткой стороны треугольника

0:45 — 0:51

(которая противолежит углу в 30°) равна х/2 ,

0:51 — 0:55

а длина стороны, противолежащей углу в 60°,

0:55 — 1:00

равна √3, умноженному на длину самой короткой стороны,

1:00 — 1:08

т.е. умноженной на х/2. Это я и хочу доказать в видео. Это будет очень полезно.

1:08 — 1:12

Давайте начнем с треугольника, с которым мы с вами очень хорошо знакомы.

1:12 — 1:17

Нарисую вот такой равносторонний треугольник

1:17 — 1:22

(нарисовать ровно всегда непросто… о, неплохо).

1:22 — 1:29

Назовем его АВС. Надеюсь, что он всё-таки равносторонний, давайте это запишем:

1:29 — 1:33

треугольник АВС равносторонний.

1:33 — 1:37

И это значит, что все его стороны равны между собой.

1:37 — 1:45

Предположим, что длина каждой стороны равна х.

1:45 — 1:50

Эта сторона равна х, эта – х и эта – х.

1:50 — 1:52

Также мы знаем (мы это учили раньше),

1:52 — 1:57

что все углы равностороннего треугольника равны 60°.

1:57 — 2:05

Т.е. этот угол равен 60°, этот и этот тоже равен 60°.

2:05 — 2:09

Теперь я опущу высоту из вершины В к основанию.

2:09 — 2:13

И по определению эта высота будет перпендикулярна основанию.

2:13 — 2:19

Т.е. это прямой угол, и это тоже прямой угол.

2:19 — 2:22

Вообще, довольно легко доказать, что это не только высота,

2:22 — 2:26

перпендикулярная основанию, но и то, что она делит это основание пополам

2:26 — 2:28

(если хотите, можете сами это сделать).

2:28 — 2:33

Т.е. вполне очевидно, что эти два треугольника равны.

2:33 — 2:38

Давайте все же докажем это. Назовем эту точку D.

2:38 — 2:46

Итак, у треугольников АВD и ВDС есть общая сторона,

2:46 — 2:55

она принадлежит им обоим. Также мы знаем, что этот угол равен этому, а этот – этому.

2:55 — 3:04

А мы знаем: если два угла в треугольниках равны, то и их третьи углы также будут равны,

3:04 — 3:06

т.е. этот угол будет равен этому.

3:06 — 3:10

У нас есть много разных признаков равенства треугольников.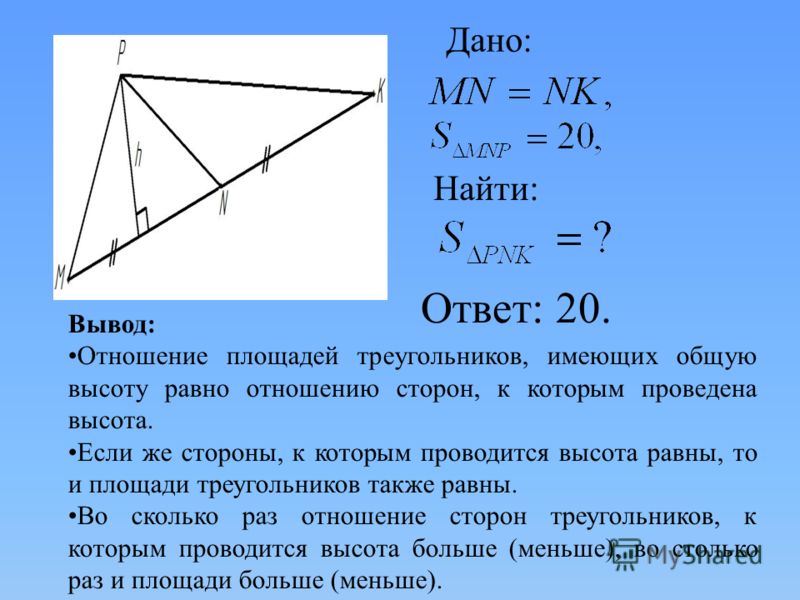

3:10 — 3:12

И здесь мы можем использовать признаки, например,

3:12 — 3:16

«сторона-угол-сторона», «угол-сторона-угол».

3:16 — 3:23

Оба они говорят нам о том, что треугольник АВD равен треугольнику СВD.

3:23 — 3:28

Мы можем использовать либо признак «сторона-угол-сторона», либо «угол-сторона-угол»,

3:28 — 3:32

они доказывают, что соответствующие стороны в этих треугольниках равны.

3:32 — 3:43

В частности, длина стороны АD равна длине стороны СD. АD равно СD,

3:43 — 3:49

это соответствующие стороны. А раз они равны и в сумме дают х,

3:49 — 3:55

значит СD=АD =х/2.

3:55 — 4:01

Теперь, зная это, а также зная, что это высота, что этот угол равен этому

4:01 — 4:10

(и в сумме они составляют 60°), мы можем сказать, что они оба равны по 30°.

4:10 — 4:17

Итак, первый интересный факт о треугольнике с углами 30-60-90 в том, что гипотенуза…

4:17 — 4:27

(напоминаю, что высота разделила наш исходный равносторонний треугольник на два равных треугольника с углами 30-60-90°)… так вот,

4:27 — 4:31

если сторона, противолежащая прямому углу, равна х,

4:31 — 4:38

то сторона, противолежащая углу в 30°, будет равна х/2.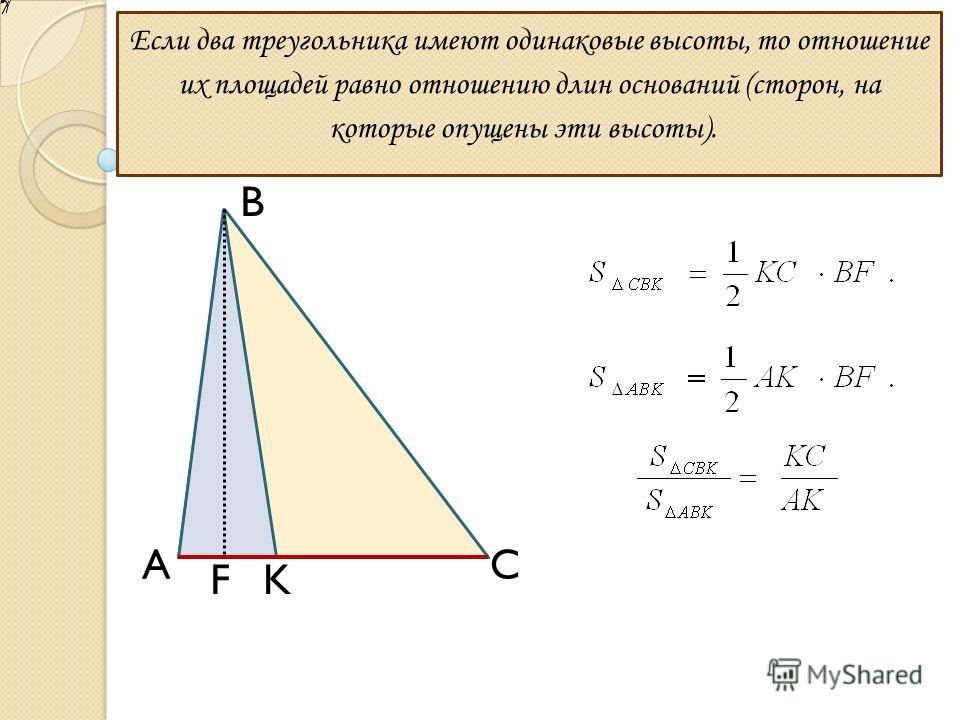

4:38 — 4:41

Здесь, слева, у нас показано то же самое.

4:41 — 4:45

Теперь давайте разберемся со стороной, противолежащей углу в 60°.

4:45 — 4:53

Стороной, противолежащей углу в 60°. Это высота, она у нас называется ВD.

4:53 — 5:01

И мы можем использовать здесь теорему Пифагора: ВD² плюс

5:01 — 5:09

DС², т.е (х/2)² равно гипотенузе в квадрате. Запишем:

5:09 — 5:21

ВD²+(х/2)²=х². Еще раз повторюсь, чтобы окончательно прояснить ситуацию,

5:21 — 5:26

чтобы мы с вами все понимали: мы рассматриваем этот треугольник и используем

5:26 — 5:30

теорему Пифагора (больший катет в квадрате плюс меньший катет в квадрате

5:30 — 5:34

равно гипотенузе в квадрате). Теперь найдем ВD.

5:34 — 5:46

ВD²+х²/4=х². В правой части можно написать 4х²/4,

5:46 — 5:51

т. к. это то же самое, что и х². Теперь, если мы вычтем

5:51 — 6:02

(¼)*х² из обеих частей равенства, то получим: ВD²=3х²/4,

6:02 — 6:28

т.к. (4/4)х²-(1/4)х²=(3/4)*х². Теперь извлечем корень из обеих частей равенства: ВD=((√3)*х)/2. А сторона ВD это и есть сторона, противолежащая углу в 60°,

6:28 — 6:33

вот мы и получили то, что хотели: если гипотенуза равна х,

6:33 — 6:38

то сторона, противолежащая углу в 30° равна х/2,

6:38 — 6:44

а сторона, противолежащая углу в 60°, – (√3/2)*х (или

6:44 — 6:50

((√3)*х)/2 – как вам больше нравится ).

6:50 —

На сегодня всё! До встречи на следующем уроке!

Соотношение углов

для калькулятора треугольников Соотношение углов

для калькулятора треугольников

Как работает калькулятор соотношения углов для треугольника?

Учитывая отношение углов треугольника a:b:c, оно определяет угловые измерения треугольника.
Этот калькулятор имеет 1 вход.

Какая 1 формула используется для расчета соотношения углов в калькуляторе треугольников?

Дан треугольник со сторонами A, B и C, тогда Ax + Bx + Cx = 180.

Дополнительные математические формулы см. в нашем досье по формулам

Какие 4 концепции рассматриваются в калькуляторе отношения углов для калькулятора треугольников?

угол: фигура, образованная двумя лучами, называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла.
Отношение углов треугольника: Величина, выражающая размер каждого угла по отношению ко всем трем углам треугольника
Отношение: указывает, сколько раз одно число содержит другое
треугольник: плоская геометрическая фигура, имеющая три стороны и три угла

Пример расчета соотношения углов для калькулятора треугольников

Соотношение углов треугольника составляет 3:5:7. Какие углы

Электронная почта: [email protected]
Тел: 800-234-2933

Математическая тревога
судоку
Раздор
Информационный бюллетень о недобросовестном преимуществе
Биографии математиков
Подкаст цены за клик
Математические Мемы
Глоссарий по математике
Предметы
бейсбольная математика

Друзья
Спонсоры
Связаться с нами
Вакансии учителя математики
Политика в отношении файлов cookie
политика конфиденциальности
Политика возврата
СМИ

Q7 Стороны треугольника относятся как 3 2 4 Если периметр треугольника равен 27 см, найдите.

Перейти к

Упражнение 11 (А)
Упражнение 11(Б)
Упражнение 11 (С)
Упражнение 11(Г)

Система счисления (закрепление чувства числа)
Оценка
Числа в Индии и международной системе (со сравнением)
Место Значение
Натуральные числа и целые числа (включая шаблоны)
Отрицательные числа и целые числа
Номер строки
HCF и LCM
Игра с числами
Наборы
Соотношение
Доля (включая словесные задачи)
Унитарный метод
Фракции
Десятичные дроби
Процент (Процент)
Представление о скорости, расстоянии и времени
Основные понятия (алгебра)
Основные операции (связанные с алгебраическими выражениями)
Замена (включая использование скобок в качестве группирующих символов)
Обрамление алгебраических выражений (включая вычисление)
Простые (линейные) уравнения (включая текстовые задачи)
Основные понятия (геометрия)
Углы (с их типами)
Свойства углов и линий (включая параллельные линии)
Треугольники (включая типы, свойства и конструкцию)
четырехугольник
Полигоны
Круг
Повторное упражнение по симметрии (включая построения по симметрии)
Распознавание твердых тел
Периметр и площадь плоских фигур
Обработка данных (включая пиктограмму и гистограмму)
Среднее и медиана

Главная > Селина Солюшнс Класс 6 Математика > Глава 11 — Соотношение > Упражнение 11 (С) > Вопрос 7

Вопрос 7 Упражнение 11(C)

В7) Стороны треугольника относятся как 3 : 2 : 4. Если периметр треугольника равен 27 см, найдите длину каждой стороны.

Ответ:

Решение:

Отношение сторон треугольника = 3:2:

Сумма отношений = 3+2+4 = 9

Периметр треугольника = 27см

Длина первой стороны = \frac{27\ times3}{9}=9см

Длина второй стороны = \frac{27\times2}{9}=6см

Длина третьей стороны = \frac{27\times4}{9}=12см

Стенограмма видео

Привет, ребята. Добро пожаловать, Билли. Не делайте сегодня, мы задаем вопрос номер 7, который заключается в том, что стороны треугольника находятся в соотношении 3 к 2 к 4, если периметр треугольника довольно тихий. Враг позади длины каждой стороны. Больше всего за неделю. Я могу умножить все члены этого отношения на яйца, потому что оно всегда кратно чему-то, поэтому его можно записать как 3 X равно 2 на X поднять до 4 следующих шагов, когда вы добавите их все, ваш ответ должен прийти 27, потому что это соотношение стороны и я умножаю его на вещи там, когда вы добавляете сообщество, должно быть 27. Итак, прежде всего, отложите наши проблемы на 5 плюс 4 равно 9фут 9 х равно 27 Следовательно. Ваш бывший будет 27 разделить на 9, если Алексис. Красиво и дают бой по бокам. Таким образом, мы должны умножить 3 на них. Итак, прежде всего три на три — это первый признак зрелости, время на сторону равно 9 и победа над Ирис, которая даст вам шесть сантиметров. И последняя третья сторона — Коридор 3, который даст вам стороны танка. Спасибо вам, ребята. Понравилось видео и подписались на мой канал? Большое спасибо

Связанные вопросы

Q1) рупий. 120 должны быть поделены между Хари и Гопи в соотношении 5:3. Сколько достанется каждой?

Q2) Разделите 72 на соотношение

Q3) Разделите 81 на три части в отношении 2 : 3 : 4.

Q4) Разделите 10 400 рупий между A, B и C в соотношении

Q5) Прибыль в размере 2500 рупий должна быть разделена между тремя лицами в отношении 6 : 9 : 10. Сколько …

Q6) Углы треугольника относятся как 3 : 7 : 8. Найдите наибольший и наименьший углы.

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 11 (a)

Упражнение 11 (b)

Упражнение 11 (c)

Упражнение 11 (d)

Главы

Система (консолидация чувства числа)

Оценка

Числа в Индии и международной системе (со сравнением)

Разрядное значение

Натуральные числа и целые числа (включая шаблоны)

Отрицательные числа и целые числа

Номерная линия

HCF и LCM

Игра с номерами

Наборы

Соотношение

Пропорция (включая задачи Word)

Unitary Method

фракции

Degimal Fracts

процент.

Как найти отношение сторон треугольника: Соотношения в треугольнике | Математика