Прямоугольный треугольник формулы — Математическая шкатулка
mathembox 14 комментариев
Треугольник называется прямоугольным, если у него один из углов является прямым. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая напротив прямого угла, гипотенузой.
Прямоугольный треугольник: основные формулы
- Пусть <A = 30°. Катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы. CB = AB:2.
- Сумма острых углов прямоугольного треугольника равна 90°. <A + <B = 90°.
- Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов. AB2 = AC2 + CB2
Прямоугольный треугольник: формулы площади и проекции
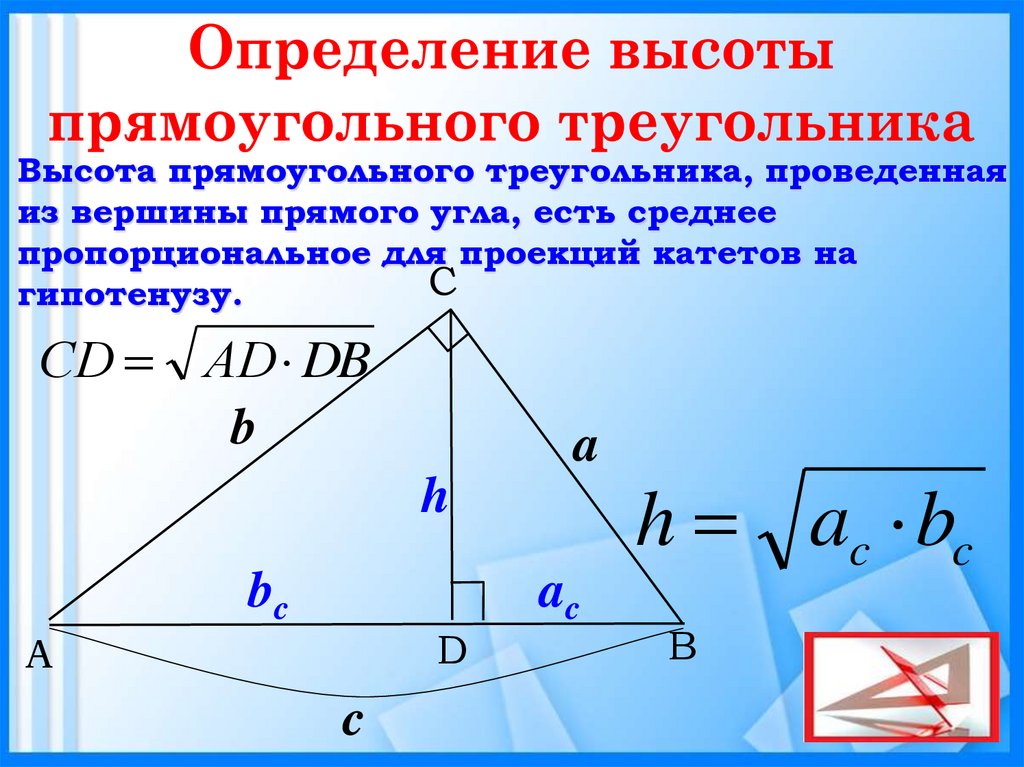
- Высота прямоугольного треугольника, проведенная к гипотенузе, равна : h = (ab):c.
- Высота прямоугольного треугольника, опущенная на гипотенузу, есть среднее пропорциональное между проекциями катетов на гипотенузу: CH2 = AH·BH.

- Катет прямоугольного треугольника — среднее пропорциональное или среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу: CA2 = AB·AH; CB2 = AB·BH.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна ее половине.
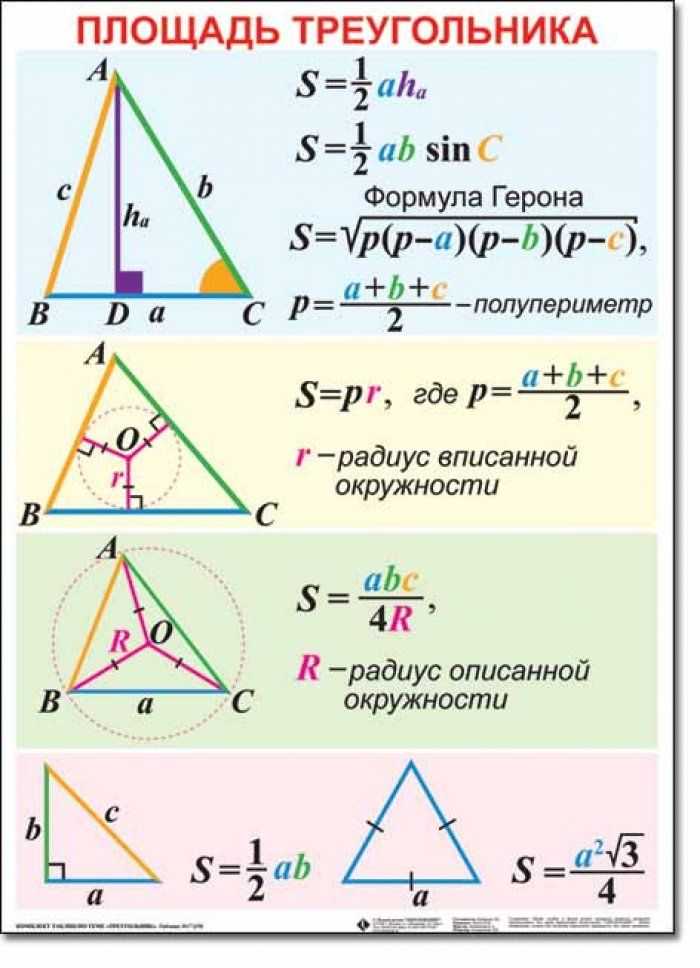
- Площадь прямоугольного треугольника равна половине произведения катетов. S = (ab):2.
- Площадь прямоугольного треугольника равна половине произведения гипотенузы и высоты. S = (hc):2.
Прямоугольный треугольник: формулы тригонометрия
- Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. cosα = AC: AB.
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. sinα = BC:AB.
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. tgα = BC:AC.
- Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему.
 ctgα = AC:BC.
ctgα = AC:BC. - Основное тригонометрическое тождество: cos2α + sin2α = 1.
- Теорема косинусов: b2 = a2 + c2 – 2ac·cosα.
- Теорема синусов: CB :sinA = AC : sinB = AB.
Прямоугольный треугольник: формулы для описанной окружности
- Радиус описанной окружности равен половине гипотенузы : R=AB:2.
- Центр описанной окружности лежит на середине гипотенузы.
Прямоугольный треугольник: формулы для вписанной окружности
Радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле: r = (a + b -c):2.
Рассмотрим применение тригонометрических формул прямоугольного треугольника при решении задания 6(вариант 32) из сборника для подготовки к ЕГЭ по математике профиль автора Ященко.
В треугольнике ABC угол С равен 90°, sinA = 11/14, AC =10√3. Найти АВ.
Решение:
- Применяя основное тригонометрическое тождество, найдем cosA = 5√3/14.

- По определению косинуса острого угла прямоугольного треугольника имеем: cosA = AC : AB, AB = AC : cosA = 10√3·14:5√3 = 28.
Ответ: AB = 28.
ЗАДАНИЕ 12 ЕГЭ МАТЕМАТИКА ПРОФИЛЬ( 20 ВАРИАНТ ЯЩЕНКО 2018)
Формулы, Формулы по геометрии прямоугольный треугольник, формулыСвойства прямоугольного треугольника. Формулы прямоугольного треугольника.
- Альфашкола
- Статьи
- Свойства прямоугольного треугольника
Прямоугольный треугольник
Треугольник с прямым углом \(90°\) называют прямоугольным треугольником.
Самая длинная сторона треугольника называется гипотенузой, а две другие стороны — катеты.
Свойства прямоугольного треугольника — это свойства, определяющие прямоугольный треугольник.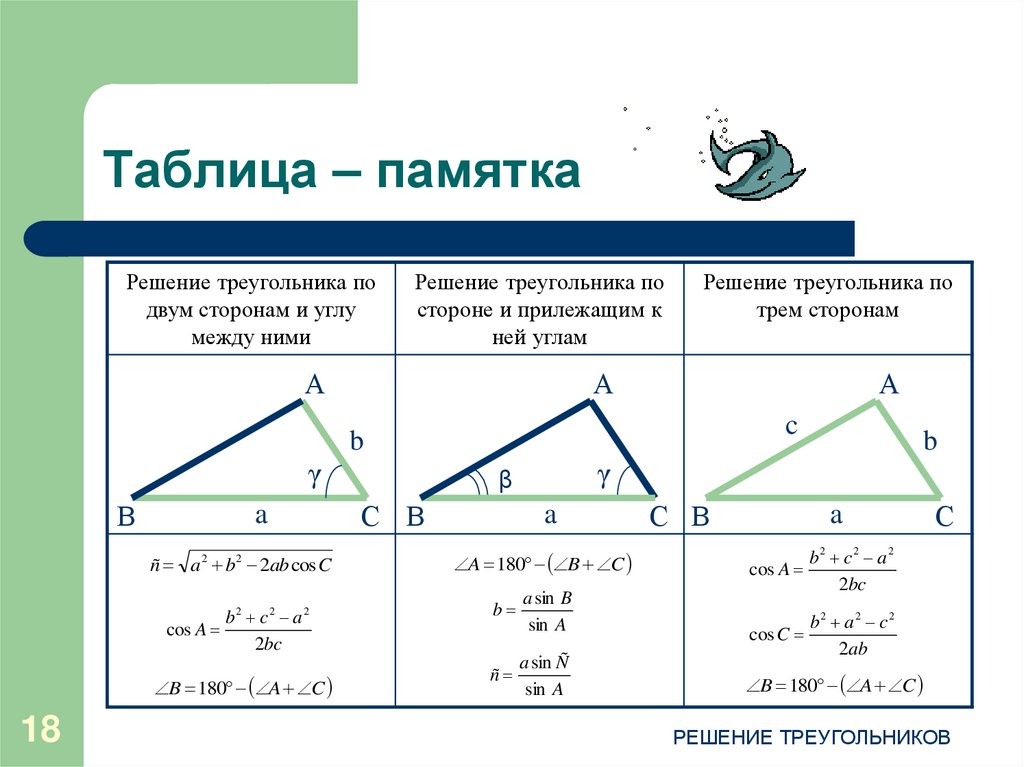 2=q*p\)
2=q*p\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Фёдор Владимирович Каузов
Репетитор по математике
Стаж (лет)
Образование:
Государственное образовательное учреждение высшего профессионального образования Ивановский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Мария Ивановна Мозина
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Оксана Николаевна Хаустова
Репетитор по математике
Стаж (лет)
Образование:
Саратовский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Подготовка к ЕГЭ по математике (базовый уровень)
- Репетитор по алгебре
- Репетитор для подготовки к ОГЭ по физике
- Репетитор по русскому языку для подготовки к ОГЭ
- Репетитор по английскому языку для подготовки к ОГЭ
- Репетитор для подготовки к ЕГЭ по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
- Подготовка к ОГЭ по литературе
- Программирование Pascal
- Scratch
Похожие статьи
- РУДН: Ландшафтная Архитектура
- ЕГЭ по математике, профильный уровень.
 Тригонометрическое уравнение
Тригонометрическое уравнение - ЕГЭ по математике, профильный уровень. Неравенства
- Задачи с логарифмическими уравнениями и неравенствами
- Задачи на движение по воде
- Как вести себя, если ребенок получает двойки?
- Летние хобби: 5 нестандартных способов рисования
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
прямоугольных треугольников
прямоугольных треугольников Давайте снова согласимся со стандартным правилом обозначения частей прямоугольного треугольника.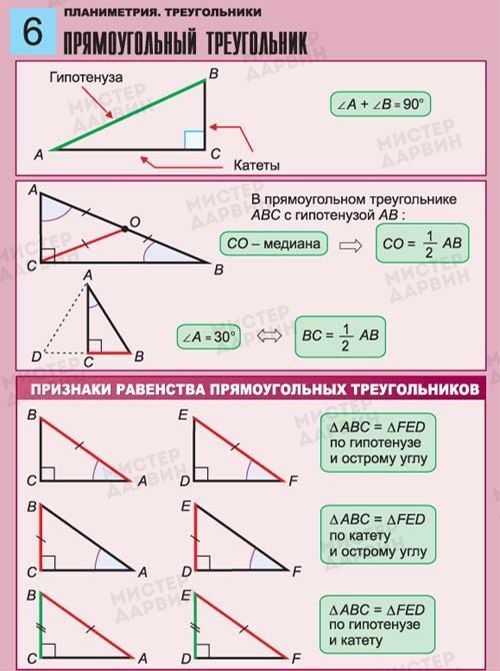 Пусть прямой угол обозначен C , а гипотенуза c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно.
Пусть прямой угол обозначен C , а гипотенуза c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно.
Решение прямоугольных треугольников
Мы можем использовать теорему Пифагора и свойства синусов, косинусов и тангенсов для решения треугольника, то есть для нахождения неизвестных частей через известные части.- Теорема Пифагора: a 2 + b 2 = c 2 .
- Синусы: sin A = a/c, sin B = b/c.
- Косинусы: cos A = b/c, cos B = a/c.
- Касательные: tan A = a/b, tan B = b/a.
 Теорема Пифагора даст нам гипотенузу. Например, если A = 10 и B = 24, затем C 2 = A 2 + B 2 = 100024 2 +24 2 = 100+576 = 676. Квадратный корень из 676 равен 26, поэтому c = 26. (Приятно привести примеры, когда из квадратных корней получаются целые числа; в жизни это обычно не так.)
Теорема Пифагора даст нам гипотенузу. Например, если A = 10 и B = 24, затем C 2 = A 2 + B 2 = 100024 2 +24 2 = 100+576 = 676. Квадратный корень из 676 равен 26, поэтому c = 26. (Приятно привести примеры, когда из квадратных корней получаются целые числа; в жизни это обычно не так.)Теперь предположим, что мы знаем гипотенузу и одну сторону, но должны найти другую. Например, если b = 119 и C = 169, затем A 2 = C 2 — B 2 = 169 2 — 119 2 = 28561 — 14161 = 140025 и квадрат из 1440024 28561 — 14161 = 14400 и квадрат из 1440024 из 140025 = 28561 — 14161 = 140025 и квадрат из 1440024 = 28561 — 14161 = 140025 и квадрат. равно 120, поэтому a = 120.
Мы можем знать только одну сторону, но мы также знаем угол. Например, если сторона a = 15 и угол A = 41°, мы можем использовать синус и тангенс, чтобы найти гипотенузу и другую сторону. Поскольку грех A = a/c, мы знаем c = a /sin A = 15/sin 41. Используя калькулятор, это 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Поскольку грех A = a/c, мы знаем c = a /sin A = 15/sin 41. Используя калькулятор, это 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Обратные триггерные функции: арксинус, арккосинус и арктангенс
Теперь давайте рассмотрим задачу нахождения углов, если известны стороны. Опять же, вы используете триггерные функции, но наоборот. Вот пример. Предположим a = 12,3 и b = 50,1. Тогда тангенс A = a/b = 12,3/50,1 = 0,2455. Раньше, когда люди использовали таблицы триггерных функций, они просто смотрели в таблицу тангенсов, чтобы увидеть, какой угол имеет тангенс 0,2455. На калькуляторе мы используем обратные триггерные функции, называемые арктангенс, арксинус и арккосинус. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием соответствующей кнопки триггера. Арктангенс 0,2455 равен 13,79., поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)
Арктангенс 0,2455 равен 13,79., поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)Вот и все.
Остальные три тригонометрические функции: котангенс, секанс и косеканс
Для большинства целей достаточно трех триггерных функций: синуса, косинуса и тангенса. Однако бывают случаи, когда нужны какие-то другие. В исчислении часто используется секанс. Вы можете спросить: «Почему шесть триггерных функций?» Это своего рода симметрия. Есть шесть способов сделать отношения двух сторон прямоугольного треугольника, и это дает шесть функций:- sin A = a/c (opp/hyp)
- cos A = b/c (adj/hyp)
- tan A = a/b (opp/adj)
- детская кроватка A = b/a (adj/opp)
- сек A = c/b (hyp/adj)
- csc A = c/a (hyp/opp)
 Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A = tan B, и косекансы являются секущими дополнительных углов, а это означает, что csc A = sec B.
Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A = tan B, и косекансы являются секущими дополнительных углов, а это означает, что csc A = sec B. Эти три другие функции также можно интерпретировать с помощью единичной круговой диаграммы.
Мы рассматриваем угол AOB. Напомним, что его касательной является прямая AC. По симметрии тангенсом угла FOB является прямая FG, но FOB является дополнительным углом AOB, , следовательно, котангенс AOB равен FG.
Далее, интерпретировать секущие геометрически. Угол AOB появляется в треугольнике COA как угол AOC, so sec AOB = sec AOC = hyp/adj = OC/OA = OC.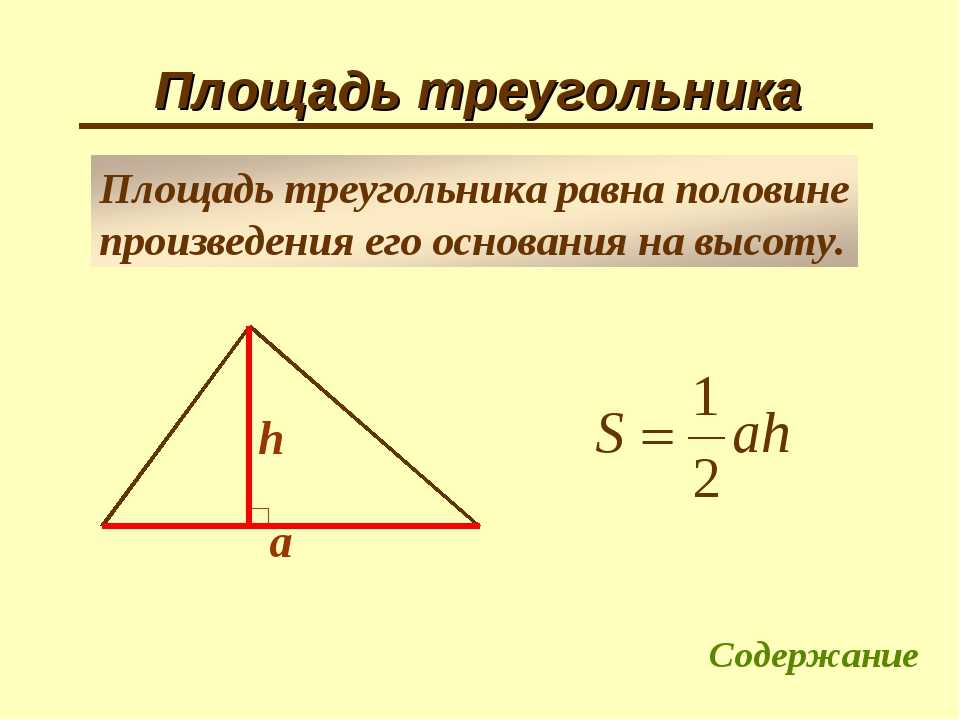 Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Аналогично, косекансом угла AOB является прямая OG , проведенная из центра окружности к прямой FG котангенса.
Упражнения
Примечание: как обычно, во всех упражнениях на прямоугольные треугольники c обозначают гипотенузу, a и b перпендикулярные стороны, A и B углы, противоположные a и б соответственно. 26. В каждом из следующих прямоугольных треугольников, две стороны которых заданы, вычислите sin, cos и тангенс углов A и B. Выразите результаты в виде обыкновенных дробей.
(и). c = 41, a = 9.
(ii). c = 37, a = 35.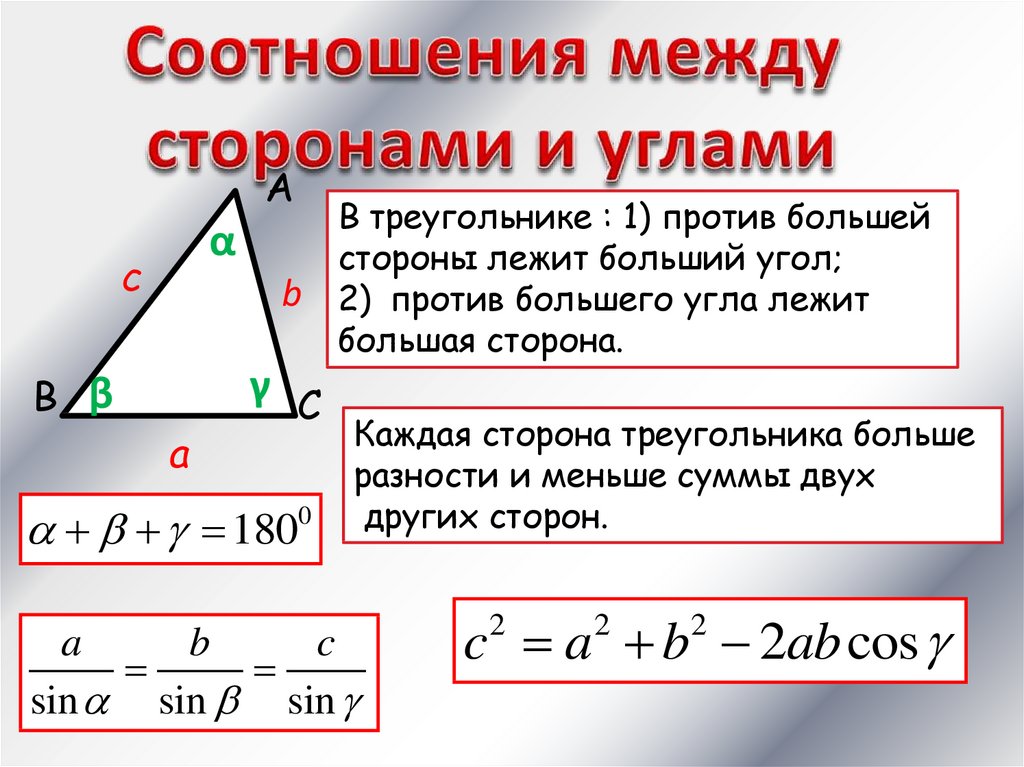
(iii). a = 24, b = 7.
31. В прямоугольном треугольнике c = 6 футов 3 дюйма и tan B = 1,2. Найдите a и b.
34. a = 1,2, b = 2,3. Найти A и c.
42. a = 10,11, b = 5,14. Найти B и c.
В следующих нескольких задачах треугольники не являются прямоугольными, но вы можете решить их, используя свои знания о прямоугольных треугольниках.
61. В косом треугольнике ABC, A = 30°, B = 45°, а перпендикуляр от C к AB имеет длину 12 дюймов. Найдите длину АВ.
67. Если сторона равностороннего треугольника равна а, найти высоту и радиусы описанной и вписанной окружностей.
202. От вершины здания высотой 50 футов углы возвышения и углубления вершины и низа другого здания равны 19° 41′ и 26° 34′ соответственно. Каковы высота и расстояние до второго здания.
Каковы высота и расстояние до второго здания.
207. С вершины маяка высотой 175 футов углы наклона вершины и низа флагштока составляют 23° 17′ и 42° 38′ соответственно. Какой высоты столб?
214. В двух точках на расстоянии 65 футов друг от друга на одной стороне дерева и на одной линии с ним углы возвышения вершины дерева составляют 21° 19′ и 16° 20′. Найдите высоту дерева.
215. Когда воздушный шар проходит между двумя точками A, и B, находящимися на расстоянии 2 миль друг от друга, углы места воздушного шара в этих точках составляют 27° 19′ и 41° 45′ соответственно. Найдите высоту воздушного шара. Возьмите A и B одного уровня.
233. Верхняя часть маяка находится на высоте 230 футов над уровнем моря. Как далеко находится объект, который находится «на горизонте»? [Предположим, что Земля представляет собой сферу радиусом 3956 миль.]
234. На какой высоте должен находиться наблюдатель, чтобы он мог видеть объект на Земле на расстоянии тридцати миль? Предположим, что Земля представляет собой гладкий шар.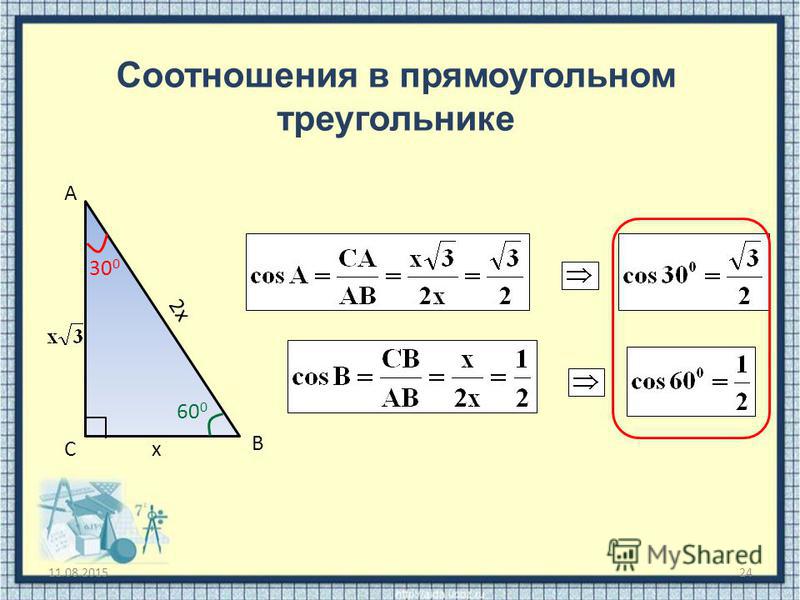
В каждой из фигур, названных в следующих нескольких задачах, объект должен выразить свою площадь (i) через радиус R, , то есть радиус описанной окружности, (ii) через апофема r, то есть радиус вписанной окружности, и (iii) по стороне а.
251. Равносторонний треугольник. [См. задачу 67 выше.]
252. Квадрат.
253. Правильный пятиугольник.
254. Правильный шестигранник.
255. Правильный восьмиугольник.
Советы
26. Вам нужны только sin, cos и тангенс углов A и B ; вам не нужны сами углы. Таким образом, вам нужна только третья сторона, которую вы можете вычислить с помощью теоремы Пифагора, а затем взять отношения двух сторон.
31. Вы знаете c и tan B. К сожалению, tan B — это отношение двух неизвестных вам сторон, а именно b/a. Существует несколько способов решения этой проблемы.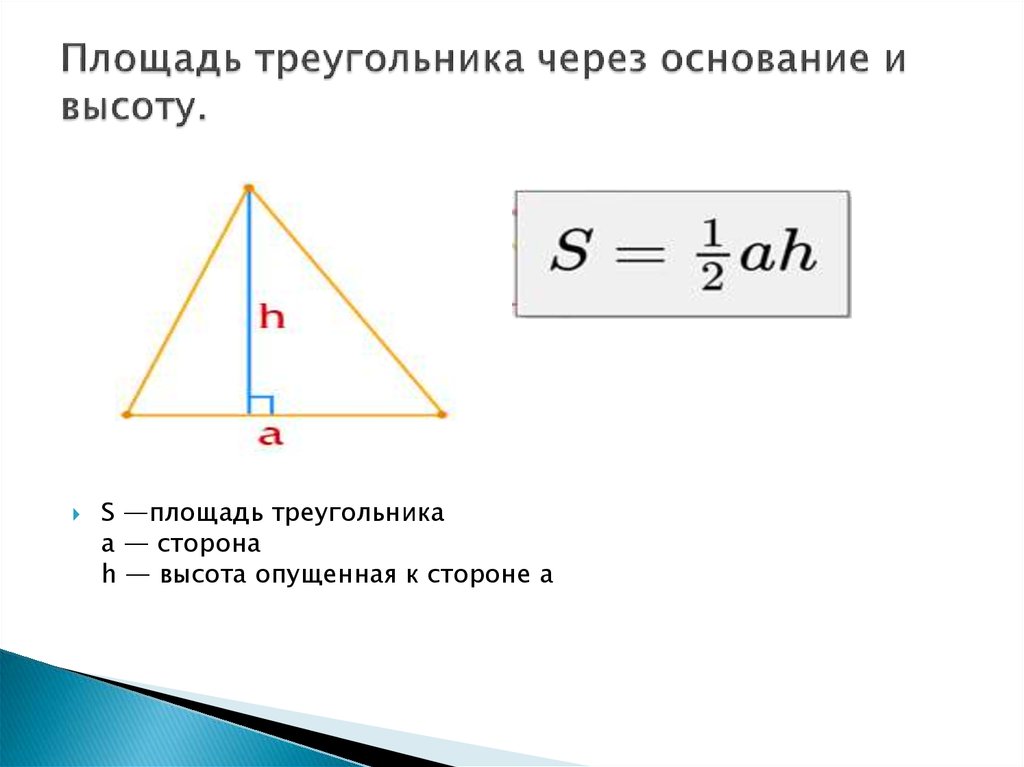 Вот два.
Вот два.
Метод 1. Возьмем уравнение 1.2 = tan B = b/a, , чтобы получить отношение между a и b, , а именно b = 1,2 a. Теорема Пифагора тогда дает 6,25 2 = a 2 + 1,44 a 2 , из которых можно определить a, и затем найти b.
Способ 2. Из тангенса B, можно определить угол B (используйте арктангенс). Отсюда вы можете найти cos B, , а затем a, , и вы можете найти sin B, , а затем b.
34. Поскольку у вас есть a и b, вы можете использовать тангенсы, чтобы найти A и теорему Пифагора, чтобы найти c.
42. Найдите B по касательной и c по теореме Пифагора.
61. Начните с рисования фигуры. Хотя треугольник ABC не является прямоугольным, он распадается на два прямоугольных треугольника. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.
Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.
67. Равносторонний треугольник ABC имеет три угла при вершине по 60°. Отбросьте перпендикуляр из одной вершины, скажем, вершины C, , и вы получите два конгруэнтных прямоугольных треугольника ACF и BCF, , и вы можете найти длину этого перпендикуляра, а это высота равностороннего треугольника. Описанная окружность — это та, которая проходит через три вершины, а вписанная окружность — это та, которая касается внутри трех сторон. Отбрасывая перпендикуляры из другой вершины равностороннего треугольника и применяя тригонометрию к полученным маленьким треугольникам, можно найти радиусы этих двух окружностей.
202. Поскольку вы знаете высоту своего здания и угол наклона к основанию другого здания, вы можете определить, как далеко оно находится. Тогда угол подъема на вершину другого здания скажет вам, насколько оно выше вашего.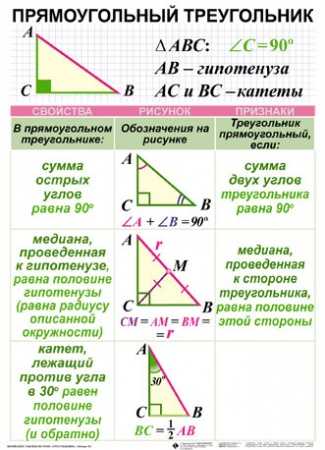
207. Подсказка похожа на 202. Смотрите, триггер может быть полезен, если вы одинокий смотритель маяка и не знаете, что делать!
214. Это полезная задача. Вы можете использовать его, чтобы найти высоты недоступных вещей. Нарисуйте фигуру. Есть два неизвестных: высота х дерева и расстояние х ближайшей точки к дереву. Дальнейшая точка — 90 003 x 90 004 + 65 футов от дерева. Используя тангенсы известных углов, вы можете составить два уравнения, которые можно решить для определения y и x.
215. Это похоже на 214, но в этой задаче шарик лежит между двумя точками. Нарисуйте фигуру. Определите свои переменные. Составьте уравнения и решите их.
233. Очень интересная задача. Различные его обратные значения использовались на протяжении веков для вычисления радиуса Земли. В этой задаче мы предполагаем, что знаем о Земле. Все, что вам нужно здесь, это теорема Пифагора. Одна сторона прямоугольного треугольника равна 90 003 r, 90 004 радиуса Земли, а гипотенуза равна 90 003 r 90 004 + 90 003 h 90 004, где 90 003 h 90 004 — высота маяка.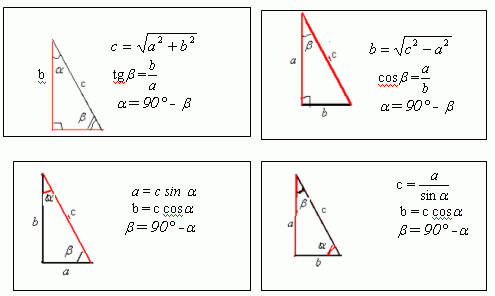 Теорема Пифагора третья сторона треугольника.
Теорема Пифагора третья сторона треугольника.
234. Поставьте эту задачу аналогично 233, но известны другие переменные.
251–255. Вы можете сделать все это сразу, оставив вычисления напоследок. Пусть n — количество сторон правильного многоугольника. Проведите линии от центра фигуры к вершинам и к серединам сторон. У вас получится 2 n маленьких треугольников. Каждый из них представляет собой прямоугольный треугольник с гипотенузой R, катетом р, и другая нога а /2. Угол в центре равен 360°/(2 n ) = 180°/ n. Используя тригонометрию, вы можете легко написать уравнения, связывающие площадь правильного многоугольника по мере необходимости.
Ответы
26. (и). B = 40. SIN A = COS B = 9/41, COS A = SIN B = 40/41, TAN A = 9/40, TAN B = 40 /9.(ii). B = 12. SIN A = COS B = 35/37, COS A = SIN B = 12/37, TAN A = 35/12, TAN B = 12 /37.
(iii). C = 25. Итак, SIN A = COS B = 24/25, COS A = SIN B = 7/25, TAN A = 24/7, TAN B = 7 /24.
31. a = 4 фута, b = 4,8 фута, около 4 футов 10 дюймов.
34. A = 27,55°, около 28°. c = 2,6.
42. B = 26,95° или 26°57′. c = 11,3.
61. AB = 12/тангенс A + 12/тангенс B = 12(√3 + 1) дюймов, примерно 33 дюйма.
67. ( a √3)/2, ( a √3)/3 и ( a √3)/6 соответственно.
202. Расстояние = 50/тангенс 26°34′ = 100 футов. Высота = 50 + 100 tan 19°41′ = 85,8′ = 85’9″.
207. Расстояние = 175/тангенс 42°38′ = 190 футов. Рост = 175 — 190 тангенс 23°17′ = 93,23′ = 9’3″.
214. Два уравнения
- 0,293052 = тангенс 16°20′ = ч /(65 + x ), и
0,3 = тангенс 21°19′ = ч/х .

Расстояние x = 196 футов. Высота ч = 76,5 футов.
215. Если ч — высота воздушного шара, а х — расстояние по земле от точки А до точки непосредственно под воздушным шаром, то два эквариона равны
- тангенс 27°19′ = ч/х и
тангенс 41°45′ = ч / (2 – x )
Высота = 0,654 мили = 3455 футов.
233. Мелочь больше 18,5 миль.
234. 600 футов.
251–255. Площадь правильного n -угольника равна A = nra /2. Чтобы найти A через R, r, или a, , используйте соотношения
- cos 180°/ n = r/R, и
тангенс 180°/ n = a /(2 r ).
- (i) в пересчете на R, площадь A = nR 2 cos 180°/ n sin 180°/ n ,
(ii) в пересчете на r, площадь A = nr 2 tan 180°/ n , и
(iii) в пересчете на а, площадь A = na 2 /(4tan 180°/ и ).
| Problem | shape | (i) R | (ii) r | (iii) a |
|---|---|---|---|---|
| 251 | triangle | (3 R 2 √3)/4 | 3 р 2 √3 | ( a 2 √3)/4 |
| 252 | квадратный | 2 Р 2 | 4 р 2 | a 2 |
| 253 | пятиугольник | (5 R 2 sin 108°)/2 | 5 r 2 tan 36° | (5 a 2 tan 54°)/4 |
| 254 | шестигранник | (3 R 2 √3)/2 | 2 р 2 √3 | (3 a 2 √3)/2 |
| 255 | восьмиугольник | 2 Р 2 √2 | 8 r 2 tan 22°30′ | 2 a 2 tan 67°30′ |
Отступление от троек Пифагора
Это не имеет ничего общего с тригонометрией, но это интересно. Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как и в задаче 26, где все три прямоугольных треугольника имели целые числа в качестве сторон, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.
Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как и в задаче 26, где все три прямоугольных треугольника имели целые числа в качестве сторон, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5. Итак, существуют ли другие специальные прямоугольные треугольники, все стороны которых являются целыми числами? Да и изучались они давно. Три числа a, b, и c такие, что a 2 + b 2 = c 2 образуют пифагорейскую тройку , в честь Пифагора. Он жил около 550 г. до н. э. и, вероятно, знаю немало из них. Но древние вавилоняне около 1800 г. до н. э. знали их все, и многие были известны в других древних цивилизациях, таких как Китай и Индия.
Прежде чем читать абзац, посмотрите, сможете ли вы найти еще несколько пифагорейских троек. Не считайте за новые те, у которых есть общий множитель, например 6:8:10, так как они будут похожи на меньшие.
В « элементах » Евклида есть описание всех возможных пифагорейских троек. Вот современный парафраз Евклида. Возьмем любые два нечетных числа m и n, с m n и взаимно простые (то есть без общих множителей). Пусть A = мн, Let B = ( N 2 — M 2 )/2 и Let C = ( N 2 + M 444444 2 + M 44444444444444444444444444444444444444444444 2 )/2. Тогда a : b : c — пифагорейская тройка. Например, если взять м = 1, а n = 3, то получится наименьшая пифагорейская тройка 3:4:5.
Формула прямоугольного треугольника— Что такое формула прямоугольного треугольника? Примеры
Треугольник – это замкнутая фигура или фигура с 3 сторонами, 3 углами и 3 вершинами. Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (размером 90º), такой треугольник называется прямоугольным треугольником или просто прямоугольным треугольником. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.
Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (размером 90º), такой треугольник называется прямоугольным треугольником или просто прямоугольным треугольником. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.
Что такое формулы прямоугольного треугольника?
Прямоугольный треугольник — это треугольник, один из внутренних углов которого равен 90 градусов. Формулы прямоугольного треугольника используются для вычисления периметра, площади, высоты и т. д. прямоугольного треугольника с использованием трех его сторон.
Формула прямоугольного треугольника
Различные формулы, связанные с прямоугольным треугольником:
- Теорема Пифагора — Формула
Определение теоремы Пифагора показывает отношение между тремя сторонами прямоугольного треугольника.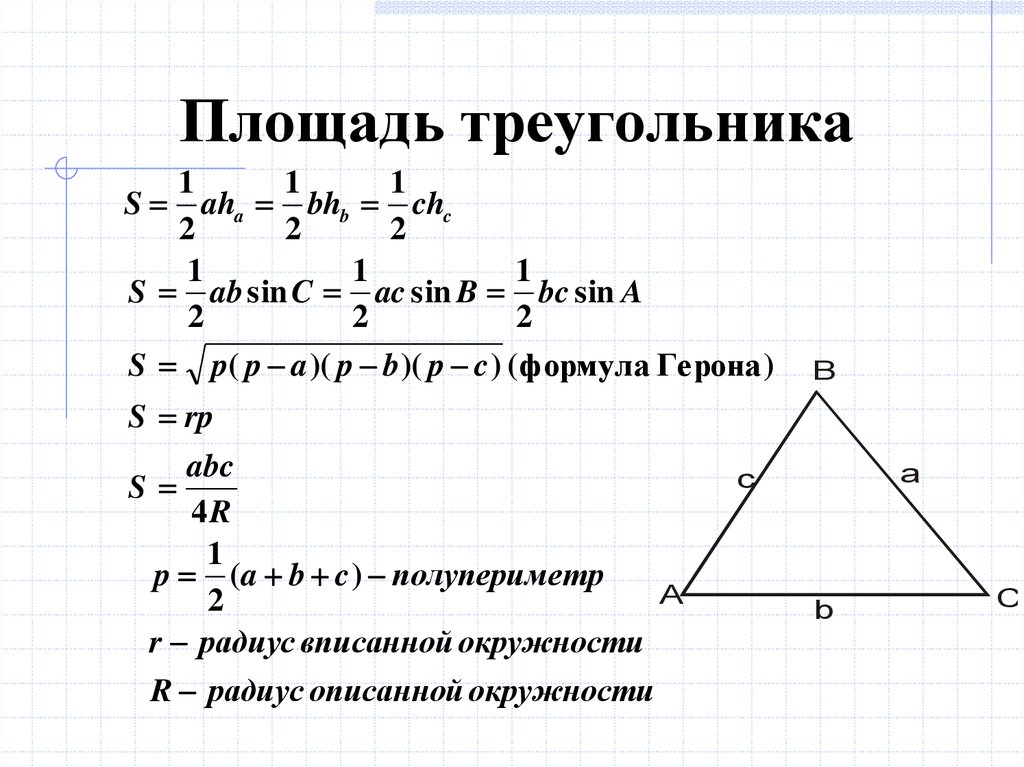 Квадрат гипотенузы равен сумме квадратов двух других катетов.
Квадрат гипотенузы равен сумме квадратов двух других катетов.
(Гипотенуза) 2 = (Перпендикуляр) 2 + (Основание) 2
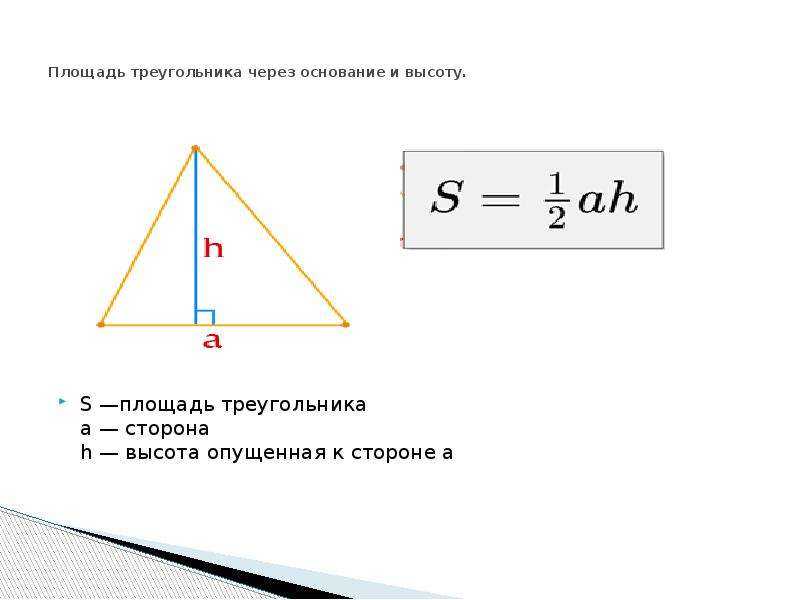
- Площадь прямоугольного треугольника формула
Формула для вычисления площади прямоугольного треугольника задается следующим образом:
Площадь = 1/2 × Основание × Высота = 1/2 × b × h
, где высота,h равна длине перпендикуляра сторона треугольника.
- Формула периметра прямоугольного треугольника
Формула для вычисления площади прямоугольного треугольника выглядит следующим образом:
Периметр = a + b + c
, где a, b и c — три стороны треугольника.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Примеры использования формул прямоугольного треугольника
Пример 1: Длина основания и перпендикуляра прямоугольного треугольника составляет 6 дюймов и 8 дюймов соответственно. Найти:
Найти:
- Длина его гипотенузы
- Периметр треугольника
- Площадь треугольника
Решение:
Найти:
Дано: длина основания = 6 дюймов, длина перпендикуляра = 8 дюймов 2 + (перпендикулярный) 2
(гипотенуза) 2 = 6 2 + 8 2 = 100
Гипотен = √100 = 10 в
ii) Используя формулу периметра прямоугольного треугольника,
Периметр = сумма всех сторон
Периметр = 6 + 8 + 10 = 24 в
iii) Используя формулу площади треугольника,
Площадь = (1/ 2) × b × h
= (1/2) × 6 × 8
= 24 дюйма 2
Ответ: гипотенуза прямоугольного треугольника = 10 дюймов, периметр прямоугольного треугольника = 24 дюйма, и площадь прямоугольного треугольника = 24 в 2 .
Пример 2: Высота и гипотенуза прямоугольного треугольника равны 12 и 13 дюймов соответственно.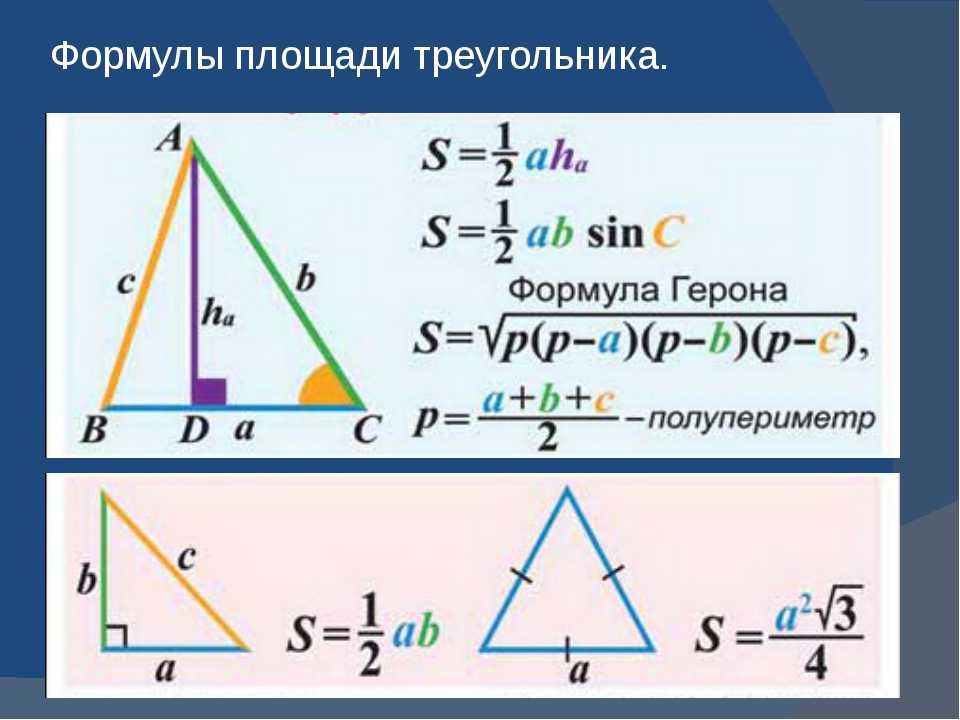 Найдите его площадь.
Найдите его площадь.
Решение:
Чтобы найти: площадь прямоугольного треугольника
Дано: высота = 12 дюймов, гипотенуза = 13 в
Используя теорему Пифагора,
2 0 2 90 090 (23) 2 + (12) 2(основание) 2 = (13) 2 — (12) 2 = 25
5 дюймов 5 0 ∆основание = 1:5 90 90 0 ∆
0002 Используя формулу площади треугольника,
Площадь = (1/2) × b × h
Площадь = (1/2) × 5 × 12
Площадь = 30 в 2
Ответ : Площадь прямоугольного треугольника = 30 в 2
Пример 3: Определить площадь прямоугольного треугольника, у которого периметр равен 30 единицам, высота – 12 единиц, а гипотенуза – 13 единиц.
Решение:
Найти: Площадь прямоугольного треугольника
Дано: периметр = 30 единиц, гипотенуза = 13 единиц, высота = 12 единиц.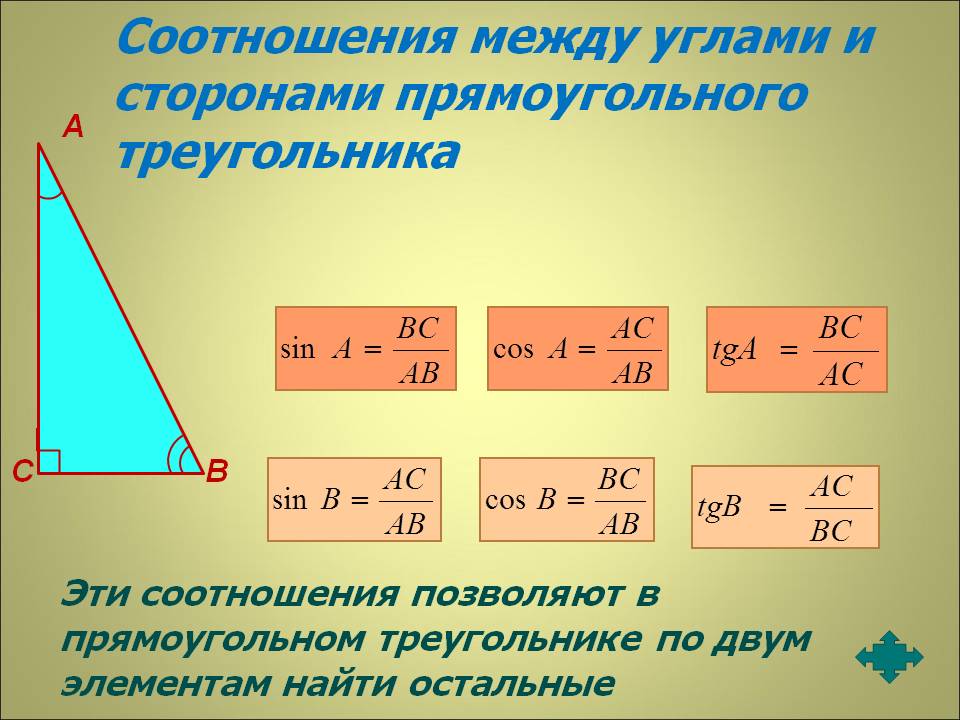 5 единиц
5 единиц
Площадь = 1/2bh = 1/2(5×12) = 30 кв. единиц.
Ответ: Площадь прямоугольного треугольника = 30 ед. В геометрии формулы прямоугольного треугольника — это формулы прямоугольного треугольника, которые используются для вычисления периметра, площади, высоты и т. д. треугольника с использованием трех его сторон — основания, высоты и гипотенузы. Эти формулы имеют вид: Существует множество применений прямоугольного треугольника в реальной жизни, наиболее распространенным является его использование в области тригонометрии, поскольку отношение между его углами и сторонами составляет основу тригонометрии. Каковы применения формулы прямоугольного треугольника?



 ctgα = AC:BC.
ctgα = AC:BC.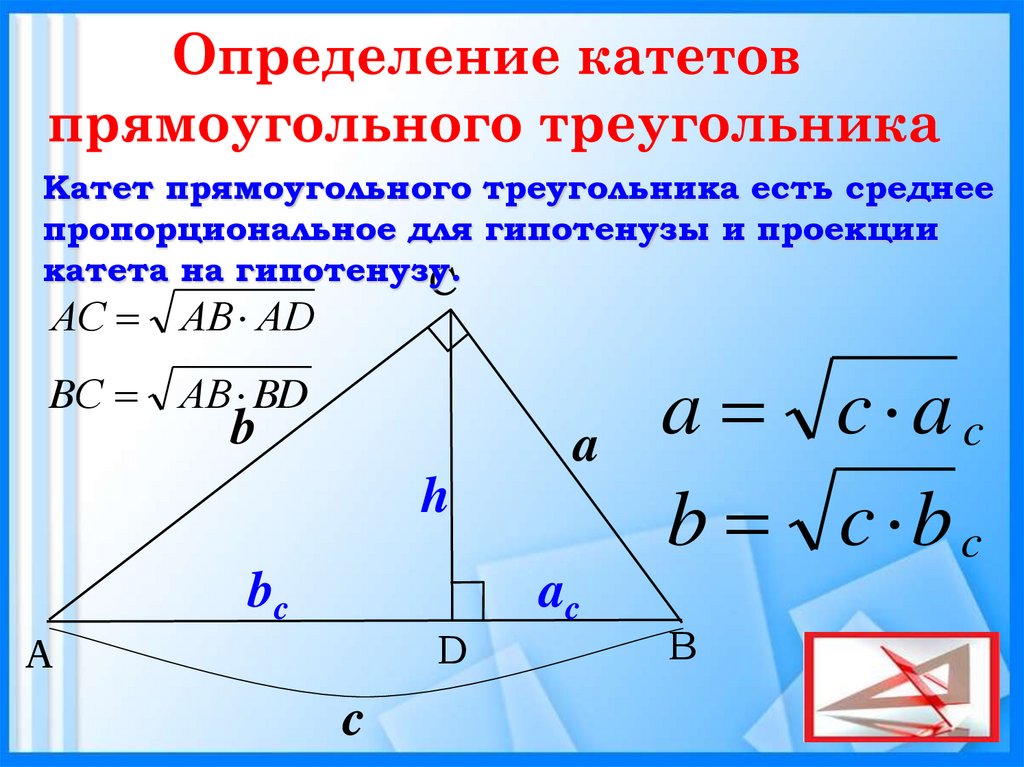
 Тригонометрическое уравнение
Тригонометрическое уравнение