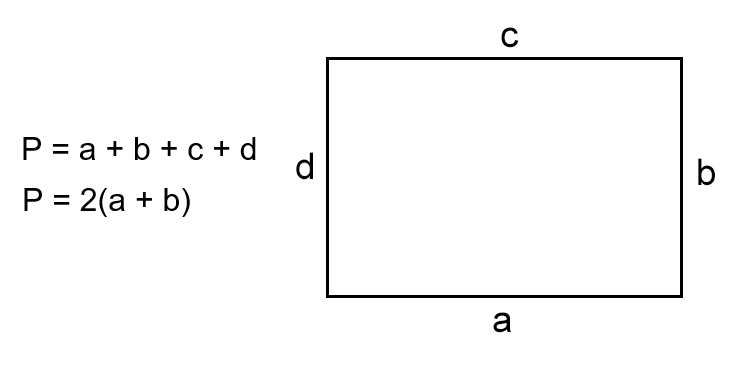
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
Задача 1
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.Задача 10
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
-
Найдите площадь фигуры, изображённой на рисунке B.
-
Найдите площадь фигуры, изображённой на рисунке C.
-
Найдите площадь фигуры, изображённой на рисунке D.
-
Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
Задачи на периметр и площадь для 4 класса
Задачи на периметр и площадь для 4 класса
Рубрики Logical words, Алгебра
Периметр — сумма сторон
Площадь — умножение сторон
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Задача 1
Найди периметр квадрата со стороной 8 см.
Решение:
8 · 4 = 32 (см)
Ответ: периметр квадрата 32 см.
Задача 2
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: длина прямоугольника 9 см.
Задача 3
Длина бассейна прямоугольной формы 15 м.
Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: периметр бассейна 46 метров
Задача 4
Периметр квадрата 8 см.
Из трех таких квадратов сложили прямоугольник.
Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: периметр прямоугольника 16 см.
Задача 5
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.
На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: ученик ошибся на 3 см²
Задача 6
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше.
Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ:площадь окна 32 дм²
Комментирование и размещение ссылок запрещено.как найти периметр квадрата по его стороне или чему он равен и какие формулы для нахождения этого
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Математика – 3 класс. Прямоугольники

Что такое прямоугольник и квадрат
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2. Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Определим PABCD.
Пример:
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см. Решение:
Нарисуем прямоугольник ABCD с исходными данными.
PABCD = 2 * (AB + BС)
Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
PABCD= 4 * AB
Пример:
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата. Решение:
Нарисуем квадрат ABCD с исходными данными.

PABCD = 4 * AB
Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.
Задачи на нахождение периметра прямоугольника
Измерь ширину и длину прямоугольников. Определи их периметр.


Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника. 3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора. 2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев. Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.). В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину. 
- S AKMO = AK * KM
- S AKMO= AK * KM = 7 см * 2 см = 14 см2.
Пример:
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
Ответ: 14 см2.
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя. Пример:
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
- S AВСО = AB * BC = AB * AB
- S AKMО = AK * KM = 8 см * 8 см = 64 см2
Пример:
Определи площадь квадрата AKMO со стороной 8 см.
Ответ: 64 см2.
Задачи на нахождение площади прямоугольника и квадрата:
- Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
- Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Источник: https://mathematics-tests.com/matematika-3-klass-urok-perimetr-ploshad-pryamougolnika
Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».
Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата
Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:
Например, перед нами квадрат со стороной 10 см:
Ответ: 40 см
Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.
Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:
S – это площадь, а – сторона квадрата.
Например, в задаче указано, что длина стороны квадрата составляет 10см.
Ответ: 100см2
Периметр и площадь прямоугольника
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два. Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см:
Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа:
- S= 5*2
- S=10см2
Ответ: 10 см2
Периметр круга (длина окружности)
Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:
L – длина окружности
π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.
π = 3.141 592 653 589 793 238 462 643 383 279 502
Для удобства вычислений обычно используют значение 3.14
R – это радиус окружности
D – Диаметр окружности
Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то
Например, перед нами круг с радиусом 3 см. Найдем его периметр:
- L= 2*3,14*3
- L=6π
- L=6*3.14
- L = 18.84 см
- Pк= 18,84 см
Ответ: 18.84 см
Отличие периметра от площади
Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ. Площадь всегда измеряется в квадратных единицах (см2, м2, мм2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.
Источник: https://topkin.ru/voprosy/nauka-voprosy/chto-takoe-perimetr-i-ploshhad/
Площадь прямоугольника
Площадь прямоугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.
Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь прямоугольника с помощью различных формул или проверить уже выполненные вычисления.
Площадь прямоугольника через две стороны

a — сторона
b — сторона
a (или b) — сторона
P — периметр
a (или b) — сторона
d — диагональ
d — диагональ
α° — угол между диагоналями
a (или b) — сторона
R — радиус описанной окружности

a (или b) — сторона
D — диаметр описанной окружности
Прямоугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками, угол между которыми равен 90 градусов и параллельные отрезки при этом равны.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Источник: https://doza.pro/art/math/geometry/area-rectangle
Задачи на нахождение площади. Математика 4 класс.
Задача 1
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Решение:
- 1) 8 ∙ 7 = 56
- Ответ: Площадь прямоугольника 56 м².
Задача 2
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Решение:
- 1) 1) 64 : 8 = 8 (сторна витрины)
- 2) 2) 8 ∙ 4 = 32 (периметр витрины)
- Ответ: 32 м.
Задача 3
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Решение:
- 1) 1) 90 ∙ 7 = 630
- Ответ: 630 см².
Задача 4
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Решение:
- 1) 48 ∙ 30 = 1440 (площадь первого участка)
- 2) 30 + 6 = 36 (ширина второго участка)
- 3) 1440 : 36 = 40
- Ответ: длина второго участка 40 м.
Задача 5
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Решение:
- 1) 36 ∙ 20 = 720 (площадь первого участка)
- 2) 36 – 6 = 30 (длина другого участка)
- 3) 720 : 30 = 24
- Ответ: ширина другого участка 24 м.
Задача 6
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Решение:
- 1) 4 ∙ 4 = 16 (площадь квадрата)
- 2) 2 ∙ 6 = 12 (площадь прямоугольника)
- 3) 16 — 12 = 4
- Ответ: площадь квадратата больше на 4 см.
Задача 7
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Решение:
- 1) 6 ∙ 6 = 36
- 2) 6 ∙ 4 = 24
- Ответ: площадь квадрата 36 см², периметр квадрата 24 см.
Задача 8
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Решение:
- 1) 7 ∙ 5 = 35
- 2) 7 ∙ 2 = 14
- 3) 5 ∙ 2 = 10
- 4) 10 + 14 = 24
- Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 9
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
- 1) 8 ∙ 8 = 64 (площадь клумбы)
- 2) 64 : 16 = 4(1/16 клумбы)
- 3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
- 4) 64 – 28 = 36
- Ответ: незабудками засажено 36 м².
Задача 10
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
- 1) 6 ∙ 2 = 12
- 2) 18 – 12 = 6
- 3) 6 : 2 = 3 (ширина прямоугольника)
- 4) 3 ∙ 6 = 18
- Ответ: площадь прямоугольника 18 м².
Задача 11
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
- 1) 4800 : 60 = 80 (длина стола)
- 2) 60 ∙ 2 = 120 см
- 3) 80 ∙ 2 = 160 см
- 4) 120 + 160 = 280 см
- Ответ: периметр стола 280 см.
Задача 12
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
- 1) 5 ∙ 2 = 10
- 2) 40 – 10 = 30
- 3) 30 : 2 = 15 (другая сторона прямоугольника)
- 4) 5 ∙ 15 = 75
- Ответ: площадь прямоугольника 75 см².
Задача 13
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
- 1) 49 : 7 = 7 (сторона квадрата)
- 2) 7 ∙ 4 = 28 (периметр квадрата)
- Ответ: периметр квадрата равен 28 дм.
Задача 14
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
- 1) 4 ∙ 2 = 8 (длина окна)
- 2) 4 ∙ 8 = 32
- Ответ: площадь окна равна 32 м².
Задача 15
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
- 1) 54 ∙ 48 = 2592 (площадь участка земли)
- 2) 2592 : 9 = 288 (1/9 площади)
- 3) 288 ∙ 5 = 1440 (5/9 площади)
- 4) 2592 – 1440 = 1152
- Ответ: капустой засадили 1152 м².
Задачи на нахождение периметра и площади
Площадь одной клетки равна 1см.
Найдите площадь фигуры, изображённой на рисунке A.
Найдите площадь фигуры, изображённой на рисунке B.
Найдите площадь фигуры, изображённой на рисунке C.
Найдите площадь фигуры, изображённой на рисунке D.
Найдите площадь фигуры, изображённой на рисунке E.Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
 Решение:
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.
 Применив формулы площади треугольника, квадрата и прямоугольника легко решим поставленную задачу
Применив формулы площади треугольника, квадрата и прямоугольника легко решим поставленную задачу
Фигура A
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура B
S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²
Ответ: площадь фигуры B 20,5 см²
Фигура C
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²
Ответ: площадь фигуры C 30,5 см²
Фигура D
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура E
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²
Ответ: площадь фигуры E 12 см²
Как найти периметр прямоугольника — Лайфхакер
Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Выбирайте формулу в зависимости от известных вам данных.
Зная все или две соседние стороны
Для полноты упомянем простейшие классические формулы.
- Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин.
- Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.

- P — искомый периметр;
- a, b, c, d — стороны прямоугольника.
Сейчас читают
🔥
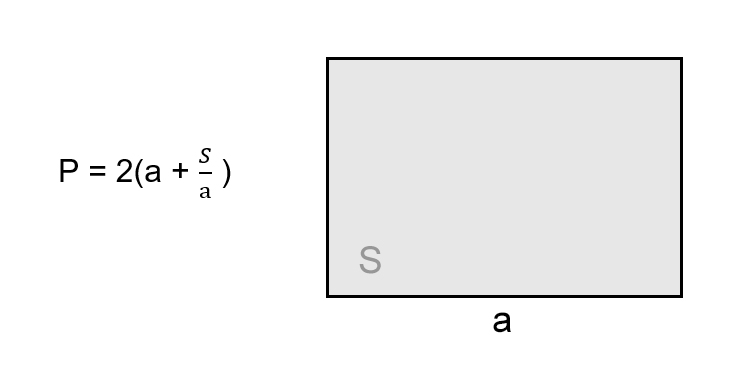
Зная любую сторону и площадь
- Поделите площадь на длину известной стороны.
- Прибавьте результат к известной стороне.
- Умножьте полученное число на два.

- P — искомый периметр прямоугольника;
- a — известная сторона;
- S — площадь прямоугольника.
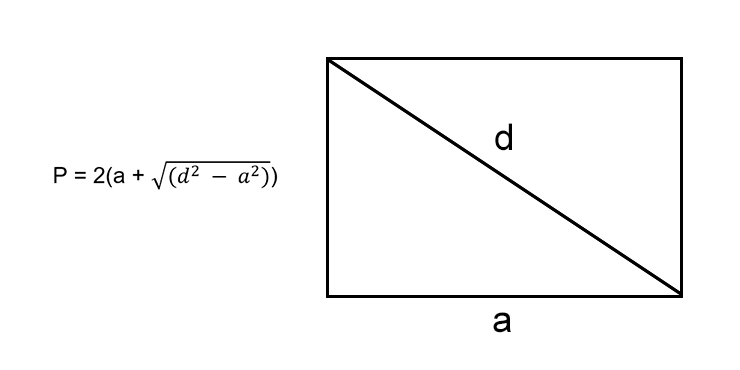
Зная любую сторону и диагональ
- Посчитайте разность квадратов диагонали и стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.

- P — искомый периметр прямоугольника;
- a — известная сторона;
- d — диагональ прямоугольника.
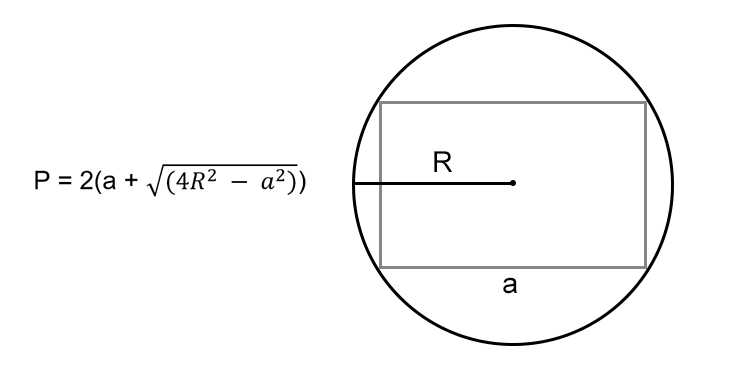
Зная одну любую сторону и радиус описанной окружности
- Умножьте квадрат радиуса на четыре.
- Посчитайте разность полученного числа и квадрата известной стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.

- P — искомый периметр прямоугольника;
- a — известная сторона;
- R — радиус окружности, описанной вокруг прямоугольника.
Читайте также
📐✂️📌
90000 Area and perimeter worksheets (rectangles and squares) 90001 90002 You are here: 90003 Home → Worksheets → Area & perimeter 90004 Find an unlimited supply of free worksheets for practicing the area and / or perimeter of rectangles & squares for grades 3-5. The worksheets are very varied, and include: 90005 90006
90007 problems for the area & perimeter of rectangles and squares, with grid images or normal images 90008
90007 word problems, including some that ask for a missing length of side when the area or perimeter is given 90008
90007 problems with complex rectangular shapes 90008
90007 write an expression for two-part rectangular areas (Common Core Standard 3.MD.7.c for 3rd grade). 90008
90015 90016 90017 Basic instructions for the worksheets 90018 90004 Each worksheet is randomly generated and thus unique. The 90020 answer key is automatically generated 90021 and is placed on the second page of the file. 90005 90004 You can generate the worksheets 90024 either in html or PDF format 90025 — both are easy to print. To get the PDF worksheet, simply push the button titled «90002 Create PDF 90003» or «90002 Make PDF worksheet 90003».To get the worksheet in html format, push the button «90002 View in browser 90003» or «90002 Make html worksheet 90003». This has the advantage that you can save the worksheet directly from your browser (choose File → Save) and then 90002 edit it 90003 in Word or other word processing program. 90005 90004 Sometimes the generated worksheet is not exactly what you want. Just try again! To get a different worksheet using the same options: 90005 90006 90007 PDF format: come back to this page and push the button again.90008
90007 Html format: simply refresh the worksheet page in your browser window. 90008
90015
90016 90046
90047
90048
90016 Draw a rectangle with given area in the grid, or find the area of a given rectangle (grades 2-3) 90004 View in browser
Create PDF 90016
90005 90053
90048
90016 Draw a rectangle with given area in the grid, or find the area of a given rectangle (grade 3) 90004 View in browser
Create PDF 90016
90005 90053
90060 90047 90048
90016 Find the area and perimeter of the given rectangle (grade 3) 90004 View in browser
Create PDF 90016
90005 90053
90048
90016 Find area, perimeter, or the missing side length (grades 3-4) 90004 View in browser
Create PDF 90016
90005 90053
90060 90047 90048
90016 Write an expression for the area of a two-part rectangle in two ways, thinking of one rectangle or two (grades 3-5).90004 This is a challenging topic for 3rd grade in the Common Core Standards (3.MD.7.c) and many children probably need lots of practice with it. It is essentially an illustration of the distributive property. 90005 90004 (If you make an html worksheet, make sure the background colors are set to be printed in your browser’s options.) 90005
90004 View in browser
Create PDF 90016
90005 90053 90048
90016 Draw a two-part rectangle to match the given number sentence for its total area (grades 3-5).90004 This is a challenging topic for 3rd grade in the Common Core Standards (3.MD.7.c) and many children probably need lots of practice with it. It is 90005 90053 90060 90092.90000 Perimeter of Square- How to Calculate Perimeter of a Square? 90001 90002 90003 90004 90003 90002 90003 90008 Classes 90002 90003 Class 1 — 3 90004 90003 Class 4 — 5 90004 90003 Class 6 — 10 90004 90003 Class 11 — 12 90004 90018 90004 90003 90008 COMPETITIVE EXAMS 90002 90003 BNAT 90004 90003 90008 CBSE 90002 90003 90008 NCERT Books 90002 90003 NCERT Books for Class 5 90004 90003 NCERT Books Class 6 90004 90003 NCERT Books for Class 7 90004 90003 NCERT Books for Class 8 90004 90003 NCERT Books for Class 9 90004 90003 NCERT Books for Class 10 90004 90003 NCERT Books for Class 11 90004 90003 NCERT Books for Class 12 90004 90018 90004 90003 90008 NCERT Exemplar 90002 90003 NCERT Exemplar Class 8 90004 90003 NCERT Exemplar Class 9 90004 90003 NCERT Exemplar Class 10 90004 90003 NCERT Exemplar Class 11 90004 90003 NCERT Exemplar Class 12 90004 90018 90004 90003 90008 RS Aggarwal 90002 90003 RS Aggarwal Class 12 Solutions 90004 90003 RS Aggarwal Class 11 Solutions 90004 90003 RS Aggarwal Class 10 Solutions 90004 90 003 RS Aggarwal Class 9 Solutions 90004 90003 RS Aggarwal Class 8 Solutions 90004 90003 RS Aggarwal Class 7 Solutions 90004 90003 RS Aggarwal Class 6 Solutions 90004 90018 90004 90003 90008 RD Sharma 90002 90003 RD Sharma Class 6 Solutions 90004 90003 RD Sharma Class 7 Solutions 90004 90003 RD Sharma Class 8 Solutions 90004 90003 RD Sharma Class 9 Solutions 90004 90003 RD Sharma Class 10 Solutions 90004 90003 RD Sharma Class 11 Solutions 90004 90003 RD Sharma Class 12 Solutions 90004 90018 90004 90003 90008 PHYSICS 90002 90003 Mechanics 90004 90003 Optics 90004 90003 Thermodynamics 90004 90003 Electromagnetism 90004 90018 90004 90003 90008 CHEMISTRY 90002 90003 Organic Chemistry 90004 90003 Inorganic Chemistry 90004 90003 Periodic Table 90004 90018 90004 90003 90008 MATHS 90002 90003 Pythagoras Theorem 90004 90003 Prime Numbers 90004 90003 Probability and Statistics 90004 90003 Fractions 90004 90003 Sets 90004 90003 Trigonometric Functions 90004 90003 Relations and Functions 90004 90003 Sequence and Series 90004 90003 Multiplication Tables 90004 90003 Determinants and Matrices 90004 90003 Profit And Loss 90004 90003 Polynomial Equations 90004 90003 Dividing Fractions 90004 90018 90004 90003 90008 BIOLOGY 90002 90003 Microbiology 90004 90003 Ecology 90004 90003 Zoology 90004 90018 90004 90003 90008 FORMULAS 90002 90003 Maths Formulas 90004 90003 Algebra Formulas 90004 90003 Trigonometry Formulas 90004 90003 Geometry Formulas 90004 90018 90004 90003 90008 CALCULATORS 90002 90003 Maths Calculators 90004 90003 Physics Calculators 90004 90003 Chemistry Calculators 90004 90018 90004 90003 90008 CBSE Sample Papers 90002 90003 CBSE Sample Papers for Class 6 90004 90003 CBSE Sample Papers for Class 7 90004 90003 CBSE Sample Papers for Class 8 90004 90003 CBSE Sample Papers for Class 9 90004 90003 CBSE Sample Papers for Class 10 90004 90003 CBSE Sample Papers for Class 11 90004 90003 CBSE Sample Pa pers for Class 12 90004 90018 90004 90003 90008 CBSE Previous Year Question Paper 90002 90003 CBSE Previous Year Question Papers Class 10 90004 90003 CBSE Previous Year Question Papers Class 12 90004 90018 90004 90003 90008 HC Verma Solutions 90002 90003 HC Verma Solutions Class 11 Physics 90004 90003 HC Verma Solutions Class 12 Physics 90004 90018 90004 90003 90008 Lakhmir Singh Solutions 90002 90003 Lakhmir Singh Class 9 Solutions 90004 90003 Lakhmir Singh Class 10 Solutions 90004 90003 Lakhmir Singh Class 8 Solutions 90004 90018 90004 90003 90008 CBSE Notes 90002 90003 Class 6 CBSE Notes 90004 90003 Class 7 CBSE Notes 90004 90003 Class 8 CBSE Notes 90004 90003 Class 9 CBSE Notes 90004 90003 Class 10 CBSE Notes 90004 90003 Class 11 CBSE Notes 90004 90003 Class 12 CBSE Notes 90004 90018 90004 90003 90008 CBSE Revision Notes 90002 90003 CBSE Class 9 Revision Notes 90004 90003 CBSE Class 10 Revision Notes 90004 90003 CBSE Class 11 Revision Notes 9000 4 90003 CBSE Class 12 Revision Notes 90004 90018 90004 90003 90008 CBSE Extra Questions 90002 90003 CBSE Class 8 Maths Extra Questions 90004 90003 CBSE Class 8 Science Extra Questions 90004 90003 CBSE Class 9 Maths Extra Questions 90004 90003 CBSE Class 9 Science Extra Questions 90004 90003 CBSE Class 10 Maths Extra Questions 90004 90003 CBSE Class 10 Science Extra Questions 90004 90018 90004 90003 90008 CBSE Class 90002 90003 Class 3 90004 90003 Class 4 90004 90003 Class 5 90004 90003 Class 6 90004 90003 Class 7 90004 90003 Class 8 90004 90003 Class 9 90004 90003 Class 10 90004 90003 Class 11 90004 90003 Class 12 90004 90018 90004 90003 Textbook Solutions 90004 90018 90004 90003 90008 NCERT Solutions 90002 90003 90008 NCERT Solutions For Class 11 90002 90003 NCERT Solutions For Class 11 Physics 90004 90003 NCERT Solutions For Class 11 Chemistry 90004 90003 NCERT Solutions For Class 11 Biology 90004 90003 NCERT Solutions For Class 11 Maths 90004 9 0003 NCERT Solutions Class 11 Accountancy 90004 90003 NCERT Solutions Class 11 Business Studies 90004 90003 NCERT Solutions Class 11 Economics 90004 90003 NCERT Solutions Class 11 Statistics 90004 90003 NCERT Solutions Class 11 Commerce 90004 90018 90004 90003 90008 NCERT Solutions For Class 12 90002 90003 NCERT Solutions For Class 12 Physics 90004 90003 NCERT Solutions For Class 12 Chemistry 90004 90003 NCERT Solutions For Class 12 Biology 90004 90003 NCERT Solutions For Class 12 Maths 90004 90003 NCERT Solutions Class 12 Accountancy 90004 90003 NCERT Solutions Class 12 Business Studies 90004 90003 NCERT Solutions Class 12 Economics 90004 90003 NCERT Solutions Class 12 Accountancy Part 1 90004 90003 NCERT Solutions Class 12 Accountancy Part 2 90004 90003 NCERT Solutions Class 12 Micro-Economics 90004 90003 NCERT Solutions Class 12 Commerce 90004 90003 NCERT Solutions Class 12 Macro-Economics 90004 90018 90004 90003 90008 NCERT Solutions For Class 4 90002 90003 NCERT Solutions For Class 4 Maths 90004 90003 NCERT Solutions For Class 4 EVS 90004 90018 90004 90003 90008 NCERT Solutions For Class 5 90002 90003 NCERT Solutions For Class 5 Maths 90004 90003 NCERT Solutions For Class 5 EVS 90004 90018 90004 90003 90008 NCERT Solutions For Class 6 90002 90003 NCERT Solutions For Class 6 Maths 90004 90003 NCERT Solutions For Class 6 Science 90004 90003 NCERT Solutions For Class 6 Social Science 90004 90003 NCERT Solutions for Class 6 English 90004 90018 90004 90003 90008 NCERT Solutions For Class 7 90002 90003 NCERT Solutions For Class 7 Maths 90004 90003 NCERT Solutions For Class 7 Science 90004 90003 NCERT Solutions for Class 7 Social Science 90004 90003 NCERT Solutions for Class 7 English 90004 90018 90004 90003 90008 NCERT Solutions For Class 8 90002 90003 NCERT Solutions For Class 8 Maths 90004 90003 NCERT Solutions For Class 8 Science 90004 90003 NCERT Solutions for Class 8 Social Science 90004 90003 NCERT Solutio ns for Class 8 English 90004 90018 90004 90003 90008 NCERT Solutions For Class 9 90002 90003 NCERT Solutions For Class 9 Social Science 90004 90018 90004 90003 90008 NCERT Solutions For Class 9 Maths 90002 90003 NCERT Solutions For Class 9 Maths Chapter 1 90004 90003 NCERT Solutions For Class 9 Maths Chapter 2 90004 90003 NCERT Solutions For Class 9 Maths Chapter 3 90004 90003 NCERT Solutions For Class 9 Maths Chapter 4 90004 90003 NCERT Solutions For Class 9 Maths Chapter 5 90004 90003 NCERT Solutions For Class 9 Maths Chapter 6 90004 90003 NCERT Solutions For Class 9 Maths Chapter 7 90004 90003 NCERT Solutions For Class 9 Maths Chapter 8 90004 90003 NCERT Solutions For Class 9 Maths Chapter 9 90004 90003 NCERT Solutions For Class 9 Maths Chapter 10 90004 90003 NCERT Solutions For Class 9 Maths Chapter 11 90004 90003 NCERT Solutions For Class 9 Maths Chapter 12 90004 90003 NCERT Solutions For Class 9 Maths Chapter 13 90004 90003 NCERT Solutions For Class 9 Maths Chapter 14 90004 90003 NCERT Solutions For Class 9 Maths Chapter 15 90004 90018 90004 90003 90008 NCERT Solutions For Class 9 Science 90002 90003 NCERT Solutions for Class 9 Science Chapter 1 90004 90003 NCERT Solutions for Class 9 Science Chapter 2 90004 90003 NCERT Solutions for Class 9 Science Chapter 3 90004 90003 NCERT Solutions for Class 9 Science Chapter 4 90004 90003 NCERT Solutions for Class 9 Science Chapter 5 90004 90003 NCERT Solutions for Class 9 Science Chapter 6 90004 90003 NCERT Solutions for Class 9 Science Chapter 7 90004 90003 NCERT Solutions for Class 9 Science Chapter 8 90004 90003 NCERT Solutions for Class 9 Science Chapter 9 90004 90003 NCERT Solutions for Class 9 Science Chapter 10 90004 90003 NCERT Solutions for Class 9 Science Chapter 12 90004 90003 NCERT Solutions for Class 9 Science Chapter 11 90004 90003 NCERT Solutions for Class 9 Science Chapter 13 90004 90003 NCERT Solutions for Class 9 Science Chapter 14 90004 90003 NCERT Solutions for Class 9 Science Chapter 15 90004 90018 90004 90003 90008 NCERT Solutions For Class 10 90002 90003 NCERT Solutions for Class 10 Social Science 90004 90018 90004 90003 90008 NCERT Solutions for Class 10 Maths 90002 90003 NCERT Solutions for Class 10 Maths Chapter 1 90004 90003 NCERT Solutions for Class 10 Maths Chapter 2 90004 90003 NCERT Solutions for Class 10 Maths Chapter 3 90004 90003 NCERT Solutions for Class 10 Maths Chapter 4 90004 90003 NCERT Solutions for Class 10 Maths Chapter 5 90004 90003 NCERT Solutions for Class 10 Maths Chapter 6 90004 90003 NCERT Solutions for Class 10 Maths Chapter 7 90004 90003 NCERT Solutions for Class 10 Maths Chapter 8 90004 90003 NCERT Solutions for Class 10 Maths Chapter 9 90004 90003 NCERT Solutions for Class 10 Maths Chapter 10 90004 90003 NCERT Solutions for Class 10 Maths Chapter 11 90004 90003 NCERT Solutions for Class 10 Maths Chapter 12 90004 90003 NCERT Solutions for Class 10 Maths Chapter 13 90004 90003 NCERT Sol utions for Class 10 Maths Chapter 14 90004 90003 NCERT Solutions for Class 10 Maths Chapter 15 90004 90018 90004 90003 90008 NCERT Solutions for Class 10 Science 90002 90003 NCERT Solutions for Class 10 Science Chapter 1 90004 90003 NCERT Solutions for Class 10 Science Chapter 2 90004 90003 NCERT Solutions for Class 10 Science Chapter 3 90004 90003 NCERT Solutions for Class 10 Science Chapter 4 90004 90003 NCERT Solutions for Class 10 Science Chapter 5 90004 90003 NCERT Solutions for Class 10 Science Chapter 6 90004 90003 NCERT Solutions for Class 10 Science Chapter 7 90004 90003 NCERT Solutions for Class 10 Science Chapter 8 90004 90003 NCERT Solutions for Class 10 Science Chapter 9 90004 90003 NCERT Solutions for Class 10 Science Chapter 10 90004 90003 NCERT Solutions for Class 10 Science Chapter 11 90004 90003 NCERT Solutions for Class 10 Science Chapter 12 90004 90003 NCERT Solutions for Class 10 Science Chapter 13 90004 90003 NCERT Solutions for Class 10 Science Chapter 14 90004 90003 NCERT Solutions for Class 10 Science Chapter 15 90004 90003 NCERT Solutions for Class 10 Science Chapter 16 90004 90018 90004 90003 NCERT Syllabus 90004 90003 NCERT 90004 90018 90004 90003 90008 Commerce 90002 90003 90008 Class 11 Commerce Syllabus 90002 90003 Class 11 Accountancy Syllabus 90004 90003 Class 11 Business Studies Syllabus 90004 90003 Class 11 Economics Syllabus 90004 90018 90004 90003 90008 Class 12 Commerce Syllabus 90002 90003 Class 12 Accountancy Syllabus 90004 90003 Class 12 Business Studies Syllabus 90004 90003 Class 12 Economics Syllabus 90004 90018 90004 90003 90008 Commerce Sample Papers 90002 90003 Class 11 Commerce Sample Papers 90004 90003 Class 12 Commerce Sample Papers 90004 90018 90004 90003 90008 TS Grewal Solutions 90002 90003 TS Grewal Solutions Class 12 Accountancy 90004 90003 TS Grewal Solutions Class 11 Accountancy 90004 90018 90004 90003 Statement Of Cash Flows 90004 90003 90004 90018 90 004 90018 90004 90018 90004 90018.90000 Area of Squares Worksheets 90001 90002 Designed for children of 3rd grade, 4th grade, and 5th grade, these area of a square worksheet PDFs feature topics like finding the area of a square whose dimensions are given as integers, decimals and fractions, finding the side length, determining the area using the perimeter and vice versa, finding the length of the diagonal using the given area and area using the diagonal length and much more to bolster your practice. Our free worksheets are a compulsive try! 90003 90004
90002 Area of Squares | Integers — Type 1 90003
90002 Calculate the area of the square by plugging in the value of the side length (a) in the formula Area = a 90008 2 90009, in these finding the area of a square worksheets for grade 3 and grade 4; providing two levels.90003
90002 Two levels of difficulty with 5 worksheets each 90003 90013
90002 Area of Squares | Integers — Type 2 90003
90002 Level up with this printable set of finding the area of a square worksheets offering exercises as geometrical figures and in word format. 90003
90002 Two levels of difficulty with 5 worksheets each 90003 90020
90002 Area of Squares | Decimals 90003
90002 Reaffirm the concept of finding the area of a square with these worksheets. The dimensions of the square are presented as decimals.Find the area by squaring the given side lengths. 90003
90002 Two different types with 5 worksheets each 90003 90027
90002 Area of Squares | Fractions 90003
90002 Figure out the area of the square in these worksheets for grade 5 presented as figures and in word format using the side lengths given as fractions; an alternate way to test the skills acquired. 90003
90002 Two different types with 5 worksheets each 90003 90034
90002 Find the Side length 90003
90002 These self-explanatory pdf worksheets for 4th grade and 5th grade children comprise examples and ample practice exercises to calculate the side length of the square by finding the square root of the given area.90003
90002 Type: Integers, Decimals (5 worksheets each) 90003 90041
90002 Area using the diagonal and vice-versa 90003
90002 Substitute the known values in the formula Area = d 90008 2 90009/2 in these two-part worksheets. Find the length of the diagonal using the area in Part A, and find the area using the diagonal length in Part B. 90003 .90000 Area and Perimeter of a Square. (Coordinate Geometry) 90001 Area and Perimeter of a Square. (Coordinate Geometry) — Math Open Reference The area and perimeter of a square can be found given the
90002
coordinates
of its
vertices (corners). 90003
Try this
Drag any vertex of the square below. It will remain a square and its dimensions calculated from its coordinates.
You can also drag the origin point at (0,0) or the square itself to move it.90004 90005 Area 90006
90003
The area of a square is calculated in the usual way once the length of a side is found.
See Square definition (coordinate geometry) to see how the side length is found.
Once the side length is known the area is found by multiplying the side length by itself in the usual way.
The formula for the area is: where 90008 s 90009 is the length of any side (they are all the same). 90004 90005 The «diagonals» method to find area 90006
90003
If you know the length of a diagonal, the area is given by: where 90002 90015 90008 d 90009 90018 is the length of either diagonal
90004 90003
The length of a diagonal can be found by using the the methods described in
Distance between two points to find the distance between say A and C in the figure above.90004 90005 Perimeter 90006
90003
A square has four sides which are all the same length.
The perimeter of a square (the total distance around the edge)
is therefore the four times the length of any side.
See Square definition (coordinate geometry) to see how the side length is calculated. The formula for the perimeter is where 90008 s 90009 is the length of any side (they are all the same). 90004 90005 Example 90006
The example below assumes you know how to calculate the side length of the square, as described in
Square (Coordinate Geometry).In the figure above, click ‘reset’. 90030
90031 90008 The side length 90009 of the square is the distance between the points A and B. (Or any two adjacent vertices).
Here, this is 22.
90034 90031 90008 Area 90009 is the side length times itself, or 22 x 22 = 484
90034 90031 90008 Perimeter 90009 is four times the side length or 4 x 22 = 88
90034
90043 90005 Things to try 90006 90046
90031 Click on «hide details» and «rotated» then drag the vertices of the square around to create an arbitrary size.From the coordinates of the corner points, calculate the side length, then the area and perimeter of the square.
Then click on «show details» to check your result. (The results shown above are rounded off to one decimal place for clarity)
90034
90031
Click «reset». Create a square that has perimeter of approximately 40, note the area.
90034
90031
Create a square that has perimeter of twice that, or 80, and note the area.
Notice how the area increases more rapidly than the perimeter.The perimeter merely doubles, but the area increases by four times.
90034
90053 90005 Limitations 90006
90003
In the interest of clarity in the applet above, the coordinates are rounded off to integers and the lengths rounded to one decimal place.
This can cause calculatioons to be slightly off.
90004 90003
For more see
Teaching Notes
90004 90005 Other Coordinate Geometry topics 90006 90003
(C) 2011 Copyright Math Open Reference.90002 All rights reserved
90004 .
b — ширина
P — периметр
S — площадь
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
Задача 1Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
Задача 10
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
Задачи на периметр и площадь для 4 класса
Задачи на периметр и площадь для 4 класса
Рубрики Logical words, Алгебра
Периметр — сумма сторон
Площадь — умножение сторон
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Задача 1
Найди периметр квадрата со стороной 8 см.
Решение:
8 · 4 = 32 (см)
Ответ: периметр квадрата 32 см.
Задача 2
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: длина прямоугольника 9 см.
Задача 3
Длина бассейна прямоугольной формы 15 м.
Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: периметр бассейна 46 метров
Задача 4
Периметр квадрата 8 см.
Из трех таких квадратов сложили прямоугольник.
Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: периметр прямоугольника 16 см.
Задача 5
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см.
На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: ученик ошибся на 3 см²
Задача 6
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше.
Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ:площадь окна 32 дм²

Пример.


Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
















- Решение:
- 1) 8 ∙ 7 = 56
- Ответ: Площадь прямоугольника 56 м².
- Решение:
- 1) 1) 64 : 8 = 8 (сторна витрины)
- 2) 2) 8 ∙ 4 = 32 (периметр витрины)
- Ответ: 32 м.
- Решение:
- 1) 1) 90 ∙ 7 = 630
- Ответ: 630 см².
- Решение:
- 1) 48 ∙ 30 = 1440 (площадь первого участка)
- 2) 30 + 6 = 36 (ширина второго участка)
- 3) 1440 : 36 = 40
- Ответ: длина второго участка 40 м.
- Решение:
- 1) 36 ∙ 20 = 720 (площадь первого участка)
- 2) 36 – 6 = 30 (длина другого участка)
- 3) 720 : 30 = 24
- Ответ: ширина другого участка 24 м.
- Решение:
- 1) 4 ∙ 4 = 16 (площадь квадрата)
- 2) 2 ∙ 6 = 12 (площадь прямоугольника)
- 3) 16 — 12 = 4
- Ответ: площадь квадратата больше на 4 см.
- Решение:
- 1) 6 ∙ 6 = 36
- 2) 6 ∙ 4 = 24
- Ответ: площадь квадрата 36 см², периметр квадрата 24 см.
- Решение:
- 1) 7 ∙ 5 = 35
- 2) 7 ∙ 2 = 14
- 3) 5 ∙ 2 = 10
- 4) 10 + 14 = 24
- Ответ: площадь прямоугольника 35 м², периметр прямоугольника 24 см.
- Решение:
- 1) 8 ∙ 8 = 64 (площадь клумбы)
- 2) 64 : 16 = 4(1/16 клумбы)
- 3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
- 4) 64 – 28 = 36
- Ответ: незабудками засажено 36 м².
- Решение:
- 1) 6 ∙ 2 = 12
- 2) 18 – 12 = 6
- 3) 6 : 2 = 3 (ширина прямоугольника)
- 4) 3 ∙ 6 = 18
- Ответ: площадь прямоугольника 18 м².
- Решение:
- 1) 4800 : 60 = 80 (длина стола)
- 2) 60 ∙ 2 = 120 см
- 3) 80 ∙ 2 = 160 см
- 4) 120 + 160 = 280 см
- Ответ: периметр стола 280 см.
- Решение:
- 1) 5 ∙ 2 = 10
- 2) 40 – 10 = 30
- 3) 30 : 2 = 15 (другая сторона прямоугольника)
- 4) 5 ∙ 15 = 75
- Ответ: площадь прямоугольника 75 см².
- Решение:
- 1) 49 : 7 = 7 (сторона квадрата)
- 2) 7 ∙ 4 = 28 (периметр квадрата)
- Ответ: периметр квадрата равен 28 дм.
- Решение:
- 1) 4 ∙ 2 = 8 (длина окна)
- 2) 4 ∙ 8 = 32
- Ответ: площадь окна равна 32 м².
- Решение:
- 1) 54 ∙ 48 = 2592 (площадь участка земли)
- 2) 2592 : 9 = 288 (1/9 площади)
- 3) 288 ∙ 5 = 1440 (5/9 площади)
- 4) 2592 – 1440 = 1152
- Ответ: капустой засадили 1152 м².
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
 Решение:
Решение:разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.
 Применив формулы площади треугольника, квадрата и прямоугольника легко решим поставленную задачу
Применив формулы площади треугольника, квадрата и прямоугольника легко решим поставленную задачуФигура A
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура B
S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²
Ответ: площадь фигуры B 20,5 см²
Фигура C
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²
Ответ: площадь фигуры C 30,5 см²
Фигура D
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура E
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²
Ответ: площадь фигуры E 12 см²