Производная сложной функции
Если g(x) и f(u) – дифференцируемые функции своих аргументов соответственно в точках x и u = g(x), то сложная функция также дифференцируема в точке x и находится по формуле
Типичная ошибка при решении задач на производные — машинальное перенесение правил дифференцирования простых функций на сложные функции. Будем учиться избегать этой ошибки.
Посмотрите на формулу 9 в таблице производных. Исходная функция является функцией от функции, причём аргумент x является аргументом лишь второй функции, а вторая функция является аргументом первой функции, или, согласно более строгому определению — промежуточным аргументом по независимой переменной x.
А теперь посмотрите на картинку ниже, которая иллюстрирует решение задач на сложные производные по аналогии с простым примером из кулинарии — приготовлении запечёных яблок, фаршированных ягодами.

Итак, «яблоко» — это функция, аргументом которой является промежуточный аргумент, а промежуточный аргумент по независимой переменной x, в свою очередь, является «фаршем» (ягодами). Представим себе, что решая задачи на производные сложной функции, сначала помещаем яблоко с фаршем в особую (физико-математическую) духовку и устанавливаем режим 1. При таком режиме духовка воздействует только на «яблоко», поскольку нужно, допустим, больше пропечь яблоко, а фарш из ягод оставить более сочным, то есть обрабатывать в другом режиме. Итак, в при режиме 1 обрабатывается яблоко, а фарш остаётся незатронутым, или, ближе к нашим задачам, находим производную функции лишь от промежуточного аргумента, то есть, «яблока». Затем в духовке устанавливается режим 2, который воздействует только на фарш, иначе говоря, записываем производную функции, являющейся промежуточным аргументом по независимой переменной x. И, в конце концов, записываем произведение производной «яблока» и производной «фарша». Можно подавать!
Пример 1.Найти производную функции
Сначала определим, где здесь «яблоко», то есть функция по промежуточному аргументу u, а где «фарш», то есть промежуточный аргумент u по независимой переменной x. Определяем: возведение в степень — это функция по промежуточному аргументу, то есть «яблоко», а выражение в скобках (разность двух тригонометрических функций) — это промежуточный аргумент, то есть «фарш».
Тогда
Далее по таблице производных (производная суммы или разности, производные синуса и косинуса) находим:
Нахождение производной сложной логарифмической функции имеет свои особенности, поэтому у нас есть и урок «Производная логарифмической функции».
Пример 2.Найти производную функции
Неправильное решение: вычислять натуральный логарифм каждого слагаемого в скобках и искать сумму производных:
Правильное решение: опять определяем, где «яблоко», а где «фарш». Здесь натуральный логарифм от выражения в скобках — это «яблоко», то есть функция по промежуточному аргументу u, а выражение в скобках — «фарш», то есть промежуточный аргумент u по независимой переменной x.
Тогда (применяя формулу 14 из таблицы производных)
Во многих реальных задачах выражение с логарифмом бывает несколько сложнее, поэтому и есть урок «Производная логарифмической функции».
Пример 3.Найти производную функции
Неправильное решение:
Правильное решение. В очередной раз определяем, где «яблоко», а где «фарш». Здесь косинус от выражения в скобках (формула 7 в таблице производных)- это «яблоко», оно готовится в режиме 1, воздействующем только на него, а выражение в скобках (производная степени — номер 3 в таблице производных) — это «фарш», он готовится при режиме 2, воздействующей только на него. И как всегда соединяем две производные знаком произведения. Результат:
Производная сложной логарифмической функции — частое задание на контрольных работах, поэтому настоятельно рекомендуем посетить урок «Производная логарифмической функции».
Первые примеры были на сложные функции, в которых промежуточный аргумент по независимой переменной был простой функцией. Но в практических заданиях нередко требуется найти производную сложной функции, где промежуточный аргумент или сам является сложной функцией или содержит такую функцию. Что делать в таких случаях? Находить производные таких функций по таблицам и правилам дифференцирования. Когда найдена производная промежуточного аргумента, она просто подставляется в нужное место формулы. Ниже – два примера, как это делается.
Кроме того, полезно знать следующее. Если сложная функция может быть представлена в виде цепочки из трёх функций
,
то её производную следует находить как произведение производных каждой из этих функций:
.
Для решения многих ваших домашних заданий может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.
Пример 4.Найти производную функции
Применяем правило дифференцирования сложной функции, не забывая, что в полученном произведении производных промежуточный аргумент по независимой переменной x не меняется:
Готовим второй сомножитель произведения и применяем правило дифференцирования суммы:
Второе слагаемое — корень, поэтому
Таким образом получили, что промежуточный аргумент, являющийся суммой, в качестве одного из слагаемых содержит сложную функцию: возведение в степень — сложная функция, а то, что возводится в степень — промежуточный аргумент по независимой переменной x.
Поэтому вновь применим правило дифференцирования сложной функции:
Степень первого сомножителя преобразуем в корень, а дифференцируя второй сомножитель, не забываем, что производная константы равна нулю:
Тогда
Пример 5.Найти производную функции
Сначала воспользуемся правилом дифференцирования суммы:
Получили сумму производных двух сложных функций. Находим первую из них:
Здесь возведение синуса в степень — сложная функция, а сам синус — промежуточный аргумент по независимой переменной x. Поэтому воспользуемся правилом дифференцирования сложной функции, попутно вынося множитель за скобки:
Теперь находим второе слагаемое из образующих производную функции y:
Здесь возведение косинуса в степень — сложная функция f[g(x)], а сам косинус — промежуточный аргумент по независимой переменной x. Снова воспользуемся правилом дифференцирования сложной функции:
Результат — требуемая производная:
Для сложных функций на основании правила дифференцирования сложной функции формула производной простой функции принимает другой вид.
Поделиться с друзьями
Весь блок «Производная»
function-x.ru
Производная сложной функции — примеры решений
Здесь мы приводим примеры вычисления производных от следующих функций:
; ; ; ; .
Если функцию можно представить как сложную функцию в следующем виде:
,
то ее производная определяется по формуле:
.
В приводимых ниже примерах, мы будем записывать эту формулу в следующем виде:
.
где .
Здесь нижние индексы или , расположенные под знаком производной, обозначают переменные, по которой выполняется дифференцирование.
Обычно, в таблицах производных, приводятся производные функций от переменной x. Однако x – это формальный параметр. Переменную x можно заменить любой другой переменной. Поэтому, при дифференцировании функции от переменной , мы просто меняем, в таблице производных, переменную x на переменную u.
Простые примеры
Пример 1
Найти производную сложной функции
.
Решение
Запишем заданную функцию в эквивалентном виде:
.
В таблице производных находим:
;
.
По формуле производной сложной функции имеем:
.
Здесь .
Ответ
.
Пример 2
Найти производную
.
Решение
Выносим постоянную 5 за знак производной и из таблицы производных находим:
.
Применяем формулу производной сложной функции:
.
Здесь .
Ответ
.
Пример 3
Найдите производную
.
Решение
Выносим постоянную –1 за знак производной и из таблицы производных находим:
;
Из таблицы производных находим:
.
Применяем формулу производной сложной функции:
.
Здесь .
Ответ
.
Более сложные примеры
В более сложных примерах мы применяем правило дифференцирования сложной функции несколько раз. При этом мы вычисляем производную с конца. То есть разбиваем функцию на составные части и находим производные самых простых частей, используя таблицу производных. Также мы применяем правила дифференцирования суммы, произведения и дроби. Затем делаем подстановки и применяем формулу производной сложной функции.
Пример 4
Найдите производную
.
Решение
Выделим самую простую часть формулы и найдем ее производную. .
Применяем правило дифференцирования сложной функции.
.
Здесь мы использовали обозначение
.
Находим производную следующей части исходной функции, применяя полученные результаты. Применяем правило дифференцирования суммы:
.
Еще раз применяем правило дифференцирования сложной функции.
.
Здесь .
Ответ
.
Пример 5
Найдите производную функции
.
Решение
Выделим самую простую часть формулы и из таблицы производных найдем ее производную. .
Применяем правило дифференцирования сложной функции.
.
Здесь
.
Дифференцируем следующую часть, применяя полученные результаты.
.
Здесь
.
Дифференцируем следующую часть.
.
Здесь
.
Теперь находим производную искомой функции.
.
Здесь
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Производная сложной функции.
Если , где, т.е. еслизависит от через посредство промежуточного аргумента , то называется сложной функцией от.
Определение 4.9. Производная сложной функции равна произведению её производной по промежуточному аргументу на производную этого аргумента по независимой переменной: или
Так, если , то формулы дифференцирования будут иметь следующий вид:
Пример №9: Найти производные следующих функций:
;
;
;
Решение:
Полагая , где, и применяя правило дифференцирования сложной функции, имеем:; ;
Полагая , получим:
Полагаем :
Задания: Найти производные следующих функций:
;
;
-
;
;
Производные показательных и логарифмических функций.
Общие формулы и их частные виды:
Для дифференцирования логарифмической функции с основанием можно предварительно преобразовать её в логарифмическую функцию с основаниемпо формуле
Пример №10: Найти производные следующих функций:
;
;
.
Решение:
;
;
.
;
;
.
Производные высших порядков
Если есть производная от функции, то производная отназывается второй производной, или производной второго порядка от первоначальной функции, и обозначается, или, или
Пример №11: Для данных функций найти производные указанных порядков:
, ;
, ;
, .
Решение:
Дифференцируя функцию , получим:. Дифференцируя производную, получим:. Дифференцируя вторую производную, получим.
. Для нахождения следующих производных здесь полезно ввести отрицательный показатель степени. ,,,.
, . При найдём .
Задания:
, ; 2),.
Производные неявной функции.
Если есть неявная функция от, т.е. задана уравнением, не разрешенным относительно, то для нахождения производнойнужно продифференцировать пообе части равенства, помня, чтоесть функция от, и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть оти;.
Пример №12: Для данных неявных функций найти производные указанного порядка:
, ;
, ;
, .
Решение:
Дифференцируем по обе части равенства, гдеесть функция от, получим:
Дифференцируя по , получим:. Подставляя заданное значениев исходное уравнение, найдём два соответствующих ему значения:,. Поэтому прии производнаяимеет два значения:;.
Прологарифмируем обе части данного уравнения (по основанию ), затем дифференцируем по, рассматриваякак функцию:;;. Отсюда найдём.
Задания:
, ;
, ;
, .
Касательная и нормаль к плоской кривой. Угол между двумя кривыми.
Если плоская кривая отнесена к прямоугольной системе координат, то уравнения касательной и нормали к ней в точке имеют вид: ; ,
где — значение в точкепроизводнойиз уравнений кривой.
Направление кривой в каждой её точке определяется направлением касательной к ней в этой точке. Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения по формуле:
, где и- угловые коэффициенты касательных к кривым в точке их пересечения, т.е. частные значения в точкепроизводных отпоиз уравнений этих кривых:;.
Задания: Составить уравнения касательной и нормали:
к параболе в точке, где;
к окружности в точках пересечения её с осью.
studfiles.net
Сложная функция. Производная сложной функции
 В этой статье мы будем говорить о таком важном математическом понятии, как сложная функция, и учиться находить производную сложной функции.
В этой статье мы будем говорить о таком важном математическом понятии, как сложная функция, и учиться находить производную сложной функции.
Прежде чем учиться находить производную сложной функции, давайте разберемся с понятием сложной функции, что это такое, «с чем ее едят», и «как правильно ее готовить».
Рассмотрим произвольную функцию, например, такую:
Заметим, что аргумент , стоящий в правой и левой части уравнения функции — это одно и то же число, или выражение.
Вместо переменной мы можем поставить, например, такое выражение: . И тогда мы получим функцию
.
Назовем выражение промежуточным аргументом, а функцию — внешней функцией. Это не строгие математические понятия, но они помогают уяснить смысл понятия сложной функции.
Строгое определение понятия сложной функции звучит так:
Пусть функция определена на множестве и — множество значений этой функции. Пусть, множество (или его подмножество) является областью определения функции . Поставим в соответствие каждому из число . Тем самым на множестве будет задана функция . Ее называют композицией функций или сложной функцией.
В этом определении, если пользоваться нашей терминологией, — внешняя функция, — промежуточный аргумент.
Производная сложной функции находится по такому правилу:
Чтобы было более понятно, я люблю записывать это правило в виде такой схемы:
В этом выражении с помощью обозначена промежуточная функция.
Итак. Чтобы найти производную сложной функции, нужно
1. Определить, какая функция является внешней и найти по таблице производных соответствующую производную.
2. Определить промежуточный аргумент.
В этой процедуре наибольшие затруднения вызывает нахождение внешней функции. Для этого используется простой алгоритм:
а. Запишите уравнение функции.
б. Представьте, что вам нужно вычислить значение функции при каком-то значении х. Для этого вы подставляете это значение х в уравнение функции и производите арифметические действия. То действие, которое вы делаете последним и есть внешняя функция.
Например, в функции
последнее действие — возведение в степень.
Найдем производную этой функции. Для этого запишем промежуточный аргумент
как
Получим
Ищем в таблице производных производную показательной функции:
Получим:
(1)
Теперь наша задача найти производную функции
Заметим, что здесь мы опять имеем дело со сложной функцией. В этом выражении последнее действие — возведение в квадрат, а промежуточный аргумент .
Получаем:
Смотрим в таблице производных производную синуса:
Получаем:
Подставим полученное значение производной в выражение (1):
И, наконец, упростим выражение, вспомнив формулу синуса двойного аргумента:
Таким образом,
Заметим, что функции иногда похожи на матрешку: промежуточный аргумент сам является сложной функции. Но тогда при нахождении производной промежуточного аргумента, нужно вновь применить правило нахождения производной сложной функции.
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Производная сложной функции. Примеры решений
На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятияКак найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень иликакие-нибудьмоменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но явсе-такипостараюсь изложить его просто и доступно.
На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.
Смотрим в таблицу на правило (№5) дифференцирования сложной функции:
Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции –и, причем функция, образно говоря, вложена в функцию. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.
Функцию я буду называтьвнешней функцией, а функцию –
внутренней (или вложенной) функцией.
! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю
неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.
Для того, чтобы прояснить ситуацию, рассмотрим: Пример 1
Найти производную функции
Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
В данном примере уже из моих объяснений интуитивно понятно, что функция – это сложная функция, причем многочленявляется внутренней функцией (вложением), а– внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобыразобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде понятно, что под синус вложен многочлен. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения при(вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет
выполнить следующее действие: , поэтому многочлени будет внутренней функцией:
Во вторую очередь нужно будет найти, поэтому синус – будет внешней функцией:
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции.
Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:
Сначала находим производную внешней функции(синуса), смотрим на таблицу производных элементарных функций и замечаем, что.Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
Обратите внимание, что внутренняя функция не изменилась, её мы не трогаем.
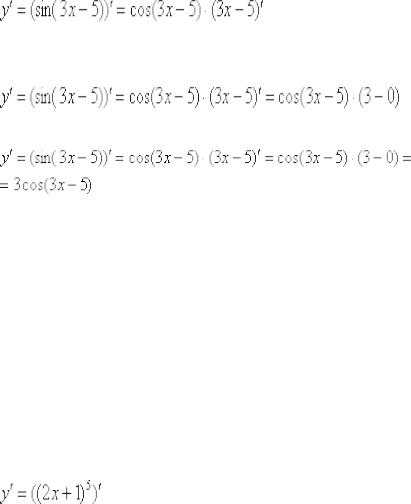
Ну и совершенно очевидно, что
Результат применения формулы в чистовом оформлении выглядит так:
Далее мы берем производную внутренней функции, она очень простая:
Постоянный множитель обычно выносят в начало выражения:
Готово
Если осталось какое-либонедопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 2
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).Пример 3
Найти производную функции Как всегда записываем:
Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение
выражения при. Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:
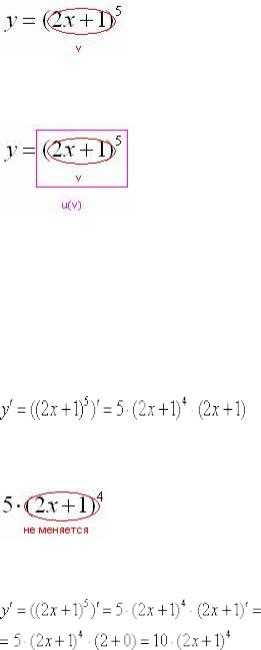
, значит, многочлен– и есть внутренняя функция:
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу:. Повторяем еще раз:любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции
следующий:
Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функцияу нас не меняется:
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:

Пример 4
Найти производную функции
Это пример для самостоятельного решения (ответ в конце урока).
Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?
Пример 5
а) Найти производную функции
б) Найти производную функции
Пример 6
Найти производную функции Здесь у нас корень, а для того, чтобы продифференцировать корень,
его нужно представить в виде степени . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
Анализируя функцию, приходим к выводу, что сумма трех слагаемых
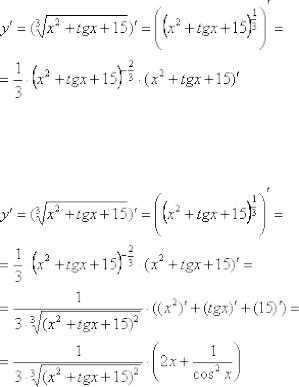
– это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :
Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:
Готово. Можно еще в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).
Пример 7
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).
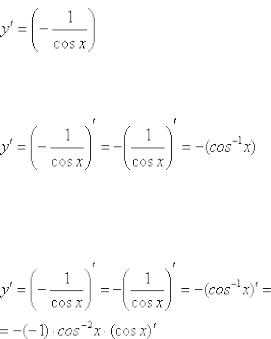
Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования
частного , но такое решение будет выглядетькак извращение необычно. Вот характерный пример:
Пример 8
Найти производную функции Здесь можно использовать правило дифференцирования частного
, но гораздо выгоднее найти производную через правило дифференцирования сложной функции:
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :
Находим производную внутренней функции, косинус сбрасываем
обратно вниз:
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила , ответы должны совпасть.
Пример 9
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).
До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрешки, одна в другую, вложены сразу 3, а то и 4-5функций.
Пример 10
Найти производную функции
Разбираемся во вложениях этой функции. Пробуем вычислить выражение с помощью подопытного значения. Как бы мы считали на калькуляторе?
Сначала нужно найти , значит, арксинус – самое глубокое вложение:

Затем этот арксинус единицы следует возвести в квадрат :
И, наконец, семерку возводим в степень :
То есть, в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.
Начинаем решать
Согласно правилу сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции:Единственное отличие – вместо «икс» у нас сложное выражение, что не отменяет справедливость данной формулы. Итак, результат применения правила дифференцирования сложной функцииследующий:
Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции

сначала нужно взять производную от степени:
Теперь все просто, находим по таблице производную арксинуса и немного «причесываем» выражение:
Готово.
Пример 11
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).
На практике правило дифференцирования сложной функции почти всегда применяется в комбинации с остальными правилами дифференцирования.
Пример 12
Найти производную функции
Сначала используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу:
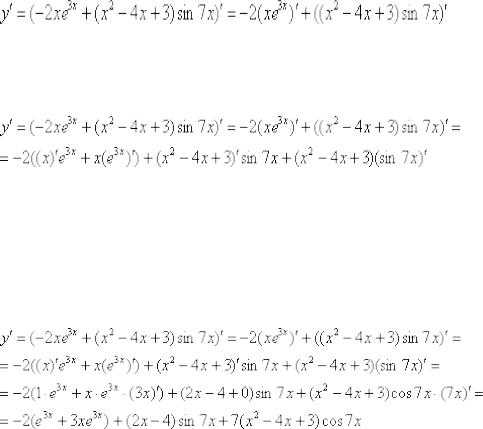
В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :
Замечаем, что под некоторыми штрихами у нас находятся сложные функции ,. Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу , получаем:
Готово.
! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.
Пример 13
Найти производную функции Это пример для самостоятельного решения (ответ в конце урока).
Пожалуй, хватит на сегодня. Хочется еще привести пример с дробью и сложной функцией, но такой пример принципиально ничем не отличается от двух последних заданий, единственное отличие –
вместо правила применяем правило.
Для закрепления темы рекомендую статью Сложные производные. Логарифмическая производная. Помимо рассмотрения дополнительных примеров, есть и новый материал! После изучения третьего урока вы будете очень уверенно себя чувствовать в ходе дальнейшего изучения математического анализа. Если задания покажутся слишком трудными (у всех разный уровень подготовки), то сначала посетите страницу Простейшие типовые задачи с производной, там рассмотрено ещё порядка15-типроизводных.
Желаю успехов!
Ответы:
Пример 2:
Пример 4: Указание: перед дифференцированием необходимо перенести степень наверх, сменив у показателя знак.
Пример 7:
Пример 9:
Пример 11:
Пример 13:
Сложные производные. Логарифмическая производная. Производная степеннопоказательной функции
Продолжаем повышать свою технику дифференцирования. На данном уроке мы закрепим пройденный материал, рассмотрим более сложные производные, а также познакомимся с новыми приемами и хитростями нахождения производной, в частности, с логарифмической производной.
Тем читателям, у кого низкий уровень подготовки, следует обратиться к статье Как найти производную? Примеры решений, которая позволит поднять свои навыки практически с нуля. Далее необходимо внимательно изучить страницуПроизводная сложной функции, понять и прорешатьвсе приведенные мной примеры. Данный урок логически третий по счету, и после его освоения Вы будете уверенно дифференцировать достаточно сложные функции. Нежелательно придерживаться позиции «Куда еще? Да и так хватит!», поскольку все примеры и приёмы решения взяты из реальных контрольных работ и часто встречаются на практике.
Начнем с повторения. На уроке Производная сложной функции мы рассмотрели ряд примеров с подробными комментариями. В ходе изучения дифференциального исчисления и других разделов математического анализа – дифференцировать придется очень часто, и не всегда бывает удобно (да и не всегда нужно) расписывать примеры очень подробно. Поэтому мы потренируемся в устном нахождении производных. Самым подходящими «кандидатами» для этого являются производные простейших из сложных функций, например:

По правилу дифференцирования сложной функции :
При изучении других тем матана в будущем такая подробная запись чаще всего не требуется, предполагается, что студент умеет находить подобные производные на автопилоте автомате. Представим, что в 3 часа ночи раздался телефонный звонок, и приятный голос спросил:
«Чему равна производная тангенса двух икс?». На это должен последовать почти мгновенный и вежливый ответ: .
Первый пример будет сразу предназначен для самостоятельного решения.
Пример 1
Найти следующие производные устно, в одно действие, например: . Для выполнения задания нужно использовать только
таблицу производных элементарных функций (если она еще не запомнилась). Если возникнут затруднения, рекомендую перечитать урок Производная сложной функции.
,,,
,,,
,,,
studfiles.net
Примеры нахождения производной сложной функции
Рассмотрим еще некоторые примеры нахождения производной сложной функции.
Решение:
Там, где возможно, перед дифференцированием примеры упрощаем:
Данная функция — сложная. Внешняя функция f=u³, внутренняя — выражение, стоящее в скобках. Дифференцируем по правилу дифференцирования сложной функции: Имеем:
2) При нахождении производных логарифмов во многих случаях возможно предварительное преобразование выражений с использованием свойств логарифмов, что позволяет существенно облегчить дифференцирование:
Здесь внешняя функция — ln u, внутренняя — выражение, стоящее под знаком логарифма. Внутренняя функция представляет собой дробь, поэтому для ее дифференцирования применяем правило нахождения производной частного:
Сокращаем числитель и знаменатель на (х²+1) и 2:
3) Здесь внешняя функция — f=arccos u, u — выражение с квадратным к0рнем. Дифференцируем:
4) Первое слагаемое — сложная показательная функция 3 в степени u, u=cos x.
Второе слагаемое дифференцируем по правилу нахождения производной произведения:
www.matematika.uznateshe.ru
Сложные производные. Логарифмическая производная. Производная степенно-показательной функции
Продолжаем повышать свою технику дифференцирования. На данном уроке мы закрепим пройденный материал, рассмотрим более сложные производные, а также познакомимся с новыми приемами и хитростями нахождения производной, в частности, с логарифмической производной.
Тем читателям, у кого низкий уровень подготовки, следует обратиться к статье Как найти производную? Примеры решений, которая позволит поднять свои навыки практически с нуля. Далее необходимо внимательно изучить страницу Производная сложной функции, понять и прорешать все приведенные мной примеры. Данный урок логически третий по счету, и после его освоения Вы будете уверенно дифференцировать достаточно сложные функции. Нежелательно придерживаться позиции «Куда еще? Да и так хватит!», поскольку все примеры и приёмы решения взяты из реальных контрольных работ и часто встречаются на практике.
Начнем с повторения. На уроке Производная сложной функциимы рассмотрели ряд примеров с подробными комментариями. В ходе изучения дифференциального исчисления и других разделов математического анализа – дифференцировать придется очень часто, и не всегда бывает удобно (да и не всегда нужно) расписывать примеры очень подробно. Поэтому мы потренируемся в устном нахождении производных. Самым подходящими «кандидатами» для этого являются производные простейших из сложных функций, например:
По правилу дифференцирования сложной функции :
При изучении других тем матана в будущем такая подробная запись чаще всего не требуется, предполагается, что студент умеет находить подобные производные на автомате. Представим, что в 3 часа ночи раздался телефонный звонок, и приятный голос спросил: «Чему равна производная тангенса двух икс?». На это должен последовать почти мгновенный и вежливый ответ:
.
Первый пример будет сразу предназначен для самостоятельного решения.
Пример 1
Найти следующие производные устно, в одно действие, например: . Для выполнения задания нужно использовать только таблицу производных элементарных функций (если она еще не запомнилась). Если возникнут затруднения, рекомендую перечитать урок Производная сложной функции.
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, ,
Ответы в конце урока
Сложные производные
После предварительной артподготовки будут менее страшны примеры, с 3-4-5 вложениями функций. Возможно, следующие два примера покажутся некоторым сложными, но если их понять (кто-то и помучается), то почти всё остальное в дифференциальном исчислении будет казаться детской шуткой.
Пример 2
Найти производную функции
Как уже отмечалось, при нахождении производной сложной функции, прежде всего, необходимо правильноРАЗОБРАТЬСЯ во вложениях. В тех случаях, когда есть сомнения, напоминаю полезный приём: берем подопытное значение «икс», например, и пробуем (мысленно или на черновике) подставить данное значение в «страшное выражение».
1) Сначала нам нужно вычислить выражение , значит, сумма – самое глубокое вложение.
2) Затем необходимо вычислить логарифм:
3) Далее косинус:
4) Потом косинус возвести в куб:
5) На пятом шагу разность:
6) И, наконец, самая внешняя функция – это квадратный корень:
Формула дифференцирования сложной функции применятся в обратном порядке, от самой внешней функции, до самой внутренней. Решаем:

Вроде без ошибок….
(1) Берем производную от квадратного корня.
(2) Берем производную от разности, используя правило
(3) Производная тройки равна нулю. Во втором слагаемом берем производную от степени (куба).
(4) Берем производную от косинуса.
(5) Берем производную от логарифма.
(6) И, наконец, берем производную от самого глубокого вложения .
Может показаться слишком трудно, но это еще не самый зверский пример. Возьмите, например, сборник Кузнецова и вы оцените всю прелесть и простоту разобранной производной. Я заметил, что похожую штуку любят давать на экзамене, чтобы проверить, понимает студент, как находить производную сложной функции, или не понимает.
Следующий пример для самостоятельного решения.
Пример 3
Найти производную функции
Подсказка: Сначала применяем правила линейности и правило дифференцирования произведения
Полное решение и ответ в конце урока.
Настало время перейти к чему-нибудь более компактному и симпатичному.
Не редка ситуация, когда в примере дано произведение не двух, и трёх функций. Как найти производную от произведения трёх множителей?
Пример 4
Найти производную функции
Сначала смотрим, а нельзя ли произведение трех функций превратить в произведение двух функций? Например, если бы у нас в произведении было два многочлена, то можно было бы раскрыть скобки. Но в рассматриваемом примере все функции разные: степень, экспонента и логарифм.
В таких случаях необходимо последовательноприменить правило дифференцирования произведения два раза
Фокус состоит в том, что за «у» мы обозначим произведение двух функций: , а за «вэ» – логарифм: . Почему так можно сделать? А разве – это не произведение двух множителей и правило не работает?! Ничего сложного нет:
Теперь осталось второй раз применить правило к скобке :
Можно еще поизвращаться и вынести что-нибудь за скобки, но в данном случае ответ лучше оставить именно в таком виде – легче будет проверять.
Готово.
Рассмотренный пример можно решить вторым способом:
Оба способа решения абсолютно равноценны.
Пример 5
Найти производную функции
Это пример для самостоятельного решения, в образце он решен первым способом.
Рассмотрим аналогичные примеры с дробями.
Пример 6
Найти производную функции
Здесь можно пойти несколькими путями:
или так:
Но решение запишется более компактно, если в первую очередь использовать правило дифференцирования частного , приняв за весь числитель:

В принципе, пример решён, и если его оставить в таком виде, то это не будет ошибкой. Но при наличии времени всегда желательно проверить на черновике, а нельзя ли ответ упростить?

Минус дополнительных упрощений состоит в том, что есть риск допустить ошибку уже не при нахождении производной, а при банальных школьных преобразованиях. С другой стороны, преподаватели нередко бракуют задание и просят «довести до ума» производную.
Более простой пример для самостоятельного решения:
Пример 7
Найти производную функции
Продолжаем осваивать приёмы нахождения производной, и сейчас мы рассмотрим типовой случай, когда для дифференцирования предложен «страшный» логарифм
Пример 8
Найти производную функции
Тут можно пойти длинным путём, используя правило дифференцирования сложной функции:
Но первый же шаг сразу повергает в уныние – предстоит взять неприятную производную от дробной степени , а потом ещё и от дроби .
Поэтому перед тем как брать производную от «навороченного» логарифма, его предварительно упрощают, используя известные школьные свойства:
! Если под рукой есть тетрадь с практикой, перепишите эти формулы прямо туда. Если тетради нет, перерисуйте их на листочек, поскольку оставшиеся примеры урока буду вращаться вокруг этих формул.
Само решение можно оформить примерно так:
Преобразуем функцию:
Находим производную:
Предварительное преобразование самой функции значительно упростило решение. Таким образом, когда для дифференцирования предложен подобный логарифм, то его всегда целесообразно «развалить».
А сейчас пара несложных примеров для самостоятельного решения:
Пример 9
Найти производную функции
Пример 10
Найти производную функции
Все преобразования и ответы в конце урока.
megaobuchalka.ru
