сложение и вычитание, умножение и деление
Сложение
При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.
Пример 1. Найти сумму рациональных чисел 2,5 и 3,2.
Решение: Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:
2,5 + 3,2 = 5,7.
Пример 2. Найти сумму отрицательных чисел (-2,5) и (-3,2).
Решение: Сначала надо сложить модули слагаемых:
2,5 + 3,2 = 5,7.
Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:
(-2,5) + (-3,2) = -5,7.
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4,7) + (+12) = 7,3, так как 12 — 4,7 = 7,3;
9 + (-15) = -6, так как 15 — 9 = 6.
Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю.
Примеры:
125 + (-125) = 0;
-34 + (+34) = 0.
Вычитание
Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.
Примеры:(+10) — (+3,4) = (+10) + (-3,4) = 6,6;
(+10) — (-3,4) = (+10) + (+3,4) = 13,4;
(-10) — (-3,4) = (-10) + (+3,4) = -6,6;
(-10) — (+3,4) = (-10) + (-3,4) = -13,4.
Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение
При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.
Примеры:
3 · 5 = 15;
3 · (-5) = -15;
-3 · 5 = -15;
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| · | — | = | — | |
| — | · | + | = | — |
| — | · | — | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 · (-1) = 1,5;
2,5 · (-1) = -2,5.
Деление
При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3;
15 : (-5) = -3;
-15 : 5 = -3;
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | — | = | — |
| — | : | + | = | — |
| — | : | — | = | + |
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число
При делении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 : (-1) = 1,5;
2,5 : (-1) = -2,5.
Действия с рациональными числами 🐲 СПАДИЛО.РУ
Что такое рациональные числа?Рациональные числа – это числа, которые можно представить в виде обыкновенной дроби, где a – целое число, а b – натуральное.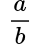
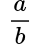
То есть все дробные и целые числа вместе образуют рациональные числа, так как любое целое можно представить в виде обыкновенной дроби, записав его в числитель, а в знаменателе надо написать 1.
Пример №1. Любые целые числа, например, 38, -24, 49 можно представить в виде обыкновенных дробей, их называют рациональными:
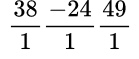
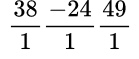
Действия с рациональными числами
Сложение (или вычитание) рационального числа и ноляДля любого рационального числа применимо правило сложения (или вычитания): а + 0 = 0, a — 0 = a
Пример №2. –25,7 + 0 = –25,7 или 0+(–67)= –67
Аналогичное правило работает и для вычитания нуля.
Пример №3. 45 – 0=45 или – 67 – 0 = – 67
Как складывать отрицательные числа?Чтобы сложить два отрицательных рациональных числа, складывают модули и перед полученным результатом ставят знак минус.
Модуль неотрицательного числа равен этому числу, модуль отрицательного числа равен числу, противоположному данному.
Пример №4. Складываем модули чисел –31 и –45, то есть модули чисел равны соответственно |–31|=31 и |–45|=45, значит, 31+45 = 76. Далее ставим минус в ответе. Запись самого решения выполняется без знака «модуля» следующим образом:
– 31+(–45)= –(31+45)= –76
Как складывать числа с разными знаками?При сложении чисел с разными знаками необходимо из числа, которое больше по модулю, вычесть число, которое меньше по модулю, а перед полученным результатом поставить знак того слагаемого, модуль которого больше.
Пример 5.
- 45+(–98) = – (98–45)= –53 здесь большее по модулю число – это 98, поэтому из него будем вычитать число 45 и ставить в ответе знак «минус».
- –43+81=81–43=38 здесь большее по модулю число это 81, поэтому из него вычитаем 43, соответственно результат будет положительный.
Чтобы вычесть из одно числа другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.
Пример №6.
- 10–18=10+(–18)= –8 здесь к уменьшаемому 10 прибавляем число противоположное 18, то есть прибавляем –18. Дальше работаем по известному правилу сложения чисел с разными знаками.
- –7–(–2)= –7+2= –5 здесь к уменьшаемому –7 прибавляем число противоположное –2, то есть 2. Далее опять работает правило сложения чисел с разными знаками.
- 15–(–12)=15+12=27 здесь к уменьшаемому 15 прибавляем число противоположное –12, то есть 12. Далее – получаем сложение положительных чисел.
Правило умножения двух рациональных чисел, содержащих разные знаки, гласит: выполняем умножение модулей этих чисел и перед полученным результатом ставим знак минус. Другими словами, при умножении двух чисел с разными знаками всегда ставится минус в ответе.
Пример №7.
- –6 80= –480
- 48 (–3)= –144
Правило умножения двух отрицательных чисел: умножаем их модули; в ответ записываем полученное положительное число. Другими словами, при умножении двух отрицательных чисел всегда получается положительное число.
Пример №8.
- –25 (–4)=100
- –21,7 (–10)=217
Правило деления двух рациональных чисел аналогично правилу умножения: при делении двух чисел с разными знаками в ответе получается отрицательное число. При делении двух отрицательных чисел получается положительное число.
Пример №9.
- –215:5= –43
- –642:(–2)= 321
- При умножении рационального числа и нуля получается нуль.
- При делении нуля на рациональное число получается нуль.
- При делении рациональных чисел нужно помнить правило о том, что на нуль делить нельзя!
Пример №10.
- –314×0=0
- 0×(–2,16)=0
- 0 : (–31)=0
Рациональные числа
Тема рациональных чисел достаточно обширна. О ней можно говорить бесконечно и писать целые труды, каждый раз удивляясь новым фишкам.
Чтобы не допускать в будущем ошибок, в данном уроке мы немного углубимся в тему рациональных чисел, почерпнём из неё необходимые сведения и двинемся дальше.
Что такое рациональное число
Рациональное число — это число, которое может быть представлено в виде дроби , где a — это числитель дроби, b — знаменатель дроби. Причем b не должно быть нулём, поскольку деление на ноль не допускается.
К рациональным числам относятся следующие категории чисел:
- целые числа (например −2, −1, 0 1, 2 и т.д.)
- обыкновенные дроби (например , , и т.п.)
- смешанные числа (например , , и т.п.)
- десятичные дроби (например 0,2 и т.п.)
- бесконечные периодические дроби (например 0,(3) и т.п.)
Каждое число из этой категории может быть представлено в виде дроби .
Примеры:
Пример 1. Целое число 2 может быть представлено в виде дроби . Значит число 2 относится не только к целым числам, но и к рациональным.
Пример 2. Смешанное число может быть представлено в виде дроби . Данная дробь получается путём перевода смешанного числа в неправильную дробь
Значит смешанное число относится к рациональным числам.
Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби . Данная дробь получилась путём перевода десятичной дроби 0,2 в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему десятичных дробей.
Поскольку десятичная дробь 0,2 может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби . Данная дробь получается путём перевода чистой периодической дроби в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему периодические дроби.
Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием — рациональные числа.
Рациональные числа на координатной прямой
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:
На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей
Попробуем понять, почему дробь вдруг расположилась между нулём и единицей.
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину
Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.
Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и равна 0,5
А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь
Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2
Значение дроби равно 1,5
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:
Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2
Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:
Пример 3.
Значение дроби равно 0,02
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3
Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3
это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.
Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь
Значение дроби равно 2,5
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 2,5
Минус перед рациональным числом
В предыдущем уроке, который назвался умножение и деление целых чисел мы научились делить целые числа. В роли делимого и делителя могли стоять как положительные, так и отрицательные числа.
Рассмотрим простейшее выражение
(−6) : 2 = −3
В данном выражении делимое (−6) является отрицательным числом.
Теперь рассмотрим второе выражение
6 : (−2) = −3
Здесь уже отрицательным числом является делитель (−2). Но в обоих случаях мы получаем один и тот же ответ −3.
Учитывая, что любое деление можно записать в виде дроби, мы можем рассмотренные выше примеры также записать в виде дроби:
А поскольку в обоих случаях значение дроби одинаково, минус стоящий либо в числителе либо в знаменателе можно сделать общим, поставив его перед дробью
Поэтому между выражениями и и можно поставить знак равенства, потому что они несут одно и то же значение
В дальнейшем работая с дробями, если минус будет нам встречаться в числителе или в знаменателе, мы будем делать этот минус общим, ставя его перед дробью.
Противоположные рациональные числа
Как и целое число, рациональное число имеет своё противоположное число.
Например, для рационального числа противоположным числом является . Располагается оно на координатной прямой симметрично расположению относительно начала координат. Другими словами, оба этих числа равноудалены от начала координат
Перевод смешанных чисел в неправильные дроби
Мы знаем что для того, чтобы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части и прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним..
Например, переведём смешанное число в неправильную дробь
Умножим целую часть на знаменатель дробной части и прибавим числитель дробной части:
(2 × 2) + 1
Вычислим данное выражение:
(2 × 2) + 1 = 4 + 1 = 5
Полученное число 5 будет числителем новой дроби, а знаменатель останется прежним:
Полностью данная процедура записывается следующим образом:
Чтобы вернуть изначальное смешанное число, достаточно выделить целую часть в дроби
Но этот способ перевода смешанного числа в неправильную дробь применим только в том случае, если смешанное число является положительным. Для отрицательного числа данный способ не сработает.
Рассмотрим дробь . Выделим в этой дроби целую часть. Получим
Чтобы вернуть изначальную дробь нужно перевести смешанное число в неправильную дробь. Но если мы воспользуемся старым правилом, а именно умножим целую часть на знаменатель дробной части и к полученному числу прибавим числитель дробной части, то получим следующее противоречие:
Мы получили дробь , а должны были получить дробь .
Делаем вывод, что смешанное число в неправильную дробь переведено неправильно:
Чтобы правильно перевести отрицательное смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части, и из полученного числа вычесть числитель дробной части. В этом случае у нас всё встанет на свои места
Отрицательное смешанное число является противоположным для смешанного числа . Если положительное смешанное число располагается в правой части и выглядит так
то отрицательное смешанное число будет располагаться в левой части симметрично относительное начала координат
И если читается как «две целых и одна вторая», то читается как «минус две целых и минус одна вторая». Поскольку числа −2 и располагаются в левой части координатной прямой — они оба являются отрицательными.
Любое смешанное число можно записать в развёрнутом виде. Положительное смешанное число в развёрнутом виде записывается как .
А отрицательное смешанное число записывается как
Теперь мы можем понять, почему смешанное число расположилось в левой части координатной прямой. Минус перед двойкой указывает, что мы сдвинулись от нуля на два шага влево, в результате оказались в точке, где находится число −2
Затем, начиная от числа −2 сдвинулись ещё влево на шага. А поскольку значение равно −0,5 то наш шаг будет половиной от полного шага.
В итоге, мы окажемся посередине между числами −3 и −2
Пример 2. Выделить в неправильной дроби целую часть, затем полученное смешанное число обратно перевести в неправильную дробь
Выполним первую часть задания, а именно выделим в неправильной дроби целую часть
Выполним вторую часть задания, а именно переведём полученное смешанное число в неправильную дробь. Для этого умножим целую часть на знаменатель дробной части и из полученного числа вычтем числитель дробной части:
Если нет желания путаться и привыкать к новому правилу, то можно смешанное число заключить в скобки, а минус оставить за скобкой. Тогда можно будет применить старое доброе правило: умножить целую часть на знаменатель дробной части и к полученному числу прибавить числитель дробной части.
Выполним предыдущее задание этим способом, а именно переведём смешанное число в неправильную дробь
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Рациональные числа, понятие и примеры.
Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.
Понятие рациональных чисел.
Определение:
Рациональные числа – это числа, которые можно представить в виде дроби \(\frac{m}{n}\), где m – целое число, а n – натуральное число.
Другими словами, можно сказать:
Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Разберем каждый пункт подробно.
- Любое натуральное число можно представить в виде дроби, например, число 5=\(\frac{5}{1}\).
- Любое целое число можно представить в виде дроби, например, числа 4, 0 и -2. Получаем 4=\(\frac{4}{1}\), 0=\(\frac{0}{1}\) и -2=\(\frac{-2}{1}\).
- Обыкновенные дроби уже записаны в рациональном виде, например, \(\frac{6}{11}\) и \(\frac{9}{2}\).
- Бесконечные периодические дроби, например, 0,8(3)=\(\frac{5}{6}\).
- Конечные десятичные дроби, например, 0,5=\(\frac{5}{10}=\frac{1}{2}\).
Множество рациональных чисел.
Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.
Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.
На рисунке можно показать множество рациональных чисел.

Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, \(\sqrt{3}\) или число \(\pi\) (читается число пи) не являются рациональными числами.
Вопросы по теме «Рациональные числа»:
Какое выражение является рациональным числом из чисел \(\sqrt{5}, -0.(3), 15, \frac{34}{1569}, \sqrt{6}\) ?
Ответ:
Корень из 5 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Бесконечная десятичная периодическая дробь -0,(3)=\(-\frac{3}{10}\) можно представить в виде дроби, поэтому это рациональное число.
Число 15 можно представить в виде дроби \(\frac{15}{1}\), поэтому это рациональное число.
Дробь \(\frac{34}{1569}\) это рациональное число.
Корень из 6 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=\(\frac{1}{1}\).
Докажите, что число \(\sqrt{0,0049}\) является рациональным?
Доказательство: \(\sqrt{0,0049}=0,07\)
Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.
Сложение рациональных чисел, правила и примеры
Сложение рациональных чисел происходит по правилам сложения дробей. В этой теме рассмотрим подробно как складывать положительные и отрицательные рациональные числа, а также рациональные числа с одинаковыми и разными знаменателями.
Тема. Сложение рациональных чисел с одинаковыми знаменателями.
Определение:
Сумма дробей с одинаковыми положительными знаменателями, есть дробь с тем же знаменателем и суммой их числителей.
Правила сложения рациональных чисел.
- Если у дробей одинаковый знаменатель, записываем его в знаменатель итоговой дроби.
- Числители складываем по правилам сложения и результат записываем в числитель итоговой дроби.
- Если требуется итоговую дробь сокращаем и преобразовываем.
Пример:
Выполните сложение рациональных чисел с одинаковыми знаменателями: а) \(\frac{-3}{4}+\frac{1}{4}\) б) \(\frac{-6}{13}+\frac{-2}{13}\) в) \(\frac{17}{47}+\frac{12}{47}\) г) \(\frac{32}{15}+\frac{-12}{15}\)
Решение:
а) Так как знаменатели у дробей одинаковые, записываем знаменатель тот же. Числители складываем по правилу сложения целых чисел. Итоговую дробь \(\frac{-2}{4}\) сокращаем на 2.
б) \(\begin{align}\frac{-6}{13}+\frac{-2}{13}=\frac{-6+(-2)}{13}=\frac{-8}{13}=-\frac{8}{13}\\\\ \end{align}\)
в) \(\begin{align}\frac{17}{47}+\frac{12}{47}=\frac{17+12}{47}=\frac{29}{47}\\\\ \end{align}\)
г) \(\begin{align}\frac{32}{15}+\frac{-12}{15}=\frac{32+(-12)}{15}=\frac{20}{15}=\frac{4 \times 5}{3 \times 5}=\frac{4}{3}=1\frac{1}{3}\\\\ \end{align}\)
Урок. Сложение рациональных чисел с разными знаменателями.
Определение:
Чтобы сложить две дроби с разными знаменателями необходимо сначала найти общий знаменатель, а потом сложить их числители.
Формула сложение рациональных чисел с разными знаменателями:
\(\begin{align}&\bf \frac{a}{b}+\frac{c}{d}=\frac{a \times d + c \times b}{b \times d} \\\\
\end{align}\)
Алгоритм действия при сложении рациональных чисел с разными знаменателями.
- Найти общий знаменатель. (Как находить общий знаменатель можете узнать, нажав на ссылку)
- Найти сумму дробей по правилам сложения рациональных чисел с одинаковыми знаменателями.
Пример:
Выполните сложение рациональных чисел с разными знаменателями: а) \(\frac{-4}{7}+\frac{5}{8}\) б) \(\frac{-3}{11}+\frac{-7}{22}\) в) \(\frac{11}{15}+\frac{9}{25}\) г) \(\frac{8}{3}+\frac{-1}{13}\)
Решение:
а) Дроби \(\frac{-4}{7}+\frac{5}{8}\) имеют разные знаменатели, поэтому нужно найти общий знаменатель. Общий знаменатель будет равен 56, поэтому первую дробь \(\frac{-4}{7}\) умножаем на 8, а вторую дробь \(\frac{5}{8}\) на 7
\end{align}\)
б) Так как у дробей разные знаменатели, находим общий знаменатель. Общий знаменатель равен 22.
\(\begin{align}\frac{-3}{11}+\frac{-7}{22}=\frac{-3 \times 2 + (-7)}{11 \times 2}=\frac{-6 + (-7)}{22}=\frac{-13}{22}=-\frac{13}{22}\\\\\end{align}\)
в) У дробей \(\frac{11}{15}\) и \(\frac{9}{25}\) разные знаменатели. Находим общий знаменатель, он равен 75. Первую дробь умножаем на 5, а вторую дробь умножаем на 3.
\(\begin{align}\frac{11}{15}+\frac{9}{25}=\frac{11 \times 5}{15 \times 5} + \frac{9 \times 3}{25 \times 3}=\frac{55}{75}+\frac{27}{75}=\frac{55+27}{75}=\frac{82}{75}=1\frac{7}{75}\\\\\end{align}\)
г) Общий знаменатель этих дробей \(\frac{8}{3}\) и \(\frac{-1}{13}\) равен 39.
\(\begin{align}\frac{8}{3}+\frac{-1}{13}=\frac{8 \times 13 + (-1) \times 3}{3 \times 13}=\frac{104+(-3)}{39}=\frac{101}{39}=2\frac{23}{39}\\\\\end{align}\)
Сложение противоположных рациональных чисел.
Правило сложения противоположных рациональных чисел.
Результатом сложения противоположных рациональных чисел будет нуль.
Пример:
Выполните сложение дробей \(\frac{-5}{18}+\frac{5}{18}\) .
Решение:
\(\begin{align}\frac{-5}{18}+\frac{5}{18}=\frac{-5+5}{18}=\frac{0}{18}=0\\\\\end{align}\)
Сложение положительных рациональных чисел.
Сложение положительных рациональных чисел сводится к сложение обыкновенных дробей. Может быть два варианта:
- Если у положительных рациональных чисел разные знаменатели, то ищем общий знаменатель.
- Если у положительных рациональных чисел одинаковые знаменатели, то переходим к сложению числителей, а знаменатель переписываем.
Примеры:
Выполните сложение положительных рациональных дробей: а) \(\frac{4}{15}+\frac{7}{15}\) б) \(\frac{3}{8}+\frac{5}{12}\).
Решение:
а) \(\begin{align}\frac{4}{15}+\frac{7}{15}=\frac{4+7}{15}=\frac{11}{15}\\\\
\end{align}\)
б) У дробей разные знаменатели нужно найти общий знаменатель. Общий знаменатель равен 24.
\(\begin{align}\frac{3}{8}+\frac{5}{12}=\frac{3 \times 3}{8 \times 3}+\frac{5 \times 2}{12 \times 2}=\frac{9}{24}+\frac{10}{24}=\frac{9+10}{24}=\frac{19}{24}\\\\\end{align}\)
Сложение отрицательных рациональных чисел.
Складываем отрицательные рациональные числа по этим правилам:
- Если знаменатели разные, то приводим к общему знаменателю.
- Если знаменатели одинаковые складываем числители по правилу сложения отрицательных целых чисел.
Пример:
Сложите отрицательные рациональные числа: а) \(-\frac{13}{19}+(-\frac{1}{19})\) б) \(-\frac{1}{49}+(-\frac{5}{14})\).
Решение:
а) \(\begin{align}-\frac{13}{19}+(-\frac{1}{19})=\frac{-13+(-1)}{19}=\frac{-14}{19}=-\frac{14}{19}\\\\
\end{align}\)
б) Для начала найдем общий знаменатель. Общий знаменатель у дробей равен 98.
\(\begin{align}-\frac{1}{49}+(-\frac{5}{14})=-\frac{1 \times 2}{49 \times 2}+(-\frac{5 \times 7}{14 \times 7})=-\frac{2}{98}+(-\frac{35}{98})=-\frac{-2+(-35)}{98}=\frac{-37}{98}=-\frac{37}{98}\\\\\end{align}\)
Сложение рациональных чисел с разными знаками, примеры.
Правило:
- Если у дробей разные знаменатели, нужно привести их к общему знаменателю.
- Если у дробей одинаковые знаменатели, нужно в итоговую дробь переписать знаменатель, а числители сложить по правилам сложения целых чисел с разными знаками.
Пример:
Выполните сложение рациональных чисел с разными знаками: а) \(-\frac{2}{5}+\frac{1}{5}\) б) \(\frac{1}{27}+(-\frac{5}{9})\)
Решение:
а) У дробей общий знаменатель, переходим к сложению числителей. Определим какой знак будет в результате. Для этого посмотри модуль какого числа больше |-2|=2 и |1|=1. Получаем 2>1, то есть модуль отрицательного числа больше модуля положительного, поэтому в ответе будет стоять знак минус. Если сказать проще, у нас два минуса и один плюс. Минусов больше поэтому в результате поставим знак минус.
\end{align}\)
б) Сначала приведем к общему знаменателю, он равен 27, а потом сложим числители. Определим знак ответа. Найдем модули чисел |-15|=15 и |1|=1. Модуль отрицательного числа больше положительного 15>1, поэтому в ответе будет знак минус.
\(\begin{align}\frac{1}{27}+(-\frac{5}{9})=\frac{1}{27}+(-\frac{5 \times 3}{9 \times 3})=\frac{1}{27}+(-\frac{15}{27})=\frac{1+(-15)}{27}=-\frac{14}{27}\\\\\end{align}\)
Рациональные числа. Сравнение рациональных чисел
Рациональные числа — это множество чисел, включающее в себя целые и дробные числа.
Множество рациональных чисел принято обозначать буквой Q.
Множество рациональных чисел содержит как дробные числа (обыкновенные и десятичные дроби, смешанные числа), так и целые числа. Любое целое рациональное число можно также представить и в виде дроби:
где a — это целое число, а b — натуральное число и b ≠ 0. Поэтому для любого целого числа a верно равенство:
| a | = | a | = | a · 2 | = | a · 3 | = | a · n | . |
| 1 | 1 · 2 | 1 · 3 | 1 · n |
Следовательно, любое целое рациональное число можно представить в виде дроби с любым знаменателем.
Сравнение рациональных чисел
Сравнить два рациональных числа — значит, узнать, какое из них больше, какое меньше, или определить, что числа равны.
Любое положительное число больше нуля и больше любого отрицательного числа.
Примеры:
1 > 0;
15 > -16;
0,001 > -100.
Любое отрицательное число меньше нуля и меньше любого положительного числа.
Примеры:
-7 < 0;
-1,25 < 0,05;
-357 < 0.
Из двух отрицательных чисел больше то, у которого модуль меньше.
Примеры:
-31 < 28, так как |-31| > |28|;
-0,5 > -0,51, так как |-0,5| < |-0,51|.
Два рациональных числа равны, если равны их модули, и они имеют одинаковый знак.
Примеры:
-31 = -31;
0 = 0;
7 = 7.
Свойства арифметических действий с рациональными числами — это правила, по которым можно обращаться с рациональными числами.

Часто для упрощения математических задач применяют основные свойства арифметических действий.
Все свойства действий с рациональными числами основываются на свойствах действий с целыми числами.
Мы выяснили, что рациональные числа можно складывать, вычитать, умножать и делить.
Но также нам известно, что на множестве рациональных чисел действие вычитание задается как обратное сложению, а действие деления как обратное умножению.
Таким образом, для рациональных чисел остается два основных арифметических действия: сложение и умножение. Свойства, касающиеся вычитания и деления легко выводятся по аналогичным принципам из свойств сложения и умножения, их мы сейчас рассмотрим.
Пусть числа a, b, c, d — некоторые рациональные числа.
Рассмотрим основные свойства действий с этими числами.
Свойства сложения рациональных чисел:
1. Переместительное свойство
При сложении рациональных чисел неважно в каком порядке идут слагаемые.
От перестановки слагаемых местами сумма не меняется.
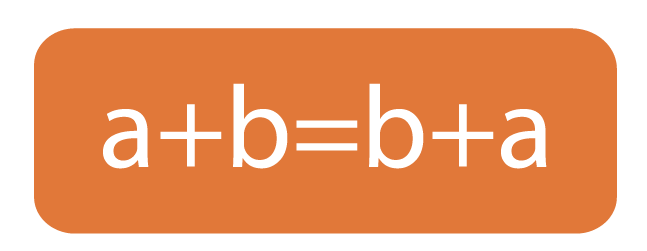
Пример:
Определим значение выражения а + b, если а = 0,5, b = 2,15
Подставим числовые значения а и b в заданное выражение, получим
а + b = 0,5 + 2,15 = 2,65
В заданном выражении а + b поменяем местами слагаемые, в результате
b+ a = 2,15 + 0,5 = 2,65.
Ответ: при перестановке слагаемых сумма выражения осталась прежней, равной 2,65.
2. Сочетательное свойство
Если выражение содержит только действия сложения чисел, то выполнять сложения этих чисел можно в любом порядке.
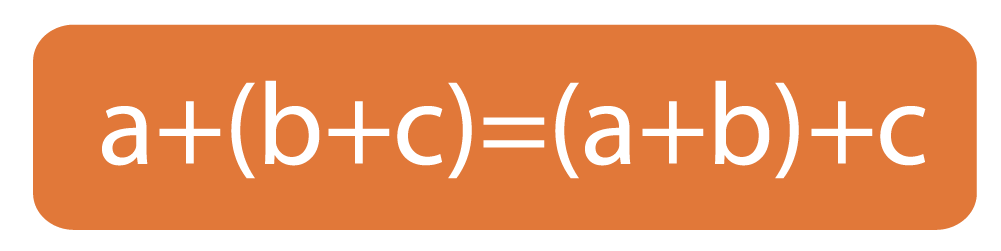
Таким образом, чтобы к сумме двух слагаемых прибавить третье число, можно к первому слагаемому прибавить сумму второго и третьего слагаемого.
Эти правила позволяют упрощать вычисления.
Если соединить переместительное и сочетательное свойства сложения, то складывать числа и их группировать можно в любом порядке.
Пример:
Найдите значения выражения а + (b + с), если
а = 7,5
b = 1,2
с = 3,3
Подставим числовые значения а, b и с в заданное выражение, получим
а + (b+ с) = 7,5 + (1,2 + 3,3) = 7,5 + 4,5 = 12
В заданном выражении а + (b+ с) поменяем порядок действий, заключив в скобки первое и второе слагаемые, в результате получим
(а + b) + с = (7,5 + 1,2) + 3,3 = 8,7 + 3,3 = 12
Ответ: при изменении порядка действий в выражении значение суммы осталось прежнее — равное 12.
Свойства умножения рациональных чисел:
Умножение, как и сложение, обладает переместительным и сочетательным свойством
1. Переместительное свойство
При умножении рациональных чисел неважно в каком порядке идут множители.
От перестановки множителей местами произведение не изменяется.
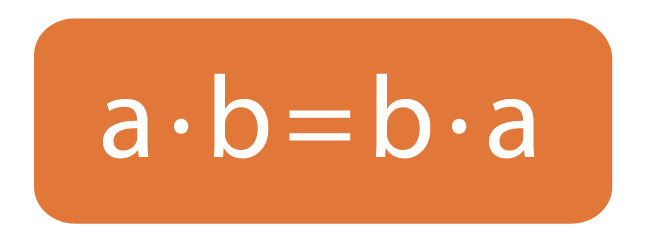
Пример:
Определим значение выражения \(\mathbf{a \cdot b}\), если а = 0,5, b = 2,1
Подставим числовые значения а и b в заданное выражение, получим
\(\mathbf{a \cdot b = 0,5 \cdot 2,1 = 1,05}\)
В заданном выражении \(\mathbf{a \cdot b}\) поменяем местами множители, в результате
\(\mathbf{b \cdot a = 2,1 \cdot 0,5 = 1,05}\)
Ответ: при перестановке множителей местами произведение осталось прежним, равным 1,05
2. Сочетательное свойство
Если выражение содержит только действия умножения чисел, то выполнять умножение этих чисел можно в любом порядке.
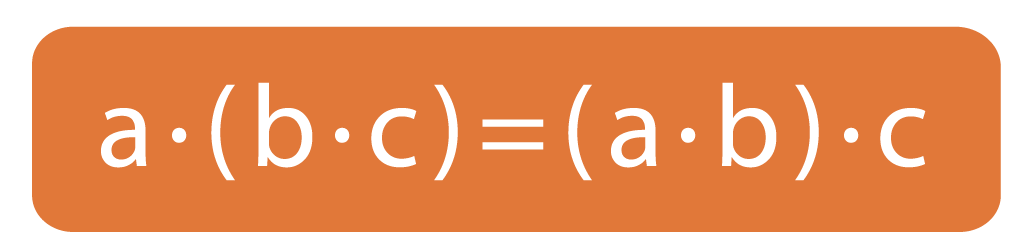
Таким образом, чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего множителя.
Переместительное и сочетательное свойство умножения позволяют в произведении переставлять и группировать множители в любом порядке, тем самым упрощая математическое выражение.
Пример:
Найдите значения выражения \(\mathbf{a \cdot (b \cdot c)}\), если
\(\mathbf{a = \frac{1}{2}}\)
\(\mathbf{b = \frac{3}{4}}\)
\(\mathbf{c = -\frac{1}{2}}\)
Подставим числовые значения а, b и с в заданное выражение, получим
\(\mathbf{a \cdot (b \cdot c) = \frac{1}{2} \cdot (\frac{3}{4} \cdot (-\frac{1}{2})) = \frac{1}{2} \cdot (-\frac{3}{8}) = -\frac{3}{16}}\)
В заданном выражении \(\mathbf{a \cdot (b \cdot c)}\) поменяем порядок действий, заключив в скобки первый и второй множитель, в результате
\(\mathbf{(a \cdot b) \cdot c = (\frac{1}{2} \cdot \frac{3}{4}) \cdot (-\frac{1}{2}) = \frac{3}{8} \cdot (-\frac{1}{2}) = -\frac{3}{16}}\)
Ответ: при изменении порядка действий в выражении значение произведения осталось прежним, равным \(\mathbf{-\frac{3}{16}}\)
Распределительное свойство относительно сложения
Рассмотрим свойство, объединяющее сложение и умножение рациональных чисел.
Для того, чтобы умножить сумму на число, можно сначала умножить первое слагаемое на это число, потом второе слагаемое на это число, а затем полученные результаты сложить.
В буквенном выражении это правило выглядит так:
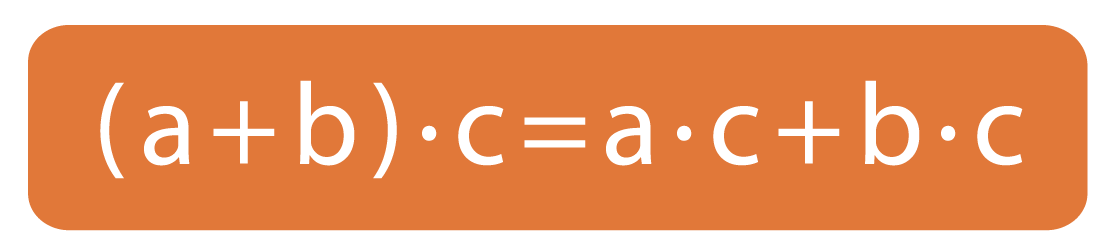
Правую часть равенства называют правилом раскрытия скобок.
Левую часть данного равенства называют правилом вынесения общего множителя за скобки.
Пример:
Найдите значение выражения \(\mathbf{(a + b) \cdot c}\), если
\(\mathbf{a = \frac{1}{2}}\)
\(\mathbf{b = \frac{3}{4}}\)
\(\mathbf{c = -\frac{1}{2}}\)
Подставим числовые значения а, b и с в заданное выражение, получим
\(\mathbf{(a + b) \cdot c = (\frac{1}{2} + \frac{3}{4}) \cdot (-\frac{1}{2}) = (\frac{2}{4} + \frac{3}{4}) \cdot (-\frac{1}{2}) = \frac{5}{4} \cdot (-\frac{1}{2}) = -\frac{5}{8}}\)
Применим к данному выражению \(\mathbf{(a \cdot b) \cdot c}\) распределительное свойство умножения относительно сложения.
Раскроем скобки в выражении \(\mathbf{(a + b) \cdot c}\), умножив первое и второе слагаемое на число с, затем, сложив полученные результаты, получаем выражение вида:
\(\mathbf{a \cdot c + b \cdot c = \frac{1}{2} \cdot (-\frac{1}{2}) + \frac{3}{4} \cdot (-\frac{1}{2}) = -\frac{1}{4} + (-\frac{3}{8}) = -\frac{2}{8} + (-\frac{3}{8}) = -\frac{5}{8}}\)
В нашем примере значение выражения \(\mathbf{(a + b) \cdot c}\) и значение выражения \(\mathbf{a \cdot c + b \cdot c}\) равны \(\mathbf{-\frac{5}{8}}\), т.е. справедливо равенство \(\mathbf{(a + b) \cdot c = a \cdot c + b \cdot c = -\frac{5}{8}}\)
90000 Rational Decision Making Model, Bringing Structure to Decision Making 90001 90002 90003 A rational decision making model provides a structured and sequenced approach to decision making. 90004 90005 90002 Using such an approach can help to ensure discipline and consistency is built into your decision making process. As the word rational suggests, this approach brings logic and order to decision making.90005 90008 Learn how to make better decisions with our e-guide bundle — 6 guides, 178 pages, 30 tools, for half price! 90009 90002 Our rational decision making model consists of a series of steps, beginning with problem / opportunity identification, and ending with actions to be taken on decisions made. 90005 90002 First though why not take a look at our comprehensive decision making e-guides with a great 90003 half price 90004 offer. You’ll find they contain our rational decision making model complete with tools, along with a comprehensive range of other guides to improve your decision making.90005 90002 It’s a great 90003 half price offer 90004. We talk through the benefits and features of our complete decision making resources in finding the right decision making model. Why not take look, you’ll see we’ve developed new models, tips and tools that you will not find elsewhere. 90005 90002 There seems to be a problem with decision making. According to Ohio State University management professor, Paul C. Nutt, we only get about 50% of our decisions in the workplace right! Half the time they are wrong, so there is clearly plenty of scope to improve on our decision making processes.Based on his research into over 300 decisions, made in a range of organizations, he discovered that 90005 90022 90002 90003 «Some tactics with a good track record are commonly known, but uncommonly practiced.» 90004 90005 90027 90002 Why? Well one reason that emerged from his research is that: 90005 90022 90002 90003 «Too often, managers make bad tactical selections … .. because they believe that following recommended decision-making practices would take too much time and demand excessive cash outlays.»90004 90005 90027 90002 Nutt argues that using good decision making practices actually costs very 90037 little 90038. Our rational decision making model is our free tool to help you improve the way you make decisions. 90005 90002 This article is part of our series on decision making. Our first article, types of decision making outlines a range of decision making approaches. Rational decision making forms part of what we have termed 90037 types of decision, categorized by process 90038.In this category we have put two contrasting approaches, that of rational decision making and that of judgement or intuitive decision making. 90005 90002 90005 90046 A General Rational Decision Making Model 90047 90002 90003 Rational decision 90004 making processes consist of a sequence of steps designed to rationally develop a desired solution. Typically these steps involve: 90005 90002 90005 90002 90055 90005 90002 90005 90002 90005 90002 90003 Identifying a problem or opportunity 90004 90005 90002 The first step is to recognise a problem or to see opportunities that may be worthwhile.A rational decision making model is best employed where relatively complex decisions have to be made. 90005 90008 Read our new book: 90009 90022 90002 90003 Uncommon Leadership: how to build competitive edge by thinking differently 90004 90005 90002 «a tour de force … all integrated into a fascinating intellectual package» 90005 90002 Professor Dennis J. Garritan, Adjunct Professor, Harvard University 90005 90027 90002 90080 90005 90002 The first decision making lesson should be to ask yourself if you really have a problem to solve or a decision to make.Then read this article for more specific advice: Problem Solving Skill: Finding the Right Problem to Solve. 90005 90002 90003 Gathering information 90004 90005 90002 What is relevant and what is not relevant to the decision? What do you need to know before you can make a decision, or that will help you make the right one? 90005 90002 90003 Analyzing the situation 90004 90005 90002 What alternative courses of action may be available to you? What different interpretations of the data may be possible? Our Problem Solving Activity uses a set of structured questions to encourage both broad and deep analysis of your situation or problem.90005 90002 90003 Developing options 90004 90005 90002 Generate several possible options. Be creative and positive. Read The Power of Positive Thinking for our five questions that create possibilities. 90005 90002 90003 Evaluating alternatives 90004 90005 90002 What criteria should you use to evaluate? Evaluate for feasibility, acceptability and desirability. Which alternative will best achieve your objectives? 90005 90002 90003 Selecting a preferred alternative 90004 90005 90002 Explore the provisional preferred alternative for future possible adverse consequences.What problems might it create? What are the risks of making this decision? 90005 90002 90003 Acting on the decision 90004 90005 90002 Put a plan in place to implement the decision. Have you allocated resources to implement? Is the decision accepted and supported by colleagues? Are they commited to to making the decision work? 90005 90002 90005 90046 Strengths and Weaknesses of the Rational Decision Making Model 90047 90002 The main strength of a rational decision making model is that it provides structure and discipline to the decision making process.90005 90008 Free infographic: 90009 90022 90002 Click on the image to download our free infographic of the rational decision making process 90005 90027 90002 90133 90005 90002 It helps ensure we consider the full range of factors relating to a decision, in a logical and comprehensive manner. These are a key feature of our comprehensive guide: Making Better Decisions. 90005 90002 However, we should always remember that whilst the model indicates 90037 what needs to be done 90038, it’s often 90037 how things are done 90038 that characterises effective decision making.90005 90002 Paul C. Nutt’s research illustrates that bad decisions were usually bad because two things were missing: 90005 90145 90146 adequate participation of stakeholders in the decision making process; 90147 90146 sufficient time spent generating a range of possible solutions. 90147 90150 90002 Too often those who should have been involved were not, and solutions were proposed and acted upon too quickly. Often with disastrous effects! 90005 90002 A second weakness arises if we attempt to use the model in isolation.This is particularly important where complex or important decisions are involved. 90005 90002 The principle assumption of the rational decision making process is that human beings make rational decisions. However, there are numerous factors which determine our decisions, many of which are not rational. In many situations decisions have to be made with incomplete and insufficient information. 90005 90002 Judgement, intuition, experience and knowledge all come together when making decisions. This critical aspect is further explored in our article: Intuition and Decision Making.90005 90046 Putting the Rational Decision Making Model to work 90047 90002 90162 Regardless of any perceived weaknesses these models are essential tools. You’ll find more on these and other practical techniques in our related e-guides (below) or in Making Better Decisions. 90005 90002 Use the tools in this guide to help your decision making: 90005 90166 90146 90003 Tool 1: Do you need to make a decision? 90004 90147 90146 90003 Tool 2: The POCA decision making model 90004 90147 90146 90003 Tool 3: Decision levels 90004 90147 90146 90003 Tool 4: 7 step decision making process 90004 90147 90146 90003 Tool 5: Team decision making 90004 90147 90146 90003 Tool 6: Evaluating alternatives 90004 90147 90191 90002 See for yourself that a rational decision making model can help us to make better decisions — and thus help us to be better managers.90005 .90000 Just a moment … 90001 90002 Please enable Cookies and reload the page. 90003 90004 This process is automatic. Your browser will redirect to your requested content shortly. 90003 90006 Please allow up to 5 seconds … 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! [ ]) + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) + !! [] +! ! []) + (! + [] + (!! []) + !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + ( + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] +! ! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] — (!! [])) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] +! ! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! []) + (+ !! [] ) + (+ !! []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! []) + (+ !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! []) + (+ !! [ ]) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! []) + (+ !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (+ !! []) + (! + [] + (!! [ ]) — []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [ ] + (!! []) — []) + (! + [] — (!! [])) + (! + [] — (!! []))) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (! ! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] +! ! []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [])) / + ((! + [] + (!! []) + !! [] + []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [ ] + (!! []) — []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (+ !! []) + (! + [] + ( !! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! []) + ( ! + [] + (!! []) — []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! [ ]) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) + !! [] + !! [] + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) — []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] +! ! []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) + !! [])) / + ((! + [] + (!! []) + !! [] + []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) +! ! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! []) + ( ! + [] + (!! []) + !! [] + !! [] + !! [] + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! [ ] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] — (!! [])) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [])) / + (( ! + [] + (!! []) — [] + []) + (! + [] + (!! []) — []) + (! + [] + (!! []) +! ! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (! ! []) + !! [] + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! [ ]) + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [ ] + !! [] + []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [ ] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (! ! []) + !! [] + !! []) + (! + [] + (!! []) + !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] — (! ! [])) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [ ] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [])) 90003 90008 + ((! + [] + (!! [ ]) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [ ] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (! ! []) + !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + !! [] + []) + (! + [ ] + (!! []) — []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] + (! ! []) + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] +! ! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! [ ]) + !! [] + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] — (!! [])) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [])) / + ((! + [] + (!! []) + !! [] + !! [] + !! [] + []) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) +! ! [] + !! []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] — (!! [])) + (! + [] — (!! [])) + (! + [] + (!! []) + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [])) 90003 90008 + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] +! ! [] + !! [] + []) + (! + [] + (!! []) — []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! []) + (+ !! []) + (! + [] + (!! []) + !! [] + !! [] +! ! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) — []) + (! + [] + (!! []) +! ! [])) / + ((! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + []) + (! + [] — (!! [])) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! [] + !! [ ]) + (! + [] + (!! []) + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! [] + !! [] + !! [] + !! [] + !! []) + (! + [] + (!! []) + !! []) + (+ !! []) + (! + [] + (!! []) — [])) 90003 .90000 The Decision-Making Process-Rational Decision Making 90001 90002 Making Economic Decisions 90003 90004 The Decision-Making Process Rational Decision Making 90005 Go to questions covering topic below 90006 Selecting an appropriate criterion (or criteria) for selecting among competing alternatives is a critical step in engineering decision making.90007 90006 If a problem involves fixed input among the possible alternatives, then the appropriate general criterion is to maximize output. For example, a company may be considering the purchase of a new office copy machine. If two competing alternatives have the same cost (fixed input), then the appropriate criterion would be to select the copy machine that in some appropriate measure has the higher output. The criterion could be as simple as the copy rate of the machine (pages per minute) or as complex as the copy rate with some measure of special features availability.90007 90006 If a problem involves fixed output among the possible alternatives, then the appropriate general criterion is to minimize input. For example, a company may be considering the installation of a new elevator. If two competing alternatives have the same output as measured in load capacity, operating speed, and so on, then the appropriate criterion would be to install the elevator with the lower cost (Minimum input). 90007 90006 If neither input nor output is fixed among the alternatives being considered, then the appropriate criterion is to maximize (output — input) or, stated more simply, to maximize profit.For example, if one of two competing production machines will be purchased, and if the machines differ in both initial cost and output rate, then the appropriate criterion is to select the machine that will generate the higher profit (benefits derived from machine output — costs). 90007 90002 Making Economic Decisions 90003 90004 The Decision-Making Process Rational Decision Making 90005 90006 Question 1 90007 90006 Question 2 90007 90006 Question 3 90007 90006 Return to The Decision-Making Process Rational Decision Making 90007 90006 Return to Making Economic Decisions Tutorials menu 90007 90006 Return to Tutorials menu 90007 90006 Question 1.90007 90006 A College of Engineering freshman is required to purchase a notebook PC upon or before enrollment. Two competing models are available through the college at the same attractive, discounted price. Both models meet the minimum performance specifications of the college, and they have identical warranty plans. They also have identical weights and footprints. 90007 90006 What economic criterion should the freshman use in selecting which PC to buy? 90007 90006 Choose an answer by clicking on one of the letters below, or click on «Review topic» if needed.90007 90006 A Choose either PC. 90007 90006 B Choose the PC with the lower cost. 90007 90006 C Choose the PC with the greater performance (output). 90007 90006 D Choose the PC with the lower (benefits — cost). 90007 90006 Review topic 90007 90006 Question 2. 90007 90006 A distribution center must purchase a new fork truck, and three competing candidates have been identified. The costs of the three alternatives vary, as do the benefits (E.g., maximum payload). 90007 90006 What economic criterion should be used in selecting a fork truck for purchase? 90007 90006 Choose an answer by clicking on one of the letters below, or click on «Review topic» if needed.90007 90006 A Choose the fork truck with the lowest cost. 90007 90006 B Choose the fork truck with the highest benefits. 90007 90006 C Choose the fork truck with the highest (cost — benefits). 90007 90006 D Choose the fork truck with the highest (benefits — cost). 90007 90006 Review topic 90007 90006 Question 3. 90007 90006 A manufacturing facility provides uniforms and uniform cleaning for its production employees. Either one of two local vendors can provide the identical service.90007 90006 What economic criterion should be used in selecting a uniform provider? 90007 90006 Choose an answer by clicking on one of the letters below, or click on «Review topic» if needed. 90007 A Choose the service provider with the lower cost B Choose the service provider with the higher service level C Choose either service provider D Alternate the selection of the provider from month to month 90006 Review topic 90007 .90000 Rational Decision-Making Model 90001 90002 The 90003 Rational Decision-Making Model 90004 is a process for making logically sound decisions. [90005 Robbins, Stephen P., and Timothy A. Judge. Organization Behavior. 12th ed. Upper Saddle River, New Jersey: Pearson Prentice Hall, 2007. 156-158. 90006] The model comes from Organization behavior. 90007 90002 90009 Method 90010 90007 90002 The Rational Decision Making emerges from Organizational Behavior. The process is one that is logical and follows the orderly path from problem identification through solution.The Rational Decision Making is a seven step model for making rational and logical reasons: 90007 90002 90009 Define the problem 90010 90007 90002 The very first step which is normally overlooked by the top level management is defining the exact problem. Though we think that the problem identification is obvious, many times it is not. The rational decision making model is a group-based decision making process. If the problem is not identified properly then we may face a problem as each and every member of the group might have a different definition of the problem.Hence, it is very important that the definition of the problem is the same among all group members. Only then is it possible for the group members to find alternate sources or problem solving in an effective manner. 90007 90002 90009 Generate all possible solutions 90010 90007 90002 The next step in the rational decision making process, after defining the exact problem, is to generate all the possible solutions. This activity is best done in groups, as different people may contribute different ideas or alternative solutions to the problem.If you are not able to generate alternative solutions, there is a chance that you might not arrive at an optimal or a rational decision. For exploring the alternatives it is necessary to gather information. Technology may help with gathering this information. 90007 90002 90009 Generate objective assessment criteria 90010 90007 90002 After going thoroughly through the process of defining the problem, exploring for all the possible alternatives for that problem and gathering information the third step says evaluate the information and the possible options to anticipate the consequences of each and every possible alternative that is thought of.At this point of time we have to also think over for optional criteria on which we will measure the success or failure of our decision taken. 90007 90002 90009 Choose the best solution which we have already generated 90010 90007 90002 Based on the criteria of assessment and the analysis done in step 3 choose the best solution which we have generated. Once we go through the above steps thoroughly, implementing the fourth step is easy job. These four steps form the core of the Rational Decision Making Model.90007 90002 90009 Other three steps 90010 90007 90002 * Implement the chosen decision 90043 * Evaluate the «success» of the chosen alternative 90043 * Modify the decisions and actions taken based on the evaluation of step 6. 90007 90002 90009 Requirements and limitations 90010 90007 90002 However, there are a lot of assumptions, requirements without which the rational decision model is a failure. Therefore, they all have to be considered. The model assumes that we have or should or can obtain adequate information, both in terms of quality, quantity and accuracy.This applies to the situation as well as the alternative technical situations. It further assumes that you have or should or can obtain substantive knowledge of the cause and effect relationships relevant to the evaluation of the alternatives. In other words, it assumes that you have a thorough knowledge of all the alternatives and the consequences of the alternatives chosen. It further assumes that you can rank the alternatives and choose the best of it. The following are the limitations for the Rational Decision Making Model: 90007 90002 * It requires a great deal of time.90043 * It requires great deal of information 90043 * It assumes rational, measurable criteria are available and agreed upon. 90043 * It assumes accurate, stable and complete knowledge of all the alternatives, preferences, goals and consequences. 90043 * It assumes a rational, reasonable, non — political world. 90007 90002 90009 The Bounded Rational Decision Making Model: a realistic approach 90010 90007 90002 The Rational Decision Making Model, amongst its many assumptions assumes that there is a single, best solution that will maximize the desired outcomes.90043 90007 90002 Now, the bounded rationality model says that the problems and the decisions are to be reduced to such a level that they will be understood. In other words, the model suggests that we should interpret information and extract essential features and then within these boundaries we take a rational decision. 90007 90002 The model turns towards compromising on the decision making process though it is a structured decision making model. The decision maker takes the decision or is assumed to choose a solution though not a perfect solution but «good enough» solution based on the limited capacity of the group leader to handle the complexity of the situation, ambiguity and information.The steps involved in the decision making are alike to the rational decision making process the model assumes that the perfect knowledge about all the alternatives are not possible for a human being to know. Hence, based on the limited knowledge he takes a good enough knowledge though not a perfect decision. 90007 90002 To cut the long story short we can say that the decision that is taken is rational but is taken in a bounded area and the choice of alternatives is though not perfect is nearer to the perfect decision.In rational process the assumption is that the exact problem, all the alternatives, should be thoroughly known to the decision maker. However, the realistic approach of human limitation is overlooked in rational decision making, but the same approach is considered mainly in the bounded rational decision making process. 90007 90002 Hence, it is also called as a Realistic Approach for Rational Decision Making Process. 90007 90002 90009 Assumptions of the model 90010 90007 90002 The rational decision making model contains a number of assumptions.90043 * Problem clarity: The problem is clear and unambiguous.The decision maker is assumed to have complete information regarding situation. 90043 * Known options: It is assumed the decision maker can identify all the relevant criteria and can list all the viable alternatives. Furthermore, the decision maker is aware of all possible consequences of each alternative. 90043 * Clear preferences: Rationality assumes that the criteria and alternatives can be ranked and weighted to reflect their importance.90043 * Constant preferences: It’s assumed that the specific decision criteria are constant and that the weights assigned to them are stable over time. 90043 * No time or cost constraints: The rational decision maker can obtain full information about criteria and alternatives because it’s assumed that there are no time or cost constraints. 90043 * Maximum payoff: The rational decision maker will choose the alternative that yields the highest perceived value. 90007 90002 90009 ee also 90010 90007 90002 * 90007 90002 90009 References 90010 90007 90002 90096 Wikimedia Foundation.2010. 90097 90007.