Периметр трапеции: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Радиусили диаметр
Стороныили диагонали
Введите 2 величины
Сторона A
Сторона B
Диагонали
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Угол γ{$ main.angles[data.angle] $}
Введите 2 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 2 величины
Сторона
Высота
Диагональ 1
Диагональ 2
Угол α{$ main.
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Высота ha
Высота hb
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Основание A
Основание C
Высота H
Дополните боковые стороны для поиска периметра
Сторона B
Сторона D
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Количество сторон многоугольника
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Введите 1 величину
Сторона A = радиусу описанной окружности (R)
Радиус вписанной окружности (r)
Результат расчёта
- Периметр: {$ result.
 p|number:4 $}
p|number:4 $} - Площать: {$ result.s|number:4 $}
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.

Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
P = 340
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
P = 390
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Площадь трапеции: формулы, определения, элементы
Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.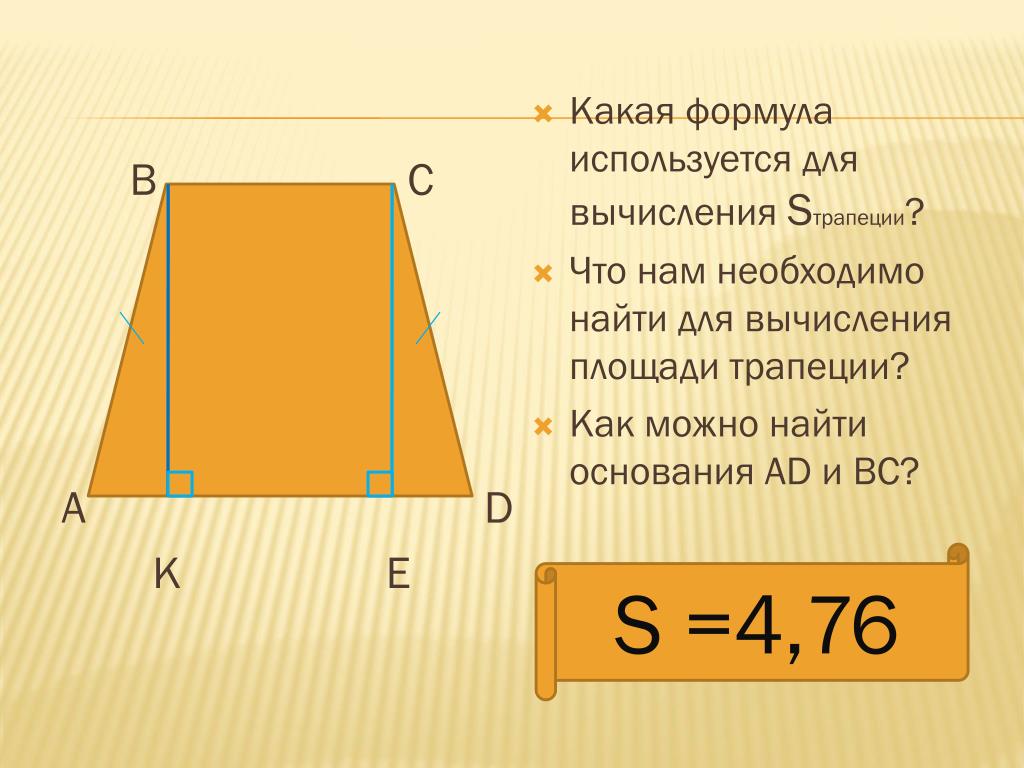
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм2, см2, м2 и км2 и так далее.
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
Содержание
- Формулы площади трапеции
- Площадь любых трапеций
- Площадь равнобедренной трапеции
- Определения трапеции
- Элементы трапеции
Формулы площади трапеции
Площадь любых трапеций
Ⅰ. Площадь трапеции через основания и высоту:
\[ S = \frac{a+b}{2} \cdot h \]
a,b — основания трапеции;
h — высота трапеции;
Ⅱ. 2}{2} \cdot \frac{\sin α \cdot \sin β}{\sin( α + β)} \]
2}{2} \cdot \frac{\sin α \cdot \sin β}{\sin( α + β)} \]
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
\[ S = ld \cdot \sin α \]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅱ. Площадь трапеции через диагонали и синус угла:
\[ S = \frac{d^2}{2} \cdot \sin α \]
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
Площадь трапеции через радиус вписанной окружности и основания:
\[ S = r( a+b) \]
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅳ. Площадь трапеции через основания:
\[ S = \sqrt{ab} \cdot {\frac{a+b}{2}} \]
a, b — основания равнобедренной трапеции;
Ⅴ. Площадь трапеции через основания и среднюю линию:
\[ S = l\sqrt{ab} \]
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅵ. Площадь трапеции через синус угла и стороны:
\[ S = c \cdot \sin α \cdot (a-c \cdot \cos α) \]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
Ⅶ.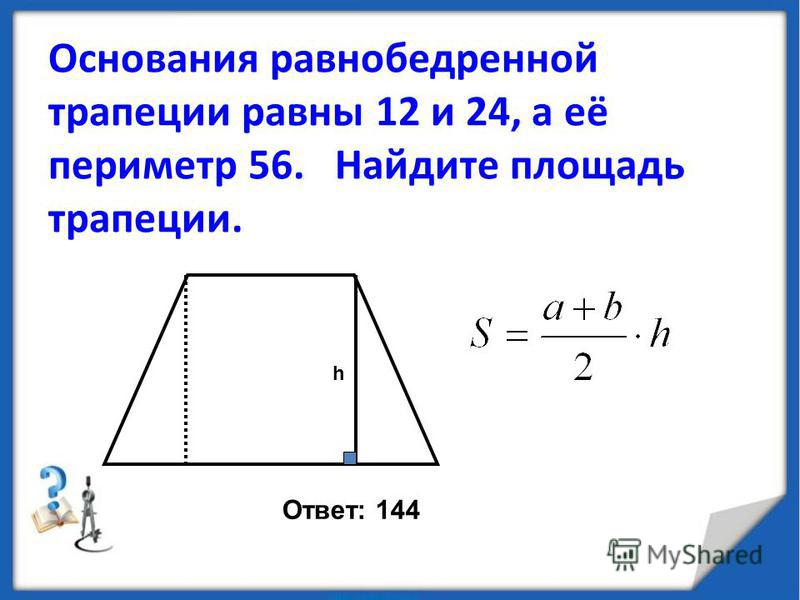 2}{\sin α} \]
2}{\sin α} \]
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
- Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
- Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны. - Прямоугольная / прямая трапеция: один из углов прямой.
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
Как найти основание трапеции в прямоугольной трапеции: Все формулы основания прямоугольной трапеции — ЭкоДом: Дом своими руками
Содержание
Все формулы основания прямоугольной трапеции
1. Формула длины оснований прямоугольной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
3.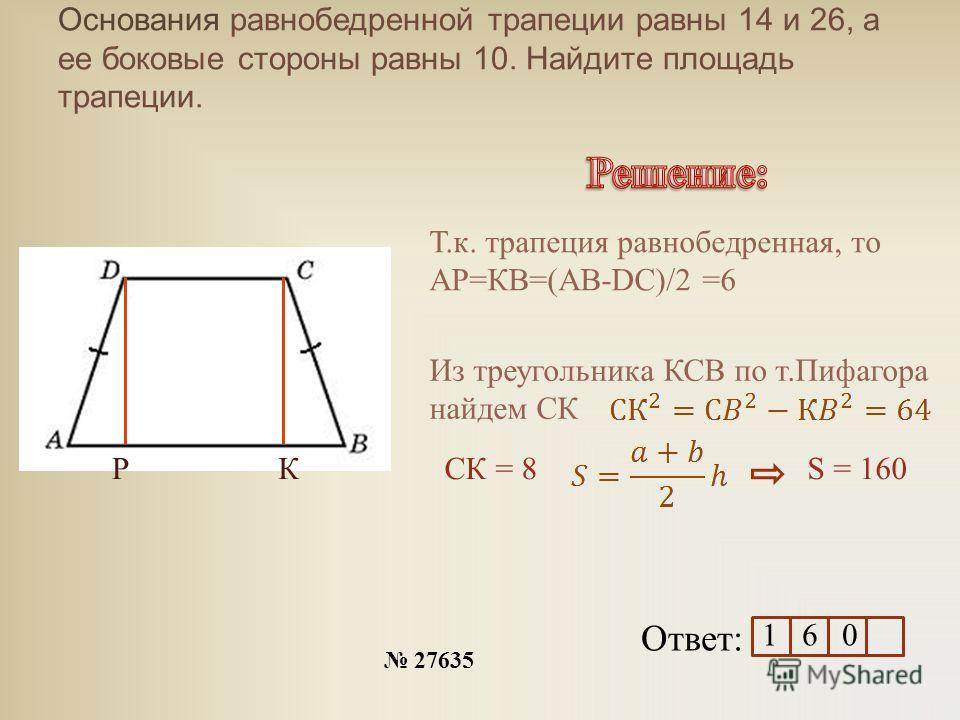 Формулы длины оснований трапеции через диагонали и угол между ними
Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
4.Формулы длины оснований трапеции через площадь
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Все формулы сторон равнобедренной трапеции
1. Формула длины основания равнобедренной трапеции через среднюю линию
Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2.Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4.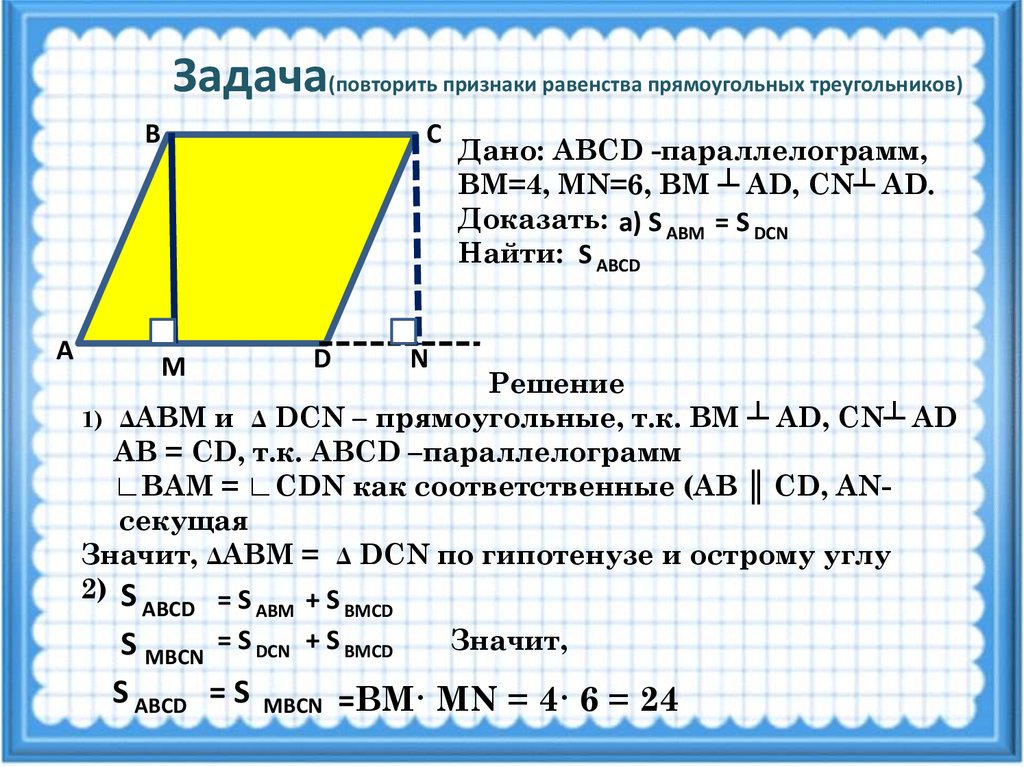 Формулы длины сторон равнобедренной трапеции через площадь
Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Все формулы боковых сторон прямоугольной трапеции
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
d — боковая сторона
α — угол при нижнем основании
h — высота трапеции
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
2. Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
c — боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
4. Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
α — угол при нижнем основании
h — высота трапеции
d — боковая сторона
Формулы длины боковой стороны (d) :
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
α — угол при нижнем основании
d — боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Прямоугольная трапеция
См.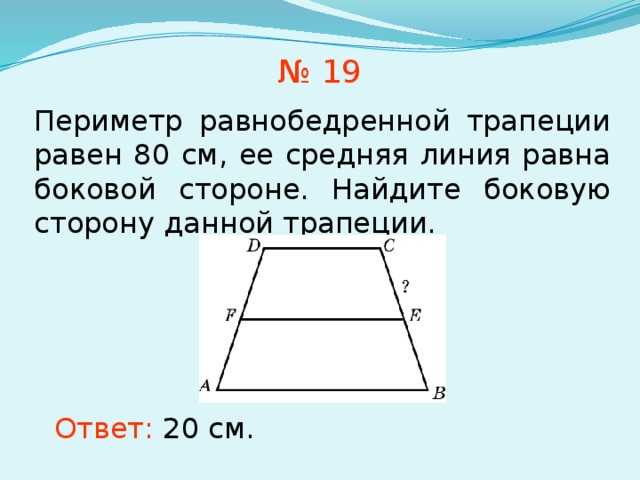 также: трапеция и ее свойства.
также: трапеция и ее свойства.
Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Формулы для прямоугольной трапеции
Обозначения формул даны на чертеже выше.
Соответственно:
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Интерпретация формул:
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
 (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
(Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона, перпендикулярная основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)
Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
(Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
(Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет
∠A.
Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD
2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + bПоскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка
AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2+ 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см
2 .
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Определение.
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий:
1. В тапеции есть два смежных прямых угла:
∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:
∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:
Высота равна меньшей боковой стороне:
h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:
a = b + d cos α = b + c ctg α = b + √d 2 — c2
b = a — d cos α = a — c ctg α = a — √d 2 — c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
| a = | d1d2 | · sin γ — b = | d1d2 | · sin δ — b |
| c | c |
| b = | d1d2 | · sin γ — a = | d1d2 | · sin δ — a |
| c | c |
3. Формулы длины оснований трапеции через площадь и другие стороны:
| a = | 2S | — b b = | 2S | — a |
| c | c |
4. Формула боковой стороны через другие стороны и угол при нижнем основании:
Формула боковой стороны через другие стороны и угол при нижнем основании:
c = √d 2 — (a — b)2 = (a — b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:
| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:
| d = | S | = | 2S |
| m sin α | (a + b) sin α |
7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
| d = | a — b | = | c | = | h | = √c2 + (a — b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1.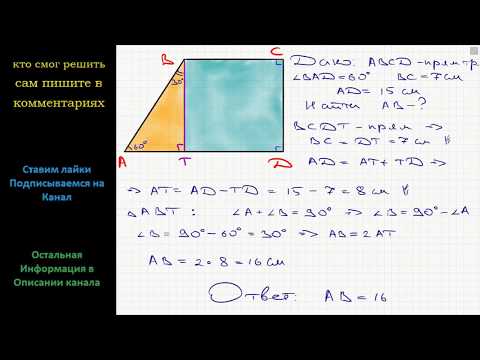 Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:
Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:
| m = | a — h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
2. Формулы средней линии через основания и боковые стороны сторону:
| m = | a — | √d 2 — c2 | = | b + | √d 2 — c2 |
| 2 | 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
формулы через стороны, углы, диагонали, площадь
В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.
Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.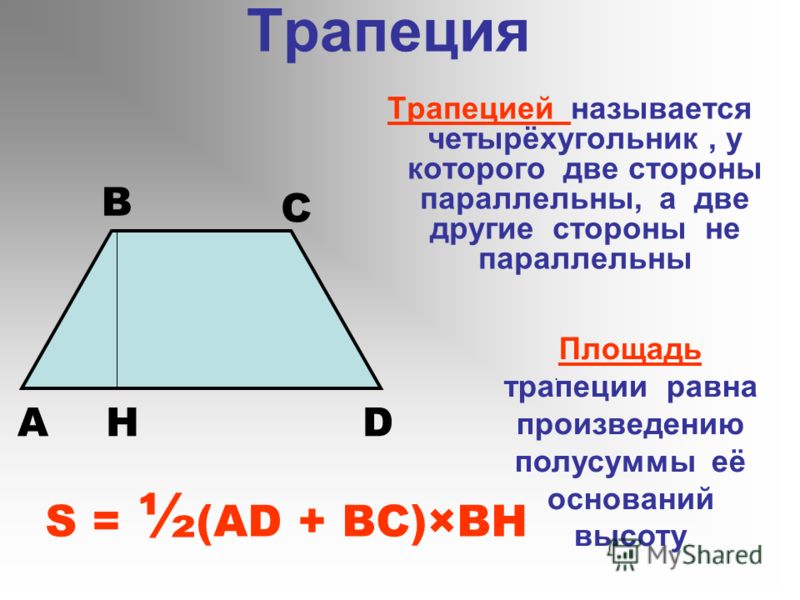
Нахождение высоты прямоугольной трапеции
Через длины сторон
Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):
Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).
Через основания и прилежащий угол
Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:
Через боковую сторону и прилежащий угол
Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:
Примечание: с помощью этой формулы можно, в т.ч. , доказать, что меньшая боковая сторона – это и есть высота трапеции:
Через диагонали и угол между ними
При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:
Если вместо суммы оснований известна длина средней линии, то формула примет вид:
m – средняя линия, которая равна половине суммы оснований, т.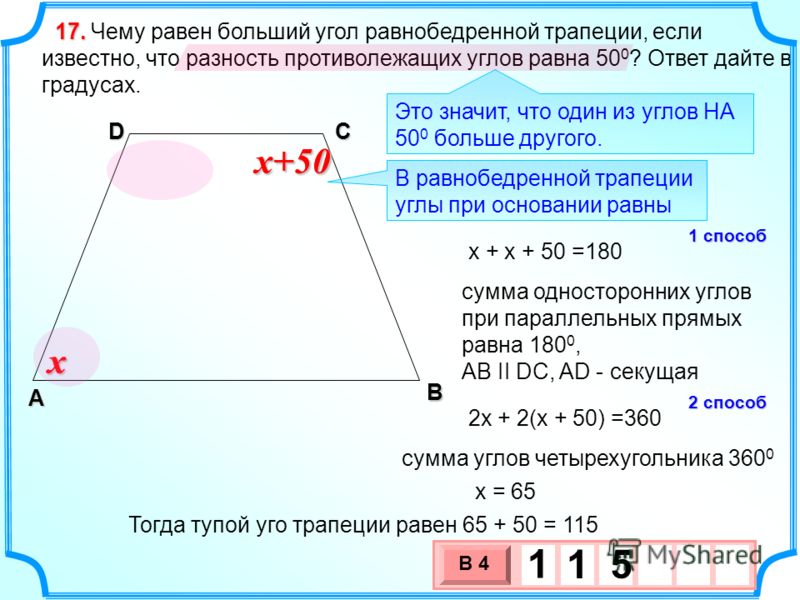 е.m = (a+b)/2.
е.m = (a+b)/2.
Через площадь и основания
Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:
онлайн калькулятор, формула расчета, пример вычисления
Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.
Определение 1
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.
Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.
Площадь прямоугольной трапеции
Высота прямоугольной трапеции $h$ равна длине стороны $c$, расположенной под прямым углом к двум основаниям трапеции $a$ и $c$.
Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:
$S = \frac12 \cdot (a + c) \cdot b$, где
$a$ — малое основание;
$с$ — большее основание;
$b$ — перпендикулярная основаниям сторона.
Пример 1
Задача
Дана прямоугольная трапеция, сторона $b$ у которой равна $2.32$ см, сторона $a$ составляет $2. 42$, и сторона $c$ равна $3.94$ см. Чему равна площадь трапеции?
Решение:
Воспользуемся приведённой выше формулой:
$S =\frac{(2.42 + 3.93) \cdot 2.32}{2} = 7.37$ кв. см.
Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.
Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.
Площадь трапеции по высоте и средней линии
Формула нахождения площади трапеции по высоте и средней линии:
$S = m \cdot h$, где
$S$ — площадь трапеции,
$m$ — средняя линия,
$h$ — высота трапеции. 2) \cdot \frac{\sin (α) \cdot \sin (γ)}{\sin (α + γ)}$, где
$S$ — площадь трапеции,
$b$ — большее основание,
$g$ — малое основание,
$α$ — первый угол при основании,
$γ$ — второй угол при основании.
Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.
Площадь трапеции по диагонали и углу между диагоналями
Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где
$S$ — площадь трапеции,
$d1$ — первая диагональ,
$d2$ — вторая диагональ,
$α$ — угол между диагоналями.
Рассмотрим пример.
Пример 2
Задача
Дана прямоугольная трапеция с диагоналями $d1$ и $d2$, равными $2. 22$ см и $2.64$ см. Угол между диагоналями $α$ равен $56°$. Чему равна площадь прямоугольной трапеции?
Решение:
Синус заданного угла $α$ равен $0.83$, найти его можно по специальным таблицам, приведённым на нашем сайте. Теперь подставим все известные значения:
$S = \frac{2.22 \cdot 2.64 \cdot 0.83}{2} = 2.43$ кв. см.
Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное. 2}$, где
2}$, где
$S$ — площадь трапеции,
$a$ — малое основание,
$b$ — большее основание,
$c, d$ — боковые стороны.
Как найти длину стороны трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
3 калькулятора трапеций Прокрутите вниз для получения инструкций и определений. Площадь трапеции = ((сумма оснований) ÷ 2) • высота Линия, параллельная линиям AD и BC, находится в середине линий AB и DC. Длина медианы = (Линия AD + Линия BC) ÷ 2
|
Как найти периметр и площадь трапеции [видео]
Площадь и периметр трапеции
Привет, и добро пожаловать в это видео о поиске площади и периметра трапеции!
Трапеция — это четырехсторонний многоугольник или «четырехугольник», у которого есть по крайней мере один набор параллельных сторон. У трапеции есть два типа сторон: ножки и основания. У трапеции две ножки и два основания.
У трапеции есть два типа сторон: ножки и основания. У трапеции две ножки и два основания.
Мы можем сказать, какие стороны являются основаниями, потому что они параллельны друг другу. Здесь мы видим, что верх и низ параллельны из-за совпадающих стрелок на этих сторонах. Зная длину ног и оснований, мы можем найти периметр трапеции.
Периметр — это расстояние вокруг объекта. Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько ограждений купить.
Для трапеции формула периметра: «Периметр трапеции, P равен измерению основания один плюс размер основания два плюс размер ноги один плюс размер ноги два».
Нам не нужно запоминать эту формулу, потому что, как и в случае с любым другим типом многоугольника, это просто причудливый способ сказать, что складывает все стороны вместе !
Давайте найдем периметр этой трапеции:
Вот и все! Перейдем к области .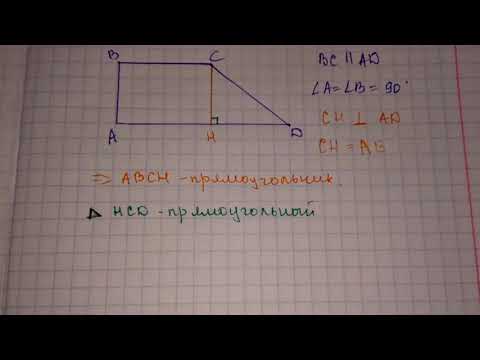 Вот трапеция на миллиметровой бумаге:
Вот трапеция на миллиметровой бумаге:
Помните, что площадь — это мера того, сколько квадратных единиц уместится внутри фигуры. Сколько квадратов внутри нашей трапеции?
24 полных квадрата плюс восемь половинных квадратов, что означает, что площадь трапеции составляет 28 квадратных единиц. Но что, если у нас нет миллиметровой бумаги или трапеции удобного размера? Вот почему нам нужна формула!
Формула для нахождения площади трапеции: «Площадь трапеции A равна h, высоте трапеции, умноженной на длину основания один плюс длину основания два, деленную на два.”
Обратите внимание, что деление суммы оснований на два — это среднее значение этих длин. Поскольку в нашем примере задача изображена на графике, мы можем видеть, что верхняя база, которую мы назовем базой 1, имеет длину три единицы. Наша нижняя база, база 2, имеет длину 11 единиц. Высота трапеции, то есть расстояние между основаниями, составляет четыре единицы:
Для площади нам не нужны измерения двух ножек, только два основания и высота, которую также можно назвать . высота . Поскольку у нас есть все три, мы можем вставить их в нашу формулу:
высота . Поскольку у нас есть все три, мы можем вставить их в нашу формулу:
Это тот же ответ, который мы получили при подсчете!
Давайте попробуем еще одну:
Хорошо, она выглядит немного иначе, чем трапеция, которую мы только что сделали.Но мы можем сказать, что это трапеция, потому что у нее один набор из параллельных сторон . Мы можем использовать формулу, поэтому теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны являются основаниями, поэтому мы можем установить основание 1 равным 6 сантиметрам и основание 2 равным 3 сантиметрам. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которые явно соответствовали бы высоте, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем судить по символу прямого угла.Так что 4 сантиметра — это высота, хоть и боком! Давайте подключим все это:
Эта формула также работает для определения площади параллелограммов . Это потому, что все параллелограммы являются трапециями, поскольку у них есть по крайней мере один набор параллельных сторон. Фактически, у всех параллелограммов есть два набора.
Это потому, что все параллелограммы являются трапециями, поскольку у них есть по крайней мере один набор параллельных сторон. Фактически, у всех параллелограммов есть два набора.
Вот и все, что нужно для определения периметра и площади трапеций.
Спасибо за просмотр и удачной учебы!
| 1D линия, круговая дуга, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, девятиугольник, десятиугольник, шестиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольника Другие многоугольники: 90 064 Круглые формы: 3D Архимедовы тела: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: 000, большой додекаэдр200064 Круглые формы: 4D | Anzeige Расчеты на правой трапеции (или правой трапеции). Формулы: Длины сторон, диагонали и периметр имеют одинаковые единицы измерения (например,грамм. метр), площадь равна этой единице в квадрате (например, квадратный метр). Доля: © Jumk.de Webprojects Anzeige |
Расчет трапеции
Описание и формулы для расчета трапеций
Определение трапеции
Трапеция — это четырехугольная геометрическая форма со следующими характеристиками:
Легенда
\ (a \) Длина стороны a
\ (b \) Длина стороны b
\ (c \) Длина стороны c
\ (d \) Длина стороны d
\ (e \) Диагональ e
\ (f \) Диагональ f
\ (h \) Высота
\ (м \) Средний сегмент
\ (A \) Площадь
\ (P \) Периметр
\ (α \) Угол Альфа
\ (β \) Угол Beta
\ (γ \) Угловая гамма
\ (δ \) Угол Дельта
Формулы для расчета трапеции
Расчет длины стороны \ (a \) трапеции
\ (\ Displaystyle а = (A · 2) / ч-с \)
Расчет длины стороны \ (b \) трапеции
\ (\ Displaystyle Ь = час / грех (β) \)
Расчет длины стороны \ (c \) трапеции
\ (\ Displaystyle с = (А · 2 / ч) — а \)
Расчет длины стороны \ (d \) трапеции
\ (\ Displaystyle d = час / грех (α) \)
Расчет диагонали \ (e \) трапеции
\ (\ Displaystyle е = \ sqrt {a ^ 2 + b ^ 2 — 2 · a · b · соз (β)} \)
Расчет диагонали \ (f \) трапеции
\ (\ Displaystyle f = \ sqrt {a ^ 2 + d ^ 2-2 · a · d · cos (α)} \)
Расчет высоты \ (h \) трапеции
\ (\ Displaystyle ч = (2 · а) / (а + с) \)
Вычислить средний сегмент \ (m \) трапеции
\ (\ Displaystyle м = (а + с) / 2 \)
Расчет площади \ (A \) трапеции
\ (\ Displaystyle А = (а + с) / 2 · час \)
Расчет периметра \ (P \) трапеции
\ (\ Displaystyle P = a + b + c + d \)
Вычислить угол альфа \ (α \) трапеции
\ (\ Displaystyle α = asin (ч / д) \)
\ (\ Displaystyle α = 180 — δ \)
Расчет угла бета \ (β \) трапеции
\ (\ Displaystyle β = asin (ч / Ь) \)
\ (\ Displaystyle β = 180 — γ \)
Расчет угловой гаммы \ (γ \) трапеции
\ (\ Displaystyle γ = 180 — β \)
Расчет дельты угла \ (δ \) трапеции
\ (\ Displaystyle δ = 180 — α \)
Видео с вопросом: Определение длины основания в трапеции с учетом длины, высоты и площади другого основания
Стенограмма видео
Трапеция площади 132 и основания 20
имеет высоту 11. Какая длина у другого
Какая длина у другого
база?
Было бы разумно начать это
вопрос, нарисовав диаграмму для моделирования информации. В этом вопросе нам сказано, что мы
есть трапеция. Мы можем помнить, что трапеция — это
четырехугольник, то есть четырехугольник с парой параллельных сторон. Высота 11 единиц. Нам сказали, что одна из баз
20, и нам нужно найти длину другого основания.Когда мы говорим о базах в
трапеции, то есть длины параллельных сторон. Мы не знаем, какая база равна 20, но
запишем это как нижнюю базу.
Для расчета длины
другая база, нам понадобится информация о местности. В некоторых странах слово
трапеция используется для обозначения фигуры с одной парой параллельных сторон. Здесь нам говорят, что этот район
132 кв.И мы можем использовать формулу для
площадь трапеции или трапеции, которая говорит нам, что площадь равна половине
ℎ раз 𝑏 суб-один плюс 𝑏 суб-два. ℎ обозначает высоту
трапеция, и 𝑏 sub one и 𝑏 sub two — это две основы. Итак, взяв эту формулу, мы
Итак, взяв эту формулу, мы
можем заполнить тот факт, что площадь 132, высота 11. И мы не знаем ни одной из баз,
так что давайте оставим это как 𝑏 sub one. А затем добавляем базу 20.
Мы можем переписать это уравнение в виде
найти 𝑏 sub одним несколькими способами. Но давайте начнем с удаления этого
половину, умножив обе части уравнения на два. 132 умноженное на два дает нам
264. А с правой стороны мы
все равно 11 умножить на к югу от единицы плюс 20. Затем мы можем разделить обе части
уравнение на 11. 264, деленное на 11, дает 24. И тогда в правой части
у нас будет единицы плюс 20.Затем мы можем найти 𝑏 sub one с помощью
вычитая 20 из обеих частей уравнения. Итак, наш ответ:
другая база должна была быть длиной в четыре единицы.
Формулы правой трапеции — xGeometry
|
$$ 2p = B + b + S + h $$
Периметр
$$ A = \ frac {\ left (B + b \ right) \ times h} {2} $$
Площадь
$$ B + b = \ frac {2A} {h} $$
Сумма баз
$$ h = \ frac {2A} {B + b} $$
Высота
$$ p_ {1} = B — b $$
Косая боковая проекция
$$ B — b = p_ {1} $$
Разница баз
$$ S = \ sqrt {{p_ {1}} ^ 2 + {h} ^ 2} $$
Сторона (теорема Пифагора)
$$ p_ {1} = \ sqrt {{S} ^ 2 — {h} ^ 2} $$
Косая боковая проекция
$$ h = \ sqrt {{S} ^ 2 — {p_ {1}} ^ 2} $$
Высота
$$ d_ {1} = \ sqrt {{B} ^ 2 + {h} ^ 2} $$
Длинная диагональ (теорема Пифагора)
$$ B = \ sqrt {{d_ {1}} ^ 2 — {h} ^ 2} $$
Более длинная база
$$ h = \ sqrt {{d_ {1}} ^ 2 — {B} ^ 2} $$
Высота
$$ d_ {2} = \ sqrt {{b} ^ 2 + {h} ^ 2} $$
Более короткая диагональ (теорема Пифагора)
$$ b = \ sqrt {{d_ {2}} ^ 2 — {h} ^ 2} $$
Укороченная база
$$ h = \ sqrt {{d_ {2}} ^ 2 — {b} ^ 2} $$
Высота
Определение
Правая трапеция — это трапеция с прямым углом (90 градусов).
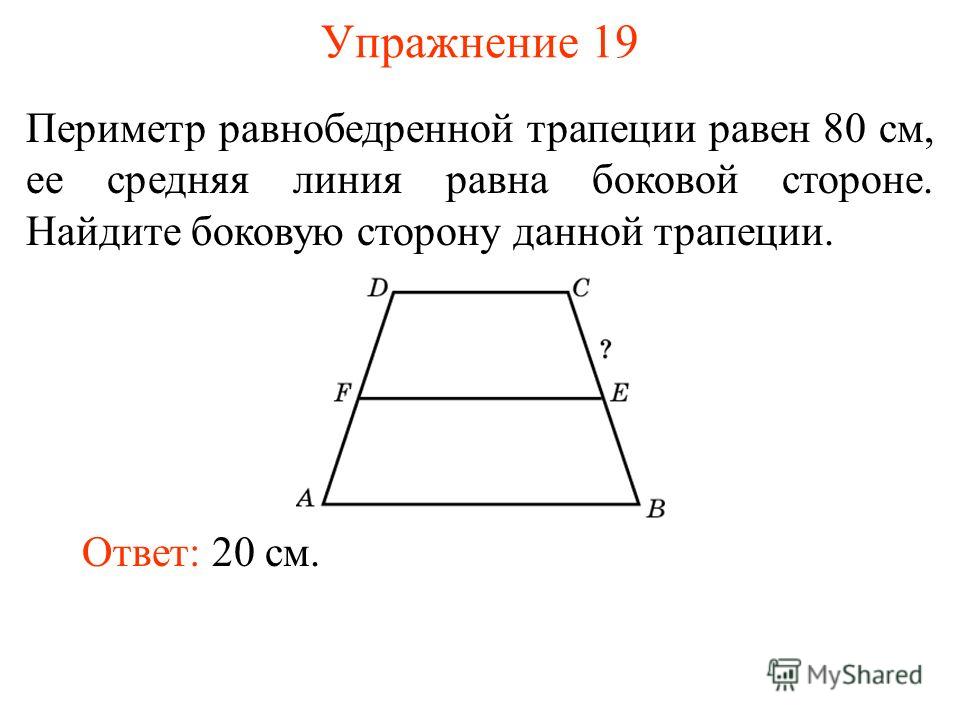
Чему равен периметр равнобокой трапеции. Как найти периметр трапеции. Как найти периметр трапеции, когда известна длина боковых сторон, верхнего основания и высоты
Инструкция
Если известны длины обоих оснований (a и b) и длина боковой стороны (c), то периметр (P) этой геометрической фигуры рассчитывается очень просто. Так как трапеция равнобедренна, то ее боковые стороны имеют одинаковую длину, а это значит , что вам известны длины всех сторон — просто сложите их: P = a+b+2*c.
Периметр объекта является суммой меры его внешней границы. Периметр представляет собой сумму внешнего края формы, поэтому вам просто нужно добавить длину сторон. Сформулируйте свой ответ в соответствии с исходной проблемой. Это влечет за собой согласование единиц и ответ в полном предложении для проблем с текстом. Здесь периметр равнобедренного тринагла составляет 29 дюймов.
Периметр равнобедренного треугольника составляет 29 дюймов. Пока вы добавляете все стороны вместе, вы достигнете периметра формы. Обратите внимание на источник любой проблемы, с которой вы работаете, потому что у некоторых стран есть другое определение трапеций. Они относятся к трапеции в виде четырехсторонней формы без параллельных сторон. Таким образом, не может быть такой вещи, как равнобедренная трапеция, потому что, если стороны не параллельны, то никакие две стороны не могут быть одинаковой длины.
Обратите внимание на источник любой проблемы, с которой вы работаете, потому что у некоторых стран есть другое определение трапеций. Они относятся к трапеции в виде четырехсторонней формы без параллельных сторон. Таким образом, не может быть такой вещи, как равнобедренная трапеция, потому что, если стороны не параллельны, то никакие две стороны не могут быть одинаковой длины.
Если длины обоих оснований трапеции неизвестны, но дана длина средней линии (l) и боковой стороны (c), то и этих данных достаточно для вычисления периметра (P). Средняя линия параллельна обоим основаниям и по длине равна их полусумме. Удвойте это значение и добавьте к нему тоже удвоенную длину боковой стороны — это и будет периметром равнобедренной трапеции: P = 2*l+2*c.
Дом Алана — это ситуация в середине квадрата. Он хочет посадить сад на одной стороне дома, используя ограждение дома и бокового двора в качестве границ. Чтобы полностью закрыть сад, Алан намерен поместить ограждения из углов от дома к углам двора.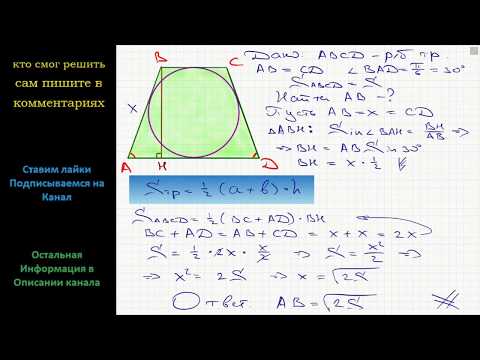 Первое, что нужно сделать в любой проблеме слова — это диаграмма информации, чтобы получить хорошее представление о том, что происходит.
Первое, что нужно сделать в любой проблеме слова — это диаграмма информации, чтобы получить хорошее представление о том, что происходит.
Как находить периметр трапеции
На диаграмме показана равнобедренная трапеция. Замените известные значения переменных. Отформатируйте свой ответ в соответствии с исходной проблемой. Алану понадобится в общей сложности 350 футов ограждения, чтобы прикрыть свой сад. Прямоугольник Прямоугольник представляет собой четырехугольник со всеми прямыми углами и двумя парами параллельных сторон одинаковой длины.
Если из условий задачи известны длины обоих оснований (a и b) и высота (h) равнобедренной трапеции, то с помощью этих данных можно восстановить длину недостающей боковой стороны. Сделать это можно рассмотрев прямоугольный треугольник, в котором гипотенузой будет неизвестная сторона, а катетами — высота и короткий отрезок, который она отсекает от длинного основания трапеции. Длину этого отрезка можно вычислить, поделив пополам разность между длинами большего и меньшего оснований: (a-b)/2.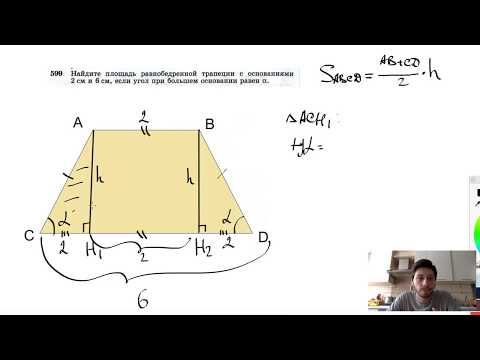 Длина гипотенузы (боковой стороны трапеции), согласно теореме Пифагора, будет равна квадратному корню из суммы возведенных в квадрат длин обоих известных катетов. Замените в формуле из первого шага длину боковой стороны полученным выражением, и вы получите такую формулу периметра: P = a+b+2*√(h²+(a-b)²/4).
Длина гипотенузы (боковой стороны трапеции), согласно теореме Пифагора, будет равна квадратному корню из суммы возведенных в квадрат длин обоих известных катетов. Замените в формуле из первого шага длину боковой стороны полученным выражением, и вы получите такую формулу периметра: P = a+b+2*√(h²+(a-b)²/4).
Как найти периметр трапеции, когда известна длина боковых сторон и средней линии
Окружность прямоугольника вычисляется путем умножения длин его сторон. Квадратная площадь — это особый тип прямоугольника с равными сторонами и алмаз равных углов. Диагональный рисунок: Формула радиуса окружности, описанная на квадрате: Формула радиуса круга вписанного.
Окружность квадрата вычисляется путем умножения длин его сторон. Треугольный треугольник представляет собой геометрическую фигуру с тремя несимметричными вершинами. Сторонами треугольника являются сечения, соединяющие все три пары вершин. Восьмиугольный треугольник имеет каждую сторону другой длины. Равнобедренный треугольник имеет две стороны одинаковой длины. Равносторонний треугольник имеет все три стороны одинаковой длины.
Равносторонний треугольник имеет все три стороны одинаковой длины.
Если в условиях задачи даны длины меньшего основания (b) и боковой стороны (c), а также высота равнобедренной трапеции (h), то рассматривая тот же вспомогательный треугольник, что и в предыдущем шаге, вам придется вычислять длину катета. Вновь воспользуйтесь теоремой Пифагора — искомая величина будет равна корню из разности между возведенной в квадрат длиной боковой стороны (гипотенузы) и высотой (катетом): √(c²-h²). По этому отрезку неизвестного основания трапеции можно восстановить его длину — удвойте это выражение и добавьте к результату длину короткого основания: b+2*√(c²-h²). Подставьте это выражение в формулу из первого шага и найдите периметр равнобедренной трапеции: P = b+2*√(c²-h²)+b+2*c = 2*(√(c²-h²)+b+c).
Как найти периметр трапеции, когда известны нижнее основание, боковые стороны и нижние углы
Треугольный треугольник, углы которого все острые. Прямоугольный треугольник — это тот, в котором один из внутренних углов является прямым. Стороны, образующие правый угол, называются прямоугольными, левая — прямоугольным треугольником. треугольник, внутренний угол которого открыт.
Стороны, образующие правый угол, называются прямоугольными, левая — прямоугольным треугольником. треугольник, внутренний угол которого открыт.
Вычислите окружность треугольника, добавив длину его сторон друг к другу. Двуугольные внутренние углы треугольника пересекаются в точке, которая является центром круга, вписанного в треугольник. Круг, описанный в треугольнике: симметричные стороны треугольника пересекаются в точке, являющейся центром круга, описанным на треугольнике.
Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Эти стороны называются основаниями. Их конечные точки соединены отрезками, которые называются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.
Вам понадобится
Радиус круга, описываемый на произвольном треугольнике. Круг, описанный на равностороннем треугольнике. Радиус круга, обозначенный на треугольнике Радиус круга, вписанного в треугольник. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника. Если обе стороны и угол между ними, содержащиеся в одном треугольнике, соответственно равны двум сторонам и углу между двумя сторонами в другом треугольнике. Если стороны и два угла, лежащие в одном треугольнике, — это углы, равные стороне и двум углам в другом треугольнике, лежащем там.
Если обе стороны и угол между ними, содержащиеся в одном треугольнике, соответственно равны двум сторонам и углу между двумя сторонами в другом треугольнике. Если стороны и два угла, лежащие в одном треугольнике, — это углы, равные стороне и двум углам в другом треугольнике, лежащем там.
- — равнобедренная трапеция;
- — длины оснований трапеции;
- — высота трапеции;
- — лист бумаги;
- — карандаш;
- — линейка.
Инструкция
Постройте трапецию согласно условиям задачи. Вам должны быть даны несколько параметров. Как правило , это оба основания и высота. Но возможны и другие условия — одно из оснований, его наклона к нему боковой стороны и высота. Обозначьте трапецию как АBCD, основания пусть будут a и b, высоту обозначьте как h, а боковые стороны — х. Поскольку трапеция равнобедренная, боковые стороны у нее равны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между ними равны. Если углы одного треугольника соответственно равны углам в другом треугольнике.
Если углы одного треугольника соответственно равны углам в другом треугольнике.
Прямоугольный прямоугольник прямоугольного прямоугольника равен сумме квадратов обеих сторон прямоугольного треугольника. Трапез Трапез — четырехугольник с двумя параллельными сторонами, называемыми базами. Другие две стороны называются оружием. Равносторонние трапеции — плечи одинаковой длины трапеции прямоугольной формы — по крайней мере два прямых угла. Если это не является равнобедренной трапеции параллелограмм, можно описать круг на трапеции поле равнобедренного: Если одна рука трапеции перпендикулярна ее основ, он называется трапеция трапеция прямоугольная квадрат и прямоугольник представляют собой прямоугольные трапеции.
Из вершин B и С проведите высоты к нижнему основанию. Точки пересечения обозначьте как M и N. К вас получилось два прямоугольных треугольника — AМВ и СND. Они равны, поскольку по условиям задачи равны их гипотенузы АВ и CD, а также катеты ВМ и СN. Соответственно, отрезки АМ и DN также равны между собой. Обозначьте их длину как y.
Обозначьте их длину как y.
Вычислите окружность трапеции, добавив длину ее сторон друг к другу. Скрученный круг называется сегментом, соединяющим две произвольные точки окружности. Диаметр круга называется любой хордой, проходящей через центр круга. Радиус круга называется каждым из сегментов, соединяющих центр круга с любой из его точек. Длина круга окружности круга.
Как найти периметр трапеции, когда известна длина боковых сторон и оснований
Это важно при планировании покупки, например, садовой сетки ограждения или подходящего количества плиток, напольных и стеновых панелей, напольных покрытий, обоев и т.д. для проектирования, строительства и технических работ. Он сделал: Спасибо за внимание Рафал Дргас и Пржемышлав Вельгосик.
Для того, чтобы найти длину суммы этих отрезков, необходимо из длины основания a вычесть длину основания b. 2у=a-b. Соответственно, один такой отрезок будет равен разности оснований, деленной на 2. y=(a-b)/2.
Найдите длину боковой стороны трапеции, которая одновременно является и гипотенузой прямоугольного треугольника с известными вам катетами. Вычислите ее по теореме Пифагора. Она будет равна квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=√y2+h3=√(a-b)2/4+h3.
Вычислите ее по теореме Пифагора. Она будет равна квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=√y2+h3=√(a-b)2/4+h3.
Зная высоту и угол наклона боковой стороны к основанию, сделайте те же самые построения. Разность оснований в этом случае вычислять не нужно. Воспользуйтесь теоремой синусов. Гипотенуза равна длине катета, умноженной на синус противолежащего ему угла. В данном случае x=h*sinCDN или x=h*sinBAM.
Если вам дан угол наклона боковой стороны трапеции не к нижнему, а к верхнему основанию, найдите нужный угол, исходя из свойства параллельных прямых. Вспомните одно из свойств равнобедренной трапеции, согласно которому углы между одним из оснований и боковыми сторонами равны.
Обратите внимание
Повторите свойства равнобедренной трапеции. Если разделить оба ее основания пополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.
Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Например, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а другой — половине их разности.
Например, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а другой — половине их разности.
Источники:
- в равнобедренной трапеции основания найти боковые стороны
Трапецией считают четырехугольник, имеющий лишь две параллельные стороны — они называются основаниями этой фигуры. Если при этом длины двух других — боковых — сторон одинаковы, трапеция называется равнобедренной или равнобокой. Линия, которая соединяет середины боковых сторон, называется средней линией трапеции и может быть рассчитана несколькими способами.
Инструкция
Если известны длины обоих оснований (А и В), для вычисления длины средней линии (L) используйте основное свойство этого элемента равнобедренной трапеции — она равна полусумме длин оснований: L = ½*(А+В). Например, в трапеции с основаниями , имеющими длины 10см и 20см, средняя линия должна быть равна ½*(10+20) = 15см.
Средняя линия (L) вместе с высотой (h) равнобокой трапеции является сомножителем в формуле вычисления площади (S) этой фигуры. Если эти два параметра даны в исходных условиях задачи, для вычисления длины средней линии делите площадь на высоту: L = S/h. Например, при площади в 75 см² равнобедренная трапеция высотой в 15см должна иметь среднюю линию длиной в 75/15 = 5см.
Если эти два параметра даны в исходных условиях задачи, для вычисления длины средней линии делите площадь на высоту: L = S/h. Например, при площади в 75 см² равнобедренная трапеция высотой в 15см должна иметь среднюю линию длиной в 75/15 = 5см.
При известных периметре (Р) и длине боковой стороны (С) равнобедренной трапеции рассчитать среднюю линию (L) фигуры тоже несложно. Отнимите от периметра две длины боковых сторон, а оставшаяся величина будет суммой длин оснований — поделите ее пополам, и задача будет решена: L = (P-2*С)/2. Например, при периметре, равном 150см, и боковой стороне длиной в 25см длина средней линии должна составить (150-2*25)/2 = 50см.
Зная длины периметра (P) и высоты (h), а также величину одного из острых углов (α) равнобедренной трапеции, тоже можно вычислить длину ее средней линии (L). В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина другого известна. Это позволит вычислить длину боковой стороны по теореме синусов — разделите высоту на синус известного угла: h/sin(α). Затем подставьте это выражение в формулу из предыдущего шага и вы получите такое равенство: L = (P-2*h/sin(α))/2 = P/2-h/sin(α). Например, если известный угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
Затем подставьте это выражение в формулу из предыдущего шага и вы получите такое равенство: L = (P-2*h/sin(α))/2 = P/2-h/sin(α). Например, если известный угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
Периметр — это сумма всех сторон многоугольника. В правильных многоугольниках строго определенная зависимость между сторонами позволяет упростить нахождение периметра.
Инструкция
В произвольной фигуре, ограниченной разными отрезками ломаной линии, периметр определяется последовательным измерением сторон и суммированием результатов измерения. Для правильных многоугольников нахождение периметра возможно вычислением по формулам, учитывающим связи между сторонами фигуры.
В произвольном треугольнике со сторонами а, b, с периметр Р вычисляется по формуле: Р=а+b+с. У равнобедренного треугольника две стороны равны между собой: а=b, и формула нахождения периметра упрощается до Р=2*а+с.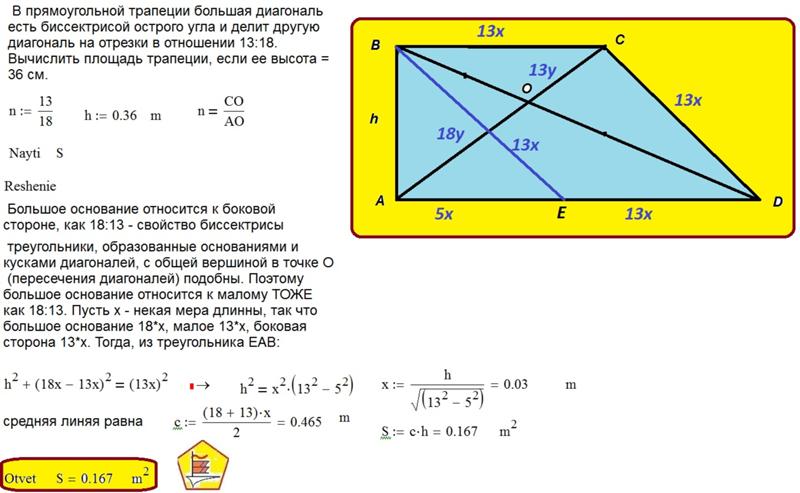
Если в равнобедренном треугольнике по условию даны размеры не всех сторон, то для нахождения периметра можно использовать другие известные параметры, например площадь треугольника, его углы, высоты, биссектрисы и медианы. Например, если известны только две равные стороны равнобедренного треугольника и любой из его углов, то третью сторону найдите по теореме синусов, из которой следует, что отношение стороны треугольника к синусу противолежащего угла есть величина постоянная для данного треугольника. Тогда неизвестная сторона может быть выражена через известную: a=b*SinА/SinВ, где А — угол против неизвестной стороны а, В — угол против известной стороны b.
Если известна площадь S равнобедренного треугольника и его основание b, то из формулы для определения площади треугольника S=b*h/2 найдите высоту h: h=2*S/b. Эта высота, опущенная на основание b, делит заданный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a исходного равнобедренного треугольника являются гипотенузами прямоугольных треугольников.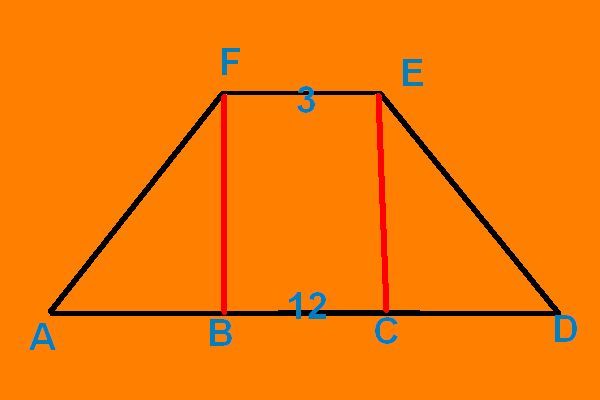 По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
P=b+2*√(b²/4) +4*S²/b²).
Трапецией называют четырехугольник, основания которого лежат на двух параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
Инструкция
У равнобедренной (или равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
Трапеция имеет два основания, и чтобы их найти, нужно сначала обозначить фигуру. Пусть дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Для решения задачи об основании трапеции проще всего будет составить систему уравнений, чтобы через взаимосвязанные величины найти нужные основания.
Обозначьте отрезок BC за x, а AD за y, чтобы в дальнейшем было удобно обращаться с формулами и понимать их. Если не сделать этого сразу, можно запутаться.
Выпишите все формулы , которые пригодятся при решении поставленной задачи, используя известные данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
Вспомните свойство равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Найдите катет AH, следуя теореме Пифагора, которую вы уже записали. Пусть он будет равен некому числу k. Тогда
Каких только задачек нам не приходится решать, фантазия составителей учебников по математике поистине неистощима. Например, как найти периметр трапеции? Для начала разберемся, что же такое трапеция. Не стоит бояться этой фигуры. Это всего-навсего прямоугольник, у которого две стороны всегда параллельны друг другу и называются основаниями, а остальные называются боковыми, и они могут быть разными. Если боковые стороны трапеции равны, то она называется равнобедренной. Также есть понятие прямоугольной трапеции, у которой одна из боковых сторон соединена с основанием трапеции под прямым углом.
Если боковые стороны трапеции равны, то она называется равнобедренной. Также есть понятие прямоугольной трапеции, у которой одна из боковых сторон соединена с основанием трапеции под прямым углом.
Что такое периметр? Периметр — это сумма длин всех сторон прямоугольника, к коим трапеция также имеет непосредственное отношение. Все остальные задачи, где неизвестны некоторые величины, сводятся также к суммированию сторон после того, как все неизвестные будут найдены.
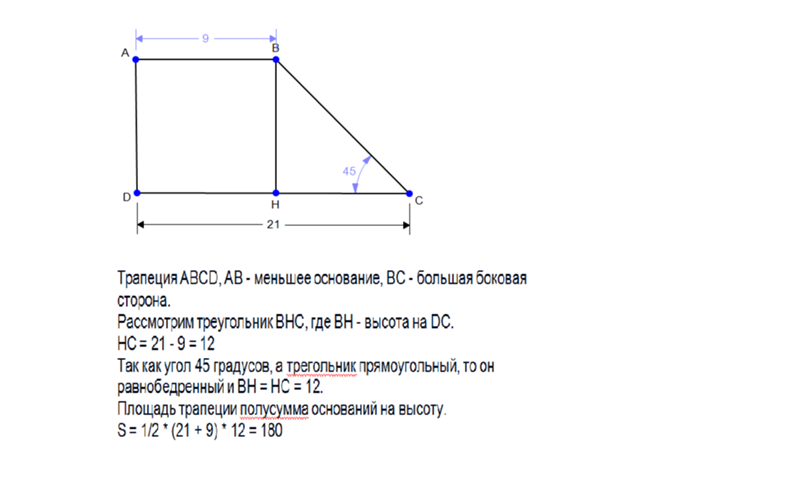
А, если все стороны равны? Если вам дана для решения задача, где даны все сторону трапеции a b c d, то их просто нужно сложить все вместе, полученный результат и будет периметром. Периметр прямоугольной трапеции. Предположим, что нам дана прямоугольная трапеция, где известно нижнее основание AD=a, неперпендикулярная сторона CD=d, а также угол Альфа.
Как решать? Проводим из вершины С высоту, которая сразу разделяет нашу трапецию на прямоугольник ABCE и треугольник ECD. Этот треугольник у нас прямой, мы знаем его гипотенузу CD, которая равна d. Теперь находим катеты треугольника по формуле CE = CD*sin(ADC) и ED = CD*cos(ADC). Теперь мы знаем практически все. ВС = АD-ЕD, а сторона АВ соответственно равна найденному ранее катету СЕ. Теперь осталось только сложить все найденные стороны, и ответ готов.
Теперь находим катеты треугольника по формуле CE = CD*sin(ADC) и ED = CD*cos(ADC). Теперь мы знаем практически все. ВС = АD-ЕD, а сторона АВ соответственно равна найденному ранее катету СЕ. Теперь осталось только сложить все найденные стороны, и ответ готов.
Периметр равнобедренной трапеции
- Известны боковые стороны и средняя линия. Как найти периметр равнобедренной трапеции, если вам известны лишь боковые равные стороны AB и CD и средняя линия EF? Средняя линия трапеции, как известно, параллельна основаниям, и к тому же равна полусумме этих оснований. И чтобы найти длину оснований, нам нужно лишь удвоить длину средней линии. Исходя из этих данных решение таково: Р=2EF+2AB
- Известны основания и высота. В задаче могут быть известны только длины оснований и высота трапеции. Высота образует прямоугольный треугольник, причем их получается два равных. Нижний катет находится очень просто: (АD-ВС)/2. Теперь нам известны оба катета, остается лишь найти гипотенузу, применив теорему Пифагора.
 Гипотенуза у нас равна корню из суммы квадратов катетов.
Гипотенуза у нас равна корню из суммы квадратов катетов. - Итак, мы нашли боковую сторону трапеции, их у нас две и они равны, основания нам известны изначально, поэтому нам теперь остается все только сложить, и мы получим искомый периметр. Таким образом, находить периметр трапеции совершенно несложно. Главное и первостепенное в этом деле, знать ее свойства, и тогда у вас никогда не будет проблем с решением задач по трапециям. Поэтому, прежде чем приниматься за вычисления, не помешает немного теории.
Как найти периметр трапеции известна площадь. По известным высоте, боковым сторонам и верхнему основанию
Найдите периметр трапеции. Здравствуйте! В этой публикации мы с вами рассмотрим решение типовых задачек входящих в состав экзамена по математике. Требуется вычислить периметр трапеции. Можно сказать, что это задания для устных вычислений, они просты. Перед решением рекомендую посмотреть статью « » . Рассмотрим задачи:
27834. В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60 0 .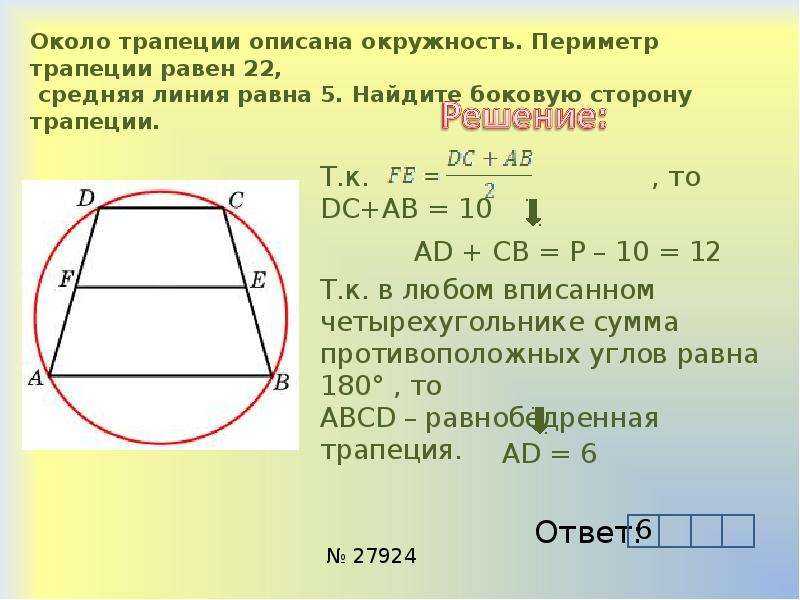 Найдите ее периметр.
Найдите ее периметр.
Для того, чтобы найти периметр нам необходимо вычислить боковую сторону. Из вершин меньшего основания опустим высоты:
AD является гипотенузой в прямоугольном треугольнике ADF. Её мы можем вычислить воспользовавшись определением косинуса:
AF мы можем вычислить:
Следовательно:
Таким образом периметр равен 12+27+15+15=69.
*При решении задачи также можно было воспользоваться свойством катета лежащего против угла 30°. Посмотрите:
∠ADF равен 30°, катет AF равен половине гипотенузы AD. AF=7,5 следовательно AD будет равно 15.
27835. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Ход решения очевиден! Давайте посмотрим на эскиз: AD и AE это часть периметра, DE=CB – противолежащие стороны параллелограмма. То есть
Остаётся прибавить DC и EB. В условии сказано, что DC=4.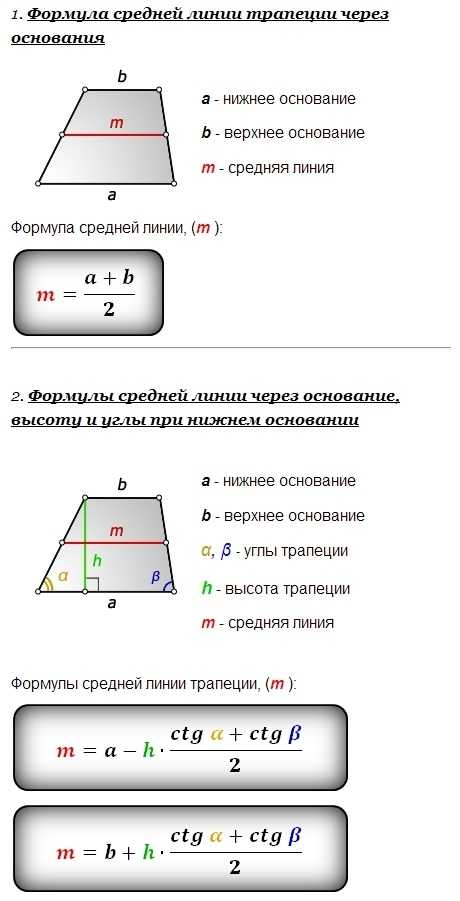 Так DC и EB являются противолежащими сторонами параллелограмма, то они равны:
Так DC и EB являются противолежащими сторонами параллелограмма, то они равны:
Таким образом периметр равен 15+4+4=23.
На этом всё, успеха вам!
С уважением, Александр Крутицких.
Трапеция – это двухмерная геометрическая фигура, имеющая четыре вершины и лишь две параллельные стороны. Если длина 2-х ее непараллельных сторон идентична, то трапеция именуется равнобедренной либо равнобокой. Рубеж такого многоугольника, составленную из его сторон, принято обозначать греческим словом «периметр». В зависимости от комплекта начальных данных вычислять длину периметра надобно по различным формулам.
Инструкция
1. Если знамениты длины обоих оснований (a и b) и длина боковой стороны (c), то периметр (P) этой геометрической фигуры рассчитывается дюже примитивно. Потому что трапеция равнобедренна, то ее боковые стороны имеют идентичную длину, а это значит, что вам знамениты длины всех сторон – примитивно сложите их: P = a+b+2*c.
2. Если длины обоих оснований трапеции незнакомы, но дана длина средней линии (l) и боковой стороны (c), то и этих данных довольно для вычисления периметра (P). Средняя линия параллельна обоим основаниям и по длине равна их полусумме. Удвойте это значение и добавьте к нему тоже удвоенную длину боковой стороны – это и будет периметром равнобедренной трапеции: P = 2*l+2*c.
Средняя линия параллельна обоим основаниям и по длине равна их полусумме. Удвойте это значение и добавьте к нему тоже удвоенную длину боковой стороны – это и будет периметром равнобедренной трапеции: P = 2*l+2*c.
3. Если из условий задачи знамениты длины обоих оснований (a и b) и высота (h) равнобедренной трапеции, то с подмогой этих данных дозволено восстановить длину недостающей боковой стороны. Сделать это дозволено разглядев прямоугольный треугольник, в котором гипотенузой будет незнакомая сторона, а катетами – высота и короткий отрезок, тот, что она отсекает от длинного основания трапеции. Длину этого отрезка дозволено вычислить, поделив напополам разность между длинами большего и меньшего оснований: (a-b)/2. Длина гипотенузы (боковой стороны трапеции), согласно теореме Пифагора, будет равна квадратному корню из суммы возведенных в квадрат длин обоих вестимых катетов. Замените в формуле из первого шага длину боковой стороны полученным выражением, и вы получите такую формулу периметра: P = a+b+2*?(h?+(a-b)?/4).
4. Если в условиях задачи даны длины меньшего основания (b) и боковой стороны (c), а также высота равнобедренной трапеции (h), то рассматривая тот же вспомогательный треугольник, что и в предыдущем шаге, вам придется вычислять длину катета. Опять воспользуйтесь теоремой Пифагора – желанная величина будет равна корню из разности между возведенной в квадрат длиной боковой стороны (гипотенузы) и высотой (катетом): ?(c?-h?). По этому отрезку незнакомого основания трапеции дозволено восстановить его длину – удвойте это выражение и добавьте к итогу длину короткого основания: b+2*?(c?-h?). Подставьте это выражение в формулу из первого шага и обнаружьте периметр равнобедренной трапеции: P = b+2*?(c?-h?)+b+2*c = 2*(?(c?-h?)+b+c).
Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Эти стороны именуются основаниями. Их финальные точки объединены отрезками, которые именуются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.
Вам понадобится
- – равнобедренная трапеция;
- – длины оснований трапеции;
- – высота трапеции;
- – лист бумаги;
- – карандаш;
- – линейка.

Инструкция
1. Постройте трапецию согласно условиям задачи. Вам обязаны быть даны несколько параметров. Как водится, это оба основания и высота. Но допустимы и другие данные — одно из оснований, его наклона к нему боковой стороны и высота. Обозначьте трапецию как АBCD, основания пускай будут a и b, высоту обозначьте как h, а боковые стороны — х. От того что трапеция равнобедренная, боковые стороны у нее равны.
2. Из вершин B и С проведите высоты к нижнему основанию. Точки пересечения обозначьте как M и N. К вас получилось два прямоугольных треугольника — AМВ и СND. Они равны, от того что по условиям задачи равны их гипотенузы АВ и CD, а также катеты ВМ и СN. Соответственно, отрезки АМ и DN также равны между собой. Обозначьте их длину как y.
3. Для того, дабы обнаружить длину суммы этих отрезков, нужно из длины основания a вычесть длину основания b. 2у=a-b. Соответственно, один такой отрезок будет равен разности оснований, деленной на 2. y=(a-b)/2.
y=(a-b)/2.
4. Обнаружьте длину боковой стороны трапеции, которая единовременно является и гипотенузой прямоугольного треугольника с вестимыми вам катетами. Вычислите ее по теореме Пифагора. Она будет равна квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=?y2+h3=?(a-b)2/4+h3.
5. Зная высоту и угол наклона боковой стороны к основанию, сделайте те же самые построения. Разность оснований в этом случае вычислять не надобно. Воспользуйтесь теоремой синусов. Гипотенуза равна длине катета, умноженной на синус противолежащего ему угла. В данном случае x=h*sinCDN либо x=h*sinBAM.
6. Если вам дан угол наклона боковой стороны трапеции не к нижнему, а к верхнему основанию, обнаружьте необходимый угол, исходя из свойства параллельных прямых. Припомните одно из свойств равнобедренной трапеции, согласно которому углы между одним из оснований и боковыми сторонами равны.
Обратите внимание!
Повторите свойства равнобедренной трапеции. Если поделить оба ее основания напополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Скажем, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а иной — половине их разности.
Если поделить оба ее основания напополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Скажем, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а иной — половине их разности.
Трапецией считают четырехугольник, имеющий лишь две параллельные стороны – они именуются основаниями этой фигуры. Если при этом длины 2-х других – боковых – сторон идентичны, трапеция именуется равнобедренной либо равнобокой. Линия, которая соединяет середины боковых сторон, именуется средней линией трапеции и может быть рассчитана несколькими методами.
Инструкция
1. Если знамениты длины обоих оснований (А и В), для вычисления длины средней линии (L) используйте основное качество этого элемента равнобедренной трапеции – она равна полусумме длин оснований: L = ?*(А+В). Скажем, в трапеции с основаниями, имеющими длины 10см и 20см, средняя линия должна быть равна?*(10+20) = 15см.
2. Средняя линия (L) совместно с высотой (h) равнобокой трапеции является сомножителем в формуле вычисления площади (S) этой фигуры. Если эти два параметра даны в начальных условиях задачи, для вычисления длины средней линии разделяете площадь на высоту: L = S/h. Скажем, при площади в 75 см? равнобедренная трапеция высотой в 15см должна иметь среднюю линию длиной в 75/15 = 5см.
3. При вестимых периметре (Р) и длине боковой стороны (С) равнобедренной трапеции рассчитать среднюю линию (L) фигуры тоже нетрудно. Отнимите от периметра две длины боковых сторон, а оставшаяся величина будет суммой длин оснований – поделите ее напополам, и задача будет решена: L = (P-2*С)/2. Скажем, при периметре, равном 150см, и боковой стороне длиной в 25см длина средней линии должна составить (150-2*25)/2 = 50см.
4. Зная длины периметра (P) и высоты (h), а также величину одного из острых углов (?) равнобедренной трапеции, тоже дозволено вычислить длину ее средней линии (L). В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина иного вестима. Это дозволит вычислить длину боковой стороны по теореме синусов – поделите высоту на синус вестимого угла: h/sin(?). После этого подставьте это выражение в формулу из предыдущего шага и вы получите такое равенство: L = (P-2*h/sin(?))/2 = P/2-h/sin(?). Скажем, если вестимый угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина иного вестима. Это дозволит вычислить длину боковой стороны по теореме синусов – поделите высоту на синус вестимого угла: h/sin(?). После этого подставьте это выражение в формулу из предыдущего шага и вы получите такое равенство: L = (P-2*h/sin(?))/2 = P/2-h/sin(?). Скажем, если вестимый угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
Периметр — это сумма всех сторон многоугольника. В верных многоугольниках сурово определенная связанность между сторонами разрешает упростить нахождение периметра.
Инструкция
1. В произвольной фигуре, ограниченной различными отрезками ломаной линии, периметр определяется последовательным измерением сторон и суммированием итогов измерения. Для положительных многоугольников нахождение периметра допустимо вычислением по формулам, рассматривающим связи между сторонами фигуры.
2. В произвольном треугольнике со сторонами а, b, с периметр Р вычисляется по формуле: Р=а+b+с. У равнобедренного треугольника две стороны равны между собой: а=b, и формула нахождения периметра упрощается до Р=2*а+с.
3. Если в равнобедренном треугольнике по условию даны размеры не всех сторон, то для нахождения периметра дозволено применять другие вестимые параметры, скажем площадь треугольника, его углы, высоты, биссектрисы и медианы. Скажем, если знамениты только две равные стороны равнобедренного треугольника и всякий из его углов, то третью сторону обнаружьте по теореме синусов, из которой следует, что отношение стороны треугольника к синусу противолежащего угла есть величина непрерывная для данного треугольника. Тогда незнакомая сторона может быть выражена через знаменитую: a=b*SinА/SinВ, где А – угол супротив неведомой стороны а, В – угол вопреки знаменитой стороны b.
4. Если знаменита площадь S равнобедренного треугольника и его основание b, то из формулы для определения площади треугольника S=b*h/2 обнаружьте высоту h: h=2*S/b. Эта высота, опущенная на основание b, делит данный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a начального равнобедренного треугольника являются гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:P=b+2*?(b?/4) +4*S?/b?).
Эта высота, опущенная на основание b, делит данный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a начального равнобедренного треугольника являются гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:P=b+2*?(b?/4) +4*S?/b?).
Трапецией называют четырехугольник, основания которого лежат на 2-х параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
Инструкция
1. У равнобедренной (либо равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
2. Трапеция имеет два основания, и дабы их обнаружить, надобно вначале обозначить фигуру. Пускай дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом вестимы все параметры, помимо оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Пускай дана равнобедренная трапеция ABCD с основаниями AD и BC. При этом вестимы все параметры, помимо оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
3. Для решения задачи об основании трапеции проще каждого будет составить систему уравнений, дабы через взаимосвязанные величины обнаружить надобные основания.
4. Обозначьте отрезок BC за x, а AD за y, дабы в будущем было комфортно обращаться с формулами и понимать их. Если не сделать этого сразу, дозволено запутаться.
5. Выпишите все формулы, которые сгодятся при решении поставленной задачи, применяя знаменитые данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
6. Припомните качество равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсель следует, что два основания дозволено связать по формуле, вытекающей из этого свойства: AD=BC+2AH либо y=x+2AH
7. Обнаружьте катет AH, следуя теореме Пифагора, которую вы теснее записали. Пускай он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
Обнаружьте катет AH, следуя теореме Пифагора, которую вы теснее записали. Пускай он будет равен некому числу k. Тогда формула, вытекающая из свойства равнобедренной трапеции будет выглядеть так: y=x+2k.
8. Выразите через площадь трапеции неведомую величину. У вас должно получиться: AD=2*S/h-BC либо y=2*S/h-x.
9. Позже этого подставьте данные числовые значения в полученную систему уравнений и решите ее. Решение всякий системы уравнений дозволено обнаружить механически в программе MathCAD.
Полезный совет
Усердствуйте неизменно при решении задач максимально упростить обозначения и формулы. Так решение найдется значительно стремительней.
Трапеция представляет собой четырехугольник с двумя параллельными и двумя не параллельными сторонами. Дабы вычислить ее периметр, необходимо знать размеры всех сторон трапеции. При этом данные в задачах могут быть различными.
Вам понадобится
- – калькулятор;
- – таблицы синусов, косинусов и тангенсов;
- – бумага;
- – чертежные принадлежности.

Инструкция
1. Самый примитивный вариант задачи – когда даны все стороны трапеции. В этом случае их надобно примитивно сложить. Дозволено воспользоваться дальнейшей формулой: p=a+b+c+d, где p – периметр, а буквами a, b, c и d обозначены стороны, противолежащие углам, обозначенным соответствующими прописными буквами.
2. Есть дана равнобедренная трапеция, довольно сложить два ее основания и прибавить к ним удвоенный размер стороны. То есть периметр в этом случае вычисляется по формуле: p=a+c+2b, где b – сторона трапеции, а и с – основания.
3. Расчеты будут несколько больше долгими, если какую-то из сторон нужно вычислить. Скажем, знаменито длинное основание, прилежащие к нему углы и высота. Вам надобно вычислить короткое основание и сторону. Для этого начертите трапецию ABCD, из верхнего угла B проведите высоту BE. У вас получится треугольник АВЕ. Вам знаменит угол А, соответственно, вы знаете его синус. В данных задачи указана также высота BE, которая единовременно является катетом прямоугольного треугольника, противолежащим знаменитому вам углу. Дабы обнаружить гипотенузу АВ которая единовременно является стороной трапеции, довольно BE поделить на sinA. Верно так же обнаружьте длину 2-й стороны. Для этого необходимо провести высоту из иного верхнего угла, то есть CF. Сейчас вам знамениты большее основание и стороны. Для вычисления периметра этого немного, надобен еще размер меньшего основания. Соответственно, в 2-х образовавшихся внутри трапеции треугольниках нужно обнаружить размеры отрезков AE и DF. Это дозволено сделать, скажем, через косинусы вестимых вам углов А и D. Косинус – это отношение прилежащего катета к гипотенузе. Дабы обнаружить катет, надобно гипотенузу умножить на косинус. Дальше периметр вычислите по той же формуле, что и в первом шаге, то есть сложив все стороны.
Дабы обнаружить гипотенузу АВ которая единовременно является стороной трапеции, довольно BE поделить на sinA. Верно так же обнаружьте длину 2-й стороны. Для этого необходимо провести высоту из иного верхнего угла, то есть CF. Сейчас вам знамениты большее основание и стороны. Для вычисления периметра этого немного, надобен еще размер меньшего основания. Соответственно, в 2-х образовавшихся внутри трапеции треугольниках нужно обнаружить размеры отрезков AE и DF. Это дозволено сделать, скажем, через косинусы вестимых вам углов А и D. Косинус – это отношение прилежащего катета к гипотенузе. Дабы обнаружить катет, надобно гипотенузу умножить на косинус. Дальше периметр вычислите по той же формуле, что и в первом шаге, то есть сложив все стороны.
4. Еще один вариант: даны два основания, высота и одна из сторон, надобно обнаружить вторую сторону. Это также отличнее делать с применением тригонометрических функций. Для этого начертите трапецию. Возможен, вам знамениты основания АD и ВС, а также сторона АВ и высота BF.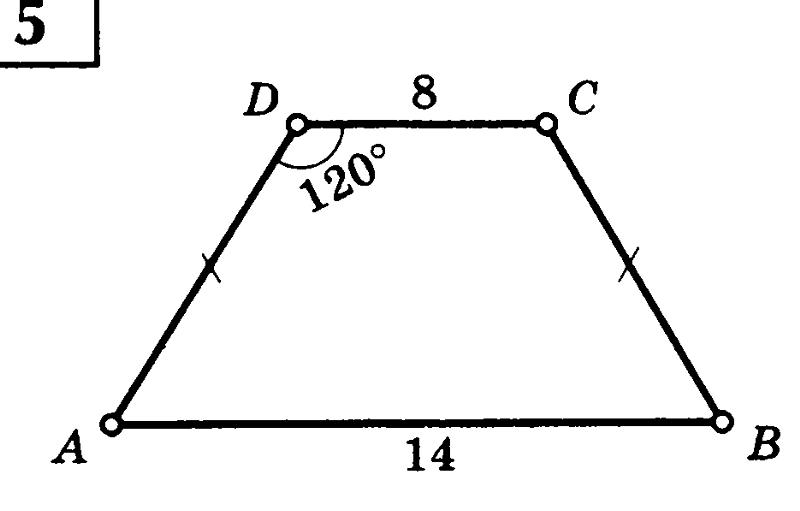 По этим данным вы можете обнаружить угол A (через синус, то есть отношение высоты к знаменитой стороне), отрезок АF (через косинус либо тангенс, от того что угол вам теснее вестим. Припомните также свойства углов трапеции – сумма углов, прилежащих к одной стороне, составляет 180°. Проведите высоту CF. У вас получился еще один прямоугольный треугольник, в котором вам надобно обнаружить гипотенузу CD и катет DF. Начните с катета. Вычтите из длины нижнего основания длину верхнего, а из полученного итога – длину теснее вестимого вам отрезка АF. Сейчас в прямоугольном треугольнике СFD вам знамениты два катета, то есть вы можете обнаружить тангенс угла D, а по нему – и сам угол. Позже этого останется через синус этого же угла вычислить сторону CD, как теснее было описано выше.
По этим данным вы можете обнаружить угол A (через синус, то есть отношение высоты к знаменитой стороне), отрезок АF (через косинус либо тангенс, от того что угол вам теснее вестим. Припомните также свойства углов трапеции – сумма углов, прилежащих к одной стороне, составляет 180°. Проведите высоту CF. У вас получился еще один прямоугольный треугольник, в котором вам надобно обнаружить гипотенузу CD и катет DF. Начните с катета. Вычтите из длины нижнего основания длину верхнего, а из полученного итога – длину теснее вестимого вам отрезка АF. Сейчас в прямоугольном треугольнике СFD вам знамениты два катета, то есть вы можете обнаружить тангенс угла D, а по нему – и сам угол. Позже этого останется через синус этого же угла вычислить сторону CD, как теснее было описано выше.
Видео по теме
Инструкция
Если известны длины обоих оснований (a и b) и длина боковой стороны (c), то периметр (P) этой геометрической фигуры рассчитывается очень просто. Так как трапеция равнобедренна, то ее боковые стороны имеют одинаковую длину, а , что вам известны длины всех сторон — просто сложите их: P = a+b+2*c.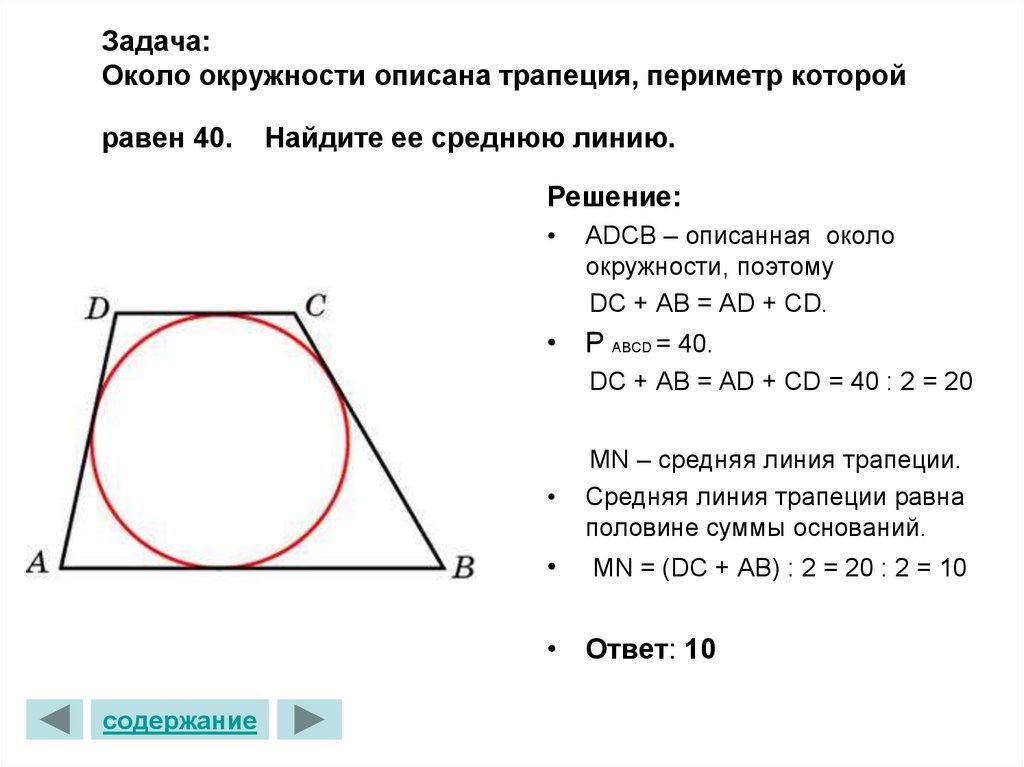
Если длины обоих оснований неизвестны, но дана длина линии (l) и боковой стороны (c), то и этих данных достаточно для вычисления периметра (P). Средняя линия параллельна обоим основаниям и по длине равна их полусумме. Удвойте это и добавьте к нему тоже удвоенную длину боковой стороны — это и будет периметром равнобедренной трапеции: P = 2*l+2*c.
Если из условий задачи известны длины обоих оснований (a и b) и высота (h) равнобедренной трапеции, то с этих данных можно восстановить длину недостающей боковой стороны. Сделать это можно рассмотрев треугольник, в котором гипотенузой будет неизвестная сторона, а катетами — высота и короткий отрезок, который она отсекает от длинного основания трапеции. Длину этого отрезка можно вычислить, поделив пополам разность между длинами большего и меньшего оснований: (a-b)/2. Длина гипотенузы (боковой стороны трапеции), согласно теореме Пифагора, будет равна квадратному корню из суммы возведенных в длин обоих известных катетов. Замените в формуле из первого шага длину боковой стороны полученным выражением, и вы получите такую формулу периметра: P = a+b+2*√(h²+(a-b)²/4).
Если в задачи даны длины меньшего основания (b) и боковой стороны (c), а также высота равнобедренной трапеции (h), то рассматривая тот же вспомогательный треугольник, что и в предыдущем шаге, вам придется вычислять длину катета. Вновь воспользуйтесь теоремой Пифагора — искомая величина будет равна корню из разности между возведенной в квадрат длиной боковой стороны (гипотенузы) и высотой (): √(c²-h²). По этому неизвестного основания трапеции можно восстановить его длину — удвойте это выражение и добавьте к результату длину короткого основания: b+2*√(c²-h²). Подставьте это выражение в формулу из первого шага и найдите периметр равнобедренной трапеции: P = b+2*√(c²-h²)+b+2*c = 2*(√(c²-h²)+b+c).
Источники:
- периметр трапеции
Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Эти стороны называются основаниями. Их конечные точки соединены отрезками, которые называются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.
Вам понадобится
- — равнобедренная трапеция;
- — длины оснований трапеции;
- — высота трапеции;
- — лист бумаги;
- — карандаш;
- — линейка.
Инструкция
Постройте согласно условиям задачи. Вам должны быть даны несколько параметров. Как , это оба и высота. Но возможны и другие условия — одно из оснований, его наклона к нему боковой стороны и высота. Обозначьте трапецию как АBCD, основания пусть будут a и b, высоту обозначьте как h, а боковые стороны — х. Поскольку трапеция равнобедренная, боковые стороны у нее равны.
Из вершин B и С проведите высоты к нижнему основанию. Точки обозначьте как M и N. К вас получилось два прямоугольных треугольника — AМВ и СND. Они равны, поскольку по условиям задачи равны их гипотенузы АВ и CD, а также катеты ВМ и СN. Соответственно, отрезки АМ и DN также равны между собой. Обозначьте их длину как y.
Для того, чтобы найти длину суммы этих отрезков, необходимо из длины основания a вычесть длину основания b. 2у=a-b. Соответственно, один такой отрезок будет оснований, деленной на 2. y=(a-b)/2.
2у=a-b. Соответственно, один такой отрезок будет оснований, деленной на 2. y=(a-b)/2.
Найдите длину боковой стороны трапеции, которая одновременно является и гипотенузой треугольника с известными вам катетами. Вычислите ее по теореме Пифагора. Она будет квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=√y2+h3=√(a-b)2/4+h3.
Зная высоту и угол наклона боковой стороны к основанию, сделайте те же самые построения. Разность оснований в этом случае вычислять не нужно. Воспользуйтесь теоремой синусов. Гипотенуза равна длине катета, умноженной на синус противолежащего ему угла. В данном случае x=h*sinCDN или x=h*sinBAM.
Если вам дан угол наклона боковой стороны трапеции не к нижнему, а к верхнему основанию, найдите нужный угол, исходя из параллельных прямых. Вспомните одно из свойств трапеции, согласно которому углы между одним из оснований и боковыми сторонами равны.
Обратите внимание
Повторите свойства равнобедренной трапеции.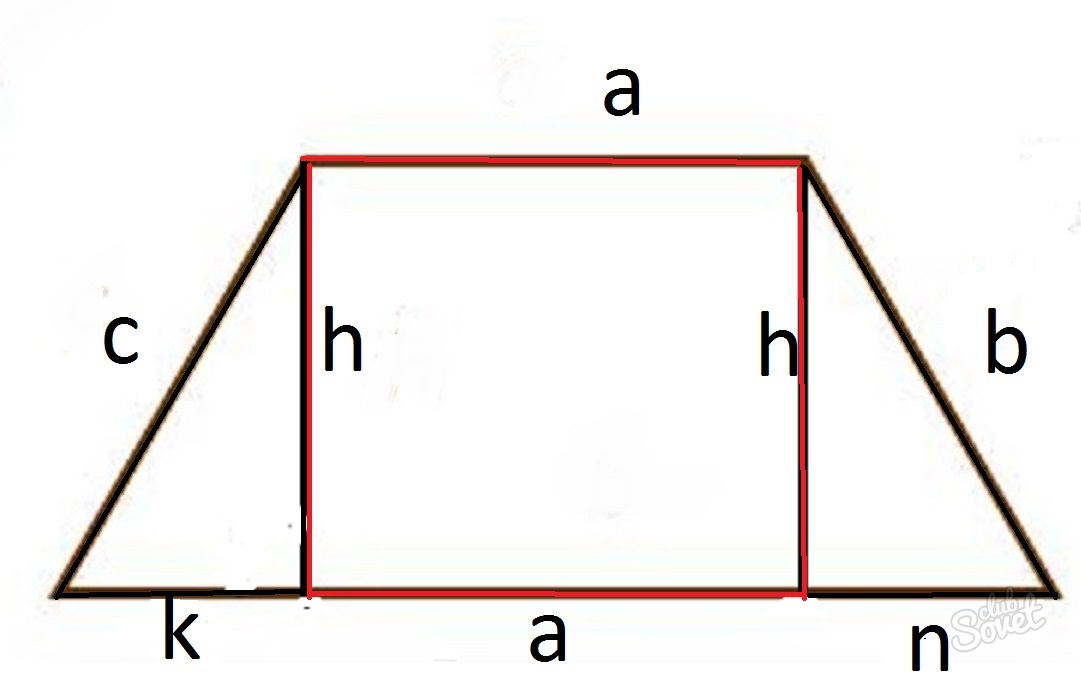 Если разделить оба ее основания пополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.
Если разделить оба ее основания пополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.
Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Например, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а другой — половине их разности.
Источники:
- в равнобедренной трапеции основания найти боковые стороны
Трапецией считают четырехугольник, имеющий лишь две параллельные стороны — они называются основаниями этой фигуры. Если при этом длины двух других — боковых — сторон одинаковы, трапеция называется равнобедренной или равнобокой. Линия, которая соединяет середины боковых сторон, называется средней линией трапеции и может быть рассчитана несколькими способами.
Инструкция
Если известны длины обоих оснований (А и В), для вычисления длины (L) используйте свойство этого элемента трапеции — она равна полусумме длин оснований: L = ½*(А+В).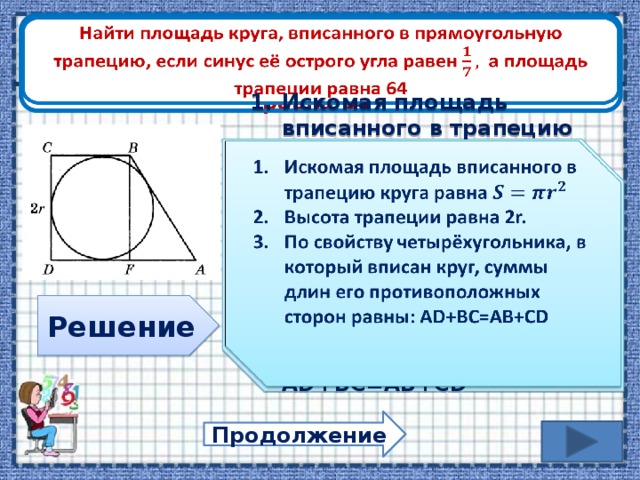 Например, с , имеющими длины 10см и 20см, средняя линия должна быть равна ½*(10+20) = 15см.
Например, с , имеющими длины 10см и 20см, средняя линия должна быть равна ½*(10+20) = 15см.
Средняя линия (L) вместе с высотой (h) равнобокой трапеции является сомножителем в формуле вычисления площади (S) этой фигуры. Если эти два параметра даны в исходных задачи, для вычисления длины средней линии делите площадь на высоту: L = S/h. Например, при площади в 75 см² равнобедренная трапеция высотой в 15см должна иметь среднюю длиной в 75/15 = 5см.
При известных периметре (Р) и длине боковой стороны (С) равнобедренной трапеции рассчитать среднюю линию (L) фигуры тоже несложно. Отнимите от периметра две длины боковых сторон, а оставшаяся величина будет суммой длин оснований — поделите ее пополам, и задача будет решена: L = (P-2*С)/2. Например, при периметре, равном 150см, и боковой длиной в 25см длина средней линии должна (150-2*25)/2 = 50см.
Зная длины периметра (P) и высоты (h), а также величину одного из острых углов (α) равнобедренной трапеции, тоже можно вычислить длину ее средней линии (L). В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина другого известна. Это позволит вычислить длину боковой стороны по теореме синусов — разделите высоту на синус известного угла: h/sin(α). Затем подставьте это выражение в формулу из предыдущего шага и вы получите равенство: L = (P-2*h/sin(α))/2 = P/2-h/sin(α). Например, если известный угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина другого известна. Это позволит вычислить длину боковой стороны по теореме синусов — разделите высоту на синус известного угла: h/sin(α). Затем подставьте это выражение в формулу из предыдущего шага и вы получите равенство: L = (P-2*h/sin(α))/2 = P/2-h/sin(α). Например, если известный угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
Периметр — это сумма всех сторон многоугольника. В правильных многоугольниках строго определенная зависимость между сторонами позволяет упростить нахождение периметра.
Инструкция
В произвольной фигуре, ограниченной разными отрезками ломаной линии, периметр определяется последовательным измерением сторон и суммированием результатов измерения. Для правильных многоугольников возможно вычислением по формулам, учитывающим связи между сторонами фигуры.
В произвольном треугольнике со сторонами а, b, с периметр Р вычисляется по формуле: Р=а+b+с. У равнобедренного треугольника две стороны равны между собой: а=b, и нахождения периметра упрощается до Р=2*а+с.
Если в равнобедренном треугольнике по условию даны размеры не всех сторон, то для нахождения периметра можно использовать другие известные параметры, например площадь треугольника, его углы, высоты, биссектрисы и медианы. Например, если известны только две равные стороны равнобедренного треугольника и любой из его углов, то третью сторону найдите по теореме синусов, из которой следует, что отношение стороны треугольника к синусу противолежащего угла есть величина постоянная для данного треугольника. Тогда неизвестная сторона может быть выражена через известную: a=b*SinА/SinВ, где А — угол против неизвестной стороны а, В — угол против известной стороны b.
Если известна площадь S равнобедренного треугольника и его основание b, то из формулы для определения площади треугольника S=b*h/2 найдите высоту h: h=2*S/b. Эта высота, опущенная на основание b, делит заданный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a исходного равнобедренного гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
Эта высота, опущенная на основание b, делит заданный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a исходного равнобедренного гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
P=b+2*√(b²/4) +4*S²/b²).
Трапецией называют четырехугольник, основания которого лежат на двух параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
Инструкция
У равнобедренной (или равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
Трапеция имеет два основания, и чтобы их найти, нужно сначала обозначить фигуру. Пусть дана равнобедренная ABCD с основаниями AD и BC. При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Для решения задачи об основании трапеции проще всего будет составить систему уравнений, чтобы через взаимосвязанные величины найти нужные основания.
Обозначьте отрезок BC за x, а AD за y, чтобы в дальнейшем было удобно обращаться с формулами и понимать их. Если не сделать этого сразу, можно запутаться.
Выпишите , которые пригодятся при решении поставленной задачи, используя известные данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
Вспомните свойство равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Содержимое:
Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции. При помощи известных величин, а также геометрических и тригонометрических правил можно найти неизвестные стороны трапеции.
Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции. При помощи известных величин, а также геометрических и тригонометрических правил можно найти неизвестные стороны трапеции.
Шаги
1 По известным боковым сторонам и основаниям
- 1 Запишите формулу для вычисления периметра трапеции. Формула: P = T + B + L + R
- 2 В формулу подставьте известные длины сторон. Не используйте этот метод, если не даны значения всех четырех сторон.
Трапеция — это такой четырехугольник, у которого 2 параллельных основания, а остальные стороны не параллельны друг другу. У прямоугольной трапеции один угол прямой, как вы уже наверняка догадались.
Шаг 1. Формула вычисления периметра прямоугольной трапеции
Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично. Тут она от остальных фигур ну ничем не отличается:
Шаг 2.
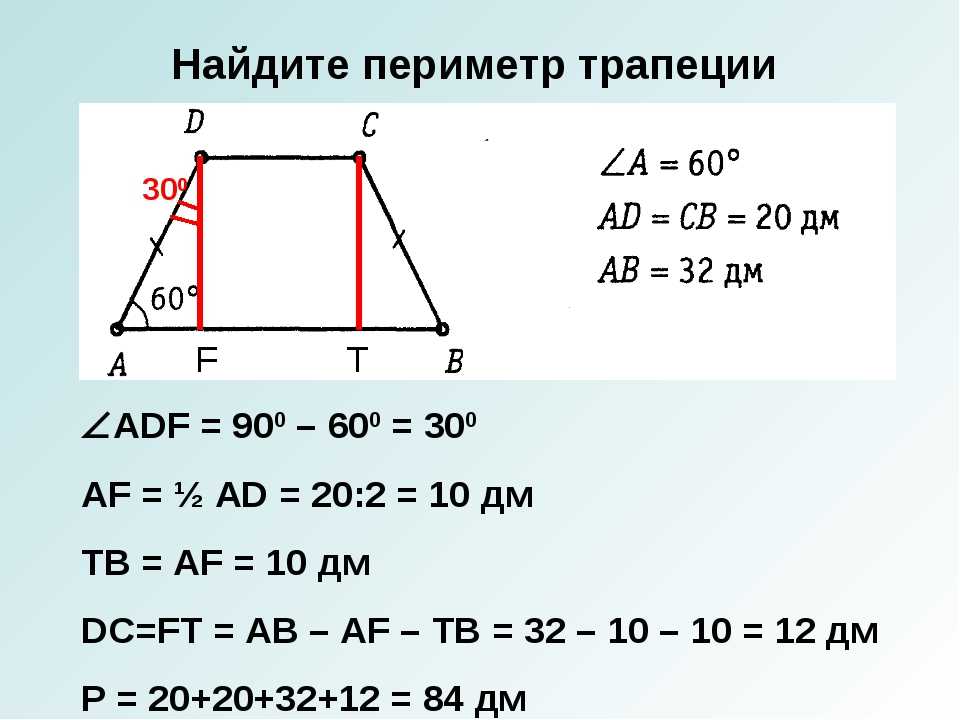 Решение задач на тему определения периметра прямоугольной трапеции
Решение задач на тему определения периметра прямоугольной трапецииЗадача №1
Нужно найти периметр прямоугольной трапеции, когда даны длины всех сторон. Тут всё просто. Складываем все 4 значения , и готово. Это самый лёгкий вариант нахождения периметра. Остальные задачи в итоге всё равно сводятся к нему, но нужно рассмотреть и остальные варианты, интересно же!
Задача №2
Нужно найти периметр всё той же прямоугольной трапеции, но в этом случае мы знаем длину нижнего основания AD , которая равна a . Одна из боковых сторон CD , которая не перпендикулярна ему, равна d . Угол между этим основанием и стороной равен Альфа .
Решение задачи №2
Катеты находятся по таким формулам: CE = CD*sin(ADC) , в свою очередь ED = CD*cos(ADC) . Верхнее основание вычисляется так: BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа) . Длина перпендикулярной стороны считается по формуле: AB = CE = d*sin(Альфа) . После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.
После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.
Задача №3
Требуется найти периметр трапеции, когда даны длины его оснований. AD = a , BC=c . Также мы знаем длину перпендикулярной стороны AB , которая равна b . Острый угол при неперпендикулярной стороне равен Альфа .
Решение задачи №3
Для начала проведите высоту трапеции на большее основание, начало которой будет лежать в вершине С . После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник ABCE , а также треугольник ECD (прямоугольный). Гипотенузой треугольника в нашем случае будет известная нам сторона CD , один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.
Для начала снова проводим перпендикуляр CE и так же получаем прямоугольник ABCE вместе с треугольником CED . Осталось найти длину гипотенузы того треугольника, который мы получили, мы с уверенностью можем сказать, что CD = AB/sin(ADC) = b/sin(Альфа) . Мы снова нашли все длины сторон. Осталось только их сложить. Надеемся, вы сможете сделать это без нас.
Площадь трапеции через периметр. Площадь трапеции: формулы и методика вычислений
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции.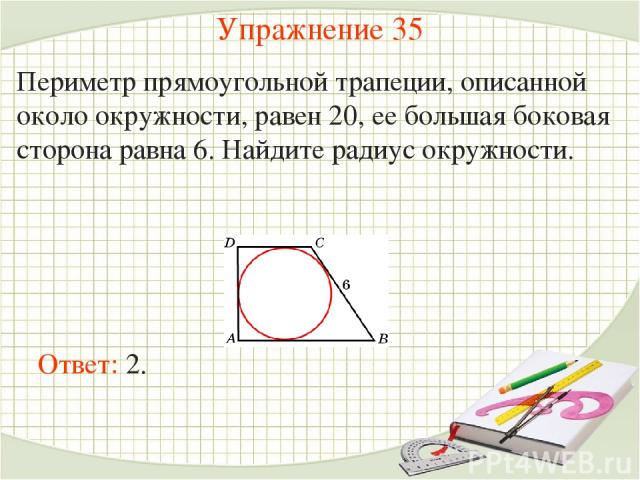 Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.

- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы.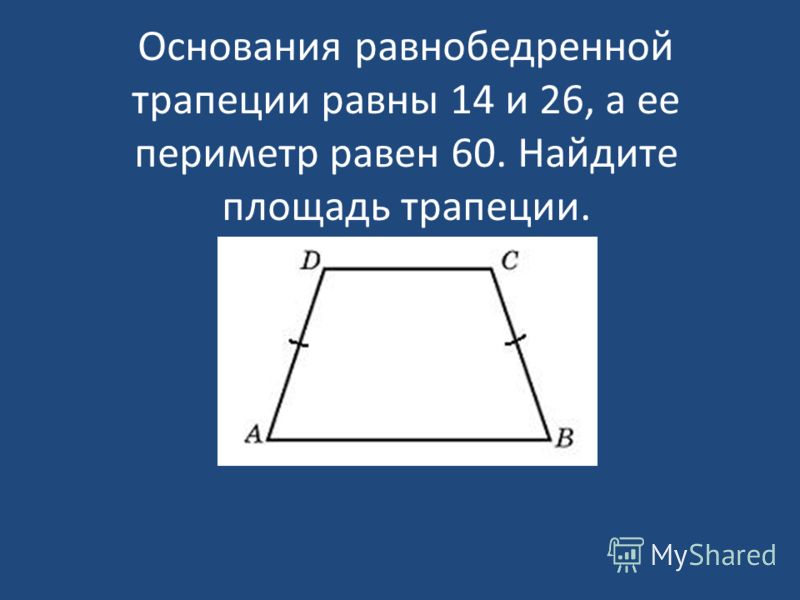 Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
Успеха вам!
С уважением, Александр.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.

По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.
Калькулятор площади правой трапеции
Создано Габриэлой Диас
Отзыв Лучано Мино
Последнее обновление: 14 марта 2022 г.
- Что такое правильная трапеция?
- Как найти площадь правильной трапеции
- Как использовать калькулятор площади правильной трапеции
- Другие калькуляторы площади трапеции
- Часто задаваемые вопросы
Добро пожаловать в калькулятор площади правильной трапеции , где вы сможете вычислить площадь любой правильной трапеции в мгновение ока! 😉
Здесь мы также узнаем:
- Что такое прямая трапеция ; и
- Как самостоятельно найти площадь правильной трапеции , даже если сначала не известна ее высота.
Начнем?
Что такое прямая трапеция?
Прямоугольная трапеция является частным случаем трапеции, четырехсторонней геометрии, по крайней мере, с одной парой противоположных сторон, параллельных друг другу. Эти параллельные стороны, также известные как основания, обозначены на изображении ниже как aaa и bbb.
В конкретном случае прямоугольной трапеции одна из двух оставшихся сторон, ccc на рисунке , перпендикулярна параллельным сторонам aaa и bbb, образуя между ними углы 90° (прямые углы).
Как найти площадь прямой трапеции
Чтобы найти площадь правильной трапеции , используйте формулу: A = (a + b) x h/2 .
Где:
-
А– Площадь трапеции; -
аиб– Основания нижние и верхние; и -
h– Высота.
Это означает, что если вы знаете все эти измерения, вы сможете вычислить площадь вашей правой трапеции напрямую.
Но что, если вы не знаете высоту h ? Сможете ли вы еще вычислить площадь? Вот тут и приходит на помощь старая добрая тригонометрия!
Глядя на изображение, мы видим прямоугольный треугольник, формирующийся из высоты h , разность оснований (а - б) и стороны d .
Отсюда, если вы знаете:
- две стороны
(a - b)иd; или - Одна сторона и один угол прямоугольного треугольника, все готово!
Если вы знаете две стороны , вычисление h вращается вокруг теоремы Пифагора как:
-
h = √(d² - (a - b)²)
С другой стороны, если у вас есть одна сторона и один угол , вы можете получить значение h с помощью функции арксинуса (инверсия синуса) как:
-
h = arcsin(δ) * д
или…
-
h = arcsin(γ - π/2) * d
Как использовать калькулятор площади правой трапеции
Чтобы использовать калькулятор площади правой трапеции:
- Ввод оснований
аиб. Например, предположим, чтоa = 10иb = 6.
- Введите значение высоты
h. В нашем примере предположим, чточ = 4. - Калькулятор отобразит результат для площади в последней строке. Для нашего расчета получаем
А = 32. Вот и все! 😀
💡 Не знаете значение высоты h ? Нажмите на расширенный режим , чтобы получить значение площади, введя углы и наклонную сторону.
Другие калькуляторы трапеций
Теперь, когда вы научились вычислять площадь правильной трапеции, почему бы не прочитать о площади неправильной трапеции или не расширить свои знания о трапециях с помощью нашего калькулятора трапеций.
Чтобы узнать о конкретных темах, касающихся трапеций, мы рекомендуем другие наши инструменты:
- Калькулятор трапеций
- Калькулятор площади трапеции
- Калькулятор периметра трапеции
- Калькулятор стороны трапеции
- Калькулятор угла трапеции
- Калькулятор высоты трапеции
- Средняя часть трапеции
- Калькулятор равнобедренной трапеции
- Калькулятор площади равнобедренной трапеции
- Калькулятор правой трапеции
- Калькулятор площади неправильной трапеции
Часто задаваемые вопросы
Может ли трапеция иметь ровно один прямой угол?
Нет, трапеция не может иметь только один прямой угол. Минимальное количество прямых углов трапеции равно двум. Эта конфигурация известна как правильная трапеция. Следующее количество прямых углов равно четырем; это случай прямоугольника.
Минимальное количество прямых углов трапеции равно двум. Эта конфигурация известна как правильная трапеция. Следующее количество прямых углов равно четырем; это случай прямоугольника.
Как найти высоту прямой трапеции?
Чтобы найти высоту прямой трапеции может встретиться один из следующих случаев:
- Если основания
аиб, а наклонная сторонаdизвестны, воспользуйтесь теоремой Пифагора:h = √(d² - (a - b)²). - Зная наклонную сторону
dи острый уголδ, используйте:h = arcsin(δ) x d. - Если известна наклонная сторона
dи тупой уголγ, используйте:h = arcsin(γ - π/2) x d.
Габриэла Диас
a (основание)
b (основание)
h (высота)
Площадь (A)
Посмотрите 21 похожий калькулятор 2d геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… Еще 18
Трапеции: примеры, формулы и характеристики
Что общего между китайской коробкой на вынос и дизайнерской сумочкой? Обратите внимание, как они представляют одну и ту же форму.
Форма параллелограмма сумки и коробки для еды на вынос, StudySmarter Originals
Теперь обратите внимание на то, что основания сумки и коробки для еды на вынос параллельны их вершинам. Поскольку эта фигура имеет четыре стороны, она классифицируется как тип четырехугольника. Однако это не квадрат, не прямоугольник и не параллелограмм. Эти формы имеют две пары параллельных сторон, в то время как форма, описанная этой сумкой и коробкой на вынос, имеет только одну пару. Есть ли у вас какие-либо предположения относительно того, какой может быть эта форма? Даю подсказку: это называется трапеция.
В этой статье будет рассмотрено определение трапеции, а также ее характеристики и типы. Мы также рассмотрим формулы, используемые для нахождения периметра и площади трапеции.
Что такое трапеция?
Как упоминалось ранее, трапеция подпадает под категорию четырехугольника, поскольку она содержит четыре стороны. Этот особый тип четырехугольника на самом деле имеет два названия: трапеция и трапеция. Имя зависит от того, где вы находитесь в мире. Здесь, в Соединенных Штатах, его обычно называют трапецией. Однако в Соединенном Королевстве ее обычно называют трапецией. Насколько это интересно? Имея это в виду, давайте начнем наше обсуждение с определения трапеции.
Имя зависит от того, где вы находитесь в мире. Здесь, в Соединенных Штатах, его обычно называют трапецией. Однако в Соединенном Королевстве ее обычно называют трапецией. Насколько это интересно? Имея это в виду, давайте начнем наше обсуждение с определения трапеции.
Трапеция — это четырехугольник с одним набором параллельных сторон.
Ниже приведено графическое изображение трапеции. Назовем эту трапецию ABCD.
Иллюстрация трапеции, StudySmarter Originals
Теперь перейдем к перечислению свойств трапеции. Таким образом, мы можем наблюдать, насколько они отличаются от правильного четырехугольника.
Характеристики трапеции
Теперь вернемся к нашей трапеции ABCD выше. Есть несколько примечательных характеристик трапеций, с которыми нам следует ознакомиться. Они перечислены ниже.
Трапеция имеет пару параллельных сторон и пару непараллельных сторон;
Обычно основания (верхнее и нижнее) треугольника ABCD параллельны друг другу.
 Это можно записать как AD//BC;
Это можно записать как AD//BC;
По определению трапеции.
Пара смежных углов, образованных между одной параллельной и одной непараллельной стороной трапеции, в сумме составляет 180°. Здесь ∠ABC + ∠BAD = 180° и ∠BCD + ∠ADC = 180°;
Сумма внутренних углов трапеции равна 360°;
Диагонали трапеции делят друг друга пополам;
Медиана (средняя линия или средний сегмент) трапеции параллельна обоим основаниям. Это показано розовой линией ниже;
Медиана трапеции, StudySmarter Originals
Медиана (или середина) трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции.
Составление других четырехугольников из трапеций
Существует три типа четырехугольников, которые могут быть получены из трапеций, а именно параллелограмм, квадрат и прямоугольник. Эти экземпляры описаны в таблице ниже.
Тип четырехстороннего | Описание | |||||||||||||||||||||||||||||
Parallelogram Parallelogram, Studysmarter youranlogram . квадрат кв.
В приведенной ниже таблице поочередно описывается каждая из этих трапеций вместе с их графическим изображением и отличительными чертами.
Периметр трапеции Трапеция — это двумерный многоугольник, лежащий на двумерной плоскости. Периметр трапеции описывается как общая длина ее границы. Другими словами, это сумма всех его сторон. Допустим, у нас есть трапеция ABCD со сторонами a, b, c и d. Периметр трапеции, StudySmarter Originals Тогда формула периметра трапеции равна P = a + b + c + d, , где P — периметр, a = AB, b = BC, c = CD и d = AD. Это также можно записать как P = AB + BC + CD + AD. Примеры с использованием формулы периметра трапецииДавайте теперь рассмотрим некоторые рабочие примеры, включающие формулу для нахождения периметра трапеции. Дана трапеция ниже, найдите ее периметр. Пример 1, StudySmarter Originals Решение Чтобы найти периметр этой трапеции, мы просто сложим измерения всех четырех сторон. P=13+21+19+34⇒P=87единиц Таким образом, периметр этой трапеции равен 87 единицам. Периметр равнобедренной трапеции равен 35 единицам. Какова длина каждой (равной) противоположной стороны, если основания равны 5 единицам и 8 единицам соответственно? Решение Здесь нам дан периметр трапеции и длины оснований. Пример 2, StudySmarter Originals Поскольку периметр представляет собой сумму всех четырех сторон этой трапеции, мы можем записать это уравнение в виде приведенного ниже уравнения. P=5+8+x+x⇒35=13+2x Преобразовывая это уравнение, получаем 2x=35-13⇒2x=22 Упрощая, получаем x=222⇒x=11единиц Таким образом, стоимость каждой противоположной стороны равна 11 единицам. Площадь трапецииПлощадь трапеции определяется пространством, заключенным внутри ее границы. Его находят путем вычисления средней длины между двумя заданными параллельными сторонами и умножения этого произведения на высоту трапеции. Обратите внимание на рисунок трапеции ABCD ниже. Площадь трапеции, StudySmarter Originals Здесь основания равны a = BC и b = AD. Высота h трапеции находится на перпендикулярном расстоянии между основаниями a и b. Его также называют высотой трапеции. Таким образом, площадь трапеции равна A=12(a+b)×h , , где A = площадь, a = длина более короткого основания, b = длина более длинного основания и h = высота. Точно так же мы можем выразить эту формулу как A=BC+AD2×ч. Примеры с использованием формулы площади трапецииДавайте теперь посмотрим на некоторые рабочие примеры с применением формулы площади трапеции. Определите площадь следующей трапеции. Пример 3, StudySmarter Originals Solution Здесь a = 6 единиц; б = 8 шт.; ч = 5 шт. Не запутайтесь в данных двух других сторонах! Они не параллельны друг другу, поэтому мы не можем использовать их меры в нашей формуле. Теперь, используя формулу площади трапеции, получаем A=12(a+b)×h⇒A=12(6+8)×5 Упрощая это, мы получаем окончательный ответ A=12(14)×5⇒A=7×5⇒A=35единиц2 Таким образом, площадь этой трапеции равна 35 единицам 2 . Найдите длину меньшего основания трапеции, зная, что площадь равна 232 единицам 2 , высота равна 16 единицам, а длина большего основания равна 17 единицам. Раствор В этом случае A = 232 единицы 2 b = 17 единиц; ч = 16 шт. Подставив эти значения в нашу формулу, получим A=12(a+b)×h⇒232=12(a+17)×16 Решив это, получим 232=16(a+17 )2⇒232=8(a+17) Расширяя это, мы получаем 232=8a+136⇒8a+136=232 Преобразовывая это уравнение и решая для a, мы получаем следующий окончательный ответ. 8а=232-136⇒8а=96⇒а=968⇒a=12единиц Следовательно, длина меньшего основания этой трапеции равна 12 единицам. Пример с участием трапецийМы закончим эту тему примером, который охватывает все, что мы узнали в ходе этого обсуждения. Дана трапеция ABCD ниже, определите ее тип, периметр и площадь. Пример 4, StudySmarter Originals Решение Тип Сначала выясним, какой это тип трапеции. Периметр Далее найдем периметр этой трапеции. Складывая все четыре стороны этой трапеции, получаем P=AB+BC+CD+AD⇒P=14+16+18+22⇒P=70единиц Таким образом, периметр этой трапеции равен 70 единицам. Площадь Здесь BC (более короткое основание) параллельно AD (более длинное основание). Высота перпендикулярна обоим этим основаниям. Таким образом, а = 16 шт.; б = 22 шт.; ч = 11 шт. Применяя формулу площади трапеции, получаем A=12(16+22)×11⇒A=12(38)×11⇒A=19×11⇒A=209единиц2 Таким образом, площадь этой трапеции равна 209 единиц 2 . Бонусный вопрос Чему равно значение угла ∠ADC, если ∠ABC = 88 o ? По свойству трапеций сумма внутренних углов равна 360°. ∠ABC+∠BCD+∠ADC+∠BAD=360°⇒88°+118°+∠ADC+103°==360° Переставляя это и решая неизвестный угол, мы получаем ∠ADC=360°- 88°-118°-103°⇒∠ADC=51° Таким образом, угол ∠ADC равен 51 o . Трапеции – основные выводы
Периметр и площадь трапеции – формулы и примерыКак найти периметр трапеции?Чтобы вычислить периметр трапеции, мы должны сложить длины всех ее сторон. Следовательно, формула для периметра трапеции:
где «a, b, c, d» представляют длины сторон трапеции. Периметр равнобедренной трапецииДве стороны равнобедренной трапеции имеют одинаковую длину, поэтому периметр можно вычислить по следующей формуле:
Как найти площадь трапеции? Чтобы найти площадь трапеции, нужно сложить длины ее оснований.
где
Доказательство формулы площади трапецииМы можем доказать формулу площади трапецию по следующей схеме: Трапецию можно разделить на два прямоугольных треугольника и один прямоугольник. Площадь трапеции равна сумме площадей двух треугольников и площади прямоугольника. Таким образом, мы должны: площадь трапеции = площадь треугольника 1 + площадь прямоугольника + площадь треугольника 2 $$A=\frac{ah}{2}+b_{1}h+\frac{ch}{2}$$ $$A=\frac{ah+2b_{1}h+ch}{2}$$ Переставляя термины и упрощая, мы имеем: $$A=\frac{h}{2}(b_ {1}+(a+b_{1}+c))$$ Теперь давайте используем $latex b_{2}$ для представления более длинного основания трапеции: $latex b_{2}=a+ b_{1}+c$ Подставив это в приведенное выше уравнение, мы получим: $latex A=\frac{h}{2}(b_{1}+b_{2})$ Периметр и площадь трапеции – Примеры с ответами Формулы периметра и площади трапеции используются для решения следующих примеров. Если длина сторон трапеции равна 6 дюймов, 8 дюймов, 5 дюймов и 7 дюймов, каков ее периметр? РешениеИспользуем формулу периметра трапеции с заданными длинами: $латекс p=a+b+c+d$ $латекс p=6+8+5+7$ $латекс p=26$ Периметр трапеции равен 26 дюймам. ПРИМЕР 2Какова площадь трапеции с основаниями длиной 8 и 12 футов и высотой 10 футов? РешениеУ нас есть следующая информация:
Используя формулу площади, мы имеем: $$A=\frac{(b_{1}+b_{2})h}{2}$$ $$=\frac{(8 +12)10}{2}$$ $$=\frac{(20)(10)}{2}$$ $$=\frac{200}{2}$$ $латекс A =100$ Площадь трапеции равна 100 м². Найдите периметр трапеции со сторонами 12 дюймов, 14 дюймов, 7 дюймов и 9 дюймов. РешениеПодставив данные длины в формулу периметра, мы получим: $латекс p=a+b+c+d$ $латекс p=12+14+7+9$ $латекс p=42$ Периметр трапеции равен 42 дюймам. ПРИМЕР 4Найдите площадь трапеции, длина основания которой 11 ярдов, а высота 15 ярдов2. РешениеУ нас есть следующее:
Применяя эти значения к формуле площади, получаем: $$A=\frac {(b_{1}+b_{2})h}{2}$$ $$=\frac{(11+15)12}{2}$$ $$=\frac{(26) (12)}{2}$$ $$ =\frac{312}{2}$$ $latex A=156$ Площадь трапеции равна 156 ярдов². У равнобедренной трапеции две параллельные стороны имеют длину 11 дюймов и 13 дюймов. Если боковые стороны трапеции равны 9дюймов, каков его периметр? РешениеУ равнобедренной трапеции две стороны равны, то есть c =9 в следующей формуле: $latex p=a+b+2c$ $latex p=11+13+ 2(9)$ $латекс p=24+18$ $латекс p=42$ Периметр трапеции равен 42 дюймам. высота трапеции, площадь которой 200 дм², основание 9дюймов, а другая база 11 дюймов. РешениеУ нас есть следующее:
В этом случае мы должны использовать формулу для площади и найти высоту: $$A=\frac{(b_{1}+b_{2})h}{2}$ $ $$200=\frac{(9+11)h}{2}$$ $латекс 400=(9+11)h$ $латекс 400=20h$ $латекс h=20$ Высота трапеции равна 20 дюймам. Периметр трапеции равен 86 футам, а три стороны имеют длину 21, 23 и 25 футов. Определить длину четвертой стороны. РешениеВ этом случае мы должны использовать формулу для периметра с заданными периметром и длинами, и мы собираемся решить для четвертой стороны: $латекс p=a+b+c+d$ $латекс 86=21+23+25+d$ $латекс d=86-21-23-25$ $латекс d=17$ Длина четвертой стороны 17 футов. площадь 240 ярдов², длина основания 11 ярдов, а длина другого основания 13 ярдов, найдите его высоту.РешениеУ нас есть следующее:
Поэтому воспользуемся формулой площади трапеции и решим для ч : $$A=\frac{(b_{1}+b_{2})h}{2}$$ $ $240=\frac{(11+13)h}{2}$$ $latex 480=(11+13)h$ $latex 480=24h$ $latex h=20$ Высота трапеции 20 ярдов. Найдите длину боковых сторон равнобедренной трапеции, периметр которой равен 64 футам, а длины параллельных сторон равны 13 футам и 17 футам. РешениеМы можем представить длину боковых сторон как c . Поэтому мы подставляем данные значения в формулу для периметра и находим c : $latex p=a+b+2c$ $latex 64=13+17+2c$ $latex 64= 30+2c$ $latex 34=2c$ $latex c=17$ Длина одной из боковых сторон равна 17 футов. следующую трапецию. 92}=48$$латекс h=6,93$ см Теперь мы можем использовать высоту и основание для вычисления площади трапеции: $$A=\frac{(b_{1}+b_{ 2})h}{2}$$ $$=\frac{(15+7)6.93}{2}$$ $$=\frac{(22)(6.93)}{2}$$ $латекс A=76,23$ Площадь трапеции 76,23 см². Периметр и площадь трапеции. Практические задачи Используйте все, что вы узнали о периметре и площади трапеции, для решения следующих задач. Если периметр трапеции равен 65 дюймов, а длина ее сторон 14 дюймов, 15 дюймов и 16 дюймов, найдите длину четвертой стороны.Выберите ответ $латекс d=18$ в $латекс d=20$ в $латекс d=22$ в $latex d=24$ in Какова площадь трапеции с основаниями 6 ярдов, 10 ярдов и высотой 5 ярдов?Выберите ответ 92}$ и базы длиной 19 футов и 27 футов. Выберите ответ $латекс h=11$ футов $латекс h=12$ футов $латекс h=13$ футов $latex h=14$ ft См. такжеХотите узнать больше о периметре и площади геометрических фигур? Взгляните на эти страницы:
Математическая задача: прямоугольная трапеция – вопрос № 7289, геометрия Прямоугольная трапеция ABCD с AB и CD основания делится диагональю АС на два равносторонних прямоугольных треугольника. Правильный ответ:S = 2883 см 2x = 62 см =62 2см≐87,6812 см c2+c2=u2 c=u/2 =62/2 =31 2 см≐43,8406 см S=2a+c=⋅c 287,6812+43,8406⋅ 43,8406=2883 см2 o1=2⋅c+u=2⋅43,8406+62≐149,6812 смo2=2⋅u+a=2⋅62+87,68126−8×1211. o1=211,6812−149,6812=62 см Вы нашли ошибку или неточность? Не стесняйтесь написать нам. Благодарю вас! Советы по использованию связанных онлайн-калькуляторов См. также наш калькулятор прямоугольного треугольника. Чтобы решить эту математическую задачу со словами, вам необходимо знать следующие знания:
Единицы физических величин:
Степень словесной задачи:
Мы рекомендуем вам посмотреть это учебное видео по этой математической задаче: АБ | = 6 см, CD | = 4 см делится на четыре треугольника диагоналями, пересекающимися в точке S. Какую часть площади трапеции составляют треугольники ABS и CDS? Прямоугольная трапеция ABCD, плечо AD которой перпендикулярно основаниям AB и CD, имеет площадь 15 кв.  см. Основания имеют длину AB = 6 см, CD = 4 см. Вычислите длину диагонали АС. см. Основания имеют длину AB = 6 см, CD = 4 см. Вычислите длину диагонали АС.Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. Участок имеет форму прямоугольной трапеции ABCD, где ABIICD с прямым углом при вершине B. Сторона AB имеет длину 36 м. Длины сторон АВ и ВС относятся как 12:7. Длины сторон AB и CD относятся как 3:2. Рассчитать минус На рисунке показана трапеция ABDC, в которой AB || CD. Отрезки RN и LM проведены параллельно AB так, что AJ=JK=KP. Если AB=0,5 м и AP=BQ=1,8 м, найдите длины AC, BD, RN и LM. угол D=угол C=60 Рассчитайте площадь четырехугольной призмы ABCDA’B’C’D’ с трапециевидным основанием ABCD. Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см.  Л ЛABDC — трапеция, в которой AB и CD — параллельные стороны, равные 6 и 9 соответственно. Углы ABC и BCD прямые. Найдите длину отрезка BD. Вычислить размер плеча b трапеции ABCD, если a = 12 см, c = 4 см, d (AC) = d (BC) и площадь S (треугольник ABC) = 9 см кв. Одна трапеция имеет длинные стороны AB=24M, BC=36M, CD=80M, DA=80M. Найдите площадь. Трапеция имеет площадь 24 квадратных см. Сколько различных трапеций можно составить? Бассейн длиной 30 м наполнен водой на глубину 1 м в мелкой части и 5 м в глубокой части, а по вертикали бассейн имеет форму трапеции с площадь определяется как S (abcd) = 1/2 (ab + cd) x ad. Что такое Трапеция ABCD имеет длину оснований в соотношении 3:10. Площадь треугольника ACD равна 825 дм². Чему равна площадь трапеции ABCD? Трапеция ABCD имеет параллельные стороны AB и CD.  Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE. Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE.Прямоугольная трапеция ABCD: /AB/ = /BC/ = /AC/. Длина медианы 6 см. Вычислите длину окружности и площадь трапеции. ABCD — это равнобедренная трапеция, на которой выполняются: |AB| = 2 |ВС| = 2 |CD| = 2 |DA|: На стороне BC есть точка K такая, что |BK| = 2 |KC|, на его стороне CD есть точка L такая, что |CL| = 2 |LD|, а на его стороне DA точка M такова, что | ДМ | = 2 |МА|. Дет В прямоугольнике ABCD длина стороны AB = 16 см, а диагональ AC = 20 см. Вычислите его периметр и площадь. В ABCD длина трапеции AB = 8 см, высота трапеции 6 см, расстояние пересечения диагоналей от AB 4 см. Вычислите площадь трапеции. Решатель задач по геометрии — трапеция Они дают треки, некоторые задачи могут решаться автоматически, числовые значения не имеют значения в различных примерах. Дорожка 1 Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Вычислите периметр и площадь трапеции.
Дорожка 2 У равнобедренной трапеции косая сторона 20 см; имеет основание большее 80 см, имеет меньшее основание 50 см. Вычислите периметр.
Трек 3 Прямоугольная трапеция имеет высоту 40 м, большее основание 80 м, меньшее основание 50 м. Вычислите периметр и площадь трапеции.
Дорожка 4 Равнобедренная трапеция имеет большее основание 80 см, меньшее основание 50 см, площадь 1300 см. Вычислите высоту трапеции.
Дорожка 5 Прямоугольник трапеции площадью 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Дорожка 6 Площадь равнобедренной трапеции 1500 см; имеет высоту 30 см. Вычисляет сумму двух оснований.
Дорожка 7 Периметр равнобедренной трапеции 150 см; имеет основание больше 50 см; имеет меньшее основание 30 см.
Дорожка 8 Периметр равнобедренной трапеции 150 см, меньшее основание 30 см, косая сторона 35 см. Вычислите длину большего основания.
Дорожка 9 Периметр равнобедренной трапеции 150 см, основание больше 50 см, наклонная сторона 35 см. Вычислите длину меньшего основания.
Дорожка 10 Прямоугольная трапеция имеет большее основание 50 см, меньшее основание 30 см; имеет косую сторону 35 см. Вычислите периметр и площадь.
Направляющая 11 Прямоугольник трапеции имеет периметр 180 см; имеет основание больше 60 см, имеет наклонную сторону 50 см; имеет высоту 40 см. Вычислите длину меньшего основания.
Направляющая 12 Прямоугольник трапеции имеет периметр 180 см; имеет меньшее основание 30 см; имеет косую сторону 50 см; имеет высоту 40 см. Вычислите длину большего основания.
Дорожка 13 Прямоугольник трапеции имеет периметр 180 см; имеет меньшее основание 30 см; имеет высоту 40 см; имеет основание больше 60 см. Вычислите длину косой стороны.
Направляющая 14 Прямоугольник трапеции имеет периметр 180 см; имеет меньшее основание 30 см; имеет косую сторону 50 см; имеет основание больше 60 см. Вычисляет длину высоты.
Дорожка 15 У равнобедренной трапеции основание больше 20 см, наклонная сторона 5 см; имеет высоту 4 см. Вычислите меньшее основание.
Дорожка 16 У равнобедренной трапеции меньшее основание 14 см; имеет косую сторону 5 см; имеет высоту 4 см. Вычисляет большее основание.
Дорожка 17 Равнобедренная трапеция имеет основание больше 20 см, косая сторона 5 см; имеет проекцию косой стороны на большее основание 3 см. Вычислите периметр.
Дорожка 18 Основание равнобедренного треугольника меньше 14 см; имеет косую сторону 5 см, имеет экранирование косой стороны на большее основание 3 см.
Дорожка 19 Равнобедренная трапеция имеет площадь 2400 см, высоту 40 см, основания составляют треть от другой. Определить периметр.
Дорожка 20 Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника равна 6 см, а разность оснований трапеции равна 4 см, вычислите площадь трапеции.
Дорожка 21 У равнобедренной трапеции косая сторона 20 см; имеет основание больше 90 см, имеет меньшее основание, равное 2/3 большего основания. Вычислите периметр.
Дорожка 22 Прямоугольная трапеция равна 1/4 квадрата с периметром 160 см. Учитывая, что высота трапеции равна 20 см, а разность оснований 6 см, вычислить площадь прямоугольника, размеры которого равны основаниям трапеции.
Дорожка 23 Трапециевидный прямоугольник, описанный в окружности, имеет длину наклонной стороны 40 см и высоту, равную 3/5 наклонной стороны.
Дорожка 24 Площадь прямоугольника трапеции равна 2250 см. Зная, что разность мер проекции косой стороны на большее основание и высоту равна 15 см и что их отношение равно 3/4, вычислить периметр трапеции.
Дорожка 25 Периметр равнобедренной трапеции 250 см, высота 30 см, малое основание 4/7 большего, равного косой стороне. Вычислите площадь трапеции.
Трасса 26 Большое основание прямоугольной формы трапеции с наклонной стороной под углом 45; зная, что основания равны 25 см и 15 см, вычислить площадь трапеции.
Дорожка 27 Равнобедренная трапеция ABCD образована тремя конгруэнтными равнобедренными треугольниками, периметр каждого из которых равен 170 см, а наклонная сторона равна 6/5 основания. Вычислите периметр трапеции.
Дорожка 28 Площадь равнобедренной трапеции ABCD равна 900 см .
Дорожка 29 Площадь равнобедренной трапеции равна 1032 см, а два основания равны 61 см и 25 см соответственно. Вычислите меру высоты и периметра.
Дорожка 30 В прямоугольной трапеции с косой стороной образуют большое основание с широким углом 30 . Два основания соответственно размером 50 см и 30 см вычисляют периметр и площадь трапеции.
Дорожка 31 В равнобедренной трапеции сумма и разность размеров двух оснований составляют соответственно 74 см и 14 см. Вычислите площадь и периметр трапеции, зная, что косая сторона равна 25 см.
Дорожка 32 Периметр равнобедренной трапеции равен 176 см. Зная, что меньшее основание составляет 4/3 наклонной стороны, а большее основание составляет 19/10 меньшего основания, вычисляют площадь трапеции.
Дорожка 33 Каждая из наклонных сторон равнобедренной трапеции составляет треть меньшего основания. Зная, что периметр равен 230 см, а большее основание равно 105 см, вычислить меру меньшего основания и площадь трапеции.
Дорожка 34 В прямоугольной трапеции нижняя диагональ перпендикулярна наклонной стороне. Зная, что эта диагональ и наклонная сторона имеют размеры 24 см и 18 см соответственно, найдите периметр и площадь трапеции.
Дорожка 35 В прямоугольной трапеции с наклонной стороной образуют большое основание с широким углом 30 . Вычислите периметр трапеции, зная, что высота равна 11,56 см, а площадь 462,42 см.
Дорожка 36 В трапеции длина большого и малого оснований 55 см, длина 30 см, периметр 140 см. Определить длину косых сторон, зная, что одна составляет 6/5 другой.
Дорожка 37 Разность оснований равнобедренной трапеции 30 см, меньшее основание 5/8 большего основания, периметр 180 см.
Дорожка 38 О равнобедренной трапеции известно, что: а) высота равна 20 см. б) разница между двумя основаниями составляет 30 см. в) основание больше 80 см. Вычислите периметр и площадь трапеции.
Дорожка 39 Периметр трапеции высотой 34,60 см равен 203,49см. Вычислите площадь трапеции, зная, что косые стороны образуют с большим основанием острые углы шириной 45 и 60 градусов.
Дорожка 40 Площадь прямоугольника-трапеции 1080 квадратных сантиметров, а высота 24 см. Вычислите размеры двух оснований, зная, что периметр равен 140 см.
Дорожка 41 Периметр равнобедренной трапеции равен 152 см, а наклонная сторона равна 26 см. Вычислите высоту и площадь трапеции, зная, что меньшее основание равно 40 см.
Дорожка 42 В прямоугольной трапеции большее основание, меньшее основание и высота соответственно 60 см, 50 см и 24 см.
Дорожка 43 Вычислите площадь трапеции, у которой большее основание составляет 8/5 меньшего основания, которое, в свою очередь, равно высоте, равной 50 см.
Дорожка 44 Сумма оснований трапеции 80 см, основание 5/3 другого, высота 2/3 меньшего основания. Вычислите размер каждой диагонали ромба, эквивалентного трапеции, зная, что диагональ равна 25/16 другой.
Дорожка 45 Трапеция образована квадратом со стороной 48 см и двумя треугольниками, каждый из которых имеет катет, совпадающий с одной из двух противоположных сторон квадрата. Гипотенуза двух треугольников равна 60 см и 50 см соответственно. Вычислите периметр и площадь трапеции.
Дорожка 46 Несимметричная трапеция имеет периметр 180 см; вычисляет все стороны, зная, что АВ = 8/5 ВС, ВС — АВ = 30 см, АД = 2/5 ВС.
Дорожка 47 В равнобедренной трапеции ABCD основание CD составляет 15/22 большего основания, косые стороны превышают 7 см 3/5 меньшего основания, периметр 124 см.
Дорожка 48 Большее основание, высота и наклонная сторона прямоугольника к трапеции соответственно размером 80 см, 48 см и 50 см. Вычислите периметр и площадь трапеции.
Дорожка 49 Круг имеет радиус 50 см; две параллельные хорды AB и CD расположены на противоположных частях относительно центра и имеют соответственно 96 см и 28 см. Вычисляет площадь и периметр трапеции, имеющей в основании две хорды.
Дорожка 50 Равнобедренная трапеция имеет высоту 20 м, большее основание 80 м, меньшее основание 50 м. Вычислите радиус окружности, описанной вокруг трапеции.
Дорожка 51 Трапеция имеет основания диаметром окружности 50 см и параллельную ей веревку длиной 30 см. Вычислите периметр и площадь трапеции.
Дорожка 52 В окружности радиусом 50 см провести две параллельные хорды, расположенные по разные стороны относительно центра и удаленные от него соответственно на 14 см и 48 см.
Дорожка 53 Прямоугольник и равнобедренная трапеция имеют равные высоты, периметр прямоугольника 140 см, разность размеров прямоугольника между ними 30 см, а косая сторона трапеции 25 см. Рассчитать :
Дорожка 54 Трапециевидный прямоугольник имеет высоту 24 см, а основания составляют 5/6 длины другого прямоугольника. Вычислите площадь круга, радиус которого равен наклонной стороне, зная, что площадь трапеции равна 1320 см.
Дорожка 55 Высота равнобедренной трапеции 24 см, а основание соответственно 28 и 8 см. Вычислите периметр, площадь и две диагонали.
Дорожка 56 Прямоугольная трапеция имеет высоту 24 см, а основания соответственно 18 и 10 см.
Дорожка 57 Прямоугольная трапеция имеет сумму оснований 110 см, высоту 24 см. Вычисляет площадь.
Дорожка 58 У равнобедренной трапеции сумма оснований 110 см, высота 24 см. Вычисляет площадь.
Дорожка 59 Площадь равнобедренной трапеции 336 см, сумма оснований 28 см. Вычислите высоту.
Дорожка 60 Прямоугольник трапеции имеет площадь 336 см, сумма оснований 28 см. Вычислите высоту.
Дорожка 61 У равнобедренной трапеции большее основание 50 см, меньшее основание 30 см. Рассчитайте высоту, зная, что косая сторона равна 26 см.
Дорожка 62 Равнобедренная трапеция имеет большее основание 72 см, меньшее основание 8 см. Вычислите радиус окружности, вписанной в трапецию, зная, что высота равна 24 см.
Дорожка 63 У равнобедренной трапеции большее основание 72 см, меньшее основание 8 см.
След 64 Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Вычислите радиус окружности, вписанной в трапецию, зная, что высота равна 24 см.
Дорожка 65 Прямоугольная трапеция имеет большее основание 48 см, меньшее основание 16 см. Вычислите диаметр окружности, вписанной в трапецию, зная, что высота равна 24 см.
Дорожка 66 У равнобедренной трапеции большее основание 80 см, меньшее основание 50 см. Вычислите диаметр окружности на трапеции, зная, что высота равна 48,75 дюйма.
Трек 67 У равнобедренной трапеции большее основание 80 см, меньшее основание 50 см. Вычислите длину окружности, окружающей трапецию, зная, что высота равна 48,75 дюйма.
Дорожка 68 У равнобедренной трапеции большее основание 80 см, меньшее основание 50 см.
Дорожка 69 У равнобедренной трапеции большее основание 80 см, меньшее основание 50 см. Рассчитать :
Направляющая 70 Трапециевидный прямоугольник имеет высоту 24 см, а основания составляют 5/6 длины другого прямоугольника. Вычислите площадь круга, радиус которого равен большему основанию, зная, что площадь трапеции равна 1320 см.
Дорожка 71 Трапециевидный прямоугольник имеет высоту 24 см, а основания составляют 5/6 длины другого прямоугольника. Вычислите площадь круга, радиус которого равен диагонали, зная, что площадь трапеции равна 1320 см.
Дорожка 72 Прямоугольная трапеция имеет высоту 24 см и основание соответственно 60 см и 50 см. Вычислите радиус окружности, конгруэнтной трапеции.
Трек 73 Прямоугольник трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого равен высоте трапеции.
Дорожка 74 Прямоугольник трапеции имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, диаметр которого равен диагонали трапеции.
Дорожка 75 Прямоугольник трапеции имеет периметр 160 см, меньшее основание 50 см, высоту 24 см и наклонную сторону 26 см. Вычислите площадь круга, диаметр которого равен основанию трапеции.
Дорожка 76 Прямоугольник трапеции имеет большое основание 60 см, малое основание 50 см, высоту 24 см. Вычислите площадь круга, длина окружности которого изопериметрична трапеции.
Направляющая 77 Трапециевидный прямоугольник имеет высоту 24 см, а основания составляют 5/6 длины другого прямоугольника. Вычислите площадь круга, радиус которого равен меньшему основанию, зная, что площадь трапеции равна 1320 см.
Дорожка 78 Равнобедренная трапеция имеет высоту 24 см, а основания одной составляют 5/7 другой. Вычислите площадь круга, радиус которого равен меньшему основанию, зная, что площадь трапеции равна 1440 см.
Дорожка 79 Равнобедренная трапеция имеет высоту 24 см, а основания одной из них составляют 5/7 другой. Вычислите площадь круга, радиус которого равен большему основанию, зная, что площадь трапеции равна 1440 см.
Дорожка 80 Трапециевидный прямоугольник имеет высоту 24 см, а основания составляют 5/6 длины другого прямоугольника. Вычислите площадь круга, радиус которого равен малой диагонали, зная, что площадь трапеции равна 1320 см.
Дорожка 81 Равнобедренная трапеция имеет высоту 10 см и основания, которые составляют одно из 7/17 другого. Вычислите площадь круга, радиус которого равен диагонали, зная, что площадь трапеции равна 240 см.
Дорожка 82 Высота равнобедренной трапеции 24 см, а основание соответственно 60 см и 50 см. Вычислите радиус окружности, конгруэнтной трапеции.
Дорожка 83 Равнобедренная трапеция имеет площадь 1320 см и основания соответственно 60 см и 50 см. Вычислите площадь круга, радиус которого равен высоте трапеции.
Дорожка 84 Прямоугольник трапеции имеет площадь 360 см и основания соответственно 10 см и 20 см. Вычислите площадь круга, диаметр которого меньше диагонали трапеции.
Дорожка 85 Площадь равнобедренной трапеции 240 см, а основания соответственно 34 см и 14 см. Вычислите площадь круга, диаметр которого равен диагонали трапеции.
Дорожка 86 Периметр равнобедренной трапеции 186 см, меньшее основание 50 см, высота 24 см, наклонная сторона 26 см. Вычислите площадь круга, диаметр которого равен основанию трапеции.
Дорожка 87 Равнобедренная трапеция имеет большое основание 70 см, малое основание 50 см, высоту 24 см. Вычислите площадь круга, длина окружности которого изопериметрична трапеции.
Дорожка 88 Вычислите площадь и периметр разносторонней трапеции, зная, что большее основание 80 см, а меньшее 50 см, а косые стороны соответственно 30 см и 20 см.
Трек 89 У равнобедренной трапеции меньшее основание 8,4 см, а проекция косой стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 90 Прямоугольная трапеция имеет меньшее основание 19,2 см и проекцию наклонной стороны на большее основание 10,8 см.
Дорожка 91 Прямоугольник трапеции имеет наклонную сторону 18 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 92 У равнобедренной трапеции косая сторона 18 см, а проекция косой стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 93 Равнобедренная трапеция имеет основание 30 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 94 Прямоугольная трапеция имеет основание 30 см и проекцию наклонной стороны на большее основание 10,8 см. Зная, что нижняя диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 95 Прямоугольная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что нижняя диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 96 Равнобедренная трапеция имеет основание 30 см и наклонную сторону 18 см. Зная, что диагональ перпендикулярна косой, вычислить периметр и площадь трапеции.
Дорожка 97 Периметр равнобедренной трапеции равен 204 см, а каждая наклонная сторона равна 30 см. Вычислите площадь и протяженность оснований, зная, что большее составляет 5/3 меньшего.
Трак 98 Большее основание равнобедренной трапеции с наклонной стороной под углом 45; зная, что основания равны 35 см и 15 см, вычисляет площадь и периметр трапеции.
************* Площадь и периметр многоугольников Существуют различные типы многоугольников, для которых нет единой формулы для определения площади и периметра. ПериметрЧасто студенты спрашивают что такое периметр ? Это вычисление длины границы любой формы . Лучший способ научиться легко находить периметр — сложить все внешние стороны фигуры. Полигон не является исключением. Короче говоря, периметр многоугольника равен сумме длины его сторон . Лучшие репетиторы по математике Поехали Площадь Найти периметр проще, но найти площадь немного сложнее. Площадь — это область, которую занимает фигура. Нет простого способа найти площадь, вам нужно будет запомнить некоторые формулы для нахождения площади. Но вопрос в том, что такое площадь многоугольника? площадь многоугольника является мерой области, ограниченной сторонами многоугольника. Периметр треугольникаДавайте начнем с чего-то, чего вы будете много раз в жизни, и да, это треугольник. Вычислить периметр треугольника очень просто. Все, что вам нужно сделать, это добавить все длины сторон. В треугольнике три стороны, а это значит, что вам нужно сложить все три стороны, чтобы найти периметр. Это основная концепция периметра треугольника, но треугольник также имеет три типа. Означает ли это, что у каждого треугольника будет свой способ нахождения периметра? Точно нет! Концепция останется той же, что и добавление трех сторон. Давайте посмотрим на это.
Above is a comparison of all three triangles с их формулами периметра. У разностороннего треугольника все стороны разные, следовательно, формула остается той же, однако с равносторонними и равнобедренными треугольниками что-то другое? Ничего не изменилось, концепция та же, но с изюминкой. Площадь треугольникаНезависимо от того, работаете ли вы с равнобедренным или разносторонним треугольником, вам потребуется только одна формула, которая может вычислить площадь треугольника. Короче говоря, эту формулу можно использовать для нахождения площади любого треугольника, с которым вы работаете. Эта формула действительна только для треугольников, вы не можете использовать ее для других многоугольников. Если у многоугольника три стороны, то площадь этого многоугольника будет: Площадь треугольника равна половине произведения основания и высоты. ПримерНайдите площадь и периметр следующего треугольника:
Площадь и периметр квадрата — самый простой из многоугольников. Все стороны равны, и этот многоугольник имеет четыре стороны. Вершины имеют угол . Возможно, вы уже догадались о периметре, да, он равен, потому что все стороны равны, а поскольку у квадрата четыре стороны, поэтому он будет равен . Чтобы найти площадь многоугольника с 4 сторонами, вам нужно умножить длину этого многоугольника на ширину (ширину) многоугольника. Поскольку все стороны равны, длина ( «l» ) умножить на ширину ( «l» ), следовательно: Все стороны равны, и этот многоугольник имеет четыре стороны. Вершины имеют угол . Возможно, вы уже догадались о периметре, да, он равен, потому что все стороны равны, а поскольку у квадрата четыре стороны, поэтому он будет равен . Чтобы найти площадь многоугольника с 4 сторонами, вам нужно умножить длину этого многоугольника на ширину (ширину) многоугольника. Поскольку все стороны равны, длина ( «l» ) умножить на ширину ( «l» ), следовательно:Все, что вам нужно, это длина любой стороны квадрата, чтобы найти площадь и периметр квадрата. ПримерВычислите площадь и периметр квадрата со сторонами. Площадь и периметр прямоугольника Не всегда длина и ширина четырехстороннего многоугольника будут одинаковыми. Если длина и ширина четырехстороннего многоугольника различны, значит, вы имеете дело с прямоугольником. Однако понятие периметра и площади будет одинаковым для четырехстороннего многоугольника. ПримерВычислите площадь и периметр прямоугольника с основанием и высотой .
РомбРомб — еще один четырехугольник, но с другими свойствами. Понятие периметра и площади будет одинаковым для ромба. Чтобы найти периметр, нам нужно сложить все четыре стороны ромба. Поскольку все стороны ромба равны, они все складываются, и самый простой способ найти периметр ромба — умножить длину одной из его сторон на четыре. Тем не менее, найти район может быть немного сложно. У ромба две диагонали, одна большая диагональ, а другая короткая. Площадь ромба будет равна половине произведения обеих диагоналей. ПримерВычислите площадь и периметр ромба, диагонали которого равны и , а его стороны равны .
Площадь и периметр ромба Ромб может выглядеть как ромб, но это не так. Возможно, вы не знакомы с названием ромбоид, он также известен как параллелограмм. ПримерВычислите площадь и периметр ромбовидной фигуры с 4 сторонами по 4,5 см и высотой 4 см.
Площадь и периметр трапецииТрапеция (также известная как «Трапеция», состоящая из пяти сторон многоугольника ). Уникальность этого многоугольника в том, что он имеет две параллельные стороны. Это делает трапецию уникальной среди всех других пятисторонних многоугольников. Площадь трапеции равна половине произведения высоты на сумму параллельных сторон. Периметр этой фигуры очень прост, достаточно сложить все граничные длины трапеции. ПримерРассчитайте область и периметр следующего трапеции: Область и Периметр Регулярного Полигана 9003. его стороны равны по длине. Обычно у многоугольников не все стороны равны, однако в случае правильного многоугольника все стороны должны быть равны. Поскольку все стороны равны, это означает, что все углы также будут равны. Чтобы найти периметр любого правильного многоугольника, достаточно умножить количество сторон на длину одной стороны. Однако найти площадь правильного многоугольника довольно сложно. Площадь будет равна половине произведения периметра и апофемы. Апофема — это расстояние от центра многоугольника до середины любой стороны правильного многоугольника. его стороны равны по длине. Обычно у многоугольников не все стороны равны, однако в случае правильного многоугольника все стороны должны быть равны. Поскольку все стороны равны, это означает, что все углы также будут равны. Чтобы найти периметр любого правильного многоугольника, достаточно умножить количество сторон на длину одной стороны. Однако найти площадь правильного многоугольника довольно сложно. Площадь будет равна половине произведения периметра и апофемы. Апофема — это расстояние от центра многоугольника до середины любой стороны правильного многоугольника.где n — количество сторон. ПримерыВычислите площадь и периметр правильного пятиугольника со сторонами . . Применяя теорему Pythagorean для одной из треугольников, мы получаем: Рассчитают Расчет области и Perameter of Arexed of Hiexed gexed. круг радиуса.
Площадь многоугольника не имеет определенной формы9000. |

 p|number:4 $}
p|number:4 $}

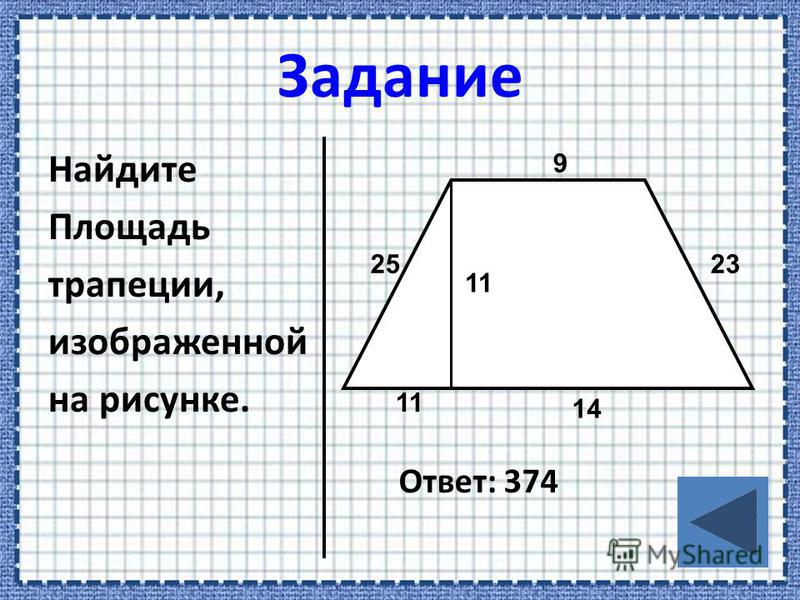
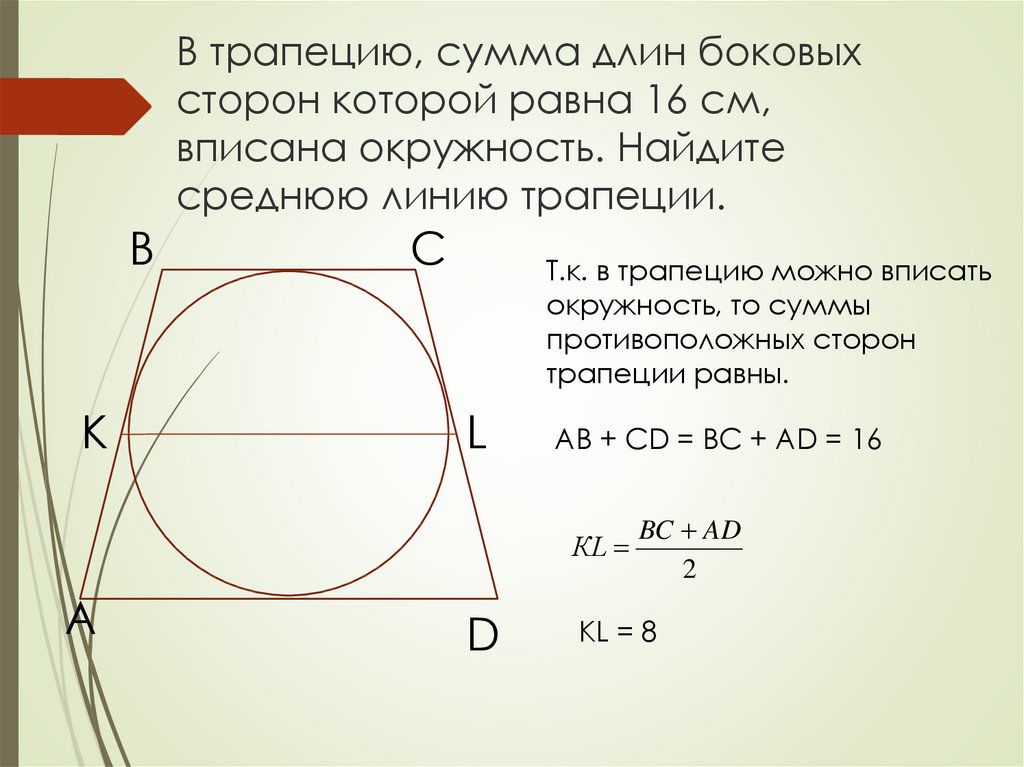

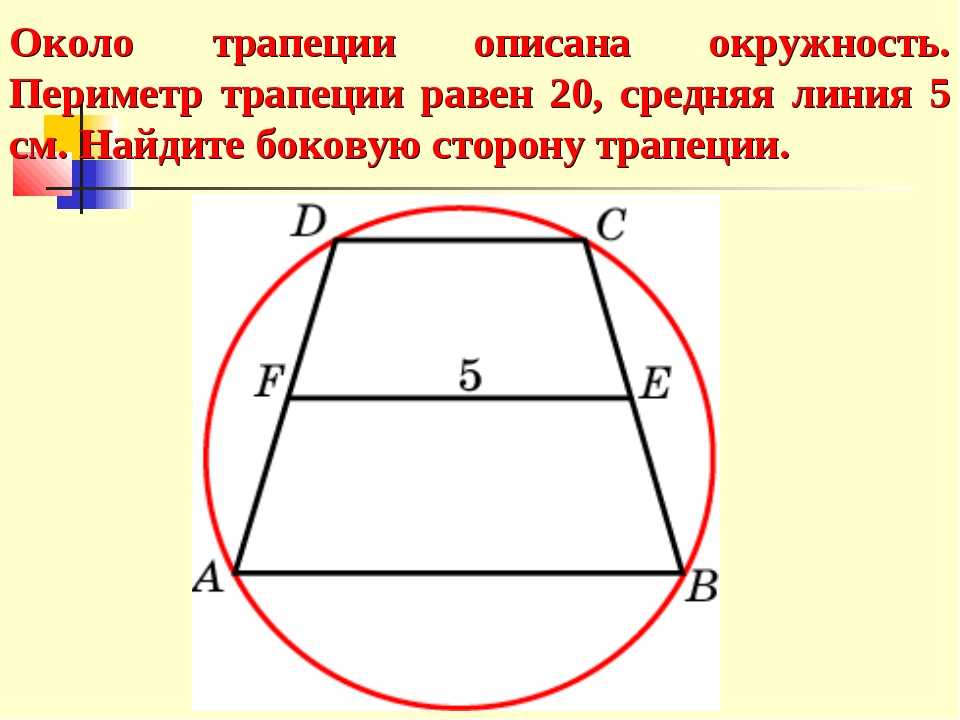

 Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рело, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой многоугольник дуги, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.
Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.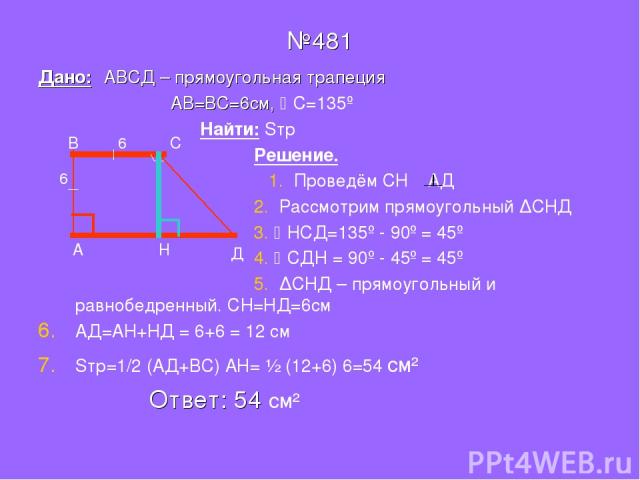 Гипотенуза у нас равна корню из суммы квадратов катетов.
Гипотенуза у нас равна корню из суммы квадратов катетов.