Как высчитать градусы угла
Содержание
- 1 Нахождение углов треугольника по заданным сторонам
- 2 Как вычислять углы
- 3 Как высчитать угол прямоугольного треугольника в градусах?
- 4 Математика
- 4.1 Строка навигации
- 5 Измерение углов и дуг круга
- 6 Как измерить угол между стен. Несколько способов.
- 6.1 Какой угол образуют стены. Первый способ – измерение.
- 6.2 Какой угол образуют стены. Второй способ – расчёт.
Нахождение углов треугольника по заданным сторонам
Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” class=”pc-math” />
a” class=”pc-math” />
b” class=”pc-math” />
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
Как вычислять углы
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 127 859.
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны, в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Как высчитать угол прямоугольного треугольника в градусах?
Если известны размеры трёх сторон, как высчитать угол в градусах?
Да, треугольник на рисунке не так, чтобы уж очень прямоугольный. 2 )/ (2*600*800)=-0,20937
2 )/ (2*600*800)=-0,20937
По табличке Брадиса или в своём супер-пупер телефоне находим: 91,2 градуса
Для вычисления углов необходимо обратиться к тригонометрии.
Нам необходимо вычислить величину острого угла А. Для этого используем формулу синуса: ВС/АС (800:1010) = 0,79207920792079.
Зная синус угла А, смотрим в таблицу Брадиса и определяем, что наш угол А равен примерно 52 градусам.
Так как сумма углов треугольника равна 180 градуса, и нам известна величина углов В и А, то мы легко можем узнать величину угла С= 180 – 90-52=38.
Ответ: угол А 52 градуса, угол С 38 градусов.
Математика
Строка навигации
Измерение углов и дуг круга
186. В самом начале курса геометрии было установлено, что значит равные углы, что значит один угол больше другого и что значит найти сумму двух углов, причем, чтобы не делать каких-либо ограничений, надо принять во внимание п. 19, где угол рассматривается, как результат поворота луча около точки (в плоскости). Благодаря этому, углы составляют систему величин, а каждый отдельный угол является определенным ее значением.
Благодаря этому, углы составляют систему величин, а каждый отдельный угол является определенным ее значением.
Так как здесь налицо те же основные положения, как и при рассмотрении отрезков, то все, что мы нашли для отрезков, справедливо и для углов: также можно измерять углы, принимая один из них за единицу, или находить отношение двух углов.
Чтобы измерять отрезки, нужно было только одно умение (пп. 165 и 172): откладывать на большем отрезке меньший. Так же точно, чтобы выполнять измерение углов, мы должны уметь откладывать меньший угол на большем, – а это мы умеем делать, умеем отличать больший угол от меньшего и умеем строить угол, равный данному.
Что же касается приближенного измерения углов (подобного изложенному в п. 181 для отрезков), то мы можем средствами геометрии лишь выполнять эти измерения с точностью до ½, ¼, 1/8, 1/16 и т. д., так как умеем угол делить только на 2, 4, 8, 16 и т. д. Равных частей. Существуют механические способы деления угла на сколько угодно равных частей.
За единицу при измерении углов принимают прямой угол, в предыдущем курсе мы часто встречались с углами, измеренными прямым углом. Например, если в равнобедренном треугольнике один угол прямой, то каждый из остальных = ½ прямого (½ d), каждый из углов равностороннего треугольника = 2/3 d, сумма внутренних углов n-угольника = 2d (n – 2) и т. д.
Но эта единица оказывается очень велика и на практике берут другую единицу, которая = 1/90 части прямого угла (1/90 d) и которая называется угловым градусом, при письме обозначают эту единицу знаком (°) и, следовательно,
угол равностороннего треугольника = 2/3 d = 60°,
сумма углов треугольника = 2d = 180° и т. д.
Затем вводят еще единицы: угловой градус делят на 60 равных частей, и такую часть называют угловою минутою, – ее знак (‘), угловую минуту делят еще на 60 равных частей и такую часть называют угловой секундою, – ее знак (”).
Например, имеем ¼ d = 22°30′, 1/16 d = 5°37’30”.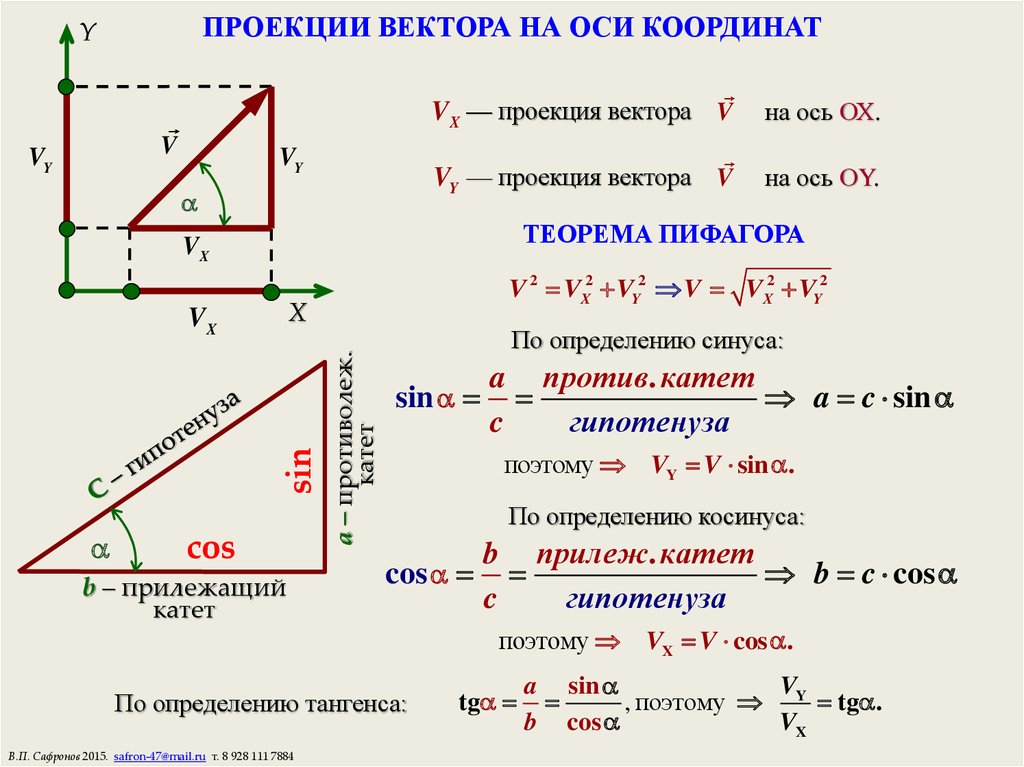
Деление прямого угла на 90 равных частей, а углового градуса на 60 равных частей и т. д. Нельзя выполнять геометрически (циркулем и линейкою), а возможно лишь выполнять механическими способами.
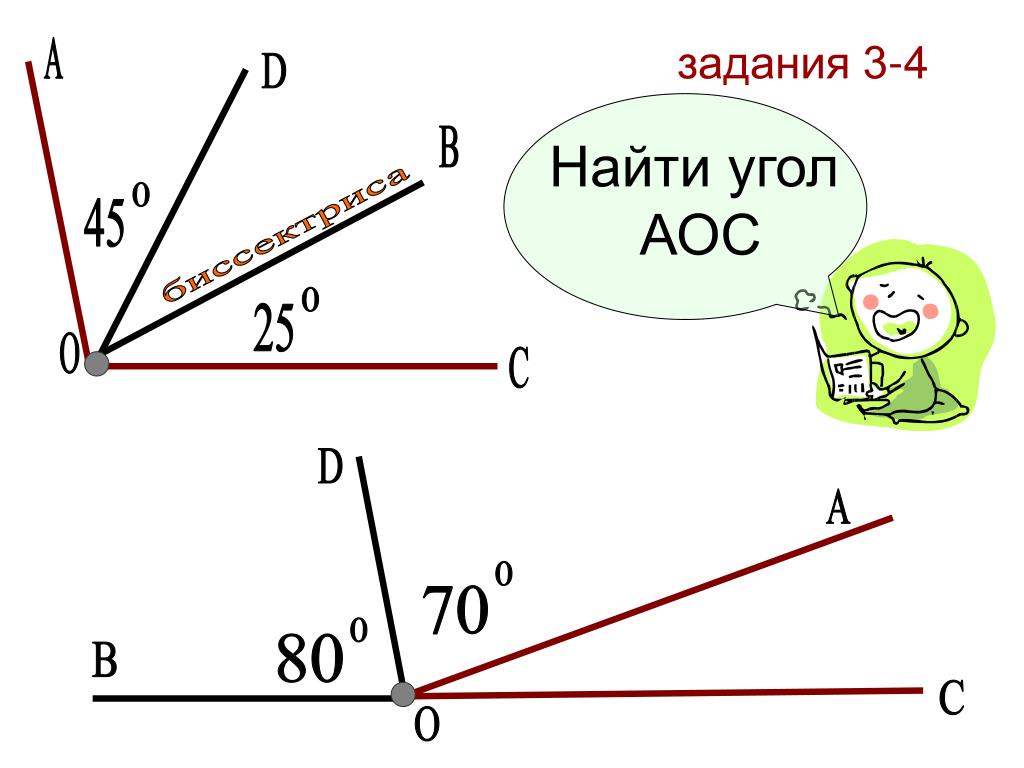
187. Упражнения. 1. Часы показывают 25 минут второго. Вычислить в градусах угол между стрелками часов.
2. Вычислить в градусах (минутах и секундах) внутренний угол правильного 8-угольника, 12-угольника, 20-угольника (его еще мы не умеем строить), 14-угольника (его геометрическими способами невозможно построить).
3. Даны 2 угла, найти отношение этих углов, полагая, что при отыскании общей меры этих углов дойдем до остатка, о котором можно, хоть приближенно, принять, что он укладывается в предыдущем целое число раз (наложение одного угла на другой надо выполнять при помощи циркуля).
188. В п. 21 мы научились различать равные дуги одного круга (или равных кругов) и неравные дуги (знаем, что значит одна дуга больше другой), составили понятие о сумме двух дуг. Надо лишь иметь в виду, что сумма нескольких дуг может оказаться больше всего круга: прикладывая к одной дуге другую, к полученной сумме третью и т. д., можем обойти весь круг и зайти за ту точку, где начинается первая дуга. На основании этих сведений мы также, как и для отрезков, можем утверждать, что дуги одного круга можно выражать числами, принимая за единицу любую дугу. Для выполнения измерения дуг необходимо лишь одно умение, – умение откладывать равные дуги, а это можно выполнять при помощи циркуля, которым можно откладывать равные хорды: равным хордам соответствуют равные дуги (п. 119).
Надо лишь иметь в виду, что сумма нескольких дуг может оказаться больше всего круга: прикладывая к одной дуге другую, к полученной сумме третью и т. д., можем обойти весь круг и зайти за ту точку, где начинается первая дуга. На основании этих сведений мы также, как и для отрезков, можем утверждать, что дуги одного круга можно выражать числами, принимая за единицу любую дугу. Для выполнения измерения дуг необходимо лишь одно умение, – умение откладывать равные дуги, а это можно выполнять при помощи циркуля, которым можно откладывать равные хорды: равным хордам соответствуют равные дуги (п. 119).
Обычно за единицу при измерении дуг принимают 1/360 часть всей окружности, разделить окружность на 360 частей геометрическими способами мы не можем, можем достигнуть этого механическими приемами (п. 148). Эта единица называется дуговым градусом , дуговой градус делят еще на 60 равных частей и эту часть называют дуговою минутою , разделив последнюю на 60 равных частей, получим дуговую секунду . Знаки для их обозначения употребляются такие же (°, ‘ и ”) как и для угловых градуса, минуты и секунды. Недоразумения здесь быть не может, так как всегда видно, об измерении угла или дуги идет речь. Например,
Знаки для их обозначения употребляются такие же (°, ‘ и ”) как и для угловых градуса, минуты и секунды. Недоразумения здесь быть не может, так как всегда видно, об измерении угла или дуги идет речь. Например,
∠AOB = 56° 8′ 24” и ◡MN = 17° 42′ 5”
(в первом случае угловые единицы, во втором — дуговые).
189. В том случае, когда две дуги одного круга или два угла несоизмеримы, отношение этих дуг или отношение этих углов признается нами равным какому-то иррациональному числу. Однако, мы не можем утверждать, что эти числа таковы же, как и те, которым равны отношения каких-либо двух отрезков: чтобы это утверждать, надо было бы убедиться, что для любой пары углов (или дуг одного круга) можно было бы построить два таких отрезка, чтобы можно было признать отношение двух углов (или дуг круга) равным отношению двух построенных отрезков, т. е. чтобы быть убежденным, что всякое рациональное число, большее одного из этих отношений, больше и другого, и всякое рациональное число, меньшее одного из этих отношений, меньше и другого. Геометрического решения указанного вопроса (построить требуемые два отрезка) вообще не возможно, но общая теория иррациональных чисел позволяет утверждать, что отношение двух несоизмеримых значений одной и той же системы величин (напр., углов) дает иррациональное число, которое можно рассматривать, как отношение двух несоизмеримых отрезков.
Геометрического решения указанного вопроса (построить требуемые два отрезка) вообще не возможно, но общая теория иррациональных чисел позволяет утверждать, что отношение двух несоизмеримых значений одной и той же системы величин (напр., углов) дает иррациональное число, которое можно рассматривать, как отношение двух несоизмеримых отрезков.
190. В частном случае мы можем легко усмотреть, что отношение двух углов равно отношению двух определенных дуг.
Построим круг O (чер. 194) и два центральных угла ∠AOB и ∠COD, которые опираются соответственно на дуги AB и CD. Рассмотрим два отношения ∠AOB/∠COD и ◡AB/◡CD. Найдем самое большое число со знаменателем n, чтобы оно было меньше первого отношения. Для этого разделим ∠COD на n равных частей (выполнить на самом деле такое построение мы можем лишь тогда, когда число n есть степень числа 2, т. е. 4, 8, 16, 32 …, если же число n какое-либо иное число, то все дальнейшее должно основываться на допущении, что существует угол, хотя мы его построить и не умеем, составляющий 1/n часть данного ∠COD) и станем такие углы укладывать на угле AOB, – допустим, что их уложится m с остатком KOB (∠KOB
Как измерить угол между стен.
 Несколько способов.
Несколько способов.Какой угол образуют стены. Первый способ – измерение.
Для проектирования мебели мы не только должны измерять длину и высоту стен в квартире или доме, но и необходимо измерить угол в который будет установлена мебель.
Для чего это нужно делать? – чтобы не возникали проблемы с монтажем, чтобы избежать огромные боковые щели, и для того чтобы еще на производстве можно было проводить необходимые корректировки.
К примеру развернутый угол не позволит смонтировать угловую кухню без дополнительных подрезов внутренних угловых модулей и столешницы. Острый угол может потянуть выход корпуса мебели за габариты установочных размеров, потому что в влотную в угол невозможно установить мебельный модуль.
Собственно, когда причины выяснили и необходимость измерения угла очевидна – дело за малым – измерить угол.
Если у Вас имеется в домашнем арсенале угломер – тогда без проблем, а если нет, то нижеописанный способ всегда прийдет на помощь.
Первое что необходимо сделать – это отметить две точки на стенах в одном уровне (на высоте где будет установлен мебельный модуль) следующим образом:
- От угла рулеткой отмеряете по левой и правой стене размер к примеру 500мм.
 и ставите точки.
и ставите точки. - Далее измеряете диагональ – т.е. расстояние между точками.
Итак например у нас есть три размера – катет 500мм., 500мм. и диагональ 700мм.
Следующий этап -это построение угла на шаблоне из любого материала. В нашем случае я покажу как это сделать в программе autоcad, но тоже можно сделать имея циркуль, линейку, транспортир и материал для шаблона.
- Чертим горизонтально отрезок 500мм. с точками “АБ”. (см. чертеж ниже.)
- Чертим окружность с радиусом 500мм. с центром в точке “В”.
- Чертим вторую окружность с радиусом 700мм. с центром в точке “А”.
- В точке пересечения окружностей ставим точку “С”.
- Соединяем точки “В” и “С” отрезком и получаем наш угол.
- Далее остается измерить угол транспортиром на шаблоне или специальным инструментом в программе autоcad. и уже имеющийся чертеж применить для проектирования.
Когда чертеж построен, мы можем в заключении сделать вывод – измеряемый угол 89градусов, угол острый и негативно повлиять на установку мебели он не сможет, т. к. 1 градус величина довольно малая.
к. 1 градус величина довольно малая.
Какой угол образуют стены. Второй способ – расчёт.
- От угла отмеряем 1000 мм (чем больше, тем лучше – погрешность меньше… конечно если вы для полочки 400*400 мм, то больше чем 400 мм отмерять не надо) на обеих стенах, и ставим отметки (если обои то можно иголками),
- Замеряем расстояние между отметками (лучше делать это вдвоем, опять же из соображений точности), допустим у нас получилось 1500 мм.
Осталось рассчитать, сколько градусов в вашем угле по формуле: cos(γ) = (a 2 + b 2 – c 2 ) / (2 • a • b)
Получив cos(γ) угла, далее через функцию
Т.е. по примеру это: (1000 2 + 1000 2 – 1500 2 ) / (2 • 1000 • 1000) = -0.125 отсюда arccos (-0.125)= 97.18 градусов.
Теги: #Как высчитать градусы угла
Как посчитать градус угла
Нахождение углов треугольника по заданным сторонам
Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” class=”pc-math” />
a” class=”pc-math” />
b” class=”pc-math” />
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
Как вычислять углы
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Количество просмотров этой статьи: 127 859.
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны, в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Измерение углов
Измерить угол — значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус — это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак ° , который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор — транспортир:
У транспортира две шкалы — внутренняя и внешняя. Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах:
Говорят: угол BOC равен 60 градусов, угол MON равен 120 градусов и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута — это угол, равный части градуса. Секунда — это угол, равный части минуты. Минуты обозначают знаком ‘ , a секунды — знаком ” . Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB. Таким образом, ∠AOB = ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Сумма углов треугольника
Сумма треугольника равна 180 градусов.
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х.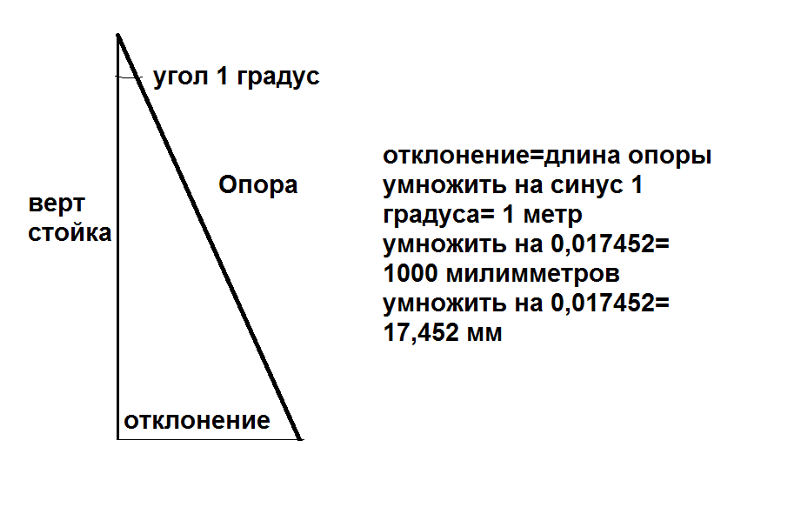 Получим уравнение
Получим уравнение
2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .
3. На рисунке угол равен , угол равен , угол равен . Найдите угол . Ответ дайте в градусах.
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Сначала найдем угол .
Угол , смежный с углом равен .
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Ты нашел то, что искал? Поделись с друзьями!
4. Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.
Пусть углы треугольника равны , и . Запишем, чему равна сумма углов этого треугольника.
Как же все-таки доказать, что сумма углов треугольника равна 180 градусов? Очень просто. На нашем рисунке угол равен углу (они накрест лежащие). Угол равен углу (тоже накрест лежащие). Развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
На нашем рисунке угол равен углу (они накрест лежащие). Угол равен углу (тоже накрест лежащие). Развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.
Угловые размеры
Угловые размеры на чертеже
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Наиболее распространенный способ измерения угловых величин – градусная мера.
Градус – «gradus», в переводе с латинского языка, означает – шаг, ступень.
При обозначении угловых размеров используется единицы измерения – градусы, минуты и секунды. После числового значения угловых размеров ставится специальные знаки:
- Градус – « ° »
- Минута – « ′ »
- Секунда – « ″ »
Размерные числа наносят над размерными линиями в зоне расположенной выше горизонтальной осевой линии со стороны их выпуклости, а в зоне расположенной ниже со стороны вогнутости размерных линий.В тех местах, где нанесена штриховка, размерные числа указывать не рекомендуется. В таких случаях размерные числа указывают на горизонтально нанесенных полках.
В таких случаях размерные числа указывают на горизонтально нанесенных полках.
Нанесение угловых размеров на чертеже
Нанесение угловых размеров
Градусы минуты секунды – n° n′ n″
Окружность, разделённая на 360° , включает в свой состав помимо градусов, минуты и секунды n° n′ n″ .
1° = 1/360 – один градус равен одной тристашестидесятой полного оборота.
1° = 60′ – один градус равен шестьдесят минут.
60′ = 60″ – шестьдесят минут ровны шестидесяти секундам.
Градусная мера полного оборота равна 360° = 21600′ = 1296000″ .
Теги: #Как посчитать градус угла
Как проверить прямой угол без угольника
При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные
конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или
разметить углы со сторонами в несколько метров.
Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.
Теорема Пифагора
Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:
a²+b²=c²
Стороны a и b — катеты, между которыми угол равен ровно 90 градусов. Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.
Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!
Это треугольник со сторонами 3, 4 и 5,
причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим
данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все
сходится!
А теперь применим теорему на практике.
Проверка прямого угла
Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.
Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих
стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно
больше, но чтобы между отметками на стенах удобно было мерить диагональ.
Калькулятор расчета диагонали прямого угла
Внимание! Для работы калькулятора необходимо включить поддержку JavaScript в вашем браузере!
Длина aДлина b
Диагональ c
Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же,
не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Поэтому можно пользоваться упрощенным методом. Нужно
лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у
прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого
метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны
быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать
о первоначальном способе совсем — в некоторых случаях он очень актуален.
Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое
нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из
понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см.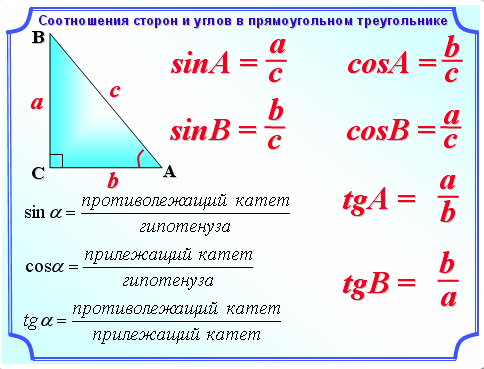 в несколько миллиметров
не даст отклонения в один целый градус.
в несколько миллиметров
не даст отклонения в один целый градус.
Как проверить внешний угол?
Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.Как разметить прямой угол рулеткой
Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.
Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся
последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на
количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!
Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах.
Картинки увеличиваются по клику!
Как разметить острый угол
Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.
Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет
вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Стоит добавить, что уметь делать это должен любой отделочник или
строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.
Смотрите также другие статьи
Расчёт угла наклона крыши Альфалес
Поскольку от его величины зависит и количество кровельного материала, то выбор угла наклона и его предварительные расчеты производят до начала закупки выбранного кровельного материала.
Что на него влияет
В зависимости от величины уклона скатов крыши зависит особенность ее эксплуатации.
Принято выделять 4 типа крыш: высокие — с углом в 45–60 градусов; скатные — с наклоном от 30 до 45 градусов; пологие — с углом уклона 10–30 градусов; плоские — с углом 10 градусов и меньше.
На выбор величины этого параметра оказывают влияние, в первую очередь, природные факторы, которые характерны для данной местности.
Ветровая нагрузка
Сильный ветер самое большое давление оказывает на кровли высокие. Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы. И если вы решили устраивать именно высокую кровлю с очень большим уклоном, то следует позаботиться и об очень прочном основании. Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.
Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы. И если вы решили устраивать именно высокую кровлю с очень большим уклоном, то следует позаботиться и об очень прочном основании. Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.
Нагрузка снеговая
Если в той местности, где строится дом, в холодное время года снегопад обильный, то следует строить кровлю с большим углом уклона. В этом случае высокая крыша вне конкуренции. На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах. Тем больший вес будет воздействовать на всю конструкцию. Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.
На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах. Тем больший вес будет воздействовать на всю конструкцию. Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.
Выбираем уклон в зависимости от используемого кровельного материала
Прошли те времена, когда для покрытия использовали всего два вида кровельных материалов: черепицу и шифер. Каждый материал имеет свои индивидуальные технические характеристики и это при расчете необходимого значения угла наклона обязательно следует учитывать. Ведь может произойти так, что понравившийся вам материал по своим параметрам просто не подойдет.
Минимальный угол наклона
Существует понятие минимального значения этого параметра. Для каждого из материалов этот параметр свой. И если угол наклона, полученный в результате ваших расчетов, окажется меньше, чем минимальная величина для выбранного вами кровельного материала, то использовать его для устройства кровли нельзя.
В дальнейшем может возникнуть очень много проблем, если нарушить это правило:
- для любых штучных наборных кровельных материалов, таких как черепица или шифер, минимальная величина уклона составляет 22 градуса. Именно при таком значении на стыках не скапливается влага и внутрь крыши влага не просачивается;
- угол наклона для рулонных материалов (рубероид, бикрост и пр.) зависит от того, какое вы планируете укладывать количество слоев. Если три слоя, то уклон может составлять 2–5 градусов. Если же два слоя, то его требуется увеличить до 15 градусов;
- производители профнастила рекомендуют при устройстве кровли из этого материала устраивать угол уклона 12 градусов.
 Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком;
Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком; - для металлической черепицы значение этого параметра равняется 14;
- для ондулина — это величина в 6 градусов;
- минимальный уклон для мягкой черепицы равняется 11 градусам. Но при этом обязательное условие — сплошная обрешетка;
- для мембранных кровельных покрытий не существует жестких требований по минимальному значению этого параметра.
Это о минимальных величинах. Дадим совет — придерживайтесь этих правил, чтобы посреди зимы не пришлось всю кровлю перестилать.
Если в регионе дожди и снега случаются часто, то оптимальной будет крыша, угол наклона скатов у которой будет составлять 45 — 60 градусов. Ведь с кровли необходимо как можно скорее снимать нагрузку от воды и снега. Потому что прочность стропильной системы не беспредельна. А благодаря большому уклону кровли дождь и снег будут сходить максимально быстро.
Если в регионе, где построен дом, постоянно сильные ветра, то с крышей поступают иначе. При меньшем наклоне снижается ее парусность. И не возникает запредельных нагрузок на кровельный материал и стропила. Также не произойдет срывания крыши при резких порывах ветра. При этом оптимальный угол уклона кровли равняется 9–20 градусов.
Очень часто в регионе есть и снега, и ветер. Например, Оренбургская область. В таком случае выбирают среднее значение угла наклона. Как правило, его величина находится в диапазоне 20 — 45 градусов. Если вы обратите внимание, большинство скатных крыш имеют именно такое его значение.
Рассчитываем его величину
Для односкатной
Поскольку односкатная крыша опирается на стены, имеющие разную высоту, то формирование заданного угла наклона производят, просто поднимая одну из стен. Проводим вдоль стены перпендикуляр L сд, берущий свое начало в точке, где оканчивается короткая стена и опирающийся на стену, имеющую максимальную дину. В итоге образуется прямоугольный треугольник.
В итоге образуется прямоугольный треугольник.
Для того, чтобы рассчитать длину стороны L bc, надо воспользоваться тригонометрической формулой.
Если длина стены L сд равняется 10 метрам, то, чтобы получить угол наклона 45 градусов, длина стены L bc должна ровняться 14.08 метра.
Для двускатной
Принцип расчета для двускатной крыши похож на предыдущий принцип.
Рассмотрим пример. Катет С — это половина ширины здания. Катет, а — это высота от перекрытия до конька. Гипотенуза является длиной ската. Если нам известны любые два параметра, то величину угла наклона можно легко рассчитать с использованием калькулятора.
Если ширина равна 8, а высота — 10 метров, то следует пользоваться формулой:
cos A = c+b
Ширина с = 8/2 = 4 метра.
В итоге формула выглядит так:
cos A = 4/10 = 0.4
По таблицам Брадиса находим значение угла, которому соответствует данная величина косинуса. Он равняется 66 градусов.
Для четырехскатной
И снова не обойтись без рулетки и таблиц Брадиса. Зная несколько параметров, можно без проблем вычислить другие. В том числе и угол наклона четырехскатной крыши. Следует помнить о том, что все размеры необходимо снимать максимально точно. А измерить уклон уже построенной крыши поможет специальный инструмент — уклономер. Ведь если вы ошибетесь, то углы наклона, длины и площади могут быть не верны. А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.
Зная несколько параметров, можно без проблем вычислить другие. В том числе и угол наклона четырехскатной крыши. Следует помнить о том, что все размеры необходимо снимать максимально точно. А измерить уклон уже построенной крыши поможет специальный инструмент — уклономер. Ведь если вы ошибетесь, то углы наклона, длины и площади могут быть не верны. А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.
Как рассчитать угол наклона крыши
Содержание статьи:
- 1 Как величина уклона зависит от используемого материала
- 2 Что влияет на наклон
- 3 Зависимость угла от места строительства
- 4 Пример расчёта
Многие хозяева загородной недвижимости говорят о том, что крыша собственного дома должна быть не только надёжной, но и красивой. Добиться максимальной функциональности и красивого внешнего вида рассматриваемой конструкции можно при правильном подборе материалов, а также вычислении необходимого уклона. В нашей статье опишем, как рассчитать угол наклона крыши. Для этого необходимо владеть данными о ветровой и снеговой нагрузке, месте строительства и свойствах покрытия.
В нашей статье опишем, как рассчитать угол наклона крыши. Для этого необходимо владеть данными о ветровой и снеговой нагрузке, месте строительства и свойствах покрытия.
Перед тем как определить угол наклона крыши в градусах нужно узнать для каких целей будет использоваться чердак. Если эта часть дома будет жилой наклон нужно делать максимальным, что позволит увеличить высоту потолков и сделает помещения просторнее. Вторым вариантом выхода со сложившейся ситуации будет устройство ломаной мансардной кровли. В большинстве случаев подобную конструкцию делают двускатной, но некоторые могут иметь и четыре ската. Здесь нужно всё тщательно высчитать, ведь при увеличении высоты конька увеличивается полезный объём мансарды. Вместе с тем повышается площадь покрытия и финансовые вложения на устройство кровли.
До того как рассчитать угол наклона кровли ознакомьтесь со следующей полезной информацией:
- При увеличении высоты конька возрастают финансовые вложения на используемые для покрытия материалы;
- На скаты со значительной площадью сильнее воздействует ветер.
 Если взять два здания с одинаковыми габаритными размерами, но имеющие разный угол наклона в градусах (например, 11 и 45), то нагрузка от одинаковых по силе потоков ветра на второй дом будет почти в 5 раз выше.
Если взять два здания с одинаковыми габаритными размерами, но имеющие разный угол наклона в градусах (например, 11 и 45), то нагрузка от одинаковых по силе потоков ветра на второй дом будет почти в 5 раз выше. - Если вы не знаете, как найти угол наклона, возьмите его большим от 60 градусов. На таких кровлях не задерживаются атмосферные осадки и снег.
- Не каждое изделие для кровли может применяться на больших по углу наклона скатах. Под углом наклона подразумевается соотношение высоты ската к половине ширины дома.
Крыши с небольшим углом уклона имеют уменьшенную площадь по сравнению с крутыми кровлями, они гораздо дешевле, но при монтаже такого покрытия тоже нужно учитывать определённые нюансы:
- Устройство специальных снегозадержателей для предотвращения схода лавин. Одним из вариантов отвода снеговых масс считается устройство специального обогрева для ускорения таянья снегов.
- При незначительных перепадах высот покрытия существует высокая вероятность проникновения влаги в конструкцию кровли через стыки.
 Чтоб крыша не дала течь необходимо использовать усиленную гидроизоляцию.
Чтоб крыша не дала течь необходимо использовать усиленную гидроизоляцию.
Как можно понять, конструкции с небольшим уклоном имеют больше недостатков, чем положительных качеств. В связи с этим каждый строитель должен знать, как определить угол наклона крыши в градусах.
Как величина уклона зависит от используемого материала
Кровля загородного дома или хозяйской постройки может иметь низкие или отвесные скаты. Во время проектирования этой конструкции необходимо рассчитать сечение стропил и расстояние между ними. Как определить угол наклона для разных кровельных материалов, пытаются понять многие, но эти значения давно уже вычислены.
Во время монтажа рулонных гидроизоляционных материалов, когда рубероид укладывается в два слоя, наклон покрытия не должен превышать 15 градусов. Многие хотели бы знать, как определить угол наклона крыши в градусах если она покрыта тремя слоями гибкой черепицы. В данном случае описываемый показатель может меняться от 2 до 5 градусов.
Обратите внимание на следующие нюансы устройства:
- Наплавляемый рубероид рекомендован к использованию при величине уклона до 25˚ в два слоя, от 0 до 10˚ – в три слоя. При наличии крыши с уклоном 10…25 градусов можно уложить один слой рулонных материалов, но лицевая поверхность такого покрытия должна иметь специальный защитный слой.
- Асбестоцементные листы используются на кровлях, имеющих уклон до 26˚.
- Минимальный уклон для натуральной черепицы составляет 33 градуса;
- Профлист или металлочерепица – 29 градусов и больше.
Расход кровельных изделий тоже зависит от рассматриваемого параметра. так конструкции с небольшими уклонами стоят гораздо дешевле аналогов, имеющих угол больше 45 градусов.
Что влияет на наклон
Все используемые кровли могут иметь различную форму и количество скатов. Например, у гаражей или других хозяйских построек может присутствовать всего один скат, у сараев таких плоскостей две, а вот кровли гражданских зданий состоят из двух или четырёх скатов.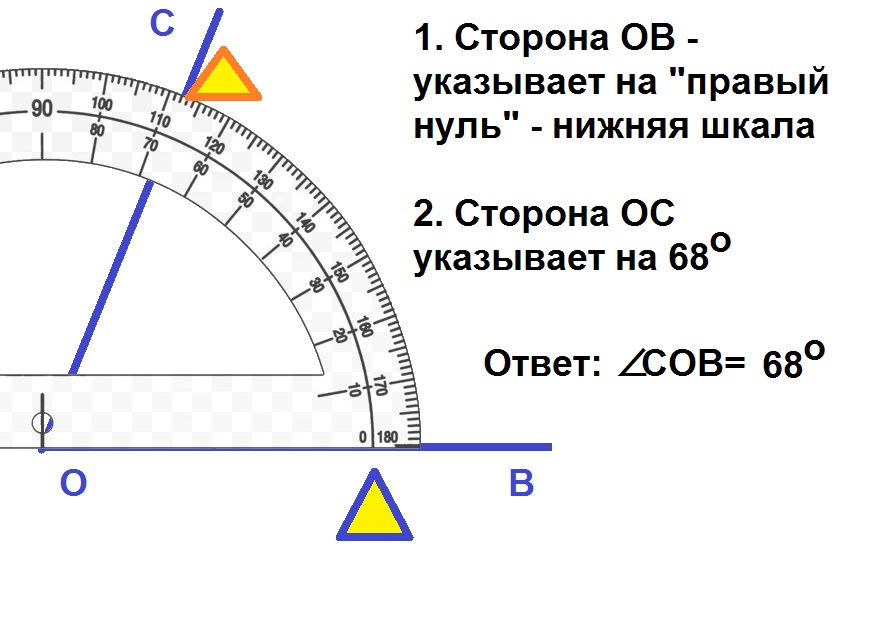 Как определить угол наклона крыши в градусах недоумевают многие строители. По мнению экспертов, подобные расчеты можно проводить при помощи специальных матриц или графиков. Кроме этого, узнать угол наклона крыши можно из курса геометрии при помощи треугольника. Чаще всего описываемый конструкционный элемент напоминает именно эту фигуру.
Как определить угол наклона крыши в градусах недоумевают многие строители. По мнению экспертов, подобные расчеты можно проводить при помощи специальных матриц или графиков. Кроме этого, узнать угол наклона крыши можно из курса геометрии при помощи треугольника. Чаще всего описываемый конструкционный элемент напоминает именно эту фигуру.
На этапе проектирования кровли нужно выбрать необходимые изделия и провести необходимые расчёты. Замечено, что тип покрытия берётся во внимание при расчёте угла любой скатной конструкции. Если хозяин постройки не знает, как посчитать наклон правильно, то эта величина находится в пределах 9-20 градусов. При проектировании кровли здания учитывайте следующие нюансы:
- предназначение постройки;
- материал, из которого изготовлено покрытие;
- климатические особенности региона строительства.
Если планируется монтаж крыши с двумя или большим количеством скатов нужно обратить внимание не только на перечисленные требования, но и на район строительства. Также необходимо брать во внимание предназначение чердачного помещения. Если мансарда будет использоваться для хранения ненужных вещей, то делать ее высокую и повышать расход кровельного материала нет смысла. При использовании жилого чердачного помещения необходимо выбирать стропила с максимальным сечением и размещать их на небольшом расстоянии друг от друга.
Также необходимо брать во внимание предназначение чердачного помещения. Если мансарда будет использоваться для хранения ненужных вещей, то делать ее высокую и повышать расход кровельного материала нет смысла. При использовании жилого чердачного помещения необходимо выбирать стропила с максимальным сечением и размещать их на небольшом расстоянии друг от друга.
Зависимость угла от места строительства
В регионах с постоянными сильными ветрами необходимо делать уклон минимальным. В связи с этим нагрузка от потоков воздуха на кровлю будет небольшой. Высокие крыши страдают от ветра гораздо больше, чем низкие. Нельзя сказать, что ветер не срывает покрытие с крыш, имеющих небольшой уклон. Далее узнаем, как найти угол наклона кровли для зданий, построенных в регионах с постоянными ветрами:
- При небольшой интенсивности воздушных потоков уклон имеет значение 34-40 градусов;
- При наличии сильных ветров этот показатель уменьшают до 15…25 градусов.
В местности с большим количеством атмосферных осадков наклон желательно увеличивать до параметров в 60˚. Такой уклон позволит быстро выводить снег и воду за пределы покрытия. Уклон крыши обычно меняется в диапазоне 9…60˚, но самыми распространёнными вариантами уклона считается диапазон 19…44 градуса.
Такой уклон позволит быстро выводить снег и воду за пределы покрытия. Уклон крыши обычно меняется в диапазоне 9…60˚, но самыми распространёнными вариантами уклона считается диапазон 19…44 градуса.
Пример расчёта
А теперь ознакомимся, как рассчитать угол наклона крыши на конкретном примере. Для начала необходимо узнать высоту конька по отношению к основанию. Этот параметр зависит от предназначения чердака. Если это помещение будет использоваться в качестве мансарды, то нам понадобится ещё одна величина – длина фронтона или основания.
Как измерить угол наклона, если высота от основания кровли до конька составляет 1,8 метра, а длина фронтона принимается кратной 6 метрам. Для начала необходимо разделить «подошву треугольника» на две части, а затем вычисляют синус угла по теореме Пифагора.
В нашем случае, это значение синуса угла, который находится из соотношения прилежащей стороны к противолежащей. Сначала делим треугольник на две равные части 6/2=3. Теперь вычисляем синус нужного угла 3/1,8= 1,6. Заглядываем в таблицу Брадиса и видим, что это значение соответствует углу в 59 градусов.
Заглядываем в таблицу Брадиса и видим, что это значение соответствует углу в 59 градусов.
Как рассчитать угол наклона крыши и получить надежную конструкцию?
21/05/2021
Как рассчитать угол наклона крыши и получить надежную конструкцию?
Содержание
Что нужно перед тем, как рассчитать угол наклона крыши?
Установка стропильных ног обычно не вызывает трудностей, если есть необходимые крепежные элементы, однако, выверяя угол, под которым будут уложены скаты, можно ошибиться, если не знать некоторых тонкостей.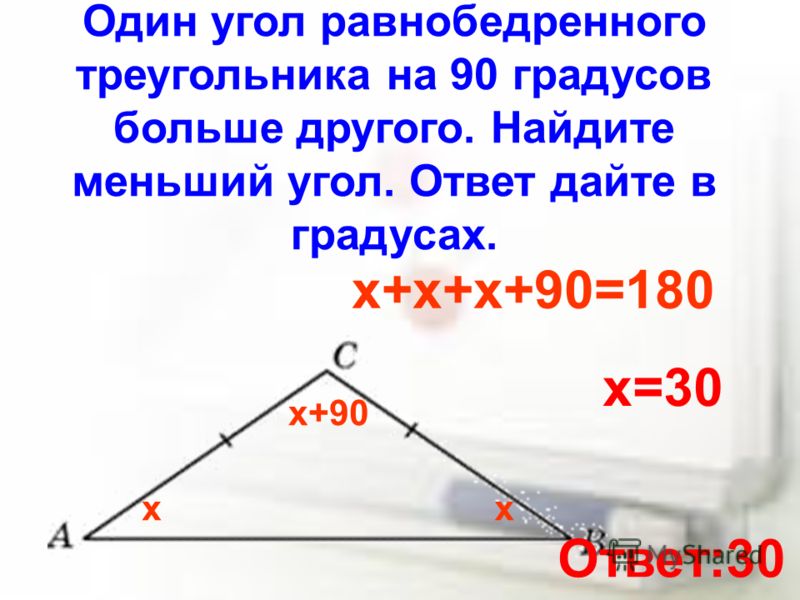 Например, очень высокая кровля в местности с сильными ветрами будет постоянно подвергаться большим нагрузкам и в итоге с большой долей вероятности будет разрушена. Следовательно, чтобы этого избежать, иногда стоит отдать предпочтение не слишком эффектной, но устойчивой низкой крыше. Таких примеров можно привести множество, но рассмотрим сами факторы, влияющие на высоту кровли. От чего она может зависеть?
Например, очень высокая кровля в местности с сильными ветрами будет постоянно подвергаться большим нагрузкам и в итоге с большой долей вероятности будет разрушена. Следовательно, чтобы этого избежать, иногда стоит отдать предпочтение не слишком эффектной, но устойчивой низкой крыше. Таких примеров можно привести множество, но рассмотрим сами факторы, влияющие на высоту кровли. От чего она может зависеть?
Как уже стало ясно, перед тем, как рассчитать угол наклона крыши, в первую очередь необходимо принять во внимание климатические особенности региона. Так, например, чем острее двускатная крыша, тем хуже на ней удерживается снег и легче стекает с нее дождевая вода. Однако, чем чреват такой крутой уклон, при сильном ветре, мы уже знаем. В тех местах, где жаркое солнце, лучше возводить скаты с минимальным уклоном или вообще обойтись без них, то есть сделать плоской поверхность кровли, которая тем сильнее получает и передает вниз тепло, чем больше ее площадь. Последняя увеличивается пропорционально крутизне уклона.
Чем более полога крыша, тем выше вероятность того, что сильными порывами ветра с дождем влага будет загоняться под края кровельного покрытия.
Помимо прочего, следует учитывать, каким образом будет использоваться пространство под стропильной системой – как чердак или в качестве жилой мансарды. В первом случае допускается расстояние до конька меньше среднего роста человека. Во втором случае необходимо, чтобы было достаточно комфортного пространства для передвижения, то есть просвет в центре помещения должен составлять не менее 2.5 метров и, желательно, не менее полутора метров в самой нижней точке потолка. Немалое воздействие на угол ската крыши может оказать материал покрытия, который можно укладывать только при определенной степени крутизны наклона.
В чем измеряется угол уклона крыши
Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i.
В СНиПе II-26-76, данная величина указывается в процентах ( % ). В данный момент не существует строгих правил по обозначению размера уклона крыши.
В данный момент не существует строгих правил по обозначению размера уклона крыши.
Единицей измерения уклона крыши считают градусы или проценты ( %). Их соотношение указаны ниже в таблице.
Уклон крыши соотношение градусы-проценты
| градусы | % | градусы | % | градусы | % |
| 1° | 1,75% | 16° | 28,68% | 31° | 60,09% |
| 2° | 3,50% | 17° | 30,58% | 32° | 62,48% |
| 3° | 5,24% | 18° | 32,50% | 33° | 64,93% |
| 4° | 7,00% | 19° | 34,43% | 34° | 67,45% |
| 5° | 8,75% | 20° | 36,39% | 35° | 70,01% |
| 6° | 10,51% | 21° | 38,38% | 36° | 72,65% |
| 7° | 12,28% | 22° | 40,40% | 37° | 75,35% |
| 8° | 14,05% | 23° | 42,45% | 38° | 78,13% |
| 9° | 15,84% | 24° | 44,52% | 39° | 80,98% |
| 10° | 17,64% | 25° | 46,64% | 40° | 83,90% |
| 11° | 19,44% | 26° | 48,78% | 41° | 86,92% |
| 12° | 21,25% | 27° | 50,95% | 42° | 90,04% |
| 13° | 23,09% | 28° | 53,18% | 43° | 93,25% |
| 14° | 24,94% | 29° | 55,42% | 44° | 96,58% |
| 15° | 26,80% | 30° | 57,73% | 45° | 100% |
Перевести уклон из процентов в градусы и наоборот из градусов в проценты можно при помощи онлайн конвертера:
Конвертер уклона — онлайн калькулятор
из градусов в проценты и из процентов в грудусы Перейти
Замер уклона крыши
Измеряют угол уклона при помощи уклономера или же математическим способом.
Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.
Математический расчёт уклона
Можно рассчитать уклон крыши не используя геодезические и другие приборы для замеров уклона. Для этого необходимо знать два размера:
- Вертикальная высота ( H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
- Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней
При помощи математического расчёта величину уклона крыши находит следующим образом:
Угол уклона ската i равен отношению высоты кровли Н к заложению L
Для того, чтобы значение уклона выразить в процентах, это отношение умножают на 100. Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.
Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.
Чтобы было понятней рассмотрим на примере:
Длина заложения 4,5 м, высота крыши 2,0 м.
Уклон равен: i = 2.0 : 4,5 = 0,44 теперь умножим на × 100 = 44 %. Переводим данное значение по таблице в градусы и получаем — 24°.
Онлайн калькулятор — уклон крыши
Расчитать уклон крыши онлайнПерейти
Минимальный уклон для кровельных материалов (покрытий)
| Вид кровли | Минимальный уклон крыши | ||
| в градусах | в % | в соотношении высоты ската к заложению | |
| Кровли из рулонных битумных материалов: 3-х и 4-х слойные (наплавляемая кровля) | 0-3° | до 5% | до 1:20 |
| Кровли из рулонных битумных материалов: 2-х слойные (наплавляемая кровля) | от | 15 | |
| Фальцевая кровля | от 4° | ||
| Ондулин | 5° | 1:11 | |
| Волнистые асбоцементные листы (шифер) | 9° | 16 | 1:6 |
| Керамическая черепица | 11° | 1:6 | |
| Битумная черепица | 11° | 1:5 | |
| Металлочерепица | 14° | ||
| Цементно-песчанная черепица | 34° | 67% | |
| Деревянная кровля | 39° | 80% | 1:1. 125 125 |
Расчет необходимой величины пологости скатов мансарды
Самое важное в любом помещении – его полезная площадь, то есть та, которую можно будет использовать для расстановки мебели и передвижения, а также для хранения вещей. В мансарде иногда бывает сложно использовать некоторые участки пространства, где располагается самая низкая точка потолочной обшивки. Впрочем, такие места как раз можно отвести под хранение вещей, сделав там встроенные шкафчики и тумбы. Другое дело – зона свободного передвижения, ее площадь напрямую зависит от высоты конька, а значит – и угла крыши.
Рассмотрим на примере. Допустим, ширина дома – 9.5 метров. Если хочется простора над головой в пределах 3 метров хотя бы по центру комнаты, то угол между скатами должен быть не менее 35 градусов, поскольку уже при 30 высота конька окажется чуть больше 2.5 метров. Однако следует учитывать, что тогда ширина пространства, доступного для свободного передвижения (до двухметрового уровня потолка), окажется немногим больше 3. 5 метров. Если придерживаться той же высоты в самых низких точках наклонного потолка, и при этом сделать угол кровли 30 градусов, то ширина комнаты сократится до 2.4 метров. Наиболее комфортно будет в мансарде под крышей с углом более 40 градусов, однако следует учитывать, что у такой конструкции, в сравнении с пологим скатом (около 10 градусов), ветровая нагрузка увеличивается почти в 5 раз.
5 метров. Если придерживаться той же высоты в самых низких точках наклонного потолка, и при этом сделать угол кровли 30 градусов, то ширина комнаты сократится до 2.4 метров. Наиболее комфортно будет в мансарде под крышей с углом более 40 градусов, однако следует учитывать, что у такой конструкции, в сравнении с пологим скатом (около 10 градусов), ветровая нагрузка увеличивается почти в 5 раз.
В целом, зависимость угла наклона кровли от высоты конька только облегчает расчеты стропильной системы.
Почему это важно?
Проектирование и строительство любой кровли – всегда очень важное и ответственное дело. Особенно, если речь идет о кровле жилого дома или сложной по форме крыше. Но даже обычная односкатная, устанавливаемая на невзрачном сарайчике или гараже, точно так же нуждается в проведении предварительных расчетов.
Если заранее не определить угол наклона кровли, не выяснить, какую оптимальную высоту должен иметь конек, то велик риск построить такую кровлю, которая рухнет после первого же снегопада, или все отделочное покрытие с нее будет сорвано даже умеренным по силе ветром.
Расчет угла наклона крыши
Также угол наклона кровли будет значительно влиять на высоту конька, на площадь и габариты скатов. В зависимости от этого можно будет более точно рассчитать количество требуемых для создания стропильной системы и отделки материалов.
Конек – важная часть стропильной системы
Цены на различные виды кровельных коньков
Калькулятор расчёта угла наклона крыши
Выберите 2 любых известных значения, введите их. Остальные значения будут рассчитаны автоматически.
| Ширина основания (W) | м |
| Высота конька (H) | м |
| Длина стропил (L) | м |
| Угол: градусов | |
Однако для вычислений нужно достаточно хорошо знать азы геометрии. Чаще всего, сечение конструкции крыши со стороны фронтонов представляет собой треугольник, равносторонний, равнобедренный или иного типа. Соответственно, пользуясь простейшими формулами, можно вычислить длину любой стороны и сопредельный с ней угол, зная основание и высоту. При этом нам, помимо измерительной рулетки, понадобится таблица Брадиса, поскольку придется столкнуться с тангенсами.
При этом нам, помимо измерительной рулетки, понадобится таблица Брадиса, поскольку придется столкнуться с тангенсами.
Итак, смотрим на фронтон и видим равносторонний треугольник, состоящий из двух прямоугольных, один из катетов для которых является общим. Существует формула, согласно которой тангенс угла А при основании равен отношению противолежащего катета к прилежащему, то есть, Tg A = H/(L/2). Иными словами, в нашем случае это высота H, деленная на половину основания L. Возьмем ту же ширину фронтона 9.5 метров, половина его будет соответствовать 4.75, на это значение делим высоту конька, которую сочтем комфортной, например, 4 метра. В итоге получаем 4/4.75 = 0.84, заглядываем в таблицу Брадиса, ищем соответствующую позицию в таблице тангенсов и видим, что нам нужен угол 40°.
Высота конька тоже зависит от угла ската
При расчетах любой кровли за ориентир всегда берется прямоугольный треугольник, где катеты – это высота ската в верхней точке, то есть в коньке или же переходе нижней части всей системы стропил в верхнюю (в случае с мансардными кровлями), а также проекция длины конкретного ската на горизонталь, которая представлена перекрытиями. Здесь есть только одна постоянная величина – это длина крыши между двумя стенами, то есть длина пролета. Высота коньковой части будет меняться в зависимости от угла наклона.
Здесь есть только одна постоянная величина – это длина крыши между двумя стенами, то есть длина пролета. Высота коньковой части будет меняться в зависимости от угла наклона.
Высота конька может меняться в зависимости от угла наклона
Спроектировать кровлю помогут знания формул из тригонометрии: tgA = H/L, sinA = H/S, H = LхtgA, S = H/sinA, где А – это угол ската, Н – высота кровли к области конька, L – ½ всей длины пролета кровли (при двухскатной крыше) либо вся длина (в случае односкатной кровли), S – длина самого ската. Например, если известно точное значение высоты коньковой части, то определяется угол наклона по первой формуле. Найти угол можно будет по таблице тангенсов. Если же в основе расчетов лежит угол кровли, то найти параметр высоты конька можно по третьей формуле. Длину стропил, имея значение угла наклона и параметров катетов, можно посчитать по четвертой формуле.
Как материал может повлиять на наклон крыши?
Любая кровля – это своего рода слоеный пирог из гидро- и пароизоляции, утеплителя, обрешетки и внешнего покрытия
. Все это уложено на стропильную систему под определенным углом, который ограничивает использование того или иного материала. Главным образом следует ориентироваться на инструкции, предложенные изготовителем, которые касаются и требований к уклону скатов. Кровельные материалы бывают рулонные, наборные (черепица и шифер), листовые, а также гибкие штучные, и для каждого типа предусмотрен минимальный угол крыши.
Все это уложено на стропильную систему под определенным углом, который ограничивает использование того или иного материала. Главным образом следует ориентироваться на инструкции, предложенные изготовителем, которые касаются и требований к уклону скатов. Кровельные материалы бывают рулонные, наборные (черепица и шифер), листовые, а также гибкие штучные, и для каждого типа предусмотрен минимальный угол крыши.
Для рулонных покрытий оптимальным считается уклон не более 15 градусов при условии, что материал укладывается в 2 слоя. Если же кровля делается трехслойной, она должна быть еще более пологой, около 5 градусов, при этом требуется дополнительная обрешетка для повышения прочности на случай увеличения временной нагрузки (снег, дождь). Но есть и исключение – мембранное покрытие, которое можно использовать при любом наклоне крыши.
Наборные материалы также не терпят крутых скатов, по той простой причине, что могут съехать под собственной тяжестью при малейшей предпосылке к этому, вроде штормового порыва ветра. Однако и слишком маленьким угол делать нельзя, поскольку в этом случае масса кровельного материала будет излишне нагружать опорные конструкции, то есть стропила, обрешетку и прочие элементы. Оптимальным считается угол 22 градуса, достаточной для того, чтобы во время дождя влага свободно стекала и не задувалась ветром под стыки.
Однако и слишком маленьким угол делать нельзя, поскольку в этом случае масса кровельного материала будет излишне нагружать опорные конструкции, то есть стропила, обрешетку и прочие элементы. Оптимальным считается угол 22 градуса, достаточной для того, чтобы во время дождя влага свободно стекала и не задувалась ветром под стыки.
В отношении профнастила и металлочерепицы минимальный уклон – 12 и 14 градусов соответственно, достаточно пологий, чтобы осадки стекали с крыши, и при этом не нарушалась ее герметичность на стыках. В большую сторону крутизна может увеличиваться без ограничений, однако с учетом того, что большая площадь кровли имеет солидную массу. Также не следует забывать про ветровую нагрузку и высокую парусность крыш с углом, близким к 45 градусам. Оптимальный наклон – порядка 27-30 градусов.
А вот у мягкой черепицы, которая состоит из отдельных кусков материала типового размера, угол кровли связан с плотностью обрешетки. Если скаты очень пологие, то расстояние между планками следует сделать как можно меньше. Это обусловлено тем, что снеговые массы могут стать непосильной нагрузкой для покрытия. В том случае, когда крутизна скатов выдержана в пределах 30-40 градусов, шаг обрешетки допускается больший, до 45 сантиметров.
Это обусловлено тем, что снеговые массы могут стать непосильной нагрузкой для покрытия. В том случае, когда крутизна скатов выдержана в пределах 30-40 градусов, шаг обрешетки допускается больший, до 45 сантиметров.
Углы скатов и кровельные материалы
Не только климатические условия будут оказывать значительное влияние на форму и угол скатов. Немаловажную роль играют и используемые для строительства материалы, в частности – покрытие крыш.
Монтаж профилированного листа для кровли
Таблица. Оптимальные углы наклона скатов для кровель из различных материалов.
| Вид материала | Угол ската, градусы |
| Профнастил (металл) | 12 |
| Металлочерепица | 14-25 |
| Рубероид в зависимости от количества слоев | 2-15 |
| Шифер | 20-35 |
| Штучный материал типа кровельных камней и черепицы | 22-25 |
| Мягкая черепица | Минимум 11 |
На заметку! Чем меньше показатель наклона кровли, тем меньший шаг используется при создании обрешетки.
Рассчитываем угол наклона скатов
Цены на металлочерепицу
Как измерить уклон
Таблица соотношения градус/процент уклона кровли.
На графике ищем наклонную линию, с которой стыкуется дугообразная стрела 2. Пересечение наклонной линии c вертикальной шкалой определяет уклон, минимально допустимый для данной крыши, который равен 50%. Нам известно, что уклон ската определяется отношением высоты конька к половине его заложения. Произведем расчет таким образом:
i = 10 метров (заложение)
h = 4 метра (высота конька)
i= h / (1/2) = 4 / (10/2) = 0,8
Для того чтобы измерить уклон в %, это отношение умножают на 100
Таким образом, уклон в 80% при соблюдении норм строительства обеспечит достаточный сброс дождевой воды со всей площади. Для кровли из рулонных полимерно-битумных, битумных и мастичных материалов с уклоном 10° необходим защитный слой для основного водоизоляционного покрова из гравия либо каменной крошки, у которой марка морозостойкости не меньше 100. Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки — 0,3-0,5 см.
Такой же защитный слой применяется для кровли крыши с помощью пленочных рулонных материалов с углом до 2,5%. Слой для защиты из гравия должен быть толщиной 1-1,6 см, а слой крупнозернистой посыпки — 0,3-0,5 см.
Причем на крышах с уклоном примерно до 2,5% с использованием эластомерных пленочных материалов в рулонах, выполненных свободной кладкой, необходим утяжеляющий слой гравия из расчета 50 кгс/кв.м.
На крышах из битумно-полимерных или битумных покрытий в рулонах с углом наклона выше 10% верхний слой гидроизоляционного покрова выполняется из крупнозернистой посыпки. На крышах из мастичных материалов с углом больше 10% предусматривается защитный слой из красочных составов.
При создании крыши из асбестоцементных листов, а также профнастила и металлической черепицы с наклоном до 20% по всей площади необходимо производить герметизацию стыков. Не более чем на 5% можно допустить отклонение уклона кровли из мелкоштучных материалов. Производя эти расчеты, можно узнать площадь помещения мансарды или чердака.
Расчёт паро- и гидроизоляции
Необходимое количество материала для изоляции крыши от пара и влаги определяют, зная площадь кровельного ската.
При расчёте количества гидроизоляционной плёнки не следует забывать о том, что 15% материала уходит на создание нахлёстов
Представим, что перед нами стоит задача закрыть пароизоляционной и водонепроницаемой плёнками крышу с двумя одинаковыми скатами длиной 5 м и шириной 4 м. В этом случае вычислительные действия будут следующими:
- Sc = 5 · 4 ·2 = 40 м² (площадь двух скатов кровли).
- S = Sc · 1,15 = 40 · 1,15 = 46 м² (необходимое количество каждого изоляционного материала с учётом нахлёста, который должен составлять 15% от площади кровли).
Без расчёта площади, высоты, нагрузок и других параметров кровли уверенность в надёжности сооружения не придёт ни к одному хозяину дома. Все размеры будущей крыши надо знать заранее, чтобы не допустить никаких накладок.
Минимальный уклон кровли
Кровельный материал, являющийся одним из главных элементов структуры верхней плоскости, также предусматривает определенные рекомендации уклона в зависимости от своего типа.
- В случае с профнастилом устанавливают угол на уровне 12 градусов, для металлочерепицы данный показатель следует увеличить до 15º.
- Ондулин или мягкую черепицу на простонародном языке можно укладывать при склоне в 11 градусов. Вот только в этом случае также есть один нюанс, который заключается в сплошной обрешетке.
- При укрытии керамической черепицы наклон должен быть минимум 22º. Также стоит учесть, что стропильная система поддается большим нагрузкам в случае небольшой наклонности ската. Во избежания перегрузок следует этот фактор взять на вооружение во время проектирования.
- К самым распространенным видам поверхностного покрытия относится шифер. При настилании асбестоцементных волнистых листов показатель склона кровли не должен превышать 28%. Те же требования и к стальным плоскостям.
- Минимальный уклон кровли из сэндвич панелей по нормам составляет 5 градусов, если планируются окна в панелях, то уклон увеличивается до 7 градусов.

По какому СНиП посмотреть уклон кровли? Оптимальный и минимальный уклон кровельного материала вы можете посмотреть в СНиП II-26-76 Кровли.
Крыша – это один из важнейших элементов любого строения. Именно она надежно защищает здание от воздействия негативных факторов окружающей среды, от атмосферных осадков.
Разумеется, хорошая конструкция должна быть водонепроницаемой, обеспечивать качественный отвод атмосферных вод, а также обладать высокой устойчивостью к огню. Вместе с тем, крыша должна быть удобной для проведения ремонта в период ее эксплуатации.
Следует помнить, что именно от надежности и качества кровли вашего дома будет напрямую зависеть, сколько прослужит само здание. В настоящее время многие домовладельцы отдают предпочтение покатой крыше.
Надо сказать, у такой конструкции есть несколько очевидных преимуществ. Кроме того, следует правильно делать расчет угла наклона крыши.
Плюсы покатой крыши
Простые конструкции, такие, как односкатные и двускатные крыши, вальмовые или мансардные, всегда были и остаются самыми качественными и надежными вариантами.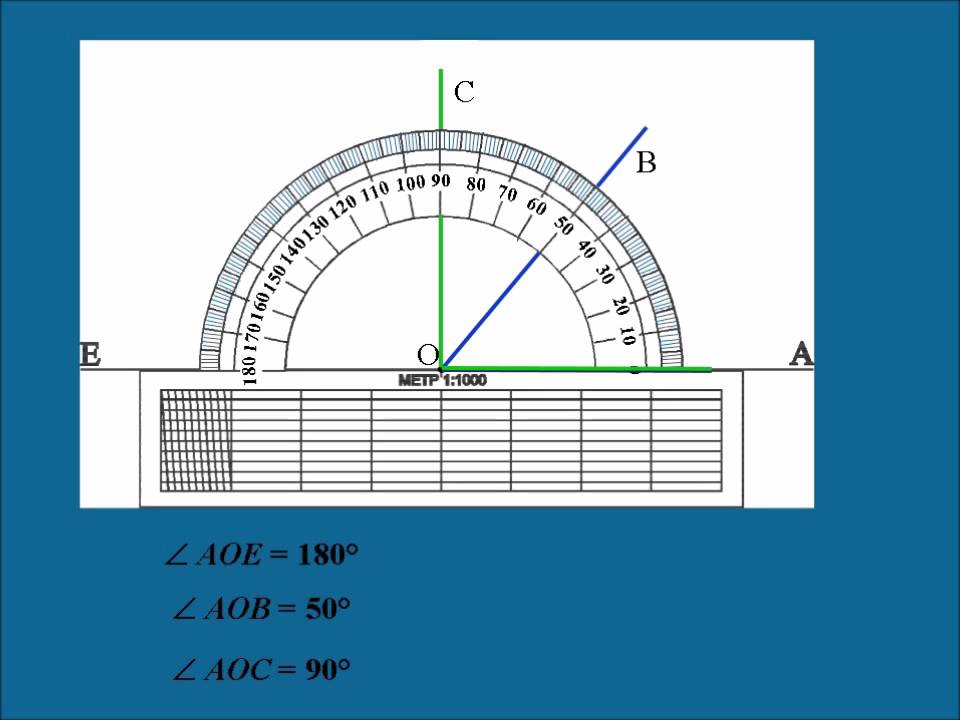 Без сомнения, преимущество покатой крыши заключается именно в гармоничном сочетании отличного качества и простоты в исполнении.
Без сомнения, преимущество покатой крыши заключается именно в гармоничном сочетании отличного качества и простоты в исполнении.
Такая крыша состоит из базового элемента кровли, а также обрешетки и стропил.
Что касается кровли, она служит для защиты здания от воздействия природных явлений, снега и дождя. Стропила же, а также обрешетки, поддерживают всю конструкцию, передают нагрузку на стены.
Рис. 1 Рассчитываем угол наклона крыши
Следует заметить, что покатая крыша защищает здание от осадков за счет определенного наклона кровли.
Прежде, чем приступить к монтажу покатой (или, как ее еще называют, скатной) крыши, необходимо произвести точный расчет угла наклона крыши.
Даже для тех людей, которые не являются специалистами в области строительства крыш, совершенно очевидно: чем угол наклона меньше, тем больше возникнет впоследствии проблем с герметичностью.
И это абсолютно не зависит от того, какой строительный материал вы выбираете для покрытия вашей крыши.
Факторы, которые влияют на выбор угла наклона
Конечно же, вам следует знать при расчете угла уклона крыши, какие факторы необходимо принимать во внимание. Так, среди важнейших параметров можно назвать:
- Ветер. Само собой разумеется, что крыша будет оказывать большее сопротивление ветру при большем наклоне. Однако слишком большой угол наклона является достаточно опасным для крыши. Так, например, при увеличении угла с минимального показателя (11 градусов) до 45 градусов, ветровая нагрузка возрастает в пять раз. Но с другой стороны, при выборе очень маленького угла наклона возникает другая проблема: при сильном порыве ветра кровлю может просто сорвать;
- Снег и дождь. Совершенно очевидно, что снег лучше сходит с крыши, имеющей большой угол наклона. Так, если он составляет более 45 градусов, обеспечено полное скатывание снега. И чем выше угол наклона, тем более герметичной будет красивая кровля вашей крыши. Объяснить это легко: дело в том, что при воздействии на крышу ветер обычно загоняет под стыки кровли атмосферную воду.
 Но чем больше вы сделаете уклон крыши, тем меньше вероятность попадания воды под стыки кровельных материалов.
Но чем больше вы сделаете уклон крыши, тем меньше вероятность попадания воды под стыки кровельных материалов.
Исходя из этих факторов, необходимо производить расчет угла наклона крыши. Для районов с сильными показателями ветра специалисты рекомендуют наклон крыши в 15-20 градусов, а для районов с нормальными показателями – около 35-40 градусов.
Однако следует помнить, что расчет угла наклона крыши обязательно нужно производить индивидуально для каждого конкретного здания.
Следует также подчеркнуть, что при расчете обязательно следует учесть особенности не только климата местности, но и конструкции самого строения.
Рис. 2 Формы скатных крыш
Способы произведения расчетов
Следует помнить, что подбор правильного угла – это очень важный этап конструирования будущей крыши здания. Обычно угол наклона крыши составляет от 11 и до 45 градусов, конечно же, бывают и исключения.
В том случае, если увеличить угол наклона, уменьшается, соответственно, снеговая нагрузка на крышу.
Но вместе с тем, чем больше будет показатель, тем воздействие ветра окажется сильнее. Это приводит к тому, что при возведении крыши требуются более прочные строительные материалы, стропила и обрешетки. А это значит, что будущая крыша обойдется вам дороже.
расчет уклона крыши
Помните: угол наклона влияет напрямую не только на качество, но и на количество материала для обустройства кровли.
Чем больше угол, тем, соответственно, больших денег будет стоить кровля.
Определенный угол уклона придается крыше в зависимости от выбранного материала, а также от климатических условий. В случае, если в районе в большом количестве наблюдаются атмосферные осадки, уклон крыши должен быть круче.
Соответствующий угол наклона будущей крыши можно определить, учитывая предполагаемую нагрузку. Как же рассчитать нагрузку? Для этого вам нужно принимать во внимание два показателя:
- Вес будущей конструкции;
- Нагрузку снега для данной местности.
Первым делом, нужно взять вес квадратного метра каждого слоя кровли, а затем сложить показатели для всех слоев. Следующий шаг: умножение получившегося результата на показатель 1,1.
Следующий шаг: умножение получившегося результата на показатель 1,1.
Наглядный пример подобных расчетов
Предположим, толщина вашей обрешетки составляет 2,5 сантиметра, и 1 квадратный метр будет весить 15 килограммов. Вы планируете класть утеплитель толщиной 10 сантиметров: вес этого материала составляет около 10 килограммов на квадратный метр.
Также вам предстоит использовать Ондулин, весом 3 килограмма на квадратный метр.
Предположим, вы решите лет через двадцать сменить кровлю, и кровельный ковер будет тяжелее, чем раньше. В данном случае и требуется тот самый коэффициент надежности 1,1 – его обязательно нужно учитывать, как коэффициент запаса.
Наконец, сделаем расчет нагрузки от собственной массы крыши. Назовем ее для простоты Н1. Она будет равна:
Н1 = 50кг/кв.м*1.1 = 55 кг/кв.м.
И непременно помните: когда вы начнете считать сечение стропильной ноги, прибавьте вес стропила к весу будущего кровельного ковра.
Учимся пользоваться таблицей Брадиса
Что касается снеговой нагрузки, коэффициент будет зависеть от того, какой угол наклона вы выбрали для вашей крыши. Итак, если наклон составляет менее 25 градусов, коэффициент составляет 1, а если от 25 до 60 градусов, то принимается во внимание коэффициент, составляющий 1,25.
А вот в том случае, если вы выбираете угол наклона более 60 градусов, учитывать нагрузку от снега не нужно.
Если вам необходимо найти угол наклона кровли, воспользуйтесь математической таблицей Брадиса (таблицей тангенсов).
Высоту в коньке следует разделить на ? длины фронтона, и по соответствующему значению в таблице найти угол наклона.
А вот для того чтобы математическим способом вычислить высоту конька, следует рассчитать ширину пролета дома, разделить этот показатель на два, а затем умножить на относительную величину, которая будет индивидуальной для определенного угла наклона.
Также для определения угла наклона и высоты конька можно воспользоваться угольником.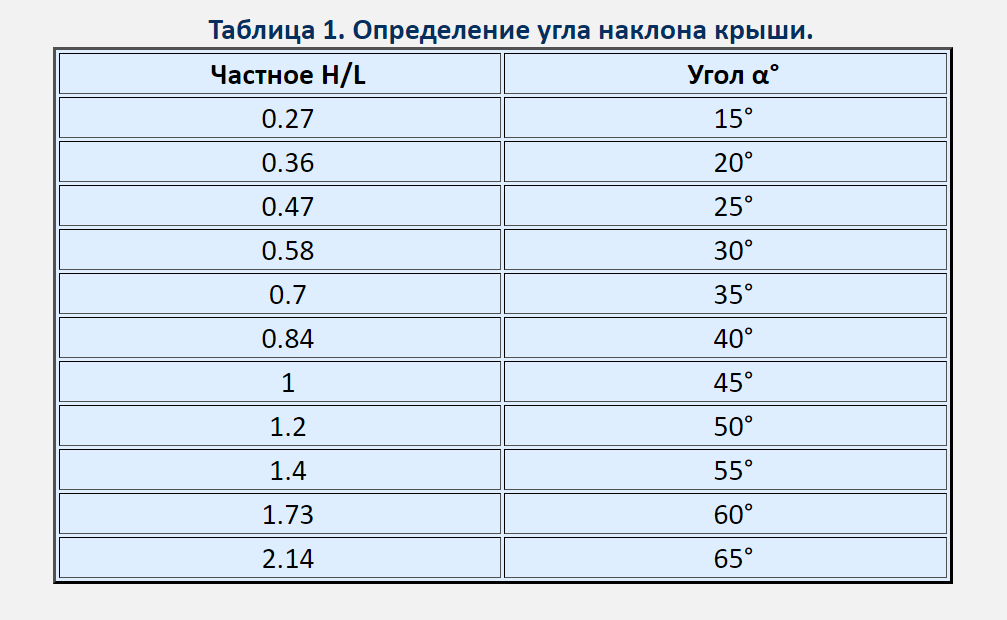
расчет наклона крыши.
Попробуем разобраться на конкретном примере. Ширина будущего здания составляет 8 метров. Делим это значение на два, получаем 4 метра.
Рис.3 Зависимость угла наклона крыши от материала для кровли
Нам нужно определить высоту поднятия стропил в случае, если уклон кровли составляет 25 градусов. Итак, находим в соответствующей таблице показатель, соответствующий данному углу наклона: он составляет 0,47.
Умножаем половину ширины нашего здания на данную относительную величину. Получаем следующий расчет: 4*0,47=1,88. Соответственно, при таком раскладе нам нужно будет поднять стропила на высоту, составляющую 1,88 метра.
Рис. 4 Схема кровельной системы
Выбор кровельного материала в зависимости от угла наклона
Следует подчеркнуть, что все материалы для обустройства кровли объединяются в отдельные группы: по их физическим свойствам, техническим характеристикам, а также ценовым параметрам.
Приведем некоторые рекомендации, которые помогут вам подобрать наиболее подходящий материал для обустройства крыши:
- В том случае, если наклон кровли совсем небольшой, и составляет где-то от 2,5 до 10 градусов, обычно применяются покрытия из каменной крошки (крупнозернистой), а также из гравия. Слой верхнего покрытия составляет для гравия – 10-15 миллиметров, для каменной крошки – 3-5 миллиметров.
- Если уклон кровли составляет от 10 градусов, и при этом была использована базовая битумная водоизоляция, необходимо выполнить верхний слой из крупнозернистого материала. В том случае, если показатель такой же, а материал выбран пленочный рулонный, то необходимо будет использовать специальный окрасочный слой для защиты.
- В том случае, если угол кровли составляет до 20 градусов, а само покрытие выполняется из металлического профнастила, или же асбестоцементных листов, следует непременно провести герметизацию всех стыков. Стоит ли выбирать металлочерепицу.
При углах до 60 градусов нужно обязательно проводить герметизацию стыков листов кровли из меди или стали. При этом стыки непременно должны быть двойными.
При этом стыки непременно должны быть двойными.
Учитывая все перечисленные параметры и делая правильные расчеты, можно сконструировать надежную крышу, которая прослужит ни один год или десяток лет.
Источник https://texnotoys.ru/ventilyaciya/ugol-kryshi.html
Источник https://stroika12.com/krysha/raschet-ugla-naklona-kryishi/
Источник
Источник
Калькулятор градусов треугольника
Если вы хотите, чтобы вычислял углы треугольника , калькулятор градусов треугольника Omni — единственный инструмент, который вам нужен.
Продолжайте читать, чтобы узнать, как вычислить степень треугольника для нескольких возможных сценариев, например,
- Когда известны три стороны;
- Когда известны два угла; и
- Когда известны две стороны и один угол
Вы также найдете пример того, как найти степень треугольника с помощью нашего инструмента.
Что такое треугольник?
Треугольник — это замкнутая кривая, имеющая три стороны (aaa, bbb и ccc на рис. 1). Он состоит из трех вершин и трех углов (∠α\угол \alpha∠α, ∠β\угол \beta∠β и ∠γ \угол \gamma∠γ).
1). Он состоит из трех вершин и трех углов (∠α\угол \alpha∠α, ∠β\угол \beta∠β и ∠γ \угол \gamma∠γ).
В следующем разделе мы попробуем научиться вычислять степень треугольника.
Рис. 1: Треугольник со сторонами a,b,c и углами α, β, γКак вычислить степень треугольника
Чтобы вычислить степень треугольника, мы можем использовать один из следующих методов: 92)}{2аб}\право ]\\\\ \end{align*}αβγ=arccos[2bc(b2+c2−a2)]=arccos[2ac(a2+c2−b2)]=arccos[2ab(a2+b2−c2)]
Если известны два угла
Замечательное свойство трех углов треугольника состоит в том, что сумма трех углов треугольника составляет 180 градусов . Мы можем использовать это свойство, чтобы найти неизвестную степень треугольника, если известны два угла.
α+β+γ=180°⟹α=180°−(β+γ)β=180°−(α+γ)γ=180°−(β+α)\footnotesize \альфа + \бета + \гамма = 180\градус \\ \начать{выравнивать*} \подразумевает \альфа & = 180\градус — (\бета + \гамма)\\ \бета & = 180\градус — ( \альфа + \гамма) \\ \гамма & = 180\градус — (\бета + \альфа) \end{align*}α+β+γ=180°⟹αβγ=180°−(β+γ)=180°−(α+γ)=180°−(β+α)
Если известны две стороны и один угол
Здесь снова мы можем использовать закон косинусов или закон синусов, чтобы найти известный градус. Например, если мы знаем значения сторон aaa, ccc и угла γ\gammaγ, по формуле закона синусов мы можем написать:
Например, если мы знаем значения сторон aaa, ccc и угла γ\gammaγ, по формуле закона синусов мы можем написать:
asin(α)=csin(γ)⟹α=arcsin[a⋅ sin(γ)c]β=180°−(α+γ)\footnotesize \frac{a}{\text{sin} (\alpha)} = \frac{c}{\text{sin} (\gamma)} \\ \начать{выравнивать*} \подразумевает \alpha &= \text{arcsin} \left[ \frac{a \cdot \text{sin} (\gamma)}{c} \right] \\ \бета &= 180\градус — ( \альфа + \гамма) \end{align*}sin(α)a=sin(γ)c⟹αβ=arcsin[ca⋅sin(γ)]=180°−(α+γ)
Если вы хотите узнать больше о треугольниках, рекомендуем воспользоваться нашим калькулятором углов треугольника.
Как пользоваться калькулятором градусов треугольника
Теперь давайте посмотрим, как найти градус треугольника, если каждая из его сторон равна 5 см.
В раскрывающемся меню выберите 3 стороны в качестве параметра заданного .
Введите размеры трех сторон , aaa, bbb и ccc, по 4 см каждая.
Инструмент отобразит градуса треугольника (∠α\угол \alpha∠α, ∠β\угол \beta∠β и ∠γ \угол \gamma∠γ) как 60°60\градус60°.

Вы также можете использовать этот калькулятор градусов треугольника, чтобы найти углы треугольника, если вы знаете либо два угла, либо один угол и две стороны.
FAQ
Как найти градус в прямоугольном треугольнике, если известен один из острых углов?
Чтобы найти градус в прямоугольном треугольнике, если известен один из острых углов, следуйте приведенным инструкциям:
В прямоугольном треугольнике один угол равен 90 градусов. Следовательно, сумма двух других углов будет 90 градусов .
Вычесть значение известного угла из 90 градусов .
Поздравляем! Вы нашли градус неизвестного угла.
В какой степени сумма углов в треугольнике?
Согласно свойству суммы углов треугольника, три внутренних угла треугольника в сумме дают 180 градусов .
Чему равен третий угол треугольника, если два его угла равны 80° и 45°?
Третий угол равен 55° . Чтобы получить этот ответ, выполните следующие действия:
Чтобы получить этот ответ, выполните следующие действия:
Найдите сумму двух известных углов , т. е. 80° + 45° = 125°.
Вычесть результат из 180° , т. е. 180° — 125° = 55°.
Вы получите 55°, градус третьего угла.
Как найти угол в прямоугольном треугольнике
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
Справка по основам геометрии » Плоская геометрия » Треугольники » Прямоугольные треугольники » Как найти угол в прямоугольном треугольнике
Найти угол угла C.
Возможные ответы:
C = 72
C = 65
Ни один из этих
C = 53
C = 70
Правильный ответ:
C = 700005
.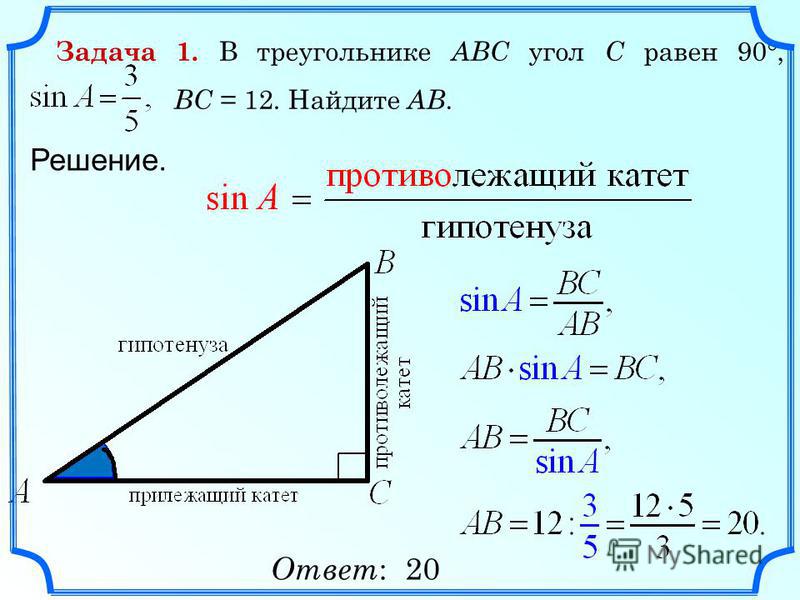 =65
=65
Пояснение:
Во-первых, знайте, что сумма всех углов треугольника равна 180 градусам.
У каждого треугольника 3 угла. Таким образом, у нас есть сумма трех углов, как показано на рисунке:
, где у нас есть углы A, B и C. В нашем прямоугольном треугольнике один угол равен 25 градусам, и мы назовем этот угол A. Другой известный угол 90 градусов, и мы назовем этот угол B. Таким образом, у нас есть
Упростите и решите для C.
Сообщить об ошибке
Какое из следующихможет быть двумя мерами угла прямоугольного треугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
В прямоугольном треугольнике не может быть тупого угла; это исключает выбор между 100 и 10.
Острые углы прямоугольного треугольника должны составлять 90 градусов. По этому критерию можно исключить три варианта:
По этому критерию можно исключить три варианта:
Оставшийся вариант правильный:
Сообщить об ошибке
Угол прямоугольного треугольника в 15 раз больше, чем у другого. Чему равен меньший угол?
Возможные ответы:
Правильный ответ:
Объяснение:
Сумма углов треугольника равна 180. В прямоугольном треугольнике один угол равен 90. Таким образом, сумма двух других углов будет равна 90.
Пусть = первый угол и = второй угол
Таким образом, уравнение для решения становится или
Таким образом, первый угол равен, а второй угол равен .
Таким образом, меньший угол равен
Сообщить об ошибке
Угол в треугольнике, показанном ниже (не в масштабе), равен 35 градусам. Что такое угол?
Возможные ответы:
градусы
градусы
градусы
градусы
Правильный ответ:
градусы
Пояснение:
Сумма внутренних углов треугольника всегда равна 180 градусам. Нам дан угол и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол равен 90 градусам. Таким образом, мы знаем 2 из 3 и можем определить третий угол.
Нам дан угол и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол равен 90 градусам. Таким образом, мы знаем 2 из 3 и можем определить третий угол.
Угол равен 55 градусам.
Сообщить об ошибке
Что из следующего нельзя верно для прямоугольного треугольника?
Возможные ответы:
Катет может быть длиннее гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Прямоугольный треугольник может быть равносторонним.
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Меры углов прямоугольного треугольника могут суммироваться.
Правильный ответ:
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Объяснение:
Все этих утверждений ложны.
Прямоугольный треугольник может быть равносторонним.
Неверно: Равносторонний треугольник должен иметь три угла, каждый из которых измеряется.
Один катет может быть длиннее гипотенузы.
Ложь: Каждый катет на 90 154 короче 90 155 гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Ложь: Оба угла прямоугольного треугольника не являются прямыми должно быть острым.
Меры углов прямоугольного треугольника могут суммироваться.
Ложь: Меры любой суммы треугольников .
Сообщить об ошибке
Чему равен угол треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для нахождения всех углов треугольника:
Чтобы найти меру угла, мы подставляем значения и . Поскольку угол прямой, мы знаем, что мера будет равна .
Поскольку угол прямой, мы знаем, что мера будет равна .
Сообщить об ошибке
Найдите градусную меру недостающего угла.
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна 180º.
Чтобы найти значение остаточного угла, вычтите известные углы из 180º:
Следовательно, третий угол равен 43º.
Сообщить об ошибке
Прямоугольный треугольник имеет два равных угла, какова их мера?
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма внутренних углов треугольника всегда равна 180 градусам, и было дано, что треугольник прямоугольный, а это означает, что один из углов равен 9. 0 градусов.
0 градусов.
Это оставляет 90 градусов, чтобы равномерно разделить два оставшихся угла, как было показано в вопросе.
Следовательно, каждый из двух равных углов имеет размер 45 градусов.
Сообщить об ошибке
Какого угла не хватает в этом прямоугольном треугольнике?
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна .
Это означает, что .
Используя тот факт, что 90 — это половина 180, мы можем вычислить, что недостающий угол x плюс 34 добавляется к оставшимся 90, и мы можем просто вычесть
.
Сообщить об ошибке
Решить:
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма углов треугольника составляет 180 градусов. Мы уже знаем, что один из углов равен 9.0 градусов, поэтому мы можем вычесть 90 из 180: два других угла должны добавиться к 90 градусам.
Мы уже знаем, что один из углов равен 9.0 градусов, поэтому мы можем вычесть 90 из 180: два других угла должны добавиться к 90 градусам.
Теперь мы можем вычесть, чтобы получить x:
Сообщить об ошибке
← Назад 1 2 3 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты2 164 практических теста Вопрос дня Карточки Learn by Conceptградусов — символ, преобразование, примеры
Градус — это единица измерения угла. Обычно используются две единицы измерения углов: радианы и градусы. В случае практической геометрии мы всегда измеряем угол в градусах. Градус обозначается знаком ° (символ градуса). Мера полного угла в градусах составляет 360 градусов (также пишется как 360°), что является мерой одного полного оборота.
В этой статье мы обсудим единицу измерения угла, известную как градус, ее символ и определение. Мы также рассмотрим взаимосвязь между радианами и градусами и их преобразование. Мы решим несколько примеров, дающих меру угла в градусах, чтобы лучше понять концепцию.
Мы также рассмотрим взаимосвязь между радианами и градусами и их преобразование. Мы решим несколько примеров, дающих меру угла в градусах, чтобы лучше понять концепцию.
| 1. | Что такое градусы? |
| 2. | Угол в градусах |
| 3. | Связь между градусами и радианами |
| 4. | Измерение угла в градусах |
| 5. | Часто задаваемые вопросы о степенях |
Что такое градусы?
Градус — единица измерения углов. Это не единица СИ, поскольку единицей измерения углов в СИ являются радианы. Как правило, в геометрии мы измеряем углы в градусах с помощью транспортира. Транспортир обычно используется в школах для измерения углов при решении различных математических задач. Давайте посмотрим, как символ градусов используется для обозначения меры угла.
Символ градусов
Мы используем маленький кружок (°) после числа в правом верхнем углу как символ градусов. Давайте посмотрим на несколько примеров, чтобы понять, как используется символ градусов:
Давайте посмотрим на несколько примеров, чтобы понять, как используется символ градусов:
- 30 градусов = 30°
- 45 градусов = 45°
- π/3 радиан = 60 градусов = 60°
- π/2 радиан = 90 градусов = 90°
Угол в градусах
Единица измерения угла в математике называется градусом. Градус угла измеряется с помощью инструмента, называемого транспортиром. Полный круг вращается на 360°, а углы можно измерять под разными углами, демонстрируя разные градусы, такие как 30°, 45°, 60° и так далее. Один оборот делится на 360 равных частей, и каждая часть называется градусом. Обозначим степень кружком °. Например, 180° означает 180 градусов. Угол, градусная мера которого дана в градусах, называется углом в градусах.
Мы можем классифицировать углы в соответствии с количеством градусов следующим образом:
- Прямой угол — Измерение прямого угла составляет 90 градусов (90°).
- Тупой угол – Измерение тупого угла больше 90° и меньше 180°
- Острый угол — измерение тупого угла меньше 90° и больше 0°
- Прямой угол — Прямой угол равен 180°
- Угол рефлекса — измерение угла рефлекса больше 180° и меньше 360°.

- Полный угол — Прямой угол равен 360°
Связь между градусами и радианами
Углы измеряются не только в градусах, но и в радианах. Радиан получается путем обертывания радиуса по кругу. Один полный оборот против часовой стрелки в радианах равен 2π. Мы можем преобразовать градусы в радианы и радианы в градусы, используя следующие две формулы:
- Чтобы преобразовать радианы в градусы, используйте формулу [Градусы = Угол в радианах × 180° / π]. Один радиан примерно равен 57,29.58 градусов.
- Для преобразования градусов в радианы используется формула [Радианы = Угол в градусах × π / 180°].
Ниже приведена таблица, показывающая эквивалентные значения радиана для соответствующих углов в градусах:
| Угол в градусах | Угол в радианах |
|---|---|
| 30° | №/6 |
| 45° | №/4 |
| 60° | №/3 |
| 90° | №/2 |
| 180° | № |
| 360° | 2π |
Как мы обсуждали в предыдущем разделе, один полный оборот равен 360 градусам или 2π радианам.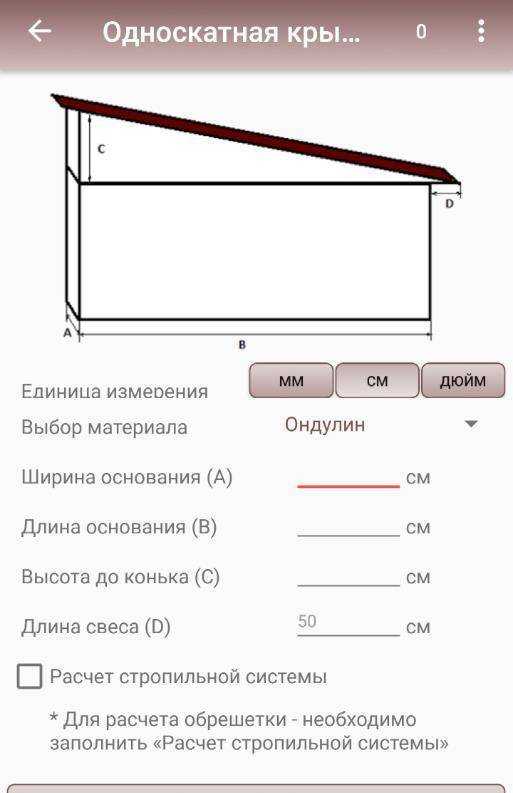 У нас есть еще одна единица измерения углов, которая называется «поворот». Один оборот равен одному полному обороту. Итак, у нас есть 1 оборот = 360° = 2π радиан.
У нас есть еще одна единица измерения углов, которая называется «поворот». Один оборот равен одному полному обороту. Итак, у нас есть 1 оборот = 360° = 2π радиан.
Измерение угла в градусах
Лучшим инструментом для измерения углов в градусах является транспортир. Изогнутый край транспортира разделен на 180 равных частей.
На транспортире два набора чисел:
- Один по часовой стрелке
- Другой против часовой стрелки
Если присмотреться, транспортир имеет градусы, отмеченные от 0° до 180° слева направо на внешней стороне и от 180° до 0° на внутренней стороне.
Внутреннее считывание и внешнее считывание дополняют друг друга. то есть они складываются, образуя угол 180°.
Посмотрите на изображение выше, если измеренный угол находится слева от центра транспортира, мы будем ориентироваться на внешние показания транспортира. В этом случае ∠POR лежит на левой стороне, следовательно, ∠POR = 80°. Если измеренный угол находится справа от центра транспортира, мы будем ориентироваться на внутренние показания транспортира. В этом случае ∠QOR лежит справа, поэтому , ∠QOR = 100°. Здесь у нас есть еще один пример измерения угла в градусах. Попробуем измерить угол ∠AOB на приведенном ниже рисунке с помощью транспортира.
Если измеренный угол находится справа от центра транспортира, мы будем ориентироваться на внутренние показания транспортира. В этом случае ∠QOR лежит справа, поэтому , ∠QOR = 100°. Здесь у нас есть еще один пример измерения угла в градусах. Попробуем измерить угол ∠AOB на приведенном ниже рисунке с помощью транспортира.
- Шаг 1: Держите транспортир так, чтобы его середина совпадала с вершиной О данной фигуры. Точно совместите транспортир с лучом OB, как показано ниже.
- Шаг 2: Начните чтение с отметки 0° в правом нижнем углу транспортира. Измерьте угол, используя внутренние показания на нижней дуге транспортира.
Следовательно, ∠AOB = 37°.
Важные замечания по градусам
- Градус — это единица измерения углов.
- Мы можем преобразовать угол в градусах в угол в радианах и наоборот, используя следующие формулы:
- Угол в градусах = Угол в радианах × 180° / π
- Угол в радианах = Угол в градусах × π / 180°
- Один полный оборот равен 360 градусам.

☛Статьи по теме
- Калькулятор радиан в градусы Калькулятор
- градусов в радианы
- Формула для поворота на 180 градусов
- Преобразование градусов в радианы
- Радиан в Градус Формула
Часто задаваемые вопросы о степенях
Что такое степени по геометрии?
градуса — это единица измерения угла. При измерении любого угла мы используем символ градусов для его обозначения. Обозначается °. Например, один полный оборот составляет 360 градусов или (360°). Один градус равен π/180 радиан.
Что такое 1 градус в радианах?
Один градус в радианах измеряется следующим образом: 1 градус = π/180° радиан = 0,0174533 радиан
Как определить градус?
Градус, обычно обозначаемый знаком ° (градус), является мерой угла. Углы могут иметь разную меру или градус, например 30°, 90°, 55° и так далее. Для измерения степени угла воспользуемся транспортиром.
Какие инструменты используются для измерения угла в градусах?
Существует 5 типов инструментов для измерения углов:
- Транспортиры
- Угловой датчик
- Линейка для измерения нескольких углов
- Пробная площадь
- Синусоида
Как преобразовать угол в градусах в радианы?
Мы можем преобразовать угол в градусах в радианы, используя формулу: Угол в радианах = Угол в градусах × π / 180°.
Как найти опорный угол в градусах?
Мы можем найти опорный угол в градусах, используя следующую формулу:
- Если заданный угол x меньше 180 градусов, то его исходный угол равен 180° — x.
- Если заданный угол x больше 180 градусов, то его опорный угол равен x — 180°.
Сколько градусов в половине оборота?
Половина оборота означает выполнение прямого угла. Измерение прямого угла в градусах равно 180°. Следовательно, в пол-оборота получается 180 градусов.
Сколько градусов составляет полный оборот?
Полный поворот означает выполнение полного угла. Измерение полного угла составляет 360°. Следовательно, в одном полном обороте 360 градусов.
Какие различные степени углов мы видим в геометрии?
Существуют различные типы углов в зависимости от их степени в геометрии. Давайте посмотрим, что они из себя представляют:
- Прямой угол. Измерение прямого угла составляет 90 градусов (90°).
- Тупой угол — Измерение тупого угла больше 90° и менее 180°
- Острый угол — измерение тупого угла меньше 90° и больше 0°
- Прямой угол — Прямой угол равен 180°
- Угол рефлекса — измерение угла рефлекса больше 180° и меньше 360°.
- Полный угол — Прямой угол равен 360°
Как рассчитать углы и параллелизм
Основные термины
o Угол
o степень
o Прямой угол
o Прямой угол
O Perpendicular
O Острый угол
o Обложенный угол
o Рефлексный угол
o Добавленный угол
Oertic
o Параллельно
o Поперечная линия
o Соответствующий угол
Цели
o Определять углы, образованные пересекающимися линиями, и знать, как использовать измерения в градусах для количественной оценки углов
o правильные предположения)
o Знать, как определяется параллелизм
o Распознавать и использовать отношения между углами, образованными, когда поперечная линия пересекает две параллельные линии
Мы начинаем углубляться в геометрию с рассмотрения параллелизма и перпендикулярности в двухмерном (плоском) пространстве. Как оказалось, то, как мы определяем эти понятия, определяет характеристики различных фигур, которые мы рассмотрим позже. Однако сначала мы рассмотрим понятие угла и то, как мы можем изображать углы на геометрических рисунках.
Как оказалось, то, как мы определяем эти понятия, определяет характеристики различных фигур, которые мы рассмотрим позже. Однако сначала мы рассмотрим понятие угла и то, как мы можем изображать углы на геометрических рисунках.
Углы
Угол (или набор углов) образуется при пересечении двух прямых (или некоторых их частей). Например, мы можем говорить о том, как холм поднимается от ровной поверхности под крутым (или большим) углом, или нам может понадобиться выбрать подходящий угол при строительстве крыши дома. Некоторыми обычными настольными инструментами для измерения или построения углов являются транспортиры и циркуль. На схеме ниже показаны два пересекающихся луча l и m , которые образуют угол α , который обозначен небольшой дугой.
Очевидно, угол α может быть больше или меньше в зависимости от ориентации l относительно м . На приведенных ниже диаграммах показано увеличение угла α , если смотреть слева направо.
На приведенных ниже диаграммах показано увеличение угла α , если смотреть слева направо.
Обратите внимание, что углы начинаются с нуля слева и увеличиваются до точки, в которой лучи вернулись в исходное совпадающее положение. Общепринятая система количественной оценки углов равна 9.0003 градуса ; самая левая диаграмма выше будет углом 0 градусов (или 0 °), а самая правая диаграмма выше будет углом 360 градусов (или 360 °). Ниже приведены некоторые примеры углов с соответствующими градусными мерами.
Хотите узнать больше? Почему бы не пройти онлайн-курс по геометрии?
Обратите внимание, что углы 0° и 360° на самом деле одинаковы: если лучи совпадают, то они совпадают! Поскольку мы можем «раскручивать» один из лучей столько раз, сколько захотим, получается, что углы 0°, 360°, 720° и так далее являются эквивалентными углами. (Другими словами, независимо от того, сколько раз вы полностью вращаетесь, вы всегда окажетесь в той же ситуации, в которой начали!) Угол 180° иногда называют углом 9°. 0003 прямой угол (например, линию можно рассматривать как образующую прямой угол). Угол 90° — это то, что мы называем прямым углом , и иногда его изображают с помощью специального символа угла на диаграмме: комбинация любого из них пересекается, образуя прямой угол, мы говорим, что они перпендикулярны . Мы также можем заметить, что когда две линии (или их части) пересекаются, они на самом деле образуют более одного угла.
0003 прямой угол (например, линию можно рассматривать как образующую прямой угол). Угол 90° — это то, что мы называем прямым углом , и иногда его изображают с помощью специального символа угла на диаграмме: комбинация любого из них пересекается, образуя прямой угол, мы говорим, что они перпендикулярны . Мы также можем заметить, что когда две линии (или их части) пересекаются, они на самом деле образуют более одного угла.
Чтобы различать эти углы, мы называем угол меньше 90° острым углом , а угол между 90° и 180° тупым углом . Углы больше 180° называются рефлекторными углами . Угол α на приведенной выше диаграмме меньше 90°, поэтому это острый угол; угол β больше 180° и, следовательно, является углом отражения. Заметим, что луч l образует острый угол α с лучом м . Если бы луч l «вращался» до тех пор, пока не оказался на вершине m , угол α был бы равен 360°. В результате можно заметить, что сумма углов α и β должна быть 360° ( l «проехала» через угол α , и ей предстоит пройти угол β . он достигает 360° — или, что то же самое, 0° — там, где он начался). Другими словами, для приведенной выше диаграммы
В результате можно заметить, что сумма углов α и β должна быть 360° ( l «проехала» через угол α , и ей предстоит пройти угол β . он достигает 360° — или, что то же самое, 0° — там, где он начался). Другими словами, для приведенной выше диаграммы
Если две линии (или их части) пересекаются не в конечной точке, а в каком-либо другом месте, могут образоваться три или четыре угла. Обратите внимание, однако, что по тем же рассуждениям, которые мы использовали выше, сумма всех углов вокруг точки пересечения по-прежнему равна 360 °.
Обратите внимание, что на крайнем левом рисунке конечная точка луча лежит на прямой. Поскольку линию можно представить как два пересекающихся луча, направленных в противоположные стороны, угол γ составляет 180°. Таким образом, сумма α и β в этом случае также составляет 180 °:
 Потому что свойства
Потому что свойства , потому что это. называются дополнительными углами . Те же рассуждения можно применить к самой правой диаграмме выше. Однако в этом случае две линии пересекаются, и поэтому мы имеем ряд отношений, которые мы можем сразу идентифицировать.
Применим эти соотношения к алгебре. Рассмотрим, например, первое и последнее выражение выше. Мы можем приравнять эти два выражения и манипулировать ими следующим образом:0155 и δ равны. Кроме того, мы можем использовать тот же тип рассуждений, чтобы заключить, что углы α и γ равны. Углы β и δ , а также углы α и γ называются вертикальными углами . Вертикальные углы – это пары противоположных углов, образованные пересечением двух прямых.
Практическая задача : Даны пересекающиеся прямые n и м на приведенной ниже схеме найдите угол α .
Решение: Мы знаем, что сумма дополнительных углов равна 180°. Таким образом, мы можем найти угол α следующим образом.
Таким образом, α равно 103°.
Практическая задача: Два отрезка q и z пересекаются, как показано ниже. Найдите угол t . Примечание: больший угол между q и z равен 121 градусу.
Решение: Как мы продемонстрировали ранее, вертикальные (противоположные) углы, образованные пересекающимися линиями (или их частями). Таким образом, угол t равен просто 121°.
Практическая задача : Определите углы на приведенной ниже диаграмме как острые, тупые или загнутые и найдите неизвестный угол b .
Решение : Угол 110 ° — это тупой угол (потому что он составляет от 90 до 180 °). Угол b является рефлекторным углом и равен разнице между 360° и тупым углом, равным 110°.
Угол b является рефлекторным углом и равен разнице между 360° и тупым углом, равным 110°.
B = 360 ° -110 ° = 250 °
Параллелизм
У большинства людей есть хорошее ощущение того, что означает, когда кто -то говорит, что две линии -для экстенса если бы мы спросили, что означает, что две прямые (на плоскости) параллельны, простой ответ мог бы состоять в том, что две прямые параллельны, если они не пересекаются. Однако мы можем применить к этому некоторую математическую строгость. Рассмотрим две строки l и м , которые показаны ниже. Кроме того, давайте разрежем (пересечем) эти две линии поперечной линией , которая представляет собой просто линию, пересекающую эти две параллельные линии. Назовем эту поперечную линию n .
Теперь мы можем заявить более математически точным образом, что мы имеем в виду, когда мы говорим, что две строки параллельны: две строки M и l параллельны, если сумма углов β и γ точно равна 180°. Вследствие этого свойства, когда прямые m и l параллельны, углы β и δ равны, как и углы α и γ . Представьте себе, например, что линия n — это «ровная площадка», а линии м и l — это башни; если мы построим эти башни перпендикулярно n , то они идут «прямо вверх» и никогда не должны пересекаться.
Вследствие этого свойства, когда прямые m и l параллельны, углы β и δ равны, как и углы α и γ . Представьте себе, например, что линия n — это «ровная площадка», а линии м и l — это башни; если мы построим эти башни перпендикулярно n , то они идут «прямо вверх» и никогда не должны пересекаться.
Мы можем применить то, что мы узнали об вертикальных углах вместе с тем, что мы обнаружили здесь, чтобы показать, что первая диаграмма с параллельными линиями имеет не более двух уникальных углов. Углы α и углы β в этом случае называются соответствующими углами (то есть все углы, равные α , являются соответствующими углами, а все углы, равные β — соответствующие углы). Обратите внимание, однако, что эти характеристики применимы только тогда, когда m и l параллельны, как мы определили этот термин выше.
Наше определение параллелизма имеет важные последствия для нашего изучения геометрии.
Практическая задача: Строки s и t параллельны и пересекаются поперечной линией r . Найдите угол p .
Решение: Во-первых, мы знаем, что по правилу дополнительных углов оба угла, смежные с углом 82°, должны быть равны 98°.
Но этот угол соответствует углу p , и поэтому он один и тот же. Итак, делаем вывод, что p = 98°.
Угол обзора — быстрое, точное и надежное отслеживание взгляда
Приблизительное время чтения: 6 минут
Концепция угла обзора имеет решающее значение для многих аспектов исследования отслеживания взгляда, но это одна из тех вещей, которыми люди почему-то просто интересуются. рассчитывал понять. Этот блог — моя попытка объяснить угол зрения так, как мне хотелось бы, чтобы кто-нибудь объяснил его мне, например, с минимумом математики… И не волнуйтесь, вы можете полностью избежать математики с этим очень полезное онлайн-приложение коллега создал!
рассчитывал понять. Этот блог — моя попытка объяснить угол зрения так, как мне хотелось бы, чтобы кто-нибудь объяснил его мне, например, с минимумом математики… И не волнуйтесь, вы можете полностью избежать математики с этим очень полезное онлайн-приложение коллега создал!
Почему углы обзора важны для отслеживания взгляда
Углы обзора используются везде в отслеживании взгляда. Исследователи могут захотеть убедиться, что их экран соответствует «отслеживаемому диапазону» их системы — где отслеживаемый диапазон составляет, например, 32 градуса по горизонтали и 25 градусов по вертикали. Другие исследователи могут захотеть убедиться, что стимулы на экране простираются ровно на 5 градусов угла зрения или что цели саккады появляются на +/- 10 градусов угла зрения от центра экрана. В то время как данные о взгляде от айтрекеров обычно сообщаются в координатах пикселя экрана, важные показатели, такие как амплитуда и скорость саккады, сообщаются в градусах угла зрения / градусах в секунду. Кроме того, данные взгляда часто разбиваются на саккады и фиксации на основе скорости движения глаза, которая измеряется айтрекерами в градусах в секунду. Наконец, многие критические показатели качества данных отслеживания взгляда (и спецификаций устройства отслеживания взгляда), такие как «точность» и «точность», сообщаются в градусах угла зрения. например EyeLink 1000 Plus имеет точность до < 0,5 градусов угла обзора.
Кроме того, данные взгляда часто разбиваются на саккады и фиксации на основе скорости движения глаза, которая измеряется айтрекерами в градусах в секунду. Наконец, многие критические показатели качества данных отслеживания взгляда (и спецификаций устройства отслеживания взгляда), такие как «точность» и «точность», сообщаются в градусах угла зрения. например EyeLink 1000 Plus имеет точность до < 0,5 градусов угла обзора.
Ясно, что базовое понимание концепции угла зрения (и возможность преобразования между пикселями экрана и градусами угла зрения) может быть очень полезным в исследованиях по отслеживанию взгляда! Основная идея проиллюстрирована ниже (в вертикальном измерении). Угол зрения (θ), на который опирается цветок, указан фиолетовой двунаправленной стрелкой.
Вычисление угла обзора
Вычисление амплитуды этого угла включает в себя некоторые очень простые математические операции, в частности тригонометрию прямостороннего треугольника. Вас, вероятно, учили этому в школе — я помню, что думал, что это никогда не пригодится в реальной жизни… Как вы можете видеть на изображениях ниже (которые переключаются на горизонтальную ось), вычисление угла зрения включает в себя выполнение сумм для одного или два прямоугольных треугольника, в зависимости от того, что именно вы хотите знать.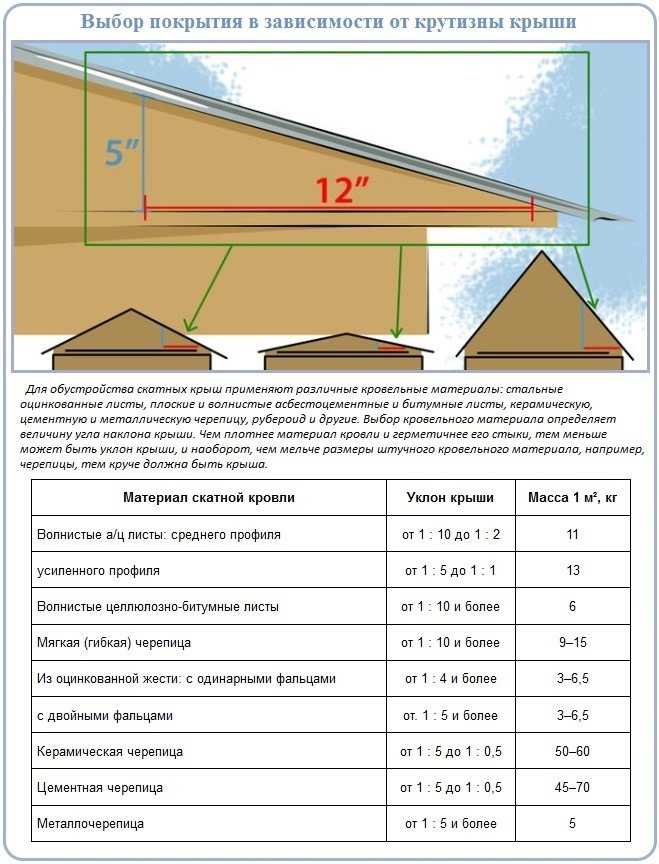
Для расчета угла обзора цели, измеренного от центра экрана (например, при отображении целей под углом +/- 10 градусов), задействован только один прямоугольный треугольник. Чтобы определить угол обзора, стягиваемый объектом, который находится в центре экрана (или угол обзора, стягиваемый самим экраном), есть два прямоугольных треугольника, расположенных рядом. Есть также два прямоугольных треугольника, если вы хотите определить угол, образуемый объектом, смещенным от центра экрана. В этом случае треугольники перекрываются, а угол обзора смещенного объекта равен углу зеленого треугольника, вычтенному из угла синего треугольника.
В каждом случае математика одна и та же — нам нужно найти угол (угол) между «противоположной» и «прилежащей» сторонами треугольника (треугольников) (длинная сторона — это гипотенуза). На изображениях выше противоположную сторону можно рассматривать как «размер», а соседнюю сторону можно рассматривать как «расстояние». Соотношение противоположных и смежных краев светло-коричневое (помните SOHCAHTOA?). Таким образом, чтобы найти угол, мы просто используем обратную функцию тангенса (также известную как атан) — θ = атан (противоположный / смежный) или θ = атан (размер / расстояние).
Таким образом, чтобы найти угол, мы просто используем обратную функцию тангенса (также известную как атан) — θ = атан (противоположный / смежный) или θ = атан (размер / расстояние).
Итак, вооружившись этими знаниями, мы можем легко вычислить угол зрения, просто измерив расстояние (Смежное) и размер (Напротив) любого просматриваемого объекта. Простую формулу для одного прямоугольного треугольника — θ = atan (размер/расстояние) можно легко скорректировать, чтобы учесть тот факт, что два прямоугольных треугольника задействованы для центрированных объектов — θ = 2*atan (размер/2*расстояние). На изображении ниже экран имеет ширину 400 мм и расстояние до него 700 мм. Таким образом, получается 2*атан(400/(2*700)) = 31,9 градуса угла обзора.
Преобразование пикселей в градусы угла зрения
Теперь, когда мы можем вычислить угол зрения для объектов, которые можно измерить в миллиметрах, переход между миллиметрами и пикселями экрана является относительно простым шагом. Если мы знаем разрешение нашего экрана в пикселях (например, 1920×1080), а также его размеры (высота и ширина в мм), очень легко определить, сколько пикселей приходится на мм. Например, в горизонтальном направлении экран с разрешением 1920 пикселей и шириной 520 мм имеет 1920/520 = 3,89 пикселей на мм. Другой способ взглянуть на вещи — сказать, что каждый пиксель на экране имеет разрешение 520/19.20 = 0,27 мм в ширину.
Например, в горизонтальном направлении экран с разрешением 1920 пикселей и шириной 520 мм имеет 1920/520 = 3,89 пикселей на мм. Другой способ взглянуть на вещи — сказать, что каждый пиксель на экране имеет разрешение 520/19.20 = 0,27 мм в ширину.
Эти коэффициенты преобразования позволяют нам легко переключаться между пикселями и миллиметрами, поэтому мы также можем вычислять градусы угла зрения на основе пикселей экрана. Например, цель, представленная в 300 пикселях справа от центра описанного выше экрана, находится на расстоянии θ = atan((300*0,27)/700) = 6,6 градуса от центра.
Онлайн-калькулятор угла обзора!
Хотя математика для вычисления градусов угла зрения не слишком сложна (если вы освоите ее), гораздо проще позволить компьютеру сделать все за вас – вот почему мой коллега Джоно из служба поддержки создала этот удобный онлайн-калькулятор угла зрения — просто введите разрешение экрана, размеры и расстояние, и он произведет преобразование между пикселями и градусами угла зрения для вас! Проверьте это — вы можете найти его и несколько других удобных приложений в разделе «Полезные приложения» на нашей странице поддержки .
Если вы хотите, чтобы мы рассказали о вашем исследовании EyeLink, у вас есть идеи для публикаций или у вас есть какие-либо вопросы о нашем аппаратном и программном обеспечении, свяжитесь с нами. Мы всегда рады помочь. Вы можете позвонить нам (+1-613-271-8686) или нажать кнопку ниже, чтобы написать по электронной почте:
Свяжитесь с нами
Подробнее
О Сэме Хаттоне
Сэм Хаттон изучал экспериментальную психологию в Университете Сассекса, и ему так понравилось, что он остался там, чтобы защитить докторскую диссертацию. Его первое знакомство с айтрекером произошло во время постдокторской стажировки в Имперском колледже в Лондоне. Он работал в отделении нейроофтальмологии в больнице Чаринг-Кросс в течение 6 лет, где научился использовать древнюю инфракрасную систему слежения за глазами для измерения основных глазодвигательных функций (просаккады / антисаккады / плавное слежение и т. д.) у пациентов с нервно-психическими и неврологическими расстройствами.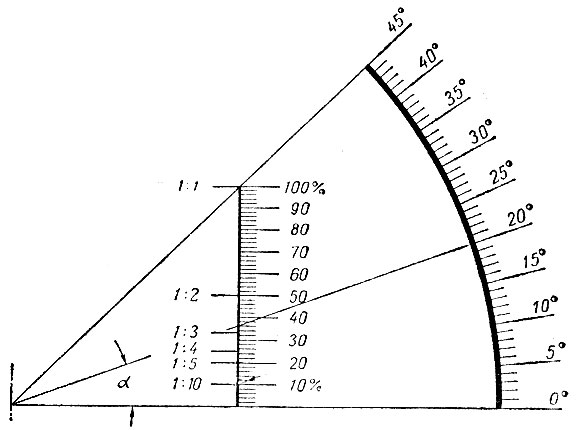 . Он попался на крючок и с тех пор так или иначе активно участвует в исследованиях по отслеживанию взгляда. Когда он не ведет блоги (например, большую часть времени…), он работает с остальной частью группы поддержки исследований SR над рядом проектов, проявляя особый интерес к вопросам, связанным с отслеживанием взгляда в клинических условиях (например, нистагм с отслеживанием взгляда / неврологические расстройства). ) и пупиллометрия. Его также можно встретить на семинарах по отслеживанию взгляда по целому ряду тем, и, как правило, он пытается убедиться, что люди не совершают тех же ошибок, что и он. Он любит следить за животными, и до сих пор ему удавалось записывать взгляды мышей, кошек, собак и утки…
. Он попался на крючок и с тех пор так или иначе активно участвует в исследованиях по отслеживанию взгляда. Когда он не ведет блоги (например, большую часть времени…), он работает с остальной частью группы поддержки исследований SR над рядом проектов, проявляя особый интерес к вопросам, связанным с отслеживанием взгляда в клинических условиях (например, нистагм с отслеживанием взгляда / неврологические расстройства). ) и пупиллометрия. Его также можно встретить на семинарах по отслеживанию взгляда по целому ряду тем, и, как правило, он пытается убедиться, что люди не совершают тех же ошибок, что и он. Он любит следить за животными, и до сих пор ему удавалось записывать взгляды мышей, кошек, собак и утки…
радиан против градусов — physicsthisweek.com
На обычном уроке физики мы несколько раз переходим от градусов к радианам и обратно. Когда следует использовать радианы и градусы? Я помогу вам решить.
Радианы и градусы
Вы должны использовать радианы, когда смотрите на объекты, движущиеся по круговым траекториям или частям кругового траектории. В частности, уравнения вращательного движения почти всегда выражаются в радианах. Начальные параметры задачи могут быть в градусах, но перед их использованием необходимо преобразовать эти углы в радианы.
В частности, уравнения вращательного движения почти всегда выражаются в радианах. Начальные параметры задачи могут быть в градусах, но перед их использованием необходимо преобразовать эти углы в радианы.
Вы должны использовать градусы, когда измеряете углы с помощью транспортира или описываете физическое изображение. У большинства людей развито интуитивное ощущение общих ракурсов. Это было бы обычным делом в задачах, связанных с векторами, включая скорости, снаряды, силы и подобные ситуации.
Предупреждение для калькуляторов
В вашем калькуляторе есть три параметра, связанные с углом.
- Режим DEG, который использует градусы в триггерных функциях,
- режим RAD, который использует радианы в триггерных функциях, и Режим
- ГРАД, который разбивает круг на 400 частей.
Убедитесь, что ваш калькулятор находится в правильном режиме в зависимости от темы, которую вы изучаете. Если вы не геодезист, скорее всего, вы никогда не будете использовать режим GRAD, кроме как по ошибке.
Хотите узнать больше? Читайте дальше для получения информации о градусах и радианах.
Градусы
В древности круг делился на 360 градусов. Существует несколько вероятных причин.
- В году 365 дней.
- Число 360 можно разбить на множество множителей: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 45, 60, 90, 120, 180, 360. Это упрощает разделить круг на равные части. (Это похоже на причину, по которой мы делим фут на 12 дюймов.)
- Число 360 является естественной частью системы счисления с основанием 60.
Одним из результатов является то, что размер степени относительно мал. Мы можем использовать транспортир и относительно легко измерить или нарисовать углы треугольника. Вероятно, вы можете нарисовать треугольник с углами 30°, 60° и 9°.0° довольно легко. Вы также можете довольно точно оценить угол наклона в 45°.
В первые недели занятий по физике мы часто используем углы, измеряемые в градусах. Градусы отображаются вместе с векторами и используются в направлениях, силах, ускорениях, наклонах и других измерениях.
Какой другой выбор в радианах или градусах?
Радиан
Радиан связан с диаметром (и, следовательно, радиусом) окружности. В древности люди поняли, что диаметр D , а длина окружности C всех окружностей имела общее отношение, т.е.
\(\color{black}{ \frac{C}{d}=3,14159…}\)
Поскольку это соотношение было фиксированным, ему был присвоен специальный символ π . Оно известно как иррациональное число, потому что его нельзя записать в виде дроби с двумя целыми числами. (Отношение 22/7 получается настолько близким, насколько это возможно).0154 D ) как…
\(\color{black}{C=\pi D \textrm{ или } C=2\pi r}\)
Радиан на самом деле безразмерный, потому что это отношение двух длин. Однако, когда мы работаем с кругами или частями кругов, мы хотим убедиться, что знаем, что говорим об этом соотношении. Следовательно, мы всегда добавляем слово радианы, чтобы показать это отношение.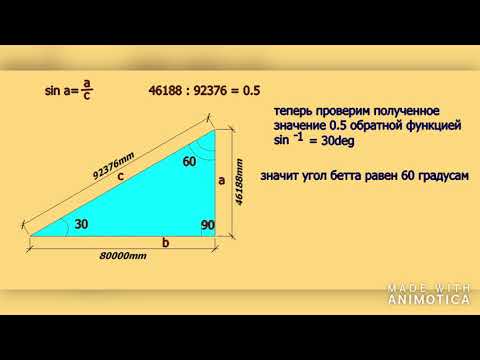
Лучше сказать, что в круге «2 π радиан», а не просто «2 π » в круге.
Проблема с радианами
Проблема с радианами заключается в том, что угол в один радиан довольно большой. На самом деле вы можете оценить его примерно в 60 градусов, хотя его истинное значение составляет около 57,32 градуса. Это все равно, что пытаться измерить длину пальцев в ярдах. Вы могли бы это сделать, но каждый из ваших пальцев будет измеряться небольшой долей ярда.
В некоторых случаях это удобно. Вы, наверное, помните, что использовали такие дроби, как π /2 = 90°, π /3 = 60°, π/9.0155 4 = 45°, а π /6 = 30° назад в классе тригонометрии.
Когда мы говорим о вращательном движении, радианы становятся предпочтительной единицей измерения углов. В конечном итоге это вытекает из описания длины дуги, с, , данного
. \(\color{black}{s = r \theta.}\)
Длина дуги частичной окружности связана с углом и радиусом.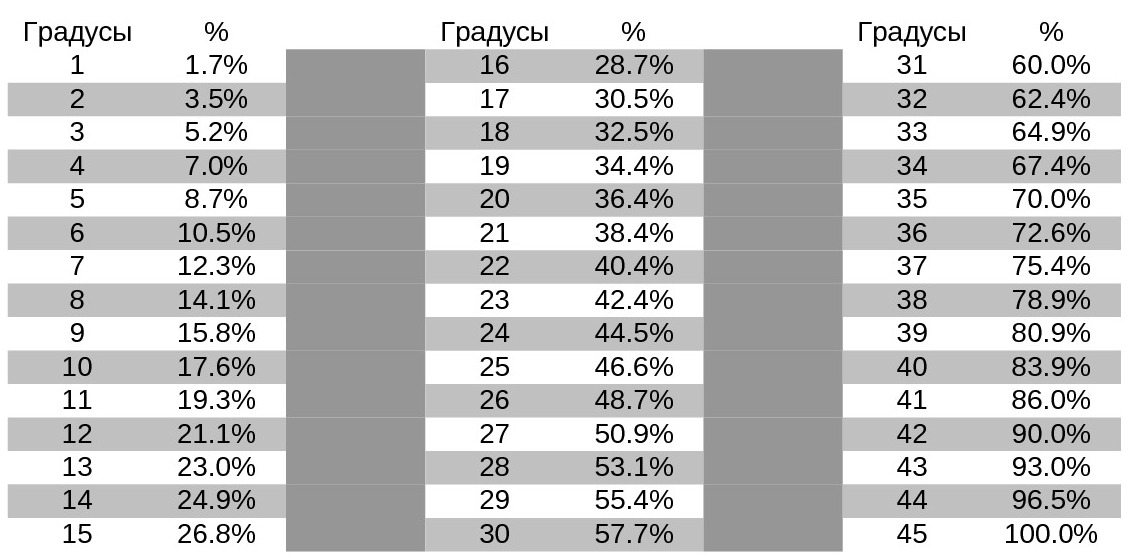
Используя это соотношение, мы можем умножить радиус на угол в радианах, чтобы определить длину дуги. Никаких преобразований не требуется.
В частности, при равномерном круговом движении угловая частота ω, связана с периодом T соотношением
\(\color{black}{\omega = \frac{2 \pi}{T},}\)
, что говорит нам о том, что если мы знаем время (период = T ), которое требуется для одного движения по окружности (угол = 2 π ), мы можем определить угловую скорость. (Для равномерного кругового движения скорость постоянна, поэтому угловая скорость и угловая частота одинаковы.)
Для частей круга расстояние, пройденное по кругу, можно найти с помощью
\(\color{black}{\omega = \frac{\theta}{t}=\frac{s}{rt}}\)
так что
\(\color{black}{s=\omega r t.}\)
Если бы мы не использовали радианы, нам пришлось бы конвертировать из градусов, чтобы это работало.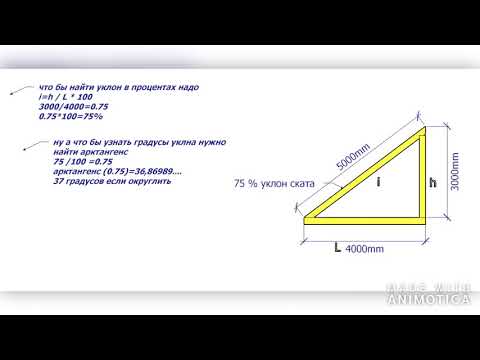

 и ставите точки.
и ставите точки.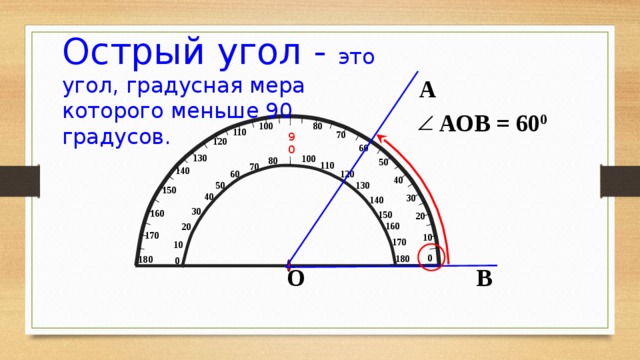 Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком;
Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком; Если взять два здания с одинаковыми габаритными размерами, но имеющие разный угол наклона в градусах (например, 11 и 45), то нагрузка от одинаковых по силе потоков ветра на второй дом будет почти в 5 раз выше.
Если взять два здания с одинаковыми габаритными размерами, но имеющие разный угол наклона в градусах (например, 11 и 45), то нагрузка от одинаковых по силе потоков ветра на второй дом будет почти в 5 раз выше. Чтоб крыша не дала течь необходимо использовать усиленную гидроизоляцию.
Чтоб крыша не дала течь необходимо использовать усиленную гидроизоляцию.

 Но чем больше вы сделаете уклон крыши, тем меньше вероятность попадания воды под стыки кровельных материалов.
Но чем больше вы сделаете уклон крыши, тем меньше вероятность попадания воды под стыки кровельных материалов.

